1 Introduction

This paper presents a topology optimization approach for strongly coupled fluid-structure interaction (FSI) problems. Such problems pose interesting challenges on the optimization method with respect to (a) describing the geometry of the structure, (b) modeling the flow, the structural response and their interactions, (c) discretizing the FSI model, and (d) solving efficiently and robustly the resulting numerical problems.

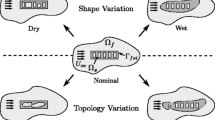
Figure 1 illustrates the two fundamental approaches for varying the structural geometry in the optimization process. We distinguish between methods that only optimize the topology and shape of the internal structure and methods that only manipulate the geometry of the fluid-structure interface. Adopting the nomenclature used in aeroelasticity for internal, “dry” surfaces and external, “wet” surfaces, we refer to these methods as “dry” and “wet” topology optimization methods in the remainder of this paper. Combining wet and dry methods leads to the most general from of topology optimization for FSI problems. This paper presents a method for optimizing the “dry” topology.

Fig. 1
figure 1

Geometry variations in FSI problems

Full size image

The structural geometry is typically defined via the distribution of two or more material phases in a given design domain. Density methods describe the material distribution locally and introduce fictitious porous materials to continuously transition between two or more materials. Alternatively, level set methods (LSMs) explicitly describe the geometry of material interfaces via the iso-contours of a level set function. The level set function is advanced either by the solution of the Hamilton-Jacobi equation or by a black-box optimization algorithm. The latter approach defines the parameters of the discretized level set function by explicit functions of the optimization variables. The interface geometry is represented in the mechanical model either by an Ersatz material approach or by immersed boundary techniques. Sigmund and Maute (2013) review recent developments of density and level set methods. In the case of “dry” topology optimization, the fluid-structure interface is explicitly defined and interface conditions can be formulated and discretized with standard methods. As outlined in the following, specialized formulations and numerical techniques are needed to treat interface conditions for “wet” topology optimization.

To accurately predict the response of a particular FSI problem, the fluid and structural models and the coupling model need to be carefully chosen. The proper choice of the fluid model depends on the Reynolds and Mach numbers of the flow. A broad range of flow regimes can be modeled by the compressible Navier-Stokes (CNS) equations, augmented by turbulence models at higher Reynolds numbers. If viscous effects can be ignored, the CNS equations can be approximated by an inviscid Euler flow model. If the Mach number is sufficiently low, compressibility phenomena can be ignored and either the incompressible Navier-Stokes (INS) equations or the hydrodynamic Boltzmann transport equations (HBTE) are typically used. For subsonic flows in aeronautical applications, potential flow models are often employed to predict the aerodynamic forces. Optimizing the “wet” topology with either a density or an Ersatz material approach, the stick conditions at the fluid-structure interface are enforced via a Brinkman penalization. Alternatively, immersed boundary techniques can be used to enforce the boundary conditions at the fluid-structure interface.

The flow models above are combined with a structural model assuming either infinitesimal or finite deformations. In density methods, the material properties are interpolated as functions of the density, typically using the Solid Isotropic Material with Penalization (SIMP) approach. Similarly, the Ersatz material interpolates the material properties as functions of either the level set field or the local volume ratio of the individual phases. For “wet” topology optimization with either density or Ersatz material methods, the fluid loads are transformed into volumetric forces and smeared along the fluid-structure interface. Immersed boundary techniques have not yet been applied to “wet” topology optimization.

In general, FSI problems are two-way coupled, i.e. the flow depends on the structural displacements and velocities and the structural response depends on the fluid forces. To capture dynamic coupling phenomena, such as flutter or limit cycle oscillations, the transient response of FSI problem needs to be resolved. In the case of small structural deformations, the FSI problem can be simplified by imposing velocity boundary conditions on the fluid that account for the deformations of the structure. These so-called transpiration boundary conditions are however insufficient to capture the influence of large geometrical changes of the flow domain due to structural deformations.

The fluid and structure models can be discretized by the same or different schemes depending on user preference for each discipline. The CNS equations are typically discretized in space by finite difference or finite volume schemes, while stabilized finite element methods (FEMs) are commonly applied to INS models. In the context of design optimization, both forms of the Navier-Stokes equations are typically integrated in time by implicit schemes. For transient problems, the CNS and INS equations are often formulated with respect to an Arbitrary Lagrangean Eulerian (ALE) reference frame. The ALE formulation allows movement of the fluid mesh as the structure deforms. Potential flow and the HBTE are discretized by specialized schemes, such as panel methods or the lattice Boltzmann method. Structural models are typically discretized by the FEM and integrated by implicit time stepping schemes.

The overall FSI problem is solved by either a staggered or a monolithic scheme. Staggered schemes satisfy the interface conditions iteratively by solving individually the fluid and structure sub-problems with appropriate Dirichlet and Neumann boundary conditions. While staggered schemes allow for modularity of fluid and structure solvers, they complicate the formulation and solution of the global sensitivity equations (Maute et al. 2003). In contrast, monolithic schemes solve the discretized fluid and structure models simultaneously, requiring an implicit treatment of the interface conditions. While this approach is often challenged by the need for solving large, ill-conditioned nonlinear systems of equations, it does not require any special consideration for deriving and solving the global sensitivity equations.

Prior work on topology optimization combines the different methods outlined above for describing the structural geometry and modeling and solving the FSI problem. The majority of FSI optimization studies employ density methods to optimize the dry topology. Guo et al. (2005) and Guo (2007) model the flow by strip and lifting theory approximations that employ the above described transpiration boundary conditions. Stanford and Ifju (2009) and Stanford (2008) predict the fluid loads by a vortex lattice method which is dependent on the panel deflection calculated by finite element analysis. Stanford and Beran (2013) consider the transient aero-thermo-elastic response of a panel, predicting the aerodynamic loads via a linear piston theory. Kennedy et al. (2014) optimized flexible aircraft wings with flutter constraints using a panel method to predict the compressible fluid response. They employ an FEM structural discretization for modeling composite structures, considering both small and large deformations. The change of the geometry of the flow domain due to structural deformations is considered in the following studies. Ghazlane et al. (2011) optimize wing-box configurations, analyzing the flow field via a finite volume discretization of the CNS equations where the overall flow domain is updated based on the converged structural response. Allen and Maute (2002), Allen and Maute (2004), and Martins et al. (2005) predict the aeroelastic response by staggered scheme, coupling a finite volume discretization of an Euler flow model and a FE discretization of a linear elastic structural model. Maute and Reich (2006) use the same scheme to optimize morphing airfoils but account for large deformations in the structural model.

Only recently optimization of the “wet” and “dry” topology is considered by Yoon (2009) and Yoon (2014). These works account for the overall flow domain dependence on structural displacements, and use a monolithic scheme to couple an INS flow model augmented by a Brinkman penalization method and a linear elastic structural model.

Density methods require a sufficiently refined mesh to resolve the structural geometry and to mitigate the appearance of jagged or blurred interfaces. The need for refined meshes and the in general large computational cost of solving FSI problems render density methods impractical for a broad class of real-world applications where the flow field needs to be resolved by numerically expensive INS and CNS models.

To obtain a crisp representation of the structural geometry with moderately refined meshes, the LSM is applied to FSI problems in the following studies, in all of which the structural response is modeled via an Ersatz material approach. Brampton et al. (2012) and Dunning et al. (2014) apply the LSM with Hamilton-Jacobi update method to the optimization of wing-box structures considering design dependent aeroelastic loading, predicted by a structural finite element model and a doublet-lattice fluid solver. Gomes and Suleman (2008) adopt an explicit LSM, employ a spectral discretization of the level set function, and optimize the aileron reversal speed of a wing torsion box. The fluid loads are computed by design dependent strip theory.

To resolve well the geometry defined by the LSM with the Ersatz material approach, a rather fine mesh is needed. Further, the Ersatz material approach may lead to similar issues as the density approach in regards to the accuracy of the FE predictions, the numerical stability of the optimization problem, and the convergence to a clearly defined geometry (Angot et al. 1999; Kreissl and Maute 2011). To mitigate these issues, in this work we combine the LSM with an immersed boundary technique to describe the structural geometry. We follow the approach of Makhija and Maute (2014b) and Villanueva and Maute (2014): We optimize the topology of structures with an explicit LSM, and predict the structural response with a generalized formulation of the extended finite element method (XFEM). We study this approach for “dry” topology optimization problems, focusing on hydro-elastic problems at steady-state. The FSI problem is modeled by coupling a stabilized finite element model of the INS equations and a linear elastic structural XFEM model. The fluid mesh is modeled as a fictitious elastic continuum and deformed in response to the structural displacements. The steady-state solution of the FSI problem is computed by a monolithic scheme and the design sensitivities are evaluated by the adjoint method. We study this LSM-XFEM topology optimization method for designing the internal structure of 2D and 3D FSI problems. We compare the LSM-XFEM results against designs found by the SIMP approach. While the numerical examples are rather academic, they illustrate the key features of the proposed method and are easily repeatable.

The remainder of this paper is organized as follows: in Section 2 we present the FSI model, followed by a description of the XFEM framework used for the solid phase. Section 3 summarizes the density and level set methods studied here. Section 4 presents three examples that provide insight into the characteristics of our LSM-XFEM approach. In Section 5 we summarize the main findings of this work.

2 Fluid-structure interaction model

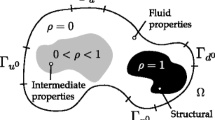
Figure 2 shows a structure immersed in fluid. The structure is composed of two material phases “A” and “B”, one of which could represent “void”. Phase “A” occupies the domain \({\Omega }^{s}_{A}\) and phase “B” the domain \({\Omega }^{s}_{B}\). The boundary between phase “A” and “B” is \({\Gamma }^{s}_{A,B}\). The structural displacements u i are defined in the structural domain Ωs with the external boundary Γs, where \({\Omega }^{s}={{\Omega }^{s}_{A}}{\cup {\Omega }^{s}_{B}}\). The fluid velocity v i and pressure p are defined in the fluid domain Ωf with the external boundary Γf. The fluid mesh is deformed within the domain Ωm to accommodate structural displacements. The fluid mesh displacements are denoted by d i and Γm is the boundary of Ωm. In this work, we update the fluid mesh in the entire fluid domain, i.e. Ωf=Ωm and Γf=Γm. The fluid-structure interface is Γfsi. Essential boundary conditions d o ,v o , and u o are defined on the fluid mesh, fluid, and solid boundaries, respectively.

Fig. 2
figure 2

Schematic representation of a FSI problem

Full size image

The fluid is modeled by the INS equations, discretized by the Streamline Upwind Petrov Galerkin (SUPG) and Pressure Stabilized Petrov Galerkin (PSPG) stabilized FE formulation of Tezduyar et al. (1992). The motion of the fluid mesh is described via linear elastic deformations of a fictitious continuum (Stein et al. 2004). The structure is modeled by linear elasticity and discretized by a generalized formulation of the XFEM, which is discussed in Section 2.2. The fluid and structure meshes match on the FSI interface, and we enforce two-way coupling of the fluid and structure weakly using a boundary integral formulation that is outlined below. Note while the internal forces in the solid are modeled via linear elasticity, i.e. infinitesimal small strains, our model accounts for finite deformations in predicting the fluid forces. This simplification of the solid model is valid as long as geometric nonlinearities can be ignored for modeling the internal forces.

2.1 Variational formulation of governing equations

The weak formulation for the stationary FSI problem is written as follows:

$$\begin{array}{@{}rcl@{}} R^{f} &=& R^{f}_{\Omega}+R^{f,IC}_{{\Gamma}^{fsi}}+R^{f}_{{\Gamma}_{f}}=0 , \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} R^{m} &=& R^{m}_{\Omega}+R^{m,IC}_{{\Gamma}^{fsi}}+R^{m}_{{\Gamma}_{m}}=0 , \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} R^{s} &=& R^{s}_{\Omega}+R^{s}_{{\Gamma}^{A,B}}+R^{s,IC}_{{\Gamma}^{fsi}}+R^{s}_{{\Gamma}_{s}}=0. \end{array} $$
(3)

The fluid residual, R f, is comprised of a volume contribution, \(R^{f}_{\Omega }\), contributions from the interface coupling at the FSI boundary, \(R^{f,IC}_{{\Gamma }^{fsi}}\), and contributions from boundary integrals along the external boundaries, \(R^{f}_{{\Gamma }_{f}}\). Similarly, the fluid mesh motion residual, R m, is comprised of integrals over the volume, \(R^{m}_{\Omega }\), and the fluid-structure interface, \(R^{m,IC}_{{\Gamma }^{fsi}}\). The contributions, \(R^{m}_{{\Gamma }_{m}}\), from integrals along the external boundary vanishes as the solution is prescribed at Γ m . The structural residual, R s, is the sum of contributions of integrals over the volume, \(R^{s}_{\Omega }\), the phase boundaries, \(R^{s}_{{\Gamma }^{A,B}}\), the fluid-structure interface, \(R^{s,IC}_{{\Gamma }^{fsi}}\), and the external boundary, \(R^{s}_{{\Gamma }_{s}}\).

Adopting an index notation, the volume contributions are:

$$\begin{array}{@{}rcl@{}} R^{f}_{\Omega} &=& {\int}_{{\Omega}^{f}}\left(\rho^{f}\psi_{i}\frac{\partial v_{i}}{\partial x_{j}}v_{j}+\frac{\partial\psi_{i}}{\partial x_{j}}\sigma^{f}_{ij}+\eta\frac{\partial v_{i}}{\partial x_{i}}\right)d{\Omega}\\ &&+ {\sum}_{e}^{N^{f}_{elems}}{\int}_{{\Omega}^{e,f}}\left(\rho^{f}\frac{\partial v_{i}}{\partial x_{k}}v_{k}-\frac{\partial \sigma^{f}_{ik}}{\partial x_{k}}\right)\\ && \qquad \left(\tau_{SUPG} \ v_{j} \frac{\partial\psi_{i}}{\partial x_{j}}+\frac{1}{\rho^{f}} \ \tau_{PSPG}\frac{\partial\eta}{\partial x_{i}}\right)d{\Omega}, \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} R^{s}_{\Omega} &=& {\int}_{{\Omega}^{s,A}}\frac{{\partial\chi^{A}_{i}}}{\partial x_{j}}\sigma^{s,A}_{ij}d{\Omega}+{\int}_{{\Omega}^{s,B}}\frac{{\partial\chi^{B}_{i}}}{\partial x_{j}}\sigma^{s,B}_{ij}d{\Omega}, \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} R^{m}_{\Omega} &=& {\int}_{{\Omega}^{f}}\frac{\partial\xi_{i}}{\partial x_{j}}\sigma^{m}_{ij}d{\Omega} , \end{array} $$
(6)

where \(N^{f}_{elems}\) is the total number of fluid elements, and Ωe,f is the domain of the e th fluid element. The test functions for the fluid momentum equations are denoted as ψ i , and η is the test function for the incompressibility condition. The stabilization parameters of the SUPG and PSPG formulations are denoted by τ S U P G and τ P S P G , respectively, and are defined in Tezduyar et al. (1992). The fluid mesh displacement test function is ξ i . The test functions of the static equilibrium equations in phase “A” and “B” are denoted by \({\chi ^{A}_{i}}\) and \({\chi ^{B}_{i}}\), respectively.

The elastic stress tensors in phase “A” and “B” are \(\sigma ^{s,A}_{ij}\) and \(\sigma ^{s,B}_{ij}\), respectively. The elastic stress tensor in the fictitious continuum describing the fluid mesh motion is \(\sigma ^{m}_{ij}\). We assume a linear elastic constitutive relation for all elastic stress tensors. The associated material parameters are denoted by ν s for the Poisson’s ratio in the solid and \({E^{s}_{A}}\) and \({E^{s}_{B}}\) for the elastic moduli in phases “A” and “B”. The Poisson’s ratio of the fictitious continuum is ν m , and the elastic modulus is E m. Note, the value E m>0 is arbitrary. Assuming a Newtonian fluid, the fluid stress tensor \(\sigma ^{f}_{ij}\) is:

$$\begin{array}{@{}rcl@{}} \sigma_{ij}^{f} = -p\delta_{ij}+\mu^{f}\left(\frac{\partial v_{i}}{\partial x_{j}}+\frac{\partial v_{j}}{\partial x_{i}}\right), \end{array} $$
(7)

where the fluid dynamic viscosity is μ f and δ i j is the Kronecker delta.

The contributions from integrals over the external boundaries of the fluid and structure subdomains are:

$$\begin{array}{@{}rcl@{}} R^{f}_{{\Gamma}_{f}} &=& {\int}_{{\Gamma}^{f}}\psi_{i}\sigma^{f}_{ij}{n^{f}_{j}}d{\Gamma}, \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} R^{s}_{{\Gamma}_{s}} &=& {\int}_{{\Gamma}^{s}}\chi^{A}\sigma^{s,A}{n^{s}_{j}}d{\Gamma}+{\int}_{{\Gamma}^{s}}\chi^{B}\sigma^{s,B}{n^{s}_{j}}d{\Gamma}, \end{array} $$
(9)

where \(R^{f}_{{\Gamma }_{f}}\) vanishes if the fluid velocity or a traction free condition is prescribed. \(R^{s}_{{\Gamma }_{s}}\) vanishes on the structural boundary if there is no external traction present. The outward facing normal vectors for the fluid and solid are n f and n s, respectively. Note that on Γfsi the two normal vectors are equal and opposite.

On the fluid-structure interface, we weakly enforce the balance of the surface traction due to the fluid and elastic stress tensors and the continuity of displacements and velocities. At steady state, the latter is equivalent to enforcing stick conditions on the flow. To enforce the force balance we follow the approach of Hubner et al. (2004) and add the structural residual contributions of degrees of freedom of nodes along the fluid-structure interface to the fluid residual contributions of the same nodes. As the interface contributions of the structural and fluid equations cancel out, only the volumetric portion of the structural residual needs to be added to the fluid residual and subtracted from the structural residual. The displacement and velocity continuity constraints are enforced via Lagrange multipliers. Formally, we write the above procedure as follows:

$$\begin{array}{@{}rcl@{}} R^{f,IC}_{{\Gamma}^{fsi}} & = & R^{s}_{\Omega\cap{\Gamma}^{fsi}}, \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} R^{s,IC}_{{\Gamma}^{fsi}} & = & -R^{s}_{\Omega\cap{\Gamma}^{fsi}}+{\int}_{{\Gamma}^{fsi}}\chi_{i}v_{i}d{\Gamma}, \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} R^{m,IC}_{{\Gamma}^{fsi}} & = & -R^{m}_{\Omega\cap{\Gamma}^{fsi}}+{\int}_{{\Gamma}^{fsi}}\xi_{i}\left(u_{i}-d_{i}\right)d{\Gamma}. \end{array} $$
(12)

The displacement degrees of freedom in the structural and the fluid mesh motion equations serve as Lagrange multipliers to enforce the stick condition of the flow and to prescribe the structural displacements for the mesh deformations, respectively.

The residual \(R^{s}_{{\Gamma }^{A,B}}\) that accounts for contributions from phase boundary conditions is defined in the subsection below.

2.2 Extended finite element discretization

We use a generalized formulation of the XFEM to predict the structural response of the solid that is comprised of two phases. The material layout is described by the level set function. Note the XFEM is only used within the solid domain.

The level set function, ϕ, defines the geometry of the material layout within the structural domain as follows:

$$ \begin{array}{ll} \phi(x_{i}) < 0, & \forall \ x_{i} \in {{\Omega}^{s}_{A}}, \\ \phi(x_{i}) > 0, & \forall \ x_{i} \in {{\Omega}^{s}_{B}}, \\ \phi(x_{i}) = 0, & \forall \ x_{i} \in {\Gamma}_{A,B}. \end{array} $$
(13)

In this work we discretize the level set function with bi-linear shape functions in 2D and tri-linear shape functions in 3D. The same mesh is used for discretizing the level set function and the structural governing equations. Figure 3 shows four configurations of the zero level set iso-contour intersecting an element in 2D. Note that due to the linear interpolation of the level set function the double-intersection shown on the far right is not possible.

Fig. 3
figure 3

Intersection configurations

Full size image

To allow for discontinuous displacement and strain fields across phase boundaries, we approximate the displacement field within an intersected element as follows:

$$ u_{i}=\sum\limits_{m=1}^{M}\left(H(-\phi)\sum\limits_{z=1}^{N^{e}_{nodes}}N_{z} \hat{u}^{A,z}_{i,m}+H(\phi)\sum\limits_{z=1}^{N^{e}_{nodes}}N_{z} \hat{u}^{B,z}_{i,m}\right), $$
(14)

with H being the Heaviside function:

$$ H(a) = \left\{ \begin{array}{ll} 1 & \text{if \(a > 0\)}\\ 0 & \text{if \(a \leq 0\)} \end{array} \right. , $$
(15)

where N z are the local shape functions, \(N^{e}_{nodes}\) is the number of nodes of the e th element, and \(\hat {u}^{q,z}_{i,m}\) is the displacement degree of freedom at node z for phase q = [A,B] in the i th direction. The enrichment level is m, with M being the maximum number of enrichment levels. The Heaviside function turns on/off two sets of shape functions associated with the phases “A” and “B”. For each phase, multiple enrichment levels, i.e. sets of shape functions, are necessary if the degrees of freedom interpolate the solution in multiple, physically disconnected regions of the same phase; see Makhija and Maute (2014b), Terada et al. (2003), and Tran et al. (2011). This generalization prevents spurious coupling and load transfer between disconnected regions of the same phase. A detailed explanation of this phenomenon is provided by Makhija and Maute (2014b). To accurately integrate the weak form of the static equilibrium (3) by standard Gauss quadrature, the intersected elements are decomposed into triangles in 2D and tetrahedrons in 3D.

Using the Heaviside enrichment approach described above does not guarantee that the displacement field is continuous across phase boundaries. Therefore, we enforce the continuity of the displacement fields across phase boundaries by a stabilized Lagrange multiplier formulation (Gerstenberger and Wall 2008; Kreissl and Maute 2012). The associated phase boundary residual \(R^{s}_{{\Gamma }^{A,B}}\) is:

$$\begin{array}{@{}rcl@{}} R^{s}_{{\Gamma}_{A,B}} & =& {\int}_{{\Gamma}^{s}_{A,B}}[\chi_{i}] \ \lambda_{i} \ d{\Gamma} + {\int}_{{\Gamma}^{s}_{A,B}}\zeta_{i} \ [u_{i}] \ d{\Gamma} \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} & +& \gamma{\int}_{{\Gamma}^{s}_{A,B}}\zeta_{i} \ \left(\lambda_{i}-\bar{\sigma}^{s}_{ij}n^{A,B}_{j}\right) \ d{\Gamma}, \end{array} $$
(17)

where [⋅] denotes the jump across the phase boundary, i.e. [z]=z A−z B, λ i is a Lagrange multiplier, and ζ i is the test function for the displacement continuity constraint and a consistency condition. The latter enforces weakly the equivalence of the Lagrange multiplier and the surface traction along the phase boundary, which defined via the mean stress \(\bar {\sigma }^{s}_{ij}\):

$$ \bar{\sigma}^{s}_{ij}=\frac{1}{2}\left(\sigma^{s,A}_{ij}+\sigma^{s,B}_{ij}\right). $$
(18)

The vector \(n_{i}^{A,B}\) denotes the normal pointing from phase “A” to phase “B”. The parameter γ scales the consistency conditions versus the displacement continuity constraint. In this work, the Lagrange multiplier is approximated element-wise constant and condensed out during the assembly of the elemental contributions. If either phase “A” or “B” represents “void” the displacement continuity condition is ignored and the residual, \(R^{s}_{{\Gamma }^{A,B}}\), in (17) vanishes.

While the spatial interpolation (14) of the state variables allows for a discontinuity across the phase boundary, this does not imply that the structural response is discontinuous with respect to a shape variation, i.e. a variation of the level set field. The reader is referred to Lang et al. (2014) who studied the XFEM approach described above for shape variations.

3 Geometry model

In this work we focus on “dry” topology optimization and do not alter the shape of the fluid-structure interface. Figure 4 depicts the geometry configuration we consider in the following. The design domain, \({{\Omega }^{s}_{D}}\), is comprised of the phase “A” and “B”, and the material arrangement is determined in the optimization process. The design domain and fluid domain are separated by a skin layer, \({{\Omega }^{s}_{C}}\), that is constrained to phase “A” and is not altered in the optimization process. Thus, phase “A” cannot represent “void”.

Fig. 4
figure 4

Geometry model

Full size image

In Section 4, we compare optimization results of the proposed LSM-XFEM approach against designs found by a density method. The geometry models of both approaches are summarized in the following subsections.

3.1 Density approach

Following the seminal work of Bendsøe and Sigmund (1999) and Zhou and Rozvany (1991), we apply a SIMP approach to optimize the internal structure. We define an independent optimization variable, \(s_{i} \in \mathcal {S}\), at each node in the design domain, with \(\mathcal {S} = \{ s_{i} \in \Re | 0 \leq s_{i} \leq 1 \}\). In the structural finite element model, the material properties are assumed to be element-wise constant. The elemental density, ρ s,e, of the e th element is computed using the following filter:

$$ \rho^{s,e} = \left({\sum\limits^{N_{nodes}}_{j=1} w_{ij}}\right)^{-1} \ \sum\limits^{N_{nodes}}_{j=1} w_{ij} s_{j} , $$
(19)

with

$$ w_{ij}={max}\left(0, (r-|\mathbf{x}^{e}_{i} - \mathbf{x}_{j}|)\right), $$
(20)

where \(\mathbf {x}^{e}_{i}\) is position vector of the center of the i th element, x j the coordinates of the j th node, N n o d e s is the total number of structural nodes, and r the filter radius. The elastic modulus, E s,e of the e th element is interpolated as follows:

$$ E^{s,e}={E^{s}_{B}}+\left({E^{s}_{A}}-{E^{s}_{B}}\right) \ \left(\rho^{s,e}\right)^{\beta}, $$
(21)

where β is the SIMP penalization parameter. If phase “B” represents “void” its elastic modulus \({E^{s}_{B}}\) is set to a small, non-zero value to prevent numerical instabilities in the finite element analysis. Note that the interplay of the linear interpolation of the density and the nonlinear interpolation of the elastic modulus penalizes intermediate density values only if the objective promotes structural stiffness subject to a mass constraint.

The optimization variables associated with nodes in the skin layer, \({{\Omega }^{s}_{C}}\), are set to one.

3.2 Level set approach

In this work, we adopt the explicit level set method presented by Kreissl and Maute (2011) and define the nodal level set values as explicit functions of the optimization variables. Similar to the density filter (19), the nodal values, ϕ i , of the discretized level set function are computed with a filter:

$$ \phi_{i} = \left({\sum\limits^{N_{nodes}}_{j=1} w_{ij}}\right)^{-1} \ \sum\limits^{N_{nodes}}_{j=1} w_{ij} s_{j} , $$
(22)

with

$$ w_{ij}={max}\left(0, (r-|\mathbf{x}_{i} - \mathbf{x}_{j}|)\right), $$
(23)

where x i is the location of node i. The level set filter (23) widens the zone of influence of the optimization variables on the level set field and thus enhances the convergence of the optimization process. In contrast to the density filter (19), however, it does neither guarantee the convergence of the optimized geometry with mesh refinement nor provide local size control; see, for example, the discussions in van Dijk et al. (2013), Sigmund and Maute (2013), and Villanueva and Maute (2014). To control globally, i.e. in an integral sense, the geometry of the optimized design, we penalize the perimeter of the phase boundary in the formulation of the LSM-XFEM optimization problems studied in Section 4. Makhija and Maute (2014b) show that penalizing or constraining the perimeter leads to smooth shapes and impedes the emergence of small features and free-floating material. Note the SIMP approach with density filter (19) does not require a perimeter penalization, as the filter already suppresses the emergence of small features (Petersson and Sigmund 1998).

The optimization variables associated with nodes in the skin layer, \({{\Omega }^{s}_{C}}\), are set to a negative value to ensure that the skin layer is occupied by phase “A” only.

4 Numerical examples

We study the proposed LSM-XFEM method and compare it against a SIMP approach with three examples. In the first two examples we maximize the stiffness of the structure in two and three dimensions. In the third example, we manipulate the internal structural layout to obtain a desired flow characteristic as the structure deforms. While these examples are rather academic and maximizing the structural stiffness often leads to structural designs that do not undergo strong FSI phenomena, they are well-suited to illustrate the main characteristics of the proposed LSM-XFEM approach and can be easily repeated. Furthermore, the third example utilizes fluid-structure coupling to meet the design objective.

The same formulations of the optimization problems are used for the LSM-XFEM and the SIMP approaches, except for an additional perimeter penalization is considered for the LSM-XFEM formulation. The need for this term is discussed in Section 3.2.

In the 2D examples of this section we discretize the fluid, mesh motion, and structural sub-problems with 4-node, bi-linear finite elements. The 3D example uses 8-node, tri-linear finite elements. In all examples, the steady-state response of the FSI problem is computed by Newton’s method. The design sensitivities of the objective and constraints are determined by the adjoint method. The Jacobian of the state equations and the gradients of objective and constraints with respect to the state variables are computed based on analytically derived expressions. The partial derivatives of the FSI residual, objective, and constraints with respect to the optimization variable are evaluated by a central difference scheme. The linear sub-problems in the forward and adjoint sensitivity analysis are solved by a direct parallel solver (Sala et al. 2008; Amestoy et al. 2000), unless stated otherwise.

The parameter optimization problems resulting from the SIMP and the proposed LSM-XFEM approaches are solved by the Globally Convergent Method of Moving Asymptotes of Svanberg (2002). We use an initial adaptation of 0.5 and 0.7 thereafter, a relative step size of 0.01, and a GCMMA penalty of 100.0. Sub-cycling of the GCMMA algorithm is suppressed for the examples shown here.

4.1 Two-dimensional beam in flow channel

We seek to determine the optimal geometry of the internal structure of beam immersed in a flow channel. The objective is to minimize the compliance of the beam subject to a constraint on the maximum structural mass. With this example, we illustrate the key features of the proposed LSM-XFEM approach. We study the optimization problem for different stiffness ratios of the material phases and compare the LSM-XFEM results against the one of a SIMP method.

This problem is similar to one of Yoon (2009) who optimizes a beam-type structure with a design dependent fluid load for minimum compliance. The problem presented here has a fixed fluid-structure boundary, and we optimize the dry topology of the structural member. The geometry of the problem is a scaled version of the COMSOL Multiphysics benchmark problem (COMSOL 2008). However, the material properties used in this study differ from the benchmark problem to magnify the strength of the fluid-structure coupling.

The problem setup is shown in Fig. 5. A flexible beam is immersed in a flow channel with stick conditions on both the top and bottom of the channel. A parabolic velocity profile is prescribed at the inlet, and a traction free condition is prescribed at the outlet. The beam is pinned along the bottom edge in both horizontal and vertical directions. The fluid and solid sub-domains are discretized with unstructured meshes that match geometrically and topologically along the fluid-structure interface. We consider two levels of mesh refinement. The properties of the fluid and the solid along with algorithmic parameters are summarized in Table 1. Using the mean inflow velocity and the beam length as reference values, the Reynolds number of the flow is 1.0.

Fig. 5
figure 5

Flexible beam in flow channel: problem setup for 2D example

Full size image
Table 1 Physical parameters of flexible beam problem
Full size table

Table 2 gives the discretization parameters for the problem where the number of active degrees of freedom (DOFs) depends on the structural element intersection configuration, and varies throughout the optimization process. The reader is referred to Makhija and Maute (2014b) for details on the dependence of the number of constrained and unconstrained DOFs on the intersection configuration.

Table 2 Discretization parameters of flexible beam problem
Full size table

The design objective is to minimize the strain energy (SE) augmented by a perimeter penalty and a constraint on the volume of solid phase “A”:

$$\begin{array}{@{}rcl@{}} \underset{s_{i}}{\text{minimize}} \ \ \ z(s_{i}) & =& k_{D} \ {\int}_{{{\Omega}^{s}_{A}}}\sigma^{s,A}_{ij} \ \epsilon^{A}_{ij} \ d{\Omega} \\ && + k_{D} \ {\int}_{{{\Omega}^{s}_{B}}}\sigma^{s,B}_{ij} \ \epsilon^{B}_{ij} \ d{\Omega} + k_{P} {\int}_{{\Gamma}^{s}_{A,B}}d{\Gamma} \\ \text{subject to} \ \ \ g\left(s_{i}\right) & =&\frac{1}{n^{V} \ {m^{s}_{T}}} \ {\int}_{{\Omega}^{s}_{A}}\rho^{s,e} \ d{\Omega}-1.0 \leq 0, \end{array} $$
(24)

where \(m_{T}^{s}\) is the total structural mass of the structure filled with \({\rho ^{s}_{A}}\), and \(\epsilon ^{q}_{ij}\) is the strain tensor for phase q = [A,B]. The structural density is:

$$ \rho^{s,e}=\left\{ \begin{array}{lll} {\rho^{s}_{A}} & \text{if} x_{i} \in {{\Omega}^{s}_{A}},\\ {\rho^{s}_{B}} & \text{if} x_{i} \in {{\Omega}^{s}_{B}}, \end{array} \right. $$
(25)

where \(\rho ^{s}_{B}\) is to zero. We limit the volume fraction of phase “A” to 60 %, i.e. n V=0.6. The smoothing radius, r, is 1.6 times the maximum solid element edge length, that is r = 0.016 m for the coarse mesh, and r = 0.014 m for the fine mesh. The weighting factors are k D =100 and k P =0.1.

The skin layer, \({{\Omega }^{s}_{C}}\), is formed by prescribing one layer of solid elements along the fluid-structure interface to phase “A”. The skin layer is approximately 0.00495 m for the coarse mesh, and 0.00280 m for the fine mesh.

The initial structural design has six holes filled with solid phase “B”; the hole diameter is 0.074 m. The hole centers are aligned at the beam center 2.05 m in the horizontal direction, and equally spaced in the vertical direction. The initial hole radius is used as the upper and lower bound on \({{\Omega }^{s}_{D}}\) for the box constraints of the optimization problem (24): [ −0.074:0.074].

4.1.1 LSM-XFEM approach

First we study the optimization problem above on the coarse mesh for the following ratios of elastic moduli of phases “A” and “B”: \({E^{s}_{B}} = [0.0;10^{-3};10^{-2};10^{-1}] \ {E^{s}_{A}}\). Note, \({E^{s}_{B}}=0\) represents phase “B” being “void”. For this case, the fluid velocity norm, the fluid pressure field, and the norm of the displacements of the fluid mesh of the initial optimized design are shown in Fig. 6. Note these solutions do not change significantly during the optimization process.

Fig. 6
figure 6

Contour plots of velocity magnitude, fluid pressure and mesh displacement magnitude in deformed configuration of initial design (left) and optimized design (right) for \({E^{s}_{B}}=0\)

Full size image

Figure 7 shows the optimized structural geometries for different \({E^{s}_{A}}/{E^{s}_{B}}\) ratios. The smaller the stiffness of phase “B”, the more phase “A” material is placed along the upstream side of the fluid-structure interface to stiffen the skin layer against large local deformation. As the stiffness of phase “B” increases, more material is placed at the root of the beam to reduce the overall bending deformation. As expected, the strain energy decreases as the stiffness for phase “B” increases.

Fig. 7
figure 7

Optimized designs and level set fields for \({E^{s}_{A}}/{E^{s}_{B}}\) ratios

Full size image

The evolutions of the objective function are depicted in Fig. 8 for different \({E^{s}_{A}}/{E^{s}_{B}}\) ratios. Note the jumps in the objective evolution, in particular for small \({E^{s}_{B}}/{E^{s}_{A}}\) ratios. The evolution convergence is smooth and faster for large \({E_{B}^{s}}\) values. The jumps are due to thin members disconnecting and resulting in large local deformations. For particular configurations of element intersections, a small change in the optimization variables leads to a change in the structural topology, accompanied by a significant change of the structural response.

Fig. 8
figure 8

Objective evolution for different \({E^{s}_{A}}/{E^{s}_{B}}\) ratios

Full size image

This issue is illustrated in Fig. 9 for the case \({E^{s}_{B}}=0.0\). Consider a design with a thin member as in Fig. 9a; the level set function in the vicinity of the thinnest section is shown. The design sensitivities of the objective promote reducing the thickness of the member. The target intersection configuration is shown in Fig. 9b: the sign of the level set value at node (i) switches from negative to positive and the edge e z is intersected twice. However, this intersection configuration is not possible as the bi-linear interpolation of level set field used in this study only allows for no more than one intersection of the zero level set iso-contour along an element edge e z. Instead, the change of the level set function promoted by the design sensitivities results in the intersection pattern shown in Fig. 9c, disconnecting the member and leading to large structural deformations seen in Fig. 9d.

Fig. 9
figure 9

Illustration of configurations leading to disconnection of structural members

Full size image

The issue discussed above is inherent to the proposed LSM-XFEM approach and may arise independent of the physics modeled. Interestingly, the jumps in the evolution of the objective have not been observed in earlier LSM-XFEM studies on structural and flow problems (Makhija and Maute 2014b, a). We speculate that the nonlinearity of the fluid-structure coupling amplifies the sensitivity of the FSI response to changes in the structural topology and leads to discontinuities discussed above. Finding remedies for this issue are beyond the scope of this paper, but are planned for future studies.

4.1.2 Comparison of LSM-XFEM and SIMP approaches

Next, we compare the LSM-XFEM to the SIMP method for two mesh refinement levels and for two different \({E^{s}_{A}}/{E^{s}_{B}}\) ratios. For the SIMP method we consider the same optimization problem formulation as the LSM-XFEM, except we omit the perimeter penalty term. The SIMP penalty factor is β = 3.5. If phase “B” is considered ”void”, the Young’s modulus of phase “B” is set to \({E_{B}^{s}}=10^{-6}\) to avoid a singular finite element problem. The smoothing radius is element dependent and set to \(h^{(e)}/\sqrt {2}\), where h (e) is the solid element edge length of element (e). Note that the smoothing radius for the SIMP approach differs from the one for the LSM-XFEM approach since the density and level set filters serve different purposes as explained previously. The structural design domain, \({{\Omega }^{s}_{D}}\), is initialized to a uniform density of 60 %.

Figure 10 shows the optimized structural designs for the LSM-XFEM and SIMP approaches where the shade indicates the material stiffness. As observed in the previous study by Villanueva and Maute (2014), the SIMP approach leads to designs with more structural members in comparison to the LSM-XFEM approach. However, the increased geometric complexity does not result in a significant increase in structural stiffness. As the results for the fine mesh show, the structural performances between LSM-XFEM and SIMP designs differ insignificantly. Both approaches exhibit mesh dependency, which is to be expected given we use a mesh dependent filtering scheme for both approaches. Efficient density and sensitivity filtering schemes have been developed for the SIMP approach to mitigate the dependence of the optimized results on mesh refinement level; see, for example, Bourdin (2001) and Sigmund (2007), and Sigmund and Maute (2012). However, similar efficient methods for LSMs are currently lacking (van Dijk et al. 2013).

Fig. 10
figure 10

Comparison of LSM-XFEM and SIMP methods for different mesh resolutions and \({E^{s}_{A}}/{E^{s}_{B}}\) ratios

Full size image

The evolution of the objectives for the LSM-XFEM and SIMP approaches along with snapshots of the designs in the course of the optimization process are given in Fig. 11. Note the values of the objectives are different for the LSM-XFEM and SIMP formulations due the scaling factors and inclusion of the perimeter penalty in (24). Comparing the evolution plots shows that the SIMP approach yields a smooth and quick convergence to the optimized solution. In contrast, the LSM-XFEM approach suffers from the jumps for reasons discussed above. Note the objective values just before the jumps in Fig. 11 seem converged and are larger after the jump. Interestingly, the final objective value is the lowest value in the optimization process. However, due to the discontinuity in the optimization process associated with the disconnecting of thin members, we cannot guarantee such a behavior.

Fig. 11
figure 11

SIMP and LSM-XFEM objective evolution for phase “B” being “void”

Full size image

4.2 Flexible plate in flow channel

We study the LSM-XFEM and SIMP approaches for optimizing the internal structural layout of a three-dimensional flexible plate immersed in a flow channel. As in the example of Section 4.1, the objective is to minimize the strain energy of the structure subject to a volume constraint on the material phase “A”. We will show with this problem that the improved geometry resolution on rather coarse meshes is an attractive feature of the proposed LSM-XFEM approach, in particular for 3D FSI problems.

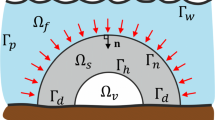
The problem setup is depicted in Fig. 12. A plate of size 3.0×1.5×0.5 m is mounted at the bottom a flow channel. The plate is centered in the z-direction. The distance between the channel inlet and the front face is 4.0 m in the x-direction, and the remaining dimensions of the channel are given in Fig. 12.The structural displacements are prescribed to zero at the bottom face of the plate. A parabolic profile for the velocity in x-direction is prescribed at channel inlet face. Stick conditions are enforced at the channel walls, and a traction free boundary condition is imposed at the channel outlet face. The fluid and structural properties along with algorithmic parameters are summarized in Table 3. The discretization parameters are given in Table 4.

Fig. 12
figure 12

Dimensions and coordinate system for the flexible plate example

Full size image
Table 3 Physical parameters of flexible plate problem
Full size table
Table 4 Discretization parameters of flexible beam problem
Full size table

Using the mean inflow velocity and the width of the plate as reference values, the Reynolds number is 3.0. We consider two levels of mesh refinement and assume that the phase “B” represents “void”, i.e. \({E^{s}_{B}}=0\) and \(\rho ^s_B=0\). The skin layer, \({{\Omega }^{s}_{C}}\), is formed by prescribing one layer of solid elements along the fluid-structure interface to phase “A”. The thickness of skin layer is approximately 0.033 m for the coarse mesh and 0.025 m for the fine mesh. Note the fine mesh leads to more than 106 degrees of freedom. As direct parallel solvers do not scale well as the number of processors increase, we solve the linear sub-problems of this example by the Generalized Minimum Residual Method (GMRES) with the Dual Threshold Incomplete LU Factorization (ILUT) preconditioning scheme (Saad 1994).

The formulations of the optimization problem for the LSM-XFEM and the SIMP approaches are the same as for the 2D problem in Section 4.1. As in Section 4.1, we limit the volume fraction of the structural design domain filled with phase “A” to 60 %, i.e. n V=0.6. For the LSM-XFEM formulation (24), the weighting factors are k D =100 and k P =0.01. The smoothing radius for the coarse mesh is r = 0.088 m and for the fine mesh is r = 0.055 m.

For the LSM-XFEM approach, the solid is initialized with 20 equally spaced spheres of phase “B” material (void): 4 in the y-direction, 5 in the z-direction, 1 in the x-direction. The radius of each initial spheres is 0.12 m. The initial sphere radius is used as the upper and lower bound for the box constraints in \({{\Omega }^{s}_{D}}\): [ −0.12:0.12]. For the SIMP approach, the design domain is initialized with a uniform density of 60 %. The smoothing radius is element size dependent and set to \(h^{(e)}/\sqrt {2}\), where h (e) is the solid element edge length of element (e). The SIMP penalty factor is β = 3.5, and the Young’s modulus of phase “B” is set to \({E_{B}^{s}}=10^{-6}\) to avoid a singular finite element problem.

The initial LSM-XFEM design in the deformed state is shown in Figs. 13 and 14. In Fig. 13, the up-stream half of the plate is not shown to expose the internal topology. Note the displacements are not amplified.

Fig. 13
figure 13

Structural response and flow field of initial LSM-XFEM design in deformed configuration: a contour plot of structural displacement magnitude with streamlines and b channel velocity magnitude contours with streamlines

Full size image
Fig. 14
figure 14

Pressure field of initial LSM-XFEM design in deformed configuration for upstream view a and downstream view b

Full size image

The optimized designs for the LSM-XFEM and the density approach are shown in Fig. 15 where the shade indicates the material stiffness. In the top row, the design from the density approach are given, and the LSM-XFEM results are on the bottom row where black is phase “A” material. Fig. 15 shows that the SIMP and LSM-XFEM approach are similar in that they both lead to column-type internal structures. They differ near the lower region of the plate, where the density approach has a thick filled in design, and the LSM-XFEM design has breaks along the z-length of the plate. Note the appearance of seemingly free-floating material in Fig. 15 arises from showing a slice in the y-z plane through the center of the structure; this material is actually connected in the out of plane (x) direction.

Fig. 15
figure 15

Material distributions of optimized designs in the y-z plane at x = 4.5m obtained with LSM-XFEM and SIMP approaches on coarse mesh (left) and the fine mesh (right)

Full size image

The LSM-XFEM performs better by achieving a lower strain energy on both refinement levels than the SIMP method. The designs acquired using the SIMP method are very different for the two mesh refinement levels. In contrast, the optimal design for the LSM-XFEM is nearly the same for both mesh refinements, suggesting that the LSM-XFEM approach converges faster as the mesh is refined. Again, we note that the SIMP convergence can be improved through density or sensitivity filter and the crispness of the density distribution can be enhanced by projection methods (Sigmund 2007; Guest 2009). Neither option is studied here. Nevertheless, the ability of the LSM-XFEM approach to capture optimal geometries on rather coarse meshes is an attractive feature of this approach, in particular for 3D FSI problems that are computationally costly.

Figure 16 shows the evolution of the objectives in the optimization process for both the LSM-XFEM and the SIMP approaches. Fig. 17 depicts the zero level set iso-surface in the course of the optimization process at different snapshots for the fine mesh. Fig. 16 shows that both the LSM-XFEM and the SIMP method objective function converge at nearly the same rate. Note in Fig. 16 the fine LSM-XFEM curve increases until the inequality constraint is satisfied, then converges after iteration 50. The 3D example does not exhibit the jumps seen in the 2D problem due to the greater redundancy of load paths in the 3D design.

Fig. 16
figure 16

Objective evolution for both SIMP and LSM-XFEM, with both mesh refinements

Full size image
Fig. 17
figure 17

Snapshots of the level set iso-surface through the optimization evolution

Full size image

4.3 Pressure tuning device

In the final example of this study we optimize a passive valve to control the pressure drop in a 2D channel. The problem is illustrated in Fig. 18. The internal structural geometry of the two vertical beams is to be designed such that upon deformation of the beams the flow exhibits a desired pressure drop, Δp d e s i r e d , across the channel. This example will illustrate that the proposed LSM-XFEM approach is applicable to design optimization problems that do not involve compliance. We will further show that the SIMP approach requires a volume penalization to converge toward a “0-1” material distribution.

Fig. 18
figure 18

Pressure tuning device example: problem setup

Full size image

The dimensions of the problem are given in Fig. 18. The fluid and structural properties along algorithmic parameters are given in Table 5. The discretization parameters are given in Table 6. The Reynolds number is 1.0 using the mean inflow velocity and the beam length L b as reference values. We assume that the phase “B” represents “void”, i.e. \({E^{s}_{B}}=0\) and \(\rho ^s_B=0\). The problem is assumed to be symmetric about the y = 1.3m line. Therefore, only half of the FSI problem is modeled, using an unstructured mesh. The skin layer, \({{\Omega }^{s}_{C}}\), is formed by prescribing the material in one layer of solid elements along the fluid-structure interface to phase “A”. For the given mesh, the thickness of the skin layer is approximately 0.0055 m. The optimization problem is to minimize the difference between the actual and the desired pressure drop. To regularize the LSM-XFEM version of the optimization problem the perimeter is also penalized. We further study the influence of penalizing the volume occupied by phase “A”. The optimization problem reads as follows:

$$\begin{array}{@{}rcl@{}} \underset{s_{i}}{\text{minimize}} \quad z(s_{i}) & =& k_{\Delta p} \ \left(\frac{\Delta p}{\Delta p_{desired}}-1.0\right)^{2} \\ & +& k_{V} \ {\int}_{{{\Omega}^{s}_{A}}}d{\Omega} + k_{P} \ {\int}_{{\Gamma}^{s}_{A,B}} d{\Gamma}, \end{array} $$
(26)

where the actual pressure drop, Δp, is computed as follows:

$$\begin{array}{@{}rcl@{}} {\Delta} p &=& {\int}_{{\Gamma}^{\text{inflow}}}\left(\frac{1}{2}\rho^{f}|v_{i}|^{2}+p\right)d{\Gamma} \end{array} $$
(27)
$$\begin{array}{@{}rcl@{}} &-& {\int}_{{\Gamma}^{\text{outflow}}}\left(\frac{1}{2}\rho^{f}|v_{i}|^{2}+p\right)d{\Gamma}. \end{array} $$
(28)
Table 5 Physical parameters of pressure-tuning problem
Full size table
Table 6 Discretization parameters of pressure-tuning problem
Full size table

To find an obtainable value for the desired pressure drop, we consider the beams made of a uniform material and study the pressure as the elastic modulus of the material changes. The results are shown in Fig. 19. The pressure drop decreases as the stiffness of the beams increase and the structural deformations decrease. This may be found counter-intuitive. As the structure deforms, the orthogonal projection of the beam onto the inlet is reduced, i.e. the beam appears shorter as seen by the inlet flow, yet the pressure drop increases. This behavior can be explained by the skin friction being the main driver of the pressure loss in the channel. As the structure deforms, the more the fluid- structure interface is aligned with the flow and, thus, the skin friction increases. To promote a beam design that exhibits some flexibility, we choose the value 0.37 for Δp d e s i r e d .

Fig. 19
figure 19

Phase “A” elastic modulus sweep results

Full size image

First we will solve the optimization problem with both LSM-XFEM and the SIMP approaches, omitting the volume penalty, i.e. k V =0. The penalty parameter for the pressure term k Δp is 10000. For the LSM-XFEM we use a perimeter penalty of k P =0.1. The LSM-XFEM approach is initialized with an equally spaced array of 2×5 holes of radius 0.045 m. The initial hole radius is used as the upper and lower bound for the box constraints in \({{\Omega }^{s}_{D}}\): [ −0.045:0.045]. For the SIMP approach, we set the penalty factor to β = 3.5 and initialize the design domain, \({{\Omega }^{s}_{D}}\),to uniform 60 % density. The Young’s modulus in the “void” phase is set to \({E_{B}^{s}}=10^{-6}\) to avoid a singular finite element problem.

The contour plots of the velocity magnitude and pressure fields of the initial configuration are given in Figs. 20 and 21 for both LSM-XFEM and SIMP approaches. The flow solution plots show the overall symmetry of the problem, and stagnation and low pressure areas.

Fig. 20
figure 20

Contour plots of fluid velocity magnitude of initial configurations for SIMP and LSM-XFEM approaches

Full size image
Fig. 21
figure 21

Fluid pressure fields of initial configurations for LSM-XFEM and SIMP approaches

Full size image

The initial and optimized geometries are given in Fig. 22 where the shade indicates the material stiffness. The convergence plots of the objectives are shown in Fig. 23. The pressure drop values and the volumes occupied by phase “A” are reported in Table 7. The LSM-XFEM approach leads to a simple design that provides flexibility to the beam through simple compliant mechanism at the bottom of the beam. In contrast, the SIMP approach leads to material distribution of intermediate density values that provides no guidance for a practical design solution. Note in this case projection methods will not improve the results (Sigmund and Maute 2013). Both optimization processes are well converged and both the LSM-XFEM and SIMP design meet well the target pressure drop. Note that the LSM-XFEM approach converges without any jumps.

Fig. 22
figure 22

Initial and optimized geometries for LSM-XFEM and SIMP approaches with no volume penalty

Full size image
Fig. 23
figure 23

Evolution of objectives for LSM-XFEM and the SIMP method with no volume penalty

Full size image
Table 7 Performance of optimized pressure tuning device
Full size table

In the absence of physical phenomena that naturally promote a “0-1” solution, the convergence of the SIMP approach toward a “0-1” material distribution relies on the interplay of an objective that promotes stiffness and a constraint or penalty on volume. To enhance the SIMP results we therefore introduce a volume penalty and solve the optimization problem for k V =10. These initial and optimized designs are given in Fig. 24 where the shade indicates the material stiffness. The evolution of the objectives are shown in Fig. 25.

Fig. 24
figure 24

Initial and optimized geometries for LSM-XFEM and SIMP approaches with volume penalty: k V =10

Full size image
Fig. 25
figure 25

Evolution of objectives for LSM-XFEM and the SIMP method with volume penalty: k V =10

Full size image

Due to the volume penalty, the SIMP approach converges to a material distribution that describes well the optimized geometry. However, the design of both the LSM-XFEM and SIMP approaches are significantly more complex and do not meet the target pressure drop as well as when omitting the volume penalty; see Table 7. Figure 25 shows that SIMP and the LSM-XFEM converge at similar rates. However, due to the formation of thin structural members, the convergence of LSM-XFEM suffers from a few jumps.

5 Conclusions

A topology optimization approach that combines an explicit level set method and the extended finite element method was presented and studied for optimizing the internal structural layout of FSI problems. The structural response was modeled assuming infinitesimal small strains and a linear elastic material behavior. The fluid loads were predicted via an incompressible Navier-Stokes model. Fluid and structure models were strongly coupled and the steady-state FSI response was computed by a monolithic scheme.

Optimization problems in 2D and 3D were studied, comparing the proposed LSM-XFEM approach against the SIMP method. For both approaches, the gradients of objective and constraints were evaluated by the adjoint method and the parameter optimization problems were solved by the Globally Convergent Method of Moving Asymptotes. The examples focused on two-phase structural designs, including both “solid-void” and “solid-solid” configurations. Objective functions were considered that increase the structural stiffness and tune the flexibility of the structure such that a target pressure drop across a flow channel is achieved. Either a penalty or constraint on the mass of the stiff phase was imposed. The LSM-XFEM problem formulations were augmented by a penalty on the perimeter. While the examples presented in this paper are rather academic and, with the exception of the third example, do not necessarily highlight the need for considering FSI phenomena in the design process, they are well-suited to gain insight into the proposed LSM-XFEM approach.

The numerical studies suggested the proposed LSM-XFEM scheme is a suitable approach to find crisp geometries of the internal structure for FSI problems. It was observed that the convergences of the LSM-XFEM designs in the optimization process may suffer from jumps. This issue was more pronounced for “solid-void” problems in 2D as the structure forms thin members. Analysis of design evolution revealed that the jumps are due to the bi-linear interpolation scheme of the level set functions that does not allow multiple intersections along an element edge. While this issue is inherent to the proposed LSM-XFEM approach, it was not observed in previous LSM-XFEM studies but seems to be more pronounced for FSI problems. In 3D the tri-linear interpolation of the level set function provides more flexibility to represent thin structural members and therefore jumps in the design evolutions are less likely.

Comparing LSM-XFEM and SIMP results showed that both approaches find designs with comparable performance. When sufficiently constraining the mass of the stiff phase, the SIMP approach converged toward a two-phase solution and typically found designs with a more complex, delicate geometry. However, the increased geometric complexity did not provide a significant mechanical advantage over the much simpler designs found by the LSM-XFEM approach. Note that for SIMP, the density filter was not used to control the feature size as the filter radius was decreased as meshes were refined. Further, it was observed that the LSM-XFEM approach results in optimized geometries with crisp phase boundaries on rather coarse meshes. In contrast, the SIMP approach requires much finer meshes to yield clearly defined boundaries. The ability of the LSM-XFEM approach to work on coarse meshes provides a practical advantage in particular for 3D FSI problems.

The numerical studies on the pressure tuning device illustrated that the LSM-XFEM approach is applicable to problems where the mass of the stiff phase is not constrained or penalized. In this case, the SIMP approach did not converge toward a two-phase solution, and a mass penalty was needed to obtain meaningful designs with the SIMP approach. Note that augmenting the SIMP approach with a projection scheme is not likely to resolve the lack of convergence as the presence of intermediate density values is not due to filtering; see, for example, the discussion in Sigmund and Maute (2013).

In future studies, the proposed LSM-XFEM approach should be refined and expanded. An alternative interpolation scheme of the level set function needs to be developed to mitigate the jumps in the design evolution. The current approach should be enhanced to allow optimizing both the “wet” and “dry” geometry. Expanding the method into finite strains and nonlinear constitutive structural models is straight forward from an algorithmic point of view. However, one needs to devise strategies to deal with structural instabilities. Applying the proposed approach to higher Reynolds and Mach number flows requires the integration of appropriate flow models and anisotropic meshing schemes to resolve relevant flow phenomena, such as boundary layer flows. To consider dynamic FSI phenomena, such as flutter and limit cycle oscillations, the transient response of the FSI system needs to be considered. Finally, the applicability of the LSM-XFEM approach should be studied in the context of practical design problems.