Abstract
Cholera is an acute intestinal infectious disease caused by the bacterium Vibrio cholerae. To explore the multiple effects of spatial mobility, spatial heterogeneity and the seasonality on the transmission of cholera, we propose a time periodic reaction–diffusion equation model with latent period. Based on the basic reproduction number \(\mathscr {R}_0\), we establish a threshold-type result. And in the case where all the parameters are constants and \(\mathscr {R}_0>1\), we show the global attractivity of the endemic steady state by constructing Lyapunov functionals. Finally, we perform some numerical simulations. Our simulations show that (i) increasing the vaccination rate of susceptible individuals and vaccine protective efficacy can reduce the transmission risk \(\mathscr {R}_0\); (ii) decreasing the transmission coefficient of contact with infected individuals, the transmission coefficient of contact with hyperinfectious vibrios and the transmission coefficient of contact with hypoinfectious vibrios can reduce the transmission risk \(\mathscr {R}_0\); (iii) it is possible to underestimate the transmission risk \(\mathscr {R}_0\) in the periodic system if the spatial averaged system is used, based on some experimental data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cholera is an acute intestinal infectious disease caused by a bacterium Vibrio cholerae. It can be transmitted by many ways, such as direct person-to-person contact or indirect transmission through the environment [21, 31]. It remains as one of the major public health threats in underdeveloped countries even though tremendous efforts have been made towards the prevention, intervention and control of the spread of the disease. According to the World Health Organization (WHO), there are approximately 1.3–4.0 million cholera cases occur worldwide annually, leading to the related deaths of 21,000–143,000 yearly [55]. It is widely accepted that mathematical models of the cholera dynamics play an important role in providing deep and useful insights into the understanding of the multiple transmission pathways of cholera (see, e.g. [1, 7, 8, 10, 11, 17, 19, 21, 31, 32, 34, 37, 43, 44, 49, 51]). Most of these models are governed by ordinary differential equations (ODEs), where model parameters are assumed to be independent of time and space so that detailed mathematical results on stabilities and bifurcations can be achieved.
It is now well known that the most effective measures for prevention, intervention and control on the spread of the cholera transmission in the long term are improvements in personal hygiene, drinking water and basic sanitation system. Unfortunately, these measures cannot be applied properly in some cholera endemic countries. Thus, vaccination becomes a useful measure, for example in 2010, WHO recommended that oral vaccines should be used in some cholera endemic countries [55]. Since then researchers have been working on mathematical models to investigate the effect of vaccination on the cholera transmission, see [24, 35, 41, 60] and the references therein.
To better understand the multiple transmission pathways of cholera, very recently, Bai et al. [5] proposed a mathematical model, by incorporating the combined effects of hyperinfectious and hypoinfectious vibrios, both human-to-human and environment-to-human transmission pathways and waning vaccine-induced immunity. Let S(t), V(t), I(t), R(t), \(B_H(t)\) and \(B_L(t)\), respectively, represent the densities of susceptible individuals, vaccinated individuals, infected individuals, recovered individuals, hyperinfectious vibrios and hypoinfectious vibrios at time t. Then, the model takes a form of
The biological meanings of parameters in model (1.1) are summarized in Table 1. The global dynamics and the control measures of cholera of model (1.1) were discussed.
In biology, spatial and temporal heterogeneity involving differences in ecological and geographic environments, demographic characteristics and socio-economic structures lead to differences in disease exposure rates, levels of human activity, pathogen growth and mortality. This, in turn, leads to a strong impact on cholera dynamics, resulting some natural questions regarding the spread of cholera transmission:
-
(i)
How does the spatial mobility of hosts and pathogens affect the spread of cholera?
-
(ii)
What factors determine cholera outbreaks that persists in some countries but not in others?
-
(iii)
Why does cholera typically spread in a certain period of a year (e.g. monsoon or rainy seasons [23, 47])?
There have been some studies on the spatial dynamics of cholera transmission. In [17, 38, 45], some ODE models based on patch/network structures were established to discuss the global dynamics of steady states. Some reaction–diffusion equation models were proposed to discuss the global dynamics of cholera dynamics [6, 10, 36, 48, 51, 56, 57]. In [11], a nonautonomous ODE model was presented to discuss periodic patterns of cholera outbreaks. Posny and Wang [34] studied the threshold dynamics of a nonautonomous ODE cholera model with general incidence rate. Wang et al. [52] studied the threshold dynamics of a reaction–convection–diffusion cholera model with spatial and temporal heterogeneity. However, to the best of our knowledge, very little has been known and undertaken on threshold dynamics for time periodic reaction–diffusion cholera transmission models with latent period. Azman et al. [2] estimated that the median incubation period of cholera is 1.4 days (95% CI 1.3–1.6). Hence, it is reasonable and helpful to incorporate nonlocal time delay into cholera transmission models.
Motivated by the aforementioned, in this study we consider a case where the latent period is taken into account. Thus, the main purpose of this paper is to propose a time periodic reaction–diffusion equation cholera transmission model with latent period and to explore its dynamics. To this end, we organize the structure of the rest of the paper as follows. We formulate a time periodic reaction–diffusion equation model with latent period according to the criteria of structural population and spatial diffusion in Sect. 2. In Sect. 3, we are dedicated ourselves to the threshold dynamics in terms of the basic reproduction number \(\mathscr {R}_0\). It is then followed by Sect. 4 where we mainly discuss the global attractivity of the endemic steady state when \(\mathscr {R}_0>1\). It is done by constructing Lyapunov functionals. We numerically illustrate our theoretical findings. Finally, we conclude our study in Sect. 6.
2 Model formulation
First, we, based on the notations in model (1.1), introduce the time- and location-dependent densities: \(S(t,\,x)\), \(V(t,\,x)\), \(I(t,\,x)\), \(R(t,\,x)\), \(B_H(t,\,x)\) and \(B_L(t,\,x)\), respectively, denote the densities of susceptible individuals, vaccinated individuals, infected individuals, recovered individuals, hyperinfectious vibrios and hypoinfectious vibrios at the time t and location x. Then, we develop the equations they satisfy. Following the standard procedure on developing model involving structured population and spatial diffusion in [20], we can get
where \(\Omega \subset \mathbb {R}^n\) is a general open bounded domain with smooth boundary \(\partial \Omega \), \(I_{1}(t,\,h,\,x)\) is the density of individuals with infection age h at time t and location x, \(\mu (t,\,x)\) represents the natural human death rate of infected individuals, independent of h, \(D_3\) is the diffusion rate of infected individuals, and \(\Delta \) is the usual Laplace operator. Assuming that \(\tau \) is the average incubation period, we have

and

We make some assumptions for the functions \(\Upsilon (t,\,h,\,x)\) and \(d(t,\,h,\,x)\) as follows:
and
A straightforward computation yields
and
In biology, we assume that \(I(t,\,\infty ,\,x)=0\) as suggested by [27]. The density of newly infected individuals \((I_{1}(t,\,0,\,x))\) is adopted by:
Based on model (1.1) and the above discussions, we propose a time periodic reaction–diffusion cholera transmission model. To make things not too complicated (as spatial and temporal heterogeneity, and nonlocal time delay have already made the problem challenging), we compromise a little bit by assuming \(\eta =0\), yielding
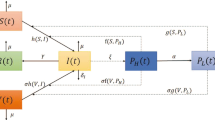
where \(D_i\) \((i=1,2,3,4,5,6)\) are the diffusion rates of susceptible individuals, vaccinated individuals, infected individuals, recovered individuals, hyperinfectious vibrios and hypoinfectious vibrios, respectively. The corresponding flowchart of cholera transmission in model (2.2) is depicted in Fig. 1.
We further make the following basic hypotheses:
\(\mathbf {(H)}\): All functions \(A\left( t,x\right) \), \(\beta _{h}\left( t,x\right) \), \(\beta _{H}\left( t,x\right) \), \(\beta _{L}\left( t,x\right) \), \(\varpi \left( t,x\right) \), \(\mu \left( t,x\right) \), \(\varUpsilon _{L}\left( t,x\right) \), \(d_{L}\left( t,x\right) \), \(\varUpsilon _{I}\left( t,x\right) \), \(d_{I}\left( t,x\right) \), \(\xi \left( t,x\right) \), \(\chi \left( t,x\right) \) and \(\delta _{L}\left( t,x\right) \) are Hölder continuous and positive on \(\mathbb {R}\times {\overline{\Omega }}\), and \(\omega \)-periodic in time \((\omega >0)\).
Next, we determine \(I_1(t,\,\tau ,\,x)\) by using the characteristics method. For \(h\in (0,\,\tau ]\) and \({\overline{r}}\ge 0\), let \({\overline{s}}({\overline{r}},\,h,\,x)=I_1(h+{\overline{r}},\,h,\,x)\). Then, one gets from (2.1) that
which has a solution
where
and \(\Gamma (t,\,s,\,x,\,y)\) with \(t>s\ge 0\) and \(x,\,y\in \Omega \) is the fundamental solution for the partial differential operator \(\partial _{t}-D_3\Delta +\mu \left( t,\cdot \right) +\varUpsilon _{L}\left( t,\cdot \right) +d_{L}\left( t,\cdot \right) \) [18, Chapter 1]. We then can verify that \( \Gamma (t,\,s,\,x,\,y)=\Gamma \left( t+\omega ,\,s+\omega ,\,x,\,y\right) \) for \(t>s\ge 0\), and \(x,\,y \in \Omega \) since \(\mu \left( t+\omega ,\,\cdot \right) =\mu \left( t,\,\cdot \right) \), \(\varUpsilon _{L} \left( t+\omega ,\,\cdot \right) =\varUpsilon _{L} \left( t,\,\cdot \right) \) and \(d_{L}\left( t+\omega ,\,\cdot \right) =d_{L}\left( t,\,\cdot \right) \) for \(t\ge 0\). Notice \(I_1(t,\,h,\,x)={\overline{s}}(t-h,\,h,\,x)\). Then, for \(h=\tau \) and \(\forall \ t\ge \tau \), we have
Since \(I_m\) in model (2.2) can be decoupled from the other equations, we now reach our main model governed by the following system (2.4) of time periodic reaction–diffusion equations to describe the cholera transmission with latent period. It is then followed by exploring its threshold dynamics and stability in Sects. 3 and 4, respectively.
3 Threshold dynamics
For the convenience of discussion in the rest study, we introduce some commonly used notations in the literature: Let \(\mathbb {X}:=C({\overline{\Omega }},\, \mathbb {R}^6)\) denote the Banach space with the supremum norm \(\Vert \cdot \Vert _{\mathbb {X}}\). For \(\tau \ge 0\), we define \(C_{\tau }:=C\left( \left[ -\tau ,\,0 \right] ,\, \mathbb {X}\right) \) with the norm \(\Vert \cdot \Vert :=\max _{\theta \in [-\tau ,\, 0]}\Vert \phi (\theta )\Vert _{\mathbb {X}},\ \, \phi \in C_{\tau }.\) Define \(\mathbb {X}^+:=C({\overline{\Omega }},\, \mathbb {R}_{+}^6)\ \, \text {and}\ \, C_{\tau }^+=C\left( \left[ -\tau ,\,0 \right] ,\, \mathbb {X}^+\right) .\) Then \((\mathbb {X},\, \mathbb {X}^+)\) and \((C_{\tau },\, C_{\tau }^+)\) are strongly ordered spaces. For \(\sigma >0\) and a function \(\gamma :[-\tau ,\, \sigma )\mapsto \mathbb {X}\), we define \(\gamma _t\in C_{\tau }\) by
3.1 The Well-posedness
Let \(\mathbb {Y}:=C({\overline{\Omega }},\, \mathbb {R})\) and \(\mathbb {Y}^+:=C({\overline{\Omega }},\, \mathbb {R}_+)\). We assume that \(T_i(t,\,s)\) \((i=1,\ldots ,6):\) \(\mathbb {Y}\rightarrow \mathbb {Y}\), are, respectively, the evolution operators associated with
subject to the zero-flux boundary conditions. By the assumption \(\mathbf {(H)}\), and using [14, Lemma 6.1] for \(t\ge s\), we then have \(T_i(t+\omega ,\,s+\omega )=T_i(t,\,s)\) for \((t,\,s)\in \mathbb {R}^2\) with \(i=1,\ldots ,6\). According to [22, Chapter II], for \((t,\,s)\in \mathbb {R}^2\) with \(t>s\), \(T_i(t,\,s)\) \((i=1,\ldots ,6)\) are compact and strongly positive. Further, denote
Then, \(T(t,\,s):\mathbb {X}\rightarrow \mathbb {X}\) is an evolution operator for \((t,\,s)\in \mathbb {R}^2\) with \(t\ge s\).
Define \(\Sigma =(\Sigma _1,\,\Sigma _2,\,\Sigma _3,\,\Sigma _4,\,\Sigma _5,\,\Sigma _6)\) \(:\,[0,\,+\infty )\times C_{\tau }^+\rightarrow \mathbb {X}\) by
for \(t\ge 0\), \(x\in {\overline{\Omega }}\), and \(\phi =(\phi _1,\,\phi _2,\,\phi _3,\,\phi _4,\,\phi _5,\,\phi _6)\in C_{\tau }^+\). Then, model (2.4) can be rewritten as
where \(\Pi (t,\,x)=(\Pi _1(t,\,x),\,\Pi _2(t,\,x),\,\Pi _3(t,\,x),\,\Pi _4(t,\,x),\, \Pi _5(t,\,x),\,\Pi _6(t,\,x)\,)\), and \(\mathbb {K}(t)=\text {diag}(\mathbb {K}_1(t),\,\mathbb {K}_2(t), \mathbb {K}_3(t),\) \(\mathbb {K}_4(t), \mathbb {K}_5(t),\,\mathbb {K}_6(t))\). Here \(\mathbb {K}_i(t)\) \((i=1,2,3,4,5,6)\) are given by:
Theorem 3.1
For any \(\phi \in C_{\tau }^+\), model (2.4) admits a unique mild solution \(z(t,\,\cdot ;\,\phi )\) on its maximal existence interval \(\left[ 0,\,{\widetilde{t}}_{\phi }\right) \) with \(z_0=\phi \), where \({\widetilde{t}}_{\phi }\le +\infty \). Moreover, \(z(t,\,\cdot ;\,\phi )\in \mathbb {X}^+\), and \(z(t,\,\cdot ;\,\phi )\) is a classical solution of model (2.4) for \(t>\tau \).
Proof
By definition of \(\Sigma \), we can easily verify that it is locally Lipschitz continuous. The conditions \((H_1)\)–\((H_2)\) in [30, Corollary 4] are obviously satisfied due to \(D=\mathbb {X}^+\). Indeed, by [30, Remark 2.2], the condition \((H_3)\) in [30, Corollary 4] is automatically satisfied since \(\mathbb {X}^+\) is convex. By the definition of the continuity, the condition \((H_4)\) is satisfied. Then, by [30, Corollary 4], it suffices to prove
For \((t,\,\phi )\in [0,\,+\infty )\times C_{\tau }^+\) and \(\theta _{1}\ge 0\), one gets
If \(\theta _{1}\) is small enough, then \(\phi (0)+\theta _{1} \Sigma (t,\,\phi )\in \mathbb {X}^+\). It follows from [30, Corollary 4] that there admits a unique mild solution \(z(t,\,\cdot ;\, \phi )\) with \(z_0=\phi \) on \(t\in \left[ 0,\, {\widetilde{t}}_{\phi }\right) \) for model (2.4), where \({\widetilde{t}}_{\phi }\le +\infty \), and \(z(t,\,\cdot ;\,\phi )\in \mathbb {X}^+\). In addition, by the analytic of \(T(t,\,s)\), \(t,\,s\in \mathbb {R}\) and \(t>s\), \(z(t,\,\cdot ;\, \phi )\) is a classical solution for \(t>\tau \). \(\square \)
Let
For any given \(\varphi \in C_{\tau }^{++}\), we define \({\widetilde{\varphi }}=\left( \varphi _1,\,\varphi _2,\,\varphi _3,\,{\widetilde{\varphi }}_4,\,\varphi _5,\,\varphi _6\right) \), where \({\widetilde{\varphi }}_4(\theta ,\,\cdot )=\varphi _4(\cdot )\in \mathbb {Y}^+\) and \(\theta \in [-\tau ,\,0]\). Then \({\widetilde{\varphi }}\in C_{\tau }^{+}\). By the uniqueness of solutions, \(\Pi (t,\,\cdot ;\,\varphi )=z(t,\,\cdot ;\,{\widetilde{\varphi }})\) for \(t\ge 0\). It follows from Theorem 3.1 that there exists a unique solution \(\Pi (t,\,\cdot ;\,\varphi )\) of model (2.4) and \(\Pi _0=\varphi \) on \(\left[ 0,\,{\widetilde{t}}_{\varphi }\right) \), where
for \(t\ge 0\) and \((\theta ,\,x)\in [-\tau ,\,0]\times {\overline{\Omega }}\).
Denote
Theorem 3.2
For any \(\varphi \in C_{\tau }^{++}\), model (2.4) admits a unique solution \(\Pi (t,\,\cdot ;\,\varphi )\) on \([0,\, +\infty )\) with \(\Pi _0=\varphi \). In addition, model (2.4) generates an \(\omega \)-periodic semiflow \(W_t:=\Pi _t(\cdot ):\, C_{\tau }^{++}\rightarrow C_{\tau }^{++}\), i.e. \(W_t(\varphi )(s,\,x)=\Pi (t+s,\,x;\,\varphi )\) for \(\varphi \in C_{\tau }^{++},\ t\ge 0\), \(s\in [-\tau ,\, 0]\) and \(x\in \Omega \), and \(W_{\omega }:\, C_{\tau }^{++}\rightarrow C_{\tau }^{++}\) has a global attractor in \(C_{\tau }^{++}\).
Proof
From the first equation of model (2.4), by the comparison theorem, we have that \(S\left( t,x;\varphi \right) \) is bounded by \(K_{1}> 0\) on \(\left[ 0,{\widetilde{t}}_{\varphi }\right) \). Similarly, \(V\left( t,x;\varphi \right) \) is bounded by \(K_{2}> 0\) on \(\left[ 0,{\widetilde{t}}_{\varphi }\right) \). Hence, the \(I\left( t,x\right) \), \(R\left( t,x\right) \), \(B_{H}\left( t,x\right) \) and \(B_{L}\left( t,x\right) \) equations of model (2.4) are dominated by the following linear reaction–diffusion system:
By the global existence of solutions of the linear system (3.2). (see, e.g. [54, Theorem 2.1.1]), we get \({\widetilde{t}}_{\varphi }=+\infty \) for each \(\varphi \in C_{\tau }^{++}\).
Since \(\frac{\partial S}{\partial t}\le D_{1}\Delta S+A\left( t,x\right) -\left[ \phi \left( t,x\right) +\mu \left( t,x\right) \right] S\), there exists a constant \(B_1>0\) such that for any \(\varphi \in C_{\tau }^{++}\), there is an integer \(L_{1}=L_{1}\left( \varphi \right) > 0\) satisfying \(S\left( t,\,x;\,\varphi \right) \le B_1\), for \(t\ge L_{1}\omega \) and \(x\in {\bar{\Omega }} \). Similarly, there exists a constant \(B_2>0\) such that for any \(\varphi \in C_{\tau }^{++}\), there is an integer \(L_{2}=L_{2}\left( \varphi \right) > 0\) satisfying \(V\left( t,\,x;\,\varphi \right) \le B_2\), for \(t\ge L_{2}\omega \) and \(x\in {\bar{\Omega }} \). In what follows, using similar arguments to [42, Theorem 2.1], we show that the solution of model (2.4) is ultimately bounded. Let \({\bar{S}}\left( t\right) =\int \limits _{\Omega }S\left( t,\,x\right) {\mathrm{d}}x\), \({\bar{V}}\left( t\right) =\int \limits _{\Omega }V\left( t,\,x\right) {\mathrm{d}}x\) and \({\bar{I}}\left( t\right) =\int \limits _{\Omega }I\left( t,\,x\right) {\mathrm{d}}x\). By integrating the first equation of model (2.4), it follows from Green’s formula that
and
and
Thus, we have
Then,
By the property of the fundamental solutions [18], integrating the third equation of model (2.4) yields
where \(k_{1}\), \(k_{2}\) and \(k_{3}\) are positive constants independent of \(\varphi \). Choose \(k_{1}\le \left( \underline{\mu }+{\underline{\Upsilon }}_{I}+{\underline{d}}_{I}\right) k_{2}\), one gets
which yields \({\overline{I}}\left( t\right) +k_{2}\left[ {\overline{S}}\left( t-\tau \right) +{\overline{V}}\left( t-\tau \right) \right] \le \frac{k_{2}k_{3}}{k_{1}}+1\), for \(t\ge L_{1}^{'}\omega +\tau \), \( L^{'}_1> L_{1}+L_2\). Since \(\Gamma \left( t,t-\tau ,x,y\right) \), S and V are bounded, then
where \(c>0\) and \(M>0\) are constants. According to the standard parabolic maximum principle, there is a constant \(B_{3}>0\) independent of \(\varphi \), and an integer \(L_{3}=L_{3}\left( \varphi \right) > (L_{1}+L_2)\left( \varphi \right) \), such that \(I\left( t,\,x,\,\varphi \right) \le B_{3}\), for \(t\geqslant L_{3}\omega +\tau \), \(x\in {\overline{\Omega }}\).
From the last three equations of model (2.4), we obtain
There exists a constant \(B_4>0\) such that for any \(\varphi \in C_{\tau }^{++}\), there is an integer \(L_{4}=L_{4}\left( \varphi \right) > 0\) satisfying \(R\left( t,\,x;\,\varphi \right) \le B_4\), for \(t\ge L_{4}\omega \) and \(x\in {\bar{\Omega }} \). There is a constant \(B_5>0\) such that for any \(\varphi \in C_{\tau }^{++}\), there is an integer \(L_{5}=L_{5}\left( \varphi \right) > 0\) satisfying \(B_{H}\left( t,\,x;\,\varphi \right) \le B_5\), for \(t\ge L_{5}\omega \) and \(x\in {\bar{\Omega }} \). There is a constant \(B_6>0\) such that for any \(\varphi \in C_{\tau }^{++}\), there is an integer \(L_{6}=L_{6}\left( \varphi \right) > 0\) satisfying \(B_{L}\left( t,\,x;\,\varphi \right) \le B_6\), for \(t\ge L_{6}\omega \) and \(x\in {\bar{\Omega }} \).
We now define a family of operators \(\left\{ W_t\right\} _{t\ge 0}\) on \(C_{\tau }^{++}\) by \(W_t(\varphi )(s,\,x)=\Pi _t(s,\,x;\,\varphi )=\Pi (t+s,\,x;\,\varphi )\) for \(t\ge 0\), \(s\in [-\tau ,\, 0]\), \(x\in {\overline{\Omega }}\), and \(\varphi \in C_{\tau }^{++}\). From the above proofs, \(W_t:\,C_{\tau }^{++}\rightarrow C_{\tau }^{++}\) is point dissipative. Similar to the proof of [61, Lemma 2.1], we can show that \({W}_{t\ge 0}\) is an \(\omega \)-periodic semiflow on \(C_{\tau }^{++}\). Furthermore, from [54, Theorem 2.1.8], \(W_t:\,C_{\tau }^{++}\rightarrow C_{\tau }^{++}\) is compact for each \(t>\tau \). In view of [29, Theorem 2.9], we deduce that \(W_{\omega }:\,C_{\tau }^{++}\rightarrow C_{\tau }^{++}\) admits a global attractor in \(C_{\tau }^{++}\). \(\square \)
3.2 Basic reproduction number
Let \(\mathbb {M}=C({\overline{\Omega }},\, \mathbb {R}^{3})\) and \(\mathbb {M}^+=C({\overline{\Omega }},\, \mathbb {R}^{3}_{+})\). Let \(C_{\omega }(\mathbb {R},\,\mathbb {M})\) be the Banach space for all \(\omega \)-periodic functions with \(\Vert \psi \Vert _{C_{\omega }(\mathbb {R},\,\mathbb {M})}:=\max _{\theta \in [0,\,\omega ]}\Vert \psi (\theta )\Vert _{\mathbb {M}}\) from \(\mathbb {R}\) to \(\mathbb {M}\) for \(\psi \in C_{\omega }(\mathbb {R},\,\mathbb {M})\).
Consider the following periodic reaction–diffusion equation:
It follows from [61, Lemma 2.1] that model (3.3) has a unique positive \(\omega \)-periodic solution \(S^{*}(t,\,\cdot )\), which is globally attractive in \({\mathbb {Y}}^{+}\). Then, the second equation of model (2.4) is asymptotic to
Similarly, model (3.4) has a unique positive \(\omega \)-periodic solution \(V^{*}(t,\,\cdot )\), which is globally attractive in \({\mathbb {Y}}^{+}\). Setting \(I=R=B_H=B_L=0\) in model (2.4), we have
Hence, by [61, Lemma 2.1] and the theory of chain transitive sets [59], there is a globally attractive positive \(\omega \)-periodic solution \((S^*(t,\,\cdot ),\,V^*(t,\,\cdot ))\) of model (3.5) in \(C({\overline{\Omega }},\, \mathbb {R}^{2}_{+}).\) Consequently, model (2.4) has a unique infection-free periodic solution \(E_{0}=\left( S^{*}\left( t,\cdot \right) ,V^{*}\left( t,\cdot \right) ,0,0,0,0\right) .\)
Linearizing model (2.4) at \(E_0\), we get the infective compartments:
To introduce the basic reproduction number, we define
for \(t\in \mathbb {R}\), \((\phi _3,\,\phi _5,\,\phi _6)\in C([-\tau ,\,0],\,\mathbb {M})\), and
where \(D=\text {diag}(D_3,\,D_5,\,D_6)\), and for \(x\in {\overline{\Omega }}\),
Assume that \(\Lambda (t,\,s)=\text {diag}(T_3(t,\,s),\,T_5(t,\,s),\,T_6(t,\,s))\) \((t\ge s)\) is the evolution operators associated with
subject to zero-flux boundary conditions. According to [14, Theorem 6.6], there are \(c_0\in \mathbb {R}\) and \(\mathbb {U}\ge 1\) such that
and \({\overline{\omega }}(\Lambda )\le c_0\), where \({\overline{\omega }}(\Lambda )\) is the exponential growth bound of \(\Lambda (t,\,s)\), and
By [22, Lemma 14.2 and Krein–Rutman Theorem], it is easy to see that
In view of [40, Proposition 5.6], \({\overline{\omega }}(\Lambda )<0\). Thus, each \({\widehat{\Sigma }}(t)\) maps \(C([-\tau ,\,0],\,\mathbb {M}^+)\) into \(\mathbb {M}^+\), and each matrix-\(\Theta (t)\) is cooperative with \({\overline{\omega }}(\Lambda )<0\).
According to [58], from a biological perspective, we assume that \(q(s,\,x)=q(s)(x)\in C_{\omega }(\mathbb {R},\,\mathbb {M})\) is the initial distribution of infected individuals, hyperinfectious vibrios and hypoinfectious vibrios at time \(s\in \mathbb {R}\) and location \(x\in {\overline{\Omega }}\). For a given \(s\ge 0\), \({\widehat{\Sigma }}(t-s)q(t-s+\cdot ,\,x)\) denotes the distribution of newly infected individuals, hyperinfectious vibrios and hypoinfectious vibrios at time \(t-s\) \((t>s)\) and location x, which is generated by infected individuals, hyperinfectious vibrios and hypoinfectious vibrios who were introduced over \([t-s-\tau ,\,t-s]\). Hence, \(\Lambda (t,\,t-s){\widehat{\Sigma }}(t-s)q(t-s+\cdot ,\,x)\) stands for the distribution of those infected individuals, hyperinfectious vibrios and hypoinfectious vibrios who were newly infected at time \(t-s\) and still survive at time t for \(t\ge s\). Thus,
is the total distribution of infected individuals, hyperinfectious vibrios and hypoinfectious vibrios at time t and location x, which are produced by all those infected individuals, hyperinfectious vibrios and hypoinfectious vibrios introduced at all previous time to t.
We define two linear next generation operators on \(C_{\omega }(\mathbb {R},\,\mathbb {M})\) are
and
Let \(\mathbb {A}\) and \(\mathbb {B}\) be two bounded linear operators on \(C_{\omega }(\mathbb {R},\,\mathbb {M})\), denoted by
and
We see that \(L=\mathbb {A} \circ \mathbb {B}\) and \({\widehat{L}}=\mathbb {B} \circ \mathbb {A}\), and L and \({\widehat{L}}\) have the same spectral radius. By [3, 16, 40, 46, 58], the basic reproduction number for model (2.4) is
where r(L) is the spectral radius of L, and \( \mathscr {R}_0:=r(L)=r\left( {\widehat{L}}\right) . \) It is known that \(\mathscr {R}_0\) plays a crucial role in the prevention, intervention and control on the spread of the cholera transmission. In epidemiology, \(\mathscr {R}_0\) is regarded as the expected number of secondary cases produced, in a completely susceptible population, by a typical infective individual [16, 26].
For \(t\ge 0\), we assume that \(\widehat{\mathbb {P}}(t)\) is the solution map of model (3.6) on \(C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \). That is, \(\widehat{\mathbb {P}}(t)\phi =q_t(\phi )\), where
and \(q(t,\,x;\,\phi )\) is the unique solution of model (3.6) with \(q(\theta ,\,x)=\phi (\theta ,\,x)\) for \((\theta ,\,x)\in [-\tau ,\,0]\times {\overline{\Omega }}\). So we get that \(\widehat{\mathbb {P}}:=\widehat{\mathbb {P}}\left( \omega \right) \) is the Poincaré map for model (3.6). By using the similar arguments to that of [27], we have \(q(t,\,x;\,\phi )\gg 0\) for all \(t>\tau \), \(x\in {\overline{\Omega }}\) and \(\phi \in C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \) with \(\phi \not \equiv 0\). Moreover, from [54, Theorem 2.1.8], \(q_{t}\) is compact on \(C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \) for \(t>\tau \). It follows that \(\widehat{\mathbb {P}}^n\) is strongly positive and compact for \(n \omega >2\tau \). In terms of [25, Lemma 3.1], \(r\left( \widehat{\mathbb {P}}\right) \) is a simple eigenvalue of \(\widehat{\mathbb {P}}\) which admits a strongly positive eigenvector \({\overline{\phi }}\). Set \(r\left( \widehat{\mathbb {P}}\right) \) as the spectral radius of \(\widehat{\mathbb {P}}\), the following results can be obtained from [58]:
Lemma 3.3
\(\mathscr {R}_0-1\) has the same sign as \(r\left( \widehat{\mathbb {P}}\right) -1\).
3.3 Threshold dynamics
Recall that the Kuratowski measure of noncompactness in \(C_{\tau }^{+}\) [15] can be defined as
for any bounded subset B of \(C_{\tau }^{+}\).
Using an analogous argument to [4, Lemma 8] (see, also [50, Lemma 3.7]) with minor modifications, the following result is obtained.
Lemma 3.4
For \(r>0\), there exists an equivalent norm \(\Vert \cdot \Vert _{r}^{*}\) on \(C_{\tau }^{+}\) such that the solution map \({\widehat{W}}(t):=z_t\) of model (2.4) satisfies \(\kappa \left( {\widehat{W}}(t)B\right) \le e^{-rt}\kappa (B)\), \(t>0\), where \(\kappa \) is the Kuratowski measure of noncompactness in \(\left( C_{\tau }^{+},\, \Vert \cdot \Vert _{r}^{*}\right) \).
Lemma 3.5
Let \(\Pi (t,\,x;\,\varphi )\) be the solution of model (2.4) with \(\Pi _0=\varphi \in C_{\tau }^{++}\). If there is some \(t_0\ge 0\) satisfying \(I(t_0,\,\cdot ;\,\varphi )\not \equiv 0\), \(R(t_0,\,\cdot ;\,\varphi )\not \equiv 0\), \(B_H(t_0,\,\cdot ;\,\varphi )\not \equiv 0\) and \(B_L(t_0,\,\cdot ;\,\varphi )\not \equiv 0\), then \(I(t,\,x;\,\varphi )>0\), \(R(t,\,x;\,\varphi )>0\), \(B_H(t,\,x;\,\varphi )>0\) and \(B_L(t,\,x;\,\varphi )>0\) for \(t>t_0\) and \(x\in {\overline{\Omega }}\). There holds \(S(t,\,x;\,\varphi )>0\) and \(V(t,\,x;\,\varphi )>0\) for \(t>0\) and \(x\in {\overline{\Omega }}\), \(\lim \nolimits _{t\rightarrow +\infty }\inf S(t,\,x;\,\varphi )\ge \vartheta \) and \(\lim \nolimits _{t\rightarrow +\infty }\inf V(t,\,x;\,\varphi )\ge \vartheta \) uniformly for \(x\in {\overline{\Omega }}\), where \(\vartheta >0\) is a \(\varphi \)-independent constant.
Proof
Let
From model (2.4), one gets
Obviously, if there is some \(t_0\ge 0\) satisfying \(I(t_0,\,\cdot ;\,\varphi )\not \equiv 0\), \(R(t_0,\,\cdot ;\,\varphi )\not \equiv 0\), \(B_H(t_0,\,\cdot ;\,\varphi )\not \equiv 0\) and \(B_L(t_0,\,\cdot ;\,\varphi )\not \equiv 0\), then \(I(t,\,x;\,\varphi )>0\), \(R(t,\,x;\,\varphi )>0\), \(B_H(t,\,x;\,\varphi )>0\) and \(B_L(t,\,x;\,\varphi )>0\) for \(t>t_0\) and \(x\in {\overline{\Omega }}\).
From Theorem 3.2, there is a constant \(B>0\) such that \(I(t,\,x;\,\varphi )\le B\), \(\forall t>0,\) \(x\in {\overline{\Omega }}\). Assume that \(v(t,\,x;\,\varphi )\) is the solution of
It follows that
Hence, we obtain
uniformly for \(x\in {\overline{\Omega }}\), where \(v^*(t,\,x)\) is the unique positive \(\omega \)-periodic solution of model (3.7).
From the first two equations of model (2.4), we have
Consider
Denote \(e={\overline{\beta }}_h B+{\overline{\beta }}_H+{\overline{\beta }}_L\). We easily find that there is a vector with positive elements
such that
and
This indicates that for any \(0<m\le 1\), \(m \kappa \) is a lower solution of model (3.8). The comparison principle implies that solutions of model (3.8) are uniformly bounded. Thus, there is a constant \({\underline{B}}>0\) such that \(S(t,\,x;\,\varphi )> {\underline{B}}\) and \(V(t,\,x;\,\varphi )> {\underline{B}}\), \(\forall t>0,\) \(x\in {\overline{\Omega }}\). Assume that \(u(t,\,x;\,\varphi )\) is the solution of
Hence, we obtain \( \liminf _{t\rightarrow +\infty }V(t,\,x;\,\varphi )\ge \vartheta _2:=\inf _{t\in [0,\omega ],\,x\in {\overline{\Omega }}}u^*(t,\,x) \) uniformly for \(x\in {\overline{\Omega }}\), where \(u^*(t,\,x)\) is the unique positive \(\omega \)-periodic solution of model (3.9). Taking \(\vartheta =\min \{\vartheta _1,\,\vartheta _2\}\), we then complete the proof. \(\square \)
Let
Then
For \(\varphi \in \mathbb {C}_0\), it follows from Lemma 3.5 that \(I(t,\,x;\,\varphi )>0\), \(B_H(t,\,x;\,\varphi )>0\) and \(B_L(t,\,x;\,\varphi )>0\) for \(t>0\) and \(x\in {\overline{\Omega }}\). Then \(W^n(\mathbb {C}_0)\subset \mathbb {C}_0\) for \(n\in \mathbb {N}\) and \(W^n=W(n\omega )\). In view of Theorem 3.2, \(W_{\omega }: C_{\tau }^{++}\rightarrow C_{\tau }^{++}\) admits a global attractor in \(C_{\tau }^{++}\).
Lemma 3.6
If \(\mathscr {R}_0>1\), there is a \(\delta ^*>0\) such that for \(\varphi \in \mathbb {C}_0\), the solution semiflow of model (2.4) satisfies
where \(\mathbb {Q}=\left( S_{0}^*,V_{0}^*,\,{\widehat{0}},0,\,{\widehat{0}},\,{\widehat{0}}\right) \), \(S^*_{0}(\theta ,\,\cdot )=S^*(\theta ,\,\cdot )\), \(V^*_{0}(\theta ,\,\cdot )=V^*(\theta ,\,\cdot )\) and \({\widehat{0}}(\theta ,\,\cdot )=0\) for \(\theta \in [-\tau ,\,0].\)
Proof
Consider the following system with a parameter \(\delta >0\):
For \(\varphi \in C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \), let \(q^{\delta }(t,\,x;\,\varphi )=\left( q^{\delta }_{3}(t,\,x;\,\varphi ), \,q^{\delta }_{5}(t,\,x;\,\varphi ),\,q^{\delta }_{6}(t,\,x;\,\varphi )\right) \) be the unique solution of model (3.10) with \(q^{\delta }_{0}(\varphi )(\theta ,\,x)=\varphi (\theta ,\,x)\) for \(\theta \in [-\tau ,\,0]\) and \(x\in {\overline{\Omega }}\), where
Assume that \(\widehat{\mathbb {P}}_{\delta }:C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \rightarrow C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \) is the Poincaré map of model (3.10), that is, \(\widehat{\mathbb {P}}_{\delta }(\varphi )=q_{\omega }^{\delta }(\varphi )\) for \(\varphi \in C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \). Due to \(\mathop {\lim }\nolimits _{\delta \rightarrow 0}r(\widehat{\mathbb {P}}_{\delta })=r(\widehat{\mathbb {P}})>1\), it follows that \(r(\widehat{\mathbb {P}}_{\delta })>1\) by fixing a small enough number \(\delta >0\). By fixing \(\delta >0\), there is a \(\delta ^*>0\) satisfying \(\Vert W(t)\varphi -W(t)\mathbb {Q}\Vert <\delta \) when \(\Vert \varphi -\mathbb {Q}\Vert <\delta ^*\) for \(t\in \left[ 0,\,\omega \right] \).
By proof of contradiction, we assume that \(\mathop {\limsup }\nolimits _{n\rightarrow +\infty }\Vert W^n(\varphi _0)-\mathbb {Q}\Vert < \delta ^*\) for some \(\varphi _0 \in \mathbb {C}_0\). Thus, there exists \(n_1\ge 1\) such that \(\Vert W^n(\varphi _0)-\mathbb {Q}\Vert < \delta ^*\) for \(n\ge n_1\). For \(t\ge n_1\omega \), letting \(t=n\omega +t^{1}\) with \(n=[t/\omega ]\), and \(t^{1}\in [0,\omega )\), one gets
and \( S(t,\,x;\,\varphi _0)>S^*(t,\,x)-\delta \,\text {,}\,V(t,\,x;\,\varphi _0)>V^*(t,\,x)-\delta \ \text {and}\ R(t,\,x;\,\varphi _0)<\delta , \) for \(t\ge n_1 \omega \) and \(x\in {\overline{\Omega }}\). Hence, we get
Since \(\Pi (t,\,x;\,\varphi _0)> 0\) for \(t>0\) and \(x\in {\overline{\Omega }}\), there is an \(\alpha _1>0\) satisfying
where \(q_{\delta }^{*}(t,\,x)\) is a positive \(\omega \)-periodic function such that \(e^{\varsigma _{\delta }t}q_{\delta }^{*}(t,\,x)\) is a solution of model (3.11), and \(\varsigma _{\delta }=\frac{\ln r(\widehat{\mathbb {P}}_{\delta })}{\omega }\). The comparison theorem yields \(\left( I(t,\,x;\,\varphi _0),\,B_H(t,\,x;\,\varphi _0),\,B_L(t,\,x;\,\varphi _0)\right) \ge \alpha _1 e^{\varsigma _{\delta }t}q_{\delta }^{*}(t,\,\cdot )\) for \(t\ge n_1\omega +\tau \) and \(x\in {\overline{\Omega }}.\) Since \(\varsigma _{\delta }>0\), then \(I(t,\,x;\,\varphi _0)\rightarrow +\infty \), \(B_H(t,\,x;\,\varphi _0)\rightarrow +\infty \) and \(B_L(t,\,x;\,\varphi _0)\rightarrow +\infty \) as \(t\rightarrow \infty \), which leads to a contradiction. \(\square \)
Theorem 3.7
Let \(\Pi (t,\,x;\,\varphi )\) be the solution of model (2.4) with \(\Pi _0=\varphi \in C_{\tau }^{++}\). Then, the following hold.
-
(i)
If \(\mathscr {R}_0<1\), the infection-free \(\omega \)-periodic solution \(E_0\) of model (2.4) is globally attractive.
-
(ii)
If \(\mathscr {R}_0>1\), there exists at least one endemic \(\omega \)-periodic solution \((S^*(t,\,x),\, V^*(t,\,x),\, I^*(t,\,x),\,R^*(t,\,x),\, B_H^*(t,\,x),\,B_L^*(t,\,x))\) of model (2.4), and there is a \({\check{\varrho }}>0\) such that for \(\varphi \in C_{\tau }^{++}\) with \(\varphi _3(\cdot ,\,0)\not \equiv 0\), \(\varphi _5(\cdot ,\,0)\not \equiv 0\) and \(\varphi _6(\cdot ,\,0)\not \equiv 0\), we have \( \liminf _{t\rightarrow +\infty }\Big (S(t,\,x;\,\varphi ),\, V(t,\,x; \,\varphi ),\, I(t,\,x;\,\varphi ),\,R(t,\,x;\,\varphi ),\, B_H(t,\,x;\,\varphi ),\,B_L(t,\,x;\,\varphi ) \Big ) \ge ({\check{\varrho }},\,{\check{\varrho }},\,{\check{\varrho }},\,{\check{\varrho }},\, {\check{\varrho }},\,{\check{\varrho }}), \) uniformly for \(x\in {\overline{\Omega }}\).
Proof
(i) If \(\mathscr {R}_0<1\), then \(r\left( \widehat{\mathbb {P}}\right) <1\), and \(\varsigma =\frac{\ln r\left( \widehat{\mathbb {P}}\right) }{\omega }<0\). Consider the following system with a parameter \(\varepsilon >0\):
For \(\psi \in C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \), let \(q^{\varepsilon }(t,\,x;\,\psi )=\left( q^{\varepsilon }_{3}(t,\,x;\,\psi ), \,q^{\varepsilon }_{5}(t,\,x;\,\psi ),\,q^{\varepsilon }_{6}(t,\,x;\,\psi )\right) \) be the unique solution of model (3.12) with \(q_0^{\varepsilon }(\psi )=\psi (\theta ,\,x)\) for \((\theta ,\,x)\in [-\tau ,\,0]\times {\overline{\Omega }}\), where
Assume that \(\widehat{\mathbb {P}}_{\varepsilon }: C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \rightarrow C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \) is the Poincaré map of model (3.12), that is, \(\widehat{\mathbb {P}}_{\varepsilon }(\psi )=q_{\omega }^{\varepsilon }(\psi )\) for \(\psi \in C\left( [-\tau ,\,0],\,\mathbb {M}^+\right) \). Since \(\mathop {\lim }\nolimits _{\varepsilon \rightarrow 0}r(\widehat{\mathbb {P}}_{\varepsilon })=r(\widehat{\mathbb {P}})<1\), there is a sufficiently small number \(\varepsilon >0\) satisfying \(r(\widehat{\mathbb {P}}_{\varepsilon })<1\). Similar to the arguments of those in [4, Lemma 5] (see also, [50, Lemma 3.5]), we can show that there is a positive \(\omega \)-periodic function \(q_{\varepsilon }^*(t,\,x)\) such that \(q^{\varepsilon }(t,\,x)=e^{\varsigma _{\varepsilon }t}q_{\varepsilon }^*(t,\,x)\), which is a solution of model (3.12), where \(\varsigma _{\varepsilon }=\frac{\ln r(\widehat{\mathbb {P}}_{\varepsilon })}{\omega }<0\). For the fixed \(\varepsilon >0\), there is a sufficiently large integer \(n_2>0\) satisfying \(n_2\omega \ge \tau ,\) \(S(t,\,x)\le S^*(t,\,x)+\varepsilon \) and \(V(t,\,x)\le V^*(t,\,x)+\varepsilon \) for \(t\ge n_2\omega -\tau \) and \(x\in {\overline{\Omega }}\). Consider
Then, for any given \(\varphi \in C_{\tau }^{++}\), there is some \(\alpha _2>0\) such that the solution of (3.13) satisfies
Then, the comparison principle yields \( (I(t,\,x;\,\varphi ),\,B_{H}(t,\,x;\,\varphi ),\,B_{L}(t,\,x;\,\varphi ))\le \alpha _2 e^{\varsigma _{\varepsilon }t}q_{\varepsilon }^{*}(t,\,\cdot ),\ t\ge n_2\omega ,\ x\in {\overline{\Omega }}. \) Hence,
uniformly for \(x\in {\overline{\Omega }}\). Using an analogous argument to [4, Theorem (i)] (see, also [50, Theorem 3.10 (i)]), we can show that \(\mathop {\lim }\nolimits _{t\rightarrow +\infty }S(t,\,x;\,\varphi )=S^*(t,\,x)\) and \(\mathop {\lim }\nolimits _{t\rightarrow +\infty }V(t,\,x;\,\varphi )=V^*(t,\,x)\) uniformly for \(x\in {\overline{\Omega }}\). Hence,
This completes the proof of the first conclusion. We next prove the second conclusion.
(ii) If \(\mathscr {R}_0>1\), then \(r(\widehat{\mathbb {P}})>1\), and \(\varsigma =\frac{\ln r(\widehat{\mathbb {P}})}{\omega }>0\). Let \( M_{\partial }:=\left\{ \varphi \in \partial \mathbb {C}_0:\, W^n(\varphi )\in \partial \mathbb {C}_0,\ n\in \mathbb {N} \right\} , \) and \(\omega (\varphi )\) be the omega limit set of the orbit \(\Pi ^{+}(\varphi )=\left\{ W^n(\varphi ):\, \forall n\in \mathbb {N} \right\} \). For any given \(\psi \in M_{\partial }\), we see that \(W^n(\psi )\in \partial \mathbb {C}_0\), and either \(I(n \omega ,\,\cdot ;\, \psi )\equiv 0\) or \(B_H(n \omega ,\,\cdot ;\, \psi )\equiv 0\) or \(B_L(n \omega ,\,\cdot ;\, \psi )\equiv 0\). For \(t\ge 0\), either \(I(t,\,\cdot ;\, \psi )\equiv 0\) or \(B_H(t,\,\cdot ;\, \psi )\equiv 0\) or \(B_L(t,\,\cdot ;\, \psi )\equiv 0\). If \(B_H(t,\,\cdot ;\,\psi )\equiv 0\) for \(t\ge 0\), then \(I(t,\,\cdot ;\, \psi )\equiv 0\). Hence, \(\lim _{t\rightarrow +\infty }R(t,\,x;\,\psi )=0\) and \(\lim _{t\rightarrow +\infty }B_L(t,\,x;\,\psi )=0\) uniformly for \(x\in {\overline{\Omega }}\). Thus, S and V equations of model (2.4) are asymptotic to (3.5). Then, \(\lim _{t\rightarrow +\infty }S(t,\,x;\,\psi )=S^*(t,\,x)\) and \(\lim _{t\rightarrow +\infty }V(t,\,x;\,\psi )=V^*(t,\,x)\) uniformly for \(x\in {\overline{\Omega }}\). If \(B_H(t_0,\,\cdot ;\, \psi )\not \equiv 0\) for some \(t_0\ge 0\), from Lemma 3.5, we have \(B_H(t,\,\cdot ;\, \psi )>0\), \(t\ge t_0\), and further get that \(B_L(t,\,\cdot ;\, \psi )\equiv 0\) or \(I(t,\,\cdot ;\, \psi )\equiv 0\), \(t\ge t_0\). For the case \(I(t,\,\cdot ;\, \psi )\equiv 0\), \(t\ge t_0\), then \(\lim _{t\rightarrow +\infty }R(t,\,x;\,\psi )=0\), and \(\lim _{t\rightarrow +\infty }B_H(t,\,x;\,\psi )=0\), \(\lim _{t\rightarrow +\infty }B_L(t,\,x;\,\psi )=0\) uniformly for \(x\in {\overline{\Omega }}\). It follows that \(\lim _{t\rightarrow +\infty }S(t,\,x;\,\psi )=S^*(t,\,x)\) and \(\lim _{t\rightarrow +\infty }V(t,\,x;\,\psi )=V^*(t,\,x)\) uniformly for \(x\in {\overline{\Omega }}\). If \(I(t_1,\,\cdot ;\, \psi )\not \equiv 0\) for some \(t_1>t_0\ge 0\), from Lemma 3.5, we have \(I(t,\,\cdot ;\, \psi )>0\), \(t\ge t_1\), and further get that \(B_L(t,\,\cdot ;\, \psi )\equiv 0\), and thus \(B_H(t,\,\cdot ;\, \psi )\equiv 0\). From the fifth equation of model (2.4), we have \(I(t,\,\cdot ;\, \psi )\equiv 0\) for \(t\ge t_1\), which leads to a contradiction. Hence, \(\omega (\psi )=\mathbb {Q}\) for any \(\psi \in M_{\partial }\), and \(\mathbb {Q}\) cannot form a cycle for W in \(\partial \mathbb {C}_0\).
Lemma 3.6 reveals that \(\mathbb {Q}\) is an isolated invariant set for W in \(C_{\tau }^{++}\), and \(W^{s}(\mathbb {Q})\cap \mathbb {C}_0=\varnothing \). It follows from [59, Theorem 1.3.1 and Remark 1.3.1] that \(W:C_{\tau }^{++}\rightarrow C_{\tau }^{++}\) is uniformly persistent for \((\mathbb {C}_0,\, \partial \mathbb {C}_0)\). That is, there is \(\eta >0\) such that
Since \(W^n=W(n\omega )\) is compact for an integer n with \(n\omega >\tau \), W is asymptotically smooth on \(C_{\tau }^{++}\). Theorem 3.2 reveals that W admits a global attractor on \(C_{\tau }^{++}\). According to [29, Theorem 3.7], W admits a global attractor \(D_0\) in \(\mathbb {C}_0.\) Note that \(D_0=W(D_0)=W(\omega )(D_0)\). We have \(\varphi _3(0,\,\cdot )>0\), \(\varphi _5(0,\,\cdot )>0\) and \(\varphi _6(0,\,\cdot )>0\) for \(\varphi \in D_0\). Let \(F_0:=\bigcup _{t\in [0,\,\omega ]}W(t)D_0\). In view of [59, Theorem 3.1.1], we deduce that \(F_0\subset \mathbb {C}_0\) and \(\mathop {\lim }\nolimits _{t\rightarrow +\infty }d(W(t)\varphi ,\, F_0)=0\) for \(\varphi \in \mathbb {C}_0\), where \(d(W(t)\varphi ,\, F_0)=\sup _{x\in W(t)\varphi }d(x,\,F_0)\). Define a continuous function \(\mathscr {P}:\,C_{\tau }^{++}\rightarrow \mathbb {R}^+\) by
Notice that \(F_0\) is a compact subset of \(\mathbb {C}_0\), we obtain \(\inf _{\varphi \in F_0}\mathscr {P}(\varphi )=\min _{\varphi \in F_0}\mathscr {P}(\varphi )>0\). Thus, there is a \({\check{\rho }}^*>0\) such that
Furthermore, there exists a \({\check{\rho }} \in (0,\,{\check{\rho }}^*)\) such that
In what follows, we demonstrate that model (2.4) has at least one endemic \(\omega \)-periodic solution. For a given real number \(r>0\), from Lemma 3.4, we equip \(\mathbb {C}\) with an equivalent norm \(\Vert \cdot \Vert _{r}^{*}\). Define
and
Let \({\widehat{W}}={\widehat{W}}(\omega )\). By the uniqueness of solutions, \({\widehat{W}}\) is point dissipative and \(\rho \)-uniformly persistent with \(\rho (\psi )=d\left( \psi ,\, \partial {\widetilde{W}}_0\right) \), and \({\widehat{W}}^n={\widehat{W}}(n\omega )\) is compact for \(n\omega >\tau \). By Lemma 3.4, \({\widehat{W}}\) is k-condensing. Thus, by [29, Theorem 4.5], model (3.1) has an \(\omega \)-periodic solution \( \big ( \Pi _1^*(t,\,\cdot ),\,\Pi _2^*(t,\,\cdot ),\,\Pi _3^*(t,\,\cdot ),\, \Pi _4^*(t,\,\cdot ),\,\Pi _5^*(t,\,\cdot ),\, \Pi _6^*(t,\,\cdot )\big ) \) with \(\left( \Pi _{1t}^{*},\,\Pi _{2t}^{*},\,\Pi _{3t}^{*},\,\Pi _{4t}^{*},\, \Pi _{5t}^{*},\,\Pi _{6t}^{*}\right) \in {\widetilde{W}}_0\). Let \(S_{0}^{*}=\Pi _{10}^{*}\), \(V_{0}^{*}=\Pi _{20}^{*}\), \(I_{0}^{*}=\Pi _{30}^{*}\), \(R_{0}^{*}=\Pi _{40}^{*}\), \(B_{H_0}^{*}=\Pi _{50}^{*}\) and \(B_{L_0}^{*}=\Pi _{60}^{*}\). The uniqueness of solutions yields that \((S^*(t,\,\cdot ),\,V^*(t,\,\cdot ),\, I^*(t,\,\cdot ),\,R^*(t,\,\cdot ), B_{H}^{*}(t,\cdot ),B^*_L(t,\cdot ))\) is a strictly positive periodic solution of model (2.4) . \(\square \)
4 Global stability of the endemic steady state
In the case where all the parameters of model (2.4) are positive constants, model (2.4) reduces to the following autonomous reaction–diffusion equations in the absence of nonlocal time delay:
Obviously, model (4.1) always admits a disease-free steady state \(E_{0}\left( S_{0},\,V_{0},\,0,\,0,\,0,\,0\right) \), where
For model (4.1), we get
If \(\mathscr {R}_{0}> 1\), from Theorem 3.7, there exists at least an endemic steady state \(E^{*}\left( S^{*},\,V^{*},\,I^{*},\,R^{*},\,B_{H}^{*},\,B_{L}^{*}\right) \). We are concerned with the global stability of the endemic steady state of model (4.1), that will be proven by Lyapunov’s stability theorem [28].
Theorem 4.1
If \(\mathscr {R}_0> 1\), the endemic steady state \(E^{*}\) of model (4.1) is globally attractive.
Proof
Denote
Then, we can construct a Lyapunov function as follows:
Differentiate \(V_1\) with respect to t and evaluate the result along the solution of model (4.1). We obtain
Then, when \(\mathscr {R}_0> 1\) we know \(V_{1}^{'}< 0\) for \(\left( S\left( t,x\right) ,V\left( t,x\right) ,I\left( t,x\right) ,B_{H}\left( t,x\right) ,B_{L}\left( t,x\right) \right) \ne \left( S^{*}, V^{*}, I^{*}, B_{H}^{*},B_{L}^{*}\right) \). It follows from Lyapunov’s stability theorem in [28] that the endemic steady state \(E^{*}\) of model (4.1) is globally attractive. \(\square \)
5 Numerical simulations
In this section, we carry out numerical simulations to discuss the influence of spatial mobility, spatial heterogeneity and the seasonality on the transmission of cholera.
According to the report of World Health Organization for cholera [9], the first round of oral cholera vaccination campaign targeting 650,000 people for the age of 1 year and above was started on 22 June and completed on 30 June 2019 in Somalia. Hence, to make better understandings on the transmission dynamics of historical human infection with Vibrio cholerae in Somalia after June 30, model (2.4) becomes:
in which the number of vaccinated individuals at the initial time equals 650,000. The values of initial variables and parameters of model (5.1) are shown in Table 2.
5.1 Numerical computation of \(\mathscr {R}_0\)
For any \(\lambda >0\), we consider the following linear system:
subject to the zero-flux boundary conditions. Assume that \(Q(t,s,\lambda )\) \((t\ge s)\) is the evolution operator on \(C([-\tau ,0],\mathbb {M})\) for model (5.2). Applying arguments similar to those in [58, Theorem 2.2] (see, also [26, Theorem 3.8]), one gets the following result.
Lemma 5.1
If \(\mathscr {R}_0>0\), then \(\mathscr {R}_0=\lambda \) is the unique solution of \(r(Q(\omega ,0,\lambda ))=1.\)
Time variation of I(t, x), \(B_H(t, x)\) and \(B_L(t, x)\) with \(\xi (t,x)=12\times {\overline{\xi }}\times (1+0.8 \cos (8\pi x))\times (1+0.5 \sin (2\pi t))\), \(\beta _h(t,x)=180\times {\overline{\beta }}_h\times (1+0.5\sin (2\pi t))\), \(\beta _H(t,x)=180\times {\overline{\beta }}_H\times (1+0.5\sin (2\pi t))\), \(\beta _L(t,x)=180\times {\overline{\beta }}_L\times (1+0.5\sin (2\pi t))\)
Time variation of I(t, x), \(B_H(t, x)\) and \(B_L(t, x)\) with \(\xi (t,x)=0.5\times {\overline{\xi }}\times (1+0.8 \cos (8\pi x))\times (1+0.5 \sin (2\pi t))\), \(\beta _h(t,x)=0.05\times {\overline{\beta }}_h\times (1+0.5\sin (2\pi t))\), \(\beta _H(t,x)=0.05\times {\overline{\beta }}_H\times (1+0.5\sin (2\pi t))\), \(\beta _L(t,x)=0.05\times {\overline{\beta }}_L\times (1+0.5\sin (2\pi t))\)
The effects of spatial heterogeneous and time periodictiy on \(\mathscr {R}_0\). a \(\xi (t,x) = {\overline{\xi }}\times \left( 1+0.8c\cos \left( 8\pi x\right) \right) \times \left( 1+0.5\sin \left( 2\pi t\right) \right) \), \(\beta _{h}(t,x)= {\overline{\beta }}_{h}\times \left( 1+0.5\cos \left( 2\pi t\right) \right) \), \(\beta _{H}(t,x)={\overline{\beta }}_{H}\times \left( 1+0.5\cos \left( 2\pi t\right) \right) \), \(\beta _{L}(t,x)= {\overline{\beta }}_{L}\times \left( 1+0.5\cos \left( 2\pi t\right) \right) \). b \(\xi (t,x) = {\overline{\xi }}\times \left( 1+0.8c\sin \left( 8\pi x\right) \right) \times \left( 1+0.5\sin \left( 2\pi t\right) \right) \), \(\beta _{h}(t,x)= {\overline{\beta }}_{h}\times \left( 1+0.5\sin \left( 2\pi t\right) \right) \), \(\beta _{H}(t,x)={\overline{\beta }}_{H}\times \left( 1+0.5\sin \left( 2\pi t\right) \right) \), \(\beta _{L}(t,x)= {\overline{\beta }}_{L}\times \left( 1+0.5\sin \left( 2\pi t\right) \right) \)
According to Lemma 5.1, we can use the standard bisection method to obtain the numerical solution \(\lambda \) to \(r(Q(\omega ,0,\lambda ))=1\), and thus, \(\mathscr {R}_0=\lambda .\) Note that for each \(\lambda >0\), \(r(Q(\omega ,0,\lambda ))\) can be computed numerically via the algorithm developed in [26, Lemma 2.5].
5.2 Long-term behaviour
We assume that \(\beta _{h}\), \(\beta _{H}\) and \(\beta _{L}\) represent, respectively, the transmission coefficient of contact with infected individuals, hyperinfectious vibrios and hypoinfectious vibrios. Denote by \({\overline{f}}\) the mean value of parameter f, where f is one of A, \(\mu \), d, \(\beta _{h}\), \(\beta _{H}\), \(\beta _{L}\), \(k_H\), \(k_L\), \(\varpi \), \(\sigma \), \(\varUpsilon \), \(\xi \), \(\chi \), \(\delta _{L}\). For the sake of simplicity, we assume that the region is a cross-sectional area of the 1 mm \(\times \) 1 mm thin wire and \(\Omega =\left( 0,1\right) \). We assume that the diffusion coefficients of S, V, I, R, \(B_H\), \(B_L\), are, respectively, \(D_1=0.09648\) mm\(^{2}\) day\(^{-1}\), \(D_2=0.05\) mm\(^{2}\) day\(^{-1}\), \(D_3=0.08\) mm\(^{2}\) day\(^{-1}\), \(D_4=0.08\) mm\(^{2}\) day\(^{-1}\), \(D_5=0.17\) mm\(^{2}\) day\(^{-1}\), \(D_6=0.11\) mm\(^{2}\) day\(^{-1}\). Assume that
and other parameters are fixed as the mean values. We find that the solution of model (5.1) converges to a positive periodic steady state (see Fig. 2) and the disease is persistent. We take
and other parameters are fixed as the mean values. We observe that the solution of model (5.1) converges to zero (see Fig. 3), and the disease vanishes.
5.3 Effects of parameters on \(\mathscr {R}_0\)
It is well known that \(\mathscr {R}_0\) plays an important role in the prevention, intervention and control on the spread of the cholera transmission, which determines transmission risk whether or not the disease persists. However, it is difficult to theoretically study the influence of environmental heterogeneity on the transmission risk \(\mathscr {R}_0\) in the periodic system. We now illustrate the effects of spatial heterogeneity and temporal periodicity on \(\mathscr {R}_0\) numerically. Let
We find that \(\mathscr {R}_0\) increases as heterogeneous coefficient c increases in the periodic system (see Fig. 4a). This implies that spatial heterogeneity may increase transmission risk \(\mathscr {R}_0\) in the periodic system, and we may underestimate \(\mathscr {R}_0\) if the spatial averaged system is used. Let
We also find that \(\mathscr {R}_0\) increases as heterogeneous coefficient c increases in the periodic system (see Fig. 4b). This implies that spatial heterogeneity may increase transmission risk \(\mathscr {R}_0\) in the periodic system, and we may underestimate \(\mathscr {R}_0\) if the spatial averaged system is used. Figure 5 shows that decreasing the transmission coefficient of contact with infected individuals, the transmission coefficient of contact with hyperinfectious vibrios and the transmission coefficient of contact with hypoinfectious vibrios can reduce \(\mathscr {R}_0\). Figures 6 and 7 show that increasing the vaccination rate of susceptible individuals \(\varpi \) and vaccine protective efficacy \(1-\sigma \) can reduce \(\mathscr {R}_0\) and decrease the number of infected individuals, which has a positive impact on cholera control.
The effects of parameters on \(\mathscr {R}_0\). a The effect of the transmission coefficient of contact with infected individuals on \(\mathscr {R}_0\). b The effect of the transmission coefficient of contact with hyperinfectious vibrios on \(\mathscr {R}_0\). c The effect of the transmission coefficient of contact with hypoinfectious vibrios on \(\mathscr {R}_0\)
a The effects of the vaccination rate of susceptible individuals on \(\mathscr {R}_0\). b The effects of the vaccination rate of susceptible individuals on infected individuals with \(\xi (t,x)=12\times \overline{\xi }\times (1+0.8 \cos (8\pi x))\times (1+0.5 \sin (2\pi t))\), \(\beta _h(t,x)=180\times \overline{\beta }_h\times (1+0.5\sin (2\pi t))\), \(\beta _H(t,x)=180\times \overline{\beta }_H\times (1+0.5\sin (2\pi t))\), \(\beta _L(t,x)=180\times \overline{\beta }_L\times (1+0.5\sin (2\pi t))\)
a The effects of the protective efficacy of vaccine on \(\mathscr {R}_0\). b The effects of the protective efficacy of vaccine on infected individuals with \(\xi (t,x)=12\times {\overline{\xi }}\times (1+0.8 \cos (8\pi x))\times (1+0.5 \sin (2\pi t))\), \(\beta _h(t,x)=180\times {\overline{\beta }}_h\times (1+0.5\sin (2\pi t))\), \(\beta _H(t,x)=180\times {\overline{\beta }}_H\times (1+0.5\sin (2\pi t))\), \(\beta _L(t,x)=180\times {\overline{\beta }}_L\times (1+0.5\sin (2\pi t))\)
6 Conclusion
In this paper, we developed a time periodic reaction–diffusion equation model with latent period and explored the multiple effects of spatial mobility, spatial heterogeneity and the seasonality on the transmission of cholera. We first introduced the basic reproduction number \(\mathscr {R}_0\) and then discussed the threshold dynamics in terms of \(\mathscr {R}_0\). It has shown that the infection-free \(\omega \)-periodic solution of model (2.4) is globally attractive if \(\mathscr {R}_0<1\), while there is at least one endemic \(\omega \)-periodic solution and the disease is uniformly persistent. In the case where all the parameters are constants, we investigated the global attractivity of the endemic steady state by using Lyapunov functionals when \(\mathscr {R}_0>1\). Finally, a case study of the cholera outbreak in Somalia was presented numerically. Note that in this paper we only studied the global stability of the endemic steady state in the case where all coefficients are constants. In [12, 13, 39], Cui et al. discussed asymptotic profiles of endemic steady states for the epidemic models in spatially heterogeneous case. In [53], Wu and Zou discussed profiles of a diffusive host-pathogen model with different diffusion rates. However, to the best of our knowledge, all these methods cannot be directly applied to time periodic reaction–diffusion equation models with latent period. We leave these interesting problems for further investigations.
It is well known that \(\mathscr {R}_0\) plays an important role in the prevention, intervention and control on the spread of the cholera transmission, which determines transmission risk whether or not the disease persists. In the current work, we defined the basic reproduction number as the spectral radius of the next-generation infection operator. Unfortunately, we could not derive a clear formula of \(\mathscr {R}_0\) if the parameters are spatially and temporally heterogeneous. From the numerical computations, we observed that environmental heterogeneity has an effect on the transmission risk \(\mathscr {R}_0\). Our results have suggested that it is possible to underestimate the transmission risk \(\mathscr {R}_0\) in the periodic system if the spatial averaged system is used, based on some experimental data.
In addition, we have observed that decreasing the transmission coefficient of contact with infected individuals, the transmission coefficient of contact with hyperinfectious vibrios and the transmission coefficient of contact with hypoinfectious vibrios can reduce the basic reproduction number \(\mathscr {R}_0\). We have also found that increasing the vaccination rate of susceptible individuals \(\varpi \) and vaccine protective efficacy \(1-\sigma \) can reduce the basic reproduction number \(\mathscr {R}_0\) and decrease the number of infected individuals, which has a positive impact on cholera control in the population.
References
Andrews, J., Basu, S.: Transmission dynamics and control of cholera in Haiti: an epidemic model. Lancet 377, 1248–1255 (2011)
Azman, A., Rudolph, K., Cummings, D., Lessler, J.: The incubation period of cholera: a systematic review. J. Infect. 66, 432–438 (2013)
Bacaër, N., Guernaoui, S.: The epidemic threshold of vector-borne diseases with seasonality. J. Math. Biol. 53, 421–436 (2006)
Bai, Z., Peng, R., Zhao, X.: A reaction–diffusion malaria model with seasonality and incubation period. J. Math. Biol. 77, 201–228 (2018)
Bai, N., Song, C., Xu, R.: Mathematical analysis and application of a cholera transmission model with waning vaccine-induced immunity. Nonlinear Anal. RWA 58, 103–232 (2021)
Bertuzzo, E., Casagrandi, R., Gatto, M., Rodriguez-Iturbe, I., Rinaldo, A.: On spatially explicit models of cholera epidemics. J. R. Soc. Interface 7, 321–333 (2010)
Capasso, V., Maddalena, L.: Convergence to equilibrium states for a reaction–diffusion system modeling the spatial spread of a class of bacterial and viral diseases. J. Math. Biol. 13, 173–184 (1981)
Capasso, V., Paveri-Fontana, S.: A mathematical model for the cholera epidemic in the European Mediterranean region. Rev. Epidemiol. Sante 27(1979), 121–132 (1973)
Cholera, Report of World Health Organization. Available from: http://www.emro.who.int/health-topics/cholera-outbre ak/cholera-outbreaks.html
Capone, F., Cataldis, V., Luca, R.: Influence of diffusion on the stability of equilibria in a reaction–diffusion system modeling cholera dynamic. J. Math. Biol. 71, 1107–1131 (2015)
Codeço, C.: Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect. Dis. 1(1), 1–14 (2001)
Cui, R., Lou, Y.: A spatial SIS model in advective heterogeneous environments. J. Differ. Equ. 261, 3305–3343 (2016)
Cui, R., Lam, K., Lou, Y.: Dynamics and asymptotic profiles of steady states of an epidemic model in advective environments. J. Differ. Equ. 263, 2343–2373 (2017)
Daners, D., Medina, K.: Abstract Evolution Equations, Periodic Problems and Applications, Pitman Research Notes in Mathematics Series, vol. 279. Longman Scientific & Technical, Harlow (1992)
Deimling, K.: Nonlinear Functional Analysis. Springer, Berlin (1985)
Diekmann, O., Heesterbeek, J., Metz, A.: On the definition and the computation of the basic reproduction ratio \(R_0\) in models for infectious diseases in heterogeneous population. J. Math. Biol. 28, 365–382 (1990)
Eisenberg, M., Shuai, Z., Tien, J., van den Driessche, P.: A cholera model in a patchy environment with water and human movement. Math. Biosci. 246, 105–112 (2013)
Friedman, A.: Partial Differential Equations of Parabolic Type. Prentice-Hall, Englewood Cliffs (1964)
Gatto, M., Mari, L., Rinaldo, A.: Leading eigenvalues and the spread of cholera. SIAM News 46(7), 1–2 (2013)
Gourley, S., Wu, J.: Delayed non-local diffusive systems in biological invasion and disease spread. In: Nonlinear Dynamics and Evolution Equations, vol. 48, pp. 137–200. American Mathematical Society, Providence (2006)
Hartley, D., Morris, J., Smith, D.: Hyperinfectivity: A critical element in the ability of V. cholerae to cause epidemics? PLoS Med. 3, 0063 (2006)
Hess, P.: Periodic-Parabolic Boundary Value Problems and Positivity, Pitman Research Notes in Mathematics, vol. 247. Longman Sci. Tech, Harlow (1991)
Islam, S., Rheman, S., Sharker, A., et al.: Climate change and its impact on transmission dynamics of cholera, Climate Change Cell, DoE, MoEF; Component 4B. CDMP, MoFDM, Dhaka (2009)
Lin, J., Xu, R., Tian, X.: Transmission dynamics of cholera with hyperinfectious and hypoinfectious vibrios: mathematical modelling and control strategies. Math. Biosci. Eng. 26, 4339–4358 (2019)
Liang, X., Zhao, X.: Asymptotic speeds of spread and traveling waves for monotone semiflows with applications. Commun. Pure Appl. Math. 60, 1–40 (2007)
Liang, X., Zhang, L., Zhao, X.: Basic reproduction ratios for periodic abstract functional differential equations (with application to a spatial model for Lyme disease). J. Dyn. Differ. Equ. 31, 1247–1278 (2019)
Lou, Y., Zhao, X.: A reaction–diffusion malaria model with incubation period in the vector population. J. Math. Biol. 62, 543–568 (2011)
Martcheva, M.: An Introduction to Mathematical Epidemilogy. Springer, New York (2015)
Magal, P., Zhao, X.: Global attractors and steady states for uniformly persistent dynamical systems. SIAM J. Math. Anal. 37, 251–275 (2005)
Martin, R., Smith, H.: Abstract functional differential equations and reaction–diffusion systems. Trans. Am. Math. Soc. 321, 1–44 (1990)
Mukandavire, Z., Liao, S., Wang, J., Gaff, H., Smith, D., Morris, J.G.: Estimating the reproductive numbers for the 2008–2009 cholera outbreaks in Zimbabwe. Proc. Natl. Acad. Sci. U.S.A. 108, 8767–8772 (2011)
Nelson, E., Harris, J., Morris, J., Calderwood, S., Camilli, A.: Cholera transmission: the host, pathogen and bacteriophage dynamics. Nat. Rev. Microbiol. 7, 693–702 (2009)
Population, Report of the website of Worldmeter. Available from: https://www.worldometers.info/popu-lation/
Posny, D., Wang, J.: Modelling cholera in periodic environments. J. Biol. Dyn. 8(1), 1–19 (2014)
Posny, D., Wang, J., Mukandavire, Z., et al.: Analyzing transmission dynamics of cholera with public health interventions. Math. Biosci. 264, 38–53 (2015)
Rinaldo, A., Bertuzzo, E., Mari, L., Righetto, L., Blokesch, M., Gatto, M., Casagrandi, R., Murray, M., Vesenbeckh, S.M., Rodriguez-Iturbe, I.: Reassessment of the 2010–2011 Haiti cholera outbreak and rainfall-driven multiseason projections. Proc. Natl. Acad. Sci. U.S.A. 109, 6602–6607 (2012)
Shuai, Z., Tien, J., van den Driessche, P.: Cholera models with hyperinfectivity and temporary immunity. Bull. Math. Biol. 74, 2423–2445 (2012)
Shuai, Z., van den Driessche, P.: Modeling and control of cholera on networks with a common water source. J. Biol. Dyn. 9(Suppl. 1), 90–103 (2015)
Song, P., Lou, Y., Xiao, Y.: A spatial SEIRS reaction–diffusion model in heterogeneous environment. J. Differ. Equ. 267, 5084–5114 (2019)
Thieme, H.: Spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity. SIAM J. Appl. Math. 70, 188–211 (2009)
Tian, X., Xu, R., Lin, J.: Mathematical analysis of a cholera infection model with vaccination strategy. Appl. Math. Comput. 361, 517–535 (2019)
Thieme, H., Zhao, X.: A non-local delayed and diffusive predator–prey model. Nonlinear Anal. RWA 2, 145–160 (2001)
Tian, J., Wang, J.: Global stability for cholera epidemic models. Math. Biosci. 232(1), 31–41 (2011)
Tien, J., Earn, D.: Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull. Math. Biol. 72(6), 1506–1533 (2010)
Tuite, A., Tien, J., Eisenberg, M., Earn, D., Ma, J., Fisman, D.: Cholera epidemic in Haiti, 2010-using a transmission model to explain spatial spread of disease and identify optimal control interventions. Ann. Intern. Med. 154(9), 593–601 (2011)
van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)
Wandiga, S.: Climate change and induced vulnerability to malaria and cholera in the Lake Victoria Region, AIACC Final Report, Project No. AF 91, The International START Secretariat, Washington, DC, USA (2006)
Wang, X., Gao, D., Wang, J.: Influence of human behavior on cholera dynamics. Math. Biosci. 267, 41–52 (2015)
Wang, J., Liao, S.: A generalized cholera model and epidemic–endemic analysis. J. Biol. Dyn. 6(2), 568–589 (2012)
Wang, W., Ma, W., Feng, Z.: Complex dynamics of a time periodic nonlocal and time-delayed model of reaction–diffusion equations for modeling CD4+ T cells decline. J. Comput. Appl. Math. 367, 112430 (2020)
Wang, X., Wang, J.: Analysis of cholera epidemics with bacterial growth and spatial movement. J. Biol. Dyn. 9, 233–261 (2015)
Wang, X., Zhao, X., Wang, J.: A cholera epidemic model in a spatiotemporally heterogeneous environment. J. Math. Anal. Appl. 468, 893–912 (2018)
Wu, Y., Zou, X.: Dynamics and profiles of a diffusive host–pathogen system with distinct dispersal rates. J. Differ. Equ. 264, 4989–5024 (2018)
Wu, J.: Theory and Applications of Partial Functional Differential Equations. Springer, New York (1996)
World Health Organization: Cholera vaccines: WHO position paper. Wkly. Epidemiol. Rec. 85, 117–128 (2010)
Yamazaki, K., Wang, X.: Global well-posedness and asymptotic behavior of solutions to a reaction–convection–diffusion cholera epidemic model. Discrete Contin. Dyn. Syst. Ser. B 21, 1297–1316 (2016)
Yamazaki, K., Wang, X.: Global stability and uniform persistence of the reaction–convection–diffusion cholera epidemic model. Math. Biosci. Eng. 14(2), 559–579 (2017)
Zhao, X.: Basic reproduction ratios for periodic compartmental models with time delay. J. Dyn. Differ. Equ. 29, 67–82 (2017)
Zhao, X.: Dynamical Systems in Population Biology, 2nd edn. Springer, New York (2017)
Zhou, X., Cui, J.: Modeling and stability analysis for a cholera model with vaccination. Math. Methods Appl. Sci. 34, 1711–1724 (2011)
Zhang, L., Wang, Z., Zhao, X.: Threshold dynamics of a time periodic reaction–diffusion epidemic model with latent period. J. Differ. Equ. 258, 3011–3036 (2015)
Acknowledgements
We are grateful to the editor and two anonymous referees for careful reading and valuable comments which led to improvements of our original manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is supported by the NNSF of China (11901360).
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhou, M., Wang, W., Fan, X. et al. Threshold dynamics of a reaction–diffusion equation model for cholera transmission with waning vaccine-induced immunity and seasonality. Z. Angew. Math. Phys. 73, 190 (2022). https://doi.org/10.1007/s00033-022-01829-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-022-01829-2
Keywords
- Cholera transmission model
- Seasonality
- Reaction–diffusion equation model
- Basic reproduction number
- Threshold dynamics