Abstract
A nonlocal and delayed cholera model with two transmission mechanisms in a spatially heterogeneous environment is derived. We introduce two basic reproduction numbers, one is for the bacterium in the environment and the other is for the cholera disease in the host population. If the basic reproduction number for the cholera bacterium in the environment is strictly less than one and the basic reproduction number of infection is no more than one, we prove globally asymptotically stability of the infection-free steady state. Otherwise, the infection will persist and there exists at least one endemic steady state. For the special homogeneous case, the endemic steady state is actually unique and globally asymptotically stable. Under some conditions, the basic reproduction number of infection is strictly decreasing with respect to the diffusion coefficients of cholera bacteria and infectious hosts. When these conditions are violated, numerical simulation suggests that spatial diffusion may not only spread the infection from high-risk region to low-risk region, but also increase the infection level in high-risk region.
Similar content being viewed by others

Avoid common mistakes on your manuscript.
1 Introduction and model formulation
Cholera is a severe infectious disease which threats a large population in the world. It was associated with the death of 50,000 refugees during the first month after 500,000-800,000 Rwandan refugees flew into Zaire in July, 1994 (Goma Epidemiology Group 1994). It caused “an extraordinary public health crisis" during the 2009 Zimbabwe outbreak (Koenig 2009). Form mid-October to late-December, 2011, cholera infected more than 170,000 people and killed more than 3,600 in Haiti (Dowell et al. 2011). Cholera is spread by Vibrio cholerae bacteria through two major transmission mechanisms: direct human-to-human infection via faecal-oral route; and indirect environment-to-human transmission from polluted aquatic reservoir (Miller et al. 1985; Mukandavire et al. 2011). The direct transmission is rare in the areas with good hygiene, but it contributes a significant proportion of cases in developing countries.
To understand the complex dynamics of cholera, one should consider the transmissions of pathogens among the human hosts and the environment (Nelson et al. 2009). Numerous cholera models incorporating both direct and indirect transmission routes have been developed and analyzed (Andrews and Basu 2011; Eisenberg et al. 2013; Hartley and J. G. M., and Smith, D. L. 2006; Joh et al. 2009; Mukandavire et al. 2011; Nelson et al. 2009; Tian and Wang 2011; Tien and Earn 2010). Most of these models were based on autonomous ordinary differential equations with constant parameters, and did not consider the spatial heterogeneity. This, however, may induce deficient and limited understanding of the spatial spread of cholera infection. As shown in Mukandavire et al. (2011); Tuite et al. (2011), the (local) basic reproduction numbers vary in 10 different regions in Zimbabwe and Haiti. In fact, spatial heterogeneity is universal due to the variance of temperature, humidity and resources at different locations. Therefore, it is important to consider spatial heterogeneity in cholera transmission, and construct a unified model that incorporates spatial variance in geographical environments, human activity and pathogen characteristics. Bertuzzo et al. (2010) introduced a spatial movement of the pathogen in cholera epidemic setting, and calculated the traveling speed of cholera wave in difference topologies. A host-pathogen model with a common diffusion on both susceptible and infected hosts but no diffusion on the pathogen was proposed in Wang et al. (2015), where threshold dynamics and bifurcation analysis was investigated. Wang et al. (2018) studied a reaction-convection-diffusion model with time-periodic coefficients and obtained the spatiotemporal dynamics of cholera transmission. In this paper, we will incorporate incubation period of cholera in the diffusions model with both direct and indirect transmissions. As remarked in Azman et al. (2013), it is important to consider incubation period in clinical practice and making decision for public health. Incubation period has been widely studied in many other infectious diseases such as dengue (Wang and Zhao 2011), HIV (Shu et al. 2013, 2018), and others. In the followings, we will propose an age-structure model and then derive an equivalent diffusion system with both time delay and nonlocal terms.
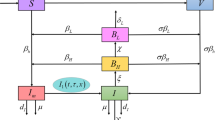
Assume that a human population lives in a bounded spatial habitat \(\Omega \) with a smooth boundary \(\partial \Omega \). Denote S(x, t), E(x, t), I(x, t) and R(x, t) as the densities of susceptible, exposed, infectious and recovered hosts at location x at time t, respectively, and B(x, t) measures the density of the bacteria in the contaminated environment at location x at time t. We further assume that a susceptible host becomes infected either by direct contact with infectious hosts or via contaminated environment with bacteria shed from infectious hosts. The second transmission mechanism does not involve direct contacts among the hosts and is thus referred to as the indirect transmission. Applying the standard SIR epidemic framework for the infection with the host population, we find the equations for susceptible and recovered populations
and the equation for the bacteria/vibrios density
where \(\nabla \) and \(\nabla \cdot \) are the gradient the divergence operators; \(\Lambda (x,S(x,t))\) is the growth rate function of susceptible hosts, which includes the influx (or, recruitment) and the natural death. The nonlinear functions f(S(x, t), I(x, t)) and g(S(x, t), B(x, t)) describe the direct (i.e., human-to-human) and indirect (i.e., environment-to-human) transmission rates, respectively. \(d_S(x)\), \(d_R(x)\) and \(d_B(x)\) are the diffusion coefficient of susceptible hosts, infectious hosts and bacteria, respectively. \(\gamma (x)\) is the recovery rate of infectious individuals, \(\mu _R(x)\) is the natural death rate of recovered hosts. \(\sigma (x)\) is the shedding rate of bacteria by infectious hosts, h(x, B(x, t)) denotes the growth rate of bacteria, and \(\mu _B(x)\) is the natural death rate of the bacteria. Here we consider a closed environment in the sense that Neumann (no-flux) boundary conditions are assumed for each of these four sub-population and bacteria.
To incorporate the latency into the model suitably, we let i(x, t, a) be the density of infected population at location x time t with infection age a, and propose the following structured population model with spatial diffusion
where \(d_i(x,a)>0\) is the diffusion rate at location x and with infection age a, and \(\mu (x,a)>0\) is the removal rate of infected population at location x and age a which combines natural and disease-induced death rates as well as recovery rate. We assume that the initial density i(x, 0, a) at any fixed location x is integrable for \(a\in \mathbb {R}_+\). Especially, \(i(x,0,\infty )=0\) for all \(x\in \Omega \). This assumption is biologically relevant because the age of infection cannot be infinitely large.
Let \(\tau \) be a cutoff age for the incubation period of the infected population, and assume the diffusion rate and mortality rate are stage-specific:
where \(d_E\), \(d_I\), \(\mu _E\) and \(\mu _I\) are continuous and positive functions on \({\bar{\Omega }}\). Now, we introduce
Given a fixed time t, we regard i(x, t, a) as the density function (up to a multiplicative constant) for the joint distribution of infected host population at location x and with infection age a. Moreover, E(x, t) and I(x, t) are proportional to the density functions for the marginal distributions of exposed and infectious host populations, respectively, at location x. It follows from (1.4) that
To solve the stage-structure model (1.4) along the characteristic line \(s=t-a\), we define \(u(x,t,s)=i(x,t,t-s)\) and rewrite (1.4) as
We treat s as a parameter and find the solution of the above equation:
where \(T_E(t)\) and \(T_I(t)\) are the \(C_0\) semigroups generated by \(\nabla \cdot (d_E\nabla )-\mu _E\) and \(\nabla \cdot (d_I\nabla )-\mu _I\), respectively, with Neumann boundary condition on \(\Omega \). Especially, we obtain
Let K(x, y, t) be the kernel function for the solution operator \(T_E(t)\). We can rewrite \(T_E(\tau )i(\cdot ,t-\tau ,0)\) as
Substituting this into the equations for E(x, t) and I(x, t) gives
where we have made use of the fact that \(i(x,t,\infty )=0\), which can be proved using the assumption \(i(x,0,\infty )=0\) and the formula \(i(x,t,s)=T_E(t)i(x,0,s-t)\) for large s. The above equations and the equations (1.1), (1.2) and (1.3) formulate a system of five reaction-diffusion equations for S, E, I, R, B. Since the equations of E and R can be decoupled from this system, we only need to study the equations for S, I, B. For convenience, we set \((d_1,d_2,d_3)=(d_S,d_I,d_B)\), \((\mu _2,\mu _3)=(\mu _I,\mu _B)\), \((u_1,u_2,u_3)=(S,I,B)\), and denote \(u_{i,-\tau }(x,t)=u_i(x,t-\tau )\) for \(i=1,2,3\). The equations (1.1), (1.6) and (1.3) can be rewritten as
for \(x\in \Omega \) and \(t>0\), where
for any \(\psi \in C({\bar{\Omega }})\). Motivated by the properties of the kernel function for the solution operator \(T_E(t)\), we generalize the above system in the sense that the kernel function is more general. For convenience, we still use the same notation but now \(K(x,y,\tau )\) is a general nonnegative kernel function satisfying the following assumption.
- \((\mathbf{H} _0)\):
-
For any \(\tau \ge 0\), \(\int _\Omega K(x,y,\tau )dy\) is continuous in \(x\in {\bar{\Omega }}\), \(\int _\Omega K(x,y,\tau )dx\) is continuous in \(y\in {\bar{\Omega }}\), and \(\int _\Omega K(x,y,\tau )\psi (y)dy>0\) for any \(x\in {\bar{\Omega }}\) and \(\psi \in C({\bar{\Omega }},\mathbb {R}_+)\) with \(\psi >0\). Moreover, there exists \(C_K(\tau )>0\) such that
$$\begin{aligned} \int _\Omega v(x)[\int _\Omega K(x,y,\tau )w(y)dy]dx\le C_K(\tau )\int _\Omega [v^2(x)+w^2(x)]dx, \end{aligned}$$(1.9)for any \(v,w\in C({\bar{\Omega }})\).
If \(K(x,y,\tau )\) is the kernel function for the solution operator \(T_E(t)\), then a standard energy estimate implies that the \(L^2\) norm of \(\int _\Omega K(\cdot ,y,\tau )w(y)dy=T_E(\tau )w\) is bounded by the \(L^2\) norm of w. This together with Cauchy inequality gives (1.9). In the rest of this paper, we will investigate the nonlocal delayed system (1.7) with general kernel function \(K(x,y,\tau )\) satisfying the assumption \((\mathbf{H} _0)\).
Let \(X=C({\bar{\Omega }},\mathbb {R}^3)\) be the Banach space equipped with the supremum norm \(\Vert \cdot \Vert _X\) and a nonnegative cone \(X^+=C(\bar{\Omega },\mathbb {R}_+^3)\). For any \(\tau \ge 0\), we also introduce the Banach space \(\mathcal {C}_\tau :=C([-\tau ,0], X)\) equipped with the supremum norm \(\Vert \phi \Vert :=\max \limits _{\theta \in [-\tau ,0]}\Vert \phi (\cdot ,\theta )\Vert _X\) and a nonnegative cone \(\mathcal {C}_\tau ^+:=C([-\tau ,0], X^+)\). It is readily seen that both \((X,X^+)\) and \((\mathcal {C}_\tau ,\mathcal {C}_\tau ^+)\) are strongly ordered (Smith 1995).
To be consistent with the derivation of (1.7), we impose the Neumann boundary condition
and nonnegative initial condition \(u(x,\theta )=\phi (x,\theta )\) for \(x\in \Omega \) and \(\theta \in [-\tau ,0]\), where \(\phi =(\phi _1,\phi _2,\phi _3)\in \mathcal {C}_\tau ^+\). Throughout this paper, we assume that the diffusion coefficients \(d_i(x)\) with \(i=1,2,3\), the shedding rate \(\sigma (x)\), and the death rates \(\mu _i(x)\) with \(i=2,3\) are positive and continuous functions on \({\bar{\Omega }}\). The only exception is in the section of numerical simulation where we will compare the steady state of diffusion system with that of diffusion-free system (\(d_i(x)=0\)). We also make the following biologically motivated assumptions.
- \((\mathbf{H} _1)\):
-
\(\Lambda \in C^{0,1}({\bar{\Omega }}\times \mathbb {R}_+)\) is decreasing with respect to the second variable. For each \(x\in {\bar{\Omega }}\), there exist a unique \({\bar{u}}_{1}(x)>0\) such that \(\Lambda (x, {\bar{u}}_{1}(x))=0.\) Moreover, \({{\bar{u}}}_1\in C(\bar{\Omega },\mathbb {R}_+)\).
- \((\mathbf{H} _2)\):
-
\(f, g\in C^1(\mathbb {R}_+\times \mathbb {R}_+)\) are strictly increasing with respect to both variables and concave down with respect to the second variable. Furthermore, \(f(v,w)=0\) (resp.\(g(v,w)=0\)) if and only if \(vw=0\).
- \((\mathbf{H} _3)\):
-
\(h\in C^{0,1}({\bar{\Omega }}\times \mathbb {R}_+)\) is nonnegative and strictly concave down with respect to the second variable. \(h(x,v)=0\) if and only if \(v=0\). For all \(x\in {\bar{\Omega }}\),
$$\begin{aligned} \lim _{v\rightarrow \infty }{h(x,v)\over v}<\mu _3(x). \end{aligned}$$(1.11)
Throughout this paper, we assume that \((\mathbf{H} _{0})\), \((\mathbf{H} _{1})\), \((\mathbf{H} _{2})\) and \((\mathbf{H} _{3})\) are satisfied. The rest of this paper is organized as follows. In Section 2, we obtain some preliminary results on well-posedness of our model system. In Section 3, we study the dynamics of a single environment model without shedding source. In Section 4, we define the basic reproduction number of infection. In Section 5, we investigate global dynamics of nonlocal and delayed cholera model. In Section 6, we consider a special case when all coefficients are spatial homogeneous. In Section 7, we conduct numerical computation and simulation for our model. In Section 8, we conclude this paper with a brief discussion.
2 Well-posedness
For each \(i=1,2,3\), let \(T_i(t)\) be the \(C_0\) semigroups generated by the second-order differential operator \(A_i=\nabla \cdot (d_i\nabla )-\mu _i\) with Neumann boundary condition, where, for convenience, we set \(\mu _1(x)=0\). It then follows from (Smith 1995, Corollary 7.2.3) that \(T_{i}(t)\) is compact and strongly positive for all \(t>0\) and \(i=1,2,3\). Moreover, \(T(t):=(T_{1}(t),T_{2}(t),T_{3}(t))\) is a \(C_{0}\) semigroup on X with an infinitesimal generator \(A=(A_1,A_2,A_3)\); see Pazy (1983). Given a vector-valued function \(u=(u_1,u_2,u_3)\in C({\bar{\Omega }}\times [-\tau ,\infty ),\mathbb {R}^3)\), we define \({\hat{u}}(t)=u(\cdot ,t+\cdot )\in \mathcal {C}_\tau ^+\) for \(t\ge 0\). The system (1.7) can be written as an abstract differential equation
with initial condition \({\hat{u}}(0)=\phi \in \mathcal {C}_\tau ^+\), where \(F=(F_1,F_2,F_3):\mathcal {C}_\tau ^+\rightarrow X\) is defined by
for any \(\varphi =(\varphi _1,\varphi _2,\varphi _3)\in \mathcal {C}_\tau ^+\). Recall that the kernel function \(K(x,y,\tau )\) is nonnegative and has a continuous total integral \(\int _\Omega K(x,y,\tau )dy\). It follows that \(K(\tau )\psi \in C({\bar{\Omega }})\) for any \(\psi \in C({\bar{\Omega }})\). This implies that \(F(\varphi )\in \mathbb {X}\) for any \(\varphi \in \mathcal {C}_\tau ^+\). Given any \(\varphi \in \mathcal {C}_\tau ^+\), there exists \(c>0\) such that \(f(\varphi _{1}(x,0),\varphi _{2}(x,0))+g(\varphi _{1}(x,0),\varphi _{3}(x,0))\le c\varphi _1(x,0)\) for all \(x\in \Omega \). It is readily seen that
By choosing \(\varepsilon >0\) sufficiently small, we have \(\varphi (\cdot ,0)+\varepsilon F(\varphi )\in X^+\). Especially,
By using (Martin and Smith 1990, Corollary 4) or (Smith 1995, Theorem 7.3.1), we establish the existence of the solution to the system (1.7). Note that \(F=(F_1,F_2,F_3)\) is mixed quasimontone, it then follows from the comparison principle that the solutions are nonnegative. To summarize, we obtain the following lemma on the existence and nonnegativity of the solution to system (1.7).
Lemma 2.1
For each initial condition \(\phi \in \mathcal {C}_\tau ^+\), the system (1.7) with Neumann boundary condition (1.10) admits a unique solution u(x, t) on a maximal interval of existence \([0,t_{max})\), and if \(t_{max}<\infty \), then \(\limsup \limits _{t\rightarrow t_{max}}\Vert u(\cdot ,t)\Vert _{\mathbb {X}}=\infty \). Moreover, \(u(x,t)\ge 0\) for all \(t\in [-\tau ,t_{max})\).
To show that \(t_{max}=\infty \), we need to prove that the solutions are bounded. First, we state the following lemma.
Lemma 2.2
Assume that the function \(\Lambda \) satisfies \((\mathbf{H} _1)\); namely, \(\Lambda \in C^{0,1}({\bar{\Omega }}\times \mathbb {R}_+)\) is decreasing with respect to the second variable; for each \(x\in {\bar{\Omega }}\), there exist a unique \({\bar{u}}_{1}(x)>0\) such that \(\Lambda (x, {\bar{u}}_{1}(x))=0\); and \({{\bar{u}}}_1\in C(\bar{\Omega },\mathbb {R}_+)\). For any positive and continuous diffusion coefficient \(d_1(x)\), the reaction-diffusion equation
admits a unique and strictly positive steady state \(w^*(x)\), which is globally asymptotically stable in \(C(\bar{\Omega },\mathbb {R}_+)\). Furthermore, if \(d(x)=d\) and \(\Lambda (x,v)=\Lambda (v)\) are independent of x, then \({{\bar{u}}}_1(x)={{\bar{u}}}_1\) is also independent of x and \(w^*(x)\equiv {{\bar{u}}}_1\).
Proof
A standard theory of parabolic equations (Pao 1992) gives existence of a compact semiflow \(\Psi _t\) for (2.1) in \(C({\bar{\Omega }},\mathbb {R}_+)\). Choose a pair of positive constants \(\varepsilon \) and M such that \(\varepsilon<{{\bar{u}}}_1(x)<M\) for all \(x\in \Omega \). By \((\mathbf{H} _1)\), we have \(\Lambda (x,\varepsilon )<0<\Lambda (x,M)\). Thus, the comparison theorem and maximum principle (Pao 1992) indicate that \(\Psi _t\) has a global compact attractor \(K\subset (\varepsilon , M)\). By (Hirsch 1984, Theorem 3.1), K contains a positive steady state \(w^*(x)\). A simple application of strong maximal principle (Protter and Weinberger 1984) and monotonicity of \(\Lambda \) with respect to the second variable shows that the positive steady state of (2.1) is unique. Finally, according to (Hirsch 1984, Theorem 3.2), \(w^*(x)\) attracts all solutions of (2.1) with nontrivial initial condition \(\phi \in C(\bar{\Omega },\mathbb {R}_+)\). This completes the proof. \(\square \)
Now, we let \(\Theta (t): \mathcal {C}_\tau ^+\rightarrow \mathcal {C}_\tau ^+\) with \(t\ge 0\) be the solution semiflow associated with (1.7); namely, if u(x, t) is the solution of (1.7) with initial condition \(\phi \in \mathcal {C}_\tau ^+\), then \(\Theta (t)\phi =u(\cdot ,t+\cdot )\in \mathcal {C}_\tau ^+\).
Theorem 2.3
For each initial condition \(\phi \in \mathcal {C}_\tau ^+\), system (1.7) has a unique global solution \(u(x,t)\ge 0\) for \(t\ge 0\). There exists a constant \(M>0\) independent of \(\phi \) such that \(\limsup \limits _{t\rightarrow \infty } u_i(x,t)\le M\) for all \(x\in \Omega \) and \(i=1,2,3\). The solution semiflow \(\Theta (t)\) admits a global compact attractor in \(\mathcal {C}_\tau ^+\).
Proof
Given any initial condition \(\phi \in \mathcal {C}_\tau ^+\), by comparison principle and Lemma 2.2, we have \(u_1(x,t)\le w(x,t)\) for all \(t\in [0,\tau _{max})\), where w(x, t) is the solution of (2.1) with initial condition \(w(x,0)=\phi _1(x,0)\). Since \(w(x,t)\rightarrow w^*(x)\) as \(t\rightarrow \infty \), \(u_1(x,t)\) is uniformly bounded for \(t\in [0,\tau _{max})\).
On account of \((\mathbf{H} _3)\), there exist \(c_0>0\) and \(c_3>0\) such that \(h(x,v)-\mu _3(x)v\le c_0-c_3v\) for all \(v\ge 0\). Especially,
Let \(T_2(t)\) and \(\widetilde{T}_3(t)\) be the \(C_0\) semigroups generated by \(\nabla \cdot (d_2\nabla )-\mu _2\) and \(\nabla \cdot (d_3\nabla )-c_3\) with Neumann boundary condition, respectively. It follows that
Let \(-\lambda _2<0\) and \(-\lambda _3<0\) be the principal eigenvalues of \(\nabla \cdot (d_2\nabla )-\mu _2\) and \(\nabla \cdot (d_3\nabla )-c_3\) with Neumann boundary condition, respectively. We have \(\Vert T_2(t)\Vert \le e^{-\lambda _2t}\) and \(\Vert \widetilde{T}_3(t)\Vert \le e^{-\lambda _3t}\). Denote \(v_i(t)=\max \limits _{x\in {\bar{\Omega }}}u_i(x,t)\). Clearly, \(v_1\) is uniformly bounded in \([0,t_{max})\). By \((\mathbf{H} _2)\) and continuity of \([{\mathcal {K}}(\tau )1](x)=\int _\Omega K(x,y,\tau )dy\) in \({\bar{\Omega }}\), there exist \(c_{12}>0\) and \(c_{13}>0\) such that \({\mathcal {K}}(\tau )[f(u_1(\cdot ,s),u_2(\cdot ,s))+g(u_1(\cdot ,s),u_3(\cdot ,s))]\le c_{12}v_2(s)+c_{13}v_3(s)\) for all \(s\in [-\tau ,t_{max})\). It then follows from the above two formulas that
where \(c_{11},c_{31}\) and \(c_{32}\) are positive constants. Substituting the second inequality into the first one gives \(v_2(t)\le C_1+\int _0^{t-\tau }C_2v_2(s)ds \le C_1+\int _0^tC_2v_2(s)ds\) for some generic positive constants \(C_1\) and \(C_2\). Thus, Gronwall’s inequality implies that \(v_2(t)\le C_1e^{C_2t}\) for \(t\in [0,t_{max})\). This together with the last inequality yields \(v_3(t)\le c_{31}+c_{32}C_1e^{C_2 t}/C_2\) for \(t\in [0,t_{max})\). In view of Lemma 2.1, \(t_{max}=\infty \) and the solution u(x, t) exists for all \(t\ge 0\).
Next, we will prove that the solution u(x, t) is ultimately bounded by a constant independent of the initial condition. By comparison principle and Lemma 2.2, we have \(\limsup \limits _{t\rightarrow \infty } u_1(x,t)\le w^*(x)\). Especially, there exist \(t_1>0\) and \(M_1>0\) such that \(u_1(x,t)\le M_1\) for all \(t\ge t_1\). By \((\mathbf{H} _2)\), there exists \(c_2>0\) such that
Now, we define \(U_{i,p}(t)=\int _\Omega u_i^p(x,t)dx\) with \(i=1,2,3\) and \(p\ge 1\). An integration of the reaction-diffusion equations for \(u_1\) and \(u_2\) gives
where \(c_1=\max \limits _{y\in {\bar{\Omega }}}\int _\Omega K(x,y,\tau )dx\ge 0\) and \(\underline{\mu _2}=\min \limits _{x\in {\bar{\Omega }}}\mu _2(x)>0\). \(c_1\) is finite because \(\int _\Omega K(x,y,\tau )dx\) is continuous for \(y\in {\bar{\Omega }}\). For \(t\ge t_1+\tau \), we choose \(c_0=\underline{\mu _2}c_1M_1|\Omega |+c_1\int _\Omega \Lambda (x,0)dx\). It then follows from the above two formulas, \(u_1(t-\tau )\le M_1\), and monotonicity of \(\Lambda \) in the second variable that
By comparison principle, we obtain \(\limsup \limits _{t\rightarrow \infty } U_{2,1}(t)\le c_0/\underline{\mu _2}\). Especially, there exist \(t_2>t_1\) and \(M_2>0\) such that \(U_{2,1}(t)\le M_2\) for all \(t\ge t_2\).
In view of (2.2), we integrate the reaction-diffusion equation for \(u_3\) on \(\Omega \) and obtain
for \(t\ge t_2\), where \({\bar{\sigma }}=\max \limits _{x\in {\bar{\Omega }}}\sigma (x)\). By comparison principle, there exist \(t_3>t_2\) and \(M_3>0\) such that \(U_{3,1}(t)\le M_3\) for all \(t\ge t_3\).
Assume \(t>t_3\). We want to estimate \(U_{2,2}(t)\) and \(U_{3,2}(t)\). First, we multiple the equation for \(u_2\) by \(u_2\) and integrate on \(\Omega \). It follows from (2.3) and (1.9) that
where \(\underline{d_2}=\min \limits _{x\in {\bar{\Omega }}}d_2(x)>0\). Similarly, we multiple the equation for \(u_3\) by \(u_3\) and integrate on \(\Omega \). It follows from (2.2) and Cauchy inequality that
where \(\underline{d_3}=\min \limits _{x\in {\bar{\Omega }}}d_3(x)>0\) and \({\bar{\sigma }}=\max \limits _{x\in {\bar{\Omega }}}\sigma (x)\). Adding the above inequalities and making use of the Gagliardo-Nirenberg interpolation inequality: there exists \(c>0\) such that
for any \(w\in W^{1,2}(\Omega )\) and small \(\varepsilon >0\), we obtain
for some generic positive constants \(C_1,C_2,C_3\). A simple application of comparison principle gives
Especially, there exist \(t_4>t_3\) and \(M_4>0\) such that \(U_{2,2}(t)+U_{3,2}(t)\le M_4\) for all \(t\ge t_4\).
Finally, we set \(L_p:=\limsup \limits _{t\rightarrow \infty }U_{2,p}(t)+U_{3,p}(t)\) and use a similar argument as in the estimation of \(L_2\) to obtain that \(L_{2p}\le Cp^{n/2}(L_p+1)^2\), where C is a generic constant independent of p and initial condition \(\phi \). To achieve this, we multiple the equation for \(u_2\) by \(2pu_2^{2p-1}\) and integrate on \(\Omega \). It follows from (2.3), (1.9), Young inequality and \(p\ge 1\) that
We also multiple the equation for \(u_3\) by \(2pu_3^{2p-1}\) and integrate on \(\Omega \). It follows from (2.2), Young inequality and \(p\ge 1\) that
Let \(\underline{d}=\min \{2\underline{d_2},2\underline{d_3}\}\) and \(C_1=8c_2C_K(\tau )+2{\bar{\sigma }}+2c_0\). Denote \(V_p(t):=U_{2,p}(t)+U_{3,p}(t)\). We add the above two inequalities and make use of (2.4) to obtain
Since \(\limsup \limits _{t\rightarrow \infty }V_p(t)=L_p\), there exist \(t_p>0\) such that \(V_p(t)\le L_p+1\) for all \(t\ge t_p\). Choose \(\varepsilon ^{-1}=pC_2\) with \(C_2=(2C_1+1)/\underline{d}\) and set \(C_3=c\underline{d}C_2^{-n/2-1}+c_0|\Omega |\). We obtain
for \(t\ge t_p\). By comparison principle, \(L_{2p}\le C_3p^{n/2}(L_p+1)^2\), where \(C_3\) is a constant independent of p and \(\phi \). We can prove by induction that \(L_{2^k}<\infty \) for all \(k=0,1,2,\cdots \). Let \(C=C_3+1\) and \(a_k\) be an infinite sequence defined recursively as \(a_{k+1}=C^{2^{-k-1}}2^{kn2^{-k-2}}a_k\) with initial condition \(a_0=L_1+1\). It is readily seen that \(L_{2^k}\le (a_k)^{2^k}\) and
Hence,
where \(M=(M_4+1)C2^{n/2}+M_1\). This implies that \(\limsup \limits _{t\rightarrow \infty } u_i(x,t)\le M\) for all \(x\in \Omega \) and \(i=1,2,3\). Especially, the semiflow \(\Theta (t)\) is point dissipative. It follows from (Wu 1996, Theorem 2.1.8) that \(\Theta (t)\) is compact for all \(t>\tau \). Hence, by (Hale 1988, Theorem 3.4.8), \(\Theta (t)\) admits a nonempty global attractor in \(\mathcal {C}_\tau ^+\). The proof is complete. \(\square \)
The following results give the positivity of the solution of (1.7) and the persistence of \(u_1(x,t)\).
Proposition 2.4
Let \(u(x,t)=(u_1(x,t),u_2(x,t),u_3(x,t))\) be the solution of (1.7) with initial condition \(\phi \in \mathcal {C}_\tau ^+\), then \(u_1(x,t)>0\) for all \(t>0\) and \(x\in \Omega \), and there exists a positive constant \(m_1\) independent of \(\phi \) such that
Moreover, if there exist some \(x_0\in \Omega \) and \(t_0\ge 0\) such that either \(u_2(x_0,t_0)>0\) or \(u_3(x_0,t_0)>0\), then \(u_i(x,t)>0\) for all \(i=2,3\), \(t>t_0+\tau \) and \(x\in \Omega \).
Proof
If \(u_1(\cdot ,0)\not \equiv 0\), then the strong maximum principle (Protter and Weinberger 1984, Theorem 4) yields to \(u_1(x,t)>0\) for \(t>0\) and \(x\in \Omega \). If \(u_1(\cdot ,0)\equiv 0\), then \({\partial u_1(x,0)\over \partial t}=\Lambda (x,0)>0\). Thus, there exists \(t_\epsilon >0\) such that \(u_1(x,t)>0\) for \(t\in (0,t_\epsilon )\) and \(x\in \Omega \), which together with strong maximum principle implies the positivity of \(u_1(x,t)\) for all \(t>0\) and \(x\in \Omega \).
We next show the persistence of \(u_1(x,t)\). By Theorem 2.3, there exist \(t_1>0\) and \(M_0>0\) such that \(u_i(x,t)<M_0\) for all \(t>t_1\) and \(x\in \Omega \). It then follows from the first equation of (1.7) and \((\mathbf{H} _2)\) that
for all \(t\ge t_1\) and some positive constant \(c_0\). Note that \(\Lambda (x,u_1)-c_0 u_1\) satisfies \((\mathbf{H} _1)\). Lemma 2.2 and comparison principle that \(u_1(x,t)\) is ultimately bounded below by a unique positive steady state \(w^*(x)\). Let \(m_1=\min \limits _{x\in {\bar{\Omega }}}w^*(x)>0\). Then \(\limsup \limits _{t\rightarrow \infty }u_1(x,t)\ge m_1\) for all \(x\in \Omega \).
Now, we assume that either \(u_2(x_0,t_0)>0\) or \(u_3(x_0,t_0)>0\) for some \(x_0\in \Omega \) and \(t_0\ge 0\). It follows from the equation for \(u_3\) and strong maximum principle that \(u_3(x,t)>0\) for all \(t>t_0\) and \(x\in \Omega \). We then apply strong maximum principle to the equation for \(u_2\) and obtain \(u_2(x,t)>0\) for all \(t>t_0+\tau \) and \(x\in \Omega \). \(\square \)
3 Dynamics of environment model without shedding source
Without shedding source, the dynamics of bacteria is determined by a single reaction-diffusion equation:
Clearly, this system is well-posed, that is, for every initial condition \(u_{30}\in C({\bar{\Omega }}, \mathbb {R}_+)\), system (3.1) admits a unique, nonnegative, and ultimately bounded solution \(B(\cdot ,t)\in C(\bar{\Omega },\mathbb {R}_+)\). Moreover, if \(u_{30}\not \equiv 0\), then \(B(x,t)>0\) for all \(t>0\) and \(x\in \Omega \). Since \(h(x,0)=0\), system (1.7) has a trivial steady state 0 and the corresponding linearized equation is
where, for simplicity, we denote
Denote \(A_3=\nabla \cdot (d_3(\cdot )\nabla )-\mu _3(\cdot )\) with Neumann boundary condition. The linearized system (3.2) becomes \(\partial _tB=(A_3+h_1)B\). We define the basic reproduction number for cholera bacterium in the environment as the spectral radius of the next generation operator \(-h_1A_3^{-1}\):
Given small initial bacteria density \(\psi (x)\), the density of survived bacteria at time t is \([T_3(t)\psi ](x)\), which generates new bacteria of density \(h_1(x)[T_3(t)\psi ](x)\), where \(T_3(t)\) is the solution semigroup associated with the differential operator \(A_3\). Now, the total density of next generation bacteria during the life cycle of initial bacteria is calculated as the integral
which implies that \(-h_1A_3^{-1}\) is the next generation operator; see (Zhao 2017, Chapter 11) for more details about basic reproduction number of biological models with diffusion. By (Du 2006, Remark 1.6) and (Wang and Zhao 2012, Theorem 3.2), \(1/R_e\) is the principal eigenvalue of the following elliptic eigenvalue problem with positive eigenfunction.
Moreover, \(R_e\) has the following variational representation:
On the other hand, we obtain from Krein-Rutman theorem that the spectral bound of \(h_1+A_3\) is the same as its principal eigenvalue and it has the following variational representation:
Since \(A_3\) is resolvent-positive with negative spectral bound and \(h_1+A_3\) is resolvent-positive, it follows from (Thieme 2009, Theorem 3.5) that \(R_e-1\) has the same sign as \(\lambda _3\), which can be also observed from the above two variational formulas.
Theorem 3.1
The trivial steady state for (3.1) is globally asymptotically stable if \(R_e\le 1\) and unstable if \(R_e>1\).
Proof
If \(R_e\le 1\), by (Du 2006, Remark 1.6) and (Wang and Zhao 2012, Theorem 3.2), there exists \(\psi (x)>0\) such that
for \(x\in \Omega \) and \(\nabla \psi (x)\cdot \nu =0\) for \(x\in \partial \Omega \). Following the idea in Cui et al. (2017), we define
where B(x, t) is a solution of (3.1). By \((\mathbf{H} _3)\) and (3.3), we have \(h(x,B(x,t))<h_1(x)B(x,t)\) and thus,
It follows from strong maximum principle that \(B(x,t_2)<c(t_1;B)\psi (x)\) and thus \(c(t_2;B)<c(t_1;B)\) for all \(t_2>t_1\ge 0\). Let \(\underline{c}:=\lim \limits _{t\rightarrow \infty }c(t;B)\). If \(\underline{c}>0\), then there exists a subsequence \(t_n\) such that \(B(x,t+t_n)\rightarrow \widetilde{B}(x,t)\) as \(n\rightarrow \infty \) and \(\widetilde{B}(x_0,t_0)\ne 0\) for some \(x_0\in \Omega \) and \(t_0>0\). By strong maximum principle, \(\widetilde{B}(x,t)>0\) for all \(t>t_0\). Using a similar argument, we have \(c(t_2,\widetilde{B})<c(t_1,\widetilde{B})\) for all \(t_2>t_1>t_0\). However, \(c(t,\widetilde{B})=\lim \limits _{n\rightarrow \infty }c(t+t_n,B)=\underline{c}\) for all \(t>t_0\), a contradiction. Thus, we have \(\underline{c}=0\). This implies that the trivial steady state 0 is globally attractive. Moreover, for any \(\varepsilon >0\), we set \(\delta =\varepsilon \min \limits _{x\in {\bar{\Omega }}}\psi (x)/\max \limits _{x\in {\bar{\Omega }}}\psi (x)\). It follows from monotonicity of c(t, B) in t that \(\Vert B(\cdot ,t)\Vert <\varepsilon \) for all \(t\ge 0\) if \(\Vert B(\cdot ,0)\Vert <\delta \). Hence, the trivial steady state 0 is also stable.
If \(R_e>1\), then the spectral bound of \(h_1+A_3\) is positive, which implies that the exponential growth bound of the solution semiflow of (3.2) is positive. Hence, the trivial steady state 0 is unstable. This completes the proof. \(\square \)
We now investigate the existence and global attractiveness of the positive steady state of (3.1) when \(R_e>1\).
Theorem 3.2
If \(R_e>1\), then system (3.1) admits a unique positive steady state \(B^*(x)\), which is globally attractive in \(\{\phi _3\in C({\bar{\Omega }}, \mathbb {R}_+): \phi _3\not \equiv 0\}\).
Proof
The steady state of (3.1) satisfies the following boundary value problem
It follows from (1.11) that there exists a sufficiently large constant \(M_1\) such that \(h(x,M_1)<\mu _3(x)M_1\) for all \(x\in \Omega \). Thus, \(M_1\) is an upper-solution of (3.5). On the other hand, \(R_e>1\) implies \(\lambda _0>0\), where \(\lambda _0\) is the principal eigenvalue of \(h_1+A_3\) with a positive eigenfunction \(\varphi (x)>0\). By chosen \(\varepsilon _0>0\) sufficiently small, we have \(\varepsilon _0\varphi (x)\le M_1\) and \(h(x,\varepsilon _0\varphi (x))\ge [h_1(x)-\lambda _0]\varepsilon _0\varphi (x)\) for all \(x\in \Omega \). Hence, \(\varepsilon _0\varphi (x)\) is a lower-solution of (3.5). By (Protter and Weinberger 1984, Theorem 2.13), there exist a solution \(B^*(x)\) such that \(\epsilon _0\psi _0\le B^*(x)\le M_1\).
We then construct a Lyapunov functional \(W: C({\bar{\Omega }},\mathbb {R}_+)\setminus \{0\} \rightarrow \mathbb {R}\) as follows.
Notice that the steady state solution \(B^*(x)\) satisfies \(-\nabla \cdot (d_3(x)\nabla B^*(x))=h(x,B^*(x))-\mu _3(x)B^*(x)\). Thus, the time derivative of W along a positive solution of system (3.1) is given by
Green’s identity and Neumann boundary condition imply that
In view of \((\mathbf{H} _3)\), h(x, B) is concave down with respect to B, which yields
Hence, we have \(dW/dt\le 0\). Since the largest invariant set on which \(dW/dt=0\) is a singleton \(\{B^*(x)\}\), By Lyapunov-LaSalle invariance principle, the positive steady state \(B^*(x)\) is globally attractive, which implies the uniqueness of the positive steady state. This ends the proof. \(\square \)
4 Basic reproduction number for infection
Recall from Lemma 2.2 that the single reaction-diffusion equation (2.1) has a unique steady state \(w^*(x)\). So, the system (1.7) has a unique infection-free steady state \((w^*(x),0,0)\). For simplicity, we denote
Linearizing system (1.7) at \((w^*(x),0,0)\) gives a single equation for \(u_1(x,t)\) and the following cooperative system for \((u_2(x,t), u_3(x,t))\):
with Neumann boundary condition, where for convenience, we denote \(u_{i,-\tau }(x,t)=u_i(x,t-\tau )\) with \(i=2,3\). Let U(t) be the solution semigroup of the above decoupled system. Denote by \(\omega (U)\) the exponential growth bound of U(t). Define
According to (Kerscher and Nagel 1984, Section 4) and Krein-Rutman theorem, we have the following lemma.
Lemma 4.1
Let F and V be given as in (4.2). The spectral bound \(s(e^{-\lambda \tau }F-V)\) is a continuous and decreasing function of \(\lambda \). Let \(\lambda _0\in \mathbb {R}\) be the unique solution of \(\lambda _0=s(e^{-\lambda _0\tau }F-V)\). We have \(\lambda _0=\omega (U)\). Furthermore, \(\lambda _0\) is the principal eigenvalue of \(e^{-\lambda _0\tau }F-V\) with positive eigenfunction and it has the same sign as \(s(F-V)\).
Let \((\varphi ,\psi )\) be the positive eigenfunction corresponding to the principal eigenvalue \(\lambda _0\) of \(e^{-\lambda _0\tau }F-V\). We have
with Neumann boundary condition. Recall that \(\lambda _3\) is the principal eigenvalue of \(A_3+h_1=\nabla \cdot (d_3\nabla )+h_1-\mu _3\) with a positive eigenfunction \(\psi _3\). We write
with Neumann boundary condition. Multiplying the last two equations by \(\psi _0\) and \(\psi _3\), respectively, and then integrating the difference of resulting equations on \(\Omega \), we find
which implies \(\lambda _0>\lambda _3\). Recall that \(\lambda _3\) has the same sign as \(R_e-1\). We have the following lemma.
Lemma 4.2
If \(R_e\ge 1\), then \(\lambda _0>0\).
Now, we assume that \(R_e<1\) and define the basic reproduction number as \(R_0=r(FV^{-1})\), the spectral radius of \(FV^{-1}\). Since \(R_e<1\), the operator \(-V\) is resolvent-positive with \(s(-V)<0\). Obviously, F is positive. Moreover, by (Thieme 2009, Theorem 3.12), \(F-V\) is resolvent-positive because it generates a positive semigroup. It follows from (Thieme 2009, Theorem 3.5) that \(R_0-1\) has the same sign as \(s(F-V)\). Recall from Lemma 4.1 that \(s(F-V)\) has the same sign as \(\lambda _0\). We obtain the following lemma.
Lemma 4.3
If \(R_e<1\) and \(R_0>1\), then \(\lambda _0>0\).
To find a more biologically relevant expression of \(R_0\), we need to make use of the following lemma.
Lemma 4.4
Let \(\displaystyle F=\begin{pmatrix} F_{11}&{}F_{12}\\ 0&{}0 \end{pmatrix}\) be a positive operator and \(\displaystyle -V=\begin{pmatrix} -V_{11}&{}0\\ -V_{21}&{}-V_{22} \end{pmatrix}\) be a resolvent-positive operator with \(s(-V)<0\). We have
Proof
Since V is lower triangular, it follows from \(s(-V)<0\) that both \(V_{11}\) and \(V_{22}\) are invertible. Furthermore, \(\displaystyle V^{-1}=\begin{pmatrix} V_{11}^{-1}&{}0\\ -V_{22}^{-1}V_{21}V_{11}^{-1}&{}V_{22}^{-1} \end{pmatrix}\). Consequently, we have
which implies that \(r(FV^{-1})=r(F_{11}V_{11}^{-1}-F_{12}V_{22}^{-1}V_{21}V_{11}^{-1})\). This completes the proof. \(\square \)
Now, we find another expression of the basic reproduction number:
where
is the next generation operator for direct (human-to-human) transmission, and
is the next generation operator for indirect (environment-to-human) transmission.
Next, we analyze the dependence of \(R_0\) of diffusion coefficients \(d_2\) and \(d_3\). For simplicity, we assume that the kernel function \(K(x,y,\tau )\) is a constant multiplication of delta function such that \(({\mathcal {K}}(\tau )\circ \psi )(x)=\kappa (\tau )\psi (x)\). We also assume that \(d_2\) and \(d_3\) are constants. By Krein-Rutman theorem, \(R_0\) is a principal eigenvalue of \(L_d+L_i\) with a positive eigenfunction, denoted by \(\phi (x)\); namely,
Define \(\lambda =\kappa (\tau )/R_0\), \(\varphi =(\mu _2-d_2\Delta )^{-1}\phi \) and \(\psi =(\mu _3-h_1-d_3\Delta )^{-1}(\sigma \varphi )\). Since \(R_e<1\), it follows from strong maximum principle that both \(\varphi \) and \(\psi \) are positive functions. Thus, we have
We treat \(d_2\) as a variable and take the derivatives with respect to \(d_2\) on both sides of the above equations to obtain
We multiply (4.6) and (4.8) by \(\varphi '\) and \(\varphi \), respectively, and then integrate the difference over \(\Omega \). The resulting equation becomes
Similarly, we multiply (4.7) and (4.9) by \(\psi '\) and \(\psi \), respectively, and then integrate the difference over \(\Omega \) to find
If the ratio \(\beta _i/\sigma \) is independent of x (especially, if both \(\beta _i\) and \(\sigma \) are constants), then we obtain from the above two equations that \(\lambda '>0\). Recall that \(\lambda =\kappa (\tau )/R_0\). We conclude that \(R_0\) is a decreasing function of \(d_2\). A similar argument shows that \(R_0\) is also a decreasing function of \(d_3\), provided that \(\beta _i/\sigma \) is a constant function. We summarize the result in the following proposition.
Proposition 4.5
Assume that \(d_2\), \(d_3\) and \(\beta _i/\sigma \) are constant functions on \({\bar{\Omega }}\). Assume further that \(({\mathcal {K}}(\tau )\circ \psi )(x)=\kappa (\tau )\psi (x)\) for all \(x\in \Omega \) and \(\psi \in C({\bar{\Omega }})\), then \(R_0\) is a decreasing function in both \(d_2\) and \(d_3\).
As we shall see later in the simulation, \(R_0\) may not be a decreasing function of \(d_2\) or \(d_3\) if \(\beta _i/\sigma \) is not a constant function.
5 Global dynamics of the nonlocal and delayed cholera model
In this section, we demonstrate that the global dynamics of (1.7) are completely determined by the basic reproduction number for cholera bacterium in the environment \(R_e\) and the basic reproduction number of infection \(R_0\).
Theorem 5.1
If \(R_e<1\) and \(R_0\le 1\), then the infection-free steady state \((w^*(x),0,0)\) for (1.7) is globally asymptotically stable.
Proof
Recall that \(R_0-1\) has the same sign as \(s(F-V)\), which, according to Lemma 4.1, has the same sign as \(\lambda _0\), where \(\lambda _0\) is the principal eigenvalue of \(e^{-\lambda \tau }F-V\) with a positive eigenfunction \((\varphi ,\psi )\); namely,
If \(R_0\le 1\), then \(\lambda _0\le 0\). Given any solution \(u=(u_1,u_2,u_3)\), define
for \(t\ge 0\). If either \(u_2\) or \(u_3\) is not identically zero, then by strong maximum principle, there exists \(t_0\ge 0\) such that \(u_2(x,t)>0\) and \(u_2(x,t)>0\) for all \(t\ge t_0-\tau \). If further, \(u_1(x,t)\le w^*(x)\) for all \(t\ge -\tau \), it then follows from \((\mathbf{H} _2)\) and \((\mathbf{H} _3)\) that
By strong maximum principle, \(u_2(x,t)<c(t_1;u)e^{\lambda _0t}\varphi (x)\) and \(u_3(x,t)<c(t_1;u)e^{\lambda _0t}\psi (x)\) for all \(t>t_1\ge t_0\). Thus, c(t; u) is strictly decreasing in t. We claim that \(u_2(x,t)\rightarrow 0\) and \(u_3(x,t)\rightarrow 0\) as \(t\rightarrow \infty \). If \(\lambda _0<0\), then the claim is obvious. If \(\lambda _0=0\), then the claim is true when \(\underline{c}=\lim _{t\rightarrow \infty }c(t;u)=0\). Assume that \(\lambda _0=0\) and \(\underline{c}>0\), then there exists a subsequence \(t_n\) such that \(u(x,t+t_n)\rightarrow \widetilde{u}(x,t)\) as \(n\rightarrow \infty \) and either \(\widetilde{u}_2(x,t)\) or \(\widetilde{u}_3(x,t)\) is not identically zero. Moreover, \(\widetilde{u}(x,t)\le w^*(x)\) for all \(t\ge -\tau \). A similar argument shows that \(c(t;\widetilde{u})\) is strictly decreasing for all sufficiently large t. However, \(c(t;\widetilde{u})=\lim _{n\rightarrow \infty }c(t+t_n;u)=\underline{c}\), a contradiction. Hence, we have proved the claim. Since the limiting system when \(u_2=u_3\equiv 0\) has a unique globally asymptotically stable steady state \(u_1=w^*\), we obtain from (Thieme 1992, Theorem 4.1) that \((w^*(x),0,0)\) attracts all initial conditions in the positively invariant set \(D:=\{\phi \in \mathcal {C}_\tau ^+:\phi _1(x)\le w^*(x)\}.\) Since \(\limsup _{t\rightarrow \infty }u_1(x,t)\le w^*(x)\), any omega limit set of any positive orbit lies in D. It follows from (Zhao 2017, Theorem 1.2.1) that \((w^*(x),0,0)\) is globally attractive.
Now, we want to prove stability of \((w^*(x),0,0)\) when \(R_0\le 1\). In view of Lemma 4.1, we have \(\omega (U)\le 0\). Especially, there exists a generic constant \(C_1>0\) such that \(\Vert U(t)\Vert \le C_1\) for all \(t\ge 0\). Let u be a solution of (1.7) with initial condition
On account of Theorem 2.3, there exists a generic constant M such that \(0\le u_i(x,t)\le M\) for all \(x\in \Omega \), \(t\ge -\tau \) and \(i=1,2,3\). By \((\mathbf{H} _1)\), we have
It then follows that
Subtracting the equations of \(u_1\) and \(w^*\) gives
It then follows from comparison principle that \(u_1(x,t)\le w^*(x)+\delta e^{-\alpha t}\) for all \(x\in \Omega \) and \(t\ge -\tau \). Making use of \((\mathbf{H} _2)\), we have
for some generic constant \(C_2>0\). Consequently,
Since \(\Vert U(t)\Vert \le C_1\), we have
for all \(x\in \Omega \) and \(t\ge 0\). On account of \((\mathbf{H} _2)\), there exists a generic constant \(C_3>0\) such that
for all \(x\in \Omega \) and \(t\ge 0\). Recall that
where \(\xi (x,t)\le -\alpha \) for all \(x\in \Omega \) and \(t\ge 0\). By comparison principle, we have \(w^*(x)-u_1(x,t)\le \delta C_3/\alpha \) for all \(x\in \Omega \) and \(t\ge 0\). Choosing a generic constant \(C=C_1+C_1C_2/\alpha +C_3/\alpha \), we have
for all \(x\in \Omega \) and \(t\ge -\tau \). This implies that the solution lies in \(CB_\delta \) if the initial condition lies in \(B_\delta \). Since C is a generic constant independent of \(\delta \), we obtain the stability of \((w^*(x),0,0)\). This together with the global attractiveness implies globally asymptotic stability of \((w^*(x),0,0)\) under the condition \(R_0\le 1\). \(\square \)
Denote
and
Let \(M_\partial \) be the largest positively invariant set in \(\partial \mathbb {X}_0\). It follows from strong maximum principle that
In view of Lemma 2.2, \((w^*(x),0,0)\) is globally attractive in \(M_\partial \). Introduce a generalized distance function \(p:\mathcal {C}_\tau ^+\rightarrow \mathbb {R}_+\) as
for each \(\phi =(\phi _1,\phi _2,\phi _3)\in \mathcal {C}_\tau ^+\). Recall that \(\Theta (t)\) denotes the solution semiflow of (1.7) on \(\mathcal {C}_\tau ^+\). By strong maximum principle, \(p(\Theta (t)\phi )>0\) for all \(\phi \in \mathbb {X}_0\). Since \(p^{-1}(0,\infty )\subset \mathbb {X}_0\), the condition (P) in (Smith and Zhao 2001, Section 3) is satisfied. We have the following uniform persistence result.
Theorem 5.2
If either \(R_e\ge 1\) or \(R_e<1<R_0\), then there exists an \(\eta >0\) such that for any \(\phi \in \mathbb {X}_{0}\) and \(u(\cdot ,t+\cdot )=\Theta (t)\phi \), we have \(\liminf \limits _{t\rightarrow \infty }u_i(x,t)\ge \eta \) for all \(i=1,2,3\) and \(x\in {\bar{\Omega }}.\) Moreover, system (1.7) admits at least one endemic steady state \((u_1^*(x),u_2^*(x),u_3^*(x))\).
Proof
If \(R_e\ge 1\), then Lemma 4.2 implies \(\lambda _0>0\). If \(R_e<1\) but \(R_0>1\), then in view of Lemma 4.3, we still have \(\lambda _0>0\). Recall from Lemma 4.1 that \(\lambda _0\) is the principal eigenvalue of \(e^{-\lambda _0\tau }F-V\) with positive eigenfunction. For any sufficiently small \(\varepsilon >0\), we consider a small perturbation of F:
By (Kerscher and Nagel 1984, Section 4), there exists a principal eigenvalue \(\lambda _\varepsilon \) with positive eigenfunction \((\varphi _\varepsilon ,\psi _\varepsilon )\) of \(e^{-\lambda _\varepsilon \tau }F-V\); namely,
By continuity of the operator, we have \(\lambda _\varepsilon \rightarrow \lambda _0>0\) as \(\varepsilon \rightarrow 0^+\). We may choose a small \(\varepsilon >0\) such that \(\lambda _\varepsilon >0\). Now, we claim that the stable manifold of \((w^*(x),0,0)\) does not intersect \(p^{-1}(0,\infty )\). Assume to the contrary that there exists \(\phi \in \mathcal {C}_\tau ^+\) with \(p(\phi )>0\) such that \(u(x,t)\rightarrow (w^*(x),0,0)\) as \(t\rightarrow \infty \), where \(u(\cdot ,t+\cdot )=\Theta (t)\phi \). Especially, \(f(u_1,u_2)/u_2\rightarrow \beta _d\) and \(g(u_1,u_3)/u_3\rightarrow \beta _i\) as \(t\rightarrow \infty \). Hence, there exists \(t_1>0\) such that \(f(u_1,u_2)>(\beta _d-\varepsilon )u_2\) and \(g(u_1,u_3)>(\beta _i-\varepsilon )u_3\) for all \(t>t_1-\tau \). Choose \(\delta >0\) such that \(u_2(x,t_1+\theta )\ge \delta e^{\lambda _\varepsilon (t_1+\theta )}\varphi _\varepsilon (x)\) and \(u_3(x,t_1+\theta )\ge \delta e^{\lambda _\varepsilon (t_1+\theta )}\psi _\varepsilon (x)\) for all \(x\in \Omega \) and \(\theta \in [-\tau ,0]\). It follows from maximum principle that \(u_2(x,t)\ge \delta e^{\lambda _\varepsilon t}\varphi _\varepsilon (x)\) and \(u_3(x,t)\ge \delta e^{\lambda _\varepsilon t}\psi _\varepsilon (x)\) for all \(x\in \Omega \) and \(t\ge t_1\), which contradicts to the fact that \((u_2,u_3)\rightarrow 0\) as \(t\rightarrow \infty \). Thus, we have proved that the stable manifold of \((w^*(x),0,0)\) does not intersect \(p^{-1}(0,\infty )\). By (Smith and Zhao 2001, Theorem 3), there exists \(\eta >0\) such that \(\liminf \limits _{t\rightarrow \infty }p(\Theta (t)\phi )\ge \eta \) for any \(\phi \in \mathcal {C}_\tau ^+\). This, together with Proposition 2.4 (by choosing \(\eta <m_1\)), implies that \(\liminf \limits _{t\rightarrow \infty }u_i(x,t)\ge \eta \) for all \(i=1,2,3\) and \(x\in {\bar{\Omega }}.\) On account of (Magal and Zhao 2005, Theorem 4.7), system (1.7) admits at least one endemic steady state \((u_1^*(x),u_2^*(x),u_3^*(x))\). This completes the proof. \(\square \)
6 Homogeneous system: a special case
In this section, we consider the special case when the system becomes homogeneous; namely, we assume that
and \([{\mathcal {K}}(\tau )1](x)=\kappa (\tau )\) for all \(x\in {\bar{\Omega }}\). Note that both heat kernel and delta kernel satisfy this condition. We further assume that \(f(v,w)=vf_2(w)\) and \(g(v,w)=vg_3(w)\). It then follows that \(w^*(x)={{\bar{u}}}_1\), where \({{\bar{u}}}_1\) is the unique positive solution of \(\Lambda ({{\bar{u}}}_1)=0\). The formula (3.4) can be simplified as \(R_e=h_1/\mu _3\), where \(h_1=h'(0)\). If \(R_e<1\), by Krein-Rutman theorem, \(L_d+L_i\) is a compact and positive operator with a positive eigenfunction 1 corresponding to a positive principal eigenvalue
where \(\beta _d={{\bar{u}}}_1f_2'(0)\) and \(\beta _i={{\bar{u}}}_1g_3'(0)\). This implies that the basic reproduction numbers for the system (1.7) and the diffusion-free (\(d_i=0\)) system are the same.
Lemma 6.1
If either \(R_e\ge 1\) or \(R_e<1<R_0\), then the system (1.7) with homogeneous coefficients has a unique positive homogeneous steady state \((u_1^*,u_2^*,u_3^*)\).
Proof
A homogeneous steady state \(u=(u_1,u_2,u_3)\) satisfies the equations
Consider \(u_1\in [0,{{\bar{u}}}_1]\) as an independent variable, and regard \(u_2\) and \(u_3\) as functions of \(u_1\) defined by \(u_2=\kappa (\tau )\Lambda (u_1)/\mu _2\) and
In view of \((\mathbf{H} _{1})\) and \((\mathbf{H} _{3})\), the above equation has a unique solution for \(u_3\ge \underline{u_3}\), where \(\underline{u_3}=0\) if \(R_e\le 1\) and \(\underline{u_3}>0\) is the unique positive solution of \(\mu _3\underline{u_3}=h(\underline{u_3})\) if \(R_e>1\). Now, we introduce the function
A homogeneous positive steady state exists if and only if G has a root in \((0,{{\bar{u}}}_1)\). Clearly, \(G(0)=\Lambda (0)>0\). If \(R_e>1\), then \(u_2=0\) and \(u_3=\underline{u_3}>0\) when \(u_1={{\bar{u}}}_1\). Consequently, \(G({{\bar{u}}}_1)=-{{\bar{u}}}_1g_3(\underline{u_3})<0\), which implies that G(u) has at least one root \(u_1^*\in (0,{{\bar{u}}}_1)\). If \(R_e<1<R_0\), then \(u_2=u_3=0\) when \(u_1={{\bar{u}}}_1\). Moreover, \(u_2'({{\bar{u}}}_1)=\kappa (\tau )\Lambda '({{\bar{u}}}_1)/\mu _2\) and \(u_3'({{\bar{u}}}_1)=\kappa (\tau )\sigma \Lambda '({{\bar{u}}}_1)/[\mu _2(\mu _3-h_1)]\). Consequently, \(G({{\bar{u}}}_1)=0\) and
It then follows that G(u) has at least one root \(u_1^*\in (0,{{\bar{u}}}_1)\). For the critical case \(R_e=1\), we still have \(u_2=u_3=0\) when \(u_1={{\bar{u}}}_1\). Thus, \(G({{\bar{u}}}_1)=0\) and
As \(u_1\) approaches \({{\bar{u}}}_1\) from the left, \(u_3\) approaches 0 from the right, and \(\mu _3-h'(u_3)\) approaches zero from the right, and consequently, \(G'(u_1)\rightarrow \infty \). Especially, \(G(u_1)<0\) for \(u_1\) close to \({{\bar{u}}}_1\). This again implies that G(u) has at least one root \(u_1^*\in (0,{{\bar{u}}}_1)\). Let \(u_2^*=\kappa (\tau )\Lambda (u_1^*)/\mu _2\) and \(u_3^*\) be the unique positive solution of \(\kappa (\tau )\sigma \Lambda (u_1^*)/\mu _2=\mu _3u_3^*-h(u_3^*)\). This proves the existence of positive homogeneous steady state.
To prove uniqueness, we consider the ordinary differential system
The set of positive homogeneous steady states of (1.7) is the same as the set of positive equilibria of the above system. For simplicity, we introduce a basic Lyapunov function \(J(z)=z-1-\ln z\), which is concave up on the positive real line and has a unique minimum at \(z=1\) with minimum value \(J(1)=0\). Now, we construct a Lyapunov function \(W:\mathbb {R}^3\rightarrow \mathbb {R}\) as
for \(\phi =(\phi _1,\phi _2,\phi _3)\in \mathbb {R}^3\). We restrict W on the solution trajectory \(u(t)=(u_1(t),u_2(t),u_3(t))\) of the ordinary differential system and take derivative with respect to t. It follows from a tedious calculation that
The last two lines are non-positive due to nonnegativity of L on the positive line. Since \(g_3\) is increasing (i.e., \(g_3'\ge 0\)) and concave down (i.e., \(g_3''\le 0\)), it follows that \([g_3(u_3)-g_3(u_3^*)][g_3(u_3)/u_3-g_3(u_3^*)/u_3^*]\le 0\). Similarly, since \(f_2\) is increasing and concave down, we have \([f_2(u_2)-f_2(u_2^*)][f_2(u_2)/u_2-f_2(u_2^*)/u_2^*]\le 0\). Consequently, the second line in the expression of \(\dot{W}(u)\) is also non-positive. Finally, the first line in the expression of \(\dot{W}(u)\) is non-positive because \(\Lambda \) is decreasing and h is concave down. Therefore, we conclude that \(\dot{W}(u)\le 0\). The largest invariant set of \(\dot{W}(u)=0\) is a singleton \(\{u^*\}\). By LaSalle-Lyapunov invariance principle, \(u^*\) is globally attractive, which implies that it is the unique positive equilibrium for the ordinary differential system, and also the unique positive homogeneous steady state for the system (1.7). This completes the proof. \(\square \)
When \(R_e\ge 1\) or \(R_e<1<R_0\), we want to prove global attractiveness of \((u_1^*,u_2^*,u_3^*)\) by making an additional assumption: \([{\mathcal {K}}(\tau )\circ \psi ](x)=\kappa (\tau )\psi (x)\) for all \(\psi \in C({\bar{\Omega }})\). This restrictive technical condition requires the kernel to be local and hence is not satisfied by the heat kernel. Recall that \(J(z)=z-1-\ln z\). We construct a Lyapunov functional \(\mathcal {W}:\mathcal {C}_\tau ^+\rightarrow \mathbb {R}\) as
where
for \(\phi =(\phi _1,\phi _2,\phi _3)\in \mathcal {C}_\tau ^+\). We restrict \(\mathcal {W}\) and W on the solution trajectory \(u(t,x)=(u_1(t,x),u_2(t,x),u_3(t,x))\) and take derivative with respect to t. After a simple (though tedious) calculation, we obtain
Note from Neumann boundary conditions that
It then follows from a similar argument as in the proof of Lemma 6.1 that \({\dot{\mathcal {W}}}=\int _\Omega \dot{W} dx\le 0\). The largest invariant subset of \({\dot{\mathcal {W}}}=0\) is the singleton \(u^*=(u_1^*,u_2^*,u_3^*)\). By LaSalle-Lyapunov invariance principle, the positive homogeneous steady state \(u^*\) is globally attractive.
To obtain globally asymptotic stability of \(u^*\) when \(R_e\ge 1\) or \(R_e<1<R_0\), we shall establish locally asymptotic stability of \(u^*\); namely, all eigenvalues of the system (1.7) linearized about \(u^*\) have negative real parts. Assume to the contrary that the linearized system has an eigenvalue \(\lambda \in \mathcal {C}\) such that \({{\,\mathrm{{Re}}\,}}\lambda \ge 0\), then there exists an eigenvalue \(\xi \ge 0\) of \(-\Delta \) with Neumann boundary condition on \(\Omega \) such that the following determinant vanishes.
A simple calculation gives
which can be rewritten as
Recall that the positive homogeneous steady state \(u^*=(u_1^*,u_2^*,u_3^*)\) satisfies the equation \(\sigma u_2^*=\mu _3u_3^*-h(u_3^*)\). Especially, in view of \(h''<0\), we have \(\mu _3-h'(u_3^*)>\mu _3-h(u_3^*)/u_3^*=\sigma u_2^*/u_3^*>0\). This together with \(\Lambda '\le 0\), \({{\,\mathrm{{Re}}\,}}\lambda \ge 0\) and \(\xi \ge 0\) implies that the left-hand side of the above equality has a modulus larger than one. However, the modulus of the right-hand side of the above equality is less than
where we have made use of \(f_2''\le 0\), \(g_2''\le 0\) and \(\kappa (\tau )u_1^*[f_2(u_2^*)+g_3(u_3^*)]=\mu _2u_2^*\). This leads to a contradiction. Therefore, \(u^*\) is locally asymptotically stable if either \(R_e\ge 1\) or \(R_e<1<R_0\).
We summarize our results in the following theorem.
Theorem 6.2
Assume \((\mathbf{H} _{0})\), \((\mathbf{H} _{1})\), \((\mathbf{H} _{2})\), and \((\mathbf{H} _{3})\), with \(\Lambda (x,v)=\Lambda (v)\), \(h(x,v)=h(v)\), \(f(v,w)=vf_2(w)\), \(g(v,w)=vg_3(w)\) and \([{\mathcal {K}}(\tau )\circ \psi ](x)=\kappa (\tau )\psi (x)\) for all \(\psi \in C({\bar{\Omega }})\). Assume further that \(d_i,\mu _i,\sigma \) are constant functions, Let \(R_e=h_1/\sigma \) with \(h_1=h'(0)\) and \(R_0\) be defined as in (6.1). We have the dichotomy result.
-
(i)
if \(R_e<1\) and \(R_0\le 1\), then the infection-free steady state \(({{\bar{u}}}_1,0,0)\) for system (1.7) is globally asymptotically stable;
-
(ii)
if \(R_e\ge 1\) or \(R_e<1<R_0\), then system (1.7) admits a unique positive steady state \((u_1^*,u_2^*,u_3^*)\) which is also homogeneous and globally asymptotically stable.
7 Numerical computation and simulation
For simplicity, we choose \(\Omega =(0,1)\) and use finite difference method to conduct numerical simulation. To implement the Neumann boundary conditions, we make use of staggered mesh points: \(x_k=(k-1/2)h\) for \(k=1,\cdots ,N\) and \(y_j=jh\) for \(j=0,1,\cdots ,N\), where N is the number of mesh points and \(h=1/N\) is the mesh size. For any given diffusion coefficient \(d_i(x)\) and death rate \(\mu _i(x)\), the operator \(A_i=\nabla \cdot (d_i\nabla )-\mu _i\) can be approximated by a tridiagonal matrix \({\hat{A}}_i\) in \(\mathbb {R}^N\). For any \(\varphi \in C[0,1]\), we approximate \((A_i\varphi )(x_k)=(d_i\varphi ')'(x_k)-\mu _i(x_k)\varphi (x_k)\) with \(k=2,\cdots ,N\) by
When \(k=1\) or \(k=N\), we use Neumann boundary conditions \(\varphi '(y_0)=\varphi '(y_N)=0\) to approximate
and
It then follows that
where o is the \((N-1)\)-dimensional zero column vector, \({\hat{d}}_i\) is the \((N-1)\)-dimensional diagonal matrix with jth diagonal term \(d_i(y_j)\), and \({\hat{\mu }}_i\) is the N-dimensional diagonal matrix with kth diagonal term \(\mu _i(x_k)\). The basic reproduction number for cholera bacterium in the environment \(R_e\) can be approximated by
where the hat symbol denotes the numerical (resp. matrix) approximation of a number (resp. operator). To approximate the basic reproduction number of infection \(R_0\), we shall first solve for the infection-free steady state \((w^*(x),0,0)\), where \(A_1w^*+\Lambda (\cdot ,w^*)=0\) with \(A_1=\nabla \cdot (d_1\nabla )\). For any \(\delta >0\), the steady state \(w^*\) is a fixed point of the map \(G(w)=(\delta -A_1)^{-1}[\delta w+\Lambda (\cdot ,w)].\) Let \(\Lambda _2(x,v)\) be the partial derivative of \(\Lambda (x,v)\) with respect to the second variable v. The Frechét derivative of G(w) with respect to \(w\in C({\bar{\Omega }})\) is \(G'(w)=(\delta -A_1)^{-1}[\delta +\Lambda _2(\cdot ,w)]\).
Proposition 7.1
Assume \((\mathbf{H} _{1})\). Denote
If \(\delta \ge {\bar{\delta }}\), then the map G(w) is a contraction on \([0,U_1]\subset C({\bar{\Omega }})\) and the iteration \(w_{k+1}=G(w_k)\) with \(k\ge 0\) converges to the unique fixed point \(w^*\) with any initial point \(w_0\in C(\bar{\Omega })\) such that \(0\le w_0(x)\le U_1\) for all \(x\in {\bar{\Omega }}\).
Proof
If follows from \((\mathbf{H} _{1})\) that \(\Lambda _2(x,v)<0\) for all \(x\in {\bar{\Omega }}\) and \(v\ge 0\). On the other hand, \((\delta -A_1)^{-1}\) is a positive operator for all \(\delta >0\). For any \(\delta \ge {\bar{\delta }}\) and \(w\in C({\bar{\Omega }})\) such that \(0\le w(x)\le U_1\) for all \(x\in {\bar{\Omega }}\), we obtain from a standard variational method that
where \(\underline{\delta }:=-\max _{x\in {\bar{\Omega }},v\in [0,U_1]}\Lambda _2(x,v)>0\). Thus, G(w) is a contraction map. The convergence of iteration follows from contraction mapping theorem. \(\square \)
In practise, we choose \(\delta ={\bar{\delta }}\). Then the number of iterations to reach an accuracy of \(\varepsilon \) is about \(\ln \varepsilon /\ln (1-\underline{\delta }/{\bar{\delta }})\). For the critical case \({\bar{\delta }}=\underline{\delta }\), we have \(\Lambda (x,v)=b(x)-\mu _1v\). By choosing \(\delta =\mu _1\), the iteration map actually gives the exact solution: \(G(w)=(\mu _1-A_1)^{-1}b=w^*\) for any \(w\in C({\bar{\Omega }})\).
Recall from (4.3) that \(R_0=r(L_d+L_i)\), where \(L_d\) and \(L_i\) and the transmission operators defined in (4.4) and (4.5), respectively. We then approximate \(R_0\) by
where \({\hat{\beta }}_d\) and \({\hat{\beta }}_i\) are approximation of \(\beta _d\) and \(\beta _i\) in (4.1), and \({\hat{{\mathcal {K}}}}(\tau )\) is the approximation of the integral operator \({\mathcal {K}}(\tau )\). Especially, if \({\mathcal {K}}(\tau )\) is a semigroup \(T_E(\tau )\) generated by the operator \(A_4:=\nabla (\cdot d_4\nabla )-\mu _4\) with Neumann boundary condition, then \({\hat{{\mathcal {K}}}}(\tau )=\exp (\tau {\hat{A}}_4)\). If \({\mathcal {K}}(\tau )\psi =\kappa (\tau )\psi \), then \({\hat{{\mathcal {K}}}}(\tau )=\kappa (\tau )I\), where I is the identity matrix.
First, we consider the homogeneous model and set \(\Lambda (S)=\mu _1(S_m-S)\), \(f(S,I)=\beta _hSI\), and \(g(S,B)=\beta _eSB/(B_e+B)\), where the parameter values are chosen as in Table 1, with time unit in week (wk). We also assume \(h(B)=h_1B/(K+B)\) with \(h_1=0.1\)/wk and \(K=10^6\) cells/ml. The diffusion coefficients are chosen as \(d_1=0.1/\text {wk},~d_2=0.01/\text {wk},~d_3=0.1/\text {wk}.\) The integral operator \({\mathcal {K}}(\tau )\) is taken to be a delta function multiplied by \(\kappa (\tau )=e^{-\mu _4\tau }\) with \(\mu _4=0.001\)/wk. As demonstrated in Section 6, the basic reproduction numbers are exactly the same. And our numerical computation supports this result. By using (7.1) and (7.2) with \(N=100\) mesh points, we obtain \({\hat{R}}_e=0.5\) and \({\hat{R}}_0=14.6\), which coincide with the values calculated from \(R_e=h_1/\mu _3\) and (6.1).
Next, we introduce spatial heterogeneity to the model system by choosing
It is readily seen that \(\beta _i/\sigma \) is a constant function, which, according to Proposition 4.5, implies that \(R_0\) is a decreasing function in both \(d_2\) and \(d_3\); see the left panel of Fig. 1. However, if we choose \(\beta _e(x)=1.5(x+0.1)\), then \(\beta _i/\sigma \) is not a constant function and \(R_0\) is no longer decreasing in \(d_2\); see the right panel of Fig. 1. When we make some changes on the other model parameters, \(R_0\) may not be decreasing in \(d_3\) (figure not shown here).
Next, we consider the heat kernel when \({\mathcal {K}}(\tau )\) is the semigroup generated by an operator \(\nabla \cdot (d_4\nabla )-\mu _4\) with Neumann boundary condition, where \(d_4(x)=0.1[1+0.5\cos (2\pi x)]\) and \(\mu _4(x)=0.001(1+9x)\). The other parameters are chosen as
The basic reproduction numbers are computed as \(R_e\approx 0.17\) and \(R_0\approx 3.38\). Theorem 5.2 implies that infection will persist and at least one endemic steady state exists. Numerical simulation supports this and further indicates that the endemic steady state should be globally attractive; see the red dashed curve in the right panel of Fig. 2. Define the local basic reproduction number for the cholera bacterium in the environment \(R_e^l(x)=h_1(x)/\mu _3(x)\), and when \(R_e^l(x)<1\), the local basic reproduction number of infection
Following the ideas in Allen et al. (2008), we then divide the spatial domain into high-risk region \(\Omega _h\) where either \(R_e^l(x)\ge 1\) or \(R_e^l(x)<1<R_0^l(x)\), and low-risk region \(\Omega _l\) where \(R_e^l(x)<1\) and \(R_0^l(x)\le 1\). Numerical calculation shows that \(R_e^l(x)<1\) for all \(x\in [0,1]\), and \(R_0^l(x)>1\) when \(x<x_c\approx 0.46\) and \(R_0^l(x)\le 1\) when \(x\ge x_c\); see the left panel of Fig. 2. Without diffusion, the infection will persist only in the high-risk region; see the blue solid curve in the right panel of Fig. 2. However, the diffusion will spread the infection from the high-risk region to the low-risk region. Numerical exploration also suggests that the diffusion may increase the level of infection even in the high-risk region, which agrees with a study of a nonlocal dispersal epidemic model in Yang et al. (2019).
8 Discussions
In this paper, we propose a general nonlocal delayed reaction-diffusion system to investigate the direct (human-to-human) and indirect (environment-to-human) transmissions of cholera in a spatially heterogeneous habitat. The general model reduces to the age-structure model when the nonlocal kernel function takes the form of a heat kernel. Global dynamics of the general model system is determined by two basic reproduction numbers for the cholera bacterium in the environment (\(R_e\)) and for the cholera disease in the host population (\(R_0\)), respectively. Our theoretical results imply that the disease will persist if the environment is seriously contaminated (\(R_e\ge 1\)). On the other hand, if the cholera bacterium can not survive in the environment without host infection (\(R_e<1\)), then the extinction threshold of cholera disease is given by \(R_0<1\), where \(R_0\) characterizes the combined effect of direct and indirect transmissions. We also study the impact of spatial diffusion on cholera dynamics. If the habitat is homogeneous, then the diffusion will always reduce cholera infection. However, in a heterogeneous environment, the relation between cholera infection and diffusion is more complicated. In the absence of spatial diffusion, the cholera infection will only persist in the high-risk region. One significant impact of diffusion is the spreading of infection from the high-risk region to the low-risk region. Simulation results indicate that diffusion may also increase the infection level in the high-risk region. Based on our study, three types of cholera control strategies are suggested: (1) reduce cholera bacterium in the environment such that \(R_e<1\); (2) reduce the spatial diffusion of infectious hosts and cholera bacterium from high-risk region to low-risk region; and (3) reduce both direct and indirect disease transmissions such that \(R_0<1\).
References
Allen LJS, Bolker BM, Lou Y, Nevai AL (2008) Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model. Discrete Contin Dyn Syst 21:1–20
Andrews JR, Basu S (2011) Transmission dynamics and control of cholera in Haiti: an epidemic model. Lancet 377:1248–1255
Azman AS, Rudolph KE, Cummings DAT, Lessler J (2013) The incubation period of cholera: a systematic review. J Infect 66:432–438
Bertuzzo E, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2010) On spatially explicit models of cholera epidemics. J Roy Soc Interface 7:321–333
Codeço CT (2001) Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect Dis 1:1
Cui R, Lam K, Lou Y (2017) Dynamics and asymptotic profiles of steady states of an epidemic model in advective environments. J Differ Equ 263:2343–2373
Dowell SF, Tappero JW, Frieden TR (2011) Public health in Haiti - challenges and progress. N Engl J Med 364:300–301
Du Y (2006) Order Structure and Topological Methods in Nonlinear Partial Differential Equations, vol 1. World Scientific, Maximum Principles and Applications
Eisenberg MC, Shuai Z, Tien JH, van den Driessche P (2013) A cholera model in a patchy environment with water and human movement. Math Biosci 246:105–112
Goma Epidemiology Group (1994) Public health impact of Rwandan refugee crisis: what happened in Goma, Zaire, in July, 1994? Lancet 345:339–344
Hale JK (1988) Asymptotic Behavior of Dissipative Systems. American Mathematical Society, Providence
Hartley DM Jr, Morris JG, Smith DL (2006) Hyperinfectivity: a critical element in the ability of V. cholerae to cause epidemics? PLOS Med 3:63–69
Hirsch MW (1984) The dynamical systems approach to differential equations. Bull Am Math Soc 11:1–64
Joh RI, Wang H, Weiss H, Weitz JS (2009) Dynamics of indirectly transmitted infectious diseases with immunological threshold. Bull Math Biol 71:845–862
Kerscher W, Nagel R (1984) Asymptotic behavior of one-parameter semigroups of positive operators. Acta Applicandae Math 2:297–309
Koenig R (2009) Public health: International groups battle cholera in Zimbabwe. Science 323:860–861
Magal P, Zhao X-Q (2005) Global attractors and steady states for uniformly persistent dynamical systems. SIAM J Math Anal 37:251–275
Martin RJ, Smith HL (1990) Abstract functional differential equations and reaction-diffusion systems. Trans Am Math Soc 321:1–44
Miller C, Feachem R, Drasar B (1985) Cholera epidemiology in developed and developing-countries new thoughts on transmission, seasonality, and control. Lancet 1:261–263
Mukandavire Z, Liao S, Wang J, Gaff H, Smith DL, Morris JG (2011) Estimating the reproductive numbers for the 2008–2009 cholera outbreaks in Zimbabwe. Proc Nat Acad Sci USA 108:8767–8772
Nelson EJ, Harris JB, Morris JG, Calderwood SB, Camilli A (2009) Cholera transmission: the host, pathogen and bacteriophage dynamics. Nat Rev Microbiol 7:693–702
Pao CV (1992) Nonlinear parabolic and elliptic equations. Springer, New York
Pazy A (1983) Semigroups of linear operators and application to partial differential equations. Springer, Berlin
Protter MH, Weinberger HF (1984) Maximum principles in differential equations. Springer, New York
Shu H, Chen Y, Wang L (2018) Impacts of the cell-free and cell-to-cell infection modes on viral dynamics. J Dyn Differ Equ 30:1817–1836
Shu H, Wang L, Watmough J (2013) Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL immune responses. SIAM J Appl Math 73:1280–1302
Smith H (1995) Monotone Dynamical Systems. An Introduction to the Theory of Competitive and Cooperative Systems, volume 41 of Mathematical Surveys and Monographs. American Mathematical Society, Providence, RI
Smith HL, Zhao X-Q (2001) Robust persistence for semidynamical systems. Nonlinear Anal 47:6169–6179
Thieme HR (1992) Convergence results and Poincaré-Bendixson trichotomy for asymptotically autonomous differential equations. J Math Biol 30:755–763
Thieme HR (2009) Spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity. SIAM J Appl Math 70:188–211
Tian JP, Wang J (2011) Global stability for cholera epidemic models. Math Biosci 232:31–41
Tien JH, Earn DJD (2010) Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull Math Biol 72:1506–1533
Tuite AR, Tien JH, Eisenberg MC, Earn DJD, Ma J, Fisman DN (2011) Cholera epidemic in Haiti, 2010: using a transmission model to explain spatial spread of disease and identify optimal control interventions. Ann Int Med 154:293–302
Wang FB, Shi J, Zou X (2015) Dynamics of a host-pathogen system on a bounded spatial domain. Commun Pure Appl Anal 14:2535–2560
Wang W, Zhao X-Q (2011) A nonlocal and time-delayed reaction-diffusion model of dengue transmission. SIAM J Appl Math 71:147–168
Wang W, Zhao X-Q (2012) Basic reproduction numbers for reaction-diffusion epidemic models. SIAM J Appl Dyn Syst 11:1652–1673
Wang X, Zhao X-Q, Wang J (2018) A cholera epidemic model in a spatiotemporally heterogeneous environment. J Math Anal Appl 468:893–912
Wu J (1996) Theory and applications of partial functional differential equations. Springer, New York
Yang F, Li W, Ruan S (2019) Dynamics of a nonlocal dispersal SIS epidemic model with Neumann boundary conditions. J Differ Equ 267:2011–2051
Zhao X-Q (2017) Dynamical Systems in Population Biology. CMS Books in Mathematics. Springer, Cham, 2 edition
Acknowledgements
HS was partially supported by the National Natural Science Foundation of China (No. 11971285) and the Fundamental Research Funds for the Central Universities (No. GK201902005).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Shu, H., Ma, Z. & Wang, XS. Threshold dynamics of a nonlocal and delayed cholera model in a spatially heterogeneous environment. J. Math. Biol. 83, 41 (2021). https://doi.org/10.1007/s00285-021-01672-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00285-021-01672-5