Cholera Models with Hyperinfectivity and Temporary Immunity

Abstract

A mathematical model for cholera is formulated that incorporates hyperinfectivity and temporary immunity using distributed delays. The basic reproduction number $\mathcal{R}_{0}$ is defined and proved to give a sharp threshold that determines whether or not the disease dies out. The case of constant temporary immunity is further considered with two different infectivity kernels. Numerical simulations are carried out to show that when $\mathcal{R}_{0}>1$, the unique endemic equilibrium can lose its stability and oscillations occur. Using cholera data from the literature, the quantitative effects of hyperinfectivity and temporary immunity on oscillations are investigated numerically.

1 Introduction

Recent severe cholera outbreaks in Haiti (Bertuzzo et al. 2011; Chao et al. 2011; Enserink 2010; Tuite et al. 2011), Zimbabwe (Koenig 2009; Mukandavire et al. 2011; WHO 2008), and Angola (WHO 2007), together with the endemicity of the disease in parts of Africa and Asia (Bhattacharya et al. 2009; Waldor et al. 2010), highlight the continuing relevance of cholera for public health. John Snow (1854) demonstrated that the consumption of contaminated water causes cholera outbreaks. Cholera is a bacterial disease caused by the bacterium Vibrio cholerae, which is an aquatic organism with a resulting waterborne transmission route for cholera, as discovered by Filippo Pacini and later Robert Koch. However, other transmission pathways for cholera exist: direct person–person transmission has been documented in a psychiatric hospital (Goh et al. 1990), and household members of cholera patients are at increased risk of infection (Oseasohn et al. 1966; Tamayo et al. 1965; Weil et al. 2009), perhaps reflecting food preparation by infected individuals (Holmberg et al. 1984) or contamination of household water storage containers (Swerdlow et al. 1992). Pathways where the pathogen can persist only for a short period of time outside of human hosts can be grouped as “direct” transmission, while pathways where the pathogen is long-lived are considered “indirect” or “delayed” transmission (Tien and Earn 2010). Furthermore, the infectivity of V. cholerae has been shown to depend upon how long ago the pathogen was shed (Alam et al. 2005; Merrell et al. 2002; Sengupta et al. 1998). This “hyper-infectivity” of freshly shed cholera bacteria has been suggested to play an important role in cholera dynamics (Hartley et al. 2006; Pascual et al. 2006).

The primary symptom of cholera is diarrhea, which can be extremely severe, leading to rapid death due to dehydration if left untreated. Some measure of infection-derived immunity is gained upon recovery. Challenge–rechallenge experiments suggest immunity on the order of 3 or more years (Levine et al. 1981). This is in contrast to more recent modeling work suggesting that mild cases may be associated with short-lived immunity on the order of weeks to months, which can significantly impact the time course of the disease (King et al. 2008).

Mathematical models have been proposed to understand the multiple transmission pathways and to control the spread of cholera; see, for example, Andrews and Basu (2011), Bertuzzo et al. (2011), Capasso and Paveri-Fontana (1979), Chao et al. (2011), Codeço (2001), Eisenberg et al. (2002), Hartley et al. (2006), Joh et al. (2009), King et al. (2008), Mukandavire et al. (2011), Sanches et al. (2011), Shuai and van den Driessche (2011), Tian et al. (2010), Tian and Wang (2011), Tien and Earn (2010) and Tuite et al. (2011). Differential infectivity can be incorporated into mathematical models by categorizing the pathogen into discrete infectious states according to their infectivity, e.g., hyper and lower infectious states (Hartley et al. 2006) or multiple infectious states (Shuai and van den Driessche 2011). The resulting models are ordinary differential equations (ODE) and their global dynamics have been completely established in Shuai and van den Driessche (2011). The effect of temporary immunity on cholera transmission has been previously studied in Sanches et al. (2011), where immunity is assumed to be lost exponentially, resulting in an ODE model.

In this paper, we formulate a cholera model that incorporates both temporary immunity and differential infectivity (where infectivity varies with the time since the pathogen was shed). Both immunity and infectivity are modeled using arbitrary kernel functions. The resulting model with two arbitrary distributed delays is formulated in Sect. 2 and analyzed in Sects. 3 and 4. In particular, the basic reproduction number $\mathcal{R}_{0}$ is defined and proved to be a threshold parameter. If $\mathcal{R}_{0} \leq 1$, then the disease dies out; otherwise, there exists a unique endemic equilibrium. In Sect. 5, numerical simulations with two different infectivity kernels show that the stability of the endemic equilibrium depends upon the temporary immunity kernel; when the endemic equilibrium is unstable, oscillations may occur due to bifurcations. The infectivity kernel affects both the parameter sets that support periodic orbits, as well as the amplitude of the orbits where they exist. A summary and discussion of results is given in Sect. 6.

2 Model Formulation

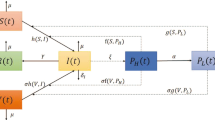
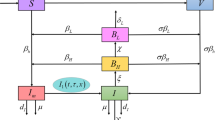
Let S(t),I(t),R(t) be the numbers of individuals at time t in the susceptible, infectious, and recovered compartments, respectively, with the total population N(t)=S(t)+I(t)+R(t). Suppose that Λ>0 denotes the constant recruitment, m>0 denotes the natural mortality rate, and α≥0 denotes the mortality rate due to the disease. The rate of change of N(t) is

$$ N'(t) = \varLambda - mN(t) - \alpha I(t), $$

(1)

where ′ represents the derivative with respect to time t. Susceptible individuals can be infected by contacting infectious individuals (direct transmission) or by drinking contaminated water in which pathogen is shed by infectious individuals (indirect transmission), and both direct and indirect transmission are modeled by mass action incidence with transmission coefficients β,λ≥0, respectively. Assume that the shedding rate ξ≥0 represents the average number of pathogen contributed per infectious individual and that the removal rate of the pathogen in the contaminated water is denoted by η>0. Let f(t)≥0, not identically zero, measure the infectivity of pathogen that was shed into the water t time units ago. Assume that f(t) is piecewise continuous on any finite interval and of exponential order η at infinity. The incidence function thus takes the form

$$\beta S(t)I(t) + \lambda S(t) \int_0^t \xi I(r) e^{-\eta (t-r)} f(t-r) \, dr. $$

Note that Pascual et al. (2006) suggest that a hyperinfective stage can be replaced by human–human transmission, but our model includes both these aspects through the terms f(t) and βS(t)I(t). Let 1/γ, γ>0, be the average infectious period, then the rate of change of I(t) is

$$ I'(t) = \beta S(t)I(t) + \lambda \xi S(t) \int _0^t I(r) e^{-\eta (t-r)} f(t-r) \, dr - (m+ \gamma+\alpha) I(t). $$

(2)

Let P(t) denote the fraction of individuals remaining in the recovered compartment t time units after becoming recovered. It is assumed that P(t)≥0 is nonincreasing, piecewise continuous and satisfies P(0⁺)=1,P(∞)=0, and $\int_{0}^{\infty}P(t) \, dt$ is finite. Thus, the number in the recovered compartment is

$$ R(t) = \int_0^t \gamma I(r) e^{-m(t-r)} P(t-r) \, dr. $$

(3)

Differentiating gives

$$ R'(t) = \gamma I(t) - mR(t) + \gamma \int _0^t I(r) e^{-m(t-r)} d_tP(t-r) \, dr, $$

(4)

where the integral is in the Riemann–Stieltjes sense and $d_{t} P(t-r)=\frac{d}{dt} P(t-r)$ whenever the derivative exists. It can be verified that R(t) given in (3) is the unique solution of (4) with the initial condition R(0)=0. Substituting (1), (2), (4) into S′(t)=N′(t)−I′(t)−R′(t) gives an equation for S′(t). Therefore, the cholera model can be written as a system with two distributed delays:

(5)

with nonnegative initial conditions S(0),I(0),R(0). Table 1 summarizes the model variables and parameters. Model (5) includes as special cases several epidemic models in the literature; see Sects. 4 and 5 for detailed discussions. Note that our model assumes mass action incidence and thus neglects saturation effects, so does not contain the models in Codeço (2001) and Hartley et al. (2006) as special cases.

Table 1 Variables and parameters with units in system (5)

The existence, uniqueness, and continuity of solutions of system (5) follow from the standard theory of Volterra integro-differential equations; see (Miller 1971, p. 338). The first equation of (5) leads to S′(t)≥0 whenever S(t)=0 and I(r)≥0 for all 0≤r≤t, and thus S(t)≥0 for all t≥0. Similarly, the second equation of (5) yields I(t)≥0 for all t≥0. The nonnegativity of R(t) follows from the expression (3). It follows from (1) that N′(t)≤Λ−mN(t), and thus $\limsup_{t\to \infty} N(t) \leq \frac{\varLambda}{m}$. Therefore, the feasible region

$$\varGamma = \biggl\{(S,I,R)\in \mathbb{R}^3 \Bigm{|} S,I,R\geq 0,\ S+I+R\leq \frac{\varLambda}{m} \biggr\} $$

is positively invariant with respect to (5).

3 Model Analysis

The model (5) always has a disease-free equilibrium (DFE) P ₀=(S ₀,0,0) in Γ, where $S_{0}=\frac{\varLambda}{m}$. Let

$$ F = \int_0^\infty e^{-\eta r} f(r) \,dr, $$

(6)

which is finite following the assumptions on f(t). Motivated by the studies on cholera models (Shuai and van den Driessche 2011; Tien and Earn 2010) and epidemic models with arbitrary distributed delay (van den Driessche et al. 2007; van den Driessche and Zou 2007), define the basic reproduction number as

$$ \mathcal{R}_0 = \frac{\beta+\lambda \xi F}{m+\gamma+\alpha} S_0, $$

(7)

which completely determines the stability of the DFE, as shown in Theorem 3.1 below. Here, 1/(m+γ+α) is the average time in the infectious compartment taking death into account. The first term in $\mathcal{R}_{0}$, namely, βS ₀/(m+γ+α), represents the contribution from direct transmission, and the second term represents that from indirect transmission through the water.

Theorem 3.1

The following results hold for (5).

• (1) If $\mathcal{R}_{0}\leq 1$, then the DFE is globally asymptotically stable in Γ.

• (2) If $\mathcal{R}_{0} >1$, then the DFE is unstable.

Proof

Since the variable R(t) does not appear in the first two equations of (5), it is sufficient to study the dynamical behavior of the reduced system consisting of the equations of S(t) and I(t). Following Li et al. (2010) and McCluskey (2009, 2010), let

$$L = S - S_0 -S_0\ln\frac{S}{S_0} + I +\lambda \xi S_0 \int_0^t I(t-r) F(r)\, dr, $$

where

$$ F(t) = \int_t^\infty e^{-\eta r} f(r) \,dr, $$

(8)

with F(0)=F. It can be easily verified that L≥0 with equality holding iff S=S ₀ and I(r)=0 for all 0≤r≤t. Differentiating L along (5) gives

(9)

It follows from integration by parts that

(10)

Combining (9) and (10), along with the facts that Λ=mS ₀, S≤S ₀ and P(t) is nonincreasing, yields

(11)

Since L′=0 implies that S=S ₀, substituting S=S ₀ into the first equation of (5) leads to I(t−r)=0 for all 0≤r≤t. Therefore, the largest invariant set where L′=0 is the singleton {P ₀}. By the LaSalle–Lyapunov theorem (see LaSalle 1976, Theorem 3.4.7), P ₀ attracts all solutions of system (5) whose initial conditions satisfy $0\leq S(0)+I(0) \leq \frac{\varLambda}{m}$. For $\mathcal{R}_{0}\le 1$, the local stability of P ₀ can be proved by using a similar argument as in Li et al. (2010, Theorem 3.1). Therefore, P ₀ is globally asymptotically stable in Γ provided $\mathcal{R}_{0}\le 1$.

If $\mathcal{R}_{0}>1$ and $I\not=0$, it follows that

$$(\mathcal{R}_0-1) (m+\gamma+\alpha)I >0, $$

which along with (11) implies that by continuity L′>0 in a small enough neighborhood of P ₀ in the interior of Γ, denoted by $\overset{\circ}{\varGamma}$. Therefore, P ₀ is unstable if $\mathcal{R}_{0}>1$. □

Biologically, Theorem 3.1 implies that if $\mathcal{R}_{0} \leq 1$, then the disease dies out eventually, irrespective of the initial conditions. In order to further study the dynamical behavior of (5) when $\mathcal{R}_{0}>1$, consider the following limiting system (see Miller 1971, p. 176):

(12)

Since system (12) consists of functional differential equations with infinite delays, a certain suitable phase space is required. Assume that there exists 0<κ<m such that $\int_{0}^{\infty}f(r) e^{-(\eta-\kappa)r} \,dr <\infty$. Define the following Banach space of fading memory type (e.g., see Atkinson and Haddock 1988)

(13)

with norm ∥ϕ∥ _κ =sup _s≤0|ϕ(s)|e ^κs. For ψ∈C(ℝ,ℝ) and t>0, let ψ _t ∈C _κ be such that ψ _t (s)=ψ(t+s),s∈(−∞,0]. Consider system (12) in the phase space

$$ X=\mathbb{R} \times C_\kappa\times \mathbb{R}. $$

(14)

Let S(0),R(0)≥0 and ϕ∈C _κ be such that ϕ(s)≥0 for all s∈(−∞,0]. The standard theory of functional differential equations (Hino et al. 1991) yields the existence, uniqueness, and continuity of solutions (S(t),I _t ,R(t)) of (12) with initial conditions (S(0),ϕ,R(0)), and gives I _t ∈C _κ for all t>0. It can be verified that

(15)

is positively invariant with respect to system (12). Let $\overset{\circ}{\varDelta}$ be the interior of Δ.

Define

$$ Q=-\int_0^\infty e^{-mt} d_tP(t) \, dt. $$

(16)

Notice that $Q = 1 - \int_{0}^{\infty}m e^{-mt} P(t) \, dt <1$. When $\mathcal{R}_{0}>1$, system (12) has a unique endemic equilibrium (EE) P ^∗=(S ^∗,I ^∗,R ^∗) in $\overset{\circ}{\varDelta}$, found by solving (12) at a stationary state with I ^∗>0.

Theorem 3.2

If $\mathcal{R}_{0}>1$, then for system (12) there exists a unique endemic equilibrium P ^∗=(S ^∗,I ^∗,R ^∗) in $\overset{\circ}{\varDelta}$, where $S^{*}=\frac{S_{0}}{\mathcal{R}_{0}}$, $I^{*}=\frac{mS_{0}(1-\frac{1}{\mathcal{R}_{0}})}{m+\alpha+\gamma(1-Q)} >0$, and $R^{*}=\frac{1-Q}{m}\gamma I^{*}$.

The stability of the EE depends on the distribution P(t). For example, when P(t) is a negative exponential, that is, P(t)=e ^−σt with σ>0, giving 1/σ as the average time of temporary immunity, the EE is always locally asymptotically stable as long as it exists (see Theorem 4.1 below). However, when P(t) is a step function, the EE can become unstable and Hopf bifurcation may occur (see Sect. 5).

4 Stability of the Endemic Equilibrium

Throughout this section, assume that P(t)=e ^−σt. It follows from the limiting system of (3) that

$$-\gamma \int_0^\infty I(t-r) e^{-mr} d_r P(r) \, dr = \sigma R(t), $$

and thus system (12) becomes

(17)

Model (17) includes model (1.19) in Jin et al. (2006) as a special case when the direct transmission is ignored, i.e., β=0. The following local stability result thus generalizes the second part of Theorem 3.1 in Jin et al. (2006).

Theorem 4.1

If $\mathcal{R}_{0}>1$, then the EE of (17) is locally asymptotically stable.

Proof

The existence of the EE P ^∗=(S ^∗,I ^∗,R ^∗) follows from Theorem 3.2. Let x=S−S ^∗, y=I−I ^∗, and z=R−R ^∗. The linearization at P ^∗ satisfies

(18)

It is sufficient to prove that the equilibrium (x,y,z)=(0,0,0) is asymptotically stable for system (18). Following Beretta and Takeuchi (1995, 1997) and Jin et al. (2006), construct a Lyapunov functional

$$V=\frac{1}{2}(x+y+z)^2 + \frac{1}{2} ay^2 + \frac{1}{2} bz^2 + \frac{1}{2} a\lambda \xi S^* \int _0^\infty e^{-\eta r} f(r) \int _{t-r}^t y^2(u) \,du \,dr, $$

where constants a,b>0 will be determined later. Differentiating V along (18) gives

(19)

Notice that in the above and also later derivations, x,y,z stand for x(t),y(t),z(t), respectively. Choose a and b such that

$$ (2m+\alpha) xy = a\bigl(\beta I^*+\lambda \xi I^* F\bigr) xy, $$

(20)

and

$$ (2m+\alpha) yz = b\gamma yz. $$

(21)

It follows from the arithmetic–geometric mean inequality that

(22)

Combining (19), (20), (21), (22), and using an equilibrium equation of (17), namely, (β+λξF)S ^∗=m+γ+α, lead to

(23)

In particular, V′=0 implies that x(t)=y(t)=z(t)=0 from (23) and y(t−r)=y(t)=0 for all 0≤r≤t from (22). Therefore, (0,0,0) is (globally) asymptotically stable for the linear system (18), and as a consequence, P ^∗ is locally asymptotically stable for (17). □

Theorem 4.1 rules out the possibility of Hopf bifurcations for system (17). The global stability of the EE of (17) is conjectured but remains open except for several special cases. For example, in the special case when immunity is permanent (σ→0), system (17) becomes an SIR model with direct and indirect transmission, i.e., the model (1.1) in Jin and Ma (2006). The global stability of the EE for this SIR model is proved in Jin and Ma (2006) for a “weak” delay; we comment that the same Lyapunov functional used in Li et al. (2010) and McCluskey (2009, 2010) can be applied to prove this for arbitrary distributed delay for the pathogen infectivity. Similar Lyapunov functionals have been applied to other delay epidemic/virus models (e.g., see Huang and Takeuchi 2011; Li and Shu 2010; Magal et al. 2010) after the successful application of Lyapunov functions in ordinary differential equation epidemic models in Korobeinikov (2004) and Korobeinikov and Maini (2004) and the extension to delay models in McCluskey (2009, 2010). The following result shows that the global stability result also holds when there is no disease-induced death (α=0) and a long period of temporary immunity (σ small).

Theorem 4.2

Suppose that α=0 and $\mathcal{R}_{0}>1$. If the inequality

$$ mS^* + \beta S^*I^* \geq \sigma R^* $$

(24)

holds, then the EE of (17) is globally asymptotically stable in $\overset{\circ}{\varDelta}$. Thus, all solutions of (5) with P(t)=e ^−σt starting in $\overset{\circ}{\varGamma}$ approach the EE of (17) given in Theorem 3.2 with Q=σ/(m+σ).

Proof

The proof is motivated by Nakata et al. (2011). It suffices to study the dynamical behavior of (17) in the invariant set $\{N=S+I+R=\frac{\varLambda}{m}\}$. Thus,

$$ R'(t) = \gamma \frac{\varLambda}{m} - \gamma S(t) - (m+\sigma+\gamma) R(t). $$

(25)

To prove the global asymptotic stability of P ^∗=(S ^∗,I ^∗,R ^∗), construct a Lyapunov functional (following Nakata et al. 2011):

where F(t) is defined as in (8). Applying the same techniques as in the proof of Theorem 3.1 and using (25), the derivative of V along (17) satisfies

Since

and the inequality 1−x+lnx≤0 for all x>0 with equality holding iff x=1, it follows that

(26)

Furthermore, it can be verified similarly as in the proof of Theorem 3.1 that the largest invariant set where V′=0 is the singleton {P ^∗}, so P ^∗ of the limiting system (17) is globally asymptotically stable in $\overset{\circ}{\varDelta}$. The second part of Theorem 4.2 follows from Theorem 7.2 in Miller (1971). □

We conjecture that Theorem 4.2 still holds after removing the assumption (24).

5 Disease Oscillations

Throughout this section, assume that P(t) is a step function, namely, P(t)=1 for all 0≤t≤w and P(t)=0 otherwise. Here, w>0 is the constant finite period of immunity. In this case,

$$\gamma \int_0^\infty I(t-r) e^{-mr} d_rP(r) \, dr = -\gamma I(t-w) e^{-mw}, $$

which appears in the first and third equations of (12). Hopf bifurcations have been shown numerically and analytically in Brauer et al. (2008) and Hethcote et al. (1981) when the indirect transmission in (12) is ignored, namely, λ=0 or ξ=0. In this section, we investigate the effect of indirect transmission on disease oscillations by choosing different kernel functions f(t).

5.1 Hyperinfectivity μ–w Model

Hyper and lower infectivity of V. cholerae have been investigated analytically in Hartley et al. (2006) and Shuai and van den Driessche (2011) by incorporating differential infectivity states of the pathogen into Codeço’s model (Codeço 2001); the resulting models are ordinary differential equation systems. In the following, by choosing an appropriate kernel function f(t), we demonstrate that our delay model (5) can also be used to investigate the effect of hyperinfectivity on cholera transmission. Let f(t) be given as follows:

$$f(t)=\left \{ \begin{array}{l@{\quad}l} \theta, & 0\leq t\leq \mu,\\ 1, & t>\mu, \end{array} \right . $$

where θ≥1 measures the ratio of hyper to lower infectivity and μ>0 is the constant period for which the pathogen is hyperinfectious. It is biologically reasonable to assume w>μ since the temporary immunity w of cholera ranges from 9 weeks to 3 years or more (Kaper et al. 1995; King et al. 2008), while μ is normally less than 1 day (Hartley et al. 2006). It follows from (6) and (7) that

$$F=\int_0^\infty e^{-\eta t} f(t) \,dt = \frac{\theta}{\eta}\bigl(1-e^{-\eta \mu}\bigr) + \frac{1}{\eta} e^{-\eta \mu} $$

and

$$ \mathcal{R}_0=\frac{\beta +\frac{\lambda \xi}{\eta} (\theta(1-e^{-\eta \mu}) + e^{-\eta \mu})}{m+\gamma+\alpha} S_0. $$

(27)

Note that, when β=0, $\mathcal{R}_{0}$ agrees with the basic reproduction number in Hartley et al. (2006) for ημ≪1. Let

$$ W(t)=\int_0^t \xi e^{-\eta (t-r)} I(r) \, dr $$

(28)

denote the number of pathogen in the contaminated water, then for t>μ:

(29)

Substituting (29) into (5) or (12) gives

(30)

The last equation of (30) follows from the differentiation of W(t) in (28). Note that in the special case of no hyperinfectivity (i.e., θ=1 or μ=0), system (30) reduces to a delay differential equation system that generalizes model (1) in Tien and Earn (2010) by incorporating temporary immunity. The initial conditions for system (30) can be generated using two associated systems:

$$ \begin{array}{rcl} S'(t) &=& \displaystyle\varLambda - \beta S(t)I(t) -\lambda \theta S(t)W(t) - mS(t),\\[5pt] I'(t) &=&\displaystyle \beta S(t)I(t) +\lambda \theta S(t)W(t) - (m+\gamma+\alpha) I(t),\\[5pt] R'(t) &=&\displaystyle \gamma I(t) - mR(t),\\[5pt] W'(t)&=&\displaystyle \xi I(t) - \eta W(t), \quad \mbox{when}\ 0\leq t \leq \mu, \end{array} $$

(31)

with initial values S(0)>0,I(0)≥0,R(0)≥0,W(0)≥0, and

$$ \begin{array}{rcl} S'(t) &=& \displaystyle\varLambda - \beta S(t)I(t) -\lambda \theta S(t) \bigl(W(t)-W(t-\mu)e^{-\eta \mu}\bigr)\\[5pt] && {}\displaystyle -\lambda S(t) W(t-\mu) e^{-\eta \mu}- mS(t),\\[5pt] I'(t) &=& \beta S(t)I(t) + \lambda \theta S(t) \bigl(W(t)-W(t-\mu)e^{-\eta \mu}\bigr) \\[5pt] &&{} \displaystyle + \lambda S(t) W(t-\mu) e^{-\eta \mu} - (m+\gamma+\alpha) I(t),\\[5pt] R'(t) &=&\displaystyle \gamma I(t) - mR(t),\\[5pt] W'(t)&=&\displaystyle \xi I(t) - \eta W(t), \quad \mbox{when}\ \mu<t\leq w. \end{array} $$

(32)

By Theorem 3.1, when $\mathcal{R}_{0}\leq 1$, the DFE of (30) is globally asymptotically stable; biologically, the cholera disease dies out eventually. If $\mathcal{R}_{0}>1$, numerical simulations show that the unique EE of (30) loses its stability when the temporary immunity w is large enough and Hopf bifurcation occurs. Simulations use parameter values from Hartley et al. (2006) (see Table 2), thus $\mathcal{R}_{0}$ agrees approximately with the basic reproduction number in Hartley et al. (2006) as ημ=0.063≪1. First, the hyperinfectivity ratio θ is assumed to equal 700 (Hartley et al. 2006), giving $\mathcal{R}_{0}=18.8$. Simulations of (30) with initial conditions (31) and (32) taking S(0)=9900,I(0)=100,R(0)=W(0)=0, using DDE23 (Shampine and Thompson 2001), show that oscillations exist for a wide range of temporary immunity w, from about 2 months to 2 years; see Fig. 1 for the prevalence I(t)/N(t) versus time. Note that for w=600 days, values of the prevalence can be very small, so stochastic effects may be important. For w=1000 days, it appears that oscillations die out and the EE regains its stability. This “stability switch” phenomenon, where increasing delays result in an equilibrium solution first losing and then regaining stability, is observed in several different delay systems (see, for example, Beretta and Kuang 2002). If the ratio θ between hyper and lower infectivity is decreased, the critical value of w destabilizing the EE is first decreased slightly and then increased; see Figs. 2–4. For example, when the difference between hyper and lower infectivity is completely ignored (θ=1), the temporary immunity w needs to be at least 5 months to destabilize the EE; see Fig. 4.

Fig. 1

The prevalence of cholera for system (30) when w=40,45,50,60,600, 1000 days, respectively, with θ=700 and parameters from Table 2, giving $\mathcal{R}_{0}=18.8$

Fig. 2

The prevalence of cholera for system (30) when w=35,40 days, respectively, with θ=375 and parameters from Table 2, giving $\mathcal{R}_{0}=11.5$

Fig. 3

The prevalence of cholera for system (30) when w=75,80 days, respectively, with θ=70 and parameters from Table 2, giving $\mathcal{R}_{0}=4.7$

Fig. 4

The prevalence of cholera for system (30) when w=150,160 days, respectively, with θ=1 and parameters from Table 2, giving $\mathcal{R}_{0}=3.2$

Table 2 Parameters taken from Hartley et al. (2006) used in the simulation for system (30)

To separate the effects of changes in $\mathcal{R}_{0}$ and θ, let $\mathcal{R}_{0}=18.8$ be fixed, vary θ, and let λ be given by

$$ \lambda=\frac{\mathcal{R}_0 \eta (m+\gamma+\alpha)}{\xi S_0(\theta(1-e^{-\eta \mu})+e^{-\eta \mu})}. $$

(33)

Figure 5 demonstrates the joint effect of hyperinfectivity (θ) and temporary immunity (w) on the existence, amplitude, and period of oscillations in cholera prevalence when $\mathcal{R}_{0}$ is held fixed. Hyperinfectivity reduces the destabilizing threshold of temporary immunity, agreeing with the simulation results in Figs. 1–4. The amplitude of the oscillations increases as the hyperinfectivity ratio increases. Hyperinfectivity may induce disease oscillations even when the basic reproduction number $\mathcal{R}_{0}$ is held constant, while the length of the temporary immunity is tightly linked to the period of these oscillations (see, for example, Fig. 1).

Fig. 5

The first row: The limit superior/inferior in cholera prevalence for system (30) when θ=1,700, respectively, with different w values, parameters from Table 2, $\mathcal{R}_{0}=18.8$ and λ as given in (33), i.e., λ=1.3×10⁻⁶ when θ=1 while λ=2.1×10⁻⁷ when θ=700. The second row: The limit superior/inferior and period of oscillation in cholera prevalence for system (30) with ω=70 days, θ ranging from 1 to 700, parameters from Table 2, $\mathcal{R}_{0}=18.8$ and λ as given in (33)

5.2 Incubation τ–w Model

Let $f(t)=\frac{1}{\eta}\delta(t-\tau)$, where δ(⋅) is the delta function, τ is the incubation time that the pathogen needs to develop in the water to become infectious or the time that it takes for the pathogen to arrive in the drinking water, and 1/η is the average time the pathogen is in the water. This assumption gives $F=\frac{1}{\eta}e^{-\eta \tau}$ and

$$ \mathcal{R}_0=\frac{\beta +\frac{\lambda \xi}{\eta} e^{-\eta \tau}}{m+\gamma+\alpha} S_0. $$

(34)

In this case system (5) or (12) becomes

(35)

There is a dichotomy of time scales involved with transmission in system (35): rapid transmission without any delay is incorporated into the direct transmission term (βSI), while the delayed transmission term can be interpreted as environmental transmission. Hyperinfectivity associated with recently shed cholera bacteria would then be incorporated into the direct transmission parameter β (see Pascual et al. 2006). System (35) includes vector-borne disease models in Beretta and Takeuchi (1995, 1997), Jin and Ma (2006) and Jin et al. (2006) as special cases if direct transmission is ignored (β=0) and/or immunity is assumed to be permanent (w→∞). The initial conditions for system (35) can be generated from a similar ordinary differential equation system as (31) and (32) associated with (30).

When $\mathcal{R}_{0}>1$ and the temporary immunity w is large enough, the EE of (35) becomes unstable. Simulations, using parameters as in Table 1, show that oscillations occur for different values of τ and w; see Fig. 6. Notice that the critical value of w destabilizing the EE increases as τ increases.

Fig. 6

Stability of the EE and the existence of stable periodic solutions for model (35) with parameters from Table 2 when τ=0.1,0.5,1 day, giving $\mathcal{R}_{0}=3.20,3.16,3.11$, respectively, with varying w days

6 Discussion

We have formulated a general cholera model with arbitrary distributed delays to incorporate hyperinfectivity and temporary immunity. The resulting model (5) is a differential equation system with two distributed delays. The basic reproduction number $\mathcal{R}_{0}$ has been defined and proved to be a threshold parameter that determines whether or not the disease dies out. When $\mathcal{R}_{0}>1$, model (5) admits a unique endemic equilibrium, and its stability depends on the distribution of temporary immunity. If this is given by a negative exponential, then the EE is locally asymptotically stable. Sufficient conditions for the global stability of the EE in this case have also been derived using the method of Lyapunov functionals. However, disease oscillations can occur for other temporary immunity distributions. For example, if temporary immunity is assumed to be of constant duration w, then the EE can become unstable. Numerical simulations show that the EE first loses and then regains its stability as w increases, with oscillations occurring when the EE is unstable. The parameter regions that support oscillations depend upon the infectivity kernel. In particular, we show numerically that hyperinfectivity of freshly shed pathogen affects both the existence as well as the amplitude of disease oscillations.

Numerical simulations indicate that other hyperinfectivity and immunity distributions besides fixed delays can also support disease oscillations. For example, stable periodic orbits can occur when immunity and infectivity are both gamma-distributed, with mean η and shape parameter 10 for infectivity, and mean w and shape parameter 1000 for immunity. For these distributions, the dynamics of system (5) are complex: multiple attractors can coexist, and global bifurcations play an important role. Figure 7 shows bistability between two stable periodic orbits coexisting for expected immune duration of 350 days. The period of the oscillations differs considerably between the two orbits (Figs. 7(b) and (c)); with the inner (outer) orbit having a period of 300 (110) days. A more extensive study of what immunity distributions support oscillations, and the effect of differential infectivity kernels other than step functions on these oscillations, would be of interest.

Fig. 7

Two stable periodic orbits coexist for model (5) with gamma-distributed infectivity and immunity kernel functions. Infectivity kernel f has a mean η=1/30 and shape parameter 10 while immunity kernel P has a mean w=350 days and shape parameter 1000. Other parameters are given in Table 2

An important parameter for cholera is the expected lifetime of V. cholerae outside of human hosts. This varies considerably depending upon environmental conditions (Feachem et al. 1983), and has the potential to be quite long, given the ability of V. cholerae to persist in a free-living state in association with plankton and detritus (reviewed in Nelson et al. 2009). We have used a value of 30 days here for the expected persistence time. Other studies have suggested shorter persistence times on the order of 5 days, so η=0.228 (Bertuzzo et al. 2008). We found that simulations with this value of η are qualitatively similar to those reported in Sect. 5.1.

A great deal of research has been devoted to examining seasonal oscillations for cholera in connection with environmental drivers such as rainfall, river discharge, chlorophyll levels, sea surface temperatures, and El Niño (Altizer et al. 2006; Bouma and Pascual 2001; Emch et al. 2008; Huq et al. 2005; King et al. 2008; Pascual et al. 2000, 2008; Ruiz-Moreno et al. 2007; Sanches et al. 2011). King et al. (2008) and Sanches et al. (2011) examine the effect of temporary immunity on cholera oscillations by incorporating this factor into models with seasonal variation in transmission. Systems (30) and (35) exhibit oscillations without any seasonal forcing of the equations, as found previously in SIRS models with constant periods of immunity (Hethcote et al. 1981). The effect of combining differential infectivity and temporary immunity distributions on disease dynamics is less obvious. Our finding that the degree of hyperinfectivity affects disease oscillations even when $\mathcal{R}_{0}$ is held constant complements work by Hartley et al. (2006), who point out that a hyperinfectious state for freshly shed cholera bacteria could correspond to much larger values of $\mathcal{R}_{0}$ than previously thought.