Dynamics of cholera outbreak with bacteriophage and periodic rate of contact

Abstract

In this paper, a cholera epidemic model with periodic transmission rate has been considered and discussed. It is shown that the disease free equilibrium point is globally asymptotically stable and also seen that the cholera disease is disappeared if the basic reproduction number is less than one. When the basic reproduction number is grater than one, then the endemic equilibrium is globally asymptotically stable. Finally, numerical simulations have been given for the existence of the analytical results.

1 Introduction

The cholera, a waterborne gastroenteric infection, remains a significant threat to public health in the developing countries. It is caused by the bacterium Vibrio cholerae. It is typically transmitted through water and food that have been contaminated with fecal matter from a person who is infected with the disease. Now-a-days, several number of mathematical models have been developed for understanding the dynamics of cholera disease. A mathematical model for cholera epidemic occurred in the European Mediterranean region had been developed and discussed by Capasso [1] in 1973. In this model, Capasso used two differential equations to describe the dynamics of infected people in the infected region and the dynamics of the bacterium V. cholerae. Codeco [2] extended the model of Capasso by introducing one additional equation of susceptible human population and described the dynamics of the persistence of the disease cholera. After that Codeco’s model was extended by Hartley [3] including hyperinfectious vibrio bacterium. Again, Hartley’s mathematical model was analysed by Liao and Wang [4].

Cholera disease is typically seasonal due to climatic factors, physical and many biological factors. It is observed that in Bangladesh the seasonality of cholera exhibits two peaks per year and differs from that of other diarrheal diseases [5]. Cholera disease typically increases from November to January and April to May. In the same time, the seasonal cholera disease is occurred in the peak form in April, May and June [6] in every year. There are many research papers on the cholera disease such as [7–13] etc.

It is known that the bacteriophage might control the natural population of pathogens. Moreover, the recent studies in marine microbiology also have revealed the elegant balance between bacteriophage and their mycobacterial prey. In 2009, Nelson et al. [14] explored that in a closed experimental system, the transmission of V. cholerae may be minimized when these two factors such as bacteriophage and bacterium are combined in the aquatic environments. Therefore, the dynamical interaction between bacteriophage and bacterium in pond water suggests that a model of cholera transmission should incorporate a measure for the rapid decay of bacterial culturability and predation by bacteriophage.

There are two hundreds species that infect V. cholerae known as vibriophage. In 2006 a mathematical model was described by Jensen et al. [15] in the role of bacteriophage in the control of cholera outbreak. They suggests that either bacteria in the environmental reservoir are hyperinfectious or most victims ingest bacteria amplified in food or drinking water contaminated by environmental water carrying few viable V. cholerae. The consequent reduction of bacteria numbers in the effluent might fully account for the decline in disease incidence and density of phage preying on these bacteria. In this interpretation, the outbreak drives the changes in phage populations, rather than the reverse. They showed that the large numbers of phage to the reservoir at the time of the bacterial bloom decreases the size of the epidemic. If there are few number of phage such $10^5$ virion per liter or less then there is virtually no effect on the epidemic. There are many research papers on baceriophage dynamics such as [16–19] etc. A cholera epidemic model of an optimal cost effectiveness study on Zimbabwe cholera seasonal data from 2008 to 2011 was developed by Sardar et al. [20] in 2013. We have modified this model by introducing the bacteriophage and discussed the dynamical behavior of the proposed cholera epidemic model.

In this paper, the dynamical behavior of the interaction between cholera pathogen V. cholerae and bacteriophage has been discussed. Then, the extinction and uniform persistence of the disease have been explored here. Also, the existence and stability of positive $\omega$-periodic solution have been discussed precisely. Finally, a numerical simulations have been presented to support the analytic results of the proposed model.

2 Model formulation

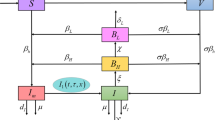
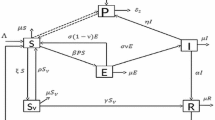
In this paper, it is considered that an area is effected with V. cholerae. So, the population N(t) at time t, consists of three kinds of populations such as (i) susceptible human S(t), (ii) infected human I(t) and (iii) recovered human R(t) i.e., $N(t)=S(t)+I(t)+R(t)$. Here, the bacterial population at time t is also considered of two types such as: (i) hyper-infectious bacteria $B_H(t)$ and (ii) low-infectious bacteria $B_L(t)$. Also here, the population of bacterio-phage P(t) has been introduced.

Now, the susceptible population is increased (i) by a constant recruitment of newborn at a rate $\Lambda _H$ and (ii) by those recovered persons who loses their temporary immunity to cholera at a rate w. It is reduced by getting infected on contact with hyper-infectious and low-infectious bacterium at a rates $\beta _H(t)\frac{B_H}{K_H+B_H}$ and $\beta _L(t)\frac{B_L}{K_L+B_L}$ respectively and also decreased by natural death at a rate $\mu _d$, where $\beta _H(t)$ and $\beta _L(t)$ have been defined in this paper as follows:

$$\begin{aligned} \beta _H(t)= & {} \beta _{H0}\left( 1+\delta cos\left( \frac{2\pi t}{365}\right) \right) \\ \beta _L(t)= & {} \beta _{L0}\left( 1+\delta cos\left( \frac{2\pi t}{365}\right) \right) \end{aligned}$$

and $\delta$ is the amplitude of seasonality.

Here, infected human is increased by those susceptible humans who get infected in contact with hyper-infectious and low-infectious vibrios and decreased by (i) those who are recovered from cholera at a rate $\gamma$, (ii) those who die due to cholera infection at a rate $\mu _c$ and (iii) those who die naturally at a rate $\mu _d$.

Again, recovered human population is increased by those infected people who get recovery from the disease at a rate $\gamma$. It is observed that the recovered population is reduced due to the loss of natural immunity to cholera at a rate w and due to the natural dies at a rate $\mu _d$.

Hyper-infectious bacterium is enriched from the amount of hyper-infectious V. cholerae bacterium in the contaminated aquatic environment due to infected human feces, vomiting etc. at a rate $\xi$.

It is assumed that hyper-infectivity bacterium losse their hyper-infectivity at a rate $\chi$. Here, it is also assumed that the both bacterium populations decrease by the consumption of phage (bacterio phage). The number of phage produced per infected bacterium (burst size) is denoted by $\beta _1$. The death rate of phage in the reservoir is $w_1$ per day. Therefore, under the above considerations a mathematical model of V. cholerae has been suggested as follows:

$$\begin{aligned} \left. \begin{array}{llll} \displaystyle \frac{dS}{dt}&{}=&{}\Lambda _H+wR-\beta _H(t)\frac{B_H S}{K_H+B_H}-\beta _L(t)\frac{B_L S}{K_L+B_L}-\mu _d S \\ \frac{dI}{dt}&{}=&{}\beta _H(t)\frac{B_H S}{K_H+B_H}+\beta _L(t)\frac{B_L S}{K_L+B_L}-(\mu _d+\mu _c+\gamma )I \,\,\,\ \\ \frac{dR}{dt}&{}=&{}\gamma I-(w+\mu _d)R \\ \frac{dB_H}{dt}&{}=&{}\xi I-\chi B_H- \gamma _1 B_H P \\ \frac{dB_L}{dt}&{}=&{} \chi B_H-\delta _L B_L-\gamma _1 B_L P \\ \frac{dP}{dt}&{}=&{} \beta _1 \gamma _1 (B_H+B_L)P-w_1P \end{array}\right\} \end{aligned}$$

(1)

The initial conditions are taken as $S(0)\ge 0,I(0)\ge 0,R(0)\ge 0,B_H(0)\ge 0,B_L(0)\ge 0, P(0)\ge 0$.

Theorem 1

The solution of the proposed model (1) $(S(t),I(t),R(t),B_H(t),B_L(t),P(t))$ is uniformly and ultimately bounded i.e., there exists a positive real number M such that $(S(t),I(t),R(t),B_H(t),B_L(t),P(t))\le (M,M,M,M,M,M)$ for $t\ge T$ where T is a fixed time.

Proof

From the first three equations of proposed model (1), it is obtained that

$$\begin{aligned} \frac{d(S+I+R)}{d t}= & {} \Lambda _H-\mu _d(S+I+R)-\mu _cI \nonumber \\\le & {} \Lambda _H-\mu _d(S+I+R) \end{aligned}$$

(2)

Solving Eq. (2) by using standard comparison theorem [21], there exists $t_1>0$ such that $S+I+R\le \frac{\Lambda _H}{\mu _d}$ for all $t\ge t_1$. Then, we have

$$\begin{aligned} S\le \frac{\Lambda _H}{\mu _d}, I\le \frac{\Lambda _H}{\mu _d} \text{ and } R\le \frac{\Lambda _H}{\mu _d}, \quad \text{ for } \text{ all }\quad t\ge t_1. \end{aligned}$$

(3)

Again, from the fourth equation of the proposed model (1), it is obtained that

$$\begin{aligned} \frac{d B_H}{d t}\le & {} \xi \frac{\Lambda _H}{\mu _d}-\chi B_H-\gamma _1 B_H P\nonumber \\\le & {} \xi \frac{\Lambda _H}{\mu _d}-\chi B_H \end{aligned}$$

(4)

Hence, again solving Eq. (4) by using standard comparison theorem, there exists $t_2\ge t_1$ such that

$$\begin{aligned} B_H(t)\le \frac{\Lambda _H}{\chi \mu _d}, \quad \text{ for } \text{ all }\quad t\ge t_2 . \end{aligned}$$

(5)

From the fifth equation of the proposed model (1), it is obtained that

$$\begin{aligned} \frac{d B_L}{d t}\le & {} \frac{\xi \Lambda _H}{\chi \mu _d}-\delta _L B_L-\gamma _1B_L P\nonumber \\\le & {} \frac{\xi \Lambda _H}{\chi \mu _d}-\delta _L B_L \end{aligned}$$

(6)

Again, also solving Eq. (6) by using standard comparison theorem, there exists $t_3\ge t_2 \ge t_1$ such that

$$\begin{aligned} B_L(t)\le \frac{\xi \Lambda _H}{\mu _d \delta _L}, \text{ for } \text{ all }\quad t\ge t_3. \end{aligned}$$

(7)

Again, from the sixth equation of the proposed model (1), it is obtained that

$$\begin{aligned} \frac{d P}{d t}\le \beta _1 \gamma _1\left( \frac{\xi \Lambda _H}{\chi \mu _d}+\frac{\xi \Lambda _H}{\mu _d \delta _L}\right) P-w_1 P \end{aligned}$$

(8)

Hence, solving Eq. (8) by using standard comparison theorem, there exists $T\ge t_1,t_2,t_3$ such that

$$\begin{aligned} P(t)\le e^{\left( \frac{\beta _1 \gamma _1 \xi \Lambda _H}{\mu _d}\left( \frac{1}{\chi }+\frac{1}{\delta _L}\right) \right) }. \end{aligned}$$

(9)

From Eqs. (3), (5), (7) and (9), let us define $M=max\{\frac{\Lambda _H}{\mu _d},\frac{ \xi \Lambda _H}{\chi \mu _d}, \frac{\xi \Lambda _H}{\delta _L \mu _d}, e^{(\frac{\beta _1 \gamma _1 \xi \Lambda _H}{\mu _d}(\frac{1}{\chi }+\frac{1}{\delta _L}))}\}$.

Thus it follows that, $S(t)\le M$, $I(t)\le M$, $R(t)\le M$, $B_H(t)\le M$, $B_L(t)\le M$ and $P(t)\le M$ for all $t\ge T$. Therefore, the solution of the system are uniformly and ultimately bounded.

3 Local stability of disease free periodic equilibrium point

Let $(R^n, R_{+}^{n})$ be the standard ordered n-dimensional Euclidean space with a norm ||.||. For $u,v\in R^n$, we denote $u\ge v$ if $u-v \in R_{+}^{n}$; $u>v$, if $u-v\in R^n$; $u\gg v$, if $u-v \in Int(R_+^n)$.

Let A(t) be a continuous, cooperative, irreducible and $\omega$ periodic $n \times n$ matrix function. Then $\phi _A(t)$ be a fundamental solution matrix of

$$\begin{aligned} \frac{d x}{d t}= A(t)x \end{aligned}$$

(10)

Let $\rho (\phi _A(\omega ))$ be the spectral radius of $\phi _A(\omega )$. According to Perron–Frobenius theorem, $\rho (\phi _A(\omega ))$ is the simple principal eigenvalue of $\phi _A(\omega )$ and it admits an eigenvector $v^*$ which is grater than equal to zero vector.

Lemma 1

(Zhang and Zhao [22]) Let $s=\frac{1}{\omega } ln \rho (\phi _A(\omega ))$, then there exists a positive $\omega$ periodic function v(t) such that $e^{st}v(t)$ is a solution of (10).

In the following, we calculate the basic reproduction number of proposed system (1). It is easy to see that the proposed system (1) has exactly one disease free equilibrium point $E_0(S_0, 0,0,0,0,0)$ where $S_0=\frac{\Lambda _H}{\mu _d}$.

Now, $F(t)= \left[ \begin{array}{ccc} 0 &{} \frac{\beta _H(t)\Lambda _H}{K_H \mu _d} &{} \frac{\beta _L(t)\Lambda _H}{K_L \mu _d} \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array}\right]$,

$V(t)= \left[ \begin{array}{ccc} (\gamma +\mu _c+\mu _d)&{} 0 &{} 0 \\ -\xi &{} \chi &{} 0 \\ 0 &{} -\chi &{} \delta _L \\ \end{array}\right]$

Let Y(t, s) is an $3\times 3$ matrix solution of the system

$$\begin{aligned} \frac{d Y(t,s)}{d t}=-V(t)Y(t,s) \end{aligned}$$

(11)

for any $t\le s$, $Y(s,s)=I$ where I is an $3\times 3$ identity matrix.

Let $C_\omega$ be the ordered banach space of all $\omega$ periodic functions from R to $R^3$ which is equipped with maximum norm $||.||_\infty$ and the positive cone $C_\omega ^+=\{\phi \in C_\omega : \phi (t)\ge 0, \text{ for } \text{ all } \text{ t } \text{ in } R\}$. Now, using Eq. (11) we consider the linear operator $L: C_\omega \longrightarrow C_\omega$ by

$$\begin{aligned} (L\phi )(t)=\int ^{+\infty }_{0} Y(t,t-a)F(t-a)\phi (t-a)da \end{aligned}$$

(12)

for any $t\in R$ and $\phi \in C_\omega$.

Finally, from the Eq. (12) we define the basic reproduction number $R_0$ for the system (1) as the spectral radius of L i.e., $R_0=\rho (L)$ which has been motivated by the concept of next generation method introduced in the article of [23–25]. From the above discussion, the following theorem for the local asymptotically stability of disease free equilibrium $E_0(S_0, 0,0,0,0,0)$ has been obtained.

Theorem 2

(Wang and Zhao [23]) The following statements are valid

• 1. $R_0=1$ if and only if $\rho (\phi _{F-V}(\omega ))=1$

• 2. $R_0>1$ if and only if $\rho (\phi _{F-V}(\omega ))>1$

• 3. $R_0<1$ if and only if $\rho (\phi _{F-V}(\omega ))<1$

Thus, we can say that the disease free equilibrium $E_0(S_0, 0,0,0,0,0)$ is locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$.

4 Global stability of disease free periodic equilibrium point

Theorem 3

If $R_0<1$, then the disease free periodic state is globally asymptotically stable.

Proof

From second, fourth and fifth equations of the system (1) we have

$$\begin{aligned} \frac{d I}{d t}= & {} \beta _H(t)\frac{B_H S}{K_H+B_H}+\beta _L(t)\frac{B_L S}{K_L+B_L}\nonumber \\&-(\gamma +\mu _d+mu_c)I\nonumber \\\le & {} \beta _H(t)\frac{B_H }{K_H+B_H}\frac{\Lambda _H}{\mu _d}+\beta _L(t)\frac{B_L }{K_L+B_L}\frac{\Lambda _H}{\mu _d}\nonumber \\&-(\gamma +\mu _d+mu_c)I\nonumber \\\le & {} \beta _H(t)\frac{\Lambda _H B_H }{K_H \mu _d}+\beta _L(t)\frac{\Lambda _H B_L }{\mu _d K_L}\frac{\Lambda _H}{\mu _d}\nonumber \\&-(\gamma +\mu _d+mu_c)I \end{aligned}$$

(13)

$$\begin{aligned} \frac{d B_H}{d t}\le & {} \xi (t)I-\chi B_H \end{aligned}$$

(14)

$$\begin{aligned} \frac{d B_L}{d t}\le & {} \chi B_H-\delta _L B_L \end{aligned}$$

(15)

Then, for all $t\ge 0$, hence $0\le S(t)\le \frac{\Lambda _H}{\mu _d}$, $B_H(t)\ge 0$, $B_L(t)\ge 0$ and $P(t)\ge 0$. Now, from the Eqs. (13), (14) and (15) we consider the following auxiliary system:

$$\begin{aligned} \frac{d I}{d t}= & {} \beta _H(t)\frac{\Lambda _H B_H }{K_H \mu _d}+\beta _L(t)\frac{\Lambda _H B_L }{\mu _d K_L}\frac{\Lambda _H}{\mu _d}\nonumber \\&-(\gamma +\mu _d+mu_c)I\nonumber \\ \frac{d B_H}{d t}= & {} \xi I-\chi B_H \nonumber \\ \frac{d B_L}{d t}= & {} \chi B_H-\delta _L B_L \nonumber \end{aligned}$$

which can be written as

$$\begin{aligned} \frac{d X}{d t}=(F(t)-V(t))X \end{aligned}$$

(16)

where $X=(I(t),B_H(t),B_L(t))^T$.

Then using above Lemma 1, there exists a positive $\omega$-periodic function $\bar{X}(t)$ such that $X(t)=e^{s t} \bar{X}(t)$ is a solution of the above Eq. (16) where $s=\frac{1}{\omega }ln \rho (\phi _{F-V}(\omega ))$. Again, from Theorem 2, we know that for $R_0{<}1, \rho (\phi _{F-V}(\omega )){<}1$, so s must be a negative constant. Therefore, when $t\rightarrow \infty$, we have $X(t)\rightarrow 0$.

$$\begin{aligned}&i.e., \lim \limits _{t\rightarrow \infty }I(t)=0, \lim \limits _{t\rightarrow \infty }B_H(t)=0 \text{ and } \lim \limits _{t\rightarrow \infty }B_L(t)=0.\\&i.e., \lim \limits _{t\rightarrow \infty }R(t)=0, \lim \limits _{t\rightarrow \infty }P(t)=0 \text{ and } \lim \limits _{t\rightarrow \infty }S(t)=\frac{\Lambda _H}{\mu _d} \end{aligned}$$

Hence, the above implies that the disease free equilibrium point $E_0$ is globally asymptotically stable.

5 Uniform persistence of the disease

Theorem 4

If $R_0>1$, there exists a positive constant $\epsilon$ such that for all initial value $(S(0),I(0),R(0),B_H(0),B_L(0),P(0))\in \{(S,I,R,B_H,B_L,P)\in R_+^6: I>0, B_H>0, B_L>0\}$, the solution of system (1) satisfies the following

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }inf I(t)\ge \epsilon , \lim \limits _{t\rightarrow \infty }inf B_H(t)\ge \epsilon \text{ and } \lim \limits _{t\rightarrow \infty }inf B_L(t)\ge \epsilon . \nonumber \end{aligned}$$

i.e., for $R_0>1$, the disease in system (1) is uniformly persistent.

Proof

Let us consider the sets $X=R_{+}^{6}$, $X_0=\{(S,I,R,B_H,B_L,P)\in R_+^6: I>0, B_H>0, B_L>0\}$ and $\partial X_0=X\setminus X_0$. Next, we define a poincare map $P:R_+^6\longrightarrow R_+^6$ satisfying $P(x^0)=u(\omega ,x^0)$,$\forall x^0\in R_+^6$ where $u(t,x^0)$ be the unique solution of system (1) satisfying $u(0,x^0)=x^0$.

At first, we show that P is uniformly persistent with respect to $(X_0,\partial X_0)$. It is easy to see from the system (1) that X and $X_0$ are positively invariant. Moreover, $\partial X_0$ is relatively closed set in X. Now from Theorem 1, it follows that the solutions of the system (1) are uniformly and ultimately bounded. Thus, the semiflow P is point dissipative on $R_+^6$ and $P:R_+^6\rightarrow R_+^6$ is compact by Theorem 3.4.8 in [26]. Then, it follows that P admits a global attractor which attracks every bounded set in $R_+^6$. Now, we define another set $M_\partial$ as

$$\begin{aligned} M\partial= & {} \{(S(0),I(0),R(0),B_H(0),B_L(0),P(0))\in \partial X_0:\nonumber \\&P^m(S_0,I_0,R_0,B_H{_0},B_L{_0},P_0)\in \partial X_0, \forall m\in N \cup {0}\}. \end{aligned}$$

Next, it is claimed that

$$\begin{aligned} M\partial =\{(S,0,R,0,0,P): S\ge 0,R\ge 0,P\ge 0\}. \end{aligned}$$

In fact, it is obvious that

$$\begin{aligned} \{(S,0,R,0,0,P): S\ge 0,R\ge 0,P\ge 0\}\subseteq M\partial \end{aligned}$$

For any $(S(0),I(0),R(0),B_H(0),B_L(0),P(0))\in \partial X_0/\{(S,0,R,0,0,P): S\ge 0,R\ge 0,P\ge 0\}$, if $I(0)=0,B_H(0)=0,B_L(0)>0$ it is clear that $S>0$ and $B_L>0$ for all $t>0$. Now from the second equation of (1) we have $\dot{I}(0)=\beta _L(t)\frac{S(0)B_L(0)}{K_L+B_L(0)}>0$ $\Rightarrow I(0)>0$. Thus from the fourth equation of (1) we have $\dot{B_H}(0)=\xi I(0)>0$ else if $I(0)=0$,$B_L(0)=0$ and $B_H>0$. Then similarly we can show that $\dot{I}(0)>0$ and $B_H(0)>0$ and similarly for other cases also. Therefore, if $(S(0),I(0),R(0),B_H(0),B_L(0),P(0))\notin \{(S,0,R,0,0,P):S\ge 0,R\ge 0,P\ge 0\}$ then $(S(t),I(t),R(t),B_H(t),B_L(t),P(t))\notin \partial X_0$ for simultaneously small $t>0$. This implies that $M_\partial \subseteq \{ (S,0,R,0,0,P):S\ge 0,R\ge 0,P\ge 0\}$. Therefore, we have $M_\partial =\{(S, 0, R, 0,0,P):S\ge 0,R\ge 0,P\ge 0\}$. Clearly, $E_0$ is one fixed point of P in $M_\partial$. If $(S(t),I(t),R(t),B_H(t),B_L(t),P(t))$ is a solution of system (1) initiating from $M_\partial$, it then follows from (1) that $S(t)\rightarrow S_0, I(t)\rightarrow 0, R(t)\rightarrow 0, B_H(t)\rightarrow 0,B_L(t)\rightarrow 0,P(t)\rightarrow 0$ as $t\rightarrow \infty$. So any solution of (1) initiating in $M_\partial$ will remain into $M_\partial$.

We will now show that $\{E_0\}$ is an acyclic covering of $E_0$. It is enough to show that $\{E_0\}$ isolated invariant subset of $M_\partial$ i.e., $W^s(E_0)\cap X_0=\emptyset$, where $W^s(E_0)$ is the stable set of $E_0$.

Let $x^0=(S(0),I(0),R(0),B_H(0),B_L(0),P(0))\in X_0$, then by the continuity of solution with respect to initial values $\forall x\in (0, \frac{\Lambda _H}{\mu _d})$, then there exists $\xi >0$ such that $\forall x^0\in X_0$ with $||x^0-E_0||\le \xi$, it follows that $||u(t,x^0)-u(t,E_0)||\le \epsilon \forall t \in [0,w]$. To show $x^0\in X_0\Rightarrow x^0\notin W^s(E_0)$, it is enough to show that $\lim \limits _{m\rightarrow \infty }d(P^m(x^0),E_0)\ge \xi$ for some $m>0$. If not let $\exists x^0 \in X_0$ such that $\lim \limits _{m\rightarrow \infty }d(P^m(x^0),E_0)<\eta$ for all $m>0$. This implies that $||u(t,P^m(x^0))-u(t,E_0)||\le \epsilon$, $\forall t\in [0,w]$.

To show, $x^0\in X_0\Rightarrow x^0\notin W^s(E_0)$, it is enough to show that $\lim \limits _{m\rightarrow \infty } sup \text{ d } (P^m(x^0),E_0) \ge \xi$ for some $m>0$. If not let $\exists x^0\in X_0$ such that $\lim \limits _{m\rightarrow \infty } sup \text{ d } (P^m(x^0),E_0)\ge \eta$ for all $m>0$. This implies that $||u(t,P^m(x^0))-u(t,E_0)||<\epsilon$, $\forall t\in [0,w]$. For any $t\ge 0$, let $t=mw+t_1$ where $t_1\in [0,w]$ and $m=[\frac{t}{w}]$ which is the greatest integer less than or equal to $\frac{t}{w}$. Then, we have $||u(t,P^m(x^0))-u(t,E_0)||=||u(t_1,P^m(x^0))-u(t,E_0)||\le \epsilon$, $\forall t\in [0,w]$.

By selecting $(S(t),I(t),R(t),B_H(t),B_L(t), P(t))=u(t,x^0)$, it follows that

$$\begin{aligned}&\frac{\Lambda _H}{\mu _d}-\epsilon \le S(t)\le \frac{\Lambda _H}{\mu _d}+\epsilon , 0\le I \le \epsilon , 0\\&\quad \le R \le \epsilon , 0 \le B_H \le \epsilon , 0\le B_L \le \epsilon , 0\le P \le \epsilon \end{aligned}$$

for all $t\ge 0$. Then, we have $\frac{S(t)}{K_H+B_H}\ge (\frac{\Lambda _H}{\mu _d K_H}-\frac{\epsilon }{K_H+\epsilon })$ and $\frac{S(t)}{K_L+B_L}\ge (\frac{\Lambda _H}{\mu _d K_L}-\frac{\epsilon }{K_L+\epsilon })$. Therefore, from system (1) we have

$$\begin{aligned} \frac{d I}{d t}\ge & {} \beta _H(t)\left( \frac{\Lambda _H}{\mu _d K_H}-\frac{\epsilon }{K_H+\epsilon }\right) B_H\nonumber \\&+\,\beta _L(t)\left( \frac{\Lambda _H}{\mu _d K_L}-\frac{\epsilon }{K_L+\epsilon }\right) B_L \end{aligned}$$

(17)

$$\begin{aligned} \frac{d B_H}{d t}= & {} \xi I-\chi B_H \end{aligned}$$

(18)

$$\begin{aligned} \frac{d B_L}{d t}= & {} \chi B_H-\delta _L B_L \end{aligned}$$

(19)

Then, from Eqs. (17),(18) and (19) a matrix $M_{\epsilon }(t)$ can be obtained as follows:

$$\begin{aligned} M_{\epsilon }(t)= \left[ \begin{array}{ccc} 0 &{}\quad \beta _H(t)\frac{\epsilon }{K_H+\epsilon } &{}\quad \beta _L(t)\frac{\epsilon }{K_L+\epsilon } \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right] \end{aligned}$$

Already, from Theorem 2, it is known that as $R_0>1$ so $\rho (\phi _{F-V}(\omega ))>1$, choosing $\epsilon$ is very very small such that $\rho (\phi _{F-V-M_{\epsilon }}(\omega ))>1$. Again, by Lemma 1 and the standard comparison principle, there exists a positive $\omega$ periodic function $f_2(t)$ such that $\jmath (t)\ge f_2(t)e^{s_2(t)}$ where $\jmath (t)=(I(t),B_H(t),B_L(t))^T$ and $s_2=\frac{1}{\omega }ln\rho (\phi _{F-V}(\omega ))>0$. This implies that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty } I(t)=\infty , \lim \limits _{t\rightarrow \infty } B_H(t)=\infty \text{ and } \lim \limits _{t\rightarrow \infty } B_L(t)=\infty \nonumber \end{aligned}$$

which is a contradiction in $M_\partial$. Hence, $W^s(E_0)\cap X_0=\emptyset$. Then, by Theorem 1.3.1 [26] we obtain that P is uniformly persistent with respect to $(X_0,\partial X_0)$. Thus, by Theorem 1.3.1 [26] it follows that the solution of (1) is uniformly persistent.

6 Periodic solution

In this section, the existence and stability of a positive periodic solution of the system (1) have been investigated in Theorem 5 as follows:

Theorem 5

If $R_0>1$, then the system (1) admits a positive $\omega$-periodic solution which is globally asymptotically stable.

Proof

We have already proved in Theorem 3 that the poincare map, $P :R^6_+\longrightarrow R^6_+$ of the system (1) is point dissipative and compact as well as P is uniformly persistent with respect to $(X_0,\partial X_0)$. Then, it follows from Theorem 1.3.6 [26] that the poincare map P has a fixed point $(\tilde{S},\tilde{I},\tilde{R},\tilde{B_H},\tilde{B_L},\tilde{P})\in Int(R^6_+)$. Hence, $u(t,(\tilde{S},\tilde{I},\tilde{R},\tilde{B_H},\tilde{B_L},\tilde{P}))\in Int(R^6_+)$ for all $t>0$. Thus, $(\tilde{S},\tilde{I},\tilde{R},\tilde{B_H},\tilde{B_L},\tilde{P})$ is a positive $\omega -$ periodic solution of system (1) due to the definition of the semiflow P. $\square$

Let $\tilde{X}=(\tilde{S},\tilde{I},\tilde{R},\tilde{B_H},\tilde{B_L},\tilde{P})$ be positive $\omega$-periodic solution of system (1) and $X(t)=(S(t),I(t),R(t),B_H(t),B_L(t),P)$ be any solution of system (1) initiating from nonnegative initial values. Then, a Lyapunov function is defined as follows:

$$\begin{aligned}&L(S,I,R,B_H,B_L,P)=|S(t)-\tilde{S}(t)|+|I(t)-\tilde{I}(t)|\nonumber \\&\quad +\,|R(t)-\tilde{R}(t)|\!+\!\frac{\mu _d}{\xi }|B_H(t)\!-\!\tilde{B_H}(t)|\nonumber \\&\quad +\,\frac{\mu _d}{\xi }|B_L(t)-\tilde{B_L}(t)|+|P(t)-\tilde{P}(t)| \end{aligned}$$

(20)

Now, the right upper derivative $D^+ L(t)$ of Eq. (20) of the system (1) is obtained as follows:

$$\begin{aligned}&D^+ L(S,I,R,B_H,B_L,P)=sign(S(t)-\tilde{S}(t))\nonumber \\&\quad \left\{ \beta _H(t) \frac{\tilde{B_H}\tilde{ S}}{K_H\!+\!\tilde{B_H}}\!+\!\beta _L(t)\frac{\tilde{B_L}\tilde{ S}}{K_L\!+\!\tilde{B_L}}\!-\!\beta _H(t) \frac{B_H S}{K_H+B_H}\right. \nonumber \\&\qquad \left. -\beta _L(t)\frac{B_L S}{K_L\!+\!B_L}\!+\!w(R-\tilde{R})-\mu _d(S-\tilde{S})\right\} \nonumber \\&\,\quad \quad +\,sign(I(t)-\tilde{I}(t))\nonumber \\&\quad \left\{ \beta _H(t)\frac{B_H S}{K_H\!+\!B_H} \!+\!\beta _L(t)\frac{B_L S}{K_L+B_L}\!-\!\beta _H(t) \frac{\tilde{B_H} \tilde{S}}{K_H\!+\!\tilde{B_H}}\right. \nonumber \\&\qquad \left. -\beta _L(t)\frac{\tilde{B_L} \tilde{S}}{K_L+\tilde{B_L}} -(\gamma +\mu _c+\mu _d)(I(t)-\tilde{I}(t))\right\} \nonumber \\&\quad +\,sign(R(t)-\tilde{R}(t))\left\{ \gamma (I(t)-\tilde{I}(t))\right. \nonumber \\&\quad \left. -\,(w+\mu _d)(R(t)-\tilde{R}(t))\right\} +sign(B_H(t)\nonumber \\&\quad -\,\tilde{B_H}(t))\frac{\mu _d}{\xi }\left\{ \xi (I(t)-\tilde{I}(t))-\chi (B_H(t)-\tilde{B_H}(t))\right. \nonumber \\&\quad \left. -\,\gamma _1(\tilde{B_H}\tilde{P}-B_H P)\right\} +sign(B_L(t)\nonumber \\&\quad -\,\tilde{B_L}(t))\frac{\mu _d}{\xi }\left\{ \chi (B_H(t)\!-\!\tilde{B_H}(t))\!-\!\delta _L(B_L(t)-\tilde{B_L}(t))\right. \nonumber \\&\quad \left. -\,\gamma _1(\tilde{B_L}(t)\tilde{P}(t)-B_L(t) P(t))\right\} +sign(P(t)-\tilde{P}(t))\nonumber \\&\quad \times \left\{ \beta _1 \gamma _1(B_H(t) P(t)-\tilde{B_H}(t) \tilde{P}(t))\right. \nonumber \\&\quad \left. + \beta _1 \gamma _1(B_L(t)P(t)\!-\!\tilde{B_L}(t)\tilde{P}(t)) \!-\!w_1(P(t)\!-\!\tilde{P}(t))\right\} \nonumber \\&\le -\mu _d|S(t)-\tilde{S}(t)|-\mu _c|I(t)-\tilde{I}(t)|-\mu _d|R-\tilde{R}|\nonumber \\&\quad -\frac{\mu _d \delta _L}{\xi }|B_L(t)-\tilde{B_L}(t)| -\,\frac{w_1}{\beta _1}|P(t)-\tilde{P}(t)|\nonumber \\&\le -K(|S(t)-\tilde{S}(t)|+|I(t)-\tilde{I}(t)|+|R-\tilde{R}|\nonumber \\&\quad +|B_L(t)-\tilde{B_L}(t)|+|P(t)-\tilde{P}(t)|) \end{aligned}$$

(21)

where $K=min\{\mu _d, \mu _c, \frac{\mu _d \delta _L}{\xi },\frac{w_1}{\beta _1}\}$.

Now, integrating the above Eq. (21) from $\bar{t}$ to $\infty$, it is obtained that

$$\begin{aligned}&L(t)+K\int ^\infty _{\bar{t}}(|S(t)-\tilde{S}(t)|+|I(t)-\tilde{I}(t)|+|R-\tilde{R}|\nonumber \\&\qquad +|B_L(t)-\tilde{B_L}(t)|+|P(t)-\tilde{P}(t)|)ds\nonumber \\&\quad \le L(\bar{t}) \end{aligned}$$

(22)

provided that $t>\bar{t}$. Then, from Eq. (22) it follows that

$$\begin{aligned}&\sup _{t\rightarrow \infty }K\int ^\infty _{\bar{t}}(|S(t)-\tilde{S}(t)|+|I(t)-\tilde{I}(t)|+|R-\tilde{R}|\\&\qquad +|B_L(t)-\tilde{B_L}(t)|+|P(t)-\tilde{P}(t)|)ds\\&\quad \le \frac{L(\bar{t})}{K}<+\infty \end{aligned}$$

$$\begin{aligned} \text{ i.e., }&\lim _{t\rightarrow \infty }|S(t)-\tilde{S}(t)|=0, \lim _{t\rightarrow \infty }|I(t)-\tilde{I}(t)|=0, \\&\lim _{t\rightarrow \infty }|R(t)-\tilde{R}(t)|=0, \\&\lim _{t\rightarrow \infty }|B_H(t)-\tilde{B_H}(t)|=0, \lim _{t\rightarrow \infty }|B_L(t)-\tilde{B_L}(t)|=0 \\&\text{ and } \lim _{t\rightarrow \infty }|P(t)-\tilde{P}(t)|=0. \end{aligned}$$

Therefore, the solution $(\tilde{S}(t),\tilde{I}(t),\tilde{R}(t),\tilde{B_H}(t),\tilde{B_L}(t),\tilde{P}(t))$ is globally asymptotically stable.

7 Numerical simulations

For numerical simulation to illustrate the proposed mathematical model, the standard software MATLAB 2010a has been used. After finding the value of $R_0$ numerically using the parametric values in Table 1, it has been shown that when disease persists and disappears from the human population.

Table 1 The parameters used in the simulations

Now, using the following initial values of the state variables such as $S(0)=800{,}000,I(0)=800,R(0)=100, B_H(0)=3{,}000{,}000,B_L(0)=3{,}000{,}000, P(0)=300{,}000$ and also taking $K_H=10^9,K_L=10^9,\delta =0.75, B_{H0}=0.2143, B_{L0}=0.2$, Fig. 1 has been drawn from which it is observed that when $R_0=0.6043<1$, then it is confirmed that the disease free equilibrium point of the system (1) is globally asymptotically stable. Therefore, it is concluded that the cholera disease will be disappeared from the human population when the basic reproduction number must be less than one in the presence of bacteriophage.

Fig. 1

The graphical structure of solution of the proposed system (1) near the disease free equilibrium point when $R_0<1$

Again, using the following initial values of the state variables such as $S(0)=8000,I(0)=800,R(0)=100, B_H(0)=30{,}000,B_L(0)=30{,}000, P(0)=3000$ and also $K_H=10^9,K_L=\frac{10^9}{7},\delta =0.75, B_{H0}=0.2143, B_{L0}=0.2$, Fig. 2 has been drawn from which it is observed that when $R_0=4.2030>1$, then it is confirmed that the disease persists in the system (1) and it is globally asymptotically stable. Therefore, it is concluded that the cholera disease will be positively persisted in the human population when the basic reproduction number is grater than one in the presence of bacteriophage.

Fig. 2

The representation of solution of the proposed system (1) near the endemic equilibrium point when $R_0>1$

Using the same parametric values and initial condition that is used in Fig. 2, Fig. 3 has been drawn and from this figure it is seen that the limit cycle of each population such as susceptible human, infected human, recovered human, hyper-infectious V. cholerae bacteria and low-infectious V. cholerae bacteria with respect to bacteriophage is stable. Again, it is known that the stable limit cycles are example of attractors. So, they imply self-sustained oscillations i.e., the closed trajectory describes perfect periodic behavior of the system and any small perturbation from this closed trajectory causes the system to return to it, making the system stick to the limit cycle.

Fig. 3

The limit cycle of the proposed system (1) with respect to the bacteriophage

8 Conclusion

In this paper, a cholera epidemic model with periodic transmission rate has been discussed. Here, the total human population is divided into three subpopulations such as (i) susceptible human (ii) infected human (iii) recovered human and total bacterial population into three subpopulations such as (i) hyper-infectious V. cholerae bacterium (ii) low-infectious bacterium (iii) bacteriophage. A transmission model that accurately predicts the magnitude of an emerging outbreak would provide public health authorities with useful information to appropriately scale their responses. Interventions that target vital steps in transmission might be effective for the prevention of the outbreak. Host immunity, pathogen hyperinfectivity and phages are all factors that can be leveraged for outbreak control. The disease free equilibrium point is globally asymptotically stable and the cholera disease is disappeared if the basic reproduction number is less than one. It is observed that when the basic reproduction number is grater than one, then the endemic equilibrium is globally asymptotically stable and the disease persists in the human population. It is also observed that the system has a stable limit cycle with respect to bacteriophage and this closed trajectory describes perfect periodic behavior of the proposed system. So, Numerical simulations of the mathematical model supports our analytical results.