Nonlocal strain gradient-based quasi-3D nonlinear dynamical stability behavior of agglomerated nanocomposite microbeams

Abstract

An efficient numerical quasi-3D beam model is introduced to analyze the effect of carbon nanotube (CNT) agglomeration on the nonlinear dynamical stability characteristics of agglomerated beams at microscale made of agglomerated CNT-reinforced nanocomposites. For this objective, the constructive material properties are estimated based upon a micromechanical homogenization scheme containing only two parameters to capture the associated agglomeration of randomly oriented CNTs, while the nonlocal strain gradient continuum theory of elasticity is enrolled to apprehend various size dependency features. The unconventional nonlinear governing differential equations of motion are solved numerically via the shifted Chebyshev–Gauss–Lobatto discretization pattern together with the pseudo-arc-length continuation strategy. The size-dependent frequency–load–deflection characteristic curves are traced corresponding to different degrees of agglomeration including complete and partial ones. It is revealed that for an agglomerated CNT-reinforced nanocomposite microbeam in which the most CNTs are inside clusters, a higher value of the cluster volume fraction results in to reduce the significance of the softening and stiffing characters associated with the nonlocal and strain gradient small-scale effects, respectively. However, for an agglomerated CNT-reinforced nanocomposite microbeam in which the most CNTs are outside clusters, increasing the value of the cluster volume fraction plays an opposite role in the size dependency features.

1 Introduction

Via incorporating nanoscaled particles into a matrix having standard properties, one of advanced materials developed within recent decades namely as nanocomposite can be achieved which has been demonstrated a wide range of applications having various disciplines. To express some cases in this regard, Pitchan et al. [1] introduced polyetherimide nanocomposites including functionalized multi-walled carbon nanotubes (CNTs) having aerospace application. Sahmani et al. [2, 3] prepared ceramic-based nanocomposite beam-type structures having biocompatibility used space holder and additive manufacturing techniques for bony implant applications. Fu et al. [4] fabricated nanocomposites having protein adsorption capability containing vaterite nanospheres using aggregation mechanism. Ciplak et al. [5] introduced graphene-based nanocomposites having supercapacitor property via low-cost and green approach. Sahmani et al. [6] employed 3D-printing method to manufacture calcium phosphate polymeric nanocomposites with periodic cellular topologies using for bone tissue applications. Oraibi and Kadhim [7] manufactured polymeric nanocomposites containing barium titanate nanoparticles using for piezoelectric applications. Somaily [8] utilized a one pot facile flash-combustion technique to prepare nickel oxide-contained nanocomposites having excellent characters for using in optoelectronic cases.

On the other hand, utilizing advanced materials such as nanocomposites in design and manufacture structures at microscale and nanoscale is one of the most interesting topics among fields of research study in recent years. For instance, Rafiee et al. [9] studied the nonlinear dynamic stability behavior of imperfect piezoelectric plates reinforced with carbon nanotubes in the presence of coupling between in-plane and lateral responses. Ansari et al. [10] explored postbuckling characteristics of Euler–Bernoulli beams at nanoscale including the small-scale effect of surface stress. Nguyen et al. [11] introduced quasi-3D isogeometric formulations for size-dependent analysis of nanoplates based on the nonlocal continuum theory. Zhang et al. [12] studied nonlinear stability response of sandwich nanocomposite plates under bi-axial compressive load. Kitipornchai et al. [13] predicted natural frequencies of nanocomposite porous beams having graded distributions of porosity and nanofillers. Sahmani and Aghdam [14] developed nonlocal strain gradient beam model for nonlinear stability analysis of lipid supramolecular microtubules. El-Borgi et al. [15] investigated torsional oscillations of viscoelastic rod at microscale on the basis of the nonlocal strain and velocity gradient elasticity theory. Fu et al. [16] proposed an analytical solution for the sound transmission as well as wave excitation in stiffened double multilayer composite plates. Duc et al. [17] carried out nonlinear dynamical behavior of nanocomposite curved shallow shells subjected to the temperature change including geometrical imperfection. Borjalilou et al. [18] studied different linear mechanical behaviors of functionally graded nanocomposite beams at nanoscale based upon the nonlocal Timoshenko beam model. Sahmani and Safaei [19] established nonlocal strain gradient beam models for nonlinear postbuckling characteristics of bi-directional graded composite microbeams under various loading conditions. Gao et al. [20] anticipated snap-buckling behavior of functionally graded sandwich nanocomposite curved nanobeams based on the nonlocal strain gradient continuum theory. Thai et al. [21] developed size-dependent meshfree models to analyze free oscillations of functionally graded CNT-reinforced nanocomposite plates at nanoscale and microscale. Yi et al. [22] predicted the influence of vibrational mode interactions on the size-dependent forced oscillation response of porous composite nanoshells including the surface stress effect. Yuan et al. [23], and Yang et al. [24] established unconventional conical shell models to capture various types of size dependency in nonlinear stability and oscillations of functionally graded inhomogeneous truncated conical microshells.

To manifest some more recent research works in this field of study, Liu et al. [25] reported critical buckling loads of axially functionally graded nanocomposite Euler–Bernoulli beams using state-space method. Yue et al. [26] established a nonlocal strain gradient Timoshenko beam model for thermoelastic analysis of nanobeams. Yang et al. [27], and Rao et al. [28] introduced isogeometric analyses to anticipate linear and nonlinear bending and vibrations of composite microplates having non-uniform thickness. Fan et al. [29] employed the nonlocal strain gradient continuum elasticity theory together with an isogeometric plate model for nonlinear vibration characteristics of composite microplates. Wu et al. [30] proposed a unified size-dependent plate formulations to examine static flexural response of plates at microscale and nanoscale. Kazemi et al. [31] explored dynamical large deformations in CNT-reinforced nanocomposite cylinders incorporating large strain within the interphase region. Naskar et al. [32] predicted the surface stress type of size effect on the electromechanical responses of functionally graded nanocomposites using a semi-analytical technique. Chu et al. [33] and Zuo et al. [34] incorporated different strain gradient tensors to analyze nonlinear free vibrations of isogeometric microplates various oscillation amplitudes. Tao and Dai [35] presented nonlinear transient responses of sandwich nanocomposite microplates integrated with porous layers incorporating the couple stress size dependency. Taati et al. [36] analyzed size-dependent nonlinear free oscillations of nanocomposite beams at nanoscale using a perturbation-based nonlocal formulations. Liu et al. [37], and Yang et al. [38] established modified couple stress-based meshfree shell models for postbuckling analysis of randomly reinforced nanocomposite microshells under axial and lateral pressures. Saiah et al. [39] calculated natural frequencies of laminated nanocomposite plates containing piece-wise graphene-reinforced layers with various lay-up arrangements. Jalaei et al. [40] explored the transient response of geometrical imperfect nanobeams made of functionally graded magnetic composites on the basis of the strain gradient elasticity. Zhao et al. [41] introduced a probabilistic nanocomposite shell model for postbuckling analysis of strain gradient-based microshells under axial and lateral compressions. Ma et al. [42] established quasi-3D beam formulations for nonlocal strain gradient nonlinear bending of functionally graded composite microplates. Wang et al. [43] indicated the hygrothermal effects on the critical buckling loads of bi-directional functionally graded composite microbeams in the presence of nonlocality and strain gradient size effect. Wei and Qing [44] developed modified couple stress-based plate model for bending, buckling and free oscillations of bi-directional graded composite circular microplates. Wang et al. [45] predicted the nonlinear stability behavior of porous plates at microscale in the presence of various microstructural-dependent strain gradient tensors.

The main aim of the current research investigation is to analyze the size-dependent quasi-3D nonlinear dynamical stability characteristics of agglomerated nanocomposite microbeams reinforced with agglomerated randomly oriented CNTs. In this regard, the nonlocal strain gradient continuum elasticity is applied to a quasi-3D beam theory incorporating the sinusoidal transverse shear and normal shape functions in conjunction with geometrical nonlinearity. The constructive material properties are extracted based upon a micromechanical homogenization scheme containing only two parameters to capture the associated agglomeration of randomly oriented CNTs. Afterwards, an efficient numerical solving process using the shifted Chebyshev–Gauss–Lobatto discretization pattern together with the pseudo-arc-length continuation strategy is employed to trace the associated size-dependent nonlinear responses.

2 Quasi-3D nonlocal strain gradient-based beam formulations

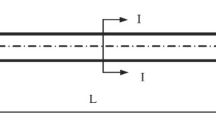
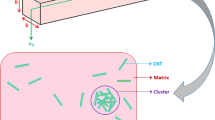
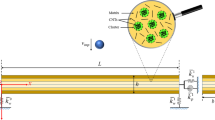
In Fig. 1, a nanocomposite microbeam having the length of $L$ and thickness of $h$ reinforced by randomly oriented CNTs is displayed. As it is shown, due to bundling as well as clustering of CNTs having low bending rigidity, it is necessary to consider the CNT agglomeration. To capture the effective material properties for a randomly oriented CNT-reinforced nanocomposite material incorporating the influence of the CNT agglomeration, Shi et al. [46] introduced a two-parameter homogenization scheme. Based upon this micromechanical model, the total CNT volume fraction related to the selected representative volume element (RVE) is divided to two parts as follows [46]:

$${V}_{\text{CNT}}={V}_{\text{CNT}}^{\text{in}-\text{cluster}}+{V}_{\text{CNT}}^{\text{out}-\text{cluster}},$$

(1)

in which ${V}_{\text{CNT}}^{\text{in}-\text{cluster}}$ and ${V}_{\text{CNT}}^{\text{out}-\text{cluster}}$ stand for the CNT volume fractions associated with inside and outside of clusters, respectively. Accordingly, in order to describe the agglomeration feature, two parameters are taken into account as [46]

$$\eta =\frac{{V}_{\text{cluster}}}{V}, \zeta =\frac{{V}_{\text{CNT}}^{\text{in}-\text{cluster}}}{{V}_{CNT}} \left(\eta \ge 0, \zeta \le 1\right),$$

(2)

where ${V}_{\text{cluster}}$ denotes the cluster volume fraction within the selected RVE. The parameter $\eta$ refers to the ratio of CNT volume fraction to the total RVE volume. On the other hand, $\zeta$ represents the ratio of the cluster volume fraction to the CNT volume fraction inside the selected RVE. Consequently, the value of $\eta =1$ indicates uniform distribution of CNT reinforcements, so reduction of $\eta$ leads to excessive agglomeration. In addition, the value of $\zeta =1$ specifies that all CNTs are located inside the clusters. Therefore, when $\eta =\zeta$, it means that there are no agglomeration in the nanocomposite microbeams.

Fig. 1

Schematic demonstration of a quasi-3D agglomerated CNT-reinforced nanocomposite microbeam

Now, by taking the two parameters of $\eta$ and $\zeta$, the bulk and shear moduli associated with inside and outside of clusters can be achieved as

$$\begin{aligned}{K}_{\text{in}-\text{cluster}}&=\frac{3\eta {K}_{m}-3\zeta {V}_{CNT}{K}_{m}+3\eta {\vartheta }_{1}{V}_{CNT}{K}_{m}+\zeta {\vartheta }_{3}{V}_{CNT}-3\zeta {\vartheta }_{1}{K}_{m}}{3\left(\eta -{V}_{CNT}\zeta +{V}_{CNT}\eta {\vartheta }_{1}\right)},\\{G}_{\text{in}-\text{cluster}}& =\frac{2\eta {G}_{m}-2\zeta {V}_{CNT}{G}_{m}+2\eta {\vartheta }_{2}{V}_{CNT}{G}_{m}+\zeta {\vartheta }_{4}{V}_{CNT}-2\zeta {\vartheta }_{2}{G}_{m}}{2\left(\eta -{V}_{CNT}\zeta +{V}_{CNT}\eta {\vartheta }_{2}\right)},\\ {K}_{\text{out}-\text{cluster}}& =\frac{3{K}_{m}-3\eta {K}_{m}+3\zeta {V}_{CNT}{K}_{m}-3{V}_{CNT}{K}_{m}+3{\vartheta }_{1}{V}_{CNT}\left({K}_{m}-\zeta {K}_{m}\right)+{V}_{CNT}\left({\vartheta }_{3}-3{K}_{m}{\vartheta }_{1}\right)\left(1-\zeta \right)}{3\left(1-\eta -{V}_{CNT}\left(1-\zeta \right)+{V}_{CNT}\left(1-\zeta \right){\vartheta }_{1}\right)}, \\ {G}_{\text{out}-\text{cluster}}& =\frac{2{G}_{m}-2\eta {G}_{m}+2\zeta {V}_{CNT}{G}_{m}-2{V}_{CNT}{G}_{m}+2{\vartheta }_{2}{V}_{CNT}\left({G}_{m}-\zeta {G}_{m}\right)+{V}_{CNT}\left({\vartheta }_{4}-2{G}_{m}{\vartheta }_{2}\right)\left(1-\zeta \right)}{2\left(1-\eta -{V}_{CNT}\left(1-\zeta \right)+{V}_{CNT}\left(1-\zeta \right){\vartheta }_{2}\right)},\end{aligned}$$

(3)

in which ${K}_{m}$ and ${G}_{m}$ in order are the bulk and shear moduli of the matrix phase, and

$$\begin{aligned}{\vartheta }_{1}& =\frac{3\left({K}_{m}+{G}_{m}\right)+{k}_{0}-{p}_{0}}{3\left({G}_{m}+{k}_{0}\right)}, \\ {\vartheta }_{2}& =\frac{16{G}_{m}^{2}+14{G}_{m}{k}_{0}+2{G}_{m}{q}_{0}+{G}_{m}{p}_{0}+2{k}_{0}{q}_{0}+{p}_{0}{q}_{0}}{15\left({G}_{m}+{k}_{0}\right)\left({G}_{m}+{q}_{0}\right)}+\frac{2{G}_{m}\left(3{K}_{m}+{G}_{m}\right)+2{G}_{m}\left(3{K}_{m}+7{G}_{m}\right)}{5{G}_{m}\left(3{K}_{m}+{G}_{m}\right)+5{r}_{0}\left(3{K}_{m}+7{G}_{m}\right)},\\{\vartheta }_{3}& =\frac{6{K}_{m}{k}_{0}+4{G}_{m}{k}_{0}+4{G}_{m}{p}_{0}+3{K}_{m}{p}_{0}+{G}_{m}{s}_{0}+{k}_{0}{s}_{0}-{p}_{0}^{2}}{3\left({G}_{m}+{k}_{0}\right)\left({s}_{0}+2{p}_{0}\right)},\\ {\vartheta }_{4}& =\frac{2\left({s}_{0}-{p}_{0}\right)}{15}+\frac{8{G}_{m}{q}_{0}}{5\left({G}_{m}+{q}_{0}\right)}+\frac{32{G}_{m}^{2}{r}_{0}+24{G}_{m}{K}_{m}{r}_{0}}{15{K}_{m}\left({r}_{0}+{G}_{m}\right)+5{G}_{m}\left(7{r}_{0}+{G}_{m}\right)}\\ &\quad+\frac{4{G}_{m}{k}_{0}-4{G}_{m}{p}_{0}+2{k}_{0}{p}_{0}-2{p}_{0}^{2}}{15\left({G}_{m}+{k}_{0}\right)}.\end{aligned}$$

(4)

As a consequence, the bulk and shear moduli of the agglomerated CNT-reinforced nanocomposite material are obtained as

$$K=\frac{{K}_{\text{out}-\text{cluster}}+\left({\Gamma }_{1}+\eta -{\Gamma }_{1}\eta \right)\left({K}_{\text{in}-\text{cluster}}-{K}_{\text{out}-\text{cluster}}\right)}{1+\left({\Gamma }_{1}-{\Gamma }_{1}\eta \right)\left(\frac{{K}_{\text{in}-\text{cluster}}}{{K}_{\text{out}-\text{cluster}}}-1\right)},$$

(5a)

$$G=\frac{{G}_{\text{out}-\text{cluster}}+\left({\Gamma }_{2}+\eta -{\Gamma }_{2}\eta \right)\left({G}_{\text{in}-\text{cluster}}-{G}_{\text{out}-\text{cluster}}\right)}{1+\left({\Gamma }_{2}-{\Gamma }_{2}\eta \right)\left(\frac{{G}_{\text{in}-\text{cluster}}}{{G}_{\text{out}-\text{cluster}}}-1\right)},$$

(5b)

where

$$\begin{aligned} & {\Gamma }_{1} =\frac{1+{\nu }_{\text{out}-\text{cluster}}}{3\left(1-{\nu }_{\text{out}-\text{cluster}}\right)}, {\Gamma }_{2}=\frac{8-10{\nu }_{\text{out}-\text{cluster}}}{15\left(1-{\nu }_{\text{out}-\text{cluster}}\right)},\\ & {\nu }_{\text{out}-\text{cluster}} =\frac{3{K}_{\text{out}-\text{cluster}}-2{G}_{\text{out}-\text{cluster}}}{6{K}_{\text{out}-\text{cluster}}+2{G}_{\text{out}-\text{cluster}}}.\end{aligned}$$

(6)

Therefore, the effective Young’s modulus and Poisson’s ratio can be extracted as

$$E=\frac{9KG}{3K+G}, \nu =\frac{3K-2G}{6K+2G}.$$

(7)

In Figs. 2 and 3, the variation of achieved effective Young’s modulus and Poisson’s ratio with the agglomeration parameters is depicted, respectively.

Fig. 2

Variations of the obtained effective Young’s modulus with agglomeration parameters corresponding to different CNT volume fractions

Fig. 3

Variations of the obtained effective Poisson’s ratio with agglomeration parameters corresponding to different CNT volume fractions

On the basis of the quasi-3D theory of elasticity, the displacement field of a beam-type structure is defined in such a way that the transverse deformation $w({x}_{1},t)$ is separated to bending ${w}_{b}({x}_{1},t)$ and shear ${w}_{s}({x}_{1},t)$ parts, and the normal strain along with the beam thickness is added to the displacement formulations with the aid a transverse normal shape function ${\mathbb{G}}\left({x}_{3}\right)$. Accordingly, one will have

$${\mathcal{U}}_{1}\left({x}_{1},{x}_{3},t\right)=u\left({x}_{1},t\right)-{x}_{3}\frac{\partial {w}_{b}\left({x}_{1},t\right)}{\partial {x}_{1}}+{\mathbb{F}}\left({x}_{3}\right)\frac{\partial {w}_{s}\left({x}_{1},t\right)}{\partial {x}_{1}},$$

(8a)

$${\mathcal{U}}_{3}\left({x}_{1},{x}_{3},t\right)={w}_{b}\left({x}_{1},t\right)+{\mathbb{G}}\left({x}_{3}\right){w}_{s}\left({x}_{1},t\right),$$

(8b)

in which the transverse shear and normal shape functions are considered as

$${\mathbb{F}}\left({x}_{3}\right)=\frac{h}{2}\text{sin}\left(\frac{\pi {x}_{3}}{h}\right)-{x}_{3},$$

(9a)

$${\mathbb{G}}\left({x}_{3}\right)=1+\frac{5}{12\pi }\text{cos}\left(\frac{\pi {x}_{3}}{h}\right).$$

(9b)

Consequently, by taking the geometrical nonlinearity into consideration, the quasi-3D-based strain components of an agglomerated nanocomposite microbeam can be expressed as

$$\begin{aligned}{\varepsilon }_{11}& =\frac{\partial u}{\partial {x}_{1}}+\frac{1}{2}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}-{x}_{3}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}+{\mathbb{F}}\left({x}_{3}\right)\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}},\\ {\varepsilon }_{33}& =\frac{d{\mathbb{G}}\left({x}_{3}\right)}{d{x}_{3}}{w}_{s}, {\gamma }_{13}=\left(\frac{d{\mathbb{F}}\left({x}_{3}\right)}{d{x}_{3}}+{\mathbb{G}}\left({x}_{3}\right)\right)\frac{\partial {w}_{s}}{\partial {x}_{1}} .\end{aligned}$$

(10)

In order to capture the size dependency features more efficiently, the physical coupling effect between strain gradient stress tensor and nonlocal stress tensor can be taken into account via the nonlocal strain gradient continuum elasticity in the following form [47]:

$${\sigma }_{ij}={\sigma }_{ij}^{(0)}-\frac{\partial {\sigma }_{ij}^{\left(1\right)}}{\partial {x}_{1}},$$

(11)

in which ${\sigma }_{ij}^{(0)}$ and ${\sigma }_{ij}^{\left(1\right)}$ stand for the stress tensors associated with the conventional strain and strain gradient tensors as follows:

$${\sigma }_{ij}^{(0)}={\int }_{0}^{L}\left\{{C}_{ijmn}{\beta }_{0}\left(x,{x}^{^{\prime}},{e}_{0}a\right)\frac{\partial {\varepsilon }_{mn}({x}^{^{\prime}})}{\partial x}\right\}dx{^{\prime}},$$

(12a)

$${\sigma }_{ij}^{(1)}={l}^{2}{\int }_{0}^{L}\left\{{C}_{ijmn}{\beta }_{0}\left(x,{x}^{^{\prime}},{e}_{1}a\right)\nabla \left(\frac{\partial {\varepsilon }_{mn}({x}^{^{\prime}})}{\partial x}\right)\right\}dx{^{\prime}},$$

(12b)

where ${C}_{ijmn}$ refers to elastic parameter, ${e}_{0}a$ and ${e}_{1}a$ represent the nonlocal parameters related to the conventional and higher order stress tensors, and $l$ denotes an internal length scale parameter for the strain gradient size effect. In addition, ${\beta }_{0}\left(x,{x}^{^{\prime}},{e}_{0}a\right)$ and ${\beta }_{1}\left(x,{x}^{^{\prime}},{e}_{1}a\right)$ are the nonlocal kernel functions corresponding to the introduced conditions by Eringen [48].

Therefore, the constitutive equation related to a beam-type structure modeled via the nonlocal strain gradient continuum mechanics can be written as

$$\begin{aligned} & \left[1-{\left({e}_{1}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right]\left[1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right]{\sigma }_{ij}\\ & \quad ={C}_{ijmn}\left[1-{\left({e}_{1}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right]{\varepsilon }_{mn} \\ & \qquad-{C}_{ijmn}{l}^{2}\left[1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right]\frac{{\partial }^{2}{\varepsilon }_{mn}}{\partial {x}_{1}^{2}}.\end{aligned}$$

(13)

With the assumption of $e={e}_{0}={e}_{1}$ considered by Lim et al. [47], the derived constitutive equation of a nonlocal strain gradient beam can be rewritten as

$$\left[1-{\left(ea\right)}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right]{\sigma }_{ij}={C}_{ijmn}\left[1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right]{\varepsilon }_{mn}.$$

(14)

In this regard, the stress–strain constitutive relations can be stated in the following form:

$$\left(1-{\left(ea\right)}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\left\{\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{33}\\ {\tau }_{13}\end{array}\right\}=\left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\left[\begin{array}{ccc}{Q}_{11}& {Q}_{13}& 0\\ {Q}_{13}& {Q}_{33}& 0\\ 0& 0& {Q}_{44}\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{11}\\ {\varepsilon }_{33}\\ {\gamma }_{13}\end{array}\right\},$$

(15)

where

$$\begin{aligned}{Q}_{11}& ={Q}_{33}=\frac{\left(1-\nu \right)E)}{\left(1-2\nu \right)\left(1+\nu )\right)} ,\\ {Q}_{13}&=\frac{\nu E}{\left(1-2\nu \right)\left(1+\nu \right)} , {Q}_{44}=\frac{E}{2\left(1+\nu \right)}.\end{aligned}$$

(16)

As a result, the strain energy stored in a quasi-3D agglomerated CNT-reinforced nanocomposite microbeams can be presented in terms of the stress resultants as follows:

$$\begin{aligned}{\Pi }_{s}& =\frac{1}{2}{\int }_{0}^{L}{\int }_{-\frac{h}{2}}^\frac{h}{2}{\sigma }_{ij}{\varepsilon }_{ij}d{x}_{3}d{x}_{1}\\ & =\frac{1}{2}{\int }_{0}^{L}\left\{{N}_{11}^{*}\left[\frac{\partial u}{\partial {x}_{1}}+\frac{1}{2}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}\right] \right. \\ & \qquad \left. +{N}_{33}^{*}{w}_{s}-{M}_{11}^{*}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}+{J}_{11}^{*}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+{Q}_{1}^{*}\frac{\partial {w}_{s}}{\partial {x}_{1}}\right\}d{x}_{1}.\end{aligned}$$

(17)

In addition, the work done by the applied external axial compressive load can be read as

$${\Pi }_{w}=\frac{1}{2}{\int }_{0}^{L}P{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}d{x}_{1},$$

(18)

in which

$$\begin{aligned}& \left\{\begin{array}{c}{N}_{11}^{*}-{\left(ea\right)}^{2}\frac{{\partial }^{2}{N}_{11}^{*}}{\partial {x}_{1}^{2}}\\ {M}_{11}^{*}-{\left(ea\right)}^{2}\frac{{\partial }^{2}{M}_{11}^{*}}{\partial {x}_{1}^{2}}\\ {J}_{11}^{*}-{\left(ea\right)}^{2}\frac{{\partial }^{2}{J}_{11}^{*}}{\partial {x}_{1}^{2}}\end{array}\right\}={\left[\begin{array}{ccc}{A}_{11}^{*}& 0& 0\\ 0& {D}_{11}^{*}& {E}_{11}^{*}\\ 0& {E}_{11}^{*}& {H}_{11}^{*}\\ 0& {F}_{13}^{*}& {K}_{13}^{*}\end{array}\right]}^{T}\left\{\begin{array}{c}\left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\left[\frac{\partial u}{\partial {x}_{1}}+\frac{1}{2}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}\right]\\ -\left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\\ \left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\\ {\left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)w}_{s}\end{array}\right\}\\ & \quad {N}_{33}^{*}-{\left(ea\right)}^{2}\frac{{\partial }^{2}{N}_{33}^{*}}{\partial {x}_{1}^{2}}={\left\{\begin{array}{c}{G}_{13}^{*}\\ {F}_{13}^{*}\\ {K}_{13}^{*}\\ {G}_{33}^{*}\end{array}\right\}}^{T}\left\{\begin{array}{c}\left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\left[\frac{\partial u}{\partial {x}_{1}}+\frac{1}{2}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}\right]\\ -\left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\\ \left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\\ \left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right){w}_{s}\end{array}\right\},\\ & \quad {Q}_{1}^{*}-{\left(ea\right)}^{2}\frac{{\partial }^{2}{Q}_{1}^{*}}{\partial {x}_{1}^{2}}={A}_{44}^{*}\left(1-{l}^{2}\frac{{\partial }^{2}}{\partial {x}_{1}^{2}}\right)\frac{\partial {w}_{s}}{\partial {x}_{1}}, \end{aligned}$$

(19)

where

$$\begin{aligned}& \left\{\begin{array}{c}{A}_{11}^{*}\\ {D}_{11}^{*}\\ {E}_{11}^{*}\\ {H}_{11}^{*}\end{array}\right\}={Q}_{11}b{\int }_{-\frac{h}{2}}^\frac{h}{2}\left\{\begin{array}{c}1\\ {x}_{3}^{2}\\ {x}_{3}{\mathbb{F}}\left({x}_{3}\right)\\ {\left({\mathbb{F}}\left({x}_{3}\right)\right)}^{2}\end{array}\right\}d{x}_{3}, {A}_{44}^{*}={Q}_{44}b{\int }_{-\frac{h}{2}}^\frac{h}{2}\left(\frac{d{\mathbb{F}}\left({x}_{3}\right)}{d{x}_{3}}+{\mathbb{G}}\left({x}_{3}\right)\right)d{x}_{3}\\ & \quad \left\{\begin{array}{c}{F}_{13}^{*}\\ {K}_{13}^{*}\\ {G}_{33}^{*}\end{array}\right\}={Q}_{33}b{\int }_{-\frac{h}{2}}^\frac{h}{2}\left\{{x}_{3}\frac{d{\mathbb{G}}\left({x}_{3}\right)}{d{x}_{3}},{\mathbb{F}}\left({x}_{3}\right)\frac{d{\mathbb{G}}\left({x}_{3}\right)}{d{x}_{3}},{\left(\frac{d{\mathbb{G}}\left({x}_{3}\right)}{d{x}_{3}}\right)}^{2}\right\}d{x}_{3}.\end{aligned}$$

(20)

In addition, the kinetic energy of a quasi-3D agglomerated CNT-reinforced nanocomposite microbeam incorporating transverse shear and normal deformations can be introduced as

$$\begin{aligned}{\Pi }_{k}& =\frac{1}{2}{\int }_{0}^{L}{\int }_{-\frac{h}{2}}^\frac{h}{2}\left\{\rho \left[{\left(\frac{\partial {\mathcal{U}}_{1}}{\partial t}\right)}^{2}+{\left(\frac{\partial {\mathcal{U}}_{3}}{\partial t}\right)}^{2}\right]\right\}d{x}_{3}d{x}_{1}\\ & =\frac{1}{2}{\int }_{0}^{L}\left\{{I}_{0}\left[{\left(\frac{\partial u}{\partial t}\right)}^{2}+{\left(\frac{\partial {w}_{b}}{\partial t}\right)}^{2}\right]-2{I}_{1}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}\partial t}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}\partial t}\right.\\ & \quad \left.+{I}_{2}{\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}\partial t}\right)}^{2}+{I}_{3}{\left(\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}\partial t}\right)}^{2}+{I}_{4}\frac{\partial {w}_{b}}{\partial t}\frac{\partial {w}_{s}}{\partial t}+{I}_{5}{\left(\frac{\partial {w}_{s}}{\partial t}\right)}^{2}\right\}d{x}_{1},\end{aligned}$$

(21)

where $\rho$ represents the mass density of the agglomerated nanocomposite microbeam as

$$\rho ={V}_{CNT}{\rho }_{CNT}+\left(1-{V}_{CNT}\right){\rho }_{m}$$

in which ${\rho }_{CNT}$ and ${\rho }_{m}$ refer to, respectively, the mass density of CNT and matrix phases, and

$$\left\{{I}_{0},{I}_{1},{I}_{2},{I}_{3},{I}_{4},{I}_{5}\right\}=b{\int }_{-\frac{h}{2}}^\frac{h}{2}\rho \left({x}_{3}\right)\left\{1,{x}_{3}{\mathbb{F}}\left({x}_{3}\right),{x}_{3}^{2},{\left({\mathbb{F}}\left({x}_{3}\right)\right)}^{2},{\mathbb{G}}\left({x}_{3}\right),{\left({\mathbb{G}}\left({x}_{3}\right)\right)}^{2}\right\}d{x}_{3}.$$

(22)

With the aid of the essential lemma of calculus associated with the variational formulations, the quasi-3D-based governing differential equations of motion can be derived as

$${A}_{11}^{*}\left[\frac{{\partial }^{2}u}{\partial {x}_{1}^{2}}-{l}^{2}\frac{{\partial }^{4}u}{\partial {x}_{1}^{4}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}-{l}^{2}\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}+3\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}+\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+3\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+3\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}+3\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}\right)\right]={I}_{0}\left(\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{4}u}{\partial {x}_{1}^{2}\partial {t}^{2}}\right),$$

(23a)

$${D}_{11}^{*}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}-{l}^{2}\frac{{\partial }^{6}{w}_{b}}{\partial {x}_{1}^{6}}\right)-{E}_{11}^{*}\left(\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}-{l}^{2}\frac{{\partial }^{6}{w}_{s}}{\partial {x}_{1}^{6}}\right)-{F}_{13}^{*}\left({w}_{s}-{l}^{2}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\right)+{A}_{11}^{*}\left[\frac{{\partial }^{2}u}{\partial {x}_{1}^{2}}\frac{\partial {w}_{b}}{\partial {x}_{1}}-{l}^{2}\left(\frac{{\partial }^{4}u}{\partial {x}_{1}^{4}}\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{{\partial }^{2}u}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\right)+\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\right)}^{2}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\right)}^{2}+\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}-{l}^{2}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\right)}^{2}+3\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+3\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+3\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}+\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\right)}^{2}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}+3\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}\right)\right]+{A}_{11}^{*}\left[\frac{\partial u}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}-{l}^{2}\left(\frac{{\partial }^{3}u}{\partial {x}_{1}^{3}}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}+\frac{\partial u}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}\right)+\frac{1}{2}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}-{l}^{2}\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}+\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}+\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}{\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\right)}^{2}\right)\right]+P\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}\right)={I}_{0}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{2}\partial {t}^{2}}\right)-{I}_{1}\left(\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{2}\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{6}{w}_{s}}{\partial {x}_{1}^{4}\partial {t}^{2}}\right)+{I}_{2}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{2}\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{6}{w}_{b}}{\partial {x}_{1}^{4}\partial {t}^{2}}\right)+{I}_{4}\left(\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{2}\partial {t}^{2}}\right),$$

(23b)

$${A}_{44}^{*}\left(\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}-{l}^{2}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}\right)-\left({E}_{11}^{*}-{F}_{13}^{*}\right)\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}-{l}^{2}\frac{{\partial }^{6}{w}_{b}}{\partial {x}_{1}^{6}}\right)+\left({H}_{11}^{*}-{K}_{13}^{*}\right)\left(\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}-{l}^{2}\frac{{\partial }^{6}{w}_{s}}{\partial {x}_{1}^{6}}\right)+\left({K}_{13}^{*}-{G}_{33}^{*}\right)\left({w}_{s}-{l}^{2}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\right)+{A}_{11}^{*}\left[\frac{{\partial }^{2}u}{\partial {x}_{1}^{2}}\frac{\partial {w}_{s}}{\partial {x}_{1}}-{l}^{2}\left(\frac{{\partial }^{4}u}{\partial {x}_{1}^{4}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+\frac{{\partial }^{2}u}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}\right)+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}{\left(\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}{\left(\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}-{l}^{2}\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+3\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{4}}{\left(\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}+3\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+3\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}+\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}{\left(\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}+3\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}\right)\right]+{A}_{11}^{*}\left[\frac{\partial u}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}-{l}^{2}\left(\frac{{\partial }^{3}u}{\partial {x}_{1}^{3}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+\frac{\partial u}{\partial {x}_{1}}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}\right)+\frac{1}{2}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}-{l}^{2}\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}{\left(\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\right)}^{2}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}{\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\right)}^{2}\right)\right]+P\left(\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{4}}\right)-{G}_{13}^{*}\left[\frac{\partial u}{\partial {x}_{1}}-{l}^{2}\frac{{\partial }^{3}u}{\partial {x}_{1}^{3}}+\frac{1}{2}{\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)}^{2}-{l}^{2}\left(\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}+\frac{{\partial }^{3}{w}_{b}}{\partial {x}_{1}^{3}}\frac{\partial {w}_{s}}{\partial {x}_{1}}+\frac{\partial {w}_{b}}{\partial {x}_{1}}\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}+\frac{\partial {w}_{s}}{\partial {x}_{1}}\frac{{\partial }^{3}{w}_{s}}{\partial {x}_{1}^{3}}+{\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}_{1}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}_{1}^{2}}\right)}^{2}\right)\right]={I}_{5}\left(\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{2}\partial {t}^{2}}\right)-{I}_{1}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{2}\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{6}{w}_{b}}{\partial {x}_{1}^{4}\partial {t}^{2}}\right)+{I}_{3}\left(\frac{{\partial }^{4}{w}_{s}}{\partial {x}_{1}^{2}\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{6}{w}_{s}}{\partial {x}_{1}^{4}\partial {t}^{2}}\right)+{I}_{4}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}-{\left(ea\right)}^{2}\frac{{\partial }^{4}{w}_{b}}{\partial {x}_{1}^{2}\partial {t}^{2}}\right).$$

(23c)

In addition, the associated boundary conditions can be expressed as

$$\begin{aligned}\delta u& =0 \text{or} \delta {N}_{11}^{*}=0\\ \delta {w}_{b}& =0 \text{or} \delta \left[\frac{{\partial }^{2}{M}_{11}^{*}}{\partial {x}_{1}^{2}}-\frac{\partial }{\partial {x}_{1}}\left({N}_{11}^{*}\frac{\partial {w}_{b}}{\partial {x}_{1}}\right)\right]=0\\ \delta {w}_{s}& =0 \text{or} \delta \left[\frac{\partial {Q}_{1}^{*}}{\partial {x}_{1}}+\frac{{\partial }^{2}{J}_{11}^{*}}{\partial {x}_{1}^{2}}-{N}_{33}^{*}+\frac{\partial }{\partial {x}_{1}}\left({N}_{11}^{*}\frac{\partial {w}_{s}}{\partial {x}_{1}}\right)\right]=0,\end{aligned}$$

(24)

• For the movable simply supported end condition:

  $${w}_{b}={w}_{s}={M}_{11}^{*}=0.$$

  (25)

• For the movable clamped end condition:

  $${w}_{b}={w}_{s}=\frac{\partial {w}_{b}}{\partial {x}_{1}}=\frac{\partial {w}_{s}}{\partial {x}_{1}}=0.$$

  (26)

3 Differential quadrature-based solution strategy

An effective numerical solving procedure namely as generalized differential quadrature (GDQ) method is employed herein to capture the solution of the developed size-dependent nonlinear problem. For this reason, an accurate discretization process is considered for the proposed nonlinear problem via putting an inconsistent function of $\mathcal{F}(\xi )$ defined within an associated territory of $\xi =\left[{\xi }_{1},{\xi }_{2},\dots ,{\xi }_{n}\right]$ to use as follows:

$$\frac{{d}^{k}\mathcal{F}(\xi )}{d{\xi }^{k}}=\sum_{i=1}^{n}{\mathfrak{P}}_{\xi }^{\left(k\right)}\mathcal{F}({\xi }_{i}),$$

(27)

where ${\mathfrak{P}}_{\xi }^{\left(k\right)}$ states the coefficients related to the weighting process of the $k$ th-order derivation that can be brought in as follows:

$${\mathfrak{P}}_{\xi }^{\left(k\right)}=\left[{\mathfrak{W}}_{ij}^{(k)}\right] i,j=\text{1,2},\dots , n , k=\text{1,2},\dots , n-1,$$

(28a)

$${\mathfrak{W}}_{ij}^{(k)}=\left\{\begin{array}{l}\text{identity matri}{\text{x}}_{n\times n} k=0\\ \frac{\prod_{p=1,i\ne p}^{n}\left({\xi }_{i}-{\xi }_{p}\right)}{\left[\left({\xi }_{i}-{\xi }_{j}\right)\prod_{p=1,j\ne p}^{n}\left({\xi }_{j}-{\xi }_{p}\right)\right]} i\ne j , k=1\\ \left\{\begin{array}{l}k\left({\mathfrak{W}}_{ij}^{(1)}{\mathfrak{W}}_{ij}^{(k-1)}-\frac{{\mathfrak{W}}_{ij}^{(k-1)}}{{\xi }_{i}-{\xi }_{j}}\right) i\ne j\\ -\sum_{p=1,p\ne i}^{n}{\mathfrak{W}}_{ip}^{\left(k\right)} i=j \end{array}\right. k\ge 2\end{array},\right.$$

(28b)

in which the gridding pattern of shifted Chebyshev–Gauss–Lobatto is utilized as

$${\xi }_{i}=\frac{L}{2}\left[1-\text{cos}\left(\frac{\left(i-1\right)\pi }{n-1}\right)\right].$$

(29)

In order to initiate the solving procedure, the regime associated with the postbuckling part of the considered problem is extracted by eliminating the inertia terms as

$${a}_{11}^{*}\left[{\mathfrak{P}}_{\xi }^{\left(2\right)}{U}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(4\right)}{U}^{*}+\frac{1}{\Upsilon}\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\right)-\frac{{\beta }^{2}}{\Upsilon}\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}\right)+3\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)+3\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)+3\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)+3\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)\right)\right]=0 ,$$

(30a)

$$\begin{aligned} &{d}_{11}^{*}\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(6\right)}{W}_{b}^{*}\right)-{e}_{11}^{*}\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(6\right)}{W}_{s}^{*}\right)-{f}_{13}^{*}\left({W}_{s}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\\ & \quad +\frac{{a}_{11}^{*}}{\Upsilon}\left[\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)-{\beta }^{2}\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)-{\beta }^{2}\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\right. \\ & \quad +\frac{1}{\Upsilon}\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit{\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\right)}^{2}+\frac{1}{\vartheta }\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\diamondsuit{\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\right)}^{2}\\ & \quad +\frac{1}{\Upsilon}\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)+\frac{1}{\vartheta }\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\\& \quad -\frac{{\beta }^{2}}{\Upsilon}\left(\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}\right)\diamondsuit{\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\right)}^{2} +3\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)+3\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\right.\\ & \quad \left.\left.+3\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)\diamondsuit{\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\right)}^{2}+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)+3\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)\right)\right]\\& \quad +\frac{{a}_{11}^{*}}{\Upsilon} \left[\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)-{\beta }^{2}\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)-{\beta }^{2}\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}\right)+\frac{1}{2\Upsilon}\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit{\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\right)}^{2}\right. \\& \quad-\frac{{\beta }^{2}}{\Upsilon}\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\right.\\ & \quad \left. \left.+\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit{\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}+{\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)}^{2}\right)\right]+\widetilde{P}\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}-{\alpha }^{2}{\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}\right)=0,\end{aligned}$$

(30b)

$$\begin{aligned}&{a}_{44}^{*}\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)-\left({E}_{11}^{*}-{F}_{13}^{*}\right)\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(6\right)}{W}_{b}^{*}\right)+\left({H}_{11}^{*}-{K}_{13}^{*}\right)\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(6\right)}{W}_{s}^{*}\right)+\left({K}_{13}^{*}-{G}_{33}^{*}\right)\left({W}_{s}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right) \\ & \quad +\frac{{a}_{11}^{*}}{\Upsilon}\left[\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)-{\beta }^{2}\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)-{\beta }^{2}\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\right. \\ & \quad +\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit{\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)}^{2}+\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\diamondsuit{\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)}^{2}-\frac{{\beta }^{2}}{\Upsilon}\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\right.\\ & \quad +3\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{b}^{*}\right)\diamondsuit{\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)}^{2}+3\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right) \\ & \quad \left.\left.+3\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)\diamondsuit{\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)}^{2}+3\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)\right)\right] \\ & \quad +\frac{{a}_{11}^{*}}{\Upsilon}\left[\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)-{\beta }^{2}\left(\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{U}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)\right)+\frac{1}{2\Upsilon}\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\diamondsuit{\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}+{\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)}^{2}\right. \\ & \quad \left. -\frac{{\beta }^{2}}{\Upsilon}\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit{\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)}^{2}\right. \right. \\ & \quad\left.\left.+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\diamondsuit{\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}+{\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)}^{2}\right)\right]\\ & \quad +\widetilde{P}\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}-{\alpha }^{2}{\mathfrak{P}}_{\xi }^{\left(4\right)}{W}_{s}^{*}\right)-{g}_{13}^{*}\left[{\mathfrak{P}}_{\xi }^{\left(1\right)}{U}^{*}-{\beta }^{2}{\mathfrak{P}}_{\xi }^{\left(3\right)}{U}^{*}+\frac{1}{2\vartheta }{\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}+{\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)}^{2}\right. \\& \quad -\frac{{\beta }^{2}}{\Upsilon}\left(\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{b}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)\right.\\& \quad \left.\left.+\left({\mathfrak{P}}_{\xi }^{\left(1\right)}{W}_{s}^{*}\right)\diamondsuit\left({\mathfrak{P}}_{\xi }^{\left(3\right)}{W}_{s}^{*}\right)+{\left({\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{b}^{*}+{\mathfrak{P}}_{\xi }^{\left(2\right)}{W}_{s}^{*}\right)}^{2}\right)\right]=0,\end{aligned}$$

(30c)

where

$$\begin{aligned}\left\{U,{W}_{b},{W}_{s}\right\}& =\left\{\frac{u}{h},\frac{{w}_{b}}{h},\frac{{w}_{s}}{h}\right\} , \left\{\xi ,\alpha ,\beta \right\}=\left\{\frac{x}{L},\frac{ea}{L},\frac{l}{L}\right\} , \Upsilon=\frac{L}{h},\\ \left\{{a}_{11}^{*},{a}_{44}^{*},{g}_{33}^{*}\right\}& =\left\{\frac{{A}_{11}^{*}}{{A}_{11}^{*}},\frac{{A}_{44}^{*}}{{A}_{11}^{*}},\frac{{G}_{33}^{*}}{{A}_{11}^{*}}\right\} , \left\{{d}_{11}^{*},{e}_{11}^{*},{h}_{11}^{*}\right\}=\left\{\frac{{D}_{11}^{*}}{{A}_{11}^{*}{h}^{2}},\frac{{E}_{11}^{*}}{{A}_{11}^{*}{h}^{2}},\frac{{H}_{11}^{*}}{{A}_{11}^{*}{h}^{2}}\right\}\\\left\{{f}_{11}^{*},{k}_{13}^{*}\right\}& =\left\{\frac{{F}_{13}^{*}}{{A}_{11}^{*}h},\frac{{K}_{13}^{*}}{{A}_{11}^{*}h}\right\},\end{aligned}$$

(31)

and \diamondsuit stands for the Hadamard product.

Consequently, one can achieve the following vectorized nonlinear stability equations:

$$\left({\mathcal{K}}_{{\varvec{l}}}-P{\mathcal{K}}_{{\varvec{g}}}\right){\mathfrak{A}}^{\boldsymbol{*}}+{\mathcal{K}}_{{\varvec{n}}{\varvec{l}}}\left({\mathfrak{A}}^{\boldsymbol{*}}\right)=0,$$

(31)

where ${\mathfrak{A}}^{\boldsymbol{*}}$ stands for the vectorzied displacement components after discretization by $n$ elements which is taken into account as

$$\begin{aligned}&{\mathfrak{A}}^{\boldsymbol{*}} =\left\{\begin{array}{c}{U}^{*}\\ {W}_{b}^{*}\\ {W}_{s}^{*}\end{array}\right\}=\left\{\begin{array}{c}{\left\{u\left({\xi }_{1}\right),u\left({\xi }_{2}\right), u({\xi }_{3})\dots ,u\left({\xi }_{n-1}\right),u\left({\xi }_{n}\right)\right\}}^{T}\\ {\left\{{w}_{b}\left({\xi }_{1}\right),{w}_{b}({\xi }_{2}),{w}_{b}({\xi }_{3}),\dots ,{w}_{b}\left({\xi }_{n-1}\right),{w}_{b}\left({\xi }_{n}\right)\right\}}^{T}\\ {\left\{{w}_{s}\left({\xi }_{1}\right),{w}_{s}({\xi }_{2}),{w}_{s}({\xi }_{3}),\dots ,{w}_{s}\left({\xi }_{n-1}\right),{w}_{s}\left({\xi }_{n}\right)\right\}}^{T}\end{array}\right\}\\ & {\mathcal{K}}_{{\varvec{n}}{\varvec{l}}}\left({\mathfrak{A}}^{{\varvec{p}}}\right) =\left\{\begin{array}{c}{\mathcal{T}}_{1}\\ {\mathcal{T}}_{2}\\ {\mathcal{T}}_{3}\end{array}\right\} , {\mathcal{K}}_{{\varvec{l}}}=\left[\begin{array}{ccc}{\mathcal{K}}_{11}& {\mathcal{K}}_{12}& {\mathcal{K}}_{13}\\ {\mathcal{K}}_{21}& {\mathcal{K}}_{22}& {\mathcal{K}}_{23}\\ {\mathcal{K}}_{31}& {\mathcal{K}}_{32}& {\mathcal{K}}_{33}\end{array}\right] , {\mathcal{K}}_{{\varvec{g}}}=\left[\begin{array}{ccc}0& 0& 0\\ 0& {\mathfrak{P}}_{\xi }^{\left(2\right)}& 0\\ 0& 0& {\mathfrak{P}}_{\xi }^{\left(2\right)}\end{array}\right],\end{aligned}$$

(32)

${\mathcal{K}}_{ij}$ and ${\mathcal{T}}_{i}$ refer to, respectively, the discretized linear stiffness components and discretized nonlinear stiffness components associated with the agglomerated CNT-reinforced nanocomposite microbeams.

At the initiate phase of the numerical solving process, the nonlinear expressions of ${\mathcal{K}}_{{\varvec{n}}{\varvec{l}}}\left({\mathfrak{A}}^{{\varvec{p}}}\right)$ are ignored, and then the critical buckling loads of the agglomerated CNT-reinforced nanocomposite microbeams are achieved and appointed as beginning point of the route of numerical solution for the examined nonlinear problem. Afterwards, a repetitious operation is applied jointly with the pseudo-arc-length continuation technique [48] to track down the correlated nonlinear stability curves.

Subsequently, the characteristics of nonlinear dynamics within postbuckling and prebuckling regimes of an agglomerated CNT-reinforced nanocomposite microbeam are captured via imposing a dynamical disturbance having an amplitude around the predicted buckled configuration. Therefore, two parts of static and dynamic ones are supposed for the associated displacement components as follows:

$$\mathfrak{A}={\mathfrak{A}}^{{\varvec{s}}}+{\mathfrak{A}}^{{\varvec{d}}}.$$

(33)

After substitution of Eq. (33) into the nonlocal strain gradient-based nonlinear differential equations of motion, one will have

$$\mathcal{M}\ddot{\mathfrak{A}}+\left({\mathcal{K}}_{{\varvec{l}}}-P{\mathcal{K}}_{{\varvec{g}}}\right)\mathfrak{A}+{\mathcal{K}}_{{\varvec{n}}{\varvec{l}}}\left(\mathfrak{A}\right)=0,$$

(34)

where $\mathcal{M}$ denotes the mass matrix taking in the related inertia components. In addition, the over dot specifies the time differentiation.

On the basis of Eq. (33) and incorporating the imposed dynamical disturbance, the dynamic governing equations can be stated in discretized form as

$$\mathcal{M}{\ddot{\mathfrak{A}}}^{{\varvec{d}}}+{\mathcal{K}}_{{\varvec{l}}}{\mathfrak{A}}^{{\varvec{d}}}+{\mathcal{K}}_{{\varvec{n}}{\varvec{l}}}\left({\mathfrak{A}}^{{\varvec{d}}}\right)=0.$$

(35)

Via taking a harmonic solution into account as ${\mathfrak{A}}^{{\varvec{d}}}={\overline{\mathfrak{A}} }^{{\varvec{d}}}{e}^{i\omega t}$, the associated eigenvalue problem is extracted in a general form, the solution of which can be introduced as

$${\mathfrak{A}}^{{\varvec{d}}}=\mathfrak{X}\mathfrak{S} ,$$

(36)

where $\mathfrak{X}$ and $\mathfrak{S}$ in order represent the decreased generalized coordinates and sparse matrix related to the basis function in the presence of Galerkin-derived mode-shapes, as

$$\mathfrak{S}=\left\{\begin{array}{c}{\mathfrak{S}}_{u}^{(1)},{\mathfrak{S}}_{u}^{(2)},\dots ,{\mathfrak{S}}_{u}^{(q)}\\ {\mathfrak{S}}_{{w}_{b}}^{(1)},{\mathfrak{S}}_{{w}_{b}}^{(2)},\dots ,{\mathfrak{S}}_{{w}_{b}}^{(q)}\\ {\mathfrak{S}}_{{w}_{s}}^{(1)},{\mathfrak{S}}_{{w}_{s}}^{(2)},\dots ,{\mathfrak{S}}_{{w}_{s}}^{(q)}\end{array}\right\}, \mathfrak{X}=\left[\begin{array}{ccc}{\mathfrak{X}}_{{\varvec{u}}}& 0& 0\\ 0& {\mathfrak{X}}_{{{\varvec{w}}}_{{\varvec{b}}}}& 0\\ 0& 0& {\mathfrak{X}}_{{{\varvec{w}}}_{{\varvec{s}}}}\end{array}\right].$$

(37)

in which

$$\begin{aligned}{\mathfrak{X}}_{{\varvec{u}}}& =\left[\begin{array}{cccc}{\left\{{\mathfrak{X}}_{u}^{\left(1\right)}\right\}}_{n\times 1}& {\left\{{\mathfrak{X}}_{u}^{\left(2\right)}\right\}}_{n\times 1}& \dots & {\left\{{\mathfrak{X}}_{u}^{\left(q\right)}\right\}}_{n\times 1}\end{array}\right]\\ {\mathfrak{X}}_{{{\varvec{w}}}_{{\varvec{b}}}}& =\left[\begin{array}{cccc}{\left\{{\mathfrak{X}}_{{w}_{b}}^{\left(1\right)}\right\}}_{n\times 1}& {\left\{{\mathfrak{X}}_{{w}_{b}}^{\left(2\right)}\right\}}_{n\times 1}& \dots & {\left\{{\mathfrak{X}}_{{w}_{b}}^{\left(q\right)}\right\}}_{n\times 1}\end{array}\right]\\ {\mathfrak{X}}_{{{\varvec{w}}}_{{\varvec{s}}}}&=\left[\begin{array}{cccc}{\left\{{\mathfrak{X}}_{{w}_{s}}^{\left(1\right)}\right\}}_{n\times 1}& {\left\{{\mathfrak{X}}_{{w}_{s}}^{\left(2\right)}\right\}}_{n\times 1}& \dots & {\left\{{\mathfrak{X}}_{{w}_{s}}^{\left(q\right)}\right\}}_{n\times 1}\end{array}\right].\end{aligned}$$

(38)

Inserting Eq. (36) in Eq. (34) and then multiplying the result of it with the Galerkin matrix operator leads to the following format of the time-dependent governing differential equations of problem:

$$\overline{\overline{\mathcal{M}}}\ddot{\mathfrak{S}}+{\overline{\overline{\mathcal{K}}}}_{{\varvec{l}}}\mathfrak{S}+{\overline{\overline{\mathcal{K}}}}_{{\varvec{n}}{\varvec{l}}}\left(\mathfrak{S}\right)=0,$$

(39)

where

$$\begin{aligned}\overline{\overline{\mathcal{M}}}& =\mathcal{Q}\mathcal{M}\mathfrak{X}, {\overline{\overline{\mathcal{K}}}}_{{\varvec{l}}}=\mathcal{Q}{\mathcal{K}}_{{\varvec{l}}}\mathfrak{X} , {\overline{\overline{\mathcal{K}}}}_{{\varvec{n}}{\varvec{l}}}\left(\mathfrak{S}\right)=\mathcal{Q}{\mathcal{K}}_{{\varvec{n}}{\varvec{l}}}\left(\mathfrak{X}\mathfrak{S}\right)\\ \mathcal{Q}& =\left[\begin{array}{ccc}{\mathfrak{X}}_{{\varvec{u}}}& 0& 0\\ 0& {\mathfrak{X}}_{{{\varvec{w}}}_{{\varvec{b}}}}& 0\\ 0& 0& {\mathfrak{X}}_{{{\varvec{w}}}_{{\varvec{s}}}}\end{array}\right]\times \left[\begin{array}{ccc}\sum_{k=1}^{n-1}\left\{{{\overline{\overline{{\varvec{\xi}}}}}^{(k)}\mathfrak{P}}_{\xi }^{\left(k\right)}\right\}& 0& 0\\ 0& \sum_{k=1}^{n-1}\left\{{{\overline{\overline{{\varvec{\xi}}}}}^{(k)}\mathfrak{P}}_{\xi }^{\left(k\right)}\right\}& 0\\ 0& 0& \sum_{k=1}^{n-1}\left\{{{\overline{\overline{{\varvec{\xi}}}}}^{(k)}\mathfrak{P}}_{\xi }^{\left(k\right)}\right\}\end{array}\right]\\ {\overline{\overline{{\varvec{\xi}}}}}^{\left(k\right)}& =\left[\begin{array}{ccccc}\frac{{\left({\xi }_{2}-{\xi }_{1}\right)}^{k+1}}{{2}^{k+1}\left(k+1\right)!}& \cdots & \frac{{\left({\xi }_{i+1}-{\xi }_{i}\right)}^{k+1}-{\left({\xi }_{i-1}-{\xi }_{i}\right)}^{k+1}}{{2}^{k+1}\left(k+1\right)!}& \cdots & -\frac{{\left({\xi }_{n-1}-{\xi }_{n}\right)}^{k+1}}{{2}^{k+1}\left(k+1\right)!}\end{array}\right]\\& \quad i =\text{2,3},\dots ,n-1.\end{aligned}$$

(40)

On the other hand, the discretization of the sparse matrix incorporating the basis function contained of $q$ number of Galerkin-derived mode-shapes results in

$$\begin{aligned}{\mathbb{T}}_{3q\times {n}_{t}}=& \left[\begin{array}{llllllll}{\left\{{\mathfrak{S}}_{{\varvec{u}}}^{\left(1\right)}\right\}}_{1\times {n}_{t}}& {\left\{{\mathfrak{S}}_{{\varvec{u}}}^{\left(2\right)}\right\}}_{1\times {n}_{t}}& \dots & {\left\{{\mathfrak{S}}_{{\varvec{u}}}^{\left(2\right)}\right\}}_{1\times {n}_{t}}& {\left\{{\mathfrak{S}}_{{{\varvec{w}}}_{{\varvec{b}}}}^{\left(1\right)}\right\}}_{1\times {n}_{t}}& {\left\{{\mathfrak{S}}_{{{\varvec{w}}}_{{\varvec{b}}}}^{\left(2\right)}\right\}}_{1\times {n}_{t}}& \cdots & {\left\{{\mathfrak{S}}_{{{\varvec{w}}}_{{\varvec{b}}}}^{\left({\varvec{q}}\right)}\right\}}_{1\times {n}_{t}}\end{array}\right.\\ & \quad \left.\begin{array}{cccc}{\left\{{\mathfrak{S}}_{{{\varvec{w}}}_{{\varvec{s}}}}^{\left(1\right)}\right\}}_{1\times {n}_{t}}& {\left\{{\mathfrak{S}}_{{{\varvec{w}}}_{{\varvec{s}}}}^{\left(2\right)}\right\}}_{1\times {n}_{t}}& \dots & {\left\{{\mathfrak{S}}_{{{\varvec{w}}}_{{\varvec{s}}}}^{\left({\varvec{q}}\right)}\right\}}_{1\times {n}_{t}}\end{array}\right],\end{aligned}$$

(42)

where ${n}_{t}$ represents the discretization node numbers within the time domain. Consequently, after putting the related discretization process for Eq. (39), it yields

$$\overline{\overline{\mathcal{M}}}{\mathbb{T}}{\mathfrak{P}}_{t}^{\left(2\right)}+{\overline{\overline{\mathcal{K}}}}_{{\varvec{l}}}{\mathbb{T}}+{\overline{\overline{\mathcal{K}}}}_{{\varvec{n}}{\varvec{l}}}\left({\mathbb{T}}\right)=0,$$

(43)

in which ${\mathfrak{P}}_{t}^{\left(\right)}$ stands for the time differentiation matrix operators which can be defined as follows:

$${\mathfrak{P}}_{t}^{\left(1\right)}=2\pi \left[{\alpha }_{i,j}\right]\to \left\{\begin{array}{l}{\alpha }_{11}=0\\ {\alpha }_{i,1}=\frac{{\left(-1\right)}^{i-1}}{2}\text{cot}\left(\frac{\pi \left(i-1\right)}{{n}_{t}}\right)\\ {\alpha }_{1,j}=\frac{{\left(-1\right)}^{{n}_{t}-j+1}}{2}\text{cot}\left(\frac{\pi \left({n}_{t}-j+1\right)}{{n}_{t}}\right)\\ {\alpha }_{i+1,j+1}={\alpha }_{i,j}\end{array} i,j=\text{2,3},4,\dots ,{n}_{t}\right.,$$

(44a)

$${\mathfrak{P}}_{t}^{\left(2\right)}=4{\pi }^{2}\left[{\beta }_{i,j}\right]\to \left\{\begin{array}{l}{\beta }_{11}=-\frac{{n}_{t}^{2}}{12}-\frac{1}{6}\\ {\beta }_{i,1}=\frac{{\left(-1\right)}^{i-2}}{2{\text{sin}}^{2}\left(\frac{\pi \left(i-1\right)}{{n}_{t}}\right)}\\ {\beta }_{1,j}=\frac{{\left(-1\right)}^{{n}_{t}-j}}{2{\text{sin}}^{2}\left(\frac{\pi \left({n}_{t}-j-1\right)}{{n}_{t}}\right)}\\ {\beta }_{i+1,j+1}={\beta }_{i,j}\end{array} i,j=\text{2,3},4,\dots ,{n}_{t}\right..$$

(44b)

As a consequence, Eq. (43) can be rewritten in a vectorized form as follows:

$$\left[\left({\mathfrak{P}}_{t}^{\left(2\right)}\otimes \overline{\overline{\mathcal{M}}}\right)+\left({\mathbf{I}}_{\mathbf{t}}\otimes {\overline{\overline{\mathcal{K}}}}_{{\varvec{l}}}\right)\right]\text{vec}\left({\mathbb{T}}\right)+\text{vec}\left({\overline{\overline{\mathcal{K}}}}_{{\varvec{n}}{\varvec{l}}}\left({\mathbb{T}}\right)\right)=0,$$

(45)

in which $\otimes$ refers to the Kronecker product.

Through encompassing Eq. (45) to a set of nonlinear algebraic-type of equations, the considered nonlinear dynamic problem can be picked up using the strategy of pseudo-arc-length continuation.

4 Numerical results and discussion

A parametric examination is now performed, on the basis of which the dimensionless linear frequency–load and nonlinear frequency ratio–deflection responses related to the nonlocal strain gradient-based nonlinear dynamic stability of the agglomerated CNT-reinforced nanocomposite microbeams within the both prebuckling and postbuckling regimes are traced.

Accordingly, the dimensionless parameters utilized in the numerical analysis are considered as

Dimensionless maximum deflection: ${W}_{\text{max}}={\left({w}_{b}+{w}_{s}\right)}_{\text{max}}/h$

Dimensionless frequency: $\omega =\Omega h\sqrt{{\rho }_{m}/{E}_{m}}$.

Dimensionless axial load: $\overline{P }=PL/{E}_{m}{h}^{3}$

In addition, the geometric parameters of the agglomerated CNT-reinforced nanocomposite microbeams considered in the present analysis are taken into account as: $b=h=10 \,\upmu\text{m}, L=100h$. For armchair CNT nanofillers having the radius of $0.1 \text{nm}$, one will have: ${k}_{0}=30 \text{GPa}, {p}_{0}=10 \text{GPa}$, ${r}_{0}=1 \text{GPa}$, ${s}_{0}=450 \text{GPa}$, and ${q}_{0}=1 \text{GPa}$ [46]. In addition, for the matrix phase, it is supposed that: ${E}_{m}=0.85 \text{GPa}, {\nu }_{m}=0.4, {\rho }_{m}=2370 \text{Kg}/{\text{m}}^{3}$ [50].

In order to explore the accuracy of the proposed beam formulations, the nonlinear frequency ratio (${\omega }_{nl}/{\omega }_{l}$) of an axially compressed isotropic nanobeam with simply supported boundary conditions are obtained based upon the nonlocal continuum theory and corresponding to different maximum beam deflections, and then they are compared with those reported by Yang et al. [51] using an analytical solution as tabulated in Table 1. An excellent agreement is detected which confirms the validity of the proposed model and the accuracy of the given numerical results in the current investigation.

Table 1 Comparison examination on the nonlocal nonlinear frequency ratio (${\omega }_{nl}/{\omega }_{l}$) of an isotropic nanobeam relevant to various maximum beam deflections

Figures 4 and 5 depict, respectively, the nonlocal strain gradient-based linear frequency–load response and nonlinear frequency ratio-load response of agglomerated CNT-reinforced nanocomposite microbeams corresponding to different values of the nonlocal and strain gradient parameters. It is revealed that the nonlocality effect on the linear frequency is opposite before and after the bifurcation point as within the prebuckling territory, it results in lower linear frequency while within the postbuckling domain, it leads to higher values of ${\omega }_{l}$. This change in the size dependency character before and after the bifurcation point can be also observed related to the strain gradient type of size effect but with an opposite pattern. On the other hand, it is found the nonlinear frequency ratio (${\omega }_{nl}/{\omega }_{l}$) associated with a specific value of the microbeam deflection increases by taking the nonlocality into account, but decreases via considering the strain gradient size effect. These features of size dependency are the same within the both prebuckling and postbuckling territories.

Fig. 4

Conventional and nonlocal strain gradient-based linear frequency–load response of agglomerated nanocomposite microbeams corresponding to various small-scale parameters ($\eta =0.4 , \zeta =0.8, {V}_{\text{CNT}}=0.1$)

Fig. 5

Conventional and nonlocal strain gradient-based nonlinear frequency ratio–deflection response of agglomerated nanocomposite microbeams corresponding to various small-scale parameters ($\eta =0.4 , \zeta =0.8, {V}_{\text{CNT}}=0.1$)

In Tables 2 and 3, the nonlocal strain gradient-based nonlinear frequency ratios (${\omega }_{nl}/{\omega }_{l}$) associated with a specific maximum deflection of axially compressed agglomerated CNT-reinforced nanocomposite microbeams are presented corresponding to different cluster volume fractions with high ($\zeta =0.9$) and low ($\zeta =0.2$) CNT amounts inside clusters, respectively. It is deduced that for an agglomerated CNT-reinforced nanocomposite microbeam in which the most CNTs are inside clusters, a higher value of the cluster volume fraction results in to reduce the significance of the softening and stiffing characters associated with the nonlocal and strain gradient small-scale effects, respectively. However, for an agglomerated CNT-reinforced nanocomposite microbeam in which the most CNTs are outside clusters, increasing the value of the cluster volume fraction plays an opposite role in the size dependency features. Moreover, it is seen that for all values of the cluster volume fraction and within the both postbuckling and prebuckling territories, this softening character related to the nonlocality is somehow more considerable than the stiffening character associated with the strain gradient size effect.

Table 2 Nonlinear frequency ratios (${\omega }_{nl}/{\omega }_{l}$) of agglomerated CNT-reinforced nanocomposite microbeams corresponding to different cluster volume fractions ($\zeta =0.9, {W}_{\text{max}}=0.5$)

Table 3 Nonlinear frequency ratios (${\omega }_{nl}/{\omega }_{l}$) of agglomerated CNT-reinforced nanocomposite microbeams corresponding to different cluster volume fractions ($\zeta =0.2, {W}_{\text{max}}=0.5$)

Tables 4 and 5 give the nonlocal strain gradient-based nonlinear frequency ratios (${\omega }_{nl}/{\omega }_{l}$) associated with a specific maximum deflection of axially compressed agglomerated CNT-reinforced nanocomposite microbeams corresponding to different CNT amounts inside clusters with high ($\eta =0.9$) and low ($\eta =0.2$) cluster volume fractions, respectively. It is demonstrated that for an agglomerated CNT-reinforced nanocomposite microbeam having a low cluster volume fraction, increasing the CNT amount inside clusters causes to enhance the significance of the softening and stiffing characters associated with the nonlocal and strain gradient small-scale effects, respectively. However, for an agglomerated CNT-reinforced nanocomposite microbeam having a high cluster volume fraction, increasing the CNT amount inside clusters plays an opposite role. These observations are repeated for all kinds of boundary conditions.

Table 4 Nonlinear frequency ratios (${\omega }_{nl}/{\omega }_{l}$) of agglomerated CNT-reinforced nanocomposite microbeams corresponding to different CNT amounts inside clusters ($\eta =0.9, {W}_{\text{max}}=0.5$)

Table 5 Nonlinear frequency ratios (${\omega }_{nl}/{\omega }_{l}$) of agglomerated CNT-reinforced nanocomposite microbeams corresponding to different CNT amounts inside clusters ($\eta =0.2, {W}_{\text{max}}=0.5$)

In Figs. 6 and 7, the nonlocal strain gradient-based linear frequency–load response and nonlinear frequency ratio-load response are illustrated, respectively, for agglomerated CNT-reinforced nanocomposite microbeams having high cluster volume fractions with various CNT amounts inside clusters. It is indicated that by increasing the CNT amount inside clusters, the bifurcation point shifts to a lower axial compressive load. In addition, it results in that the linear frequency of the agglomerated nanocomposite microbeam before the bifurcation point increases, but reduces after the bifurcation point. Furthermore, for a specific maximum deflection induced in the microbeam, the nonlinear frequency ratio gets larger by decreasing the CNT amount outside clusters. These anticipations are repeated for all kinds of end supports.

Fig. 6

Influence of CNT amount inside clusters on the nonlocal strain gradient-based linear frequency–load path of agglomerated nanocomposite microbeams ($\eta =0.9 , {V}_{\text{CNT}}=0.1$)

Fig. 7

Influence of CNT amount inside clusters on the nonlocal strain gradient-based nonlinear frequency ratio–deflection path of agglomerated nanocomposite microbeams ($\eta =0.9 , {V}_{\text{CNT}}=0.1$)

Figures 8 and 9 show the nonlocal strain gradient-based linear frequency–load response and nonlinear frequency ratio-load response are illustrated, respectively, for agglomerated CNT-reinforced nanocomposite microbeams having high CNT amount inside clusters with various cluster volume fractions. It can be found that by decreasing the cluster volume fraction, the bifurcation point shifts to a higher axial compressive load. Moreover, it causes that the linear frequency of the agglomerated nanocomposite microbeam before the bifurcation point reduces, but enhances after the bifurcation point. In addition, for a specific maximum deflection induced in the agglomerated microbeam having high CNT amount inside clusters, the nonlinear frequency ratio becomes smaller by increasing the CNT amount outside clusters. These observations can be detected for all kinds of end supports.

Fig. 8

Influence of cluster volume fraction on the nonlocal strain gradient-based linear frequency–load path of agglomerated nanocomposite microbeams ($\zeta =0.9 , {V}_{\text{CNT}}=0.1$)

Fig. 9

Influence of cluster volume fraction on the nonlocal strain gradient-based nonlinear frequency–deflection path of agglomerated nanocomposite microbeams ($\zeta =0.9 , {V}_{\text{CNT}}=0.1$)

5 Concluding remarks

The prime objective of the present research study was to analyze the size-dependent quasi-3D nonlinear dynamical stability characteristics of agglomerated nanocomposite microbeams reinforced with randomly oriented CNTs. In this regard, the nonlocal strain gradient continuum elasticity was applied to a quasi-3D beam theory incorporating the sinusoidal transverse shear and normal shape functions in conjunction with geometrical nonlinearity. The constructive material properties were extracted based upon a micromechanical homogenization scheme containing only two parameters to capture the associated agglomeration of randomly oriented CNTs. Afterwards, an efficient numerical solving process was employed to trace the associated size-dependent nonlinear responses.

It was observed that the nonlocality effect on the linear frequency is opposite before and after the bifurcation point as within the prebuckling territory, it results in lower linear frequency while within the postbuckling domain, it leads to higher values of ${\omega }_{l}$. This change in the size dependency character before and after the bifurcation point can be also found for the strain gradient type of size effect but with an opposite pattern. It was indicated that for an agglomerated CNT-reinforced nanocomposite microbeam having a low cluster volume fraction, increasing the CNT amount inside clusters causes to enhance the significance of the softening and stiffing characters associated with the nonlocal and strain gradient small-scale effects, respectively. However, for an agglomerated CNT-reinforced nanocomposite microbeam having a high cluster volume fraction, increasing the CNT amount inside clusters plays an opposite role. These observations were repeated for all kinds of boundary conditions. In addition, for a specific maximum deflection induced in the microbeam, the nonlinear frequency ratio gets larger by decreasing the CNT amount outside clusters.