1 Introduction

As an emerging and modern and inhomogeneous material class, functionally graded materials (FGMs) meet several requirements of engineering applications including effective stress control leading the creation of several application areas for these materials. Kumar et al. [1] developed polymer–ceramic continuous quartz fiber reinforced FGM composites to be applied in thermos-structural aerospace applications. Qin and his colleagues investigated wave propagation behavior of FGM porous plates reinforced with graphene platelets [2] and conducted analytical study on impact response of sandwich cylindrical shell with a FGM porous core [3]. Besides, they have carried out a series of studies on vibrations of FGM plates and shells with non-classic boundary conditions [4,5,6], which benefits the application of plates and shells in engineering fields. On the other hand, advanced composite materials have widely utilized for several applications such as dynamic sensors [7], reinforced beam structures [8,9,10,11,12], lithium–ion battery [13], digital microscopes [14, 15], and dampers [16].

In the past decade, new fabrication processes have been proposed incorporating FGM composite concept in micro-electro-mechanical structures and systems. In this regard, it of great importance to take various size dependency features in mechanical properties of microstructures made of FGM composite. For example, Jung and Han [17] studied Sigmoid FGM composite microplate mechanical behaviors based on modified couple stress elasticity. Li and Pan [18] predicted FGM piezoelectric microplate static bending when symmetric couple stress tensor was present. Simsek [19] developed a nonlocal strain gradient Euler–Bernoulli beam model for nonlinear vibration behaviors of FGM composite nanobeam structures according to a novel Hamiltonian method. Sahmani and Aghdam [20] applied surface elasticity theory to investigate imperfection sensitivity of postbuckling behaviors of pressurized FGM composite cylindrical nanoshells. Liu et al. [21] investigated biaxial buckling and nonlocal oscillations properties of double viscoelastic FGM composite nanoplates under in-plane edge loads. Sahmani and Aghdam [22,23,24] determined critical buckling loads and postbuckling equilibrium paths of hybrid FGM composite cylindrical nanoshells based on nonlocal continuum theory. Phung-Van et al. [25] developed a generalized shear deformation plate theory for nonlinear transient response of piezoelectric FGM plates subjected to thermos-electro-mechanical loads using isogeometric technique. Nguyen et al. [26] employed a refined quasi-3D plate model incorporating couple stress size for FM composite microplates. Van et al. [27] derived a suitable computational equation for size-dependent nonlinear transient behaviors of FGM composite nanoplates based on isogeometric analysis. Chu et al. [28] predicted flexoelectric effect on FGM piezoelectric microbeam bending behaviors based on general modified strain gradient elasticity.

Recently, Khakalo et al. [29] modeled size-dependent 2D triangular lattices on the basis of strain gradient model for the analysis of mechanical responses of auxetics and sandwich beams. She et al. [30] studied the oscillations and nonlinear bending of FGM porous microtubes based on nonlocal strain gradient elasticity. Pang et al. [31] analytically explored viscoelastic nanoplate transverse oscillations using simply supported boundary conditions including high-order surface stress size effect. Sahmani et al. [32,33,34,35] predicted the nonlinear vibration and bending properties of graphene platelet-reinforced FGM porous third-order shear deformable microbeams based on nonlocal strain gradient continuum mechanics. Phung-Van et al. [36] investigated numerically the porosity-dependent nonlinear transient characteristics of FGM nanoplates with the aid of isogeometric method. Li et al. [37] used modified strain gradient theory of elasticity for the analysis of vibrations and static bending of organic solar cells surrounded by Winkler–Pasternak elastic foundation. Thanh et al. [38] established a modified couple stress-based Reddy plate model for the simulation of composite laminated microplate thermal bending behaviors. Sahmani and Safaei [39,40,41] analyzed size-dependent nonlinear mechanical responses of bi-directional FGM microbeams. Fan et al. [42,43,44] anticipated FGM porous microplate size-dependent responses according to various non-classical continuum theories. Ghorbani et al. [45] combined Gurtin–Murdoch and nonlocal strain gradient theories of elasticity to derive cylindrical microshell size-dependent natural frequencies. Yuan et al. [46,47,48] established size-dependent conical shell models to evaluate FGM composite conical microshell nonlinear mechanical properties. Ghobadi et al. [49] developed a continuous size-dependent electro-mechanical model for the analysis nonlinear thermos-electro-mechanical vibration behaviors of FGM flexoelectric nanoplate structures. Thai et al. [50] proposed a nonlocal meshfree model for the determination of size-dependent frequencies and deformations of FGM carbon nanotube-reinforced nanoplates. Yuan et al. [51] investigated shear buckling behaviors of FGM composite skew nanoplates under surface residual stress and surface elasticity. Yi et al. [52], and Li et al. [53] took into account the interactions among vibration modes for the analysis of surface elastic-based large-amplitude free vibrations of porous FGM composite nanoplates. Fan et al. [54] analyzed the couple stress effect on the dynamic stability of FGM conical microshells having magnetostrictive facesheets surrounded by a viscoelastic foundation. Sarafraz et al. [55], and Xie et al. [56] established a surface elastic beam model to predict the nonlinear secondary resonance of FGM porous nanobeams under periodic excitation. Yang et al. [57] employed a perturbation-based solving process for postbuckling analysis of hydrostatic pressurized nonlocal strain gradient FGM microshells.

The aim of this research was to develop nonlocal strain gradient quasi-3D nonlinear flexural solving process for FGM microplates with various thickness variation patterns. Therefore, a quasi-3D plate model based on nonlocal strain gradient continuum mechanics with sinusoidal transverse shear and trigonometric normal functions were employed. Then, the proposed refined quasi-3D nonlocal strain gradient plate model was combined with isogeometric technique incorporating geometric description and finite element approximation for accurately solving nonlinear problems for different thickness variation patterns.

2 Nonlocal strain gradient quasi-3D FGM variable thickness plate model

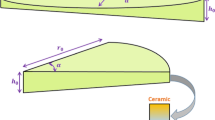
Here, as shown in Fig. 1, two sector and elliptical shapes have been taken into account for FGM composite microplates with variable thickness \(h(x,y)\). For elliptical shape, \(a\) and \(b\) denote long and short axes, respectively. For sector microplates, \(\alpha\) and \({r}_{0}\) represent angle and radius, respectively.

Fig. 1
figure 1

Schematic representation of a FGM sector microplate with variable thickness under uniform distributed load

Full size image

For estimating effective material characteristics of Poisson’s ratio \(\nu (z)\) and Young’s modulus \(E(z)\) of FGM composite microplates, Mori–Tanaka scheme homogenization scheme were considered. Therefore, effective bulk and shear moduli were determined according to homogenization model as:

$$K\left(z\right)={K}_{m}+\frac{{\left(\frac{1}{2}+\frac{z}{h}\right)}^{k}}{\frac{1}{{K}_{c}-{K}_{m}}+\frac{3\left[1-{\left(\frac{1}{2}+\frac{z}{h}\right)}^{k}\right]}{3{K}_{m}+4{G}_{m}}},$$
(1a)
$$G\left(z\right)={G}_{m}+\frac{{\left(\frac{1}{2}+\frac{z}{h}\right)}^{k}}{\frac{1}{{G}_{c}-{G}_{m}}+\frac{6\left({K}_{m}+2{G}_{m}\right)\left[1-{\left(\frac{1}{2}+\frac{z}{h}\right)}^{k}\right]}{5{G}_{m}\left(3{K}_{m}+4{G}_{m}\right)}},$$
(1b)

where \(k\) is material property gradient index and

$${K}_{m}=\frac{{E}_{m}}{3\left(1-2{\nu }_{m}\right)} , {K}_{c}=\frac{{E}_{c}}{3\left(1-2{\nu }_{c}\right)} , {G}_{m}=\frac{{E}_{m}}{2\left(1+{\nu }_{m}\right)} , {G}_{c}=\frac{{E}_{c}}{2\left(1+{\nu }_{c}\right)} .$$
(2)

Also, subscripts \(c\) and \(m\) denote ceramic and metal phases of FGM composite microplates, respectively.

To determine microplate thickness variations for sector and elliptical shapes, the following functions were considered for a sector microplates:

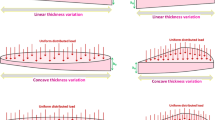
$$h\left(x,y\right)={h}_{0}\left[1-\frac{1}{2}{\left(\frac{\sqrt{{x}^{2}+{y}^{2}}}{{r}_{0}}\right)}^{\eta }\right],$$
(3)

where \(\eta\) and \({h}_{0}\) are thickness variation constant showing variable thickness type and maximum plate thickness, respectively. Therefore, concave, linear, and convex thickness variation types are related to \(\eta >1\), \(\eta =1\) and \(\eta <1\), respectively.

Figures 2 and 3 compare linear thickness variations with convex and concave ones, respectively, for various thickness variation constants.

Fig. 2
figure 2

Illustration of convex and linear variations of the plate thickness for sector microplates corresponding to different thickness variation constants

Full size image
Fig. 3
figure 3

Illustration of concave and linear variations of the plate thickness for sector microplates corresponding to different thickness variation constants

Full size image

The quasi-3D modelling of a microplate was stated as follows by taking into account normal strains using a transverse normal shape function \({\mathbb{g}}(z)\) and dividing transverse displacement component into shear bending and variables:

$${\mathcal{U}}_{x}\left(x,y,z\right)=u\left(x,y\right)-z{w}_{b,x}\left(x,y\right)+{\mathbb{F}}\left(z\right){w}_{s,x}\left(x,y\right),$$
(4a)
$${\mathcal{U}}_{y}\left(x,y,z\right)=v\left(x,y\right)-z{w}_{b,y}\left(x,y\right)+{\mathbb{F}}\left(z\right){w}_{s,y}\left(x,y\right),$$
(4b)
$${\mathcal{U}}_{z}\left(x,y,z\right)={w}_{b}\left(x,y\right)+{\mathbb{G}}\left(z\right){w}_{s}\left(x,y\right),$$
(4c)

where \({w}_{s}(x,y)\) and \({w}_{b}\left(x,y\right)\) are shear and bending displacement variables according to hybrid quasi-3D-based higher order shear deformation plate model. By assuming normal shape and transverse shear functions as sinusoidal trigonometric ones, it was found that

$${\mathbb{F}}\left(z\right)=\mathrm{sin}\left(\pi z/h\right)-z ,$$
(5a)
$${\mathbb{G}}\left(z\right)=1+\left(5/12\pi \right)\mathrm{cos}\left(\pi z/h\right).$$
(5b)

Considering von-Karman nonlinear kinematics including large deflections and moderate rotations, the associated hybrid quasi-3D-based strain components were stated as:

$${\varepsilon }_{xx}={u}_{,x}+\frac{{\left({w}_{b,x}+{w}_{s,x}\right)}^{2}}{2}-z{w}_{b,xx}+{\mathbb{F}}\left(z\right){w}_{s,xx},$$
$${\varepsilon }_{yy}={v}_{,y}+\frac{{\left({w}_{b,y}+{w}_{s,y}\right)}^{2}}{2}-z{w}_{b,yy}+{\mathbb{F}}\left(z\right){w}_{s,yy},$$
$${\varepsilon }_{zz}={\mathbb{G}}_{,z}\left(z\right){w}_{s},$$
$${\gamma }_{xy}={u}_{,y}+{v}_{,x}+\left({w}_{b,x}+{w}_{s,x}\right)\left({w}_{b,y}+{w}_{s,y}\right)-2z{w}_{b,xy}+2{\mathbb{F}}\left(z\right){w}_{s,xy},$$
(6)
$${\gamma }_{xz}=\left({\mathbb{F}}_{,z}\left(z\right)+{\mathbb{G}}\left(z\right)\right){w}_{s,x},$$
$${\gamma }_{yz}=\left({\mathbb{F}}_{,z}\left(z\right)+{\mathbb{G}}\left(z\right)\right){w}_{s,y}.$$

Consequently, stress–strain constitutive relationships were written as:

$${\sigma }_{xx}=\frac{E(z)}{\left(1+\nu \left(z\right)\right)\left(1-2\nu \left(z\right)\right) }{\varepsilon }_{xx}+\frac{\nu \left(z\right)E(z)}{\left(1+\nu \left(z\right)\right)\left(1-2\nu \left(z\right)\right)}\left({\varepsilon }_{yy}+{\varepsilon }_{zz}\right),$$
$${\sigma }_{yy}=\frac{E(z)}{\left(1+\nu \left(z\right)\right)\left(1-2\nu \left(z\right)\right)}{\varepsilon }_{yy}+\frac{\nu \left(z\right)E(z)}{\left(1+\nu \left(z\right)\right)\left(1-2\nu \left(z\right)\right)}\left({\varepsilon }_{xx}+{\varepsilon }_{zz}\right),$$
(7)
$${\sigma }_{zz}=\frac{E(z)}{\left(1+\nu \left(z\right)\right)\left(1-2\nu \left(z\right)\right)}{\varepsilon }_{zz}+\frac{\nu \left(z\right)E(z)}{\left(1+\nu \left(z\right)\right)\left(1-2\nu \left(z\right)\right)}\left({\varepsilon }_{xx}+{\varepsilon }_{yy}\right),$$
$${\tau }_{xy}=\frac{E(z)}{2\left(1+\nu \left(z\right)\right)}{\gamma }_{xy} , {\tau }_{yz}=\frac{E(z)}{2\left(1+\nu \left(z\right)\right)}{\gamma }_{yz} , {\tau }_{xz}=\frac{E(z)}{2\left(1+\nu \left(z\right)\right)}{\gamma }_{xz}.$$

By employing nonlocal strain gradient continuum elasticity, total stress tensor was stated as [58]:

$${\Phi }_{ij}={\sigma }_{ij}-\nabla {\sigma }_{ijm}^{*} ,$$
(8)

where classical and higher order stresses, respectively, were described:

$${\sigma }_{ij}={\int }_{V}{\chi }_{1}\left({x}^{^{\prime}},x,{e}_{1}\right){C}_{ijkl}{\varepsilon }_{kl}dV,$$
(9a)
$${\sigma }_{ijm}^{*}={l}^{2}{\int }_{V}{\chi }_{2}\left({x}^{^{\prime}},x,{e}_{2}\right){C}_{ijkl}{\varepsilon }_{kl,m}dV,$$
(9b)

where \({e}_{1}\) and \({e}_{2}\) represent nonlocal parameters corresponding to size dependency due to nonlocal stress. Also, \(l\) is length scale parameter incorporating strain gradient size effect. \({C}_{ijkl}\), \({\varepsilon }_{kl}\), \({\mathrm{and } \, \varepsilon }_{kl,m}\) are elastic coefficients, strain components, and strain gradient components, respectively. Based on nonlocal strain gradient theory, it was assumed that \({\chi }_{1}\left({x}^{^{\prime}},x,{e}_{1}\right)\) and \({\chi }_{2}\left({x}^{^{\prime}},x,{e}_{2}\right)\) two kernel functions had to equilibrate the conditions introduced by Eringen [59] as:

$${\sigma }_{ij}-{e}_{1}^{2}\left({\sigma }_{ij,xx}+{\sigma }_{ij,yy}\right)={C}_{ijkl}{\varepsilon }_{kl},$$
(10a)
$${\sigma }_{ijm}^{*}-{e}_{2}^{2}\left({\sigma }_{ijm,xx}^{*}+{\sigma }_{ijm,yy}^{*}\right)={l}^{2}{C}_{ijkl}{\varepsilon }_{kl,m}.$$
(10b)

Therefore, generalized constitutive equation based on nonlocal strain gradient elasticity was stated as:

$$\left[1-{e}_{1}^{2}\left({}_{,xx}+{}_{,yy}\right)\right]\left[1-{e}_{2}^{2}\left({}_{,xx}+{}_{,yy}\right)\right]{\Phi }_{ij}=\left[1-{e}_{1}^{2}\left({}_{,xx}+{}_{,yy}\right)\right]{C}_{ijkl}{\varepsilon }_{kl}-{l}^{2}\left[1-{e}_{2}^{2}\left({}_{,xx}+{}_{,yy}\right)\right]{C}_{ijkl}\left({\varepsilon }_{kl,xx}+{\varepsilon }_{kl,yy}\right).$$
(11)

Assuming \({e}_{1}={e}_{2}=e\), it was found that

$${\Phi }_{ij}-{e}^{2}\left({\Phi }_{ij,xx}+{\Phi }_{ij,yy}\right)={C}_{ijkl}{\varepsilon }_{kl}-{l}^{2}{C}_{ijkl}\left({\varepsilon }_{kl,xx}+{\varepsilon }_{kl,yy}\right).$$
(12)

Therefore, strain energy variations for quasi-3D nonlocal strain gradient FGM microplates with various shapes and thicknesses were written as:

$$\delta {\Pi }_{S}={\int }_{S}{\int }_{-\frac{h(x,y)}{2}}^{\frac{h(x,y)}{2}}{\Phi }_{ij}\delta {\varepsilon }_{ij}dzdS.$$
(13)

In addition, the induced virtual work by external distributed load \(q\) was stated as:

$$\delta {\Pi }_{W}={\int }_{S}q\delta wdS.$$
(14)

Virtual work principle was employed along with the substitution of Eqs. (6) and (7) into Eq. (13) resulting in

$${\int }_{S}\left\{\delta \left({\mathfrak{P}}_{{\varvec{b}}}^{T}\right){{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{P}}_{{\varvec{b}}}-{l}^{2}\delta \left({\nabla }^{2}{\mathfrak{P}}_{{\varvec{b}}}^{T}\right){{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{P}}_{{\varvec{b}}}+\delta \left({\mathfrak{P}}_{{\varvec{s}}}^{T}\right){{\varvec{\xi}}}_{{\varvec{s}}}{\mathfrak{P}}_{{\varvec{s}}}-{l}^{2}\delta \left({\nabla }^{2}{\mathfrak{P}}_{{\varvec{s}}}^{T}\right){{\varvec{\xi}}}_{{\varvec{s}}}{\mathfrak{P}}_{{\varvec{s}}}\right\}dS={\int }_{S}\left(1-{e}^{2}{\nabla }^{2}\right)\mathcal{q}\delta wdS,$$
(15)

where

$${\mathfrak{P}}_{{\varvec{b}}}={\left[\begin{array}{cccc}{u}_{,x}+{\left({w}_{b,x}+{w}_{s,x}\right)}^{2}/2& -{w}_{b,xx}& {w}_{s,xx}& 0\\ {v}_{,y}+{\left({w}_{b,y}+{w}_{s,y}\right)}^{2}/2& -{w}_{b,yy}& {w}_{s,yy}& 0\\ {u}_{,y}+{v}_{,x}+\left({w}_{b,x}+{w}_{s,x}\right)\left({w}_{b,y}+{w}_{s,y}\right)& -2{w}_{b,xy}& 2{w}_{s,xy}& 0\\ 0& 0& 0& {w}_{s}\end{array}\right]}^{T},$$
$${{\varvec{\xi}}}_{{\varvec{b}}}=\left[\begin{array}{cccc}{\mathbf{A}}_{\mathbf{b}}& {\mathbf{B}}_{\mathbf{b}}& {\mathbf{C}}_{\mathbf{b}}& {\mathbf{E}}_{\mathbf{b}}\\ {\mathbf{B}}_{\mathbf{b}}& {\mathbf{D}}_{\mathbf{b}}& {\mathbf{F}}_{\mathbf{b}}& {\mathbf{G}}_{\mathbf{b}}\\ {\mathbf{C}}_{\mathbf{b}}& {\mathbf{F}}_{\mathbf{b}}& {\mathbf{H}}_{\mathbf{b}}& {\mathbf{K}}_{\mathbf{b}}\\ {\mathbf{E}}_{\mathbf{b}}& {\mathbf{G}}_{\mathbf{b}}& {\mathbf{K}}_{\mathbf{b}}& {\mathbf{J}}_{\mathbf{b}}\end{array}\right] , {\mathfrak{P}}_{{\varvec{s}}}=\left[\begin{array}{c}{w}_{s,x}\\ {w}_{s,y}\end{array}\right],$$
(16)
$${{\varvec{\xi}}}_{{\varvec{s}}}={\int }_{-\frac{h(x,y)}{2}}^{\frac{h(x,y)}{2}}{\left({\mathbb{F}}_{,z}\left(z\right)+{\mathbb{G}}\left(z\right)\right)}^{2}\left[\begin{array}{cc}{Q}_{44}(z)& 0\\ 0& {Q}_{55}(z)\end{array}\right]dz,$$

where stress-based stiffness parameters was defined as:

$$\left\{{\mathbf{A}}_{\mathbf{b}},{\mathbf{B}}_{\mathbf{b}},{\mathbf{C}}_{\mathbf{b}}\right\}={\int }_{-\frac{h(x,y)}{2}}^{\frac{h(x,y)}{2}}\left[\begin{array}{cccc}\frac{1}{1-2\nu (z)}& \frac{\nu \left(z\right)}{1-2\nu (z)}& 0& \frac{\nu \left(z\right)}{1-2\nu (z)}\\ \frac{\nu \left(z\right)}{1-2\nu (z)}& \frac{1}{1-2\nu (z)}& 0& \frac{\nu \left(z\right)}{1-2\nu (z)}\\ 0& 0& 1/2& 0\\ \frac{\nu \left(z\right)}{1-2\nu (z)}& \frac{\nu \left(z\right)}{1-2\nu (z)}& 0& \frac{1}{1-2\nu (z)}\end{array}\right]\frac{E(z)}{1+\nu (z)}\left\{1,z,{\mathbb{F}}\left(z\right)\right\}dz,$$
$$\left\{{\mathbf{D}}_{\mathbf{b}},{\mathbf{E}}_{\mathbf{b}}\right\}={\int }_{-\frac{h(x,y)}{2}}^{\frac{h(x,y)}{2}}\left[\begin{array}{cccc}\frac{1}{1-2\nu (z)}& \frac{\nu \left(z\right)}{1-2\nu (z)}& 0& \frac{\nu \left(z\right)}{1-2\nu (z)}\\ \frac{\nu \left(z\right)}{1-2\nu (z)}& \frac{1}{1-2\nu (z)}& 0& \frac{\nu \left(z\right)}{1-2\nu (z)}\\ 0& 0& 1/2& 0\\ \frac{\nu \left(z\right)}{1-2\nu (z)}& \frac{\nu \left(z\right)}{1-2\nu (z)}& 0& \frac{1}{1-2\nu (z)}\end{array}\right]\frac{E(z)}{1+\nu (z)}\left\{{z}^{2},{\mathbb{G}}_{,z}\left(z\right)\right\}dz,$$
(17)
$$\left\{{\mathbf{F}}_{\mathbf{b}},{\mathbf{G}}_{\mathbf{b}},{\mathbf{H}}_{\mathbf{b}}\right\}={\int }_{-\frac{h(x,y)}{2}}^{\frac{h(x,y)}{2}}\left[\begin{array}{cccc}\frac{1}{1-\nu 2(z)}& \frac{\nu \left(z\right)}{1-2\nu (z)}& 0& \frac{\nu \left(z\right)}{1-2\nu (z)}\\ \frac{\nu \left(z\right)}{1-2\nu (z)}& \frac{1}{1-2\nu (z)}& 0& \frac{\nu \left(z\right)}{1-2\nu (z)}\\ 0& 0& 1/2& 0\\ \frac{\nu \left(z\right)}{1-2\nu (z)}& \frac{\nu \left(z\right)}{1-2\nu (z)}& 0& \frac{1}{1-2\nu (z)}\end{array}\right]\frac{E(z)}{1+\nu (z)}\left\{z{\mathbb{F}}\left(z\right),z{\mathbb{G}}_{,z}\left(z\right),{\mathbb{F}}^{2}\left(z\right)\right\}dz,$$
$$\left\{{\mathbf{K}}_{\mathbf{b}},{\mathbf{J}}_{{\varvec{b}}}\right\}={\int }_{-\frac{h(x,y)}{2}}^{\frac{h(x,y)}{2}}\left[\begin{array}{cccc}\frac{1}{1-2\nu (z)}& \frac{\nu \left(z\right)}{1-2\nu (z)}& 0& \frac{\nu \left(z\right)}{1-2\nu (z)}\\ \frac{\nu \left(z\right)}{1-2\nu (z)}& \frac{1}{1-2\nu (z)}& 0& \frac{\nu \left(z\right)}{1-2\nu (z)}\\ 0& 0& 1/2& 0\\ \frac{\nu \left(z\right)}{1-2\nu (z)}& \frac{\nu \left(z\right)}{1-2\nu (z)}& 0& \frac{1}{1-2\nu (z)}\end{array}\right]\frac{E(z)}{1+\nu (z)}\left\{{\mathbb{F}}\left(z\right){\mathbb{G}}_{,z}\left(z\right),{\left({\mathbb{G}}_{,z}\left(z\right)\right)}^{2}\right\}dz.$$

3 Isogeometric finite element framework

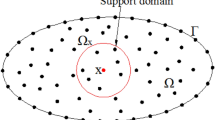
Isogeometric technique is a new solution method for connecting finite element and computer aided design approaches to determine geometrical description and an efficient numerical approximation [60,61,62,63,64,65,66,67,68]. The considered cubic elements for a sector microplate is depicted in Fig. 4.

Fig. 4
figure 4

Representation of cubic elements for a sector microplate

Full size image

Considering rational functions of B-splines, displacement field in a plate-type domain satisfying C−1-requirement essential for the developed quasi-3D plate model was approximated as:

$${\left\{{\stackrel{\sim }{u}}^{i},{\stackrel{\sim }{v}}^{i},{\stackrel{\sim }{w}}_{b}^{i},{\stackrel{\sim }{w}}_{s}^{i}\right\}}^{T}=\sum_{i=1}^{m\times n}{G}_{i}\left(x,y\right)\left\{\begin{array}{c}{u}^{i}\\ {v}^{i}\\ {w}_{b}^{i}\\ {w}_{s}^{i}\end{array}\right\},$$
(18)

where

$${G}_{i}\left(x,y\right)=\left[\begin{array}{cccc}{\mathfrak{X}}_{i}(x,y)& 0& 0& 0\\ 0& {\mathfrak{X}}_{i}(x,y)& 0& 0\\ 0& 0& {\mathfrak{X}}_{i}(x,y)& 0\\ 0& 0& 0& {\mathfrak{X}}_{i}(x,y)\end{array}\right].$$
(19)

According to Eqs. (18) and (19), strain components were rewritten as:

$${\mathfrak{F}}_{{\varvec{b}}}={\mathfrak{F}}_{{\varvec{b}}}^{{\varvec{L}}}+{\mathfrak{F}}_{{\varvec{b}}}^{{\varvec{N}}{\varvec{L}}}=\sum_{i=1}^{m\times n}{\boldsymbol{\Upsilon}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}{\mathbb{X}}+\sum_{i=1}^{m\times n}\frac{1}{2}{\boldsymbol{\Upsilon}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}{\mathbb{X}} , {\mathfrak{F}}_{{\varvec{s}}}=\sum_{{\varvec{i}}=1}^{{\varvec{m}}\times {\varvec{n}}}{\boldsymbol{\Upsilon}}_{{\varvec{s}}}^{{\varvec{i}}}{\mathbb{X}} ,$$
(20)

where

$${\boldsymbol{\Upsilon}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}={\left\{\begin{array}{cccc}{\boldsymbol{\Upsilon}}_{{\varvec{b}}1}^{{\varvec{i}}}& {\boldsymbol{\Upsilon}}_{{\varvec{b}}2}^{{\varvec{i}}}& {\boldsymbol{\Upsilon}}_{{\varvec{b}}3}^{{\varvec{i}}}& {\boldsymbol{\Upsilon}}_{{\varvec{b}}4}^{{\varvec{i}}}\end{array}\right\}}^{{\varvec{T}}}\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ },\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{\boldsymbol{\Upsilon}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}={\left\{\begin{array}{cccc}{\boldsymbol{\Upsilon}}_{{\varvec{b}}5}^{{\varvec{i}}}& 0& 0& 0\end{array}\right\}}^{{\varvec{T}}}{\boldsymbol{\Upsilon}}_{{\varvec{G}}}^{{\varvec{i}}},{\mathbb{X}}=\left\{\begin{array}{c}{u}^{i}\\ {v}^{i}\\ {w}_{b}^{i}\\ {w}_{s}^{i}\end{array}\right\},$$
$${\boldsymbol{\Upsilon}}_{{\varvec{b}}1}^{{\varvec{i}}}=\left[\begin{array}{cccc}{\mathfrak{X}}_{i,x}(x,y)& 0& 0& 0\\ 0& {\mathfrak{X}}_{i,y}(x,y)& 0& 0\\ {\mathfrak{X}}_{i,y}(x,y)& {\mathfrak{X}}_{i,x}(x,y)& 0& 0\\ 0& 0& 0& 0\end{array}\right]\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ },\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{\boldsymbol{\Upsilon}}_{{\varvec{b}}2}^{{\varvec{i}}}=-\left[\begin{array}{cccc}0& 0& {\mathfrak{X}}_{i,xx}\left(x,y\right)& 0\\ 0& 0& {\mathfrak{X}}_{i,yy}\left(x,y\right)& 0\\ 0& 0& 2{\mathfrak{X}}_{i,xy}\left(x,y\right)& 0\\ 0& 0& 0& 0\end{array}\right],$$
$${\boldsymbol{\Upsilon}}_{{\varvec{b}}3}^{{\varvec{i}}}=\left[\begin{array}{cccc}0& 0& 0& {\mathfrak{X}}_{i,xx}(x,y)\\ 0& 0& 0& {\mathfrak{X}}_{i,yy}(x,y)\\ 0& 0& 0& 2{\mathfrak{X}}_{i,xy}(x,y)\\ 0& 0& 0& 0\end{array}\right]\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ },\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{\boldsymbol{\Upsilon}}_{{\varvec{b}}4}^{{\varvec{i}}}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& {\mathfrak{X}}_{i}(x,y)\end{array}\right],$$
(21)
$${\boldsymbol{\Upsilon}}_{{\varvec{b}}5}^{{\varvec{i}}}=\left[\begin{array}{cc}{w}_{b,x}+{w}_{s,x}& 0\\ 0& {w}_{b,y}+{w}_{s,y}\\ {w}_{b,y}+{w}_{s,y}& {w}_{b,x}+{w}_{s,x}\end{array}\right]\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ },\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{\boldsymbol{\Upsilon}}_{{\varvec{G}}}^{{\varvec{i}}}=\left[\begin{array}{cccc}0& 0& {\mathfrak{X}}_{i,x}(x,y)& {\mathfrak{X}}_{i,x}(x,y)\\ 0& 0& {\mathfrak{X}}_{i,y}(x,y)& {\mathfrak{X}}_{i,y}(x,y)\end{array}\right].$$

Therefore, strain tensor variations were derived as:

$$\delta \left({\mathfrak{F}}_{{\varvec{b}}}\right)=\delta \left({\mathfrak{F}}_{{\varvec{b}}}^{{\varvec{L}}}\right)+\delta \left({\mathfrak{F}}_{{\varvec{b}}}^{{\varvec{N}}{\varvec{L}}}\right)=\sum_{i=1}^{m\times n}\left({\boldsymbol{\Upsilon}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}+{\boldsymbol{\Upsilon}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)\left\{\begin{array}{c}\delta {u}^{i}\\ \delta {v}^{i}\\ \delta {w}_{b}^{i}\\ \delta {w}_{s}^{i}\end{array}\right\} , \delta \left({\mathfrak{F}}_{{\varvec{s}}}\right)=\sum_{i=1}^{m\times n}{\boldsymbol{\Upsilon}}_{{\varvec{s}}}^{{\varvec{i}}}\left\{\begin{array}{c}\delta {u}^{i}\\ \delta {v}^{i}\\ \delta {w}_{b}^{i}\\ \delta {w}_{s}^{i}\end{array}\right\}.$$
(22)

In the continuation of solution methodology, the nonlinear differential equations of the system could be obtained in a discretized form as:

$$\mathfrak{A}\left({\mathbb{X}}\right){\mathbb{X}}={\mathbb{S}},$$
(23)

where \(\mathfrak{A}\left({\mathbb{X}}\right)\) is global stiffness matrix containing two nonlinear and linear parts as:

$${\mathfrak{A}}_{L}={\int }_{S}\left\{{\left({\mathfrak{F}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{F}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}-{l}^{2}{\nabla }^{2}{\left({\mathfrak{F}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{F}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}+{\left({\mathfrak{F}}_{{\varvec{s}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{s}}}{\mathfrak{F}}_{{\varvec{s}}}^{{\varvec{i}}}-{l}^{2}{\nabla }^{2}{\left({\mathfrak{F}}_{{\varvec{s}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{s}}}{\mathfrak{F}}_{{\varvec{s}}}^{{\varvec{i}}}\right\}dS,$$
(24)
$${\mathfrak{A}}_{NL}\left({\mathbb{X}}\right)={\int }_{S}\left\{\frac{1}{2}{\left({\mathfrak{F}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{F}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}-\frac{{l}^{2}}{2}{\nabla }^{2}{\left({\mathfrak{F}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{F}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}+{\left({\mathfrak{F}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{F}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}-{l}^{2}{\nabla }^{2}{\left({\mathfrak{F}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{F}}_{{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}+\frac{1}{2}{\left({\mathfrak{F}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{F}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}-\frac{{l}^{2}}{2}{\nabla }^{2}{\left({\mathfrak{F}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right)}^{{\varvec{T}}}{{\varvec{\xi}}}_{{\varvec{b}}}{\mathfrak{F}}_{{\varvec{N}}{\varvec{L}}{\varvec{b}}}^{{\varvec{i}}}\right\}dS.$$
(25)

In addition, the load vector associated with uniform distributed load \(\mathcal{q}\) was stated as:

$${\mathbb{S}}={\int }_{S}\left(1-{e}^{2}{\nabla }^{2}\right)\mathcal{q}\left\{\begin{array}{c}0\\ 0\\ {\mathfrak{X}}_{i}(x,y)\\ {\mathfrak{X}}_{i}(x,y)\end{array}\right\}dS.$$
(26)

Then, an iterative procedure based on Newton–Raphson technique was applied to derive the solution of Eq. (23).

4 Numerical results and discussion

Following the application of the developed solution method, the dimensionless nonlocal strain gradient nonlinear and linear load–deflection behaviors of FGM microplates with a sector shape with variable thicknesses were drawn. It was assumed that FGM microplate bottom and top surfaces were fully metal and fully ceramic, respectively. Material properties were: \({E}_{m}=70 \, \mathrm{GPa}\), \(\nu =0.35\) for metal constituent and \({E}_{c}=210 \, \mathrm{GPa}\), \(\nu =0.24\) for ceramic constituent [69]. In addition, dimensionless maximum deflection was considered as \({W}_{\max}={w}_{\max}/h\) and dimensionless load was described as \(\stackrel{-}{P}=\mathcal{q}{r}_{0}^{2}/{E}_{m}{h}^{2}\). Furthermore, the geometric parameters of sector microplates with \({h}_{0}\) initial thickness were considered as \({h}_{0}=25 \, \mu \mathrm{m} \, \mathrm{and} \, 2{r}_{0}=50{h}_{0}\).

Firstly, the proposed solving methodology was validated. To do so, neglecting couple stress size dependency terms, the nonlinear load–deflection curves drawn for geometrically nonlinear flexural behaviors of square composite plates were compared with those reported by Singh et al. [70], as shown in Fig. 5. A great agreement was witnessed which confirmed the reliability of the developed numerical solution process.

Fig. 5
figure 5

Comparison study on the load–deflection plots obtained for the nonlinear bending of a composite square plate under inform distributed load

Full size image

Figure 6 demonstrates dimensionless nonlocal strain gradient linear and nonlinear load–deflection responses corresponding to the flexural behavior of FGM sector microplates, with linear thickness variations (\(\eta =1\)). To compare, the findings of classical quasi-3D continuum elasticity were also adopted. It was shown that increase of nonlocal parameter to plate thickness ratio enhanced nonlocality importance. However, decrease of the abovementioned ratio resulted in the tendency of both nonlinear and linear flexural behaviors of sector microplates to their classical counterparts. Similar findings were obtained for strain gradient size effect. Also, it was witnessed that considering nonlocal size effect resulted in higher extracted deflections obtained from nonlocal strain gradient quasi-3D plate model than those derived from classical continuum elasticity because of the softening property of nonlocal size effect, while strain gradient microstructural size dependency acted in opposite way and represented a stiffening property.

Fig. 6
figure 6

Comparison of the classical and nonlocal strain gradient plate models for linear and nonlinear flexural responses of FGM sector microplate with variable thickness (\(k=0.5, \eta =1,\boldsymbol{ }\alpha =\pi /3\))

Full size image

Tables 1 and 2 summarize the dimensionless distributed loads for specific values of maximum deflection in the presence of nonlocality and absence of strain gradient small scale effect for simply supported and clamped boundary conditions, respectively. The same findings are given in Tables 3 and 4 for strain gradient size effect and ignoring nonlocality, respectively. It was witnessed that by moving to deeper parts of load–deflection response, which takes into account higher maximum deflections, the significance of nonlocality softener character and strain gradient size dependency stiffer character somehow decreased. This finding was repeated for all thickness variation patterns and for both clamped and simply supported boundary conditions. However, it was found that changing material gradient index value changed FGM sector microplate flexural stiffness, but the emphasis of both small scale effect kinds remained unchanged. This prediction was similar for both initial and deeper parts of flexural responses. Also, it was concluded that for all material gradient index values and thickness variation patterns, strain gradient size effect stiffer character was more prominent than nonlocality softener character acting in a specific value of maximum deflection.

Table 1 Dimensionless classical and nonlocal strain gradient distributed loads associated with the nonlinear bending response of FGM sector microplates with simply supported boundary conditions corresponding to different nonlocal parameters and thickness variation constants
Full size table
Table 2 Dimensionless classical and nonlocal strain gradient distributed loads associated with the nonlinear bending response of FGM sector microplates with clamped boundary conditions corresponding to different nonlocal parameters and thickness variation constants
Full size table
Table 3 Dimensionless classical and nonlocal strain gradient distributed loads associated with the nonlinear bending response of FGM sector microplates with simply supported boundary conditions corresponding to different strain gradient parameters and thickness variation constants
Full size table
Table 4 Dimensionless classical and nonlocal strain gradient distributed loads associated with the nonlinear bending response of FGM sector microplates with clamped boundary conditions corresponding to different strain gradient parameters and thickness variation constants
Full size table

Material gradient index effects on linear and nonlinear flexural responses of FGM sector microplates are presented in Fig. 7. Analyses were conducted for both classical and nonlocal strain gradient quasi-3D models. It was found that increase of material gradient index value, which resulted in moving from fully ceramic sector microplate to fully metal one, increased maximum deflection for a given uniform transverse load because of lower volume fractions of ceramic constituent. Also, it was found that in both nonlinear and linear flexural responses, increase of transverse load value enhanced the significance of material gradient index.

Fig. 7
figure 7

Influence of material gradient index on the nonlocal strain gradient linear and nonlinear flexural responses of FGM sector microplate with variable thickness (\(\eta =1, \alpha =\pi /3\))

Full size image

Figure 8 shows nonlocal strain gradient linear and flexural characteristics for FGM composite sector microplates with various thickness variation patterns. It was found that the gaps between load–deflection curves for concave, convex, and linear thickness variation patterns were increased by altering the boundary conditions of FGM composite sector microplates from clamped to simply supported. In addition, it was found that at higher transverse loads, the effect of thickness variation pattern was enhanced.

Fig. 8
figure 8

Influence of thickness variation parameter on the nonlocal strain gradient linear and nonlinear flexural responses of FGM sector microplate with variable thickness (\(k=0.5, e=l=150 \, \mu \mathrm{m}, \alpha =\pi /3\))

Full size image

Figure 9 shows the influences of geometrical parameters on nonlocal strain gradient linear and nonlinear flexural behaviors of FGM sector microplates. It was deduced that decrease of \(\alpha\) in sector microplates increased their bending stiffness resulting in lower deflections for specific applied transverse loads. In addition, it was found that taking into account this variation in the geometrical parameter of sector microplates, the difference between nonlinear and linear flexural analyses was increased representing the increase of associated geometrical nonlinearity.

Fig. 9
figure 9

Influence of the angle on the nonlocal strain gradient linear and nonlinear flexural responses of FGM sector microplate with variable thickness (\(k=0.5, \eta =1, e=l=150 \, \mu \mathrm{m}\))

Full size image

5 Concluding remarks

In this research, microstructural-dependent nonlinear and linear flexural properties of FGM microplates with a sector shape and different thicknesses were studied. To do so, nonlocal strain gradient continuum mechanics was applied in a hybrid quasi-3D-based higher order shear deformation plate model along with von Karman geometrical nonlinearity. Then, isogeometric finite element method was applied to derive nonlocal strain gradient nonlinear and linear load–deflection plots along with classical continuum elastic-based counterparts.

It was shown that by moving to deeper parts of load–deflection responses which took into account higher maximum deflections, the significance of strain gradient size dependency stiffer character and nonlocality softener character was somehow decreased. Furthermore, for all thickness variation patterns and material gradient index values, strain gradient size effect stiffer character was more prominent than nonlocality softener character acting in a specific value of maximum deflection. This anticipation was similar for both initial and deeper parts of flexural responses. Furthermore, it was found that at higher applied transverse loads, the importance of thickness variation pattern effect was enhanced.