1 Introduction

Carbon nanotube (CNT) is known as its extraordinary mechanical and physical properties [1, 2]. As ideal candidates of reinforcements for nanocomposites, CNTs can provide remarkable improvements to the mechanical properties of composites [3]. In the recent years, inspired by the concept of functionally graded material (FGM), the functionally graded carbon nanotube reinforced composite (FG-CNTRC) was developed by dispersing CNTs into the matrix according to the uniform or non-uniform distribution patterns, which can utilize the CNTs much better and bring considerable enhancements to the composite structures. Structures made of FG-CNTRCs have greatly potential applications in aerospace, aeronautics, precision instruments and other engineering fields [4,5,6], and the investigations on the mechanical responses of those structures are of great importance [7,8,9,10,11,12,13,14,15].

Literature review indicates that the mechanical responses of FG-CNTRC structures have been extensively investigated [16,17,18]. Zhong et al. [19] performed a vibration analysis of FG-CNTRC circular, annular and sector plates with arbitrary boundary conditions. Four types of the CNT distribution pattern are considered and their influences on the structures’ vibration behaviors are discussed comprehensively. Ansari et al. [20] mainly analyzed the thermal buckling response of FG-CNTRC quadrilateral plates. Bhagat et al. [21] investigated the buckling and free vibration behaviors of FG-CNTRC cylindrical panels exposed to uniform thermal loads. Duc et al. [22] studied the free vibration of FG-CNTRC plates with cracks by using the third-order shear deformation theory and phase field theory. It is worth to note that in most of the representative works of predicating mechanical properties of CNTRCs, the nanofiller agglomerations that are widely observed are not taken into account. However, agglomeration of nanotubes in manufacturing of CNT reinforced composites in large scale is, in fact, inevitable and should be included for better understanding the reinforcing effects of CNTs [23]. Bisheh et al. [24] used the Mori–Tanaka micromechanical model to investigate the wave propagation characteristics of piezocomposite cylindrical shells reinforced with agglomerated CNTs. Tornabene et al. [25] researched the effects of agglomeration on the natural frequencies of functionally graded carbon nanotube reinforced laminated composite doubly curved shells. Though some encouraging results have been reported, the studies that focus on the agglomeration of CNTs are still limited. Therefore, devoting more efforts on exploring the nanotube agglomeration influences on the mechanical behaviors of composite structures is meaningful for better applying the excellent mechanical properties of CNTs in different engineering fields.

Beam is one of the most fundamental structures that primarily used to resist loads, its mechanical characteristics such as the stability, vibration behaviors and dynamic response have attracted extensive research interest from engineers [26,27,28,29,30]. The low-velocity impact is a kind of traditional, permanent and often being observed external load in many engineering fields; thus, the mechanical responses of beams under low-velocity impacts have been experimentally and theoretically studied [31, 32]. Yalamanchili et al. [33] analyzed the contact problem between a rigid cylindrical indenter and FG beam, in which the indentation of homogeneous beam is considered. Kiani et al. [34] carried out a study of low-velocity impact responses of the FGM beams. SiSi et al. [35] investigated the repeated low-velocity impacts on a laminated beam using the higher-order shear deformation beam theory. In addition to considering the traditional composite beam structures, the scholars also took the CNTRC beams as research objective to investigate their low-velocity impact responses. Salami [36] performed a comprehensive analysis on the low-velocity impacts of the sandwich beams with CNTRC face sheets using extended high-order sandwich panel theory. Wang et al. [37] presented an investigation on mechanical response of FG-CNTRC plates and sandwich plates subjected to a low-velocity impact. Jam and Kiani [38] researched the low-velocity impact response of FG-CNTRC beams utilizing a polynomial Ritz method in conjunction with Timoshenko beam theory. Although the low-velocity impact response of FG-CNTRC beams have been reported in some available works, it is found, as mentioned before, no works exhibited the effects of CNT agglomerations on the low-velocity impact behaviors of the CNTRC beams.

In this paper, we present a study on the damped low-velocity impact response of a functionally graded carbon nanotube reinforced composite (FG-CNTRC) viscoelastic beam with elastic boundary constraints. The beam is constructed by a multiplayer beam model with the weight fraction of carbon nanotubes (CNTs) being constant in each layer but varying according to a layer-wise rule in the thickness direction. The effective elastic moduli and Poisson’s ratio are evaluated by the Mori–Tanaka micromechanics model considering CNT agglomeration with matrix, while the viscoelastic properties of beams are assumed based on Kelvin–Voigt theory. In addition, the energy expressions of the system are derived using a hyperbolic shear deformation theory with the aid of the artificial spring technique of quantifiably accounting for the elastic boundary conditions. The Gram–Schmidt process is implemented to produce admissible functions in a general orthogonal polynomial form to model the general elastic end constraints. The Lagrange methods are employed to derive the governing equations of motions. Furthermore, the Newmark-β method is adopted to obtain the low-velocity impact responses of the FG-CNTRC beam in time domain. A detailed parametric study is performed to investigate the effects of the CNT agglomeration, CNT distribution patterns and artificial spring parameters on the damped low-velocity impact response of the beam.

2 Problem description

2.1 Agglomerated FG-CNTRC beams with general boundary conditions

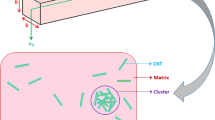
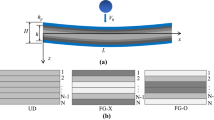
Figure 1 displays the schematic of an FG-CNTRC beam subjected to a low-velocity impact load and with general boundary conditions. The length, width and thickness of the beam are L, b and h, respectively, and the origin of the coordinate system is set at the center of the left end of the beam. An impactor drops vertical to the upper surface of the beam and contacts the beam with a velocity of vimp. Three artificial springs with stiffnesses of \(\overline{k}_{u}\), \(\overline{k}_{\varphi }\), \(\overline{k}_{w}\) at each end of the beam are set to model the general boundary conditions.

Fig. 1
figure 1

Schematic of an FG-CNTRC beam with general boundary condition

Full size image

In the current work, the nanocomposite beam is constructed by a multiplayer beam model with the weight fraction of carbon nanotubes (CNTs) being constant in each layer but varying according to a layer-wise rule in the thickness direction. The matrix of the nanocomposite is polymer. The CNTs can provide superior mechanical properties to the polymer matrix; however, CNTs are easy to agglomerate in the polymer due to their small diameters and small elastic modulus in the radial direction and high aspect ratio. Therefore, the agglomeration of CNTs within the matrix occurs inevitably, as shown in Fig. 1, and the degeneration of the stiffness of the beams introduced by the agglomerations has to be considered in the evaluation of modulus of elasticity of the nanocomposites. Herein, we use a two-parameter micromechanics [39] model to show the effects of agglomeration on the mechanical properties of nanocomposites.

2.2 A two-parameter model

Experimental results demonstrated that the spatial distribution of CNTs in the matrix is non-uniform, and some local regions have a higher concentration of CNTs than the average volume fraction in the material, as shown in Fig. 1. These local regions with more CNTs are considered as “cluster,” assumed to be spherical shapes, and possess different elastic properties from the surrounding matrix.

In this work, the beam is constructed by a multiplayer beam model and in each layer, and a given CNTRC layer has uniformly distributed CNTs within the matrix. In the given layer, choose a representative volume element (RVE) of the nanocomposite, and the total volume of CNTs in the RVE is denoted as Vr which contains CNTs inside and outside the sphere cluster in the matrix. Vr can written as:

$$V_{r} = V_{r}^{{{\text{cluster}}}} + V_{r}^{m}$$
(1)

in which \(V_{r}^{{{\text{cluster}}}}\) and \(V_{r}^{m}\) represent the volume of CNTs inside and outside the sphere cluster in the matrix, respectively. In addition, the total volume of RVE, V, can be given by the following:

$$V = V_{r} + V_{m}^{{}}$$
(2)

where Vm is the volume of matrix. In order to describe the agglomeration of CNTs, the following two parameters ξ and ζ are introduced:

$$\xi = \frac{{V_{{{\text{cluster}}}} }}{V},\zeta = \frac{{V_{r}^{{{\text{cluster}}}} }}{{V_{r} }}\quad 0 \le \xi ,\zeta \le {1}$$
(3)

in which Vcluster denotes the volume of the sphere cluster in the RVE. ξ is the volume fraction of clusters with respect to the total volume V of the RVE. It is clear that ξ = 1 means the clusters occupy the whole domain of RVE and the CNTs uniformly disperse in the matrix. As ξ decreases, a more severe agglomeration of CNTs will take place.

The parameter ζ represents the volume ratio of CNTs dispersed in clusters and the total volume of the nanotubes. ζ = 1 means that all the CNTs are in the sphere cluster. ξ = ζ means that the volume fraction of CNTs outside the clusters is equal to the volume fraction of CNTs inside the cluster; in other words, all the CNTs are dispersed uniformly. For a given value of ξ, the bigger the value ζ with ζ > ξ, the more heterogeneous the spatial distribution of CNTs. The average volume fraction fr of CNTs in the composite is defined as:

$$f_{r} = \frac{{V_{r} }}{V}$$
(4)

The volume fraction fr can be given as:

$$f_{r} = \frac{{g_{{{\text{CNT}}}} }}{{g_{{{\text{CNT}}}} + \left( {{\raise0.7ex\hbox{${\rho_{{{\text{CNT}}}} }$} \!\mathord{\left/ {\vphantom {{\rho_{{{\text{CNT}}}} } {\rho_{{{\text{matrix}}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{{{\text{matrix}}}} }$}}} \right)\left( {1 - g_{{{\text{CNT}}}} } \right)}}$$
(5)

in which gCNT is the mass fraction of CNTs, ρCNT and ρmatrix represent the density of CNTs and matrix, respectively.

Due to the existence of agglomeration, the CNTRCs are considered as a system of containing sphere clusters embedded in a hybrid matrix. Both the matrix and the inclusions contain CNTs. In order to calculate the overall properties of the whole system, the effective elastic stiffnesses of the clusters and the surrounding matrix are determined firstly. The Mori–Tanaka method is applied to calculate the elastic moduli of the matrix, in which the CNTs are assumed to be transversely isotropic. In the clusters, the CNTs are assumed to be randomly oriented and, therefore, the inclusions are isotropic. The effective bulk moduli Kin and Kout and the effective shear moduli Gin and Gout of the clusters and the matrix can be given, respectively, as:

$$K_{{{\text{in}}}} = K_{m} + \frac{{\left( {\delta_{r} - 3K_{m} \alpha_{r} } \right)f_{r} \zeta }}{{3\left( {\xi - f_{r} \zeta + f_{r} \zeta \alpha_{r} } \right)}}$$
(6a)
$$K_{{{\text{out}}}} = K_{m} + \frac{{f_{r} \left( {\delta_{r} - 3K_{m} \alpha_{r} } \right)\left( {1 - \zeta } \right)}}{{3\left[ {1 - \xi - f_{r} \left( {1 - \zeta } \right) + f_{r} \left( {1 - \zeta } \right)\alpha_{r} } \right]}}$$
(6b)
$$G_{{{\text{in}}}} = G_{m} + \frac{{\left( {\eta_{r} - 2G_{m} \beta_{r} } \right)f_{r} \zeta }}{{2\left( {\xi - f_{r} \zeta + f_{r} \zeta \beta_{r} } \right)}}$$
(6c)
$$G_{{{\text{out}}}} = G_{m} + \frac{{f_{r} \left( {\eta_{r} - 2G_{m} \beta_{r} } \right)\left( {1 - \zeta } \right)}}{{2\left[ {1 - \xi - f_{r} \left( {1 - \zeta } \right) + f_{r} \left( {1 - \zeta } \right)\beta_{r} } \right]}}$$
(6d)

in which

$$\alpha_{r} = \frac{{3\left( {K_{m} + G_{m} } \right) + k_{r} { - }l_{r} }}{{3\left( {G_{m} + k_{r} } \right)}}$$
(7a)
$$\beta_{r} = \frac{1}{5}\left\{ {\frac{{4G_{m} + 2k_{r} + l_{r} }}{{3\left( {G_{m} + k_{r} } \right)}} + \frac{{4G_{m} }}{{G_{m} + p_{r} }} + \frac{{2\left[ {G_{m} \left( {3K_{m} + G_{m} } \right) + G_{m} \left( {3K_{m} + 7G_{m} } \right)} \right]}}{{G_{m} \left( {3K_{m} + G_{m} } \right) + m_{r} \left( {3K_{m} + 7G_{m} } \right)}}} \right\}$$
(7b)
$$\delta_{r} = \frac{1}{3}\left[ {n_{r} + 2l_{r} + \frac{{2\left( {k_{r} + l_{r} } \right)\left( {3K_{m} + 2G_{m} - l_{r} } \right)}}{{G_{m} + k_{r} }}} \right]$$
(7c)
$$\eta_{r} = \frac{1}{5}\left[ {\frac{2}{3}\left( {n_{r} - l_{r} } \right) + \frac{{8G_{m} p_{r} }}{{G_{m} + p_{r} }} + \frac{{8m_{r} G_{m} \left( {3K_{m} + 4G_{m} } \right)}}{{3K_{m} \left( {m_{r} + G_{m} } \right) + G_{m} \left( {7m_{r} + G_{m} } \right)}} + \frac{{2\left( {k_{r} - l_{r} } \right)\left( {2G_{m} + l_{r} } \right)}}{{3\left( {G_{m} + k_{r} } \right)}}} \right]$$
(7d)

kr, lr, mr, nr and pr are the Hill’s elastic moduli of the CNTs, and Km and Gm are the bulk and shear moduli of the matrix, respectively, and can be determined by the well-known expression of the theory of elasticity:

$$K_{m} { = }\frac{{E_{m} }}{{3\left( {1 - 2\nu_{m} } \right)}}$$
(8a)
$$G_{m} { = }\frac{{E_{m} }}{{2\left( {1 + \nu_{m} } \right)}}$$
(8b)

Em, νm are the modulus of elasticity and Poisson’s ratio of the matrix. Finally, the effective bulk modulus K and the effective shear modulus G of the composite are derived from the Mori–Tanaka method as:

$$K{ = }\,K_{{{\text{out}}}} \left[ {1 + \frac{{\xi \left( {\frac{{K_{{{\text{in}}}} }}{{K_{{{\text{out}}}} }} - 1} \right)}}{{1 + \alpha \left( {1 - \xi } \right)\left( {\frac{{K_{{{\text{in}}}} }}{{K_{{{\text{out}}}} }} - 1} \right)}}} \right]$$
(9a)
$$G{ = }\,G_{{{\text{out}}}} \left[ {1 + \frac{{\xi \left( {\frac{{G_{{{\text{in}}}} }}{{G_{{{\text{out}}}} }} - 1} \right)}}{{1 + \beta \left( {1 - \xi } \right)\left( {\frac{{G_{{{\text{in}}}} }}{{G_{{{\text{out}}}} }} - 1} \right)}}} \right]$$
(9b)

in which \(\alpha { = }\frac{{1 + \nu_{{{\text{out}}}} }}{{3\left( {1 - \nu_{{{\text{out}}}} } \right)}},\;\beta { = }\frac{{2\left( {4 - 5\nu_{{{\text{out}}}} } \right)}}{{15\left( {1 - \nu_{{{\text{out}}}} } \right)}},\;\nu_{{{\text{out}}}} { = }\frac{{3K_{{{\text{out}}}} { - }2G_{{{\text{out}}}} }}{{2\left( {3K_{{{\text{out}}}} + G_{{{\text{out}}}} } \right)}}\). The effective overall modulus of elasticity E and Poisson’s ratio ν of the agglomerated CNTRC layer is given by

$$E{ = }\frac{9KG}{{3K + G}}$$
(10a)
$$\nu { = }\frac{3K - 2G}{{6K + 2G}}$$
(10b)

Based on the rule of mixture, the mass density of the CNTRCs can be given as:

$$\rho = f_{r} \rho_{{{\text{CNT}}}} + \left( {1 - f_{r} } \right)\rho_{{{\text{matrix}}}}$$
(11)

In the current work, the modulus of elasticity of the matrix is Em = 1.9 GPa, Poisson’s ratio is νm = 0.3, and mass density is ρmatrix = 1090 kg/m3. The density of the CNTs is 1200 kg/m3, and the Hill’s elastic modulus for the CNTs used in Eq. (7) is listed in Table 1 [24, 40].

Table 1 Hill’s elastic moduli for the CNTs
Full size table

The nanocomposite beam made of 20 CNTRC layers with the same thickness means the total layer number NL is 20 (NL = 20). As mentioned above, the weight fraction of CNTs changes from one layer to another, while CNTs are distributed evenly and oriented randomly in every layer. Thus, each layer of the CNTRC beam is isotropic homogeneous. Table 2 presents tree patterns of CNT distribution across the beam thickness. They are UD, FGO as well as FGX. Consequently, the volume fraction of CNTs of the k-th layer for the respective distribution patterns is also defined in Table 2.

Table 2 Values of the weight fraction indices and the maximum weight fraction
Full size table

3 Theory and formulations

3.1 A new hyperbolic shear deformation theory

Herein, a general form of the high shear deformation theory is given as follows [41]:

$$\left\{ \begin{aligned} & u = u_{0} \left( {x,t} \right) - z\frac{{\partial w_{0} \left( {x,t} \right)}}{\partial x} + f\left( z \right)\varphi \left( {x,t} \right) \\ & w = w_{0} \left( {x,t} \right) \\ \end{aligned} \right.$$
(12)

where u and w are the displacement components of any point within the beam; the symbols u0 and w0 represent the x- and z-direction displacements of any point of the geometrical neutral plane (z = 0); and φ is the shear deformation at the geometrical neutral plane. In Eq. (12), \(f\left( z \right)\) is the shear–strain function being in form of a function of thickness coordinate z. It is well known that the different selections of this function can generate various shear deformation theories. For example, \(f\left( z \right){ = }z\left( {1 - \frac{{4z^{2} }}{{3h^{2} }}} \right)\) is from Reddy’s third-order shear deformation theory (TSDT) [42, 43], \(f\left( z \right){ = }\frac{z}{\pi }\sin \left( {\frac{\pi z}{h}} \right)\) is a sinusoidal shear deformation theory (SSDT) [44, 45], while \(f\left( z \right){ = }z\) represents the first-order shear deformation theory (FSDT). In the current study, a new hyperbolic shear–strain function, which was originally proposed by Grover et al. [46, 47], is considered and its form is given as follows:

$$\left\{ \begin{aligned} & f\left( z \right) = \sinh^{ - 1} \left( \frac{rz}{h} \right) + \Xi z \\ & \Xi = \frac{ - 2r}{{h\sqrt {r^{2} + 4} }} \\ \end{aligned} \right.$$
(13)

where r = 3 is a constant being independent of z. The value of r is obtained by comparing the results with elasticity solutions in a post processing step given in [48]. The distribution of the transverse shear strains exactly satisfies the zero shear stress on the upper and lower beam surfaces, so a shear correction factor is not required.

3.2 Energy expression

The total energy of the system consists of the total potential and kinetic energies of the beam and the impactor. Given the assumption of small deformations and small rotations, the linear strains associated with the displacement field in Eq. (12) are expressed as follows:

$$\left\{ \begin{aligned} & \varepsilon_{xx} = \frac{{\partial u_{0} }}{\partial x} + f\left( z \right)\frac{\partial \varphi }{{\partial x}} - z\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} \\ & \varepsilon_{xz} = \frac{\partial f}{{\partial z}}\varphi \\ \end{aligned} \right.$$
(14)

The linear stress–strain relation for the FG-CNTRC beam is expressed as follows:

$$\left\{ \begin{gathered} \sigma_{xx} = C_{11} \left( z \right)\varepsilon_{xx} \hfill \\ \sigma_{xz} = C_{55} \left( z \right)\varepsilon_{xz} \hfill \\ \end{gathered} \right.$$
(15)

where Cii denotes the viscoelastic constants. Based on the viscoelastic Kelvin–Voigt model \(C_{11} \left( z \right) = Q_{11} \left( z \right)\left( {1 + \mu \frac{\partial }{\partial t}} \right)\),\(C_{55} \left( z \right) = Q_{55} \left( z \right)\left( {1 + \mu \frac{\partial }{\partial t}} \right)\), μ is the viscosity coefficient. \(Q_{11} \left( z \right) = \frac{E\left( z \right)}{{1 - \nu^{2} }}\), \(Q_{55} \left( z \right) = \frac{E\left( z \right)}{{2\left( {1 + \nu } \right)}}\) denotes the elastic constants that are dependent on beam thickness, and ν denotes the Poisson’s ratio.

The strain energy Ub and kinetic energy Tb of the beam are given as follows:

$$U_{b} = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A}^{{}} {\left( {\sigma_{xx} \varepsilon_{xx} + \sigma_{xz} \varepsilon_{xz} } \right){\text{d}}A{\text{d}}x} }$$
(16a)
$$T_{b} = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A}^{{}} {\rho \left( z \right)\left( {\left( {\frac{\partial u}{{\partial t}}} \right)^{2} + \left( {\frac{\partial w}{{\partial t}}} \right)^{2} } \right){\text{d}}A{\text{d}}x} }$$
(16b)

Substituting Eqs. (14)–(15) into Eq. (16) and using the displacement components in Eq. (8), the strain energy and kinetic energy for the FG-CNTRC beams are expressed as follows:

$$U_{b} = \frac{1}{2}\int\limits_{0}^{L} {\left( \begin{gathered} A_{11} \left( {\frac{{\partial u_{0} }}{\partial x}} \right)^{2} + A_{ff} \left( {\frac{\partial \varphi }{{\partial x}}} \right)^{2} + D_{11} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)^{2} + A_{55} \left( z \right)\varphi^{2} \hfill \\ + 2A_{f} \frac{{\partial u_{0} }}{\partial x}\frac{\partial \varphi }{{\partial x}} - 2B_{11} \frac{{\partial u_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - 2A_{zf} \frac{\partial \varphi }{{\partial x}}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} \hfill \\ \end{gathered} \right){\text{d}}x}$$
(17a)
$$T_{b} = \frac{1}{2}\int\limits_{0}^{L} {\left( \begin{gathered} I_{0} \left( {\frac{{\partial u_{0} }}{\partial t}} \right)^{2} + I_{ff} \left( {\frac{\partial \varphi }{{\partial t}}} \right)^{2} + I_{2} \left( {\frac{{\partial^{2} w_{0} }}{\partial t\partial x}} \right)^{2} + I_{0} \left( {\frac{{\partial w_{0} }}{\partial t}} \right)^{2} \hfill \\ + 2I_{f} \frac{{\partial u_{0} }}{\partial t}\frac{\partial \varphi }{{\partial t}} - 2I_{1} \frac{{\partial u_{0} }}{\partial t}\frac{{\partial^{2} w_{0} }}{\partial t\partial x} - 2I_{zf} \frac{\partial \varphi }{{\partial t}}\frac{{\partial^{2} w_{0} }}{\partial t\partial x} \hfill \\ \end{gathered} \right){\text{d}}x}$$
(17b)

The stiffness components in Eq. (17a) are defined as follows:

$$\left\{ \begin{aligned} & \left[ {\begin{array}{*{20}c} {A_{11} } & {B_{11} } & {D_{11} } & {A_{f} } & {A_{zf} } & {A_{ff} } \\ \end{array} } \right] = b\int\limits_{ - h/2}^{h/2} {C_{11} \left( z \right)\left[ {\begin{array}{*{20}c} 1 & z & {z^{2} } & f & {zf} & {f^{2} } \\ \end{array} } \right]{\text{d}}z} \\ & A_{55} = \int\limits_{ - h/2}^{h/2} {C_{55} \left( z \right)\left( {\frac{{{\text{d}}f}}{{{\text{d}}z}}} \right)^{2} {\text{d}}z} \\ \end{aligned} \right.$$
(18)

Additionally, the inertia related terms in Eq. (17b) are defined as follows:

$$\left[ {\begin{array}{*{20}c} {I_{0} } & {I_{1} } & {I_{2} } & {I_{zf} } & {I_{ff} } \\ \end{array} } \right] = b\int\limits_{ - h/2}^{h/2} {\rho \left( z \right)\left[ {\begin{array}{*{20}c} 1 & z & {z^{2} } & {zf} & {f^{2} } \\ \end{array} } \right]{\text{d}}z}$$
(19)

The energies of the impactor contain two parts: potential energy of the contact force Ui and the kinetic energy of the impactor Ti. The contact force is obtained based on the Hertz contact law, and the potential energy Ui is given as follows:

$$U_{i} { = }\frac{2}{5}K_{i} \left[ {y\left( t \right) - w_{0} \left( {x_{c} ,\;t} \right)} \right]^{\frac{5}{2}}$$
(20)

where xc is the position of the impact occurring. y is the displacement of the impactor, and w0(xc, t) represents the transverse displacement of beam at the location of x = xc. In physics, the contact indentation α(t) is described as the depth of the impactor entering the beam during the impact process and can be obtained by the displacement difference between the impactor and beam as:

$$\alpha \left( t \right){ = }y\left( t \right) - w_{0} \left( {x_{c} ,\;t} \right)$$
(21)

in which Ki represents the contact stiffness which can be determined by [49]:

$$K_{i} { = }\frac{4}{3}\sqrt {R_{{{\text{imp}}}} } \left( {\frac{1}{{E_{c} }} + \frac{{1 - \nu_{s}^{2} }}{{E_{{\text{s}}} }}} \right)^{ - 1}$$
(22)

in which Rimp is the radius of the impactor, Ec is the transverse elastic modulus of the beam surface, which is equal to the corresponding value of the top layer. Es and νs denote the modulus of elasticity and Poisson’s ratio of the impactor. The kinetic energy of the impactor is calculated by the following formula:

$$T_{i} { = }\frac{1}{2}M_{{{\text{imp}}}} \dot{y}^{2}$$
(23)

where Mimp represents the mass of the impactor.

As mentioned in Fig. 1, the general boundary conditions of the beam are represented using the artificial spring technique. Three artificial springs, namely two translational springs and one rotational spring, are set at each end of the beam. At right end, the stiffness parameters of the springs are written as \(\overline{k}_{u}^{0}\), \(\overline{k}_{\varphi }^{0}\) and \(\overline{k}_{w}^{0}\), and the ones at left end are written as \(\overline{k}_{u}^{1}\), \(\overline{k}_{\varphi }^{1}\) and \(\overline{k}_{w}^{1}\). It is well known that by assigning proper values to the stiffness of the artificial springs, arbitrary boundary conditions can be obtained, including the classical boundary conditions. The potential energy stored in those springs can be considered as follows:

$$U_{bs} { = }\frac{1}{2}\left\{ {\int\limits_{0}^{L} {\left[ {\overline{k}_{u}^{0} u_{0}^{2} + \overline{k}_{\varphi }^{0} \varphi_{{}}^{2} + \overline{k}_{w}^{0} w_{0}^{2} } \right]_{x = 0} {\text{d}}x} + \int\limits_{0}^{L} {\left[ {\overline{k}_{u}^{1} u_{0}^{2} + \overline{k}_{\varphi }^{1} \varphi_{{}}^{2} + \overline{k}_{w}^{1} w_{0}^{2} } \right]_{x = L} {\text{d}}x} } \right\}$$
(24)

The classical boundary conditions as well as the corresponding spring parameters are given as follows:

  1. (1)

    Clamped: u0 = φ = w0 = 0,

    $$k_{u}^{{}} { = }k_{\varphi }^{{}} { = }k_{w}^{{}} { = }\log \left( {\frac{{\overline{k}_{u}^{{}} }}{{E_{M} }}} \right) = \log \left( {\frac{{\overline{k}_{\varphi }^{{}} }}{{E_{M} }}} \right) = \log \left( {\frac{{\overline{k}_{w}^{{}} }}{{E_{M} }}} \right) = 8$$

    .

  2. (2)

    Hinged: u0 = w0 = 0, φ ≠ 0,

    $$k_{u}^{{}} { = }k_{w}^{{}} { = }\log \left( {\frac{{\overline{k}_{u}^{{}} }}{{E_{M} }}} \right) = \log \left( {\frac{{\overline{k}_{w}^{{}} }}{{E_{M} }}} \right) = 8,\;\;k_{\varphi }^{{}} { = }\log \left( {\frac{{\overline{k}_{\varphi }^{{}} }}{{E_{M} }}} \right){ = } - 8$$

    .

  3. (3)

    Free: u0 ≠ 0, φ ≠ 0, w0 ≠ 0,

    $$k_{u}^{{}} { = }k_{\varphi }^{{}} { = }k_{w}^{{}} { = }\log \left( {\frac{{\overline{k}_{u}^{{}} }}{{E_{M} }}} \right) = \log \left( {\frac{{\overline{k}_{\varphi }^{{}} }}{{E_{M} }}} \right) = \log \left( {\frac{{\overline{k}_{w}^{{}} }}{{E_{M} }}} \right) = - 8$$

    .

The Lagrange’s method is employed to determine the dynamic response problem including the impact load, and the Lagrange energy function L of the system can be expressed as follows:

$$L = T_{b} + T_{i} { - }U_{b} { - }U_{i} { - }U_{bs}$$
(25)

3.3 Solution strategies

3.3.1 Gram–Schmidt orthogonal polynomials

In the current work, the end restraints are transformed into quantifiable forms via the artificial spring method, in which the selection of admissible function is significant for analyzing the mechanical performances of the composite beam. In general, the displacement fields for the beams with arbitrary boundary conditions can be written as:

$$\left\{ \begin{aligned} & u_{0} (x,t) = \sum\limits_{n = 1}^{N} {\overline{U}_{n} \left( t \right)f_{n} \left( x \right)} \\ & w_{0} (x,t) = \sum\limits_{n = 1}^{N} {\overline{W}_{n} \left( t \right)f_{n} \left( x \right)} \\ & \varphi (x,t) = \sum\limits_{n = 1}^{N} {\overline{V}_{n} \left( t \right)f_{n} \left( x \right)} \\ \end{aligned} \right.$$
(26)

where \(\left( {\overline{U}_{n} ,\overline{W}_{n} ,\overline{V}_{n} } \right)\) denote the unknown coefficients corresponding to time and expressed as follows: \(\left( {\overline{U}_{n} ,\overline{W}_{n} ,\overline{V}_{n} } \right) = \left( {U_{n} ,W_{n} ,V_{n} } \right)e^{{i\omega_{n} t}}\), \(i = \sqrt { - 1}\), where ωn denotes the vibration frequency. fn(x) denotes the polynomial admissible functions. Herein, to enhance significantly the computational stability, the admissible functions are orthogonalized in the domain [0, L] via the Gram–Schmidt process as follows [50, 51]:

(i) Select a polynomial term, f1(x), that satisfies at least essential or geometric boundary condition as the initial term. For the arbitrary boundary conditions: \(f_{1} \left( x \right) = 1\).

(ii) The second term of the admissible function is: \(f_{2} \left( x \right) = \left( {x - b_{1} } \right)f_{1} \left( x \right)\).

(iii) The subsequent terms (n ≥ 2) can be derived from the following procedure:

$$f_{n + 1} \left( x \right) = \left( {x - b_{n} } \right)f_{n} \left( x \right){ - }c_{n} f_{{n{ - }1}} \left( x \right)$$

in which \(b_{n} { = }\frac{{\int_{0}^{L} {x\left[ {f_{n} \left( x \right)} \right]^{2} {\text{d}}x} }}{{\int_{0}^{L} {\left[ {f_{n} \left( x \right)} \right]^{2} {\text{d}}x} }}\), \(c_{n} { = }\frac{{\int_{0}^{L} {xf_{n} \left( x \right)f_{{n{ - }1}} \left( x \right){\text{d}}x} }}{{\int_{0}^{L} {\left[ {f_{{n{ - }1}} \left( x \right)} \right]^{2} {\text{d}}x} }}\) (n ≥ 2).

3.3.2 Lagrange method for dynamic response

Substituting Eq. (23) into the total energy functional (Π) in Eq. (24) for dynamic response analysis and then using the Lagrange equation as follows:

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{q}_{i} }}} \right) + \frac{\partial L}{{\partial q_{i} }} = 0$$
(27)

where qi represents the unknown coefficients (\(\overline{U}_{n} ,\overline{W}_{n} ,\overline{V}_{n}\) and y), and the over-dot denotes the partial derivative with respect to time. Subsequently, this results in the following form of the motion equation:

$$\left[ {\mathbf{K}} \right]{\mathbf{q}} + \left[ {\mathbf{C}} \right]{\dot{\mathbf{q}}} + \left[ {\mathbf{M}} \right]{\mathbf{\ddot{q}}} = \left\{ {\mathbf{F}} \right\}$$
(28)
$$M_{{{\text{imp}}}} y{ = } - F$$
(29)

where [K] denotes the structural stiffness matrix, [M] denotes the mass matrix, and [C] is viscoelastic matrix. Additionally, {F} denotes a vector generated by the impact load as follows:

$$\left\{ {\mathbf{F}} \right\} = \left\{ \begin{gathered} {\mathbf{0}} \hfill \\ {\text{F}}f_{i} \left( x \right) \hfill \\ {\mathbf{0}} \hfill \\ \end{gathered} \right\}$$
(30)

Since prior to impact, the composite beam is initially at rest and the initial conditions are:

$$\begin{aligned} & u_{0} = \varphi = w_{0} = 0 \\ & \dot{u}_{0} = \dot{\varphi } = \dot{w}_{0} = 0 \\ & y = 0,\;\dot{y} = v_{{{\text{imp}}}} \\ \end{aligned}$$
(31)

With help of the Newmark-β method, the equation of motion Eqs. (28)–(29) in time domain can be solved. The details of the Newmark-β method can be found in Ref. [52, 53] and were not given here for conciseness purpose. At each time step, the dynamic deflections of beams w, contact indentation α and contact forces F during the impact process can be obtained.

4 Convergence and validation studies

Prior to detail parameter study, the validation and accuracy of proposed modeling and computational code have to be verified. The results of natural frequencies and dynamic responses of FGM beams are computed using and compared with ones from the published studies.

Example 1

Free vibration response of an FGM beam.

A functionally graded beam composed of alumina (Al2O3, Ec = 380 GPa, ρc = 3800 kg/m3, vc = 0.23) and aluminum (Al, Em = 70 GPa, ρm = 2700 kg/m3, vm = 0.23) is considered. The top of the beam is fully ceramic, while the bottom is fully metallic. The dimensionless fundamental frequencies of the beam with various length-to-height ratios are calculated by using the proposed method and are compared with those from the analytical method [54]. The following dimensionless frequency parameter (Ω) is used:

$$\Omega_{n} = \frac{{\omega_{n} L^{2} }}{h}\sqrt {{{\int\limits_{ - h/2}^{h/2} {\rho \left( z \right){\text{d}}z} } \mathord{\left/ {\vphantom {{\int\limits_{ - h/2}^{h/2} {\rho \left( z \right){\text{d}}z} } {\int\limits_{ - h/2}^{h/2} {E\left( z \right){\text{d}}z} }}} \right. \kern-\nulldelimiterspace} {\int\limits_{ - h/2}^{h/2} {E\left( z \right){\text{d}}z} }}}$$
(32)

Table 3 lists the comparison results of the beams with power law index of 0.3. As shown in Table 3, our results coincide with the reported ones very well. This demonstrates that the modeling reported in present work is effective and accurate for the free vibration analysis of the FGM beam. In addition, the term number N = 10 is selected by observation of the convergency trend in Table 3.

Table 3 Comparisons of the dimensionless fundamental frequency of the FGM beam
Full size table

Example 2

Dynamic response of an FGM beam under low-velocity impacts.

In this section, the validation of the proposed theory and computational code on the dynamic response of a simply supported FGM beam subjected to low-velocity impacts is performed. A power-law FGM beam with length of 135 mm, width of 15 mm and thickness of 10 mm with linear composition rule (power-law index = 1) is considered. The upper surface of the beam is ceramic-rich (silicon nitride, E = 322.2175GPa, ρ = 2370 kg/m3, ν = 0.28), while the lower surface is metal-rich (stainless steel, E = 207.7877GPa, ρ = 8166 kg/m3, ν = 0.28). An impactor of mass m0 = 10 g, contact velocity V0 = 1 m/s and radius R = 12.7 mm is impacted to the upper surface of the beam at the middle point. The modified contact stiffness for the FGM beams is given reference [34] and not provided here for briefness. The contact force between the impactor and the beam is calculated and compared with those from the work of Kiani et al. [34]. Figure 2 shows that the present results agree well with existing results, and thus, the validity can be confirmed.

Fig. 2
figure 2

Comparisons of the contact force between the beam and the impactor

Full size image

From the two validation examples, it is concluded that the proposed theory and computational modeling are valid and accurate to predict the free vibration behavior and dynamic response of the beam subjected to the moving mass.

5 Results and discussion

In this section, the model and methodology outlined in present work is applied to investigate the dynamic characteristics of FG-CNTRC beams subjected to a low-velocity steel spherical impactor. The matrix material is isotropic epoxy. In the parametric study, the contact force and central deflection of the composite beam are calculated and plotted to check the effects of CNT agglomeration, distribution patterns, weight fraction, viscoelasticity and elastic boundary conditions on dynamic response of the beam. In order to facilitate the presentations, the following dimensionless spring stiffness parameters is used:

$$k_{\eta } = \log_{10} \left( {\frac{{\overline{k}_{\eta } }}{{E_{M} }}} \right)$$
(33)

where \(\overline{k}_{\eta }\) and EM denote the spring stiffness and elastic modulus of the epoxy matrix, respectively. Otherwise stated specially, the geometries of the composite beam are: L = 0.5 m, h = 0.025 m and b = 2 h, and the mechanical properties of the matrix and CNTs are given in Sect. 2. The radius of the impactor is 10 mm and is made of the steel with materials properties of E = 200GPa, ρ = 7850 kg/m3 and ν = 0.3.

5.1 Effect of various beam theories

Firstly, we compare the results obtained by different beam theories. In this comparison, the third-order shear deformation theory (TSDT), sinusoidal shear deformation theory (SSTD), first-order shear deformation theory (FSDT) and present hyperbolic shear deformation theory are considered. A composite beam with FGX distribution pattern and clamped–clamped boundary condition is implemented. The velocity of impactor is 3.0 m/s. Figure 3a, b present the time histories of the contact forces and central deflections of beams, respectively, obtained by different beam theories. One can see that the contact forces obtained by different beam theories are almost the same, indicating that the selection of beam theories has no obvious effect on the predication of contact forces. However, for the central deflections of beams, a remarkable difference between the results from various beam theories can be found. The FSDT results the highest prediction, followed by TSDT and SSDT. The result curve of present model is accord with the one of TSDT.

Fig. 3
figure 3

Effect of beam theories on low-velocity impact behaviors of composite beams

Full size image

5.2 Effect of agglomeration of CNTs

In this subsection, the effects of CNT agglomeration on the low-velocity impact behaviors of CNT-reinforced beams are investigated. As mentioned before, agglomeration parameter ξ stands for the volume fraction of inclusions in the composite and parameter ζ represents the volume fraction of CNTs concentrated in the inclusions. We consider an extreme case of agglomeration in which all CNTs are concentrated in spherical subregions, i.e., ζ = 1. The other agglomeration parameter ξ varies from 0.2 to 1.0. FGO distribution pattern is selected in this example. Figure 4 presents the time histories of the contact force and central deflections of the agglomerated CNTs-reinforced beams. It is observed from Fig. 4a that as ξ increases the peak values of contact force increase while the contact time decreases. From Fig. 4b, we can find that an increase in ξ leads to a descent of the peak values of central deflections. This phenomenon can be explained that ξ represents a volume fraction of clusters, a smaller value ξ means less clusters in matrix, and in the assumption of ζ = 1, a smaller value of ξ reflects a more server agglomeration of CNTs. Therefore, an increase in ξ demonstrates a weakening agglomeration degree of CNTs, indicating the progressively larger elastic modulus of the CNTRCs. Thus, a greater value of ξ can result in a greater contact stiffness, a shorter contact time and lower central deflections.

Fig. 4
figure 4

Effect of CNT agglomeration on low-velocity impact behaviors of composite beams with ζ = 1

Full size image

For a more general case of partial agglomeration of CNTs (ξ ≤ ζ), the value of ξ is fixed and the ζ varies. Figure 5 presents the variation of contact forces and central deflections with respct to time. It is observed that an increase in agglomeration parameter ζ leads to an decrease peak values of contact forces, while the contact duration and beam central deflections increase as ζ increases. That is because a greater ζ means that a more amount of CNTs concnetrates in the inclusions and the effective modulus of elasticity the CNTs reinforced nanocomposite decrease. Thus, the upper surface of the beam becomes softer and the contact stiffness decreases, leading to a lower contact force and longer contact duration. On the other hand, the decrease of effective modulus of elasticiy results in a decrease of the structural stiffness and the dynamic responses of the beams become larger.

Fig. 5
figure 5

Effect of CNT agglomeration on low-velocity impact behaviors of composite beams

Full size image

In addition, from Figs. 4 and 5 it is found that when ξ = ζ, the beams have the highest values of contact force, lowest contact durations and lowest dynamic deflections. This is because in the case of ξ = ζ, there is no agglometrtion within the nanocomposite and the CNTs are dispersed uniformly in the matrix, maximum value of the effective stiffness can be obtained.

5.3 Effect of viscoelastic parameter

The effect of viscoelasticity of the composite beams on the low-velocity impact behaviors is examined in this example. The agglomeration parameters are ξ = 0.5 and ζ = 0.75. FGX distribution pattern is considered herein. Figure 6a–c shows the time histories of the contact force, contact indentation and central deflection of the composite beams with various values of viscoelastic parameter μ. As seen from Fig. 6, as μ increases the peak values of the contact forces and indentations slightly increases, but it is interesting to find that the curves of the contact force and indentation are very close, demostrating that the viscoelasticity is of little influence on the contact stiffness. It is reasonable although the viscoelasticity can lead to an energy dissipation, however, the contat time is extremely short in the contact progress and the energy dissipation in so short duration can be neglected. Moreover, the dynamic deflections decrease as μ increases because the energy dissipation of the composite beam due to the viscoelasticity cannot be neglected and introduce an great decay of the dynamic responses.

Fig. 6
figure 6

Effect of viscoelastic parameters on low-velocity impact behaviors of CNTRC beams

Full size image

5.4 Effect of CNT distributions

Figure 6 shows the influence of CNT distribution patterns on the time histories of the contact force and central deflection of functionally graded multilayer agglomerated CNTRC beams with clamped–clamped boundary conditions. All the three distribution patterns considered in present work, namely UD, FGX and FGO, are used and no viscoelasticity is taken into account. As observed from the plots in Fig. 7a, the case of FGX has the least contact time and the largest contact force. In contrast, FGO distribution leads to the smallest peak contact force and the longest contact time. The reason explaining this phenomenon is that for FGX pattern the composite beam has the most CNTs on the upper surface and can result in the greatest contact stiffness at the contact location and largest contact force. For the central deflections observed in Fig. 7b, the FGX beam has the lowest peak value of the dynamic central deflection among all the three considered distribution patterns, while the FGO beam has the greatest ones. For instance, the peak central deflection of FGX beam is, respectively, about 85.27% of that of UD type composite beam and 67.72% of that of FGO beams when the gCNT = 20%. This is attributed to the considerably improved overall beam stiffness due to the addition of the CNTs and this reinforcing effect is the maximum in the FGX beam.

Fig. 7
figure 7

Effect of CNT distribution pattern on the impact response of the FG-CNTRC beams

Full size image

5.5 Effect of CNT weight fraction

Figure 8 depicts the effect of total CNT weight fraction gCNT on the time histories of the contact force and central deflection of the FGX agglomerated beam, along with those of the pure epoxy beam for comparison. It is expectable that an increase in CNT weight fraction results in a shorter contact time and larger peak contact force due to the increase in contact stiffness. Besides, the peak central deflection remarkably decreases as the CNT weight fraction increases.

Fig. 8
figure 8

Effect of CNT content on the impact response of the FG-CNTRC beams

Full size image

Moreover, we investigate the effects of agglomeration parameter on the reinforcing efficiency of the CNTs by the estimation of central deflections of the composite beams under low-velocity impact. The case of ξ = 0.25 is taken into account and the parameter ζ varies ranging from 0.25 to 1.0. A parameter η, which is defined as \(\eta = \left[ {\frac{{\left( {w_{{{\text{mid}}}} } \right)_{{{\text{matrix}}}} - \left( {w_{{{\text{mid}}}} } \right)_{{{\text{CNT}}}} }}{{\left( {w_{{{\text{mid}}}} } \right)_{{{\text{matrix}}}} }}} \right]\%\), is introduced to represent the reinforcing efficiency of the addition of CNT nanofillers. (wmid)matrix is the peak value of central deflections of the beam made of pure polymer matrix and (wmid)CNT is the peak value for the central deflections of the beam made of CNTRCs. Based on the results of Table 2, it is worth noticing that the agglomeration of the nanofillers significantly affects the dynamic responses. The results in Table 2 indicate that the influence of the agglomeration parameters on the dynamic response of the composite beams is more pronounced for a greater amount of CNT additions. For instance, when gCNT = 5.0%, an increase in agglomeration parameter ζ from 0.25 to 1.0 leads to a decrease in the reinforcing efficiency η from 50.16% to 19.17%, while when gCNT = 20.0%, the reduction of η ranges from 72.17% to 20.97%. Meanwhile, it is noticed that the role of CNT volume fraction becomes gradually weaker as the agglomeration parameter ζ increases. When the CNTs are all in the cluster (fully agglomerated), adding more CNTs in the matrix has no obvious improvement to the mechanical properties of the beams. It can be explained in physics that the dynamic response of a structure basically depends on its stiffness and mass, and the existence of CNT agglomerations makes the contribution of CNTs to the mass become greater, while the contribution to the beam stiffness becomes smaller (Table 4).

Table 4 The effect of CNT weight fraction on the low-velocity impact response of the composite beam (vimp = 1.0 m/s, FGX)
Full size table

5.6 Effect of elastic boundary

In this section, the effects of elastic boundary conditions on the low-velocity impact behaviors of the FG-CNTRC beams are discussed. The left end of the beam is clamped, while the right end is elastically restricted. When investigating the effects of the spring parameter, only the considered spring parameter varies in the range from -8 to 8, and the others are all set to be 8. The contact forces, contact indentations and central deflections of the beams are calculated and plotted. Figures 9, 10 and 11 present the time histories of contact forces, contact indentations and central deflections of the viscoelastic nanocomposite beam under the low-velocity impact load with vimp = 1.0 m/s. FGO distribution pattern and gCNT = 10% are considered. From Figs. 9 and 10, we can find that the variation of ku and kϕ has no influence on the contact forces and indentation of the beam, a extremely slight decrease can be found as the kw increases. This is because the the elastic ends have no obvious influence on the contact stifness between the beam and the impactor, and thus, the changing of the boundary conditions cannot produce remarkable changes to the contact forces and indentations.

Fig. 9
figure 9

Effect of elastic boundary conditions on the contact force of the FG-CNTRC beams

Full size image
Fig. 10
figure 10

Effect of elastic boundary conditions on the contact indentations of the FG-CNTRC beams

Full size image
Fig. 11
figure 11

Effect of elastic boundary conditions on the dynamic central deflection of the FG-CNTRC beams

Full size image

Figure 11 shows the effect of elastic boundary conditions on the central deflections of the nanocomposite beams under low-velocity impact. It is clear that the dynamic central deflections of the beams are affected dramatically by the variation of the spring parameters. As the artifical spring parameters decrease, the dynamic deflections increase. That is because as the artifical spring parameters decrease, the boundary end restrains are gradually relax, reducing the stiffness of the system.

5.7 Effect of impact velocity

In the last, we focus on the effects of impact velocity on the responses of the beams during the impact process. The agglomeration parameters are ξ = 0.25 and ζ = 0.75. UD distribution pattern is considered herein. Other parameters are presented in Fig. 12. The time histories of the contact force, contact indentation and central deflection of the composite beams subjected to the impact with various velocities are plotted in Fig. 12a–c. Three different initial velocities of vimp = 1.0 m/s, 3.0 m/s and 5.0 m/s are considered in this example. As expected, an increase in the impact velocity results in hihger peak values of contact forces and indentations but the lower contact times. However, the effect of imact velocity is much more pronounced on the peak contact force/indentation than the contact time. Moreover, the a larger impact velocity causes a greater central deflection.

Fig. 12
figure 12

Effect of impact velocity on the impact response of the FG-CNTRC beams

Full size image

6 Conclusions

In the current work, the low-velocity impact responses of an FG-CNTRC viscoelastic beam with general boundary constraints are studied. The beam is constructed by a multiplayer beam model with the weight fraction of carbon nanotubes (CNTs) being constant in each layer but varying according to a layer-wise rule in the thickness direction. The Mori–Tanaka micromechanics model is used to calculate the effective elastic moduli and Poisson’s ratio of the nanocomposites, in which the CNT agglomeration is considered with the aid of a two-parameter model. The viscoelastic properties of beams are assumed based on Kelvin–Voigt theory. A high-order shear deformation theory in conjunction with the artificial spring method of quantifiably accounting for the elastic boundary conditions is developed to present the energy expressions of the system. The governing equations of motions are derived by means of the Lagrange method with the help of a Gram–Schmidt process to produce admissible functions in a general orthogonal polynomial form and solved by the Newmark-β method in time domain. The numerical examples are carried out to reveal the effects of CNT weight fractions, CNT distribution patterns, CNT agglomeration and artificial spring parameters on the dynamic response of the beams. A few conclusions can be summarized from the numerical results:

  1. 1.

    The selection of beam theories has no remarkable effect on the predication of contact forces, while it has a relatively obvious effect on the predication of central deflections of beams.

  2. 2.

    CNT agglomerations weaken reinforcing efficiency of the nanofillers and the modulus of elasticity of the CNTRCs decrease. As the agglomeration become gradually severe, the contact forces decrease and the peak values of dynamic deflection increase.

  3. 3.

    Dispersing more CNT nanofillers near the beam’s top and bottom surfaces is the most effective way to enhance the resistance of the beam to low-velocity impact loads. Adding CNT nanofillers can improve the stiffness of the beam and reduce the peak values of dynamic deflections of the beam under low-velocity impact loads. However, the improvements of CNTs to the beam stiffness become more and more insignificant when the CNT weight fractions are in a higher value and the agglomerations effect is severe.

  4. 4.

    The elastic boundary conditions have no remarkable influences of artificial springs on the contact forces and indentations, while have dramatically effects on the dynamic deflections of the beams.

  5. 5.

    The viscoelasticity has remarkable effects on the contact forces and contact indentations of the nanocomposite beam under low-velocity impact, but has significant influences on the central deflections of the beam. The viscoelasticity of the nanocomposites can introduce an great decay of the dynamic responses.