1 Background

1.1 Impact of size on structural domain

On account of their distinctive characteristic and wide area of applications, small-scaled elements like nanobeams have attracted immense attentions. According to various experimental observations [1,2,3,4], it has been verified that the size-dependency phenomenon plays a crucial role in the mechanical behavior of small-sized structures, which are the main building blocks of miniaturized devices like micro- and nanoelectromechanical systems (MEMS and NEMS). Given that no length scale parameter exists in its constitutive relations, classical theory (CT) of continuum cannot suitably reflect the size-dependent features of small-scaled mechanical segments. With the purpose of resolving this limitation of classical theory, by making use of length scale parameters, nonclassical continuum theories such as couple stress theory [5], nonlocal theory (NT) [6], modified couple stress theory (MCST) [7], strain gradient theory (SGT) [8] and nonlocal strain gradient theory (NSGT) [9] have been introduced and extended. According to the values reported for the length scale parameter employed in MCST, this theory is more suitable for size-dependent analysis of structural elements with micro dimensions. The nonlocal theory relies on this assumption that the stress at an arbitrary point is a function of strains at all points of the body. In the strain gradient theory, the classical and higher order stresses are associated with the classical strains and additional higher order strain gradient terms. In general, nonlocal theory reflects only stiffness softening characteristic at small scales, whereas strain gradient theory captures the impact of stiffness enhancement. In order to incorporate these two entirely different aspects of size effect into a unified model, by combining the nonlocal and strain gradient theories, Lim et al. [9] established a hybrid nonclassical theory, which is called nonlocal strain gradient theory. In recent years, many investigations have been devoted to assessment of size-dependent mechanical behavior of small-scaled structures with the help of nonclassical continuum theories. Some of this articles are reviewed in what follows: Farokhi and Ghayesh [10] utilized MCST to assess size effect on nonlinear dynamics of axially loaded microarches. Zheng et al. [11] examined the impact of scale parameter of MCST on the stability of axially graded microtubes conveying fluid. Borjalilou et al. [12] showed that MCST predicts lower values for thermoelastic damping (TED) in microbeams in comparison with CT. In the work of Arshid et al. [13], MCST has been applied to evaluate size-dependent vibration and buckling of magneto-thermal functionally graded (FG) porous microbeams. Yang et al. [14] used MCST to determine linear and nonlinear response of arbitrary-shaped FG microplates. Borjalilou and Asghari [15] investigated the size effect on TED in electrically actuated microbeams via MCST. In the article of Soleimani and Beni [16], shell elements together with MCST have been exploited to analyze the vibrations of nanotubes. By employing NT, Li and Esmaeili [17] indicated that nonlocal effect increases TED in circular nanoplates. Glabisz et al. [18] used NT to highlight small-scale effect on the stability of initially stressed Timoshenko nanobeams. In the study of Alipour and Shariyat [19], NT has been utilized to determine hygro-thermal stresses of sandwich annular nanoplates. On the basis of three-dimensional NT, Wang et al. [20] accomplished an exact analysis on the static problem of nanoplates. With the aid of NT, Borjalilou et al. [21] conducted an analytical study to provide exact solutions for static bending, buckling and free vibration problems of FG carbon nanotube reinforced composite (CNTRC) nanobeams. Arefi and Civalek [22] appraised static problem of nonlocal FG shells embedded in elastic media. Yang et al. [23] illustrated that making use of NT leads to higher magnitudes of TED in rectangular nanoplates. Sahmani and Aghdam [24] carried out a size-dependent analysis on postbuckling behavior of FG nanoshells in thermal environment. By employing SGT, Borjalilou and Asghari revealed that length scale parameters yield smaller amount of TED in microbeams [25] and microplates [26]. Sobhy [27] applied NSGT to estimate the effect of scale parameters on bending response of graphene platelet (GPL) sandwich circular nanoplates. In the work of Dindarloo and Zenkour [28], NSGT has been used to provide a size-dependent thermomechanical model for bending problem FG spherical nanoshells. According to NSGT, Bai et al. [29] analyzed forced vibrations of nanobeams in hygro-thermo-magneto media. Zhu et al. [30] investigated size-dependent oscillations of spinning FG nanotubes conveying fluid by means of NSGT.

1.2 Small-scale effect on thermal area

For the sake of characterizing the propagation of heat in solid bodies, a variety of heat conduction models have been suggested. The classical thermoelasticity (CTE) theory has been established on the basis of the well-known Fourier law of heat conduction. According to theoretical and empirical studies, the Fourier law cannot present an exhaustive formulation for description of heat transfers occurring in small-scale times or sizes [31]. Accordingly, several non-Fourier heat conduction models have been proposed in order to eliminate the imperfections of classical model. By incorporating a single-phase lag parameter within the Fourier model, Lord and Shulman [32] introduced a famous nonclassical model. The Lord–Shulman (LS) model is able to take into account small-scale effect only in time. By inclusion of two-phase lag parameters, which allows capturing small-scale effect in both time and space, Tzou [33] established the dual-phase-lag (DPL) model. By characterizing the heat conduction process via phonon scattering model and solving the linearized phonon Boltzmann transport equation, Guyer and Krumhansl [34] provided a powerful mathematical description to reflect both the lagging and nonlocal aspects of nanoscale heat transfers.

1.3 Thermoelastic coupling effect on behavior of small-sized structures

Thermoelastic damping (TED) is one of the main energy loss mechanisms in which energy is dissipated in a thermoelastic medium owing to the coupling of strains and temperature through the thermal expansion coefficient. Indeed, when a thermoelastic structure undergoes bending oscillations, entropy generation due to irreversible heat current occurs. So, TED cannot be totally omitted and hence, narrows the quality factor of small-sized structures. The first theoretical investigations of TED have been carried out by Zener [35], who derived an analytical relation in the form of infinite series for estimation of TED value in thin beams. Lifshitz and Roukes [36] established a single explicit expression for TED in Euler–Bernoulli beams by adopting a one-dimensional model for heat conduction. Thermoelastic coupling effect on the vibrations of small-sized beams has been analyzed by some researchers. In what follows, the most important of these investigations are reviewed. By means of classical Euler–Bernoulli beam theory and Fourier heat conduction model, Guo and Rogerson [37] evaluated the frequency shift arose from thermoelastic coupling. By making use of LS model, Sun et al. [38] surveyed the impact of coupled thermoelasticity on the vibration characteristics of classical slender beams. In another research of Sun and his colleagues [39], frequency shift of classical thin beams subjected to pulsed laser heating have been approximated in the context of LS model. With the aid of SGT and LS model, Taati et al. [40] determined the role of nonclassical scale parameters in thermoelastic response of a Timoshenko microbeam under mechanical load. In the work of Zenkour [41], thermoelastic coupling effect on the vibrations of a thin microbeam resting on a viscoelastic foundation has been evaluated. Green-Naghdi (GN) model has been employed in that study to describe the heat conduction process. By applying the Laplace transform, Abouelregal and Zenkour [42] derived thermoelastic response of nonlocal nanobeams under dynamic load with dual-phase-lag heat conduction. Hosseini [43] utilized nonlocal theory and GN model to ascertain the impact of nonclassical parameters on transient response of Rayleigh nanobeams. The investigation of Kumar and Mukhopadhyay [44] has been devoted to assessment of thermoelastic coupling effect on dynamic response of classical slender microbeams with heat transfer process defined by Moore–Gibson–Thompson (MGT model). By incorporating nonlocal and surface energy effect into constitutive relations and employing GN model, Alizadeh Hamidi et al. [45] provided an analytical model to study the effect of TED on the vibrations of Euler–Bernoulli nanobeams. Kumar [46] exploited MCST in conjunction with three-phase-lag (TPL) model to clarify the impact of nonclassical structural and thermal parameters on thermoelastic response of Timoshenko beams. Kumar and Mukhopadhyay [47] conducted an analytical study on the basis of MCST and DPL model to specify the influence of size on thermoelastic oscillations of Timoshenko microbeams.

1.4 Contributions of the current study to the field

As inferred from the literature review, taking into account small-scale effect on both structure and heat transfer is indispensable to better reflect thermoelastic behavior of miniaturized mechanical elements. To the authors’ best knowledge, size effect on structure in coupled thermoelastic problems of small-scaled beams has been mainly captured via nonlocal, modified couple stress and strain gradient theories, not NSGT. Moreover, in most cases, size effect on heat conduction in coupled thermoelastic problems of miniaturized beams has been taken into account by means of LS, DPL, three-phase-lag (TPL) and Green–Naghdi (GN) models, not GK model. Although the impact of NSGT and GK model on the uncoupled problems of beams has been analyzed separately, there is no investigation in the available literature concerning the size-dependent coupled thermoelastic vibrations of Timoshenko nanobeams in the framework of nonlocal strain gradient theory (NSGT) and Guyer–Krumhansl (GK) heat conduction model. The paper at hand intends to fill this gap. For the sake of achieving this aim, the size-dependent governing equations, namely motion and heat conduction equations are established in the first step. Some parameters are then defined to normalize the coupled thermoelastic equations. With the help of Laplace transform, analytical solution of thermoelastic vibrations of a simply supported Timoshenko nanobeam subjected to dynamic load is determined. Several numerical results are provided to illuminate how the nonclassical structural and thermal parameters can affect thermoelastic response of nanobeams.

2 Primary theoretical principles

2.1 Nonlocal strain gradient theory

On the basis of nonlocal strain gradient theory (NSGT) introduced by Lim et al. [9], the total stress tensor is written as follows:

$${\varvec{t}} = {\varvec{\sigma}} - \nabla {\varvec{\sigma}}^{\left( 1 \right)} ,$$
(1)

in which \({\varvec{\sigma}}\) and \({\varvec{\sigma}}^{\left( 1 \right)}\) represent the classical and higher order stress tensors, respectively, which are determined via the following relations:

$${\varvec{\sigma}} = \int_{V} {\alpha_{0} \left( {{\varvec{x}}^{\prime } ,{\varvec{x}},e_{0} a} \right){\varvec{C}}:{\varvec{\varepsilon}}^{\prime } dV^{\prime } } ,$$
(2a)
$${\varvec{\sigma}}^{\left( 1 \right)} = l^{2} \int_{V} {\alpha_{1} \left( {{\varvec{x}}^{\prime } ,{\varvec{x}},e_{1} a} \right){\varvec{C}}:\nabla {\varvec{\varepsilon}}^{\prime } dV^{\prime } } ,$$
(2b)

where \(e_{0} a\) and \(e_{1} a\) denote the nonlocal parameters defined to capture the effect of nonlocal stress field. In addition, \(l\) is the material length scale parameter introduced to include the impact of strain gradient stress field. Parameters \({\varvec{C}}\) and \({\varvec{\varepsilon}}\) represent the fourth-order elasticity and strain tensors, respectively. The apostrophes appeared in equations above refer to the neighboring points of reference point \({\varvec{x}}\) within the domain \(V\). Moreover, \(\alpha_{0} \left( {{\varvec{x}}^{\prime } ,{\varvec{x}},e_{0} a} \right)\) and \(\alpha_{1} \left( {{\varvec{x}}^{\prime } ,{\varvec{x}},e_{1} a} \right)\) stand for nonlocal attenuation Kernel functions which comply with the conditions formulated by Eringen [6], that is, the linear nonlocal differential operators can be utilized in the nonlocal functions by way of following definitions:

$$L_{0} = 1 - \left( {e_{0} a} \right)^{2} \nabla^{2} \quad {\text{and}}\quad L_{1} = 1 - \left( {e_{1} a} \right)^{2} \nabla^{2} .$$
(3)

By applying these linear differential operators on both sides of Eq. (1) and considering Eqs. (2a) and (2b), one can arrive at the following constitutive relation:

$$\left[ {1 - \left( {e_{1} a} \right)^{2} \nabla^{2} } \right]\left[ {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right]{\varvec{t}} = \left[ {1 - \left( {e_{1} a} \right)^{2} \nabla^{2} } \right]{\varvec{C}}:{\varvec{\varepsilon}} - l^{2} \left[ {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right]\nabla \left( {{\varvec{C}}:\nabla {\varvec{\varepsilon}}} \right).$$
(4)

In the interest of convenience, by adopting \(e_{0} = e_{1} = e\), the simplified form of constitutive relation (4) can be expressed as follows:

$$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]{\varvec{t}} = \left[ {1 - l^{2} \nabla^{2} } \right]{\varvec{C}}:{\varvec{\varepsilon}}.$$
(5)

It is important to emphasize that in the absence of strain gradient length scale parameter \(l\), constitutive relation of NSGT reduces to that of nonlocal theory. As the nonlocal parameter \(ea\) is set to zero, Eq. (5) is converted to constitutive relation of pure strain gradient theory. Lastly, when both strain gradient length scale and nonlocal parameters vanish, constitutive relation of NSGT is replaced with that of classical continuum theory.

2.2 Guyer–Krumhansl heat conduction model

According to the nonclassical heat conduction model of Guyer and Krumhansl (GK model), heat transfer in isotropic materials complies with the following relation [34]:

$${\varvec{q}} + \tau \frac{{\partial {\varvec{q}}}}{\partial t} = - k\nabla \theta + \zeta^{2} \left[ {\nabla^{2} {\varvec{q}} + 2\nabla \left( {\nabla .{\varvec{q}}} \right)} \right],$$
(6)

where \({\varvec{q}}\) represents the heat flux vector. Variable \(\theta = T - T_{0}\) is temperature deviation in which \(T_{0}\) refers to the environmental temperature. Furthermore, Material constant \(k\) denotes the thermal conductivity. Parameter \(\tau\) is known as relaxation time that enables the model to incorporate phase-lagging effect within heat propagation process. Additionally, parameter \(\zeta\) is called thermal nonlocal parameter, which makes it possible to capture nonlocal effect. Note that in the absence of thermal nonlocal parameter \(\zeta\), the constitutive relation of GK model corresponds to that of LS model. Moreover, when \(\zeta\) and \(\tau\) are set to zero, Eq. (6) is converted to the well-known equation of Fourier law. For an isotropic body, the equation of conservation of energy has the following form [33]:

$$- \nabla .{\varvec{q}} + S = \rho c_{v} \frac{\partial \theta }{{\partial t}} + T_{0} \beta \frac{{\partial \varepsilon_{mm} }}{\partial t},$$
(7)

where \(S\), \(\rho\) and \(c_{v}\) stand for volumetric heat source, mass density and specific heat per unit mass, respectively. Parameter \(\beta = E\alpha /\left( {1 - 2\nu } \right)\) is also known as thermal modulus in which \(E\), \(\alpha\) and \(\nu\) represent the Young modulus, thermal expansion coefficient and the Poisson ratio, respectively. By merging Eqs. (6) and (7) and eliminating heat flux \({\varvec{q}}\), one can readily get the governing equation of heat conduction in terms of temperature increment \(\theta\):

$$\left( {1 + \tau \frac{\partial }{\partial t} - 3\zeta^{2} \nabla^{2} } \right)\left( {\rho c_{v} \frac{\partial \theta }{{\partial t}} + T_{0} \beta \frac{{\partial \varepsilon_{mm} }}{\partial t} - S} \right) = k\nabla^{2} \theta .$$
(8)

3 Nonclassical coupled thermoelastic equations of Timoshenko beams

3.1 Equations of motion

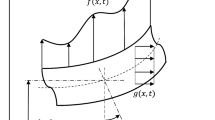
The coordinate system and loading of a Timoshenko beam with length \(L\), uniform thickness \(h\) and width \(b\) are displayed in Fig. 1. The total volume and cross-section area of the beam are also denoted by \(V\) and \(A\), respectively. Based on the Timoshenko beam model, the components of displacement field are given by the following definitions:

$$u_{x} = u\left( {x,t} \right) - z\varphi \left( {x,t} \right),\quad u_{y} = 0,\quad u_{z} = w\left( {x,t} \right).$$
(9)
Fig. 1
figure 1

Geometry and coordinate system of a Timoshenko beam

Full size image

Here, \(u_{x}\), \(u_{y}\) and \(u_{z}\) denote displacements along the axes \(x\), \(y\) and \(z\), respectively. Moreover, \(u\left( {x,t} \right)\) refers to axial displacement of the middle surface of beam. Functions \(\varphi \left( {x,t} \right)\) and \(w\left( {x,t} \right)\) represent the angle of rotation of cross sections and lateral deflection, respectively. In accordance with the first-order shear deformation beam theory, the nonzero components of strain tensor are derived via the relations below:

$$\varepsilon_{xx} = \frac{\partial u}{{\partial x}} - z\frac{\partial \varphi }{{\partial x}},\quad \varepsilon_{xz} = \varepsilon_{zx} = \frac{1}{2}\left( {\frac{\partial w}{{\partial x}} - \varphi } \right).$$
(10)

In the framework of NSGT, the virtual strain energy of a Timoshenko beam is written as follows:

$$\delta U = \int_{V} {\left( {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{xx}^{\left( 1 \right)} \nabla \delta \varepsilon_{xx} + 2\sigma_{xz} \delta \varepsilon_{xz} + \sigma_{xz}^{\left( 1 \right)} \nabla \delta \varepsilon_{xz} } \right)dV} .$$
(11)

By implementing integration by parts and employing Eq. (1), equation above takes the following form:

$$\delta U = \mathop \int \limits_{V}^{{}} \left( {t_{xx} \delta \varepsilon_{xx} + 2t_{xz} \delta \varepsilon_{xz} } \right)dV + \left[ {\mathop \int \limits_{A}^{{}} \left( {\sigma_{xx}^{\left( 1 \right)} \delta \varepsilon_{xx} + 2\sigma_{xz}^{\left( 1 \right)} \delta \varepsilon_{xz} } \right)dA} \right]_{x = 0}^{x = L} .$$
(12)

Substitution of Eq. (10) into (12) and rearrangement of the result gives the following:

$$\begin{aligned} \delta U & = \int_{0}^{L} {\left[ {N\delta \left( {\frac{\partial u}{{\partial x}}} \right) - M\delta \left( {\frac{\partial \varphi }{{\partial x}}} \right) + Q\delta \left( {\frac{\partial w}{{\partial x}}} \right) - Q\delta \varphi } \right]dx} \\ & + \left[ {N^{\left( 1 \right)} \delta \left( {\frac{\partial u}{{\partial x}}} \right) - M^{\left( 1 \right)} \delta \left( {\frac{\partial \varphi }{{\partial x}}} \right) + Q^{\left( 1 \right)} \delta \left( {\frac{\partial w}{{\partial x}}} \right) - Q^{\left( 1 \right)} \delta \varphi } \right]_{x = 0}^{x = L} , \\ \end{aligned}$$
(13)

in which axial forces \(N\) and \(N^{\left( 1 \right)}\), bending moments \(M\) and \(M^{\left( 1 \right)}\), and shear forces \(Q\) and \(Q^{\left( 1 \right)}\) are defined by way of following expressions:

$$\left( {N,M,Q} \right) = \int_{A} {\left( {t_{xx} ,zt_{xx} ,t_{xz} } \right)dA} ,$$
(14a)
$$\left( {N^{\left( 1 \right)} ,M^{\left( 1 \right)} ,Q^{\left( 1 \right)} } \right) = \int_{A} {\left( {\sigma_{xx}^{\left( 1 \right)} ,z\sigma_{xx}^{\left( 1 \right)} ,\sigma_{xz}^{\left( 1 \right)} } \right)dA} .$$
(14b)

Finally, by reusing integration by parts, virtual strain energy relation (13) becomes as follows:

$$\begin{aligned} \delta U & = \int_{0}^{L} {\left[ { - \left( {\frac{\partial N}{{\partial x}}} \right)\delta u + \left( {\frac{\partial M}{{\partial x}} - Q} \right)\delta \varphi - \left( {\frac{\partial Q}{{\partial x}}} \right)\delta w} \right]dx} \\ & + \left[ {N\delta u - M\delta \varphi + Q\delta w + N^{\left( 1 \right)} \delta \left( {\frac{\partial u}{{\partial x}}} \right) - M^{\left( 1 \right)} \delta \left( {\frac{\partial \varphi }{{\partial x}}} \right) + Q^{\left( 1 \right)} \delta \left( {\frac{\partial w}{{\partial x}} - \varphi } \right)} \right]_{x = 0}^{x = L} . \\ \end{aligned}$$
(15)

The virtual work done by external loads can be given by the following:

$$\delta W = \int_{0}^{L} {\left( {f\delta u + q\delta w} \right)dx} + \left[ {\overline{M}\delta \varphi - \overline{Q}\delta w} \right]_{x = 0}^{x = L} ,$$
(16)

where \(f\left( {x,t} \right)\) and \(q\left( {x,t} \right)\) refer to distributed axial and transverse loads, respectively. Further, \(\overline{M}\) and \(\overline{Q}\) denote the external bending moment and shear force, respectively.

The first variation of kinetic energy can be determined through the following relation:

$$\delta K = \int_{V} {\rho \left[ {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)\delta \left( {\frac{{\partial u_{x} }}{\partial t}} \right) + \left( {\frac{{\partial u_{y} }}{\partial t}} \right)\delta \left( {\frac{{\partial u_{y} }}{\partial t}} \right) + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)\delta \left( {\frac{{\partial u_{z} }}{\partial t}} \right)} \right]dV} .$$
(17)

For an isotropic beam, by substituting Eq. (9) into (17), one can achieve the following relation for the virtual kinetic energy:

$$\delta K = \rho A\left( {\frac{\partial u}{{\partial t}}} \right)\delta \left( {\frac{\partial u}{{\partial t}}} \right) + \rho I\left( {\frac{\partial \varphi }{{\partial t}}} \right)\delta \left( {\frac{\partial \varphi }{{\partial t}}} \right) + \rho A\left( {\frac{\partial w}{{\partial t}}} \right)\delta \left( {\frac{\partial w}{{\partial t}}} \right),$$
(18)

where \(I = \int_{A} {z^{2} dA}\) represents the area moment of inertia of cross sections. In order to extract the equations of motion and edge conditions, the Hamilton principle is employed as follows:

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta U - \delta W - \delta K} \right)dt} = 0.$$
(19)

Ultimately, substitution of Eqs. (15), (16) and (18) into (19) and integration by parts with respect to time yields the following relations for motion equations:

$$\delta u:\quad \frac{\partial N}{{\partial x}} + f = \rho A\frac{{\partial^{2} u}}{{\partial t^{2} }}$$
(20a)
$$\delta \varphi :\quad Q - \frac{\partial M}{{\partial x}} = \rho I\frac{{\partial^{2} \varphi }}{{\partial t^{2} }}$$
(20b)
$$\delta w:\quad \frac{\partial Q}{{\partial x}} + q = \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }}.$$
(20c)

The classical boundary conditions at end sections \(x = 0\) and \(x = L\) are obtained as follows:

$$N = 0\quad {\text{OR}}\quad \delta u = 0$$
(21a)
$$M - \overline{M} = 0\quad {\text{OR}}\quad \delta \varphi = 0$$
(21b)
$$Q - \overline{Q} = 0\quad {\text{OR}}\quad \delta w = 0.$$
(21c)

In addition, nonclassical boundary conditions at these end edges are derived as follows:

$$N^{\left( 1 \right)} = 0\quad {\text{OR}}\quad \delta \left( {\frac{\partial u}{{\partial x}}} \right) = 0$$
(22a)
$$M^{\left( 1 \right)} = 0\quad {\text{OR}}\quad \delta \left( {\frac{\partial \varphi }{{\partial x}}} \right) = 0$$
(22b)
$$Q^{\left( 1 \right)} = 0\quad {\text{OR}}\quad \delta \left( {\frac{\partial w}{{\partial x}} - \varphi } \right) = 0.$$
(22c)

In view of Eq. (5), thermoelastic constitutive relations of isotropic Timoshenko beams in the context of NSGT are derived as follows [48]:

$$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]t_{xx} = \left[ {1 - l^{2} \nabla^{2} } \right]E\left( {\varepsilon_{xx} - \alpha \theta } \right)$$
(23a)
$$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]t_{xz} = \left[ {1 - l^{2} \nabla^{2} } \right]G\gamma_{xz} ,$$
(23b)

in which \(G = E/2\left( {1 + \nu } \right)\) refers to the shear modulus of beam. It is also to be noted that \(\gamma_{xz} = 2\varepsilon_{xz}\). By referring to definition of stress resultants (14a) and using strain–displacement relations (10), one can get the following:

$$\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]N = EA\left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{\partial u}{{\partial x}} - \left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]N_{T}$$
(24a)
$$\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]M = - EI\left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{\partial \varphi }{{\partial x}} - \left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]M_{T}$$
(24b)
$$\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]Q = K_{s} GA\left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\left( {\frac{\partial w}{{\partial x}} - \varphi } \right),$$
(24c)

where \(K_{s}\) is the shear correction factor. In addition, \(N_{T}\) and \(M_{T}\) stand for thermal axial force and thermal moment which are determined via the relations as follows:

$$N_{T} = E\alpha \int_{A} {\theta dA} = E\alpha b\int_{ - h/2}^{ + h/2} {\theta dz} ,$$
(25a)
$$M_{T} = E\alpha \int_{A} {\theta zdA} = E\alpha b\int_{ - h/2}^{ + h/2} {\theta zdz} .$$
(25b)

At the final stage, by applying the operator \(1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}\) on both sides of equilibrium Eqs. (20a)–(20c) and combining the results with constitutive relations (24a)–(24c), one can arrive at the coupled thermoelastic equations of motion of nonlocal strain gradient Timoshenko beams in terms of displacement variables:

$$EA\left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{{\partial^{2} u}}{{\partial x^{2} }} - \left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{{\partial N_{T} }}{\partial x} + \left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]f = \rho A\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{{\partial^{2} u}}{{\partial t^{2} }}$$
(26a)
$$K_{s} GA\left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\left( {\frac{\partial w}{{\partial x}} - \varphi } \right) + EI\left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{{\partial M_{T} }}{\partial x} = \rho I\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{{\partial^{2} \varphi }}{{\partial t^{2} }}$$
(26b)
$$K_{s} GA\left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{\partial \varphi }{{\partial x}}} \right) + \left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]q = \rho A\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }}.$$
(26c)

As it is apparent, the differential equation of axial displacement \(u\) is independent of those of angle of rotation of cross sections \(\varphi\) and transverse displacement \(w\).

3.2 Equations of heat conduction

According to the components of strain tensor given in Eq. (10), the cubical dilatation \(\varepsilon_{mm}\) is calculated through the following relation:

$$\varepsilon_{mm} = \frac{\partial u}{{\partial x}} - z\frac{\partial \varphi }{{\partial x}}.$$
(27)

In the absence of external heat source, i.e. \(S = 0\), substitution of equation above into Eq. (8) gives the following:

$$\begin{aligned} & \rho c_{v} \frac{\partial \theta }{{\partial t}} + \tau \rho c_{v} \frac{{\partial^{2} \theta }}{{\partial t^{2} }} + T_{0} \beta \left( {\frac{{\partial^{2} u}}{\partial x\partial t} - z\frac{{\partial^{2} \varphi }}{\partial x\partial t}} \right) + \tau T_{0} \beta \left( {\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - z\frac{{\partial^{3} \varphi }}{{\partial x\partial t^{2} }}} \right) \\ & = k\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial z^{2} }}} \right) + 3\zeta^{2} \rho c_{v} \left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} \partial t}} + \frac{{\partial^{2} \theta }}{{\partial z^{2} \partial t}}} \right) + 3\zeta^{2} T_{0} \beta \left( {\frac{{\partial^{4} u}}{{\partial x^{3} \partial t}} - z\frac{{\partial^{4} \varphi }}{{\partial x^{3} \partial t}}} \right). \\ \end{aligned}$$
(28)

By multiplying the relation above by \(E\alpha bz\), integrating the result over the thickness of beam and employing the definition of thermal moment presented in Eq. (25b), one can obtain the following:

$$\begin{aligned} & \rho c_{v} \frac{{\partial M_{T} }}{\partial t} + \tau \rho c_{v} \frac{{\partial^{2} M_{T} }}{{\partial t^{2} }} - T_{0} \beta E\alpha I\frac{{\partial^{2} \varphi }}{\partial x\partial t} - \tau T_{0} \beta E\alpha I\frac{{\partial^{3} \varphi }}{{\partial x\partial t^{2} }} \\ & = k\frac{{\partial^{2} M_{T} }}{{\partial x^{2} }} + kE\alpha b\mathop \int \limits_{ - h/2}^{ + h/2} \frac{{\partial^{2} \theta }}{{\partial z^{2} }}zdz + 3\zeta^{2} \rho c_{v} \frac{{\partial^{2} M_{T} }}{{\partial x^{2} \partial t}} + 3\zeta^{2} \rho c_{v} E\alpha b\mathop \int \limits_{ - h/2}^{ + h/2} \frac{{\partial^{2} \theta }}{{\partial z^{2} \partial t}}zdz - 3\zeta^{2} T_{0} \beta E\alpha I\frac{{\partial^{4} \varphi }}{{\partial x^{3} \partial t}}. \\ \end{aligned}$$
(29)

Top and bottom sides of beam are supposed to be thermally insulated, that is \(\partial \theta /\partial z = 0\) at \(z = \pm h/2\). For such a beam, the variation of temperature can be considered as follows [38, 40, 47]:

$$\theta \left( {x,z,t} \right) = \Theta \left( {x,t} \right)\sin \left( {pz} \right)\quad {\text{with}}\quad p = \pi /h.$$
(30)

From the relation above, one can conclude that

$$E\alpha b\int_{ - h/2}^{ + h/2} {\frac{{\partial^{2} \theta }}{{\partial z^{2} }}zdz} = - p^{2} E\alpha b\int_{ - h/2}^{ + h/2} {\theta zdz} = - p^{2} M_{T} .$$
(31)

By using equation above in Eq. (29) and simplifying the result, the heat equation on the basis of GK model takes the following final form:

$$\begin{aligned} & \frac{{\partial M_{T} }}{\partial t} + \tau \frac{{\partial^{2} M_{T} }}{{\partial t^{2} }} - \frac{{EI\Delta_{E} }}{1 - 2\nu }\frac{{\partial^{2} \varphi }}{\partial x\partial t} - \tau \frac{{EI\Delta_{E} }}{1 - 2\nu }\frac{{\partial^{3} \varphi }}{{\partial x\partial t^{2} }} \\ & = \chi \frac{{\partial^{2} M_{T} }}{{\partial x^{2} }} - \chi p^{2} M_{T} + 3\zeta^{2} \frac{{\partial^{3} M_{T} }}{{\partial x^{2} \partial t}} - 3\zeta^{2} p^{2} \frac{{\partial M_{T} }}{\partial t} - 3\zeta^{2} \frac{{EI\Delta_{E} }}{1 - 2\nu }\frac{{\partial^{4} \varphi }}{{\partial x^{3} \partial t}}, \\ \end{aligned}$$
(32)

in which parameters \(\chi = k/\rho c_{v}\) and \({\Delta }_{E} = E\alpha^{2} T_{0} /\rho c_{v}\) are called thermal diffusivity and relaxation strength, respectively.

3.3 Dimensionless governing equations

In the interest of generalization of the governing equations and highlighting the impact of nonclassical material constants on the results, some parameters are introduced as follows:

$$x^{*} = \frac{x}{L},\quad t^{*} = \frac{t}{L}\sqrt {\frac{E}{\rho }} ,\quad w^{*} = \frac{w}{L},\quad \varphi^{*} = \varphi ,\quad M_{T}^{*} = \frac{{M_{T} L}}{EI},\quad q^{*} = \frac{{qL^{3} }}{EI},\quad \tau_{1} = L\sqrt {\frac{\rho }{E}} ,\quad \tau_{2} = \frac{{L^{2} }}{\chi }.$$
(33)

With the help of these nondimensional quantities, the normalized forms of motion Eqs. (26b) and (26c), and heat Eq. (32) are extracted as follows:

$$A_{1} \frac{{\partial^{4} \varphi^{*} }}{{\partial x^{*4} }} - A_{2} \frac{{\partial^{2} \varphi^{*} }}{{\partial x^{*2} }} + A_{3} \varphi^{*} + A_{4} \frac{{\partial^{3} w^{*} }}{{\partial x^{*3} }} - A_{3} \frac{{\partial w^{*} }}{{\partial x^{*} }} + A_{1} \frac{{\partial^{3} M_{T}^{*} }}{{\partial x^{*3} }} - A_{5} \frac{{\partial M_{T}^{*} }}{{\partial x^{*} }} = - A_{5} \frac{{\partial^{2} \varphi^{*} }}{{\partial t^{*2} }} + A_{6} \frac{{\partial^{4} \varphi^{*} }}{{\partial x^{*2} \partial t^{*2} }}$$
(34a)
$$A_{4} \frac{{\partial^{4} w^{*} }}{{\partial x^{*4} }} - A_{3} \frac{{\partial^{2} w^{*} }}{{\partial x^{*2} }} - A_{4} \frac{{\partial^{3} \varphi^{*} }}{{\partial x^{*3} }} + A_{3} \frac{{\partial \varphi^{*} }}{{\partial x^{*} }} + A_{6} \frac{{\partial^{2} q^{*} }}{{\partial x^{*2} }} - A_{5} q^{*} = - \frac{{\partial^{2} w^{*} }}{{\partial t^{*2} }} + A_{7} \frac{{\partial^{4} w^{*} }}{{\partial x^{*2} \partial t^{*2} }}$$
(34b)
$$A_{8} \frac{{\partial^{2} M_{T}^{*} }}{{\partial x^{*2} }} - A_{9} M_{T}^{*} = A_{10} \frac{{\partial^{2} M_{T}^{*} }}{{\partial t^{*2} }} + A_{11} \frac{{\partial M_{T}^{*} }}{{\partial t^{*} }} - A_{12} \frac{{\partial^{3} M_{T}^{*} }}{{\partial x^{*2} \partial t^{*} }} - A_{13} \frac{{\partial^{2} \varphi^{*} }}{{\partial x^{*} \partial t^{*} }} - A_{14} \frac{{\partial^{3} \varphi^{*} }}{{\partial x^{*} \partial t^{*2} }} + A_{15} \frac{{\partial^{4} \varphi^{*} }}{{\partial x^{*3} \partial t^{*} }}.$$
(34c)

The dimensionless coefficients appeared in equations above are defined as follows:

$$\begin{gathered} A_{1} = \frac{1}{12}\left( \frac{h}{L} \right)^{2} \left( \frac{l}{L} \right)^{2} ,\quad A_{2} = K_{s} \left( \frac{G}{E} \right)\left( \frac{l}{L} \right)^{2} + \frac{1}{12}\left( \frac{h}{L} \right)^{2} ,\quad A_{3} = K_{s} \left( \frac{G}{E} \right),\quad A_{4} = K_{s} \left( \frac{G}{E} \right)\left( \frac{l}{L} \right)^{2} , \hfill \\ A_{6} = \frac{1}{12}\left( \frac{h}{L} \right)^{2} \left( \frac{ea}{L} \right)^{2} ,\quad A_{7} = \left( \frac{ea}{L} \right)^{2} ,{\quad}A_{8} = \left( {\frac{{\tau_{1} }}{{\tau_{2} }}} \right)\left( \frac{h}{L} \right)^{2} , \hfill \\ A_{9} = \pi^{2} \left( {\frac{{\tau_{1} }}{{\tau_{2} }}} \right),\quad A_{10} = \left( {\frac{\tau }{{\tau_{1} }}} \right)\left( \frac{h}{L} \right)^{2} ,\quad A_{11} = \left( \frac{h}{L} \right)^{2} + 3\pi^{2} \left( {\frac{\zeta }{L}} \right)^{2} ,\quad A_{12} = 3\left( \frac{h}{L} \right)^{2} \left( {\frac{\zeta }{L}} \right)^{2} , \hfill \\ A_{13} = \frac{{\Delta_{E} }}{1 - 2\nu }\left( \frac{h}{L} \right)^{2} ,\quad A_{14} = \frac{{\Delta_{E} }}{1 - 2\nu }\left( {\frac{\tau }{{\tau_{1} }}} \right)\left( \frac{h}{L} \right)^{2} ,\quad A_{15} = \frac{{3\Delta_{E} }}{1 - 2\nu }\left( \frac{h}{L} \right)^{2} \left( {\frac{\zeta }{L}} \right)^{2} . \hfill \\ \end{gathered}$$
(35)

4 Case study

4.1 Boundary conditions and loading

In the current work, a case study is undertaken on simply supported (SS) Timoshenko nanobeams. The axial distributed force \(f\left( {x,t} \right)\), external bending moment \(\overline{M}\) and external shear force \(\overline{Q}\) are set to zero. According to classical boundary conditions (21b) and (21c), and nonclassical boundary conditions (22b) and (22c), the end conditions of a simply supported Timoshenko nanobeam at \(x = 0\) and \(x = L\) (equivalently at \(x^{*} = 0\) and \(x^{*} = 1\)) are given by the following:

$$w = M = Q^{\left( 1 \right)} = \frac{\partial \varphi }{{\partial x}} = 0.$$
(36)

In view of Eq. (20b), one can write the following:

$$\frac{{\partial^{2} M}}{{\partial x^{2} }} = \frac{\partial Q}{{\partial x}} - \rho I\frac{{\partial^{3} \varphi }}{{\partial x\partial t^{2} }}.$$
(37)

On the other hand, utilization of Eq. (20c) leads to the following:

$$\frac{\partial Q}{{\partial x}} = - q + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }}.$$
(38)

By substituting Eq. (38) into (37) and inserting the result into Eq. (24b), the following relation is derived for bending moment \(M\):

$$M = \left( {ea} \right)^{2} \left[ { - q + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} - \rho I\frac{{\partial^{3} \varphi }}{{\partial x\partial t^{2} }}} \right] - EI\left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\frac{\partial \varphi }{{\partial x}} - \left[ {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]M_{T} .$$
(39)

With the aid of Eqs. (1), (14a) and (14b), one can obtain:

$$Q = Q^{\left( 0 \right)} - \frac{{\partial Q^{\left( 1 \right)} }}{\partial x} \quad {\text{with}}\quad Q^{\left( 0 \right)} = \int_{A} {\sigma_{xz} dA} .$$
(40)

In addition, by employing Eqs. (2a), (2b) and (5), the following relations are derived [49]:

$$\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\sigma_{xz} = G\gamma_{xz}$$
(41a)
$$\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]\sigma_{xz}^{\left( 1 \right)} = l^{2} G\frac{{\partial \gamma_{xz} }}{\partial x}.$$
(41b)

According to definitions of \(Q^{\left( 0 \right)}\) and \(Q^{\left( 1 \right)}\), by using the relations above and considering the shear correction factor, one can get the following:

$$\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]Q^{\left( 0 \right)} = K_{s} GA\left( {\frac{\partial w}{{\partial x}} - \varphi } \right)$$
(42a)
$$\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]Q^{\left( 1 \right)} = l^{2} K_{s} GA\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{\partial \varphi }{{\partial x}}} \right).$$
(42b)

Comparison between (42a) and (42b) results in the following relation:

$$\frac{{\partial Q^{\left( 0 \right)} }}{\partial x} = \frac{1}{{l^{2} }}Q^{\left( 1 \right)} .$$
(43)

Rearrangement of Eq. (42b) gives the following:

$$\frac{{\partial^{2} Q^{\left( 1 \right)} }}{{\partial x^{2} }} = \frac{1}{{\left( {ea} \right)^{2} }}\left[ {Q^{\left( 1 \right)} - l^{2} K_{s} GA\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{\partial \varphi }{{\partial x}}} \right)} \right].$$
(44)

Substitution of Eq. (40) into motion Eq. (42) yields the following:

$$\frac{{\partial Q^{\left( 0 \right)} }}{\partial x} - \frac{{\partial^{2} Q^{\left( 1 \right)} }}{{\partial x^{2} }} = - q + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }}.$$
(45)

At last, by inserting Eqs. (43) and (44) into (45), one can attain the following explicit relation for \(Q^{\left( 1 \right)}\):

$$Q^{\left( 1 \right)} = \frac{{\left( {ea} \right)^{2} l^{2} }}{{\left( {ea} \right)^{2} - l^{2} }}\left[ { - q + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} - \frac{{l^{2} }}{{\left( {ea} \right)^{2} }}K_{s} GA\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{\partial \varphi }{{\partial x}}} \right)} \right].$$
(46)

It is also assumed that the nanobeam is under the exponentially time-decaying transverse load \(q\left( {x,t} \right) = q_{0} e^{ - \Omega t}\). By considering the normalized form of \(q\) defined in Eq. (33), one can write as follows:

$$q^{*} \left( {x^{*} ,t^{*} } \right) = q_{0}^{*} e^{{ - \Omega \tau_{1} t^{*} }} .$$
(47)

in which \(q_{0}^{*}\) can be expanded by way of the Fourier series as follows:

$$q_{0}^{*} = \frac{{q_{0} L^{3} }}{EI} = \sum\nolimits_{n = 1}^{\infty } {Q_{n} \sin \left( {n\pi x^{*} } \right)} \quad {\text{with}}\quad 0 \le x^{*} \le 1.$$
(48)

The quantity \(Q_{n}\) can be determined by the following relation:

$$Q_{n} = 2\int_{0}^{1} {q_{0}^{*} \sin \left( {n\pi x^{*} } \right)dx^{*} } = \frac{{4q_{0}^{*} }}{n\pi }\quad {\text{for}}\quad n = 1, 3, 5, \ldots .$$
(49)

The temperature of end edges of nanobeam is supposed to be constant. So, in view of definition (25b), by imposing isothermal condition at \(x = 0\) and \(x = L\) (equivalently at \(x^{*} = 0\) and \(x^{*} = 1\)), we have the following:

$$M_{T} = 0.$$
(50)

4.2 Analytical solution

According to the Navier method, the following expansions are adopted as the solutions of unknown functions \(\varphi^{*}\), \(w^{*}\) and \(M_{T}^{*}\):

$$\varphi^{*} \left( {x^{*} ,t^{*} } \right) = \sum\nolimits_{n = 1}^{\infty } {\Phi_{n} \left( {t^{*} } \right)\cos \left( {n\pi x^{*} } \right)}$$
(51a)
$$w^{*} \left( {x^{*} ,t^{*} } \right) = \sum\nolimits_{n = 1}^{\infty } {W_{n} \left( {t^{*} } \right)\sin \left( {n\pi x^{*} } \right)}$$
(51b)
$$M_{T}^{*} \left( {x^{*} ,t^{*} } \right) = \sum\nolimits_{n = 1}^{\infty } {M_{n} \left( {t^{*} } \right)\sin \left( {n\pi x^{*} } \right)} ,$$
(51c)

in which \(0 \le x^{*} \le 1\) and \(t^{*} \ge 0\). By considering the relations of \(M\) and \(Q^{\left( 1 \right)}\) presented in Eqs. (39) and (46), and the Fourier sine series of \(q_{0}^{*}\) given in Eq. (48), it can be readily seen that the series solution satisfies all mechanical boundary conditions (36) and thermal boundary conditions (50). Substitution of Eqs. (48) and (51a)–(51c) into normalized governing Eqs. (34a)–(34c) yields the following system of ordinary differential equations:

$$\left[ {A_{1} \left( {n\pi } \right)^{4} + A_{2} \left( {n\pi } \right)^{2} + A_{3} } \right]\Phi_{n} - \left[ {A_{4} \left( {n\pi } \right)^{3} + A_{3} \left( {n\pi } \right)} \right]W_{n} - \left[ {A_{1} \left( {n\pi } \right)^{3} + A_{5} \left( {n\pi } \right)} \right]M_{n} = - \left[ {A_{6} \left( {n\pi } \right)^{2} + A_{5} } \right]\frac{{\partial^{2} \Phi_{n} }}{{\partial t^{*2} }}$$
(52a)
$$\left[ {A_{4} \left( {n\pi } \right)^{3} + A_{3} \left( {n\pi } \right)} \right]\Phi_{n} - \left[ {A_{4} \left( {n\pi } \right)^{4} + A_{3} \left( {n\pi } \right)^{2} } \right]W_{n} + A_{5} Q_{n} e^{{ - \Omega \tau_{1} t^{*} }} = \left[ {A_{7} \left( {n\pi } \right)^{2} + 1} \right]\frac{{\partial^{2} W_{n} }}{{\partial t^{*2} }}$$
(52b)
$$\begin{aligned} \left[ {A_{8} \left( {n\pi } \right)^{2} + A_{9} } \right]M_{n} & = - A_{10} \frac{{\partial^{2} M_{n} }}{{\partial t^{*2} }} - \left[ {A_{12} \left( {n\pi } \right)^{2} + A_{11} } \right]\frac{{\partial M_{n} }}{{\partial t^{*} }} \\ & - A_{14} \left( {n\pi } \right)\frac{{\partial^{2} \Phi_{n} }}{{\partial t^{*2} }} - A_{13} \left( {n\pi } \right)\frac{{\partial \Phi_{n} }}{{\partial t^{*} }} - A_{15} \left( {n\pi } \right)^{3} \frac{{\partial \Phi_{n} }}{{\partial t^{*} }}. \\ \end{aligned}$$
(52c)

To determine the unknown functions \(\Phi_{n}\), \(W_{n}\) and \(M_{n}\), by applying the Laplace transform to Eqs. (52a)–(52c) with respect to \(t^{*}\) and assuming homogeneous initial conditions, the ordinary differential equations are converted to the algebraic ones as follows:

$$B_{1} \phi_{n} \left( s \right) - B_{2} w_{n} \left( s \right) - B_{3} m_{n} \left( s \right) = 0$$
(53a)
$$B_{2} \phi_{n} \left( s \right) - B_{4} w_{n} \left( s \right) = - B_{5} Q_{n}$$
(53b)
$$B_{6} \phi_{n} \left( s \right) + B_{7} m_{n} \left( s \right) = 0,$$
(53c)

where \(s\) is the variable of Laplace transform, and functions \(\phi_{n} \left( s \right)\), \(w_{n} \left( s \right)\) and \(m_{n} \left( s \right)\) represent the Laplace transform of functions \(\Phi_{n} \left( {t^{*} } \right)\), \(W_{n} \left( {t^{*} } \right)\) and \(M_{n} \left( {t^{*} } \right)\), respectively. In addition, the coefficients \(B_{1}\) to \(B_{7}\) are obtained through the following relations:

$$\begin{gathered} B_{1} = C_{1} + C_{2} s^{2} ,\quad B_{2} = C_{3} ,\quad B_{3} = C_{4} ,\quad B_{4} = C_{5} + C_{6} s^{2} , \hfill \\ B_{5} = C_{7} /\left( {s + \Omega \tau_{1} } \right),\quad B_{6} = C_{8} s + C_{9} s^{2} ,\quad B_{7} = C_{10} + C_{11} s + C_{12} s^{2} . \hfill \\ \end{gathered}$$
(54)

in which

$$\begin{gathered} C_{1} = A_{1} \left( {n\pi } \right)^{4} + A_{2} \left( {n\pi } \right)^{2} + A_{3} ,\quad C_{2} = A_{6} \left( {n\pi } \right)^{2} + A_{5} ,\quad C_{3} = A_{4} \left( {n\pi } \right)^{3} + A_{3} \left( {n\pi } \right), \hfill \\ C_{4} = A_{1} \left( {n\pi } \right)^{3} + A_{5} \left( {n\pi } \right),\quad C_{5} = A_{4} \left( {n\pi } \right)^{4} + A_{3} \left( {n\pi } \right)^{2} ,\quad C_{6} = A_{7} \left( {n\pi } \right)^{2} + 1, \hfill \\ C_{7} = A_{5} ,\quad C_{8} = A_{13} \left( {n\pi } \right) + A_{15} \left( {n\pi } \right)^{3} ,\quad C_{9} = A_{14} \left( {n\pi } \right), \hfill \\ C_{10} = A_{8} \left( {n\pi } \right)^{2} + A_{9} ,\quad C_{11} = A_{12} \left( {n\pi } \right)^{2} + A_{11} ,\quad C_{12} = A_{10} . \hfill \\ \end{gathered}$$
(55)

By solving the system of algebraic Eqs. (53a)–(53c), one can achieve the solution of functions \(\phi_{n} \left( s \right)\), \(w_{n} \left( s \right)\) and \(m_{n} \left( s \right)\) as follows:

$$\phi_{n} \left( s \right) = \frac{{a_{0} + a_{1} s + a_{2} s^{2} }}{{\left( {s + \Omega \tau_{1} } \right)\left( {d_{0} + d_{1} s + d_{2} s^{2} + d_{3} s^{3} + s^{4} + d_{5} s^{5} + d_{6} s^{6} } \right)}}Q_{n}$$
(56a)
$$w_{n} \left( s \right) = \frac{{b_{0} + b_{1} s + b_{2} s^{2} + b_{3} s^{3} + b_{4} s^{4} }}{{\left( {s + \Omega \tau_{1} } \right)\left( {d_{0} + d_{1} s + d_{2} s^{2} + d_{3} s^{3} + d_{4} s^{4} + d_{5} s^{5} + d_{6} s^{6} } \right)}}Q_{n}$$
(56b)
$$m_{n} \left( s \right) = - \frac{{c_{1} s + c_{2} s^{2} }}{{\left( {s + \Omega \tau_{1} } \right)\left( {d_{0} + d_{1} s + d_{2} s^{2} + d_{3} s^{3} + d_{4} s^{4} + d_{5} s^{5} + d_{6} s^{6} } \right)}}Q_{n} ,$$
(56c)

where

$$a_{0} = C_{3} C_{7} C_{10} ,\quad a_{1} = C_{3} C_{7} C_{11} ,\quad a_{2} = C_{3} C_{7} C_{12}$$
(57a)
$$\begin{gathered} b_{0} = C_{1} C_{7} C_{10} ,\quad b_{1} = C_{1} C_{7} C_{11} + C_{4} C_{7} C_{8} ,\quad b_{2} = C_{1} C_{7} C_{12} + C_{2} C_{7} C_{10} + C_{4} C_{7} C_{9} , \hfill \\ b_{3} = C_{2} C_{7} C_{11} ,\quad b_{4} = C_{2} C_{7} C_{12} \hfill \\ \end{gathered}$$
(57b)
$$c_{1} = C_{3} C_{7} C_{8} ,\quad c_{2} = C_{3} C_{7} C_{9}$$
(57c)
$$\begin{gathered} d_{0} = C_{1} C_{5} C_{10} - C_{3}^{2} C_{10} ,\quad d_{1} = C_{1} C_{5} C_{11} + C_{4} C_{5} C_{8} - C_{3}^{2} C_{11} , \hfill \\ d_{2} = C_{1} C_{5} C_{12} + C_{1} C_{6} C_{10} + C_{2} C_{5} C_{10} + C_{4} C_{5} C_{9} - C_{3}^{2} C_{12} , \hfill \\ d_{3} = C_{1} C_{6} C_{11} + C_{2} C_{5} C_{11} + C_{4} C_{6} C_{8} , \hfill \\ d_{4} = C_{1} C_{6} C_{12} + C_{2} C_{5} C_{12} + C_{2} C_{6} C_{10} + C_{4} C_{6} C_{9} . \hfill \\ \end{gathered}$$
(57d)

By taking the inverse Laplace transform of \(\phi_{n} \left( s \right)\), \(w_{n} \left( s \right)\) and \(m_{n} \left( s \right)\), one can arrive at the solution of \(\Phi_{n} \left( {t^{*} } \right)\), \(W_{n} \left( {t^{*} } \right)\) and \(M_{n} \left( {t^{*} } \right)\) in the time domain. Finally, by inserting these functions into Eqs. (51a)-(51c), the dimensionless dynamic response of nanobeam is utterly specified.

5 Numerical results and discussion

In this section, several graphical data are given to evaluate size-dependent thermoelastic vibrations of Timoshenko nanobeams. First, for the sake of assessment of the validity of presented formulation, a comparison study is conducted between the results of this study and those reported in the literature. Next, by presenting several numerical results, a detailed parametric study is performed to illuminate the impact of some key factors like strain gradient length scale, structural and thermal nonlocal parameters on thermoelastic response of Timoshenko nanobeams.

5.1 Comparison study

To the best of authors’ knowledge, there are no experimental data useful for direct validation of the presented formulation. In order to check the validity of presented model, a comparison study is carried out between the findings of this study with those of the research of Taati et al. [40]. In that work, coupled thermoelastic oscillations of Timoshenko microbeams have been examined in the framework of modified strain gradient theory (MSGT) and LS heat conduction model. To compare the outcomes of this article with those of [40], thermoelastic deflection of a Timoshenko beam made of silicon (Si) is considered according to classical continuum theory and LS model. Mechanical and thermal constants of silicon are listed in Table 1 for environmental temperature \(T_{0} = 293 K\). The conditions of the beam analyzed in this article are similar to those of the beam examined by Taati et al. [40], except that in [40] it has been supposed that the beam is under transverse load \(q\left( {x,t} \right) = q_{0} \delta \left( t \right)\). Hence, the function \(w_{n} \left( s \right)\) becomes as follows:

$$w_{n} \left( s \right) = \frac{{b_{0} + b_{1} s + b_{2} s^{2} + b_{3} s^{3} + b_{4} s^{4} }}{{d_{0} + d_{1} s + d_{2} s^{2} + d_{3} s^{3} + d_{4} s^{4} + d_{5} s^{5} + d_{6} s^{6} }}Q_{n} .$$
(58)
Table 1 Mechanical and thermal properties of silicon at \(T_{0} = 293 K\) [40]
Full size table

In addition, the dimensionless deflection introduced in [40] has the following form:

$$\tilde{w} = \frac{w}{h}.$$
(59)

Comparison between the definitions of dimensionless deflection in Eqs. (33) and (59) gives the following:

$$\tilde{w} = \left( \frac{L}{h} \right)w^{*} .$$
(60)

The shear correction factor in [40] has been assumed to be \(K_{s} = 1\). By considering \(L/h = 10\) and \(q_{0} = EAh/L^{2}\), the dynamic dimensionless midspan deflection (\(\tilde{w}\)) predicted by Taati et al. [40] and estimated via presented formulation is depicted in Fig. 2. It is readily observed that the result extracted on the basis of developed formulation in this article is in close agreement with that reported by Taati et al. [40].

Fig. 2
figure 2

Comparison study on dynamic dimensionless deflection of midspan of a Timoshenko beam

Full size image

5.2 Parametric study

In this section, several numerical examples are provided to appraise the sensitivity of thermoelastic vibrations of Timoshenko nanobeams to nonlocal parameter \(ea\), strain gradient length scale parameter \(l\) and thermal nonlocal parameter \(\zeta\). Results are presented for a Timoshenko nanobeam made of silicon with fixed thickness \(h = 2{\text{ nm}}\) and aspect ratio \(L/h = 10\). The phase lag of silicon is taken as \(\tau = 3.88 ps\) [50]. The shear correction factor is also chosen as \(K_{s} = 5/6\). In addition, the coefficients that appeared in the relation of transverse load \(q\left( {x,t} \right) = q_{0} e^{ - \Omega t}\) are supposed to be equal to \(\Omega = 4*10^{10}\) and \(q_{0} = EI/L^{3}\). To our knowledge, no experimental data have been reported in the open literature for structural nonlocal parameter \(ea\) of different materials. However, by fitting the results predicted by molecular dynamics (MD) simulation and theoretical method, some researchers have presented different ranges \(\left( {0 \le \left( {ea} \right)^{2} \le 4{\text{ nm}}^{2} } \right)\) for a type of single-walled carbon nanotube (SWCNT) [51]. In another research, Wang and Wang [52] estimated that \(ea\) should be smaller than \(2 \;{\text{nm}}\) for a SWCNT. Furthermore, by comparison between the results of nonlocal model [53] and MD simulation [54] for buckling analysis of a multi-walled CNT, the value of \(\left( {ea} \right)^{2}\) has been reported as \(0.82{\text{ nm}}^{2}\). In this study, based on a conservative approximation, it is assumed that the structural nonlocal parameter varies in the interval of \(0\) to \(2 {\text{nm}}\). This range of \(ea\) has been utilized by many researchers. Similar to structural nonlocal parameter \(ea\), the strain gradient length scale parameter \(l\) can be specified by matching the results of theoretical methods with those of MD simulation [55]. For a (15,15) SWCNT, by comparing the results of NSGT model [56] and MD simulation [57], the value of \(l\) has been approximated as \(0.235 \;{\text{nm}}\). In a similar manner, for a (10,10) SWCNT, the magnitude of \(l\) has been estimated as \(0.610\;{\text{ nm}}\) [58]. Moreover, in many studies about NSGT it has been considered that the strain gradient length scale parameter \(l\) varies in the interval \(0 \le l \le 2 \;{\text{nm}}\). Accordingly, in this work, \(l\) is supposed to be in the range of \(0\) and \(2\; {\text{nm}}\). As for thermal nonlocal parameter \(\zeta\), which can be characterized by the phonon mean free path, different values have been reported for various materials. For instance, thermal nonlocal parameter of silicon is about \(20 - 100\; {\text{nm}}\) [59, 60]. The average value of thermal nonlocal parameter of graphene at room temperature has also been estimated as \(100 \;{\text{nm}}\) [61]. In another investigation, by conducting MD simulations, thermal nonlocal parameter of graphene has been reported to be equal to \(80 \;{\text{nm}}\) [62]. According to these values, except where otherwise noted, the thermal nonlocal parameter is assumed to be \(\zeta = 50 \;{\text{nm}}\). On the basis of foregoing explanations, it seems that the range and order of magnitude considered for structural and thermal scale parameters (i.e. \(ea\), \(l\) and \(\zeta\)) is appropriate and makes physical sense.

5.2.1 Thermoelastic coupling effect

Figure 3 demonstrates the dimensionless midspan deflection of Timoshenko nanobeam versus the dimensionless time with and without considering thermoelastic coupling effect. Note that in order to disregard the impact of thermoelastic coupling, it is sufficient to set thermal expansion coefficient \(\alpha\) to zero in present formulation. The curves are plotted according to the classical theory (CT) of continuum. Although due to exponentially decaying load, the amplitude of dynamic deflection of both coupled and uncoupled cases lessens with time, it is obvious that as a result of energy dissipation caused by TED, the damping rate of vibration amplitude for the coupled case is much more than that for the uncoupled one, so that by taking into account thermoelastic coupling effect, the dynamic deflection reaches its quasi-steady state solution in a shorter time. This issue implies the significance of considering thermoelastic coupling effect in assessment of dynamical behavior of small-sized structures.

Fig. 3
figure 3

Dimensionless deflection of midspan of nanobeam versus dimensionless time a without thermoelastic coupling effect, b with thermoelastic coupling effect

Full size image

5.2.2 Effect of nonlocal and strain gradient length scale parameters

In Fig. 4, the dynamic dimensionless deflection at the midspan of nanobeam in the dimensionless time range 0–100 is displayed for different values of nonlocal and strain gradient length scale parameters. As it is observed, with the increase of \(l\), the amplitude of deflection diminishes, and the vibration frequency becomes greater. This result is compatible with the stiffness hardening aspect of NSGT at small scales. It is also apparent that as the value of \(ea\) gets larger, the amplitude of deflection ascends, while the frequency of oscillation decreases. This issue affirms the stiffness softening characteristic of NSGT. Accordingly, these curves reveal that NSGT is able to reflect both stiffness softening and stiffness enhancement feature of small-sized structures.

Fig. 4
figure 4

Dynamic dimensionless deflection of midspan of nanobeam a for different values of strain gradient length scale parameter (\(ea = 1 \;{\text{nm}}\)) , b for different values of nonlocal parameter (\(l = 1 \;{\text{nm}}\))

Full size image

Given the short dimensionless time range, attenuation of deflection is barely distinguished from Fig. 4. To better illustrate the reduction of deflection, it is prevalent that the peak values of dimensionless deflection are plotted in the form of envelope curves in a longer time interval. Figure 5 depicts the envelope curves of dimensionless midspan deflection for various values of nonlocal and strain gradient length scale parameters in the dimensionless time range 0–109. Similar to Fig. 4, these curves signify two absolutely different attributes of structures at small scales, that is by increasing the amount of \(l\) and stiffness enhancement, the time required to arrive at quasi-steady state response descends, while the increase of the amount of \(ea\) lengthens this time due to stiffness softening effect.

Fig. 5
figure 5

Peak values of dimensionless midspan dynamic deflection a for different values of strain gradient length scale parameter (\(ea = 1 \;{\text{nm}}\)), b for different values of nonlocal parameter (\(l = 1 \;{\text{nm}}\))

Full size image

Figure 6 demonstrates the impact of nonlocal and strain gradient length scale parameters on transient dimensionless thermal moment at the midspan of nanobeam. From these curves, one can realize that parameters \(l\) and \(ea\) have contrary influence on thermal moment, so that for higher values of \(l\), the amplitude of thermal moment is smaller, whereas the increase of amount of \(ea\) enlarges the amplitude of thermal moment.

Fig. 6
figure 6

Transient dimensionless thermal moment of midspan of nanobeam a for different values of strain gradient length scale parameter (\(ea = 1\;{\text{ nm}}\)), b for different values of nonlocal parameter (\(l = 1 nm\))

Full size image

Figures 7 and 8 compare the dynamic dimensionless deflection at the midspan of nanobeam predicted by different elasticity theories. As it is clear, depending on the relative values of two scale parameters of NSGT, the nonclassical model of Timoshenko nanobeam can represent either softening or hardening behavior in comparison with the classical one, so that the nanobeam exhibits the highest and lowest stiffness corresponding to SGT and NT, respectively. Indeed, by reduction of scale parameter ratio \(l/ea\), the amplitude of deflection gets greater, the frequency of vibration diminishes, and the nanobeam requires a longer time to reach its quasi-steady state response. This means that when the strain gradient effect prevails, i.e. \(l > ea\), the stiffness hardening aspect of NSGT becomes more influential, while as the nonlocal effect is dominant, i.e. \(l < ea\), the stiffness softening aspect of NSGT preponderates.

Fig. 7
figure 7

Dynamic dimensionless deflection of midspan on the basis of SGT (\(l = 2\; {\text{nm}}\)), NSGT (\(l > ea\)) (\(l = 2 \;{\text{nm}}\) and \(ea = 1 \;{\text{nm}}\)), CT, NSGT (\(l > ea\)) (\(l = 1 \;{\text{nm}}\) and \(ea = 2 \;{\text{nm}}\)), and NT (\(ea = 2 \;{\text{nm}}\))

Full size image
Fig. 8
figure 8

Envelope curves of dimensionless midspan dynamic deflection in the framework of SGT (\(l = 2\;{\text{ nm}}\)), NSGT (\(l > ea\)) (\(l = 2 \;{\text{nm}}\) and \(ea = 1 \;{\text{nm}}\)), CT, NSGT (\(l > ea\)) (\(l = 1 \;{\text{nm}}\) and \(ea = 2\; {\text{nm}}\)) and NT (\(ea = 2\; {\text{nm}}\))

Full size image

5.2.3 Effect of thermal nonlocal parameter

With the intention of evaluating the thermal nonlocal effect on thermoelastic vibrations of a Timoshenko nanobeam, the alteration of dynamic dimensionless deflection at the midspan is plotted in Figs. 9 and 10. Classical elasticity theory is employed to provide these curves. As it is seen, at the beginning of vibration, the response determined by GK model almost corresponds to that estimated by CTE model. As time passes, the discrepancy between the predictions of GK and CTE models becomes more noticeable, so that GK model approximates larger values for the amplitude of deflection in comparison with CTE model. This matter betokens that by inclusion of thermal nonlocal effect, energy loss stemmed from thermoelastic coupling lessens. It is also clear that for larger magnitudes of thermal nonlocal parameter \(\zeta\), nanobeam exhibits greater amplitude of deflection. Note that the duration of vibration in the curves of Fig. 9 is equal. As another outcome, one can observe that taking into account thermal nonlocal parameter does not lead to a remarkable change in the frequency of vibration. The envelope curves of dimensionless deflection plotted in Fig. 10 confirm that CTE model estimates more energy dissipation in comparison with GK model, so that the CTE model of nanobeam reaches its quasi-steady state response more swiftly than the GK model of nanobeam.

Fig. 9
figure 9

Dynamic dimensionless deflection of midspan of nanobeam predicted by CTE and GK models in the dimensionless time interval a 0–100, b 50,000,000–50,000,100

Full size image
Fig. 10
figure 10

Envelope curves of dimensionless midspan dynamic deflection in the framework of CTE and GK models

Full size image

6 Concluding remarks

In this article, by incorporation of small-scale effect within the constitutive and heat conduction relations via nonlocal strain gradient theory (NSGT) and Guyer–Krumhansl (GK) heat conduction model, a size-dependent generalized thermoelasticity model has been developed to appraise thermoelastic vibrations of Timoshenko nanobeams. In the first step, the nonclassical equations of motion and heat conduction have been extracted. Then, by introducing some dimensionless parameters, normalized forms of governing coupled thermoelastic equations have been derived. For the sake of analytically solving this system of partial differential equations, the Laplace transform has been utilized. Several illustrative numerical examples have been presented to illuminate the impact of various factors like nonlocal parameter, strain gradient length scale parameter, and thermal nonlocal parameter on thermoelastic vibrations of a simply supported Timoshenko nanobeam under dynamic load. The outline of findings of present study can be given as follows:

  • Owing to energy loss induced by thermoelastic damping, taking into account thermoelastic coupling effect attenuates the amplitude of deflection and time required to reach the quasi-steady state situation.

  • For higher values of strain gradient length scale parameter \(l\), the stiffness enhancement aspect of NSGT strengthens, so that nanobeam exhibits smaller amplitude of deflection and larger frequency of vibration.

  • With the increase of nonlocal parameter \(ea\), the stiffness softening feature of nanobeam intensifies in such a way that the amplitude of deflection takes greater values, the frequency of vibration descends, and the time needed to arrive at the quasi-steady state response increases.

  • According to relative magnitudes of two scale parameters \(l\) and \(ea\), NSGT can represent either stiffness softening or stiffness hardening characteristic of nanobeam, so that when \(l > ea\) the stiffness enhancement aspect prevails, and when \(l < ea\) the stiffness softening feature becomes dominant.

  • Although the results of CTE and GK models are approximately identical at the beginning of vibration, the difference between the predictions of these two models enlarges over time, so that on account of more energy dissipation caused by TED, the CTE model of nanobeam tends to its quasi-steady state situation more rapidly than the GK model of nanobeam.