Design of super twisting disturbance observer-based controller for magnetic levitation system

Abstract

The magnetic levitation systems are mismatched systems with inherent unstable nonlinear dynamics. This work has examined a control strategy that control and stabilize the magnetic levitation system from difficult start-up circumstances to the desired operating points in presence of uncertainties and disturbances. A cascaded super twisting disturbance observer (STDO)-based sliding mode controller is devised for both the electrical and electromechanical loops of the system. The overall stability of the system has been established. The performance of suggested control scheme is evaluated using simulation and experimentation. The performance of the suggested controller is compared with a classic proportional integral and derivative (PID) controller and a state and disturbance observer (SDO)-based controller. Performance criteria used for comparison are Integrated Squared Error(ISE), Integrated Absolute Error(IAE) and Time Weighted Absolute Error(ITAE). The suggested super twisting disturbance observer-based control scheme outperforms the other two and is able to control and stabilize magnetic levitation system in presence of parametric uncertainties and disturbances with smooth control.

1 Introduction

Magnetic Levitation (Maglev) systems employ electromagnetic force to keep ferromagnetic items in the proper position in the air. An electromagnetic field created by maglev systems provides the electromagnetic force necessary for this technology. As a result of this capability, friction is removed, and material wear is decreased. Ground transportation has profited greatly from maglev systems, which may be used as active suspension systems [1, 2]. They were regarded and used as the basic foundation for the development of magnetic train technology [3, 4]. Maglev systems may be used in a variety of applications, including vibration isolation in sensitive equipment and high precision chip plate placement in photo-lithography [5] . When the system model is linearized in a small region, linear controllers are adequate, but they do not account for nonlinearities in the real system model. In contrast, nonlinear controllers regulate the system’s dynamics globally rather than locally, allowing for real-time control. The search for a good topology for developing optimum nonlinear controllers will never stop, and the best one will meet the desired performance in a timely and promising manner. When choosing a nonlinear controller, the most important thing to evaluate is whether it provides a quick and efficient dynamic response, such as a short rising time, a short settling time, a decreased peak value, a low overshoot or undershoot, and a small steady-state error. Because real-world systems are subject to model uncertainty and external shocks, steady-state error is a possibility [6]. The nonlinear controller should be dealt with as smoothly and effectively as feasible. The bulk of nonlinear controllers perform poorly or not at all in the presence of uncertainty and disturbances. As a result, the primary goal of this study is to create a robust nonlinear controller for controlling the maglev system that can effectively deal with uncertainties and disturbances while maintaining optimal dynamic behavior.

The design of control systems for Magnetic levitation and magnetic levitation-based systems is a well established and much addressed topic in the literature. An integral type control was built in [7], for bringing the magnetic bearing systems rotor to desired point and maintaining it at the appropriate location. The regulation of the maglev system was the subject of a comparative control analysis published in [8]. Experiments were carried out in order to compare the sliding mode controller (SMC) with a conventional controller. Further SMC strategies for the control of maglev and the systems based on maglev were presented in [9] and [10]. The employment of SMCs [9], static and dynamic type, ensured that the maglev system was controlled asymptotically while dealing with friction force and other unknowns. Intelligent SMC based on a radial basis function (RBF) network in [10] provides position tracking for the maglev system. Experiments in [11] demonstrated the performance of nonlinear adaptive and robust controllers on the regulation of the maglev system. In [12] a self-tuning stabilizing adaptive controller is proposed for the control of the repelling maglev system. In the mentioned investigation, the developed controller offered overall system stability and regulating precision without requiring a precise understanding of numerous components. Walter Barie and John Chiasson discuss how to construct and test nonlinear and linear state space controllers using velocity observers in [13]. The control systems used in the study were both based on linearized system models. The maglev system’s location tracking problem was solved utilizing a resilient nonlinear control architecture by Yang et al. [14]. Physical parameter uncertainties, as well as modeling mistakes generated by these uncertainties, were accounted for in the control design, and the controller was built to tolerate them. The maglev system was controlled with proportional integral derivative (PID) type SMC controller as well as PID type dynamic SMC controllers in [15] . Another PID control solution to deal with the imbalanced vibration difficulties of an active magnetic bearing system was provided in [16]. To improve its efficiency, the described PID controller included a fuzzy gain tuning mechanism. Over the previous ten years, this issue has remained popular. The work presented in [17], mentioned the design of a PID controller enhanced with a velocity observer and a nonlinear feed forward technique to increase control quality and motion stability of a laboratory maglev system. A mix of linear quadratic Gaussian control, fault-tolerant control and multi-objective optimization were used to control an electromagnetic suspension system in [18]. In [19], a PID control based on real-time particle swarm optimization (PSO) was used to provide stability, balance, and propulsive placement for a maglev transit system. As suggested by Lin et al. in [20], another control method combination is made feasible using the PSO and the PID. An adaptive PID controller is integrated with a PSO approach in this study to give the best learning rates for the adaptation rule, which work assured maglev system position monitoring. An adaptive control approach for the maglev system regulation was presented in [21], based on an online algebraic estimate of system parameters, linearization, and extended proportional-integral control. In [22], position tracking for a maglev suspension system was implemented using a nonlinear disturbance observer-based design of a robust nonlinear controller, whereas exponential tracking control of the maglev system was described in [23]. In [24], based on the back-stepping approach, a cognitive online auto-tune algorithm, a unique position tracking control algorithm, for a maglev system was developed. During the previous decade, the SMC technique has remained popular for controlling maglev systems.

Two of the different SMC examples of maglev control systems that can be found in the literature are the cascade structured SMC designs given in [5] and [25]. One more cascaded SMC approach based on two time-scale observer is proposed in [26]. Fractional order PID to ensure maglev system control is designed in [27]. In the aforementioned work, to accomplish fractional order PID control, model reference adaptive control was used in a closed-loop state and PID included a disturbance rejection mechanism. According to Uroš Sadek et al. [28], an upgraded adaptive fuzzy back-stepping controller was created for controlling the maglev system even in presence of uncertainty including parametric and structural. To regulate maglev systems, Baris Bidikli and Alper Bayrak [29] created and utilized a self-tuning robust integral of signum of error (RISE)-based controller in a cascade control system. The electromagnetic levitation system was controlled with a robust control architecture based on approximate feedback linearization in [30]. In [31], Fatih Adıgüzel et al. proposed an adaptive back-stepping control solution aimed to compensate for an iron ball’s inaccuracy in position monitoring in a maglev system. To obtain a high-performance step response of the maglev system, Deepti Khimani et al. [32] built a nonlinear state feedback controller architecture. Humaidi in [33] proposed controllers for magnetic levitation systems based on linear and nonlinear active disturbance rejection. For magnetic suspension control of a low-speed maglev train, Yougang Sun et al. [34] developed a PID controller and an adaptive neural fuzzy SMC. For maglev system control, Sun et al. [35] has proposed SMC based on an exponential reaching law with RBF neural network estimator. For the nonlinear suspension system of maglev vehicles, Chen et al. [36] presented a unique RBF network approximation-based sliding mode adaptive controller architecture. When the popularity of the issue is taken into account, these examples may readily be broadened. The inspiration for this work came from a rigorous examination and evaluation of several controllers for the control of MagLev systems that were given in the literature. Issues in the controllers that are now in use are dissected and studied and solutions to these challenges are suggested. In order to construct an uncertainty and disturbance compensation approach that decreases the trade-off between performance and stability while boosting robustness, SMC is the most extensively used in the literature to handle the control issues of Maglev. While going through all these controllers mentioned in the literature, one can understand that SMC-based controllers are able to tackle uncertainties and external disturbances. The well-known problem of SMC is chattering which is not suitable for such applications. Many techniques are mentioned in the literature to address the issue of chattering. A super twisting algorithm(STA) has been identified as one of the most powerful second-order continuous SMCs to tackle the same [37]. It was first published in [38], and it has since been used in a number of applications [39]. STA is a second-order sliding mode controller that can be used to control any generalized system using first-order sliding variable control. It has the advantage of just requiring information about the output sliding variable. It allows for and simultaneously gives convergence to the origin in a short amount of time. STA gives a smoother control effort due to the reduced chattering [40]. To make use of STA’s smoothing capabilities, this work employs STA as an uncertainty and disturbance observer [41] and SMC as the primary controller.

The following are the primary contributions of the work.

• 1. The performance of a robust cascaded super twisting disturbance observer based SMC control technique is validated for model uncertainties and disturbance.

• 2. The developed control technique is used for maglev position control, and it perfectly matches the required trajectory with quicker convergence.

• 3. The use of the super twisting principle generates chattering free, smooth and continuous signal.

• 4. On the basis of the time-domain performance criteria , the results of STDO-based SMC controller are compared with SDO-based SMC and traditional PID controllers. STDO-based controller outperforms the others.

• 5. Extensive quantitative simulation and hardware experiments are used to prove the efficacy of the suggested method.

The robust control strategy has certainly been widely used for the control of a wide range of systems to cope with uncertainty, parametric and structural both, which are important issues in maglev system management. The input voltage is utilized to create the required electromagnet current in the electrical subsystem, which is then used to move the ferromagnetic material to the appropriate location. The required electromagnet current is first determined by STA-based uncertainty and disturbance observer-based controller designed for the electromechanical subsystems and then the current value so determined is obtained from the electrical subsystem via similar type of controller.

The remainder of the paper is organized as follows: The basic idea of Maglev systems is outlined in Sect. 2, along with critical parameters and mathematical modeling. The STA-based uncertainty and disturbance observer-based controller design and architecture is discussed Sect. 3. The simulation results for the designed controller are a explained in this section as well. In Sect. 4 the conventional PID controller and state and disturbance observer-based controller are explained in brief and simulation results along with performance analysis of all three methods is given and explained. Experimental validation is given in 5 followed by discussion and comparison of results and the conclusion in Sect. 6

Fig. 1

Magnetic Levitation System Circuit Diagram

2 The magnetic levitation system: mathematical modeling

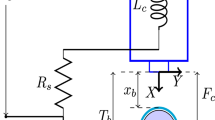
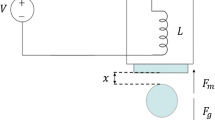
Figure 1 shows a circuit diagram for the Maglev system. A magnetic force is generated by a ferromagnetic coil, which lifts a steel ball into the correct position in the system. The placement of the ball is determined by the current flowing through the ferromagnetic coil and a sensor positioned at the base position. The Maglev system is comprised of two subsystems, one of them is an electrical system and another electromechanical system.

2.1 Electrical system

When a voltage of $V_c$ is applied to a ferromagnetic coil, as shown in Fig. 1, an electromagnetic field is formed. If Kirchhoff’s voltage law is used for electrical loop the formula for $V_c$ is obtained as:

$$\begin{aligned} \frac{1}{L_c}{V_c} =\frac{dI_c}{dt} + \frac{(R_c+R_s)}{L_c}{I_c} \end{aligned}$$

(1)

The coil inductance is $L_c$, the coil current is $I_c$, and the coil resistance and current sensor resistance are $R_c$ and $R_s$, respectively.

2.2 Electro mechanical system

The coil produces an electromagnetic field that acts on the ball, as denoted by the symbol $F_c$ given by

$$\begin{aligned} F_c&= {\frac{K_mI_c^2}{2z^2_b}} \end{aligned}$$

(2)

The electromagnetic force constant is $K_m$, and the air gap between the ball and the electromagnet’s face is $z_b > 0$. The gravitational attraction $F_g$ exerted on the ball in the opposite direction is written as

$$\begin{aligned} F_g = M_bg \end{aligned}$$

(3)

where the mass of the ball is represented by $M_b$ and g represents gravitational acceleration. The ball’s equation of motion can be written as,

$$\begin{aligned} {\frac{d^2 z_b}{dt^2} = {-\frac{K_mI_c^2}{2M_bz^2_b} + {g}}} \end{aligned}$$

(4)

In state space, the Maglev system is represented as

$$\begin{aligned} \left. \begin{aligned} {\dot{z}}_1&=z_2\\ {\dot{z}}_2&={-\frac{K_mz^2_3}{2M_bz^2_1} + {g}}\\ {\dot{z}}_3&={-\frac{(R_c+R_s)}{L_c}{z_3}}+{\frac{1}{L_c}{u}} \end{aligned} \right\} \end{aligned}$$

(5)

which is obtained by placing, $z_1=z_b$, $z_2={\dot{z}}_b$, $z_3=I_c$ and $u=V_c$.

The main role of the controller is to control the position of the ball and make it follow the reference trajectory r. As indicated in the state space model, the dynamics of the system includes $L_c$, $R_s$, g, $M_b$, $R_c$, and $K_m$, which are all unknown parameters. Furthermore, the system is not matched because the dynamics of $z_2$ are uncontrollable. To address the aforementioned challenges, the next section introduces a new approach of super twisting uncertainty and disturbance observer-based control for electromechanical as well as electrical subsystems.

3 Controller Design

A maglev system control is split into two components. In the first, the specified controller is used to obtain the electromagnet current for the electromechanical subsystem. This current is then utilized to regulate the electrical subsystem as a reference input.

As previously said, it is a mismatched system and in order to address the issue of uncertainty in the mismatched system, a virtual control input $z_{3d}$ is developed, and a super twisting observer-based control is designed such that $z_3$ will follow $z_{3d}$. Defining the errors $e_1=z_1-r$, $e_2=z_2-{\dot{r}}$ and $e_3=z_3-z_{3d}$. In the error states form, the model in (5) may be expressed as

$$\begin{aligned} {\dot{e}}_1&=e_2 \end{aligned}$$

(6)

$$\begin{aligned} {\dot{e}}_2&=-a_1e_1-a_2e_2+z_{3d}+\delta _1 \end{aligned}$$

(7)

$$\begin{aligned} {\dot{e}}_3&=-a_3z_3+bu+\delta _2 \end{aligned}$$

(8)

where $a_1$, $a_2$ and $a_3$ are nonzero constants and $\delta _1$ and $\delta _2$ are the disturbances expressed as

$$\begin{aligned} \delta _1&=a_1e_1+a_2e_2{-\frac{K_mz^2_3}{2M_bz^2_1} + {g}}-z_{3d}-\ddot{r} \end{aligned}$$

(9)

$$\begin{aligned} \delta _2&=a_3z_3-bu-\frac{(R_s+R_c)}{L_c}z_3+\frac{1}{L_c}u-z_{3d} \end{aligned}$$

(10)

3.1 Super twisting disturbance observer-based controller design for electro mechanical system

In order to track the desired trajectory, being mismatched system, the virtual control input $z_{3d}$ is obtained by using super twisting disturbance observer-based control. In compact form, the dynamics of $e_1$ and $e_2$ may be represented as:

$$\begin{aligned} \left. \begin{aligned} {\dot{e}}&=Ae+Bv+B\delta _1\\ y&=Ce \end{aligned} \right\} \end{aligned}$$

(11)

where $v=z_{3d}$, A, B, and C are matrices and are represented as,

$$\begin{aligned} {A=\begin{bmatrix} 0 &{} 1\\ -a_1 &{} -a_2 \end{bmatrix}}; {B=\begin{bmatrix} 0\\ 1 \end{bmatrix}}; {C=\begin{bmatrix} 1&0 \end{bmatrix}}; \end{aligned}$$

Where the vector e is : ${e=\begin{bmatrix} e_1&e_2 \end{bmatrix}} ^T$.

Defining sliding surface for this as ,

$$\begin{aligned} \sigma _1=Ge \end{aligned}$$

(12)

where ${G=\begin{bmatrix} c_1&1 \end{bmatrix}}$ and the constant $c_1$ is positive. When you differentiate (12) and use (11), you get (13) as

$$\begin{aligned} \dot{\sigma _1}=GAe+GBv+GB\delta _1 \end{aligned}$$

(13)

Design v as, $v=v_{eq}+v_n$. Where $v_{eq}$ is designed such that it will compensate known terms as

$$\begin{aligned} v_{eq}=-(GB)^{-1}(GAe+k_1\sigma _1) \end{aligned}$$

(14)

where $k_1$ is positive constant. Substituting (14) in (13) and solving (13) and $v_n$ is designed to compensate unknown terms

$$\begin{aligned} v_n=-{\hat{\delta }}_1 \end{aligned}$$

(15)

The estimate ${\hat{\delta }}_1$ is obtained as

$$\begin{aligned} {\hat{\delta }}_1&= k_2{\vert \sigma _1 \vert }^{1/2} + v_1 \end{aligned}$$

(16)

$$\begin{aligned} \dot{v_1}&= k_3 sat(\sigma _1) + {\dot{\delta }}_1 \end{aligned}$$

(17)

$$\begin{aligned} \dot{\sigma _1}&= -k_1 \sigma _1+ G B {\tilde{\delta }}_1 \end{aligned}$$

(18)

where ${\tilde{\delta }}_1=\delta _1-{\hat{\delta }}_1$ represents an uncertainty estimation error.

Where $k_1$, $k_2$, $k_3$ are selected as positive constants. The function $sat(\sigma _1)$ is given as,

$$\begin{aligned} sat(\sigma _1) = {\left\{ \begin{array}{ll} sign(\sigma _1) &{} \quad \text {if } \vert \sigma _1\vert >\epsilon _1 \\ \frac{\sigma _1}{\epsilon _1} &{} \quad \text {if } \vert \sigma _1\vert <\epsilon _1 \end{array}\right. } \end{aligned}$$

where $\epsilon _1$ is a small positive constant.

3.2 Controller for the electrical subsystem

In order to achieve the objective of forcing $z_3=z_{3d}$, a new approach of Super twisting disturbance observer-based control is proposed and explained in this section. Let us define another sliding surface as

$$\begin{aligned} \sigma _2&=e_3 \end{aligned}$$

(19)

after differentiating (19) and using (8)

$$\begin{aligned} {\dot{\sigma }}_2&=-a_3z_3+bu+\delta _2 \end{aligned}$$

(20)

u. is designed as $u={u}_{k}+{u}_n$. Where $u_k$ is intended to compensate for known terms as,

$$\begin{aligned} {u}_{k}=-\frac{1}{b}(-a_3z_3+k_4\sigma _2) \end{aligned}$$

(21)

and ${u}_n$ is designed for unknown terms as

$$\begin{aligned} {u}_n= -\frac{{\hat{\delta }}_2}{b} \end{aligned}$$

(22)

The estimate ${\hat{\delta }}_2$ is obtained as

$$\begin{aligned} {\hat{\delta }}_2&=k_5{ \vert \sigma _2\vert }^{1/2}+v_2 \end{aligned}$$

(23)

$$\begin{aligned} {\dot{v}}_2&=k_6sat(\sigma _2)+{\dot{\delta }}_2 \end{aligned}$$

(24)

$$\begin{aligned} {\dot{\sigma }}_2&=-k_4\sigma _2+{\tilde{\delta }}_2 \end{aligned}$$

(25)

where $k_4$, $k_5$, $k_6$ are the positive constants and

$$\begin{aligned} {\tilde{\delta }}_2=\delta _1-{\hat{\delta }}_1 \end{aligned}$$

(26)

function $sat(\sigma _2)$ is defined as,

$$\begin{aligned} sat(\sigma _2) = {\left\{ \begin{array}{ll} sign(\sigma _2) &{} \quad \text {if } \vert \sigma _2\vert >\epsilon _2\\ \frac{\sigma _2}{\epsilon _2} &{} \quad \text {if } \vert \sigma _2\vert <\epsilon _2 \end{array}\right. } \end{aligned}$$

where $\epsilon _2$ is a small positive constant. The block diagram representing the proposed controller is shown in Fig. 2

Fig. 2

Block diagram for proposed controller

3.3 The controller’s stability analysis

In this section the stability of the proposed controller, is analyzed as stated in [6]. From the proposed controller, the part of control input that deals with uncertainty and disturbance is the switching term as given in equation (16) and (17) can be written as shown in equation (27) below

$$\begin{aligned} v_n&=-k_2{\vert \sigma _1\vert }^{1/2}sign(\sigma _1)-k_3\int sign(\sigma _1)dt \end{aligned}$$

(27)

where $k_2$ and $k_3$ are given as mentioned in [6] as:

$$\begin{aligned}&k_3>\frac{\zeta }{\Gamma }_{min} \end{aligned}$$

(28)

$$\begin{aligned}&{(k_2)^2}>\frac{4\zeta \Gamma _{max}(k_3+\zeta )}{\Gamma _{min}^2\Gamma _{min}(k_3-\zeta )} \end{aligned}$$

(29)

with conditions

$$\begin{aligned} \zeta >\vert \frac{d\dot{\sigma _1}}{dt}+\frac{\dot{\sigma _1}}{dz}[f(z,t)+b(t)v(t)+\delta _1(t)]\vert \end{aligned}$$

(30)

and

$$\begin{aligned} 0\le \Gamma _{min}\le \vert \frac{d\dot{\sigma _1}}{dt}\vert \le \Gamma _{max} \end{aligned}$$

(31)

The requirements to meet for the system to be stable are: V is positive definite and radially unbounded, where as ${\dot{V}}$ is negative definite .

Using the Lyapunov candidate function as follows:

$$\begin{aligned} V=\frac{1}{2} \sigma _1^2 \end{aligned}$$

(32)

The first two requirements are met by Eq. (32), the time derivative of Eq. (32) is as follows:

$$\begin{aligned} {\dot{V}}=\sigma _1\dot{\sigma _1} \end{aligned}$$

(33)

Substituting $\dot{\sigma _1}$ from Eq. (13) in Eq. (33)

$$\begin{aligned} {\dot{V}}=\sigma _1(GAe+GBv+GB\delta _1) \end{aligned}$$

(34)

putting the value of v from section 3 in Eq.(34) and simplifying

$$\begin{aligned} {\dot{V}}&=\sigma _1(-k_1\sigma _1-k_2{\vert \sigma _1\vert }^{1/2}sign(\sigma _1) \nonumber \\&\quad -k_3\int sign(\sigma _1)dt-GB\delta _1) \end{aligned}$$

(35)

Further simplifying

$$\begin{aligned} {\dot{V}}&=-k_1\sigma _1^2-k_2{\vert \sigma _1\vert }^{1/2}\vert \sigma _1\vert \nonumber \\&\quad -k_3\int \vert \sigma _1\vert \ dt-GB\sigma _1\delta _1 \end{aligned}$$

(36)

Equation (36) demonstrates that ${\dot{V}}$ is negative definite, which implies that setting parameters ( $k_3$ and $k_2$) in accordance with (28) and (29) will ensure the controller’s asymptotic stability.

4 Simulation results

This section uses simulation to assess the efficacy of the proposed control strategy. The results of the proposed method are compared to those of a PID and SDO controller. PID is referred to as “Approach I”, SDO is referred to as “Approach II”, and the suggested method is referred to as “Approach III”. The nominal plant parameters that were used in the simulation are shown in Table 1. A simulation is done using MATLAB/Simulink on the Maglev system depicted in Fig.  1 to demonstrate the effectiveness of the proposed controller. The following are the initial conditions of system states :

$$\begin{aligned} x(0)=\begin{bmatrix}0.014&0&0 \end{bmatrix}^T, \end{aligned}$$

Approach-I: A PID controller with a feed forward (PID-FF)component is suggested by [42] for the maglave system control is applied and tested for the system. The electromechanical loop in maglave is controlled with PID plus FF control and Proportional Integral(PI) control is applied to the electrical loop. Both the PID and feed forward controller gains are determined by root locus selection of closed loop poles that match the performance requirements. In PID controller design, three independent gains are employed, resulting in two zeros and a pole at the origin, converting the system to a Type 1 system with zero steady-state error. Adjusting for gravitational bias is the goal of the feed forward control operation. When the PID controller adjusts for dynamic disturbances around the linear operating point, the feed forward control action reduces the changes in gravitational bias-induced force. The nonlinear mathematical model of the plant was built using fundamental physical concepts and around the equilibrium point, the nonlinear equation was linearized using Taylor’s series. Simple mathematical gain equations to obtain the needed response have been established by combining the tuning philosophy of PID controllers with the notion of LQR theory. The testing findings showed that the proposed strategy was effective not only in stabilizing the ball but in tracking the various reference trajectories that were provided as input. With the controller settings, $Ki_b=524$, $K_{pb}=208$, $K_{vb}=3$, and $K_{ff}=153$, the ball will track the required reference trajectory. A PI controller is used in the current loop to keep the actual current $z_3$ at the intended current level $z_{3d}$. $kp=219$ and $ki=50,000$ are the PI controller settings.

Approach-II: Cascaded sliding mode control is used for magnetic levitation systems, as designed in [25]. A disturbance observer-based sliding mode controller is utilized for the electrical loop, while a state and disturbance observer (SDO)-based sliding mode controller is used for the electromechanical loop. The SDO is used to estimate both the state and the uncertainty at the same time. The controller proposed for electrical loop is explained in brief. The observer dynamics are defined as

$$\begin{aligned} \left. \begin{aligned} \dot{{\hat{e}}}&=A{\hat{e}}+Bv+B{\hat{\delta }}_1+M(y-{\hat{y}})\\ y&=Ce \end{aligned} \right\} \end{aligned}$$

(37)

where A, B, and C are matrices as defined earlier. M is observer gain matrix. The sliding surface is defined as,

$$\begin{aligned} \sigma _3=G_1{\hat{e}} \end{aligned}$$

(38)

where ${G_1=\begin{bmatrix} c_1&1 \end{bmatrix}}$ and $c_1$ is a positive constant. After differentiating (38) and using (37) gives,

$$\begin{aligned} \dot{\sigma _3}=G_1A{\hat{e}}+G_1Bv+G_1B{\hat{\delta }}_1+G_1M(y-{\hat{y}}) \end{aligned}$$

(39)

Design v as,

$$\begin{aligned} v=-\frac{1}{G_1B}(G_1A{\hat{e}}+k_7\sigma _3+k_8sat{(\sigma _3)})-{\hat{\delta }}_1 \end{aligned}$$

(40)

where $k_7$ and $k_8$ are positive constants.

Table 1 Maglev system nominal parameters

Fig. 3

Simulation Results for proposed Controller with nominal plant

Fig. 4

Simulation Results for proposed Controller with nominal plant

Fig. 5

Simulation Results for proposed Controller with $20\%$ uncertainty in plant

Fig. 6

Simulation Results for proposed Controller with $20\%$ uncertainty in plant

Fig. 7

Comparison of simulation Results for proposed Controller with nominal plant and with uncertainty

Disturbance observer-based control strategy is suggested to achieve the goal of making $z_3=z_{3d}$. The sliding surface defined is:

$$\begin{aligned} \sigma _4&=e_3 \end{aligned}$$

(41)

differentiating (41)

$$\begin{aligned} \dot{\sigma _4}&=-a_3z_3+bu+\delta _2 \end{aligned}$$

(42)

Lets take $u=u_{k}+u_n$. Where $u_{k}$ is designed to compensate for known terms as

$$\begin{aligned} {u_{k}=-\frac{1}{b}(-a_3z_3+k_9\sigma _4+k_{10}sat(\sigma _4))} \end{aligned}$$

(43)

where the positive constants $k_9$ and $k_{10}$ are used. Design

$$\begin{aligned} {u_n=-\frac{{\hat{\delta }}_2}{b}} \end{aligned}$$

(44)

where $\hat{\delta _2}$ is a estimate of $\delta _2$, obtained using DO as

$$\begin{aligned} {\hat{\delta }}_2=p+q_2\sigma _4 \end{aligned}$$

(45)

where $q_2$ is user defined constant

$$\begin{aligned} {\dot{p}}=-q_2 \dot{\sigma _4} \end{aligned}$$

(46)

The controller parameters of SDO-based controller applied to the electromechanical subsystem and Do based controller for electrical subsystem are set as $k_7=35$, $k_8=35$, $k_9 =3$, $\epsilon _3=0.05$ and $\epsilon _4=0.05$.

Table 2 Performance comparison of controllers for nominal system

Table 3 Performance comparison of controllers for system with $20 \%$ uncertainty

Fig. 8

Experimental Results for proposed Controller

Fig. 9

Experimental Results for SDO based controller

Fig. 10

Experimental Results for PID controller

Approach-III: Proposed super twisting disturbance observer-based controller is referred as approach-III. The controller parameters for electromechanical loop are $k_1=25$, $k_2=10$, $k_3 =0.01$, $\epsilon _1=0.05$ and for electrical loop are $k_4=50$, $k_5=2$, $k_6 =45$, and $\epsilon _2=0.05$. The simulation results are shown in Fig. 3– 7. From Fig. 3a, it can be seen that the proposed controller makes the ball position, $z_1$ successfully track the reference r. The required current and the control input generated to make the ball position track the reference trajectory with proposed approach is shown in Fig. 3b, c respectively. The generated control input and current to achieve desired tracking performance are both within the maximum permitted limits. The designed super twisting estimator is able to estimate uncertainties $d_1$ and $d_2$ in two loops of the maglave. The plots of $d_1$ and $d_2$ with its respective estimate ${\hat{d}}_1$ and ${\hat{d}}_2$is given in Fig.  4a, b respectively. To compensate for the influence of uncertainties, the suggested control law employs the opposite of these estimations. Sliding surfaces used for the control of electromechanical and electrical loops are shown in Fig. 4c, d respectively.

The same plant is simulated by taking parametric uncertainty of $20\%$ and the tracking performance along with control input, current, uncertainty estimation is shown in Figs. 5 and 6. The comparative tracking results for all three controllers are depicted in Fig. 7a, b for nominal and system with uncertainty. It clearly shows that proposed controller is performing better than the other two controllers.

5 Experimental Results

The proposed controller architecture is validated experimentally utilizing a magnetic levitation laboratory setup [43] shown in Fig. 8a. A solid one inch steel ball is suspended by an electromagnetic suspension mechanism in the Maglev system. It is basically made up of an electromagnet located towards the top of the apparatus, which is capable of lifting the steel ball from its pedestal and sustaining it in free space. Two system variables are instantly monitored and offered for feedback on the configuration. The two variables are the coil current and the ball distance from the magnetic face. The ferromagnetic ball travels between 0 and 14 mm, however the linear range of the optical sensor used to detect ball location is between 6 and 14 mm . The range of the control input is between 0 to 24 V and the input current range is between 0 to 3 A . The controller parameters and initial conditions of Approach-I, II and III are set to the same values as in the simulation. The tracking performance, control input voltage and input current graphs are shown for all three controllers in Figs. 8,  9 and 10. The experimental validation indicates that the tracking performance of the proposed controller is better as compared to the other.

5.1 Comparison of proposed controller with PID and SDO

The efficacy of the suggested method is evaluated in this part using simulation and experimentation. The suggested scheme’s results are compared to those of a linear PID controller and an SDO-based controller. The suggested controller’s efficacy is tested for nominal systems and systems with $20\%$ parametric uncertainty. The graphical depiction demonstrates that the suggested technique provides improved tracking by keeping control input within a given limits. The outcomes are assessed using error-based performance metrics such as IAE, ITAE, and ISE. Table 2 summaries the performances of all three types of controller on the basis of error-based criteria for system with nominal parameters. Table 3 shows performance comparison for all three controllers when applied for plant with $20\%$ uncertainty. The results in the table clearly demonstrate that the proposed controller’s performance is superior to the other two .

6 Conclusion

Cascaded super twisting disturbance observer-based SMC, SDO-based SMC and PID controllers are applied and discussed for tracking control of a magnetic levitation plant. The proposed control scheme is immune to uncertainties and the reference trajectory to be tracked, contrasting methods that depend on approximate linearization. The whole system’s stability has been demonstrated. In simulation and experimental validation, the suggested approach outperforms conventional PID- and SDO-based controller. The performance of proposed controller is compared on the basis of error-based criteria with other two controllers and the comparison shows superiority of the proposed scheme over the others. The findings demonstrate that the suggested controller can stabilize the magnetic levitation system from difficult start-up circumstances to the desired operating points with smooth control. It is capable of dealing with intrinsically unstable nonlinear dynamics and can deal with uncertain model with external noise as well.