1 Introduction

Ocean is a valuable source of energy, it plays important role in predicting changes in the climatic conditions of the earth. As a result, various experimentation have been performed for exploration of underwater natural resources and intervention with help of underwater robots and vehicles. Due to good maneuvering capabilities and high precision path tracking along the specified path, AUVs are mostly preferred in underwater interventions.

AUV operate in uncertain oceanic environment subjected to unpredictable non vanishing forces like sea waves, tides, underwater currents. Being highly non-linear and exposure to different operating conditions, controlling motion of AUV with desired trajectory tracking performance is the challenging problem for control engineers and researchers.

When deep water waves formed by a storm or cyclone, a group of waves get superimposed on each other. It causes the underwater currents and an interaction can take place which results in a shortening of the wave frequency, ultimately fast under currents are developed [1]. Therefore, it is required to design and develop a strategy to control AUV against the fast unpredictable disturbances. Traditional controllers such as linear PD/PID controller are unable to handle such difficulties properly and results in poor tracking performance [2]. Furthermore, output feedback controller are designed to complete the path tracking of mission, however, these techniques are required to know the accurate modelling of AUV and also raise the complexity in controller’s structure. Sliding mode controller (SMC) is a robust controller which controls nonlinear and uncertain systems affected by unpredictable external disturbances. Many authors have proposed SMC control technique for trajectory tracking problems of AUV. To deal with AUV’s non linear dynamics, uncertain models and disturbances, SMC was designed by Yoerger and Slotine [3]. Since then researchers have modified and extended SMC to second-order SMC in order to compensate the unmodelled dynamics of the vehicle. The techniques are also used to rejects and ovecome the effects of unpredictable disturbance caused due to sea waves, low tides, high tides, and underwater currents in order to stabilize an AUV [4, 5]. SMC and adaptive controller are combined together for addressing trajectory tracking problem in AUV’s [6, 7]. For precise maneuvering capabilities in underwater operations of AUV spatial trajectory tracking based on intelligent and hybrid control schemes like fuzzy logic, neural networks, adaptive fuzzy, fuzzy SMC etc. are proposed and performance robustness is verified using simulations [8,9,10,11,12,13,14].

Recently in literature linear and non-linear disturbance estimators and observer based strategies are designed to deal effects of complex marine environment, multi-axis non-linear motion, strong cross-coupling effects, non-holonomic constraints, perturbations in hydrodynamic coefficients and unpredictable external disturbances in AUV. A linear estimator like UDE based SMC (UDE-SMC) control for linearised model of AUV is designed and the numerical simulations were performed to validate the design [15]. Adaptive disturbance observer based control is designed and validated through real time experimentation on AUV tracking [16]. Disturbance estimator with adaptive fuzzy controller and S-Surface control for optimising stable performance is proposed in [17]. A disturbance observer based fractional control is designed for simulation of 6-dof model of AUV. [18]. Nonlinear disturbance observer with cordinate controller for autonomous underwater vehicle manipulator is simulated for meeting desired trajectories different erros in maniplator [19].

To deal with the control challenges of AUVs in order to design uncertainty and disturbance compensation strategy which shall scale down the trade off between performance and stability to improve robustness, SMC is most commonly used in the literature. To avoid well known problem of SMC i.e. chattering, the several methodologies are proposed. Among these, a super twisting algorithm (STA) is found to be one of the most powerful second order continuous SMC. It was first introduced in [20] and since then has been used in many applications [21]. Being second order sliding mode controller, STA is applicable to any generalised system of any order, in which control appears in the first derivative of the sliding variable. It’s benefit is that it only requires the information of the output sliding variable \(\sigma \). It generates continuous control signal resulting attenuation in the chattering. Also, it provides finite-time convergence to the origin for \(\sigma \) and \({\dot{\sigma }}\) at the same time. Thus, due to attenuation of chattering STA gives a smoother control effort [22].

In order to exploit the smoothing capability of STA, in this work STA as a disturbance observer [23] and SMC being a main controller is designed. The main contributions of the work are summarized as follows:

  1. (i)

    A robust super twisting disturbance observer based SMC strategy is designed and the performance is validated for slow and fast disturbances.

  2. (ii)

    The designed control scheme is employed for motion control of AUV, due to faster convergence it precisely tracks the desired trajectory.

  3. (iii)

    The STA-SMC generates smooth and continuous control signal, consequently overcomes the chattering in SMC.

  4. (iv)

    The STA-SMC scheme has fast following accuracy under influence of fast disturbances as compared to UDE-SMC and DO based SMC.

  5. (v)

    The efficacy of the control scheme is validated through extensive numeric simulation.

The paper is organised as follows. Section 2 presents the mathematical model of AUV along with the linearisation in horizontal plane and vertical plane. Section 3 presents the problem formulation and observer based sliding mode control design approach with numerical simulation. Application of the strategies in Sect. 3 are extended to linearised model of AUV in Sect. 4. Stability analysis is discussed in Sect. 5. Numerical simulation results and comparative perfomance analysis of the control strategies for AUV in Sect. 6 and conclusion in Sect. 7.

2 Modelling of an AUV

Mathematical modelling method based on geometrical analysis is preferred in this work. It deals with the determination of model parameters, defined by Newton’s second law on the motion of a rigid body in liquid environment. Modelling of AUV includes vehicle statics which is primarily concerned with the equilibrium of vehicle body at rest or moving at constant velocity. While dynamics is concerned with accelerated motion of the vehicle’s body. The equations governing the motion of the AUV belongs to the Underwater Robotic Vehicle (URV) class. The vehicle body can be dynamically regarded as a rigid solid with six degrees of freedom (6 DOF): three coordinates for displacement movements and three others for rotational movements in the ocean.

The AUV’s dynamics are highly non-linear, time varying and coupled in nature. This is attributed due to various parameters like hydrodynamic drag, damping and lift forces, Coriolis and centripetal forces, gravity, buoyancy forces and thrust.

2.1 Vehicle coordinate system

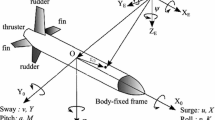
To analyse the AUV motion, two special coordinate frames are considered to set up a non-linear 6-DOF mathematical model as shown in Fig. 1. The fixed reference is earth or inertial coordinate system frame and a motion reference frame is body-fixed coordinate system frame. The vehicles are built in a symmetrical structure thus, it is practical to assume that the body-fixed coordinate is placed with neutral buoyancy at the center of gravity. For vehicle maneuvering, two stern planes and two stern rudder underneath the hull are used. Out of six independent co-ordinates, three coordinates are used to describe the translation motion i.e. forward, lateral and vertical movement respectivel. While, other coordinates describe the rotational motions i.e. roll, pitch and yaw respectively. Table 1 shows the recommended standard notation utilized in tracking and control design of AUV [24].

Fig. 1
figure 1

Coordinate systems in AUV

Full size image
Table 1 Notation used for AUV modelling
Full size table

2.2 Vehicle kinematics

According to the SNAME (1950) notation, the general motion of AUV in 6-DOF are described by the following vectors [25]:

$$\begin{aligned} \eta= & {} [\eta _{1} \; \eta _{2}]^{T} \quad \eta _{1}=[x \; y \; z]^{T} \quad \eta _{2}=[\phi \; \theta \; \psi ]^{T}\\ \nu= & {} [\nu _{1} \; \nu _{2}]^{T} \quad \nu _{1}=[u \; v \; w]^{T} \quad \nu _{2}=[p \; q \; r]^{T}\\ \tau= & {} [{\tau }_{1} \; {\tau }_{2}]^{T} \quad \tau _{1}=[X \; Y \; Z]^{T} \quad \tau _{2}=[K \; M \; N]^{T} \end{aligned}$$

where, \(\eta \in \mathfrak {R}^{6 \times 1}\) denotes the vector of position and orientation in the inertial frame, \(\nu \in \mathfrak {R}^{6 \times 1}\) represents the vector of the linear and angular velocities in body-fixed frame, and \(\tau \in \mathfrak {R}^{6 \times 1}\) is the vector of external forces and moments.

The following coordinate transform relates translational velocities and rotational velocities between body fixed and inertial or earth fixed coordinates obtained from the laws of linear and angular moments.

$$\begin{aligned} {\dot{\eta }}= J(\eta )\nu \end{aligned}$$
(1)

where,

$$\begin{aligned} J(\eta )= & {} \left[ \begin{array}{cc} J_{1}(\eta _{2}) &{} \quad 0 \\ 0 &{} \quad J_{2}(\eta _{2}) \\ \end{array} \right] \\ J_{1}(\eta _{2})= & {} \left[ \begin{array}{ccc} c\psi c\theta &{} \; -s\psi c\phi + c\psi s\theta s\phi &{} \; -s\psi s\phi + c\psi s\theta c\phi \\ s\psi c\theta &{} \; -c\psi c\phi + s\psi s\theta s\phi &{} \; -c\psi s\phi + s\psi s\theta c\phi \\ -s\theta &{}\; -c\theta s\phi &{} \; c\theta c\phi \\ \end{array} \right] \\ J_{2}(\eta _{2})= & {} \left[ \begin{array}{ccc} 1 &{}\; s\phi t\theta &{}\; c\phi t\theta \\ 0 &{}\; s\phi /c\theta &{} \; c\phi / c\theta \\ \end{array} \right] \\ \hbox {where}, s= & {} \mathrm{sin}, \; c = \mathrm{cos}, \; t =tan \end{aligned}$$

2.3 Linearising AUV model

In this work, the non-linear model of the NPS AUV II type underwater vehicle as shown in Fig. 2 is considered. For purpose of the controller design, its non-linear 6-DOF dynamics are linearised to yaw and pitch planes. The dynamics are decoupled into steering and diving planes as given in [24, 26]. The AUV mathematical model is is linearised in horizontal plane and vertical plane as discussed in [15].

Fig. 2
figure 2

NPS AUV II vehicle schematic

Full size image

The steering system in AUV is for the control of heading errors, it’s automatic control is done through a rudder or a pair of thrusters.

The vehicle dynamics in matrix form are

$$\begin{aligned}&\begin{bmatrix} m - Y_{{\dot{v}}} &{} 0 &{} 0 \\ -N_{{\dot{v}}} &{} I_{z} - N_{{\dot{r}}} &{}0 \\ 0 &{} 0 &{} 1 \end{bmatrix} \begin{bmatrix} {\dot{v}}\\ {\dot{r}}\\ {\dot{\psi }} \end{bmatrix} \nonumber \\&\quad +\begin{bmatrix} Y_v &{} -Y_r + mu_0 &{} 0\\ N_v &{} -N_r &{}0\\ 0 &{} -1 &{} 0 \end{bmatrix} \begin{bmatrix} v\\ r\\ \psi \end{bmatrix} = \begin{bmatrix} Y_\delta \\ N_\delta \\ 0 \end{bmatrix} \delta _r \end{aligned}$$
(2)

\(\delta _r\) is the rudder deflection control.

Rearranging it in state-space form,

$$\begin{aligned} \begin{array}{l} {\dot{x}}=Ax + b\delta _r \\ y = c^T x \end{array} \end{aligned}$$
(3)

here, \(x = [v \; r \; \psi ]\)

The depth errors are controlled by diving system. Two horizontal fins are used to control deflection of stern planes as a result it changes the pitch moment, pitch angle and ultimately depth.

$$\begin{aligned} \begin{bmatrix} {\dot{q}}\\ {\dot{\theta }}\\ {\dot{z}} \end{bmatrix} = \begin{bmatrix} \frac{M-q}{I_y - M_{{\dot{q}}}} &{} -\frac{{\tilde{B}}G_zW}{I_y - M_{{\dot{q}}}} &{} 0\\ 1&{} 0 &{}0\\ 0&{}-u_0 &{}0 \end{bmatrix}\begin{bmatrix} q\\ \theta \\ z \end{bmatrix} + \begin{bmatrix} \frac{M_{\delta _s}}{I_y - M_{{\dot{q}}}} \\ 0\\ 0 \end{bmatrix} \delta _s \end{aligned}$$
(4)

where, \(\delta _s\) is the stern plane deflection control.

$$\begin{aligned} \begin{array}{l} {\dot{x}}=Ax + B\delta _s \\ y = C^T x \end{array} \end{aligned}$$
(5)

here, \(x = [q, \; \theta , \; z]^T\)

3 Control design

3.1 Problem formulation

Let us consider a uncertain system

$$\begin{aligned} {\dot{x}}=Ax + \Delta Ax + Bu + d \end{aligned}$$
(6)

where, \(x \in \mathfrak {R}\) is a state vector, \(u \in \mathfrak {R}\) is the control input vector, \(d \in \mathfrak {R}\) is an external unknown matched disturbance vector, \(\Delta A\) unmodelled dynamics while A and B are the system and input matrix.

The objective of designing a control u is to follow the reference trajectory \(x_r\), despite presence of unmodeled dynamics, uncertainties and unknown disturbances in the system.

Assumption 1

\(\Delta A\) and d satisfies matching condition given by following equation in order to guarantee invariance and robustness property of SMC based design.

$$\begin{aligned} \Delta A= & {} BD \end{aligned}$$
(7)
$$\begin{aligned} d= & {} BF \end{aligned}$$
(8)

D and F are the unknown matrices.

Hence, system equation in (6) can be written as

$$\begin{aligned} {\dot{x}}=Ax + BDx + Bu + BF \end{aligned}$$
(9)

The uncertainty and disturbance in form of a lumped term e(x, t) is represented as

$$\begin{aligned} e(x,t)= Dx+F \end{aligned}$$
(10)

The system is written as

$$\begin{aligned} {\dot{x}}=Ax + Bu + Be(x,t) \end{aligned}$$
(11)

Assumption 2

The lumped uncertainty term e(x, t) and its derivative are bounded by known positive scaler function. The disturbance rate of change is negligible as compared to the estimation error dynamics of the estimator.

3.2 Observer based sliding mode control design

In the SMC design, the main task is to choose a sliding surface, that shall drive the plant dynamics on the sliding surface in order to follow trajectory and become robust against lumped uncertanities and disturbances. Therefore, sliding surface is chosen as

$$\begin{aligned} \sigma = S(x - x_r) = S{\tilde{x}} \end{aligned}$$
(12)

where, S is sliding surface coefficients vector.

When \(\sigma \rightarrow 0, {\tilde{x}}\rightarrow 0\). It require the sliding condition \(\sigma {\dot{\sigma }}< 0\), to be satisfied.

Taking derivative on both side, results,

$$\begin{aligned} \begin{array}{l} {\dot{\sigma }} = S({\dot{x}}-\dot{x_r}) \\ {\dot{\sigma }} = SAx + SBu + SBe - S\dot{x_r} \end{array} \end{aligned}$$
(13)

The control signal u, is splitted as

$$\begin{aligned} u = u_{eq} + u_n \end{aligned}$$
(14)

where, \( u_{eq}\) is used to address known terms of the system and \(u_n\) to addresses lumped uncertainty and disturbance term e.

Putting (14) in (13), we get

$$\begin{aligned} {\dot{\sigma }} = SAx + SBu_{eq} + SBu_n + SBe - S\dot{x_r} \end{aligned}$$
(15)

The equivalent control is obtained as,

$$\begin{aligned} u_{eq} = -(SB)^{-1} [SAx + K\sigma - S\dot{x_r}] \end{aligned}$$
(16)

K is a constant and it is always positive.

In order to counter the uncertainties and unknown disturbances in (11), control signal \(u_n\) is selected as

$$\begin{aligned} \begin{array}{l} u_n = -(SB)^{-1}(SBe) \\ u_n = -{\hat{e}} \end{array} \end{aligned}$$
(17)

Using (16) and (17), we get

$$\begin{aligned} \begin{array}{l} {\dot{\sigma }} = - K\sigma +SB(e-{\hat{e}}) \\ {\dot{\sigma }} = - K\sigma +SB {\tilde{e}} \end{array} \end{aligned}$$
(18)

The estimation error \({\tilde{e}}\) is given as

$$\begin{aligned} {\tilde{e}} = e -{{\hat{e}}} \end{aligned}$$
(19)

As e is unknown so it must be estimated as \({\hat{e}}\). When \({\tilde{e}}\rightarrow 0\), sliding condition is satisfied and \(\sigma \) will asymptotically approach to zero.

In this study, the following observers are designed in order to estimate lumped uncertainity e.

3.2.1 \(\mathrm{sign}(x)\) as a disturbance observer

A first order system is considered as follows

$$\begin{aligned} {\dot{x}} = u + d \end{aligned}$$
(20)

where, \(x \in \mathfrak {R}, \; u = -K \mathrm{sign}(x) \in \mathfrak {R}\) and \(d \in \mathfrak {R}\) are the state vector for control input and matched external disturbance respectively. Despite the bounded disturbance value, system trajectory will converge to origin in finite time subjected to the magnitude of gain K and shall be more than maximum bound of matched disturbance.

When \(x = 0\), the equivalent control is obtained by setting \({\dot{x}} = 0\), means it implies \(d = [k \mathrm{sign}(x)]_{eq}\). Where, \([k \mathrm{sign}(x)]_{eq}\) is nothing but the estimated value of \([k \mathrm{sign}(x)]\). It means the lumped uncertainty and non vanishing disturbance term e can be estimated practically, but it is discontinuous in nature. Hence, when the system is in sliding mode i.e. \(x = 0 \) then, \(\mathrm{sign}(x)\) acts as a disturbance observer (signDO) [27].

The control term \(u_n\) in (14), in order to estimate e is

$$\begin{aligned} u_n = -{\hat{e}}=-K_1\;\mathrm{sign}(\sigma ) \end{aligned}$$
(21)

Though this approach is estimating the disturbance, practically it is discontinuous control signal and gives chattering which is undesirable for actuators. To overcome this drawback and in order to obtain smooth control signal, it is estimated by passing through a low pass filter by following technique.

3.2.2 Uncertainty and disturbance estimator (UDE)

UDE is a robust control technique for uncertain systems introduced by Zhong and Rees in [28]. It is used for estimating slow varying uncertainties and disturbances. It is based on the assumption that a low pass filter of a proper bandwidth can be used to approximate and estimate a signal. Then the opposite of estimate is used in control term to counter the presence of lumped uncertainty [29, 30]. In order to ensure \({\tilde{e}}\) is bounded, it is assumed that,

Assumption 3

e(x, t) is continuous and satisfy

$$\begin{aligned} \left| \frac{d^{(i)}e(x,t)}{dt^{(i)}} \right| \le \eta \;\;\; \; for \; i=0,1,2,\ldots ,m \end{aligned}$$
(22)

where, \(\eta \) is a positive number.

Using UDE, e(x, t) is estimated as

$$\begin{aligned} {\hat{e}} = G_f(s) e \end{aligned}$$
(23)

\(G_f(s)\) is a strictly proper low-pass filter with unity steady-state gain and large possible bandwidth.

$$\begin{aligned} G_f(s) = \frac{1}{1+s\tau } \end{aligned}$$
(24)

where, value of \(\tau \) shall be positively as small as possible. If \(\tau \) is chosen small then (24), is written as

$$\begin{aligned} {\hat{e}}\approx e \end{aligned}$$
(25)

Hence, estimation accuracy depends on the value of \(\tau \). As mentioned in [15] the estimate is

$$\begin{aligned} u_n=-{\hat{e}} = -\frac{(SB)^{-1}}{\tau }[\sigma + K_2 \int \sigma ] \end{aligned}$$
(26)

From (23) and (24),

$$\begin{aligned} \dot{{\tilde{e}}}=-\frac{1}{\tau } {\tilde{e}} + {\dot{e}} \end{aligned}$$
(27)

Remark

If e is constant, then \({\dot{e}}=0\), and \({\tilde{e}}\) asymptotically goes to zero; otherwise it is bounded. As a consequence \(\sigma \rightarrow 0\), if \(K > 0\) and \(\tau > 0\).

Though UDE offers smooth and robustness in control designing, there are some limitations and challenges in UDE based design which are summerise as follows:

  • Selection of the error feedback gain K and the time constant of the filter \(\tau \).

  • If \(\tau \) is small, the system is stable. However, it has large control and hence the value of \(\tau \) has to be compromised.

  • The accuracy of estimation can be improved by an appropriate choice of low pass filter. eg. First order filter, Second order filter, \(\alpha \) filter etc.

  • UDE alone can not be used for mismatch systems.

  • UDE needs to be tuned for varying disturbances or it is not suitable for fast varying disturbances.

  • UDE-SMC suitable for bounded perturbations.

3.2.3 Super twisting as a disturbance observer

Among the second order sliding mode controllers, super twisting control technique is found to be the most promising algorithms. It is designed to achieve finite-time estimation of the lumped uncertainty and disturbance and generates smooth and continuous control signal to overcome chattering problem in conventional SMC. It drives the sliding variable \(\sigma \) and it’s derivative \({\dot{\sigma }}\) to zero in finite time [22].

Mathematically, the STA is represented as

$$\begin{aligned} \begin{array}{l} u = -\alpha \left| x \right| ^{1/2}\mathrm{sign}(x) + v \\ {\dot{v}} = -\beta \mathrm{sign}(x) \end{array} \end{aligned}$$
(28)

Putting (28) in (20), we get

$$\begin{aligned} \begin{array}{l} {\dot{x}} = -\alpha \left| x \right| ^{1/2}\mathrm{sign}(x) + v + d\\ {\dot{v}} = -\beta \mathrm{sign}(x) \end{array} \end{aligned}$$
(29)

It means when system is on the sliding mode i.e. \(x = 0\), so in finite time, it implies \(d = - v \). Where, \(\alpha \) and \(\beta \) are the positive constants.

Therefore, disturbance is given as

$$\begin{aligned} \begin{array}{l} d = -v \\ {\dot{v}} = -\beta \mathrm{sign}(x) \end{array} \end{aligned}$$
(30)

It means d is estimated and cancelled out. It retains the disturbance rejection property but with continuous control rather than earlier discontinuous control. Here the reason is that, the high frequency switching term \(\mathrm{sign}(x)\) is hidden under the integral term.

When the system is on the sliding surface then \(u_n\) is given as

$$\begin{aligned} \begin{array}{l} u_n=-{\hat{e}} = -K_3 \left| \sigma \right| ^{1/2}\mathrm{sign}(\sigma ) + \sigma \\ {\dot{\sigma }} = -K_4 \mathrm{sign}(\sigma ) \end{array} \end{aligned}$$
(31)

In case, when initial disturbance is non zero, the sliding mode will start after some finite time \(t \ge \tau \) where, \(\tau \) can be selected as small as possible and choosing proper values of gains \(K_3\) and \(K_4\) as given in [31]. Means, whenever the system is on sliding surface it is governed by the designed control \(u_n\), which is stable by design. The complete control structure with closed loop form is depicted in Fig. 3. The STA is sufficient to overcome effect of vanishing and non vanishing disturbance which gurantees the controller’s convergence [32]. Therefore, separate stability proof is not required for the system.

Fig. 3
figure 3

Control schematic of STA-SMC scheme

Full size image
Fig. 4
figure 4

\(\mathrm{sign}(x)\) as a DO based SMC control in presence of slow disturbance \(\mathrm{sin}(0.2*t)\): a Plant states b Control u.

Full size image
Fig. 5
figure 5

UDE based SMC control in presence of slow disturbance \(\mathrm{sin}(0.2*t)\): a Plant states b Control u

Full size image
Fig. 6
figure 6

STA as a DO based SMC control in presence of slow disturbance \(\mathrm{sin}(0.2*t)\): a Plant states b Control u

Full size image
Fig. 7
figure 7

\(\mathrm{sign}(x)\) as a DO based SMC control in presence of fast disturbance \(5*\mathrm{sin}(1.2*t)\): a Plant states b Control u

Full size image
Fig. 8
figure 8

UDE based SMC control in presence of fast disturbance \(5*\mathrm{sin}(1.2*t)\): a Plant states b Control u

Full size image
Fig. 9
figure 9

STA as a DO based SMC control in presence of fast disturbance \(5*\mathrm{sin}(1.2*t)\): a Plant states b Control u

Full size image

3.2.4 Numerical simulation and comparative analysis of observer based sliding mode control schemes

The effectiveness of discussed observer based SMC control strategies are analyzed through numerical simulation for following uncertain third order plant as

$$\begin{aligned} \begin{array}{l} \dot{x_1} = x_2 \\ \dot{x_2} = x_3 \\ \dot{x_3} = u + d \\ y = x_1 \end{array} \end{aligned}$$
(32)

where, \([x_1, x_2, x_3]^T\) is plant state vector, u is the control signal and d is matched disturbance. The sliding surface parameters are obtained using LQR method \(S=[1 \; 0.96 \; 0.2]\). As per Eq. (14), \(u=u_{eq} + u_n\) where, \(u_{eq}\) is mentioned in (16). The initial conditions of states considered for simulation are \([1 \; 1 \; 1]^T\).

For signDO control \(u_n\) is chosen as mentioned in (21), where controller gain chosen is \(K_1 = 2\). Fig. 4 shows how the states are converging with respect to time despite slow disturbance \(\mathrm{sin}(0.2*t)\) applied to the system and the required control signal. But it is observed that the control effort contains discontinuity or chattering. If the same system is exposed to fast varying disturbance \(5*\mathrm{sin}(1.2*t)\), it can be noted from Fig. 7 that the states are not converging. For the convergence of states, the gain needs to tuned but the chattering increases to higher extent.

For UDE-SMC \(u_n\) is as mentioned in (26), the UDE parameters are given as \(\tau =0.1, K_2=5\). Figure 5 shows that the problem of chattering is addressed here and the control signal evolved is smooth. For slow disturbance the states are converging to origin but for fast disturbance the states are not converging hence the controller is not effective for fast disturbance as shown in Fig. 8.

For STA-SMC, \(u_n\) is chosen as mentioned in (31). For the simulation the controller gains are selected as \(K_3 = 0.2\) and \(K_4 = 5\). Here, the states are converging to origin for slow as well as fast disturbance with smooth evolution control signal as shown in Figs. 6 and 9.

The effectiveness of the control schemes has been verified for slow disturbance and fast disturbance. It is observed that, for slow disturbances UDE-SMC and STA-SMC are performing precisely but for fast disturbance UDE-SMC is not suitable though, the control is continuous and smooth.

4 Stability analysis of observer based sliding mode control design

For stability analysis \(i = 1\) is considered in (22). The bounds on \({\tilde{e}}\) and \(\sigma \) are obtained by following Lyapunov function,

$$\begin{aligned} \vee (\sigma ,{\tilde{e}})=\frac{1}{2}\sigma ^2+\frac{1}{2}{\tilde{e}}^2 \end{aligned}$$
(33)

Differntiating it across (18) and (27).

$$\begin{aligned}&{\dot{\vee }} (\sigma ,{\tilde{e}})= -K\sigma ^2 + Sb\sigma {\tilde{e}}-\frac{1}{\tau }{\tilde{e}}^2+{\tilde{e}}{\dot{e}} \end{aligned}$$
(34)
$$\begin{aligned}&\le \;\; -K\sigma ^2+\left| Sb \right| \left| \sigma \right| \;\left\| {\tilde{e}} \right\| -\frac{1}{\tau }\left\| {\tilde{e}} \right\| ^2+\left\| {\tilde{e}} \right\| \eta \end{aligned}$$
(35)

As per Young’s inequality,

$$\begin{aligned}ab\le \frac{a^2 + b^2}{2} \end{aligned}$$

for real a and b, we get

$$\begin{aligned}&{\dot{\vee }} (\sigma ,{\tilde{e}})\le -K\sigma ^2 +\frac{\left| Sb \right| }{2}(\left| \sigma ^2 \right| +\left\| {\tilde{e}} \right\| ^2)-\frac{1}{\tau }\left\| {\tilde{e}} \right\| ^2\nonumber \\&\quad +\left\| {\tilde{e}} \right\| \eta \end{aligned}$$
(36)
$$\begin{aligned}&{\dot{\vee }} (\sigma ,{\tilde{e}})\le - \left| \sigma ^2 \right| \left( K-\frac{\left| Sb \right| }{2}\right) -\left\| {\tilde{e}} \right\| ^2\left( \frac{1}{\tau }-\frac{\left| Sb \right| }{2} \right) \nonumber \\&\quad +\left\| {\tilde{e}} \right\| \eta \end{aligned}$$
(37)
$$\begin{aligned}&{\dot{\vee }} (\sigma ,{\tilde{e}})\le - \left| \sigma ^2 \right| \left( K-\frac{\left| Sb \right| }{2}\right) \nonumber \\&\quad -\left\| {\tilde{e}} \right\| \left[ \left\| {\tilde{e}} \right\| \left( \frac{1}{\tau } -\frac{\left| Sb \right| }{2} \right) -\eta \right] \end{aligned}$$
(38)

with \(\left( K-\frac{\left| Sb \right| }{2}\right) >0\) and \(\left( \frac{1}{\tau } -\frac{\left| Sb \right| }{2} \right) >0\), the system shall be bounded. From equation (38), the bounds on \({\tilde{e}}\) and \(\sigma \) are,

$$\begin{aligned} \left\| {\tilde{e}} \right\|\le & {} \frac{\mu }{\left( \frac{1}{\tau } -\frac{\left| Sb \right| }{2} \right) } \nonumber \\ \left\| \sigma \right\|\le & {} \frac{\left| Sb \right| \mu }{K\left( \frac{1}{\tau } -\frac{\left| Sb \right| }{2} \right) } \end{aligned}$$
(39)

It proves that \({\tilde{e}}\) and \(\sigma \) are essentially bounded and bounds can be minimised by adjusting K and \(\tau \).

5 Application of Super Twisting Disturbance Observer based Control for Trajectory Tracking of AUV

Two different single input and single output STA-SMC are designed for steering and diving plane dynamics of AUV, as shown in Fig. 10. In this work, forward speed is kept constant and effect of a stern plane on the forward speed is neglected. As the rudder and stern plane relationships of the AUV are moderately separable. Therefore the control scheme are simplified into two separate implementations as follows: (i) The rudder deflection \(\delta _r\) as a control input with yaw (\(\psi \)), roll (\(\phi \)) and sway (y) as an output parameters.

(ii) The stern plane deflections \(\delta _s\) as a control input with depth (z), pitch (\(\theta \)) and heave (w) as output parameters [13].

The hydrodynamic coefficients for NPS AUV II vehicle is taken from [24] with constant surge speed. The linearised steering and diving model of the vehicle is considered from Eqs. (2) and (4) respectively from Sect. 2.

The steering model with uncertanity and disturbance is

$$\begin{aligned} {\dot{x}}_y= & {} A_yx_y + \Delta A_y + b_y\delta _r+d_y \end{aligned}$$
(40)
$$\begin{aligned} y_y= & {} c_y^Tx_y \end{aligned}$$
(41)

where, \(x_y=[v \; r \; \phi ]\) steering state vector, \(b_y\) is input matrix, \(y_y=\psi , d_y \) and \(\Delta A_y\) are the external non vanishing disturbances and parametric uncertainties in steering plane. Applying the assumption I, the lumped uncertainty in steering plane is

$$\begin{aligned} e_y = D_yx_y + F_y \end{aligned}$$
(42)

where, \(D_y\) and \(F_y\) are unknown matrices. Hence, (40) is written as

$$\begin{aligned} {\dot{x}}_y = A_yx_y + b_y\delta r + b_y e_y \end{aligned}$$
(43)

From Eqs. (14), (16) and (17) the steering control is obtained as

$$\begin{aligned} \delta _r=-(S_yb_y)^{-1}[S_yA_yx_y+K\sigma _y-S_y{\dot{x}}_{dy}]-{\hat{e}}_y \end{aligned}$$
(44)

where, \(x_{dy}\) is reference trajectory.

In diving plane, system is represented as

$$\begin{aligned} {\dot{x}}_z= & {} A_zx_z + \Delta A_z + b_z\delta _s + d_z \end{aligned}$$
(45)
$$\begin{aligned} y_z= & {} c_z^Tx_z \end{aligned}$$
(46)

Modifying the system as per Eq. (43) as

$$\begin{aligned} {\dot{x}}_z = A_zx_z + b_z \delta _r + b_z e_z \end{aligned}$$
(47)

where, \(e_z = D_z x_z +F_z \) with unknown matrices, \(D_z\) and \(F_z\). The depth control law is

$$\begin{aligned} \delta _s=-(S_zb_z)^{-1}[S_zA_zx_z+K\sigma _z -S_z{\dot{x}}_{dz}]-{\hat{e}}_z \end{aligned}$$
(48)

The errors \(e_y\) and \(e_z\) are estimated using observers mentioned in Sect. 2. Finally, the STA-SMC control law obtained by putting (31) in (44) and (48).

Fig. 10
figure 10

Control schematic for NPS AUV II

Full size image
Fig. 11
figure 11

Depth control with ocean currents \(\mathrm{sin}(0.2*t)\) and 20% uncertainties

Full size image
Fig. 12
figure 12

Steering control with ocean currents \(\mathrm{sin}(0.2*t)\) and 20% uncertainties

Full size image
Fig. 13
figure 13

Depth control with ocean currents \(2.5*\mathrm{sin}(t + \pi /2)\) and 20% uncertainties

Full size image
Fig. 14
figure 14

Steering control with ocean currents \(2.5*\mathrm{sin}(t + \pi /2)\) and 20% uncertainties

Full size image
Fig. 15
figure 15

Depth control with ocean currents \(2+5*\mathrm{sin}(1.8*t - \pi /2)\) and 20% uncertainties

Full size image
Fig. 16
figure 16

Steering control with ocean currents \(2+5*\mathrm{sin}(1.8*t - \pi /2)\) and 20% uncertainties

Full size image

6 Numerical Simulation Study and Performance Analysis

The effectiveness of the designed control law is analysed in steering and diving planes by numerical simulations of AUV models. The efficacy of the control scheme is verified under slow and fast ocean current disturbance with \(20 \%\) uncertainties or unmodeled dynamics. To demonstrate the potency of the designed controller, the method is compared with UDE-SMC and generalised signDO based SMC. The term \({\hat{e}}\) in control law i.e. estimate of lumped uncertainty and disturbance in steering and diving plane are calculated as per Eqs. (21), (26) and (31) respectively.

The parameters of the sliding surface for steering and depth control for closed-loop stable and high performance design of system are obtained using LQR method respectively as follows.

\(S_y = [0.017\; 0.082\; 0.051]\)

\(S_z=[0.016\; 0.065\; 0.039]\)

The gains for different observers are \(K_1 = 1\), \(K_2 = 5\), \(K_3 = 0.2\) and \(K_4 = 5\). Time constant for first order low pass filter is considered as \(\tau =0.1\).

The ocean current acting on steering and diving plane are modeled as mentioned in [1, 33]. The slow ocean currents are considered as follows:

$$\begin{aligned} \begin{array}{l} d_y = \mathrm{sin}(0.2t) \\ d_z = \mathrm{sin}(0.2t) \end{array} \end{aligned}$$
(49)

The fast ocean current acting on steering and diving planes are considered as follows:

$$\begin{aligned}&\begin{array}{l} d_y = 2.5*\mathrm{sin}(t+pi/2) \\ d_z = 2.5*\mathrm{sin}(t+pi/2) \end{array} \end{aligned}$$
(50)
$$\begin{aligned}&\begin{array}{l} d_y = 2+5*\mathrm{sin}(1.8*t-pi/2) \\ d_z = 2+5*\mathrm{sin}(1.8*t-pi/2) \end{array} \end{aligned}$$
(51)

The control laws mentioned in (44) and (48) are used for generating rudder plane and stern plane angle to track the trajectories for desired steering and depth. AUV model is simulated in both planes for the slow and fast ocean current profile in presence of lumped uncertanity.

It can be observed from Fig. 11 that, under the influence of \(20\%\) uncertainty in lumped disturbance form, AUV follows the required depth trajectory. The corresponding depth response and pitch rate can be seen in Fig. 11a and b, which shows the depth trajectory is tracked precisely. The STA-SMC and UDE-SMC technique offer smooth control signal compared to the signDO based SMC technique. This depicts, though the required control performance is achieved by signDO based SMC but it is subjected to chattering as shown in Fig. 11c while Fig. 11e shows actual lumped uncertainty e and its estimate \({\hat{e}}\) for slow ocean currents in presence of \(20\%\) uncertainties for the designed STA-SMC scheme. Fig 11c shows the changes in stern plane defflections during the depth tracking. It is observed that when a step change in depth is detected, the sliding surface at zero gets deviated, whereas designed control scheme gives tight tracking control under the influence of lumped disturbance and uncertainity.

Figure 12 shows the simulated response to sinusoidal steering control with precise steering tracking for slow ocean current as a disturbance and \(20\%\) parametric uncertainty for STA-SMC, UDE-SMC and signDO based SMC control technique. Though the performance of signDO based SMC is comparable with the designed control scheme, it is subjected to chattering phenomenon as shown in Fig. 12c. To verify it, the sliding surface is depicted in Fig. 12d, while the other schemes provide smooth control signal and Fig. 12b shows change in yaw rate. It is observed that the designed STA-SMC and UDE-SMC technique are precisely estimating the lumped uncertainty.

In order to evaluate the robustness and performance of the designed control scheme in steering and diving planes, it is exposed to fast underwater ocean currents as mentioned (50) and (51) under the effect of \(20\%\) uncertainties in hydrodynamic parameters. From the results in Figs. 13 and 14, it is observed that the designed STA-SMC controller is capable to counter the parametric uncertainties as compared to UDE-SMC and signDO based SMC. The simulation results show that, for fast undercurrents, the tracking performance of UDE-SMC and signDO based SMC becomes deteriorates, though the control signal of UDE-SMC is smooth. This indicate that both the controllers have limited stability range while tracking trajectory under influence of fast underwater currents in the form of lumped uncertainty.

Figures 15 and 16 confirms the effectiveness and smooth tracking capability of the designed STA-SMC control technique as compared to other techniques. It is observed that the UDE-SMC and signDO based SMC failed to reject the disturbance. The output in both the contol scheme oscillates with chattering in signDO based SMC. It is to be noted that the designed STA-SMC controller provides smooth and accurate tracking against fast varying disturbance within the acceptable range of control signals.

7 Conclusion

In this work, SMC technique is integrated with super twisting algorithm as a disturbance observer for handling slow and fast disturbances. The numerical simulation using different observer based SMC designs have embody that, the proposed STA-SMC method has enhance performance as contrast to UDE-SMC and signDO based SMC techniques under uncertain working conditions. Furthermore, the proposed STA-SMC scheme has been successfully implemented for trajectory tracking of AUV in vertical and horizontal planes. The effectiveness of the control scheme has been validated using numerical simulation of an AUV under the influence of slow as well as fast underwater ocean currents and uncertainties in the hydrodynamic coefficients of the vehicle. The proposed STA-SMC method accurately estimates and eliminates the effect of lumped uncertainty acting on the vehicle. It has the simple design and control structure. Also it is to be noted from the simulations that the designed control scheme gives smooth and desired control performance under the effect of lumped uncertainty. The essential boundness of lumped uncertainty estimation error and sliding manifold is demonstrated by Lyapunov theory.