Advanced control strategy for magnetic levitation system: a higher order sliding mode observer approach

Abstract

This paper delves into the control of magnetic levitation systems, which inherently exhibit instability due to their nonlinear nature. The main goal is to develop a control strategy that can effectively manage and stabilize these systems, especially during challenging startup scenarios, when uncertainties and disturbances are present. To accomplish this objective, a control approach based on a cascaded higher-order sliding mode observer (HOSMO) is proposed. This approach not only estimates the system’s states but also ensures a smooth control output even in the presence of uncertainties and disturbances. To evaluate the effectiveness of the suggested control method, a combination of simulations and experiments is performed. The performance of the proposed controller is benchmarked against three alternative controllers: a conventional proportional–integral–derivative controller, a controller based on state and disturbance observation (SDO), and another based on supertwisting disturbance observation. Evaluation metrics such as integrated squared error, integrated absolute error, and integral time absolute error are used for performance comparison. The outcomes of the study illustrate that the HOSMO based control approach outperforms the other three controllers. It excels in its capacity to effectively control and stabilize magnetic levitation systems, even when faced with uncertainties and disturbances.

1 Introduction

Advanced controllers for Magnetic Levitation (Maglev) are required to extend their applications to numerous real-world systems in automation, transportation, and other relevant research areas of study. The maglev system has shown tremendous success in a variety of industries. It has been used in high-speed maglev trains, frictionless bearings, spaceships, rocket-guiding projects, gyroscopes, microrobotics, contactless melting, wafer distribution systems, nuclear reactor centrifuges, vibration isolation systems, and a variety of other important applications [1, 2]. Researchers have recognised maglev’s potential as a useful research tool. The absence of mechanical contact, which eliminates friction and abrasion, is a typical feature of maglev applications. This function extends the system’s operating lifespan, improves labour productivity, and lowers maintenance expenses.

Maglev technology suspends items in the air using electromagnetic forces. These magnetic fields have the ability to oppose gravity force as well as other opposing accelerations. As a result, when affected by external noise, sensor noise, and unknown dynamic components, maglev systems exhibit severe nonlinearity and instability. While the potential uses of magnetic levitation are attractive, the system’s open-loop instability and significant nonlinearity make control difficult. Despite having a total of six degrees of freedom (DOF) in space, magnetic levitation objects have been thoroughly explored as standard challenges in modern control methods. For magnetic levitation systems, a number of control strategies have been put forth, such as adaptive control [3], PID [4, 5], robust control [6], accurate linearization control [7], and fuzzy H1 robust control [8]. The mathematical model is often linearized around the nominal working point in several of these techniques. For example, PID controllers [4, 5] provide a straightforward and straightforward-to-design solution, but their performance may be constrained since the mathematical model of the system is ignored. We need to consider the non-linear dynamics of the plant to create a functional controller. In addition, it is crucial to take into consideration variations in the mass of the levitated object as well as variations in the resistance and inductance of the current coil brought on by the heating of the electromagnets.

By creating nonlinear controllers, the feedback linearization technique’s robustness problems are resolved. Due to its resistance to parametric uncertainties and outside disturbances, SMC has become one of them. Conventional SMC has some drawbacks, including (a) the requirement to know the boundaries of uncertainties and disturbances, (b) the potential for excessive actuator wear from discontinuous control, and (c) the requirement that all the states shall be available for measurement prior to controller implementation. There have been numerous initiatives to resolve the issues with traditional SMC. Disturbance observer (DO) [9, 10]; generalised extended state observer (GESO) [11], inertial delay control (IDC) [12, 13] etc. Many researchers have employed observers in the context of magnetic levitation. For instance, in the work of Kim et al. [14], a reduced-order extended Luenberger observer is utilized for the controlled levitation of permanent magnets. Similarly, Venkatraman and van der Schaft [15] employ a full-order observer employing a passivity-based approach. Wu and Karkoub [16] combine states estimated through fuzzy observers with a variable structure system, applied to magnetic levitation. Additionally, Baranowski and Piatek [17] present a report on observer-based state feedback for magnetic levitation. It has been suggested by Slotine et al. [18] that sliding mode observers make SMC implementable by allowing the estimate of states.

To control maglev systems, Bidikli et al. [19] a self-tuning robust integral of signum of error (RISE) based controller is designed. In the control design, unlike the classical RISE controller, ‘tanh’ function is used instead of ‘signum’ function to obtain a more smooth control signal linearization was applied. In one study by Baris Bidikli [20], stabilization and control problem of a maglev system is solved by designing a robust adaptive controller. To get rid of the velocity measurement necessity in the designed controller, the control input is combined with a nonlinear velocity observer design that is able to compensate the lack of velocity measurement by estimating the velocity of the iron ball during its movement. A bi-loop frequency shifted internal model control(ĬIMC) proportional derivative (FSIMC-PD) strategy is suggested by Arunima Sagar et al. [21] for controlling the position of the ball in a laboratory based Maglev setup. Three controllers (inner, outer and stabilizing are suggested which makes the system complex and increases the tunning parameters.

The authors of the paper [22] has proposed a controller for a magnetic levitation system that combines linear and nonlinear active disturbance rejection techniques. In a related effort aimed at controlling the magnetic suspension of a low-speed maglev train, Sun et al. [23] have introduced two distinct controllers: a PID controller and an adaptive neural fuzzy Sliding Mode Control (SMC). Addressing the challenges of nonlinear suspension systems in maglev vehicles, Chen et al. [24] introduced an innovative sliding mode adaptive controller architecture that relies on RBF network approximation. It is worth noting that these approaches can be readily expanded upon, particularly considering their relevance and popularity in the field. Number of control design examples to control maglev systems utilizing sliding mode control (SMC) have been documented in the literature. These include cascade designs referenced as [25, 26]. Mane et al suggests a cascaded SMC approach with two time scale observers [27]. Dongardive et al. has suggested cascaded supertwisting uncertainty and disturbence observer [28] that gives smooth controller output designed for Maglev system.

Many control algorithms discussed are not able to handle the uncertainty and disturbances in the system. Implementation of most of the control schemes discussed requires whole state vector is available for measurement but it is not the case. The velocity of the ball needs to obtained by taking the differentiation of the output of position sensor. That results in the amplification of the noise. Controllers based on SMC are able to handle the uncertainty and disturbance, but they need to know the bounds of these parameters. The major problem of the SMC based control scheme is the chattering which affects functioning of final control elements resulting into wear and tear. In order to tackle these together HOSMO combined with supertwisting control is suggested. The scheme has following advantages:

• 1. The proposed scheme estimates all the states of the system reducing the cost required for sensors.

• 2. The proposed method simultaneously estimates the disturbance and uncertainty and eliminates its effect.

• 3. Unlike conventional SMC based control it provides chattering free, smooth and continuous control.

• 4. The HOSMO combined with supertwisting control gives finite time and exact convergence.

• 5. It can effectively manage and stabilize these systems, especially during challenging startup scenarios, when uncertainties and disturbances are present.

The work’s main contributions are listed below.

• Higher orders sliding mode observer to estimate the states of the maglev system is designed and demonstrated.

• Chattering free smooth controller performance is obtained applying super twisting algorithm (STA) along with HOSMO.

• When the proposed controller’s results are compared against SDO-based SMC, STA-SMC, and typical PID controllers using the time-domain performance criterion, HOSMO surpasses the others.

• The effectiveness of the proposed approach is validated through a combination of hardware experiments and thorough quantitative simulations

The robust control method has undeniably found extensive application in regulating a diverse array of systems, effectively handling uncertainties related to parameters and structure. These uncertainties are crucial considerations in the administration of the maglev system. Within this context, the electrical subsystem facilitates the transportation of ferromagnetic material to its intended destination. Initially, it generates the necessary electromagnet current by utilizing the input voltage. To determine the requisite electromagnet current, a controller based on the HOSMO framework is employed for the electromechanical subsystem. Similarly, a controller with a comparable design is utilized to retrieve the computed current value from the electrical subsystem.

The subsequent sections of the paper are organized as follows: In Sect. 2, an explanation of the core principles underlying maglev systems is presented, along with an exploration of essential parameters and the development of mathematical model. Moving on to Sect. 3, an exploration of the design and structure of the HOSMO-based cascaded controller is discussed. This section also encompasses an elucidation of the simulation outcomes obtained from the implemented controller. Section 4 delves into an elaborate description of multiple controller techniques, including the standard PID controller, the state and disturbance observer-based controller, and the supertwisting disturbance observer-based controller. This section further includes an analysis of simulation results and performance for all four methods. The validation of these concepts through experimentation is outlined in Sect. 5, followed by a comprehensive examination and comparison of outcomes in Sect. 6. Finally, the paper concludes with a summary of findings in Sect. 7.

Fig. 1

Circuit diagram of a magnetic levitation system

2 Magnetic levitation system and its mathematical model

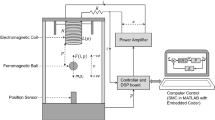
Magnetic levitation system utilizes the magnetic force generated by a ferromagnetic coil to lift a steel ball and accurately position it within the setup. Figure 1 illustrates the schematic representation of the circuitry for the maglev system. The final position of the ball is determined by both the current passing through the ferromagnetic coil and the input received from a sensor situated at the base of the system. To facilitate current measurement, a resistor marked as $R_s$ is incorporated in series with the coil. The mathematical depiction of the maglev system encompasses two distinct subsystems: an electrical system and an electromechanical system. An electromagnetic field comes into existence when a ferromagnetic coil is supplied with a voltage of $V_c$, as illustrated in Fig. 1. The formula for $V_c$ can be obtained by applying Kirchhoff’s law of voltage to an electrical loop, and the derivation is as follows:

$$\begin{aligned} \frac{1}{L_c}{V_c} =\frac{dI_c}{dt} + \frac{(R_c+R_s)}{L_c}{I_c} \end{aligned}$$

(1)

The coil resistance is $R_c$ and current sensor resistance is $R_s$ whereas the coil inductance is $L_c$, and coil current is $I_c$. As indicated by the symbol $F_c$ used by the coil, an electromagnetic field created by the coil operates upon the ball is given by

$$\begin{aligned} F_c&= {\frac{K_mI_c^2}{2z^2_b}} \end{aligned}$$

(2)

The electromagnetic force constant is $K_m$, and there is an air gap of $x_b>0$ between the ball and the electromagnet’s face. The symbol $F_g$ represents the gravitational pull of the opposite direction on the ball and is given as follows:

$$\begin{aligned} F_g = M_bg \end{aligned}$$

(3)

where g denotes the gravitational acceleration and $M_b$ denotes the ball’s mass. The equation of motion for the ball is:

$$\begin{aligned} {\frac{\textrm{d}^2 x_b}{\textrm{d}t^2} = {-\frac{K_mI_c^2}{2M_bx^2_b} + {g}}} \end{aligned}$$

(4)

The Maglev system is modelled as follows in state space:

$$\begin{aligned} \left. \begin{aligned} \dot{x}_1&=x_2\\ \dot{x}_2&={-\frac{K_mx^2_3}{2M_bx^2_1} + {g}}\\ \dot{x}_3&={-\frac{(R_c+R_s)}{L_c}{x_3}}+{\frac{1}{L_c}{u}}\\ \end{aligned} \right\} \end{aligned}$$

(5)

This is achieved by substituting $x_1$ with $x_b$, $x_2$ with $\dot{x}_b$, $x_3$ with $I_c$, and u with $V_c$. The primary objective of the controller is to regulate the position of the ball and compel it to adhere to the reference trajectory r. The system’s dynamics, as illustrated in the state space model, encompass various unknown parameters: $L_c$, $R_s$, g, $M_b$, $R_c$, and $K_m$. Additionally, the system remains unmatched due to the uncontrollable nature of the dynamics of $x_2$. To address these challenges, the following section introduces an innovative control strategy based on a higher order sliding mode observer for both electromechanical and electrical subsystems.

3 Higher order sliding mode observer based controller design

The control of a maglev system is divided into two main components. In the initial stage, designed controller is employed to acquire the current for the electromagnets within the electromechanical subsystem to lift the ferromagnetic ball to the desired position. This current is subsequently obtained from the control of electrical subsystem.

As mentioned earlier, the system is characterized by a lack of alignment, and to tackle the challenge of dealing with uncertainty within this misaligned system, a virtual control input denoted as $x_{3}^{*}$ is formulated. Subsequently, a control strategy utilizing higher order sliding mode observer based control is developed, such that $x_3$ will follow $x_{3}^{*}$. Defining the errors $e_1=x_1-r$, $e_2=x_2-\dot{r}$ and $e_4=x_3-x_{3}^{*}$. The model in (5) can be represented as follows in the error states form:

$$\begin{aligned} \dot{e}_1&=e_2 \end{aligned}$$

(6)

$$\begin{aligned} \dot{e}_2&=-a_1e_1-a_2e_2+x_{3}^{*}+d_1 \end{aligned}$$

(7)

$$\begin{aligned} \dot{e}_4&=-a_3e_4+bu+d_2 \end{aligned}$$

(8)

where the constants $a_1$, $a_2$ and $a_3$ are non-zero, and $d_1$ and $d_2$ are the disturbances, respectively represented as

$$\begin{aligned} d_1&=a_1e_1+a_2e_2{-\frac{K_mx^2_3}{2M_bx^2_1} + {g}}-x_{3}^{*}-\ddot{r} \end{aligned}$$

(9)

$$\begin{aligned} d_2&=a_3e_4-bu-\frac{(R_s+R_c)}{L_c}x_3+\frac{1}{L_c}u-\dot{x_{3}^{*} } \end{aligned}$$

(10)

3.1 Higher order sliding mode observer (HOSMO)

As previously mentioned, the maglev system is mismatched system, and as a result, the virtual control input $x_3*$ is defined. It is necessary to determine the position and velocity of the ball in order to construct the controller for this system that will cause the ferromagnetic ball to follow the designed trajectory, but only position sensor is available. A HOSMO is created to estimate the states of the maglev system in, and then supertwisting controller algorithm is used for electromechanical system to control the position of the ball to make it track the given trajectory.

The HOSMO design is suggested by Chalanga et al. [29] for double integrator purterbed system. On the same ground HOSMO is designed for electromechanical system in maglev using Eqs. (6) and (7) as explained below:

$$\begin{aligned} \left. \begin{aligned} \dot{\hat{e}}_1&=\hat{e}_2+z_1\\ \dot{\hat{e}}_2&=-a_1\hat{e_1}-a_2\hat{e_2}+\hat{e}_3+u+z_2\\ \dot{\hat{e}}_3&=z_3\\ \end{aligned} \right\} \end{aligned}$$

(11)

where $\hat{e_1}$ and $\hat{e_2}$ are the estimates of $e_1$ and $e_2$ respectively and $z_1,z_2$ and $z_3$ are the correction terms defined as:

$$\begin{aligned} \left. \begin{aligned} z_1&=k_1|e_1-\hat{e}_1|^{2/3}sign(e_1-\hat{e}_1)\\ z_2&=k_2|e_1-\hat{e}_1|^{1/3}sign(e_1-\hat{e}_1)\\ z_3&=k_3sign(e_1-\hat{e}_1)\\ \end{aligned} \right\} \end{aligned}$$

(12)

where $k_1,k_2$ and $k_3$ are positive constants. Let the estimated errors be $\tilde{e_1}=e_1-\hat{e_1}$, $\tilde{e_2}=e_2-\hat{e_2}$ and $\tilde{e_3}=-\hat{e_3}+d_1$. It is assumed that $d_1$ is Lipschitz and $|\dot{d_1}|<\varDelta$. The error dynamics of the estimated errors are:

$$\begin{aligned} \left. \begin{aligned} \dot{\tilde{e_1}}&=-k_1|\tilde{e_1}|^{2/3}sign(\tilde{e_1})+\tilde{e_2}\\ \dot{\tilde{e_2}}&=-k_2|\tilde{e_1}|^{1/3}sign(\tilde{e_1})+\tilde{e_3} \\ \dot{\tilde{e_3}}&=-k_3|\tilde{e_1}|^{1/3}sign(\tilde{e_1})+\dot{d_1}\\ \end{aligned} \right\} \end{aligned}$$

(13)

The above equation is finite time stable as proved in [30, 31]. It can be concluded that by selecting the appropriate gains $k_1,k_2,k_3$ as suggested by Levant [32], $\tilde{e_1}, \tilde{e_2}$ and $\tilde{e_3}$ will converge to zero in finite time.

Now in order to design the controller the sliding surface is defined as

$$\begin{aligned} \hat{\sigma }_1=c_1e_1+\hat{e}_2 \end{aligned}$$

(14)

Differentiation of Eq. (14) gives

$$\begin{aligned} \dot{\hat{\sigma }}_1=c_1\hat{e}_2-a_1\hat{e}_1-a_2\hat{e}_2+\hat{e}_3+z_2+x_3^* \end{aligned}$$

(15)

design the control $x_3^*$ as

$$\begin{aligned} x_{3}^*=&-\left( c_1\hat{e_2}-a_1\hat{e_1}-a_2\hat{e_2}+\hat{e_3}+z_2\right. \nonumber \\&\left. +L_1|{\hat{\sigma }}_1|^{1/2}sign({\hat{\sigma }}_1)+L_2\int _{0}^{t}sign({\hat{\sigma }}_1)\,\textrm{d}t\right) \end{aligned}$$

(16)

where $L_1$ and $L_2$ are user defined constants. The estimation of unknown uncertainty and disturbance $d_1$ is given by

$$\begin{aligned} \hat{d}_1=\hat{e}_3 \end{aligned}$$

(17)

Now ${x_3}*$ obtained is the desired value of the current to make the ball track the given reference trajectory. This value of the current is obtained with similar HOSMO based controller design for electrical loop. The design is explained in the following equations

$$\begin{aligned} e_4&=x_3-x_3^* \end{aligned}$$

(18)

$$\begin{aligned} \dot{\hat{e}}_4&=-a_3\hat{e}_4+bu+\hat{e}_5+z_4 \end{aligned}$$

(19)

$$\begin{aligned} \dot{\hat{e}}_5&=z_5 \end{aligned}$$

(20)

where the correction terms are

$$\begin{aligned} z_4&=k_4|\tilde{e_4}|^{2/3}sign(e_4-\hat{e}_4) \end{aligned}$$

(21)

$$\begin{aligned} z_5&=k_5sign(e_4-\hat{e}_4) \end{aligned}$$

(22)

Let’s define the sliding surface as

$$\begin{aligned} {\hat{\sigma }}_2=\hat{e}_4 \end{aligned}$$

(23)

Now taking differentiation of ${\hat{\sigma }}_2$ and design u as

$$\begin{aligned} u=&-(1/b)\left( -a_3\hat{e}_4+\hat{e}_5+z_4\right. \nonumber \\&\left. +L_3|{\hat{\sigma }}_2|^{1/2}sign({\hat{\sigma }}_2)+L_4\int _{0}^{t}sign({\hat{\sigma }}_2)\,\textrm{d}t\right) \end{aligned}$$

(24)

where $L_3$ and $L_4$ are user defined constants. The estimation of disturbance ${d}_2$ is given by

$$\begin{aligned} \hat{d}_2=\hat{e}_5 \end{aligned}$$

(25)

Fig. 2

Block diagram for proposed controller

The block diagram of the controller is as shown in Fig. 2A. Stability of the Controller The primary objective is to design a continuous control signal, denoted as ${x_3}^*$ in a manner that leads to the realization of second-order sliding mode within a finite time on the designated sliding surface. To achieve this goal, the control strategy is determined based on the following proposition. The control input designed in electromechanical loop results in the attainment of Second-Order Sliding Mode (SOSM) on within a finite time. Moreover, when $\hat{\sigma _1}$ reaches zero, it also implies the asymptotic stability of both $e_1$ and $e_2$ [29]. The control input ${x_3}^*$ as mentioned in (refeq.16) is given by

$$\begin{aligned} x_{3}^*=&-\left( c_1\hat{e_2}-a_1\hat{e_1}-a_2\hat{e_2}+\hat{e_3}+z_2\right. \nonumber \\&\left. +L_1|{\hat{\sigma }}_1|^{1/2}sign({\hat{\sigma }}_1)+L_2\int _{0}^{t}sign({\hat{\sigma }}_1)\,\textrm{d}t\right) \end{aligned}$$

(26)

where $L_1>0$ and $L_2>0$ By putting the value of this control input in Eq. (15) and representing Eq. (14) in the domain of $e_1$ and $\hat{\sigma _1}$

$$\begin{aligned} \dot{e_1}=&\hat{\sigma _1}-c_1e_1+{e}_2 \end{aligned}$$

(27)

$$\begin{aligned} \dot{\hat{\sigma }}_1=&c_1e_2-L_1|{\hat{\sigma }}_1|^{1/2}sign({\hat{\sigma }}_1)+v_1 \end{aligned}$$

(28)

$$\begin{aligned} \dot{v_1}=&-L_2sign({\hat{\sigma }}_1) \end{aligned}$$

(29)

As stated earlier with reference to Eq. (13) by selecting the appropriate gains $k_1,k_2,k_3$ as suggested by Levant in [32], $\tilde{e_1}, \tilde{e_2}$ and $\tilde{e_3}$ will converge to zero in finite time. The Eqs. (28) and (29) is a supertwisting control and by selecting $L_1, L_2$ as per [28] $\hat{\sigma _1}=0$ and $\dot{\hat{\sigma _1}}=0$ which further implies, that the closed loop system is given as

$$\begin{aligned} \dot{e_1}&=-c_1e_1 \end{aligned}$$

(30)

$$\begin{aligned} \dot{e_2}&=-c_1e_1 \end{aligned}$$

(31)

Therefore, both the states $e_1$ and $e_2$ are asymptotically stable by choosing $c1 > 0$

4 Performance evaluation with simulation

In this part, MATLAB/Simulink is used to gauge how well the suggested control method works. The outcomes of the proposed approach are contrasted with those of super twisting disturbance observer based controller (STDO), state and disturbance observer based controller(SDO) and PID controller. Table 1 contains a list of the nominal plant parameters of the magnetic levitation system that were used in the simulation and for experimental validation. By employing MATLAB/Simulink, we execute a simulation of the Maglev system illustrated in Fig. 1 to showcase the efficacy of the suggested controller. The initial conditions for the system states are set as follows: position of the ball $x(0)=0.014$, velocity $\dot{x}(0)=0$ and current $x_3=0$.

A PID controller integrated with a feed-forward (PID-FF) component is implemented and assessed for controlling the system, following the design principles outlined in the work by [33]. Within this framework, the electromechanical loop within the maglev system is governed by a combination of PID and feed-forward control, while the electrical loop is managed through Proportional Integral (PI) control. The gains for the PID controller and the feed-forward component are as per the recommendations of the authors as $Ki_b=524$, $K_pb=208$, $K_vb=3$, and $K_ff=153$. To maintain the real current $x_3$ at the desired current level, $x_{3}^*$, a PI controller is utilised in the current loop. The PI controller’s parameters are $ki=50,000$ and $kp=219$, respectively.

Magnetic levitation systems is controlled using cascaded sliding mode control, according to Ginoya et al. [26]. The electromechanical loop utilizes a sliding mode controller that relies on a state and disturbance observer (SDO). Meanwhile, the electrical loop employs a sliding mode controller centered around a disturbance observer. The SDO serves the purpose of concurrently estimating both the system’s state and uncertainty

The SDO-based controller used for the electromechanical subsystem and the DO based controller used for the electrical subsystem both have the controller parameter settings is mentioned in the said paper as $k_{l1}=35$, $k_{s1} =3$, $\epsilon _1=0.05$ and $k_{l2}=35$,$k_{s2} =3$, $\epsilon _2=0.05$ respectively.

A Super twisting disturbance observer(STDO) based controller is suggested by Dongardive et al. [28] to control the position of ball in maglev system. The control strategy has STDO designed for both the subsystems, electromechanical and electrical. The controller parameters used by the designer for electromechanical loop are $k_1=25$, $k_2=10$, $k_3 =0.01$, $\epsilon _1=0.05$ and for electrical loop are $k_4=50$, $k_5=2$, $k_6 =45$, and $\epsilon _2=0.05$.

Table 1 Nominal parameters of maglev system

With the nominal plant characteristics listed in Table 1, the proposed HOSMO-based controller is tested for the magnetic levitation system. In addition to being able to estimate the states of the system, the developed observer-based controller can estimate the disturbance and parametric uncertainty $d_1$ and $d_2$ in two loops of the Magalve system.

Fig. 3

Simulation results for proposed controller with nominal plant

Fig. 4

Plant states and its estimation for nominal plant and plant with $20\%$ uncertainty

Fig. 5

Simulation results for proposed controller with nominal plant

Fig. 6

Simulation outcomes for proposed controller under plant uncertainty of $20\%$

Fig. 7

Simulation outcomes for the proposed controller under a plant uncertainty of $20\%$

Fig. 8

Ball tracking comparison of all controllers with nominal plant and with uncertainty

Fig. 9

Current input comparison of all controllers with nominal plant and with uncertainty

Fig. 10

Control input comparison of all controllers with nominal plant and with uncertainty

The controller parameters used for electromechanical loop are $c_1=120$, $k_1=50$, $k_2=90$, $k_3 =40$, $L_1=2.4$, $L_2=3$, $\epsilon _1=0.001$ and for electrical loop are $k_4=50$, $k_5=25$, $L_3=14$, $L_4=20$, and $\epsilon _2=0.001$.

The simulation results for proposed controller for tracking of the desired trajectory, required control input current and control input voltage are shown in Fig. 3a–c respectively. Figure 5a, b show the plots of $d_1$ and $d_2$ with their corresponding estimates of $\hat{d_1}$ and $\hat{d_2}$, respectively. The designed HOSMO estimates the states of the system under nominal plant conditions and in presence of added uncertainty as shown in Fig. 4a, b and c and d respectively. Figure 5c, d respectively depict sliding surfaces used for controlling electromechanical and electrical loops. The generated control input and current are both within the maximum allowable limits and provide the desired tracking performance. The tracking performance together with control input, current, and uncertainty estimation are presented in Figs. 6 and 7 for the same plant when parametric uncertainty of $20\%$ is used to mimic it. Figure 8a, b, respectively, for nominal and system with uncertainty, show the comparative tracking results for all four controllers. The camprision of required control input is shown in Fig. 9a, b and current input required for nominal and uncertain plant are shown in Fig. 10a, b respectively. It is evident that the proposed controller outperforms the other two controllers.

5 Experimental results

The suggested controller architecture’s experimental verification is carried out utilizing a magnetic levitation laboratory apparatus by Quanser [34], depicted in Fig. 11.

Fig. 11

Magnetic levitatirolleron setup (Quanser Inc.2010)

Fig. 12

Results for proposed controller (experimental)

Fig. 13

Results for STDO based controller (experimental )

Fig. 14

Results for SDO based controller (experimental)

Fig. 15

Results for PID controller (experimental)

Within this setup, a robust one-inch steel ball is suspended utilizing an electromagnetic suspension mechanism within the maglev facility. Positioned atop the apparatus is an electromagnet capable of raising the steel ball from its base, sustaining it within open space. Two distinct system variables are immediately monitored and accessible for configuration feedback. These variables encompass the coil current and the gap between the magnetic surface and the ball. The ferromagnetic ball’s movement spans from 0 to 14 mm, while the optical sensor designed for ball detection operates within a linear range of 6–14 mm. Control input varies from 0 to 24 V, while input current ranges from 0 to 3 A. For all four controller types, the controller parameters and initial conditions are established to correspond with those utilized in the simulation. Figures 12, 13, 14 and 15 exhibit the reference tracking, required control input voltage, and input current graphs for all controllers respectively. According to the experimental validation, the proposed controller performs tracking better than the alternatives and keeping the current and voltage input within limit.

6 Performance evaluation of the proposed controller in comparison to the other three controllers

The efficacy of the proposed strategy is examined in this section through simulation. A comparison is drawn between the proposed method and the outcomes generated by a linear PID controller, an SDO-based controller, and an STA-based controller. The effectiveness of the suggested controller is evaluated across nominal system and nominal system with a 20$\%$ parametric uncertainty. Utilizing graphical representations, it becomes evident that the suggested technique excels in tracking performance within a predefined operational range. The evaluation of outcomes incorporates error-centric performance metrics like ISE, IAE, and ITAE. The summarized performance evaluation for all four controller types, nominal plant scenarios and based on error-related criteria with nominal parameters, is presented in Table 2.

The performance analysis of the controllers applied to a plant with a 20$\%$ uncertainty is shown in Table 3. The data in the table indisputably establishes that the suggested controller outperforms the other three approaches.

Table 2 Performance analysis of all controllers for nominal plant

Table 3 Performance analysis of all controllers for nominal plant with $20 \%$ uncertainty

7 Conclusion

In this work higher order sliding mode observer(HOSMO) based control is proposed for nonlinear, mismatched maglev system with uncertainties. The proposed strategy not only estimate the states of the system but it is also able to tackle uncertainties and disturbances with smooth control action. The recommended approach performs better than conventional PID, SDO-based and STDO based controls which is observed through simulation and experimental validation. The outcomes clearly indicate that the recommended controller proficiently stabilizes the magnetic levitation system even during challenging startup scenarios, seamlessly guiding it to the targeted operational states. It adeptly handles uncertain models subjected to external noise and effectively manages inherently unstable nonlinear dynamics.