1 Introduction

Magnetic levitation, also referred to as maglev, is an art by which a ferromagnetic object is levitated or suspended at a desired position using an electromagnet without any mechanical support. Such a method offers numerous advantages such as the elimination of lubrication systems and lowered rotating losses, providing higher speed and long-life services [1]. Due to those, maglev systems have found applications in many sophisticated areas including aircraft launch systems [2], maglev trains [3], nanoscale positioning systems [4], and vibration isolation of sensitive devices [5].

However, maglev systems have an unstable equilibrium point and nonlinear dynamic structures, which makes them challenging from a control point of view [5]. In addition, just like any other systems, they are susceptible to parameter uncertainties and external disturbances. This makes preserving the nominal performance of maglev systems with conventional controllers impossible under such severe conditions. As a result, maglev system has attracted a lot of attention from control society [5,6,7,8,9,10,11,12,13], and a variety of techniques have been proposed with the desire to achieve and maintain nominal performance. Among them are internal model-based robust regulator [6], adaptive robust control by K-filter approach [7], robust position estimation based on least square identification [8], nonlinear model predictive control [9], 2-DOF PID controller [10], neural-network-based control [11], sliding mode control [12], active disturbance rejection control [13], etc. The majority of those and other methods reported so far are advanced.

But despite all the advanced methods available, the conventional cascade configuration is worth reconsidering as a basic scheme owing to its practicality and ability to be decoupled during design for nominal performance. Also, cascade control structure is one of the most common control strategies in industrial processes to dramatically improve the performance of single-loop control, reducing both the maximum deviation and the integrated error of the disturbance response [14].

The controller that is commonly used in cascade configuration is proportional–integral (PI). Compared to other kinds, it is more suitable for practical implementation. And its main advantage is the ability to ensure zero steady-state error under low-frequency disturbances and model uncertainties as long as the closed-loop system is stable. However, the transient performance of PI controller depends on the system parameters, external disturbance, and input constraints [15]. Hence, this controller might be regarded as feasible but not robust enough.

Due to its practical importance, the design of a robust controller for systems affected by system parameter uncertainties and unmeasurable external disturbances has also been an area of active research. Therefore various approaches have been also proposed [16]. One well-known strategy is based on estimation and compensation, wherein effect of uncertainties and disturbances on the system is estimated and compensated by augmenting the controller designed for a nominal system [17,18,19,20,21,22,23,24,25]. The design procedure of such a disturbance observer-based controller has two stages. The first one focuses on stabilizing the plant performance under nominal conditions, while the other is about designing a disturbance observer (DOB) to compensate for the disturbance effects. Then, the designed DOB is integrated with the controller.

Motivated by Beale and Shafai [26] and Kim and Son [27], this paper proposes an approach in which a conventional cascade configuration controller, which can maintain nominal performance basically in the absence of system parameter uncertainty and external disturbance, is to be modified: by integrating it with two proportional–integral observers (PIOs) the system can maintain nominal performance even in their presence. The novelty of the method lies not in the use of PIO (or DOB) but in the use of dual PIOs for a nonlinear maglev system. In various cases, the proposed method has outperformed the ones that employed a single PIO [26]. Since the proposed controller suggests enhancement of robustness by modifying an already existing controller, it can be said that the advantage of the proposed control scheme is it’s ability to eliminate the need to design a new controller.

A theoretical analysis is also performed on such augmented system to illustrate the performance recovery property of the PIO from system uncertainties. The key tool used in that course is the singular perturbation theory [28], which arises from the fast PIO dynamics. A stability condition for the fast boundary-layer system is found out to determine observer gains such that the real uncertain system recovers the nominal plant without uncertainties. While the stability condition depends on a real system parameter, it can be made Hurwitz by adjusting the observer parameters. Under the condition, it is shown that the quasi-steady-state system closely approximates the nominal plant as the observer poles are placed sufficiently left of the complex s-plane.

This paper’s contributions may be summarized as follows:

  1. 1.

    A new cascade control approach is presented for a single-axis magnetic levitation system by combining a PI–PI cascade control and two nested PIOs to maintain desirable performance of the conventional closed-loop system even in the presence of uncertainties and disturbances.

  2. 2.

    Theoretical analysis is carried out on the performance of the closed-loop magnetic levitation system with the PIO, which confirms the desired approximation of the augmented system to the conventional closed-loop system without uncertainties.

  3. 3.

    Comparative computer simulations are conducted to verify the theoretical analysis.

The rest of the paper is organized as follows. Section 2 introduces the maglev system under consideration and its mathematical model. And subsequently, the conventional cascade controller design is presented along with a simulation result to study its performance under the influence of parameter uncertainty and disturbances. Based on the simulation, its weakness and the way it can be corrected are discussed. In Sect. 3 a PIO is briefed, and the proposed controller is designed. After the design, the robustness of the observer is analyzed in Sect. 4 using the singular perturbation theory. In Sect. 5 significant simulation results are presented verifying the performance of the proposed controller. In particular, the performances of various versions of the proposed controller are compared. Finally the next section concludes the paper.

2 System Model and Conventional Control Scheme

2.1 System Model

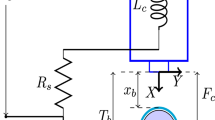
The basic principle of a magnetic levitation system operation is to apply a voltage to an electromagnet to generate sufficient magnetic force to keep a ferromagnetic object levitated. The magnetic levitation system considered here is a single-axis system (Fig. 1). That is, the ball can only move in the vertical direction. The current of the overhead electromagnet can be adjusted either to make the ball stay at a given position or to drive the ball to track a desired trajectory [12, 13].

Fig. 1
figure 1

Schematic diagram of the maglev system

Full size image

The equations describing the motion of the ferromagnetic ball and the current of the electric circuit are respectively

$$\begin{aligned} {\ddot{x}}&= g-\frac{G_{i}}{m}{\left( \frac{i}{x}\right) }^2, \end{aligned}$$
(1a)
$$\begin{aligned} L\frac{di}{dt}&= -Ri + V \end{aligned}$$
(1b)

where x represents the air gap or equivalently the ball’s position, i is the current passing through the electromagnet, m is the ball mass, g is the gravitational acceleration, \(G_i\) denotes the magnetic force constant for the electromagnet/ball pair at hand, R is the total resistance of the circuit, and L is the coil inductance. The \(G_{i}{\left( {i}/{x}\right) }^2\) term in (1a) characterizes the nonlinear relationship among the magnetic force, the current, and the ball position [12].

According to (1a), if the gravitational force (\(F_g\)) and the magnetic force (\(F_m\)) acting on the ball balance, then \({\ddot{x}} =0\). Thus the current that can bring such a steady state is

$$\begin{aligned} i_{e}=x_{e} \sqrt{\frac{gm}{G_i}} \end{aligned}$$
(2)

where \(x_e\) is the desired constant position and \(i_{e}\) is the corresponding current.

Theoretically, it is possible to achieve steady levitation of the ball by continuously providing the electromagnet with \(i_e\). But this cannot be guaranteed due to the open-loop unstable nature of the magnetic levitation system [13]. Therefore, to keep the ball in a steady state, a real-time closed-loop controller is required so that the two forces can always cancel out.

2.2 Conventional Control Scheme

One of the most popular control schemes applied to systems concatenated as in (1), consists of multiple controllers in a cascade configuration [29]. By treating the electromechanical system (1a) and the electrical system (1b) as separate subsystems, one can design two individual controllers. Equation (1a) will be used to design a ball position controller in the outer loop that tracks a desired reference ball position. That controller produces the reference current to be tracked by the inner-loop controller which amounts to the current controller. (The electromechanical and the electrical subsystem are labeled as Sys. 1 and Sys. 2 respectively in Figs. 2 and 5. Likewise, throughout the paper the subscript a is used to represent outer-loop equations and components, while the subscript b inner-loop counterparts.)

Fig. 2
figure 2

PI–PI cascade configuration controller, where \(d_a\) and \(d_b\) stand for the equivalent disturbances in the outer and inner-loop system respectively

Full size image

In order to design the outer-loop controller, (1a) needs to be linearized at point \((x_e, i_e)\) to yield

$$\begin{aligned} {\ddot{x}}&=\frac{2G_{i}i^2_{e}}{x^3_{e}m}x-\frac{2G_{i}i_{e}}{x^2_{e}m}i \end{aligned}$$
(3a)
$$\begin{aligned}&\triangleq a_Mx -b_M i. \end{aligned}$$
(3b)

Once the linearized equation is obtained, a state feedback controller is designed using the state space representation

$$\begin{aligned} \left[ \begin{array}{c}{{{\dot{\xi }}}}_1 \\ {{{\dot{\xi }}}}_2 \\ {{\dot{\zeta }}}_{x} \end{array}\right] =\left[ \begin{array}{ccc}0 &{}\quad 1 &{}\quad 0 \\ a_M &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 \ \end{array}\right] \left[ \begin{array}{c} \xi _1 \\ \xi _2 \\ \zeta _{x} \end{array}\right] +\left[ \begin{array}{c} 0 \\ -b_M \\ 0 \end{array}\right] i. \end{aligned}$$
(4)

where \(\xi _1 = x\), \(\xi _2 = {\dot{x}}\), and \(\zeta _{x}\) is the extra state variable used to calculate the I gain. The reference current provided by the outer-loop controller is given

$$\begin{aligned} i_c =-k_{P1}\left( \xi _1-x_e\right) -k_{P2}\xi _2 - k_{I1}\int _0^t {\left( \xi _1-x_e\right) d\tau } \end{aligned}$$
(5)

where \(k_{P1}\), \(k_{P2}\) and \(k_{I1}\) are the controller gains.

For the subsystem (1b) the inner-loop controller is designed using the corresponding state equation

$$\begin{aligned} \left[ \begin{array}{c}{{\dot{\xi }}}_3 \\ \dot{\zeta _i} \end{array}\right] =\left[ \begin{array}{cc}-{R}/{L} &{}\quad 0 \\ 1 &{}\quad 0 \end{array}\right] \left[ \begin{array}{c}\xi _3 \\ \zeta _i \ \end{array}\right] +\left[ \begin{array}{c}{1}/{L} \\ 0 \end{array}\right] V \end{aligned}$$
(6)

where the state \(\xi _3 = i\), and \(\zeta _i\) is the state variable serving same purpose as \(\zeta _{x}\) above. Then, the inner-loop controller is to supply the control input

$$\begin{aligned} V = -k_{P3}\left( \xi _3-i_c \right) -k_{I2}\int _0^t{\left( \xi _3-i_c \right) d\tau }. \end{aligned}$$
(7)

2.3 Limitations of Conventional Controller

The performance of the conventional controller has been analyzed through a computer simulation. The simulation tests and shows the controller’s performance under four conditions in Fig. 3: nominal (the green line), with system parameter uncertainties (the blue dotted line), with the influence of external disturbance (the red dashed line), and with the uncertainty and disturbance combined (the black line). Those conditions are more detailed in Sect. 5.

Fig. 3
figure 3

Simulation result illustrating the performance degradation of the PI–PI cascade configuration controller due to system parameter uncertainty and time-varying disturbance

Full size image

From Fig. 3 it can be seen that the conventional controller solely maintains nominal performance in the circumstance free from system parameter uncertainties and external disturbance. The presence of system parameter uncertainty degrades the transient-state response of the system, while that of external disturbance disrupts the system’s steady-state performance. Also, the controller fails to regain nominal performance when the external disturbance takes a form of a time-varying function. Hence, the conventional controller is not considered robust enough.

3 Robust Performance via PIO-Based Controller

In this section, a proportional–integral observer is briefly introduced and then two individual PIOs will be designed for both control loops mentioned in the previous section.

3.1 Proportional–Integral Observer (PIO)

A PIO is a type of disturbance observer (DOB). The primary role of DOBs is to compensate an uncertain system affected by disturbance so that the controller designed, just for the nominal disturbance-free model of the plant, recovers robust stability and performance [18, 20, 21]. PIO uses two feedback loops to reconstruct system states and the equivalent disturbance which is a combination of the effects of unknown inputs, system parameter uncertainties and unmodeled system dynamics or modeling errors. Once the equivalent disturbance is estimated, it is subtracted from the original control input to cancel out the undesired influence (as can be seen in Fig. 4). Therefore, important is to find \({{\hat{d}}}\), the equivalent disturbance estimate.

Fig. 4
figure 4

Controller with a PIO, where r is the reference signal, u is the control input, d is external disturbance, and y is the system output

Full size image

The state-space model of an nth order, p input, q output plant with p independent disturbances of constant value can be represented by

$$\begin{aligned} {\dot{x}}&= Ax+B(u+d),\;\;\;\; y=Cx, \end{aligned}$$
(8a)
$$\begin{aligned} \dot{d}&= 0.&\end{aligned}$$
(8b)

The equations above can be put together defining a new state vector \(z=\left[ \begin{array}{cc}x^T,&d^T \end{array}\right] ^T\). Thus, the augmented model of the plant can be written

$$\begin{aligned} {\dot{z}}&= \left[ \begin{array}{cc}A &{}\quad B\\ 0 &{}\quad 0\end{array}\right] \left[ \begin{array}{c}x\\ d\end{array}\right] +\left[ \begin{array}{c}B\\ 0 \end{array}\right] u \;\;\triangleq \;\; A_z z+B_z u \end{aligned}$$
(9a)
$$\begin{aligned} y&= \left[ \begin{array}{cc}C&\quad 0\end{array}\right] \left[ \begin{array}{c}x \\ d\end{array}\right] \;\; \triangleq \;\; C_z z. \end{aligned}$$
(9b)

Now a PIO is designed as below.

$$\begin{aligned} \dot{{{\hat{z}}}} = A_z {{\hat{z}}} + B_z u + L_z\left( C_z z- C_z{{\hat{z}}}\right) \end{aligned}$$
(10)

where \(L_z=\left[ \begin{array}{cc}L_P^T&L_I^T \end{array}\right] ^T\). Then the dynamics of the estimation error turns out

$$\begin{aligned} \dot{e}_z \triangleq \; {\dot{z}} - \dot{{{\hat{z}}}} = (A_z-L_zC_z)e_z. \end{aligned}$$
(11)

Thus, as long as the matrix \(A_z-L_zC_z=\left[ \begin{array}{cc}A-L_PC &{}\quad B\\ -L_IC &{}\quad 0\end{array}\right]\) is Hurwitz, the error between actual and estimated state variables will decay to zero as time goes to infinity.

3.2 Dual PIO-Based Controller

To maintain its advantage, this paper employs a control structure composed of two PI controllers in a conventional cascade configuration. Instead, two PIOs are supplemented to the control loops to enhance robustness. With their assistance, the controller proposed, as can be seen in Fig. 5, takes the effect of the disturbance into consideration and counteracts its undesired influence.

Fig. 5
figure 5

Controllers with two PIOs in cascade configuration, where \({{\hat{d}}}_a\) and \({{\hat{d}}}_b\) represent the equivalent disturbance estimates in their respective loops

Full size image

The \(PIO_a\) for the outer loop is designed for the subsystem (3). So, following (10) its model is

$$\begin{aligned} \dot{{{\hat{z}}}}_a = A_a{{\hat{z}}}_a + B_a i + L_a\left( C_a z_a -C_a{{\hat{z}}}_a\right) \end{aligned}$$
(12)

where \({z}_a = \left[ \begin{array}{ccc} z_1&\quad z_2&\quad {d}_a \end{array}\right] ^T = \left[ \begin{array}{ccc} x&\quad {\dot{x}}&\quad {d}_a \end{array}\right] ^T\), and coefficient matrices \(A_a\), \(B_a\), \(C_a\) and \(L_a\) are

$$\begin{aligned} \begin{array}{c} A_a=\left[ \begin{array}{ccc}0 &{}\quad 1 &{}\quad 0\\ a_M &{}\quad 0 &{}\quad -b_M\\ 0&{}\quad 0&{}\quad 0 \end{array}\right] ,\; B_a=\left[ \begin{array}{c}0\\ -b_M \\ 0\end{array}\right] , \\ C_a=\left[ \begin{array}{ccc}1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \end{array}\right] , \;\; L_a = \left[ \begin{array}{ccc}l_{11} &{}\quad l_{21} &{}\quad l_{31} \\ l_{12} &{}\quad l_{22} &{}\quad l_{32}\end{array}\right] ^T. \end{array} \end{aligned}$$

The \(PIO_a\) is to estimate the ball’s position (x) and velocity (\({\dot{x}}\)). It additionally does the equivalent disturbance present in the subsystem \({{\hat{d}}}_a\). Using these estimates the reference current is set to

$$\begin{aligned} i_r = i^* - {{\hat{d}}}_a \end{aligned}$$
(13)

where \(i^* =-k_{P1} {{\bar{z}}}_1 -k_{P2} {{{\hat{z}}}_2}-k_{I1}\int _0^t{{{\bar{z}}}_1 d\tau }\) with \({{\bar{z}}}_1 = {{\hat{z}}}_1 - x_e\) like (5). Therefore, the reference current \(i_r\) modified by the proposed controller is obtained by subtracting the estimated equivalent disturbance, \({{\hat{d}}}_a\), from the original reference current \(i^*\).

Meanwhile, the inner-loop observer is designed through the same procedure. For the electrical subsystem (1b), the model of \(PIO_b\) is

$$\begin{aligned} \dot{{{\hat{z}}}}_b = A_b{{\hat{z}}}_b + B_b V + L_b\left( C_b z_b -C_b{{\hat{z}}}_b\right) \end{aligned}$$
(14)

where \(z_b = \left[ \begin{array}{cc} z_3&\quad {d}_b \end{array}\right] ^T = \left[ \begin{array}{cc} i&\quad d_b \end{array}\right] ^T\), \(L_b\) is the observer gain matrix, and the remaining matrices are

$$\begin{aligned} A_b=\left[ \begin{array}{cc}-{R}/{L} &{}\quad {1}/{L}\\ 0&{}\quad 0\end{array}\right] , B_b=\left[ \begin{array}{c}{1}/{L}\\ 0\end{array}\right] , C_b=\left[ \begin{array}{cc}1&\quad 0\end{array}\right] . \end{aligned}$$
(15)

Obviously, \(PIO_b\) estimates the current denoted by \(z_3\) and the disturbance \(d_b\). Consequently the control input, which is the output of the inner-loop controller, becomes

$$\begin{aligned} V = -k_{P3}\left( {{\hat{z}}}_3 - i_r\right) -k_{I2}\int _0^t \left( {\hat{z}}_3 - i_r \right) d\tau - {{\hat{d}}}_b. \end{aligned}$$
(16)

4 Theoretical Performance Analysis

In here, the performance of the feedforward compensation by \(PIO_a\) is analyzed according to the singular perturbation theory [28]. The \({{\hat{d}}}_a\) is the estimation of \(d_a\), which represents the combined effect of the external disturbance and the system uncertainties in the outer loop. When \(i = i_r = i^* - {{\hat{d}}}_a\), the outer-loop system is governed by

$$\begin{aligned} {\dot{x}}_1&= x_2 \end{aligned}$$
(17a)
$$\begin{aligned} {\dot{x}}_2&= a_Mx_1 - b_M(i^*-{\hat{d}}_a +d). \end{aligned}$$
(17b)

If the model of \(PIO_a\) in (12) is written out, it appears

$$\begin{aligned} \dot{{{\hat{x}}}}_1&= {{\hat{x}}}_2 + l_{11}{{\tilde{x}}}_1 + l_{12}{{\tilde{x}}}_2 \end{aligned}$$
(18a)
$$\begin{aligned} \dot{{{\hat{x}}}}_2&= {{\hat{a}}}_M{{\hat{x}}}_1 - {{\hat{b}}}_M i^* + l_{21} {{\tilde{x}}}_1 + l_{22}{{\tilde{x}}}_2 \end{aligned}$$
(18b)
$$\begin{aligned} \dot{{{\hat{d}}}}_a&= l_{31} {{\tilde{x}}}_1 + l_{32}{{\tilde{x}}}_2 \end{aligned}$$
(18c)

where \({{\tilde{x}}}_i = x_i - {{\hat{x}}}_i\) (\(i = 1,2\)), \({{\hat{a}}}_M\) and \({{\hat{b}}}_M\) are the nominal values of \(a_M\) and \(b_M\) respectively, unaltered by system parameter uncertainty.

When \(a_M={{\hat{a}}}_M\), \(b_M={{\hat{b}}}_M\), and \(d=d_a\), the observer error dynamics in (11) leads to

$$\begin{aligned} \left[ \begin{array}{c}\dot{{{\tilde{x}}}}_1 \\ \dot{{{\tilde{x}}}}_2 \\ \dot{{{\tilde{d}}}}_a \end{array}\right] = \left[ \begin{array}{ccc} -l_{11} &{}\quad -(l_{12}-1) &{}\quad 0 \\ -(l_{21}-{{\hat{a}}}_M) &{}\quad -l_{22} &{}\quad -{{\hat{b}}}_M \\ -l_{31} &{}\quad -l_{32} &{}\quad 0\end{array}\right] \left[ \begin{array}{c} {{\tilde{x}}}_1 \\ {{\tilde{x}}}_2 \\ {{\tilde{d}}}_a \end{array}\right] \end{aligned}$$
(19)

where \({\tilde{d}}_a = d_a - {\hat{d}}_a\). By using the observer gain

$$\begin{aligned} L_a = \left[ \begin{array}{ccc} {k_1}/{\epsilon } &{}\quad {{\hat{a}}}_M &{}\quad 0 \\ 1 &{}\quad {k_2}/{\epsilon } &{}\quad -k_3/({{\hat{b}}}_M \epsilon ^2) \end{array}\right] ^T, \end{aligned}$$
(20)

one can obtain the characteristic equation of (19) as follows:

$$\begin{aligned} \left( s + \frac{k_1}{\epsilon }\right) \left( s^2 + \frac{k_2}{\epsilon }s + \frac{k_3}{\epsilon ^2}\right) = 0. \end{aligned}$$
(21)

Therefore, if \(\epsilon > 0\) and \(k_i > 0\) (\(i = 1,2,3\)), (21) is Hurwitz. When \(k_1 = k_3 = 1\) and \(k_2 =2\), for example, three roots are located all at \(s = -1/\epsilon\).

On the other hand, when \({{\hat{a}}}_M \ne a_M\), \({{\hat{b}}}_M \ne b_M\) and \(d_a \ne d\), the observer error dynamics changes to

$$\begin{aligned} \dot{{{\tilde{x}}}}_1&= -\frac{k_1}{\epsilon }{{\tilde{x}}}_1 \end{aligned}$$
(22a)
$$\begin{aligned} \dot{{{\tilde{x}}}}_2&= -\frac{k_2}{\epsilon }{{\tilde{x}}}_2 + b_M{{\hat{d}}}_a + \delta \end{aligned}$$
(22b)
$$\begin{aligned} \dot{{{\hat{d}}}}_a&= -\frac{1}{{{\hat{b}}}_m}\frac{k_3}{\epsilon ^2}{{\tilde{x}}}_2 \end{aligned}$$
(22c)

where \(\delta = (a_M-{{\hat{a}}}_M)x_1 - b_Md - (b_M-{{\hat{b}}}_M)i^*\).

Introducing a pair of new state variables

$$\begin{aligned} \eta _1 = \frac{1}{\epsilon }{\tilde{x}}_1, \quad \eta _2 = \frac{1}{\epsilon }{\tilde{x}}_2, \end{aligned}$$
(23)

(17) and (22) can be put into the standard singular perturbation form;

$$\begin{aligned} {\dot{x}}_1&= x_2 \end{aligned}$$
(24a)
$$\begin{aligned} {\dot{x}}_2&= a_Mx_1 - b_M(i^* - {\hat{d}}_a + d) \end{aligned}$$
(24b)
$$\begin{aligned} \epsilon {{\dot{\eta }}}_1&= -k_1\eta _1 \end{aligned}$$
(24c)
$$\begin{aligned} \epsilon {{\dot{\eta }}}_2&= -k_2\eta _2 + b_M{{\hat{d}}}_a + \delta \end{aligned}$$
(24d)
$$\begin{aligned} \epsilon \dot{{{\hat{d}}}}_a&=- \frac{k_3}{{{\hat{b}}}_M} \eta _2. \end{aligned}$$
(24e)

To find the quasi-steady-state solution of (24), stability of the boundary-layer system should be checked. To this end, the characteristic equation of the boundary-layer system (24c)–(24e) is earned

$$\begin{aligned} \left( s + k_1\right) \left( s^2 + k_2 s + \frac{b_M}{{{\hat{b}}}_M}k_3\right) = 0, \end{aligned}$$
(25)

implying to the fact that if \(b_M/{{\hat{b}}}_M > 0\), (25) is Hurwitz because \(k_i > 0\) (\(i = 1,2,3\)).

When (25) is Hurwitz and \(\epsilon \ll 1\), according to the singular perturbation analysis, the quasi-steady-state solution satisfies the following property.

$$\begin{aligned} \eta _1 = \eta _2 = 0\quad \text {and}\quad b_M{\hat{d}}_a=-\delta . \end{aligned}$$
(26)

Substitution of the property in (24b) enables to derive the quasi-steady-state system version of (24):

$$\begin{aligned} {\dot{x}}_1&= x_2 \end{aligned}$$
(27a)
$$\begin{aligned} {\dot{x}}_2&= {\hat{a}}_Mx_1-{\hat{b}}_Mi^*. \end{aligned}$$
(27b)

Hence, it can be said that the system of (17)–(18) behaves like the nominal system as \(\epsilon \rightarrow 0\) under the stability condition of (25). (The performance analysis on the feedforward compensation by \(PIO_b\) can be similarly done.)

Remark 1

When only the position information is available for the outer-loop \(PIO_a\), the output matrix reduces to \(C_a=\left[ \begin{array}{ccc}1&\quad 0&\quad 0 \end{array}\right]\). Using the observer gain

$$\begin{aligned} L_a = \left[ \begin{array}{ccc} {k_1}/{\epsilon },&\quad {\hat{a}}_M + {k_2}/{\epsilon ^2},&\quad -{k_3}/({{{\hat{b}}}_M}\epsilon ^3) \end{array}\right] ^T, \end{aligned}$$
(28)

one can obtain the same performance recovery property if the next equation is Hurwitz.

$$\begin{aligned} s^3 + k_1 s^2 + k_2 s+ \frac{b_M}{{{\hat{b}}}_M}k_3 = 0. \end{aligned}$$
(29)

Certainly, it can be made Hurwitz by adjusting the parameters based on the physical bound of \(b_M\) and the root locus method [18].

5 Simulation Results

The performance of the proposed controller, in the presence of system parameter uncertainties and external disturbances, has been verified by comparative computer simulations. In the simulations, the desired elevation, \(x_e\), that needs to be tracked by the outer-loop controller is constantly 7 mm. And the corresponding current, \(i_e\), that needs to be tracked by the inner-loop controller equals to 1 A. Thus, the simulations aim to prove that the proposed controller can maintain the desired operation values under such severe conditions. The initial values of the states variables \(\left[ \begin{array}{ccc}x&\quad {\dot{x}}&\quad i\end{array}\right] ^T\) were chosen to be \(\left[ \begin{array}{ccc}0.01&\quad 0&\quad 0\end{array}\right] ^T\). In order to reflect physical constraints, the control input in the simulations was limited to 100V in magnitude.

5.1 Robustness Improvement

System parameter variations are introduced in a manner that can reflect component performance deterioration and other environmental influences such as temperature change. The nominal and actual values of the system parameters are specified in Table 1.

Table 1 System parameter values
Full size table

External disturbances are also inserted into both loops separately: two time-varying noise signals and one constant disturbance. The inner-loop disturbance added to the control input in the fashion of a varying noise consists of two different signals, of which one is a constant between 0.5 and 0.6 s, while the other is a random time-varying signal of unknown function. The outer-loop disturbance is designed to mimic a physical disturbance (a downward pull of 3 mm at \(t = 1\) s) acting on the ball. Designing the external disturbance in that way allows to see how well both PIOs can estimate the disturbance in their respective loop. It also helps evaluate the effect a disturbance in one loop has on the performance of the other loop’s controller.

It has been mentioned previously that one of the advantages of cascade configuration is its ability to be implemented on control systems that can be decoupled during design. This allows the option of integrating only one of the control loops with a PIO. In this context, The first is designed with a PIO only in the outer-loop (Controller 1 in Table 2 and the blue dotted line in Fig. 6), the second with a PIO only in the inner loop (Controller 2 in Table 2 and the red dashed line in Fig. 6), and finally the third with a PIO in each loop (Controller 3 in Table 2 and the black solid line in Fig. 6). The original control scheme discussed in Sect. 2 is referred to as Controller 0 in Table 2.

Table 2 Control schemes considered
Full size table

The controller’s performance is evaluated in terms of its ability to track the reference ball position in the presence of system parameter uncertainty, to recover from external disturbance, and to estimate the equivalent disturbances. As follows are the simulation results.

Fig. 6
figure 6

Simulation result showing the performances of the three versions of the PIO-based controller

Full size image

From the ball position simulation result in Fig. 6, it can be seen that the controller integrated with dual PIOs (black line) performs best out of the three non-nominal cases. It recovers fastest from disturbances (seen in the steady state performance), resists the effect of system parameter uncertainties (seen in the transient state performance), and tracks the reference signal most accurately. Therefore, in view of this controller’s ability to closely approximate the nominal performance(green line), it is proposed as a robust controller for maglev systems. It can also be discovered in Fig. 7 that the proposed controller applies control input of appropriate magnitude to the system faster than the other two versions.

Fig. 7
figure 7

Control input

Full size image
Fig. 8
figure 8

Estimated equivalent disturbance in the outer loop

Full size image
Fig. 9
figure 9

Estimated equivalent disturbance in the inner loop

Full size image
Fig. 10
figure 10

Control performance improvement in ball position

Full size image
Fig. 11
figure 11

Control performance improvement in control input

Full size image

5.2 Disturbance Estimation

The simulations also reveal that the performance of the controller depends on its ability to access to an estimated disturbance. See Figs. 8 and 9. The controller equipped only with \(PIO_b\) (red dashed line in Fig. 6) fails to compensate for the effect of the outer-loop disturbance. Hence it is unable to quickly recover from it as shown in the figure. Meanwhile, the controller only with \(PIO_a\) (blue dotted line in Fig. 6) cannot counteract the effect of the inner-loop disturbance (as can be seen from its performance between 0.5 and 0.6 s). But it rapidly recovers from the outer-loop disturbance showing a good steady-state performance. It is owing to the inner-loop PI controller’s ability to ensure zero steady-state error.

This means that when integrating a PIO with a cascade configuration controller, all the loops need to have individual PIOs to guarantee that the nominal performance of each control loop is well maintained. It is noteworthy that the performance of the observer in Figs. 8 and 9 can be further enhanced by performing multiple integrations of the estimation error and the measurement output simultaneously [19, 30].

The controller and observer gains were obtained by pole placement techniques. The poles were chosen following the rule of cascade control. The inner-loop system, which is an electrical system, is much faster than the electromechanical outer-loop system. Therefore, since the inner-loop controller and observer are expected to be faster than their outer-loop counterparts, the poles of the inner-loop controller and observer are placed further away from the imaginary axis than those of outer-loop controller and observer. Similarly, since the observer in each loop is expected to be significantly faster than the controller, the locations of the observer poles are chosen further away leftward from the controller poles.

The outer-loop controller gains result from placing the closed-loop poles at \(-\,20\pm j10\) and \(-\,50\). They are

$$\begin{aligned} k_{P1} = -\,270.41,\; k_{P2} = -\,4.59,\; k_{I1} = -\,1275.50. \end{aligned}$$
(30)

And the outer-loop PIO poles are placed at \(-\,250, -\,250\) and \(-\,275\) to obtain the observer gains:

$$\begin{aligned} L_a = \left[ \begin{array}{cc} 2.50\times 10^2 &{}\quad 1\\ 2.80\times 10^3 &{}\quad 5.25\times 10^2\\ 0 &{}\quad -3.51\times 10^3 \end{array}\right] . \end{aligned}$$
(31)

For the inner-loop, controller gains are obtained as follows by placing the two closed-loop poles equally at \(-\,300\).

$$\begin{aligned} k_{P3} = 2.59\times 10^2, k_{I2} = 4.05\times 10^4. \end{aligned}$$
(32)

And the PIO poles are placed equally again at \(-\,1250\), resulting in an observer gain matrix

$$\begin{aligned} L_{b} = \left[ \begin{array}{c} 2.48\times 10^3\\ 7.03 \times 10^5\end{array}\right] . \end{aligned}$$
(33)

The overall improvement made on the result of the existing control scheme can be observed in Figs. 10 and 11. They are summarized as follows.

  1. 1.

    Improved transient response in view of the overshoot and the settling time. The original controller’s settling time 0.86 has reduced to 0.37 s.

  2. 2.

    Stronger resistance to external disturbance and faster recovery as seen from \(t=1\) to 2 s.

  3. 3.

    Smaller control input as seen in Fig. 11.

6 Conclusion

Maglev systems belong to a class of systems that are challenging but at the same time implemented in delicate applications where reliable control systems are in demand. Moreover, the existence of system parameter uncertainties and external disturbances makes the challenge even greater.

In this context, this paper has proposed a robust controller that can overcome those negative influences for a single-axis magnetic levitation system. The new control system has been designed by cascading two PI controllers each with a nested PIO. The design procedure was detailed and theoretical analysis was carried out according to the singular perturbation theory to verify that the resultant integrated system can approximate the nominal system even under severe conditions.

The performance of the proposed controller was also tested by simulations and its ability to robustly maintain nominal performance was proved. It has also been confirmed from the simulation results that optimum system performance is guaranteed only when every control loop is unexceptionally integrated with a PIO. However, if the control loop that is highly vulnerable to parameter uncertainty and disturbance can be identified and if those in the other loop are negligible, then the results may indicate that adequate performance can be obtained even when a PIO is included only in the former control loop. Since the system under consideration in this paper is a single axis magnetic levitation system, the future work aims at tackling a more practical, and yet complex magnetic levitation system with more degrees of motional freedom.