1 Introduction

In various areas of the acoustic NDT starting from nano and micro scales to geophysical scales, the high frequency Stoneley waves can give essential information on the physical properties of the adjacent layers along with information on possible interfacial cracks and other defects. The Wiechert condition imposed on the relation between bulk wave velocities of the contacting layers, play an important role in acoustic analyses, especially at analyzing high-frequency Stoneley waves arising and propagating along the interfaces. The present study concerns with a non-propagating condition for Stoneley waves at the vicinity of the Wiechert condition.

In the original paper [1] Stoneley deduced an equation for finding speed of propagation of an interface surface wave travelling along the interface between two elastic isotropic halfspaces in mechanical contact

$$ \begin{aligned} P(c) & \equiv c^{4} \left( {\left( {\uprho_{1} - \uprho_{2} } \right)^{2} - \left( {\uprho_{1} A_{2} + \uprho_{2} A_{1} } \right)\left( {\uprho_{1} B_{2} + \uprho_{2} B_{1} } \right)} \right) \\ & \quad + 2Kc^{2} \left( {\uprho_{1} A_{2} B_{2} - \uprho_{2} A_{1} B_{1} - \uprho_{1} + \uprho_{2} } \right) \\ & \quad + K^{2} \left( {A_{1} B_{1} - 1} \right)\left( {A_{2} B_{2} - 1} \right) = 0, \\ \end{aligned} $$
(1)

where \(c\) is the desired Stoneley wave velocity; \(\uprho_{1} ,\,\,\uprho_{2}\) are the material densities of the halfspaces; and

$$ \begin{aligned} & K = 2\left( {\uprho_{1} \upbeta_{1}^{2} - \uprho_{2} \upbeta_{2}^{2} } \right),\quad A_{k} = \sqrt {1 - \frac{{c^{2} }}{{\upalpha_{k}^{2} }}} ,\\ & B_{k} = \sqrt {1 - \frac{{c^{2} }}{{\upbeta_{k}^{2} }}} ,\quad k = 1,2. \end{aligned} $$
(2)

In Eqs. (2) \(\upalpha_{k} ,\,\,\upbeta_{k}\) are respectively longitudinal and shear bulk wave velocities in the corresponding halfspaces:

$$ \upalpha_{k} = \sqrt {\frac{{\uplambda_{k} + 2\upmu_{k} }}{{\uprho_{k} }}} ,\quad_{k} = \sqrt {\frac{{\upmu_{k} }}{{\uprho_{k} }}} ,\quad k = 1,2, $$
(3)

where \(\uplambda_{k}\) and \(\upmu_{k}\) are Lame constants.

The main attention in Stoneley’s work was paid to the important in geophysics case when elastic properties of both media satisfy the Wiechert condition [2]:

$$ \frac{{\upalpha_{1} }}{{\upalpha_{2} }} = \frac{{\upbeta_{1} }}{{\upbeta_{2} }} = 1. $$
(4)

Stoneley’s asymptotic analysis of Eq. (1) based on Taylor’s expansions of expressions for \(A_{k} ,\,\,B_{k}\) at small \(c\) allowed him to conclude that at the condition (4) there is the unique real root of Eq. (1):

$$ {\text{Im}} (c) = 0. $$
(5)

Stoneley also asserted that such a root satisfies the following condition

$$ \upbeta \ge c \ge 0. $$
(6)

Note that at condition (4) there is no need in indices of the bulk wave velocities.

The Eq. (1) was numerically analyzed by Sezawa and Kanai [3] for the case of Poisson’s media, when

$$ \uplambda_{k} = \upmu_{k} ,\quad k = 1,2. $$
(7)

The condition (7) is satisfied at Poisson’s ratios \(\nu_{k} = \tfrac{1}{4},\,\,\,\,\,k = 1,2\). Numerical analysis of Eq. (1) at condition (7) gave the following range of the Stoneley wave existence [3]

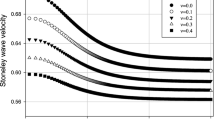
In Fig. 1 dashed diagonal line corresponds to the media satisfying Wiechert condition (4); and the region of existence is the narrow part between two curves; while curves correspond to the limiting cases of existing real and positive roots of Eq. (1) that satisfy the following relation

$$ c \le \mathop {\min }\limits_{k = 1,2} \left( {\upbeta_{k} } \right). $$
(8)
Fig. 1
figure 1

Region of existence of Stoneley waves at Poisson’s condition (7) [3]

Full size image

Note that relation (8) ensures real coefficients of Eq. (1). The plots initially obtained through numerical analysis by Sezawa and Kanai [3] were also (numerically) confirmed by Cagniard [4] and Scholte [5, 6].

Despite quite a large number [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] of studies on Stoneley waves propagating in isotropic and anisotropic media, existence of Stoneley waves at the vicinity of the point \(A\) (see Fig. 1), where both contacting media have identical physical properties, has not been questioned. However, it will be demonstrated below that not only a singular point \(A\), but also it’s open vicinity does not belong to the region of existence. The fact of nonexistence of Stoneley waves in a broader range at the vicinity of point \(A\), can have various applications starting from non-destructive testing of stratified composites containing micro and nano layers to geophysics.

2 Theoretical considerations

Consider point \(A\), where according to the Wiechert condition Eq. (4) and Poisson’s relation (7):

$$ \uplambda_{1} = \uplambda_{2} = \upmu_{1} = \upmu_{2} ;\quad \uprho_{1} = \uprho_{2} . $$
(9)

Thus, acoustically both contacting media become identical, so the two halfspaces eventually form a single homogeneous space without any interfaces. But, in a homogeneous space no surface waves can propagate [22], so at least one point \(A\) should be excluded from the region of existence.

Moreover, direct verification reveals that Eq. (1) at condition (9) yields

$$ 4\uprho^{2} c^{4} \sqrt {1 - \frac{{c^{2} }}{{\upalpha^{2} }}} \sqrt {1 - \frac{{c^{2} }}{{\upbeta^{2} }}} = 0, $$
(10)

where in view of (9) indices at \(\uprho ,\upalpha ,\,\,\upbeta\) are omitted. Now, Eq. (10) has eight roots

$$ c_{1,2,3,4} = 0,\quad c_{5,6} = \pm \upalpha ,\quad c_{7,8} = \pm \upbeta , $$
(11)

none of which satisfies conditions for the propagating Stoneley wave.

Now, it is necessary to show that along with the point \(A\), an open vicinity of that point should also be excluded from the region of existence. To prove that consider the left-hand side of Eq. (1) which can be considered as a continuous function of the \(c\) variable:

$$ P(c):\,\,{\mathbb{C}} \to \,{\mathbb{C}}, $$
(12)

\({\mathbb{C}}\) is the complex plane. In view of continuity of \(P(c)\), solutions of Eqs. (1), (5) and (6) form a closed subset \(B \subset {\mathbb{C}}\). Thus, the region of existence should be closed, however, exclusion point \(A\) from \(B\) makes the solution subset \(B\backslash A\) being not closed, but the latter means that an open vicinity of the point \(A\) should also be excluded.

3 Numerical analysis

Computing the roots of Eq. (1) obeying conditions (5), (6) for Poisson’s media satisfying condition (7) and other media with equal Poisson’s ratios, yields the following results for the region of Stoneley wave existence, presented in Fig. 2.

Fig. 2
figure 2

Region of existence of Stoneley waves marked in grey at Poisson’s ratios: a 0.0; b 0.25; c 0.499

Full size image

The plots in Fig. 2 clearly indicate that along with point \(A\) with coordinates \((1;1)\) a vicinity of that point also does not belong to the region of existence of Stoneley waves for the studied Poisson’s ratios. Computations were made using multiprecision algorithms [23] with long mantissas up to ~ 1000 decimal digits to minimize possible round of errors in finding roots of Eq. (1).

4 Concluding remarks

Both theoretical and numerical analyses revealed a more complicated structure of the Stoneley wave region of existence. In particular, for contacting halfspaces with Poisson’s ratios varying from 0.0 to 0.499, the corresponding regions of existence are doubly connected, see Fig. 2.

The obtained result may be relevant in various geophysical applications, since in the pioneering works [1,2,3,4,5], and in quite a large number of the subsequent studies in theoretical and applied geophysics and wave dynamics [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22, 24,25,26,27,28,29,30] it was implicitly assumed that the region of existence for Stoneley waves is simply connected with point (1;1) belonging to that region.