1 Introduction

Stoneley waves propagating along an interface between two dissimilar isotropic and homogeneous halfspaces in a contact are analyzed by applying Cauchy sextic formalism coupled with the exponential fundamental matrix method [1, 2]. That formalism was initially developed for study of guided wave propagation in stratified plates, and later on, it was modified for application to acoustics of functionally graded (FG) plates [3]. In the current research, the main attention is paid to the case when physical properties of the contacted halfspaces satisfy the Wiechert condition [4, 5] with relation to velocities of the interfacial Stoneley waves [6].

In [7,8,9], it was observed that at high frequencies Lamb waves propagating in stratified media are transformed into Stoneley waves, if the adjacent layers satisfy Wiechert condition. It was also observed that the number of different Stoneley waves propagating in stratified plates with periodic structure depends upon symmetric (with the odd number of alternating layers) or asymmetric layout of layers (with the even number of layers) [9].

Herein, it is shown both theoretically and numerically that the speed of propagation of Stoneley waves along Wiechert line is monotonically decreasing in the range \(q\in (1,\,\infty )\) where q is the dimensionless Wiechert parameter; for the definition, see Sect. 2. The observed monotonic variation delivers the unique possibility for applying acoustic methods to nondestructive evaluation of physical parameters of contacting media obeying Wiechert condition; see Remark 3.2. Moreover, the observed monotonic variation of Stoneley wave velocity takes place for all studied (nonnegative) values of Poisson’s ratio; see Sect. 3.3.

It should be noted that the Wiechert condition was originally proposed to describe the physical properties of the layered structure of the Earth’s crust [4, 5]; since that time, the Wiechert condition plays an important role in the problems of Stoneley wave existence [7,8,9,10,11,12,13,14,15,16,17]. In this respect, the Wiechert line plays an important role in deriving conditions of existence. The Wiechert line is defined as the straight line in a 3D space of the dimensionless physical parameters of the contacting isotropic media with equal Poisson’s ratios; it is discussed in Sect. 2 in more detail.

Another remark concerns analyzing the non-homogeneous Stoneley waves [18, 19] corresponding to the pulse of arbitrary shape, in contrast to harmonic waves in both space and time, considered in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. The non-homogeneous waves are usually studied by analyzing refractions and reflections of bulk waves at the interface; see Ref. [20].

2 Wiechert condition

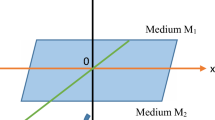
Consider stratified inhomogeneous space consisting of two isotropic and homogeneous halfspaces with ideal mechanical contact between them. Introduce the following dimensionless parameters

$$\begin{aligned} \tilde{{\lambda }}=\frac{\lambda _{1} }{\lambda _{2} },\,\,\,\,\,\,\tilde{{\mu }}=\frac{\mu _{1} }{\mu _{2} },\,\,\,\,\,\,\tilde{{\rho }}=\frac{\rho _{1} }{\rho _{2} }, \end{aligned}$$
(2.1)

where \(\lambda _{k} ,\,\,\mu _{k} ,\,\,\,k=1,2\) are Lame’s constants and \(\rho _{k} ,\,\,k=1,2\) are material densities of the corresponding halfspaces, .

Now, the Wiechert condition can be written as the following relation between dimensionless parameters

$$\begin{aligned} \tilde{{\lambda }}=\tilde{{\mu }}=\tilde{{\rho }}=q. \end{aligned}$$
(2.2)

where q is the dimensionless Wiechert parameter. Taking into account (2.1), Eq. (2.2) ensures

$$\begin{aligned} \frac{\lambda _{1} }{\rho _{1} }=\frac{\lambda _{2} }{\rho _{2} },\,\,\,\,\,\,\,\,\,\,\frac{\mu _{1} }{\rho _{1} }=\frac{\mu _{2} }{\rho _{2} }, \end{aligned}$$
(2.3)

from where it follows that the corresponding bulk wave velocities in the contacting halfspaces are equal:

$$\begin{aligned} \alpha _{1} =\alpha _{2} ,\quad \beta _{1} =\beta _{2} . \end{aligned}$$
(2.4)

In Eq. (2.4) \(\alpha _{k}\), \(\beta _{k}\), \(k=1,2\) are, respectively, longitudinal and shear bulk wave velocities:

$$\begin{aligned} \alpha _{k} =\sqrt{\frac{\lambda _{k} +2\mu _{k} }{\rho _{k} }},\quad \beta _{k} =\sqrt{\frac{\mu _{k} }{\rho _{k} }} . \end{aligned}$$
(2.5)

However, if \(\rho _{1} \ne \rho _{2} \), but the Wiechert condition is satisfied, the two contacting media are identical in terms of their bulk waves, but their acoustic impedances are different.

Remark 2.1

  1. (A)

    Note that condition (2.2) does not necessary mean that Poisson’s ratios of the contacting halfspaces coincide. However, if the contacting media have equal Poisson’s ratios, the condition (2.2) implies:

    $$\begin{aligned} \tilde{{E}}=\tilde{{\rho }}, \end{aligned}$$
    (2.6)

    where \(\tilde{{E}}\) is the dimensionless Young’s modulus

    $$\begin{aligned} \tilde{{E}}=\frac{E_{1} }{E_{2} } \end{aligned}$$
    (2.7)

    and \(E_{k}\), \(k=1,2\) are Young’s moduli of the contacted halfspaces.

  2. (B)

    The Wiechert condition defines a straight line in the 3D space generated by dimensionless parameters \(\tilde{{\lambda }}\), \(\tilde{{\mu }}\), \(\tilde{{\rho }}\). Introducing guide cosine \(l_{k} ,\; k=1,2,3\) of that line, Eq. (2.2) ensures

    $$\begin{aligned} l_{1} =l_{2} =l_{3} =1\big /\sqrt{3}. \end{aligned}$$
    (2.8)

    The straight line passing through the origin with the guide cosines (2.8) will be called as the Wiechert line.

  3. (C)

    Since Rayleigh polynomial equation for Rayleigh wave velocity depends solely on the bulk wave velocities, and at Wiechert condition the bulk wave velocities satisfy relation (2.4); that ensures equal velocities of Rayleigh waves propagating in the contacting halfspaces. For the high-frequency Lamb waves in stratified and FG plates that fact was numerically demonstrated by applying Cauchy sextic formalism coupled with the exponential fundamental matrix method [9].

With notations (2.1), (2.5) equations of motion take the form

$$\begin{aligned} \alpha _{k}^{2} \nabla \text{ div }\,{\mathbf{u}}^{(k)}-\beta _{k}^{2} \text{ rot }\,\text{ rot }\,{\mathbf{u}}^{(k)}={\mathbf{\ddot{{u}}}}^{(k)},\quad k=1,2, \end{aligned}$$
(2.9)

where \({\mathbf{u}}^{(k)}\) are the displacement fields in the corresponding halfspaces.

Equations (2.9) should be accomplished by the interfacial continuity conditions

$$\begin{aligned} \left\{ {\begin{array}{l} \left. {{\mathbf{u}}^{(1)}} \right| _{\partial \Omega _{\nu } } =\left. {{\mathbf{u}}^{(2)}} \right| _{\partial \Omega _{\nu } } \\ \left. {{\mathbf{t}}_{\varvec{\upnu }}^{(1)} } \right| _{\partial \Omega _{\nu } } =\left. {{\mathbf{t}}_{\varvec{\upnu }}^{(2)} } \right| _{\partial \Omega _{\nu } } \\ \end{array}} \right. \end{aligned}$$
(2.10)

where \(\partial \Omega _{\varvec{\upnu }} \) stands for the interface plane with the unit outward normal \(\varvec{\upnu }\) (thus, direction of \(\varvec{\upnu }\) depends upon the halfspace) and \({\mathbf{t}}_{\varvec{\upnu }}^{(k)} \) denotes the corresponding surface traction fields on the \(\partial \Omega _{\varvec{\upnu }} \)-plane. Boundary conditions should be accomplished by the Sommerfeld attenuation condition

$$\begin{aligned} \left\{ {\begin{array}{l} \lim \limits _{{\mathbf{x}}\cdot \varvec{\upnu }\rightarrow -\infty } {\mathbf{u}}^{(k)}=0 \\ \lim \limits _{{\mathbf{x}}\cdot \varvec{\upnu }\rightarrow -\infty } {\mathbf{t}}^{(k)}=0 \\ \end{array}} \right. \end{aligned}$$
(2.11)

where \({\mathbf{t}}_{k} \) is the stress field acting in the corresponding halfspace. Note that it is assumed that in Eq. (2.11) direction of \(\varvec{\upnu }\) varies depending on the considered halfspace. Equations (2.9)–(2.11) are in principal, sufficient for constructing secular equation for Stoneley wave velocity.

3 Stoneley waves at the Wiechert condition

Both theoretical and numerical analyses in [10,11,12,13,14,15,16,17,18,19] and in later publications [7,8,9] revealed that if physical parameters of the contacting media satisfy the Wiechert condition (2.2), then Stoneley waves exist. It should also be mentioned that various analytical and numerical methods for modeling Stoneley interfacial waves are developed in [21,22,23].

3.1 Secular equation

The following proposition is actually due to Stoneley [6]:

Proposition 3.1

In a stratified inhomogeneous space consisting of two isotropic homogeneous halfspaces in a contact which mechanical properties satisfy Wiechert condition (2.2), the interfacial Stoneley wave exists.

According to Stoneley’s work [3], the secular equation for velocity of the corresponding wave can be written in the following form

$$\begin{aligned} P(c)\equiv & {} c^{4}\left( {\left( {\rho _{1} -\rho _{2} } \right) ^{2}-\left( {\rho _{1} A_{2} +\rho _{2} A_{1} } \right) \left( {\rho _{1} B_{2} +\rho _{2} B_{1} } \right) } \right) \nonumber \\&\quad +\,2Kc^{2}\left( {\rho _{1} A_{2} B_{2} -\rho _{2} A_{1} B_{1} -\rho _{1} +\rho _{2} } \right) +K^{2}\left( {A_{1} B_{1} -1} \right) \left( {A_{2} B_{2} -1} \right) =0, \end{aligned}$$
(3.1)

where c is the Stoneley wave velocity, and

$$\begin{aligned} K=2\left( {\rho _{1} \beta _{1}^{2} -\rho _{2} \beta _{2}^{2} } \right) , \quad A_{k} =\sqrt{1-\frac{c^{2}}{\alpha _{k}^{2} }} ,\quad B_{k} =\sqrt{1-\frac{c^{2}}{\beta _{k}^{2} }} ,\quad k=1,2. \end{aligned}$$
(3.2)

other parameters in Eq. (3.1) were defined previously.

At the Wiechert condition, Eq. (3.1) takes the following form

$$\begin{aligned} P(c)\equiv c^{4}\left( {\left( {\tilde{{\rho }}-1} \right) ^{2}-AB\left( {\tilde{{\rho }}+1} \right) ^{2}} \right) +2\tilde{{K}}c^{2}\left( {AB-1} \right) \left( {\tilde{{\rho }}-1} \right) +\tilde{{K}}^{2}\left( {AB-1} \right) ^{2}=0, \end{aligned}$$
(3.3)

where

$$\begin{aligned} \tilde{{K}}=2\beta ^{2}\left( {\tilde{{\rho }}-1} \right) \end{aligned}$$
(3.4)

and indices at \(A,\,\,B,\,\,\beta \) are omitted in view of Eq. (2.4).

Remark 3.1

  1. (A)

    In contrast to Rayleigh secular equation, Eq. (3.1) is not polynomial with respect to the phase velocity c, since it contains square roots in multipliers \(A_{k} ,\,\,B_{k} \).

  2. (B)

    Supposing the Wiechert condition is satisfied, and both material densities coincide, then

    $$\begin{aligned} \tilde{{\rho }}=1. \end{aligned}$$
    (3.5)

    At condition (3.5), the secular equation becomes

    $$\begin{aligned} P(c)\equiv -4ABc^{4}=0, \end{aligned}$$
    (3.6)

    revealing that it has no roots, except trivial ones. Thus, no Stoneley wave can propagate at the Wiechert condition and condition (3.5). Note that in view of Eq. (2.2), the analogous result on nonexistence of Stoneley waves is valid for any other dimensionless parameters equal to unity. The latter result implies nonexistence of Stoneley waves in a homogeneous space at \(q=1\).

3.2 Incremental variation of the phase velocity along Wiechert line

Suppose now that physical properties of the two contacting halfspaces vary along the Wiechert line (see Remark 2.1.B), then physical properties of these halfspaces can be represented in the form

$$\begin{aligned} \begin{array}{l} \lambda _{1} =\lambda +\tfrac{\lambda }{\sqrt{3} }s,\quad \mu _{1} =\mu +\tfrac{\mu }{\sqrt{3} }s,\quad \rho _{1} \,=\rho +\tfrac{\rho }{\sqrt{3} }s \\ \lambda _{2} =\lambda ,\quad \upmu _{2} =\upmu ,\quad \rho _{2} \,=\rho \\ \end{array}. \end{aligned}$$
(3.7)

The corresponding dimensionless parameters are

$$\begin{aligned} \tilde{{\lambda }}=1+\tfrac{1}{\sqrt{3} }s,\quad \tilde{{\mu }}=1+\tfrac{1}{\sqrt{3} }s,\quad \tilde{{\rho }}=1+\tfrac{1}{\sqrt{3} }s. \end{aligned}$$
(3.8)

Note that physical parameters (3.7) satisfy the Wiechert condition, and

$$\begin{aligned} s=\sqrt{3} \left( {q-1} \right) . \end{aligned}$$
(3.9)

In view of Eqs. (2.5), (3.7), condition (2.4) is satisfied and the following proposition takes place

Proposition 3.2

The secular equation (3.3) depends solely upon one variable parameter \(\tilde{{\rho }}\), with other parameters in Eq. (3.3) remaining constant along Wiechert line.

That results in the following expression, where derivative of an implicit function is used

$$\begin{aligned} \frac{\mathrm{d}c}{\mathrm{d}s}=-\frac{\tfrac{\partial P}{\partial \tilde{{\rho }}}\tfrac{\partial \tilde{{\rho }}}{\partial s}}{\tfrac{\partial P}{\partial c}}. \end{aligned}$$
(3.10)

Performing differentiation in (3.3) yields

$$\begin{aligned} \frac{{\mathrm{d}}c}{\mathrm{d}s}=-\frac{1}{\sqrt{3} }\frac{X(c,\tilde{{\rho }})}{Y(c,\tilde{{\rho }})}. \end{aligned}$$
(3.11)

where

$$\begin{aligned} \begin{array}{l} X(c,\tilde{{\rho }})=\alpha ^{2}\beta ^{6}\left( {\left( {1+B^{2}} \right) ^{2}+4A^{2}B^{2}} \right) AB \\ Y(c,\tilde{{\rho }})=2\left( {c^{4}\left( {1+4\gamma ^{2}} \right) -4\beta ^{2}c^{2}\left( {2+\gamma ^{2}} \right) +8\beta ^{4}\gamma ^{2}} \right) \\ \quad \qquad \quad +\left( {c^{4}\frac{\left( {\tilde{{\rho }}+1} \right) }{\left( {\tilde{{\rho }}-1} \right) }+4\beta ^{2}\left( {1+B^{2}} \right) } \right) AB \\ \end{array}, \end{aligned}$$
(3.12)

in (3.12) \(\gamma =\tfrac{\alpha }{\beta }\). Expressions (3.12) reveal that \(X(c,\tilde{{\rho }})\) does not depend upon \(\,\tilde{{\rho }}\); \(Y(c,\tilde{{\rho }})\) is a fractional rational function of \(\tilde{{\rho }}\) and both \(X(c,\tilde{{\rho }})\) and \(Y(c,\tilde{{\rho }})\) are algebraic functions with respect to c. Equation (3.11) yields the desired expression for incremental variation of the phase velocity along Wiechert line.

Stoneley assertion [6] that at the Wiechert condition the propagating Stoneley wave velocity satisfies inequality

$$\begin{aligned} c<\beta , \end{aligned}$$
(3.13)

along with analysis of the right-hand side of Eqs. (3.12), allows us to formulate

Proposition 3.3

Incremental variation of Stoneley wave phase velocity \({c}'(s)\) along Wiechert line does not vanish at \(q\in (0,\,\,1)\cup (1,\,\,\infty )\).

Corollary

The only extremum for the Stoneley wave phase velocity on the Wiechert line may occur at \(q=1\).

Remark 3.2

The preceding Corollary delivers possibly unique method for acoustic determination of physical properties of the contacting halfspaces that obey Wiechert condition. Indeed, according to Eq. (2.4) and Remark 2.1.C, bulk and Rayleigh waves in the contacting media propagate with the equal corresponding velocities, and hence in terms of these waves such media are not distinguishable. Thus, Stoneley wave velocity remains the only acoustic parameter that is specific for specifying physical properties. And, according to the Corollary, Stoneley wave velocity is a monotonic function of the Wiechert parameter in the range \(q\in \left( {1,\,\,\infty } \right) \).

3.3 Stoneley velocity variation along Wiechert line

Herein, variation of Stoneley wave velocity along Wiechert line is plotted and analyzed by numerically finding an appropriate root of the secular Eq. (3.3) satisfying condition (3.13) and the non-attenuating condition

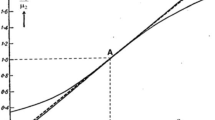
$$\begin{aligned} {\mathrm{Im}}(c)=0. \end{aligned}$$
(3.14)

The plots in Fig. 1 corresponding to different Poisson’s ratio values reveal that the dimensionless Stoneley wave velocities \(\tilde{{c}}\):

$$\begin{aligned} \tilde{{c}}=\frac{c}{\alpha } \end{aligned}$$
(3.15)

have almost identical variation along Wiechert line, except the obvious shift along vertical axis.

Fig. 1
figure 1

Variation of dimensionless Stoneley wave velocity vs the Wiechert parameter (q) at different Poisson’s ratios (\(\nu )\)

Full size image

The plotted curves show that according to the Corollary there are no extremums except at \(q\rightarrow 1\) where the corresponding derivatives of all the curves vanish. Asymptotic values at \(q\rightarrow \infty \) correspond to Rayleigh wave velocities. That has an obvious physical explanation; at very large elastic moduli and very large density of one of the contacting halfspaces, the other one can be considered as having negligible acoustic stiffness, resembling the case of theory of Rayleigh waves, when a halfspace contacts with vacuum.

At \(q\rightarrow 1\), both contacting halfspaces tend to have identical properties and Stoneley wave degenerates into the shear bulk wave that propagates in a homogeneous space (at \(q=1)\) with velocity \(\beta \).

4 Concluding remarks

Propagation of the dispersionless Stoneley waves in a heterogeneous medium consisted of two dissimilar homogeneous and isotropic perfectly connected halfspaces was analyzed at the Wiechert condition (2.2) imposed on the physical parameters of the halfspaces.

It was theoretically proved that the Stoneley wave velocity variation along the Wiechert line is a monotonically decreasing function of the dimensionless Wiechert parameter q at \(q\in (1,\,\infty )\). That fact was also numerically confirmed (see Fig. 1) by solving the Stoneley secular equation (3.3) at different (nonnegative) Poisson’s ratio values. The monotonic variation delivers the unique method for acoustic determination of physical properties of the contacting halfspaces that obey Wiechert condition as, according to Eqs. (2.4) and Remark 2.1.C bulk and Rayleigh waves in the contacting media propagate with the equal corresponding velocities, and hence, in terms of bulk and Rayleigh waves such media are not distinguishable.