1 Introduction

It is known (Stoneley 1924; Sezawa 1938; Sezawa and Kanai 1939; Scholte 1942a,b, 1947; Yamaguchi and Sato 1955; Chadwick and Borejko 1994; Bostron et al. 2013) that along an interface between two elastic isotropic halfspace or layers satisfying the widely used in various geophysical applications Wiechert condition (Wiechert and Geiger 1910; Wiechert 1919; Malischewsky 1987; Kuznetsov 2020), Stoneley waves arise and propagate with velocity that is independent from frequency. Similarly, Stoneley waves may arise and propagate along an interface between two contacting dissimilar anisotropic halfspaces or anisotropic layers in a stratified plate (Lim and Musgrave 1970; Chadwick and Currie 1974; Barnett et al. 1985; Goda 1992; Vinh and Seriani 2010; Ting 2011).

Suppose now that the interface, along which Stoneley wave propagates, becomes diffused, as can be anticipated in some real situations, Fig. 1.

Fig. 1
figure 1

The abrupt (left) and diffused (right) interfaces between two media in a contact

Full size image

It could naturally be supposed that if Stoneley wave exists in a system containing two homogeneous layers with the abrupt interface, then such a wave should also exist in a system with the same layers and a sufficiently thin FG layer between them; see Fig. 2.

Fig. 2
figure 2

Three layered medium with thin FG intermediate layer with schematic variation of physical properties (right); dotted lines indicate median planes of the layers

Full size image

However, a recent proof on non-existence of Stoneley waves in functionally graded (FG) plates with continuous transverse inhomogeneity (Kuznetsov 2021) may indicate that in real situations, when no abrupt change of material properties occurs, Stoneley waves arise less frequently than it can be supposed. The current analysis is targeted to elucidate the situation of vanishing Stoneley waves when the initially abrupt interface between elastic halfspaces starts to diffuse. The developed method is based on solving dispersion equations for both cases of abrupt and diffused interfaces; construction of dispersion equations relies on Cauchy sextic formalism and the exponential fundamental matrix method (Kuznetsov 2020).

2 Wiechert condition

The Wiechert condition plays an important role in seismology (Stevens and Day 1986) and various geotechnical and geophysical applications (Pfender and Villinger 2006; Ou and Wang 2019). As was mentioned earlier, the Wiechert condition ensures existence of the interfacial Stoneley waves, propagating along an interface between contacting halfspaces at any frequency, and in case of contacting layers of finite thickness at \(\upomega \to \infty\) (Malischewsky 1987).

Denoting respectively longitudinal and shear bulk wave velocities in the adjacent isotropic homogeneous layers or halfspaces, as

$$\upalpha_{k} = \sqrt {\frac{{\uplambda_{k} + 2\upmu_{k} }}{{\uprho_{k} }}} ,\quad \upbeta_{k} = \sqrt {\frac{{\upmu_{k} }}{{\uprho_{k} }}} ,\quad k = 1,2,$$
(1)

where \(\uplambda_{k} ,\,\upmu_{k}\) are Lame’s constants and \(\uprho_{k} ,\,k = 1,2\) are the material densities, the Wiechert condition could be written as (Ewing et al. 1957)

$$\frac{{\upalpha_{1} }}{{\upalpha_{2} }} = \frac{{\upbeta_{1} }}{{\upbeta_{2} }} = 1.$$
(2)

In view of (1), Wiechert condition (2) can be rewritten in terms of Lame’s constants moduli and material densities

$$\frac{{\uplambda_{1} }}{{\uplambda_{2} }} = \frac{{\upmu_{1} }}{{\upmu_{2} }} = \frac{{\uprho_{1} }}{{\uprho_{2} }} = \upeta ,$$
(3)

where \(\upeta \in (0;\,1) \cup (1;\,\infty )\) is the dimensionless parameter, at \(\upeta = 1\) both contacting media become acoustically identical implying that no Stoneley wave can propagate (Chadwick and Borejko 1994).

Another observation flowing out from Eq. (3) and an easily verified monotonic variation of a function of Poisson’s ratio

$$f(\upnu ) \equiv \frac{\uplambda }{\upmu } = \frac{2\upnu }{{(1 - 2\upnu )}},\quad \upnu \in ( - 1;\,0.5),$$
(4)

yields: Wiechert condition implies equal Poisson’s ratios of the contacting media, and taking into account (3), the Rayleigh wave velocities in media that satisfies Wiechert condition, are necessary equal.

3 Dispersion equations

Herein, the case of a stratified plate is considered; the plate contains either two homogeneous layers with single abrupt interface (Fig. 1) or three layers with thin FG layer (Fig. 2) modeling the diffused interface.

3.1 Equations of motion

Equation of motion for a heterogeneous elastic anisotropic medium can be written in a form (Achenbach 1987)

$${\text{div}}_{{\mathbf{x}}} {\mathbf{C}}({\mathbf{x}}) \cdot \cdot \nabla_{{\mathbf{x}}} {\mathbf{u}}({\mathbf{x}},t) = \uprho ({\mathbf{x}})\partial_{tt}^{2} {\mathbf{u}}({\mathbf{x}},t),$$
(5)

where \({\mathbf{C}}\) is the elasticity tensor, assumed to be positive definite; \({\mathbf{u}}\) is the displacement field; \(\uprho\) is the material density; \({\mathbf{x}}\) is spatial coordinate; and \(t\) is time. The harmonic surface wave with the plane wave front admits the following representation

$${\mathbf{u}}({\mathbf{x}},t) = {\mathbf{m}}({\mathbf{x}} \cdot {{\varvec{\upnu}}})\exp \left( {ir({\mathbf{x}} \cdot {\mathbf{n}} - ct)} \right),$$
(6)

where \({\mathbf{m}}\) is the wave polarization; \({{\varvec{\upnu}}}\) is the unit normal to the median plane of a layer; \({\mathbf{n}}\) is the unit wave normal; \(c\) is the phase velocity; and \(r\) is the wave number, usually (but not necessary) defined as:

$$r = \frac{\upomega }{c},$$
(7)

herein \(\upomega\) is the circular frequency.

Considering transverse inhomogeneity in Eq. (5) and substituting displacement field (6) into Eq. (5), yields the equation of motion in terms of Cauchy sextic formalism (Kuznetsov 2020)

$$\frac{\partial }{{\partial x^{\prime}}}{\mathbf{Y}}(x^{\prime}) = {\mathbf{G}}(x^{\prime}) \cdot {\mathbf{Y}}(x^{\prime}),$$
(8)

where

$$x^{\prime} = ir({\mathbf{x}} \cdot {\mathbf{\nu )}}$$
(9)

is the transverse imaginary coordinate, and

$${\mathbf{Y}}(x^{\prime}) = \left( {\begin{array}{*{20}c} {{\mathbf{m}}(x^{\prime})} \\ {{\mathbf{w}}(x^{\prime})} \\ \end{array} } \right); \quad {\mathbf{w}}(x^{\prime}) = \frac{\partial }{{\partial x^{\prime}}}{\mathbf{m}}(x^{\prime}); \quad {\mathbf{G}}(x^{\prime}) = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - {\mathbf{A}}_{1}^{ - 1} (x^{\prime}) \cdot {\mathbf{A}}_{3} (x^{\prime})} & { - {\mathbf{A}}_{1}^{ - 1} (x^{\prime}) \cdot {\mathbf{A}}_{2} (x^{\prime})} \\ \end{array} } \right),$$
(10)

\(3 \times 3\)-matrices \({\mathbf{A}}_{k} ,\,k = 1,2,3\) are as follows

$$\begin{aligned} {\mathbf{A}}_{1} (x^{\prime}) &= {{\varvec{\upnu}}} \cdot {\mathbf{C}}(x^{\prime}) \cdot {{\varvec{\upnu}}} \hfill \\ {\mathbf{A}}_{2} (x^{\prime}) &= {{\varvec{\upnu}}} \cdot {\mathbf{C}}(x^{\prime}) \cdot {\mathbf{n}}+ {\mathbf{n}} \cdot {\mathbf{C}}(x^{\prime}) \cdot {\varvec{\upnu}}+{\varvec{\upnu}} \cdot \partial_{{x^{\prime}}} {\mathbf{C}}(x^{\prime}) \cdot {{\varvec{\upnu}}} \hfill \\ {\mathbf{A}}_{3} (x^{\prime}) &= {\mathbf{n}} \cdot {\mathbf{C}}(x^{\prime}) \cdot {\mathbf{n}}- {\varvec{\uprho}}(x^{\prime})c^{2} {\mathbf{I}} + {\varvec{\upnu}} \cdot \partial_{{x^{\prime}}} {\mathbf{C}}(x^{\prime}) \cdot {\mathbf{n}} \hfill \\ \end{aligned}.$$
(11)

In (10), (11) the \(3 \times 3\)-matrices \({\mathbf{0}}\) and \({\mathbf{I}}\) denote zero and unity matrices respectively. In case of homogeneous layer, both elasticity tensor and material density are independent of coordinate \(x^{\prime}\) with the corresponding simplifications in Eq. (11).

3.2 Boundary and interfacial conditions: two-layered plate

In case of a two layered system when the interface between homogeneous layers is abrupt, the traction free boundary conditions at the outer upper and bottom surfaces can be written as

$$\begin{gathered} \left. {{\mathbf{t}}_{\nu }^{(1)} ({\mathbf{x}},t) \equiv {{\varvec{\upnu}}} \cdot {\mathbf{C}}^{(1)} \cdot \cdot \nabla_{{\mathbf{x}}} {\mathbf{u}}^{(1)} ({\mathbf{x}},t)} \right|_{{{\mathbf{x}} \cdot {\varvec{\upnu}}= + h_{1} }} = 0 \hfill \\ \left. {{\mathbf{t}}_{\nu }^{(2)} ({\mathbf{x}},t) \equiv {{\varvec{\upnu}}} \cdot {\mathbf{C}}^{(2)} \cdot \cdot \nabla_{{\mathbf{x}}} {\mathbf{u}}^{(2)} ({\mathbf{x}},t)} \right|_{{{\mathbf{x}} \cdot {\varvec{\upnu}} = - h_{2} }} = 0 \hfill \\ \end{gathered},$$
(12)

where indices \(1,\,2\) are referred to the upper and bottom (homogeneous) layers.

Equations (12) can be rewritten in terms of vector \({\mathbf{Y}}(x^{\prime})\):

$$\begin{gathered} \left. {\left( {{\mathbf{A}}_{4}^{(1)} ;{\mathbf{A}}_{1}^{(1)} } \right) \cdot {\mathbf{Y}}^{(1)} (x^{\prime})} \right|_{{x^{\prime}= + irh_{1} }} = 0 \hfill \\ \left. {\left( {{\mathbf{A}}_{4}^{(2)} ;{\mathbf{A}}_{1}^{(2)} } \right) \cdot {\mathbf{Y}}^{(2)} (x^{\prime})} \right|_{{x^{\prime}= - irh_{2} }} = 0 \hfill \\ \end{gathered},$$
(13)

where \({\mathbf{A}}_{4}^{(k)} ,\,\,k = 1,2\) are \(3 \times 3\)-matrices:

$${\mathbf{A}}_{4}^{(k)} = {{\varvec{\upnu}}} \cdot {\mathbf{C}}^{(k)} \cdot {\mathbf{n}},\quad k = 1,2.$$
(14)

At the interface between layers the continuity conditions imply

$$\begin{gathered} \left. {{\mathbf{u}}^{(1)} ({\mathbf{x}},t)} \right|_{{{\mathbf{x}} \cdot {\varvec{\upnu}} = - h_{1} }} = \left. {{\mathbf{u}}^{(2)} ({\mathbf{x}},t)} \right|_{{{\mathbf{x}} \cdot {\varvec{\upnu}} = + h_{2} }} \hfill \\ \left. {{\mathbf{t}}_{\nu }^{(1)} ({\mathbf{x}},t)} \right|_{{{\mathbf{x}} \cdot {\varvec{\upnu}} = - h_{1} }} = \left. {{\mathbf{t}}_{\nu }^{(2)} ({\mathbf{x}},t)} \right|_{{{\mathbf{x}} \cdot {\varvec{\upnu}} = + h_{2} }} , \hfill \\ \end{gathered}$$
(15)

or in terms of vector \({\mathbf{Y}}(x^{\prime})\):

$$\left. {{\mathbf{Z}}^{(1)} \cdot {\mathbf{Y}}^{(1)} (x^{\prime})} \right|_{{x^{\prime}= - irh_{1} }} = \left. {{\mathbf{Z}}^{(2)} \cdot {\mathbf{Y}}^{(2)} (x^{\prime})} \right|_{{x^{\prime}= +irh_{2} }},$$
(16)

where \({\mathbf{Z}}^{(k)} ,\,k = 1,2\) are \(6 \times 6\) impedance matrices; see (Kuznetsov 2020):

$${\mathbf{Z}}^{(k)} = \left( {\begin{array}{*{20}c} {\mathbf{I}} & {\mathbf{0}} \\ {{\mathbf{A}}_{4}^{(k)} } & {{\mathbf{A}}_{1}^{(k)} } \\ \end{array} } \right).$$
(17)

Note, that due to the assumed positive definiteness of the elasticity tensor, the impedance matrices are non-degenerate.

3.3 Boundary and interfacial conditions: three-layered plate with FG intermediate layer

In case of a three layered system with a FG intermediate layer (Fig. 3), modeling the diffused interface, the outer boundary conditions are analogous to conditions (12), (13) with necessary renumbering bottom layer (\(k = 3\)), reserving \(k = 2\) for the FG intermediate layer:

$$\begin{gathered} \left. {\left( {{\mathbf{A}}_{4}^{(1)} ;{\mathbf{A}}_{1}^{(1)} } \right) \cdot {\mathbf{Y}}^{(1)} (x^{\prime})} \right|_{{x^{\prime}= + irh_{1} }} = 0 \hfill \\ \left. {\left( {{\mathbf{A}}_{4}^{(3)} ;{\mathbf{A}}_{1}^{(3)} } \right) \cdot {\mathbf{Y}}^{(3)} (x^{\prime})} \right|_{{x^{\prime}= - irh_{3} }} = 0\hfill \\ \end{gathered},$$
(18)
Fig. 3
figure 3

Dispersion portrait of Lamb waves in a two-layered plate satisfying Wiechert condition; dashed lines denote the high frequency asymptotes, related to (1) Rayleigh wave; (2) bulk S-wave; (3) Stoneley wave

Full size image

In view of presence of the intermediate FG layer the interfacial continuity conditions become

$$\begin{gathered} \left. {{\mathbf{Z}}^{(1)} \cdot {\mathbf{Y}}^{(1)} (x^{\prime})} \right|_{{x^{\prime}= - irh_{1} }} = \left. {{\mathbf{Z}}^{(2)} (x^{\prime}) \cdot {\mathbf{Y}}^{(2)} (x^{\prime})} \right|_{{x^{\prime}= + irh_{2} }} \hfill \\ \left. {{\mathbf{Z}}^{(2)} (x^{\prime}) \cdot {\mathbf{Y}}^{(2)} (x^{\prime})} \right|_{{x^{\prime}= - irh_{2} }} = \left. {{\mathbf{Z}}^{(3)} \cdot {\mathbf{Y}}^{(3)} (x^{\prime})} \right|_{{x^{\prime}= + irh_{3} }} \hfill \\ \end{gathered},$$
(19)

where \({\mathbf{Z}}^{(2)} (x^{\prime})\) depends upon \(x^{\prime}\)-coordinate.

3.4 Dispersion equation: two-layered plate

Taking into account Eqs. (12)–(16) and the exponential solution of Eq. (8) written as (Logemann and Ryan 2014; Kuznetsov 2020)

$${\mathbf{Y}}(x^{\prime}) = \exp (x^{\prime}{\mathbf{G}}) \cdot {\mathbf{Y}}_{0} ,$$
(20)

where \({\mathbf{Y}}_{0}\) is defined by boundary conditions, the desired dispersion equation takes the form (Kuznetsov 2020):

$$\det \left( {({\mathbf{0}},{\mathbf{I}}) \cdot {\mathbf{Z}}^{(2)} \cdot \exp ( - 2irh_{2} {\mathbf{G}}^{(2)} ) \cdot \left( {{\mathbf{Z}}^{(2)} } \right)^{ - 1} \cdot {\mathbf{Z}}^{(1)} \cdot \exp ( - 2irh_{1} {\mathbf{G}}^{(1)} ) \cdot \left( {{\mathbf{Z}}^{(1)} } \right)^{ - 1} \cdot \left( {\begin{array}{*{20}c} {\mathbf{I}} \\ {\mathbf{0}} \\ \end{array} } \right)} \right) = 0.$$
(21)

Equation (21) admits another interpretation; it states that a map from the three-dimensional subspace generated by vanishing surface tractions acting on the upper surface into three-dimensional subspace of surface tractions acting on the bottom surface is degenerate. That ensures existence of the non-trivial magnitudes \({\mathbf{m}}^{(1)} ( + irh)\).

3.5 Dispersion equation: three-layered plate with FG layer

In case, when a FG intermediate layer is present, the exponential solution for FG layer is of a more complicated form (Logemann and Ryan 2014; Kuznetsov 2020):

$${\mathbf{Y}}(x^{\prime}) = \exp \left( {{\mathbf{F}}(x^{\prime})} \right) \cdot {\mathbf{Y}}_{0} ,$$
(22)

where \({\mathbf{F}}(x^{\prime})\) is an anti-derivative of \({\mathbf{G}}(x^{\prime})\): \(\partial_{{x^{\prime}}} {\mathbf{F}}(x^{\prime}) = {\mathbf{G}}(x^{\prime})\).

Combining Eqs. (18)–(22), the desired dispersion equations takes the form; see Kuznetsov 2020):

$$\det \left( {({\mathbf{0}},{\mathbf{I}}) \cdot \left( \begin{array}{l} {\mathbf{Z}}^{(3)} \cdot \exp ( - 2irh_{3} {\mathbf{G}}^{(3)} ) \cdot \left( {{\mathbf{Z}}^{(3)} } \right)^{ - 1} \hfill \\ \cdot {\mathbf{Z}}^{(2)} \cdot \exp \left( {{\mathbf{F}}^{(2)} ( - irh_{2} ) - {\mathbf{F}}^{(2)} (irh_{2} )} \right) \cdot \left( {{\mathbf{Z}}^{(2)} } \right)^{ - 1} \hfill \\ \cdot {\mathbf{Z}}^{(1)} \cdot \exp ( - 2irh_{1} {\mathbf{G}}^{(1)} ) \cdot \left( {{\mathbf{Z}}^{(1)} } \right)^{ - 1} \hfill \\ \end{array} \right) \cdot \left( {\begin{array}{*{20}c} {\mathbf{I}} \\ {\mathbf{0}} \\ \end{array} } \right)} \right) = 0.$$
(23)

4 Stoneley wave analysis

It is known, that the interfacial Stoneley wave in layered plates may arise at high frequencies, when conditions of existence are satisfied (Chadwick and Borejko 1994; Bostron et al. 2013).

4.1 Two-layered plate with abrupt interface

Herein, a two-layered plate with homogeneous layers and abrupt interface is considered with layers having the following physical and geometrical properties

$$\begin{gathered} E^{(1)} = 1;\quad \uprho^{(1)} = 1;\quad \upnu^{(1)} = 0.25;\quad 2h_{1} = 1 \hfill \\ E^{(2)} = 10;\quad \uprho^{(2)} = 10;\quad \upnu^{(2)} = 0.25;\quad 2h_{2} = 1\hfill \\ \end{gathered}.$$
(24)

Parameters  (24) ensure satisfying Wiechert condition (3) with the dimensionless \(\upeta = 2\).

Computing dispersion curves by dispersion Eq. (21), results in the following dispersion portrait shown in Fig. 3. Computations were done with the dimensionless variables

$$\frac{\upomega H}{\upalpha },\quad \frac{c}{\upalpha },$$
(25)

where \(\upomega\) is the circular frequency; \(H\) is the overall thickness of the plate; and \(\upalpha\) is the common (for both of the layers) bulk \(P\)-wave velocity; \(c\) is the phase velocity. The corresponding dimensionless Rayleigh, Stoneley and \(S\)-wave velocities are obtained by solving the Rayleigh polynomial equation for Rayleigh wave (Achenbach 1987); the modified Scholte algebraic equation (Kuznetsov 2020) for Stoneley wave; and Eq. (1) for the \(S\)-bulk wave velocity, yielding

$$\frac{{c_{{{\text{Rayleigh}}}} }}{\upalpha } \approx {0}{\text{.488}};\quad \frac{{c_{{{\text{Stoneley}}}} }}{\upalpha } \approx 0.547; \quad \frac{\upbeta }{\upalpha } \approx 0.577,$$
(26)

The fundamental symmetric and asymmetric (flexural) branches in Fig. 3 are marked as \(S_{0}\) and \(A_{0}\) respectively; \(A_{1}\) branch stands for the first asymmetric mode.

The plots in Fig. 3 reveal presence of three distinct asymptotes numbered 1,2,3 corresponding to the relative velocity values given in (26). Note that at high frequencies the first asymmetric branch \(A_{1}\) transforms into Stoneley wave. Note also, that as Fig. 3 shows, the first asymmetric branch \(A_{1}\) transforms into Stoneley wave at high frequencies. Note that intersections of the dispersion curves were studied in (Kausel et al. 2015) and in regard of dispersion of Love and SH waves, see (Ilyashenko et al. 2018; Kuznetsov 2006).

4.2 Three-layered plates with intermediate FG layer

Now, a three-layered plate with the same outer layers and a median FG layer, is considered. Physical properties of the layers are as follows

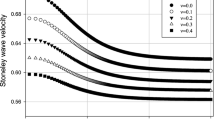
$$\begin{aligned} E^{(1)} &= 1;\quad \uprho^{(1)} = 1;\quad \upnu^{(1)} = 0.25;\quad 2h_{1} = 1 \hfill \\ E^{(2)} &= E^{(1)} + \frac{{E^{(1)} - E^{(3)} }}{{2h_{2} }}\left( {\frac{{x^{\prime}}}{ir} - h_{2} } \right);\quad \uprho^{(2)} = \rho^{(1)} + \frac{{\rho^{(1)} - \rho^{(3)} }}{{2h_{2} }}\left( {\frac{{x^{\prime}}}{ir} - h_{2} } \right);\quad \upnu^{(2)} = 0.25 \hfill \\ E^{(3)} &= 2;\quad \uprho^{(3)} = 2;\quad \upnu^{(3)} = 0.25;\quad 2h_{3} = 1 \hfill \\ \end{aligned},$$
(27)

where \(x^{\prime}\) is defined by (9). Conditions (27) ensure continuity of the physical properties across thickness of the plate, and the same values of the bulk wave velocities across thickness of the FG layer. Four different thickness values of the FG layer modeling the diffused interface, were considered: \(2h_{2} = 1;\,0.1;\,0.05;\,0.025\).

Comparing dispersion portraits shown in Fig. 4 reveals (i) absence of the vertical asymptote relating to the high frequency interfacial Stoneley waves, for all the considered cases; (ii) the first asymmetric branch \(A_{1}\) at presence of the FG layer, tends asymptotically to vertical asymptote related to the bulk \(S\)-wave; (iii) at any fixed frequency the distances between \(A_{1}\) and the closest \(S_{1}\) branch increases with the decreasing thickness of the FG layer.

Fig. 4
figure 4

Dispersion portrait of Lamb waves in three-layered plates containing intermediate FG layer of thickness, a 1.0; b 0.1; c 0.05; d 0.025; the high frequency asymptotes relate to (1) Rayleigh wave; (2) bulk S-wave

Full size image

Thus, the observed disappearance of Stoneley waves in layered media with the diffused interfaces between layers may indicate that in real situations Stoneley waves are hardly to arise, or at least they are much less frequent than it can be assumed.

The main computations in this subsection were done by applying the high precision numerical algorithms (Bailey and Borwein 2015; Kuznetsov 2020) with long mantissas having 250 decimal digits.

5 Concluding remarks

Comparing dispersion portraits shown in Figs. 3 and 4 reveals: (i) the only dispersion asymmetric branch \(A_{1}\) leads to appearing interfacial Stoneley wave in case of media with abrupt interface, Fig. 3; (ii) in case of the diffused interfaces (Fig. 4) the vertical asymptote relating to Stoneley wave, disappears; (iii) the first asymmetric branch \(A_{1}\) at presence of the FG layer, tends asymptotically to vertical asymptote related to the bulk \(S\)-wave; (iv) in case of the FG layer and at any fixed frequency the distances between \(A_{1}\) and the closest \(S_{1}\) branch increases with the decreasing thickness of the FG layer.

Thus, the observed absence of Stoneley waves in layered media with the diffused interfaces between layers may indicate that in real situations the genuine Stoneley waves are less frequent than it can be assumed. Another remark concerns energy needed to generate a monochromatic Lamb wave. It is known (Achenbach 1987; Ewing et al. 1957) that both fundamental (monochromatic) \(A_{0} ,\,\,S_{0}\) modes need less energy for their generation than needed for generating all higher modes. In this respect, the plots in Fig. 3 demonstrate that in case of the abrupt interface and at fixed frequency, Rayleigh waves demand less energy for their generation than the interfacial Stoneley waves.