1 Introduction

Herein, propagation of the interfacial Stoneley waves in layered media satisfying a more general condition, than the original Wiechert condition, is analyzed. (In more details, Wiechert condition is discussed in the next subsection.) The Wiechert condition [1, 2] plays an important role in various applications in acoustics and, especially in studies of the interfacial Stoneley waves. In this respect, in the pioneering Stoneley work [3] existence of Stoneley waves propagating on an interface between two dissimilar isotropic halfspaces was studied at an assumption that physical properties of the halfspaces obey Wiechert condition; in [3] an explicit algebraic secular equation for Stoneley wave velocity was also derived.

The vast majority of the subsequent studies on Stoneley wave propagation in layered isotropic media were concerned with the Wiechert condition [4,5,6,7,8,9,10,11,12,13,14,15,16]. In [4, 5], regions of existence for Stoneley waves plotted in terms of their relative physical parameters were constructed numerically, revealing that the Wiechert line belongs to the region of existence. Various forms of secular equations for Stoneley wave velocity were constructed in [6,7,8,9,10,11,12]. Several analytical methods for solving secular equations for Stoneley wave velocity were suggested in [13,14,15]. In [16], it was demonstrated that the studied regions of existence for Stoneley waves are multiply connected, instead of the previously assumed simply connected ones. Appearance of high-frequency Stoneley waves generated by propagation of Lamb waves in layered plates was studied numerically in [17,18,19] and by constructing high-frequency asymptotics in [20, 21].

Stoneley waves propagating on an interface between anisotropic halfspaces were mainly studied by applying either three-dimensional formalism [22] or by complex sextic formalisms [23,24,25].

1.1 Wiechert condition

The original Wiechert condition asserts that the dimensionless physical parameters responsible for acoustic properties of the contacting media are proportional to a single parameter q. Consider inhomogeneous space consisting of two isotropic homogeneous halfspaces in a contact. Acoustical properties of the contacting halfspaces can be described by the following dimensionless parameters

$$\begin{aligned} {\tilde{\rho }}=\frac{\rho _{1} }{\rho _{2} },\,\,\,\,\,\,{\tilde{\mu }}=\frac{\mu _{1} }{\mu _{2} },\,\,\,\,\,\,\,{\tilde{\lambda }}=\frac{\lambda _{1} }{\lambda _{2} }, \end{aligned}$$
(1.1)

where \(\rho _{k} \) are the material densities, and \(\,\mu _{k} ,\,\,\lambda _{k} ,\,\,k=1,2\) are the corresponding Lame’s constants of the contacting halfspaces.

The Wiechert condition imposes the following restriction on the dimensionless parameters

$$\begin{aligned} {\tilde{\rho }}={\tilde{\mu }}={\tilde{\lambda }}=q. \end{aligned}$$
(1.2)

where q is the dimensionless variable, known also as the Wiechert parameter; see [15].

Taking into account definitions (1.1), Eq. (1.2) ensures

$$\begin{aligned} \frac{\mu _{1} }{\rho _{1} }=\frac{\mu _{2} }{\rho _{2} },\,\,\,\,\,\frac{\lambda _{1} }{\rho _{1} }=\frac{\lambda _{2} }{\rho _{2} }. \end{aligned}$$
(1.3)

Equation (1.3) ensures that the corresponding bulk wave velocities in the contacting halfspaces coincides

$$\begin{aligned} \alpha _{1} =\alpha _{2} ,\,\,\,\,\,\,\,\beta _{1} =\beta _{2} . \end{aligned}$$
(1.4)

where \(\alpha _{k} \) and \(\beta _{k} \) are correspondingly P and S wave velocities in the contacting halfspaces.

It can be easily shown that condition (1.4) implies also

$$\begin{aligned} c_{R_{1} } =c_{R_{2} } , \end{aligned}$$
(1.5)

where \(c_{R_{k} } ,\quad k=1,2\) are the corresponding Rayleigh wave velocities. Thus, Wiechert condition imposes strong restrictions on the possible values of P, S and Rayleigh wave velocities.

Remarks 1.1

  1. (A)

    Despite equal P, S and Rayleigh wave velocities of the halfspaces obeying Wiechert condition (1.2), the corresponding acoustic impedances \(Z_{k} \equiv \alpha _{k} \rho _{k} \) and \(Z_{k}^{*} \equiv \beta _{k} \rho _{k} ,\quad k=1,2\) need not be equal.

  2. (B)

       Condition (1.2) does not necessary require equal Poisson’s ratios of the contacting media. However, if Poisson’s ratios are identical, condition (1.2) implies:

    $$\begin{aligned} {\tilde{\rho }}={\tilde{E}}, \end{aligned}$$
    (1.6)

    herein, \({\tilde{E}}\) is relative Young’s modulus

    $$\begin{aligned} {\tilde{E}}=\frac{E_{1} }{E_{2} } \end{aligned}$$
    (1.7)

    and \(E_{k} ,\,\,\,k=1,2\) are Young’s moduli of the contacted media.

  3. (C)

    Considering 3D space defined by the dimensionless parameters \({\tilde{\rho }},\,\,{\tilde{\lambda }},\,\,{\tilde{\mu }}\), it can be observed that Wiechert condition in this space corresponds to a straight line with guide cosines

    $$\begin{aligned} l_{1} =l_{2} =l_{3} =1/{\sqrt{3}}. \end{aligned}$$
    (1.8)

    The line passing through the origin with guide cosines (1.8) is known as Wiechert line [16].

1.2 Generalization of the Wiechert condition

In [15], variation of Stoneley wave velocity along Wiechert line analyzed by the freezing coefficient method [26] revealed unimodal (single extremum) behavior with extremal value reached at \(q\rightarrow 1\pm 0\) when both media have identical physical properties and Stoneley wave degenerates into S wave. However, Stoneley wave velocity variation along other directions in the 3D space defined by the dimensionless Lame’s constants \({\tilde{\lambda }};\,\,{\tilde{\mu }}\) and dimensionless density \({\tilde{\rho }}\), remains unexplored.

Herein, a natural generalization of the Wiechert condition by introducing two independent dimensionless variables

$$\begin{aligned} {\tilde{\lambda }}={\tilde{\mu }}=q_{1} ;\,\,\,\,\,\,\,{\tilde{\rho }}=q_{2} \end{aligned}$$
(1.9)

is proposed, and in more details generalization (1.9) is discussed in Sec. 4.

Numerical analysis of Stoneley wave velocity variation under condition (1.9) is given in Sec. 5. Computations at different Poisson’s ratios revealed almost identical regions of existence of Stoneley waves and similar shapes (not values) of the corresponding 3D plots. However, Stoneley wave velocity values heavily depend upon Poisson’s ratios.

2 Stoneley secular equation

Stoneley waves propagate along a plane interface of two dissimilar halfspaces in a contact with constant velocity that depends solely on physical properties of the contacting media. The secular equation for Stoneley wave velocity constructed in [3] may be represented the following form

$$\begin{aligned} \begin{array}{l} P(c)\equiv c^{4}\left( {\left( {\rho _{1} -\rho _{2} } \right) ^{2}-\left( {\rho _{1} A_{2} +\rho _{2} A_{1} } \right) \left( {\rho _{1} B_{2} +\rho _{2} B_{1} } \right) } \right) \\ \quad -2Kc^{2}\left( {\rho _{1} A_{2} B_{2} -\rho _{2} A_{1} B_{1} -\rho _{1} +\rho _{2} } \right) +K^{2}\left( {A_{1} B_{1} -1} \right) \left( {A_{2} B_{2} -1} \right) =0 \\ \end{array}, \end{aligned}$$
(2.1)

where c is the Stoneley wave velocity, and

$$\begin{aligned} K=2\left( {\rho _{2} \beta _{2}^{2} -\rho _{1} \beta _{1}^{2} } \right) ,\quad A_{k} =\sqrt{1-\frac{c^{2}}{\alpha _{k}^{2} }} ,\quad B_{k} =\sqrt{1-\frac{c^{2}}{\beta _{k}^{2} }} ,\quad k=\,\,1,2. \end{aligned}$$
(2.2)

In Eqs. (2.1), (2.2) \(\rho _{k} ,\,\,k=1,2\) are material densities; \(\alpha _{k} ,\,\,\,\,\beta _{k} ,\,\,\,\,k=1,2\) are, respectively, longitudinal and shear bulk wave velocities:

$$\begin{aligned} \alpha _{k} =\sqrt{\frac{\lambda _{k} +2\mu _{k} }{\rho _{k} }} ,\,\,\,\,\,\,\,\beta _{k} =\sqrt{\frac{\mu _{k} }{\rho _{k} }} , \end{aligned}$$
(2.3)

herein, \(\lambda _{k} ,\,\,\mu _{k} ,\,\,\,k=1,2\) are the corresponding Lame’s constants.

A more convenient form of the secular equation was proposed by Scholte [6,7,8] in the dimensionless form

$$\begin{aligned} P({\tilde{c}})\equiv L{\tilde{c}}^{4}+2M\,{\tilde{c}}^{2}+N=0, \end{aligned}$$
(2.4)

where \({\tilde{c}}\) is the dimensionless velocity

$$\begin{aligned} {\tilde{c}}=\frac{c}{\beta _{2} } \end{aligned}$$
(2.5)

and

$$\begin{aligned} \begin{array}{l} L=\left( {\left( {1-{\tilde{\rho }}} \right) ^{2}-\left( {{\tilde{\rho }}{\tilde{A}}_{2} +{\tilde{A}}_{1} } \right) \left( {{\tilde{\rho }}{\tilde{B}}_{2} +{\tilde{B}}_{1} } \right) } \right) \\ M={\tilde{K}}\left( {1+{\tilde{\rho }}{\tilde{A}}_{2} {\tilde{B}}_{2} -{\tilde{A}}_{1} {\tilde{B}}_{1} -{\tilde{\rho }}} \right) \\ N={\tilde{K}}^{2}\left( {1-{\tilde{A}}_{1} {\tilde{B}}_{1} } \right) \left( {1-{\tilde{A}}_{2} {\tilde{B}}_{2} } \right) \\ \end{array}. \end{aligned}$$
(2.6)

In (2.6), coefficient \({\tilde{K}}\) has the form

$$\begin{aligned} {\tilde{K}}=2\left( {1-{\tilde{\rho }}{\tilde{\beta }}^{2}} \right) \end{aligned}$$
(2.7)

and

$$\begin{aligned} {\tilde{A}}_{k} =\sqrt{1-{\tilde{c}}^{2}\frac{\beta _{2}^{2} }{\alpha _{k}^{2} }} ,\,\,\,\,\,\,\,\,\,\,{\tilde{B}}_{k} =\sqrt{1-{\tilde{c}}^{2}\frac{\beta _{2}^{2} }{\beta _{k}^{2} }} ,\,\,\,\,\,\,\,\,\,k=\,\,1,2. \end{aligned}$$
(2.8)

Secular equation in a form (2.4) will be used in the further analysis.

3 Generalized Wiechert condition

A better suited for modeling real geophysical formations is the generalized Wiechert condition containing two independent dimensionless parameters:

$$\begin{aligned} {\tilde{\rho }},\quad {\tilde{\lambda }}={\tilde{\mu }}. \end{aligned}$$
(3.1)

It will also be assumed that both media have identical Poisson’s ratios.

Taking into account expressions (2.3) for bulk waves yields

$$\begin{aligned} {\tilde{\alpha }}\equiv \frac{\alpha _{1} }{\alpha _{2} }=\chi ,\quad {\tilde{\beta }}\equiv \frac{\beta _{1} }{\beta _{2} }=\chi , \end{aligned}$$
(3.2)

where

$$\begin{aligned} \chi =\sqrt{\frac{{\tilde{\mu }}}{{\tilde{\rho }}}} . \end{aligned}$$
(3.3)

Taking into account Eqs. (3.2), the adjacent media can have different velocities of bulk waves, and consequently different Rayleigh wave velocities, obeying the analogous relation

$$\begin{aligned} {\tilde{c}}_{R} \equiv \frac{c_{R_{1} } }{c_{R_{2} } }=\chi . \end{aligned}$$
(3.4)

The natural physical restrictions imply

$$\begin{aligned} {\tilde{\rho }}>0,\quad {\tilde{\mu }}>0, \end{aligned}$$
(3.5)

and in view of (3.1)\(_{\mathrm {2}}\) both media may have either positive or negative, but identical Poisson’s ratios; thus, the case when one medium has positive Poisson’s ratio, while another negative one, is prohibited.

Remarks 3.1

  1. (A)

    Condition (3.1) defines a Q-plane in the 3D space of dimensionless parameters \({\tilde{\rho }},\,\,{\tilde{\lambda }},\,\,{\tilde{\mu }}\). It is easy to show that the Q-plane contains a straight line defined by the Wiechert condition (1.2); see Remark 1.1.C.

  2. (B)

    The following condition that is actually due to Stoneley [3] ensures attenuation of Stoneley wave with depth in both halfspaces

    $$\begin{aligned} {\tilde{c}}<\min (\chi ;\,\,1). \end{aligned}$$
    (3.6)

4 Stoneley secular equation at the generalized Wiechert condition

At conditions (3.1) coefficients (2.6) of the secular equation (2.4) take the form

$$\begin{aligned} \begin{array}{l} L=\left( {\left( {1-{\tilde{\rho }}} \right) ^{2}-\left( {{\tilde{\rho }}{\tilde{A}}_{2} +{\tilde{A}}_{1} } \right) \left( {{\tilde{\rho }}{\tilde{B}}_{2} +{\tilde{B}}_{1} } \right) } \right) \\ M={\tilde{K}}\left( {1+{\tilde{\rho }}{\tilde{A}}_{2} {\tilde{B}}_{2} -{\tilde{A}}_{1} {\tilde{B}}_{1} -{\tilde{\rho }}} \right) \\ N={\tilde{K}}^{2}\left( {1-{\tilde{A}}_{1} {\tilde{B}}_{1} } \right) \left( {1-{\tilde{A}}_{2} {\tilde{B}}_{2} } \right) \\ \end{array}. \end{aligned}$$
(4.1)

In (4.1) coefficient \({\tilde{K}}\) becomes

$$\begin{aligned} {\tilde{K}}=2\left( {1-{\tilde{\rho }}{\tilde{\chi }}^{2}} \right) \end{aligned}$$
(4.2)

and

$$\begin{aligned} {\tilde{A}}_{1} =\sqrt{1-\frac{{\tilde{c}}^{2}}{\chi ^{2}\gamma ^{2}}} ,\,\,\,\,\,\,\,\,\,{\tilde{A}}_{2} =\sqrt{1-\frac{{\tilde{c}}^{2}}{\gamma ^{2}}} ,\,\,\,\,\,\,\,\,\,\,{\tilde{B}}_{1} =\sqrt{1-\frac{{\tilde{c}}^{2}}{\chi ^{2}}} ,\quad ,{\tilde{B}}_{2} =\sqrt{1-{\tilde{c}}^{2}} , \end{aligned}$$
(4.3)

where

$$\begin{aligned} \gamma =\sqrt{2} \sqrt{\frac{1-\nu }{1-2\nu }} . \end{aligned}$$
(4.4)

In (4.4), \(\nu \) is the common Poisson’s ratio of both media; at \(\nu \in (-1;\,\,0.5)\)parameter \(\gamma \in \left( {\frac{2}{\sqrt{3} };\,\,\infty } \right) \).

With coefficients (4.1)–(4.3), the considered secular equation (2.4) becomes a three parametric one with parameters \({\tilde{\rho }},\,\,{\tilde{\chi }}\) and \(\gamma \) or \(\nu \).

Fig. 1
figure 1

Poisson’s ratio 0.0; a region of existence; b 3D plot for velocity variation; c projection onto the Wiechert plane

Full size image
Fig. 2
figure 2

Poisson’s ratio 0.25; a region of existence; b 3D plot for velocity variation; c projection onto the Wiechert plane

Full size image
Fig. 3
figure 3

Poisson’s ratio 0.49 a region of existence; b 3D plot for velocity variation; c projection onto the Wiechert plane

Full size image

5 Stoneley waves at the generalized Wiechert condition

This section concerns with numerical analysis of the real and positive root of secular equation (2.4) with coefficients defined by Eq. (4.1). In view of the non-monotonic behavior of the algebraic function \(P({\tilde{c}})\) in the left-hand side of Eq. (2.4), search of the appropriate root was done by the dichotomy algorithm coupled with the secant line method at the interval where the negative product

$$\begin{aligned} P({\tilde{c}}_{j} )P({\tilde{c}}_{j+1} )<0 \end{aligned}$$
(5.1)

at two adjacent values \({\tilde{c}}_{j} ;\,\,{\tilde{c}}_{j+1} \) is achieved along with condition \(ImP({\tilde{c}}_{j} )=0;\,\,\,\,ImP({\tilde{c}}_{j+1} )=0\). In view of condition (3.6), search of a root was done in the interval \(\left( {0;\,\,\min (\chi ;\,1)} \right) \); at the first dichotomy stage, the speed interval was divided into \(10^{3}\) subintervals; and 10–20 iterations at second stage of root refinement by the secant line method. With these parameters, accuracy of the root determination

$$\begin{aligned} \left| {P({\tilde{c}}_{\hbox {root}} )} \right| \le \varepsilon \end{aligned}$$
(5.2)

was about \(10^{-20}\). To minimize effect of possible round off errors, all computations were performed with long mantissas having more than 60 decimal digits [27, 28].

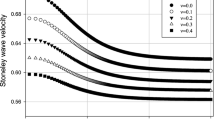
Plots in Figs. 1, 2 and 3 show (a) regions of existence in a 2D space defined by those values of parameters \({\tilde{\mu }},\,\,{\tilde{\rho }}\) that ensure existence of Stoneley wave; (b) 3D plots of dimensionless Stoneley wave velocity variation \({\tilde{c}}\) (vertical axis) vs dimensionless parameters \({\tilde{\mu }},\,\,{\tilde{\rho }}\); and (c) projection of the corresponding 3D plots onto vertical plane containing vertical axis \({\tilde{c}}\) and Wiechert line [15];    the latter is defined as line \({\tilde{\mu }}=\,{\tilde{\rho }}\); see Figs. 1c, 2c and 3c. This vertical plane will be called Wiechert plane.

The plots correspond to three Poisson’s values \(\nu =0;\,\,0.25;\,\,0.49\)

The plots in Figs. 1a, 2a and 3a reveal that the regions of existence have almost identical shapes; large similarity can be observed at comparing shapes (not values) of the corresponding 3D velocity plots (Figs. 1b, 2b, 3b), while projections of the velocity plots onto the Wiechert plane are substantially different, see Figs. 1c, 2c and 3c.

6 Concluding remarks

A generalization of the Wiechert condition by introducing two independent dimensionless parameters \({\tilde{\lambda }}={\tilde{\mu }}=q_{1} ;\,\,\,\,\,\,\,{\tilde{\rho }}=q_{2} \) instead of a single parameter \({\tilde{\lambda }}={\tilde{\mu }}=\,{\tilde{\rho }}=q\) in the original Wiechert condition is proposed.

Variation of Stoneley wave velocity at varying two parameters of the generalized Wiechert condition at different Poisson’s ratios reveals a substantial discrepancy in the Stoneley wave velocity profiles. While regions of existence (Figs. 1a, 2a, 3a) are visually almost undistinguishable, the Stoneley wave velocity profiles show a substantial discrepancy (Figs. 1c, 2c, 3c) in both shape and values.

Considering 3D plots showing variation of Stoneley wave velocity \({\tilde{c}}\) vs two varying parameters \({\tilde{\lambda }}={\tilde{\mu }}\) and \({\tilde{\rho }}\) (Figs. 1b, 2b, 3b), it should be noted that their shapes are similar; however, velocity values are different, as plots in Figs. 1c, 2c and 3c show.

And the final remark concerns an assertion [6, 7] that Poisson’s ratio does not considerably affect Stoneley wave velocity. Such a conclusion was inspired by comparison of regions of existence at different Poisson ratios. However, as our analysis reveals, Stoneley wave velocity heavily depends upon Poisson’s ratio; see Figs. 1c, 2c and 3c.