Size-dependent vibration of sandwich cylindrical nanoshells with functionally graded material based on the couple stress theory

Abstract

Vibration of functionally graded sandwich (FGS) cylindrical nanoshell is investigated. For this purpose, the first shear deformable shell theory as well as material length scale parameter as considered by the couple stress theory is used, and Hamilton’s principle is employed to derive the equations of motion of the FGS cylindrical nanoshell and the boundary conditions. In the end, using Navier solution, the natural frequency is determined for three types of FGS cylindrical nanoshells. Results of the new model are compared with the classical theory. According to the results, the rigidity of the FGS cylindrical nanoshell in the couple stress theory is higher than that in the classical theory, which leads to increased natural frequency. Besides, the effect of the material length scale parameter on natural frequency of the FGS cylindrical nanoshell in different wavenumbers and lengths is considerable.

1 Introduction

Modern achievements in the nanoscience have encouraged the researchers to more seriously consider the use of micro/nanoshells for modeling micro/nanostructures. The minute size of the structure of nanoshells has impeded the study of the dynamic behaviors of such components with conventional methods. Hence, researchers have to use various procedures such as experimental methods and continuum theories in this respect. Most experimental methods, however, are not economical due to their high costs and lengthy processes. Therefore, researchers have recently begun to use continuum theories which take the effect of material length scale (MLS) parameter into consideration. Those theories include non-local elasticity theory [1–8], couple stress theory [9–18], strain gradient theory [19–22], and surface stress theory [23–26].

Functionally graded materials are non-homogeneous materials which enhance the mechanical and thermal properties of structures by modifying nanoscopic structures. They are used for constructing sandwich structures which are widely used in different industries due to their high strength to weight ratio. Common sandwich structures are made up of a core and two faces, which can be made of functionally graded materials. In recent years, bucking and vibration of functionally graded sandwich (FGS) microbeams have been studied by the researchers. For instance, Nguyen et al. [27] examined the vibration and buckling of the FGS beam. In doing so, they used three FGS beams in different boundary conditions. Pradhan et al. [28] examined the vibration of the FGS beam and demonstrated that an increase in Pasternak foundation is accompanied by an increase in FGS beam frequency. Using finite elements method, Vo et al. [29] studied the vibration and buckling of FGS beam for different boundary conditions. Fereidoon et al. [30] investigated the bending of a curved FGS beam by using Euler–Bernoulli beam for modeling. They computed the beam deflection for the variations of Young’s modulus.

In recent years, researchers have used couple stress theory to study the behavior of nano/microbeams and nano/microshells. In couples stress theory, strain energy is dependent on both strain and strain variation [31–34]. Mindlin’s strain gradient theory was initially simplified by Fleck and Hutchinson and was named strain gradient theory, only to be rewritten later on by Lam et al. who eliminated the asymmetric part of the strain gradient tensor from the equations. Instead of the five constants developed by Mindlin, the modified strain gradient theory has only three constants for handling the effect of the MLS parameter. Couple stress theory is developed by setting two MLS parameters out of the three parameters to zero [35, 36]. Thai et al. [37] investigated the critical load and natural frequency of an FGS microbeam. They showed that an increase in the MLS parameter leads to an increase in the beam’s natural frequency and a decrease in its deformation. Researches have started to investigate the dynamic behavior of micro/nanostructures using the shell theory because modeling in this model enjoys more accuracy than that in the beam model. Using strain gradient theory, Zeighampour et al. [38] developed the governing equations of a nanoshell. In their model, by using Donnell shell theory, they showed that in shorter nanoshell lengths, the effect of MLS parameter on nanoshell natural frequency is stronger. Also, in another study, using first shear deformable shell theory and couples stress theory, Zeighampour et al. [39] attempted to examine the effect of vibration frequency on the nanoshell, demonstrating that an increase in MLS parameter leads to an increase in natural frequency. Zhang et al. [40], using strain gradient theory, investigated the vibration of an FG cylindrical microshell. They determined the natural frequency of the FG cylindrical microshell for various values of length and diameter of the microshell, wavenumber, and MSL parameter. Using Donnell shell theory, first shear deformable shell theory, and couple stress theory, Tadi et al. [41] investigated the vibration of an FG cylindrical microshell.

A review of the related literature demonstrates that sandwich nanostructures based on shell model have not been investigated sufficiently so far. Nanostructure modeling has been mainly based upon the beam model [37]. Besides, as regards the shell case, most nanostructure modeling has addressed homogeneous [38, 39] and FG materials [40, 41]. Hence, the present paper attempts to investigate the vibration of sandwich nanostructures. In doing so, the couple stress theory is used to take into account MLS, and the first shear deformable shell theory is employed in nanostructure modeling. In addition, three different sandwich nanostructures are used to model the nanoshell. Hamilton’s principle is employed to derive the equations of motion and boundary conditions, and the Navier solution is used to compute the frequency of FGS cylindrical nanoshell on the assumption that the nanoshell is simply supported. Finally, the effect of the MLS parameter, wavenumber and nanoshell length on natural frequency is investigated and it is demonstrated that the MLS parameter has a strong impact on natural frequency.

2 Preliminaries

2.1 Modified couple stress theory

Strain energy in the modified couple stress theory incorporates a non-classical constant of the MLS parameter as well as classical constants. In this theory, the strain energy for elastic and isotropic material in area $\varLambda$ (for an element at volume V) with infinitesimal deformation is expressed as [35]:

$$U = \frac{1}{2}\int_{ \, \varOmega } {\left( {\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} } \right){\text{d}}V}$$

(1)

where $\varepsilon_{ij}$ and $\chi_{ij}$ are the strain tensor and symmetric rotation gradient tensor, respectively, which are defined as

$$\varepsilon_{ij} = \frac{1}{2}\left( {\partial_{i} u_{j} + \partial_{j} u_{i} } \right)$$

(2)

$$\chi_{ij} = \frac{1}{4}\left( {e_{ipq} \varepsilon_{qj,p} + e_{jpq} \varepsilon_{qi,p} } \right)$$

(3)

where $u_{i}$ and $e_{jpq}$ are the displacement vector components and permutation symbol, respectively. Also, $\sigma_{ij}$ is the Cauchy stress tensor and $m_{ij}^{s}$ is the higher-order stress tensor, respectively, which are defined as

$$\sigma_{ij} = C_{ijkl} \varepsilon_{kl}$$

(4)

$$m_{ij} = 2l\mu \chi_{ij}$$

(5)

In Eq. (5), $l$ is the additional and independent MLS parameter associated with the symmetric rotation gradients.

The stress–strain equations in the plane stress case $(\sigma_{zz} = 0)$ for the first shear deformable isotropic shell model are expressed as:

$$\left\{ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{x\theta } \hfill \\ \sigma_{zx} \hfill \\ \sigma_{z\theta } \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} {C_{11} (z)} & {C_{12} (z)} & 0 & 0 & 0 \\ {C_{12} (z)} & {C_{22} (z)} & 0 & 0 & 0 \\ 0 & 0 & {C_{33} (z)} & 0 & 0 \\ 0 & 0 & 0 & {C_{44} (z)} & 0 \\ 0 & 0 & 0 & 0 & {C_{55} (z)} \\ \end{array} } \right]\left\{ \begin{aligned} \, \varepsilon_{xx} \hfill \\ \, \varepsilon_{\theta \theta } \hfill \\ 2k_{\text{s}} \varepsilon_{x\theta } \hfill \\ 2k_{\text{s}} \varepsilon_{zx} \hfill \\ 2k_{\text{s}} \varepsilon_{z\theta } \hfill \\ \end{aligned} \right\}$$

(6)

In Eq. (6), the elastic constants are defined as:

$$C_{11} (z) = C_{22} (z) = \frac{E(z)}{{1 - \nu^{2} (z)}},\quad C_{12} (z) = \frac{\upsilon (z)E(z)}{{1 - \nu^{2} (z)}},\quad {\text{C}}_{33} (z) = \frac{E(z)}{{2\left( {1 + \nu (z)} \right)}},\quad k_{\text{s}} = 5/6.$$

(7)

where $G$, E, ν, and $k_{\text{s}}$ represent shear modulus, Young’s modulus, Poisson’s coefficient, and shear coefficient, respectively. And, material distribution in the FGS cylindrical nanoshell along the direction of thickness and based on power-law form is expressed as:

$$P(z) = \left( {P_{\text{c}} - P_{\text{m}} } \right)V_{\text{c}} + P_{\text{m}}$$

(8)

In Eq. (8), P _c and P _m stand for Young’s modulus and Poisson’s coefficients of the density of ceramic and metal materials, respectively.

This paper uses three types of models to model FGS cylindrical nanoshell: Cylindrical nanoshell type ‘a’ with FG faces and homogeneous ceramic core, cylindrical nanoshell type ‘b’ with FG faces and homogeneous metal core, and cylindrical nanoshell type ‘c’ with homogeneous ceramic and metal faces and FG core. Figure 1 displays the three types of models.

Fig. 1

Modeling of FGS cylindrical nanoshell

The volume fraction of the ceramic phase $V_{\text{c}}^{j}$ for FGS cylindrical nanoshell is expressed for the three types as:

$V_{\text{c}}^{j}$ for type ‘a’ is expressed as (Fig. 1a):

$$V_{\text{c}}^{j} \left( z \right) = \left\{ {\begin{array}{*{20}l} {V_{\text{c}}^{1} \left( z \right) = \left( {\frac{{z - h_{2} }}{{h_{1} - h_{2} }}} \right)^{p} } \hfill & { - h/2 \le z \le - h/6} \hfill \\ {V_{\text{c}}^{2} \left( z \right) = 0} \hfill & { - h/6 \le z \le h/6} \hfill \\ {V_{\text{c}}^{3} \left( z \right) = \left( {\frac{{z - h_{3} }}{{h_{4} - h_{3} }}} \right)^{p} } \hfill & {h/6 \le z \le h/2} \hfill \\ \end{array} } \right.$$

(9)

$V_{\text{c}}^{j}$ for type ‘b’ is expressed as (Fig. 1b):

$$V_{\text{c}}^{j} \left( z \right) = \left\{ {\begin{array}{*{20}l} {V_{\text{c}}^{1} \left( z \right) = \left( {\frac{{z - h_{1} }}{{h_{2} - h_{1} }}} \right)^{p} } \hfill & { - h/2 \le z \le - h/6} \hfill \\ {V_{\text{c}}^{2} \left( z \right) = 0} \hfill & { - h/6 \le z \le h/6} \hfill \\ {V_{\text{c}}^{3} \left( z \right) = \left( {\frac{{z - h_{4} }}{{h_{3} - h_{4} }}} \right)^{p} } \hfill & {h/6 \le z \le h/2} \hfill \\ \end{array} } \right.$$

(10)

$V_{\text{c}}^{j}$ for type ‘c’ is expressed as (Fig. 1c):

$$V_{\text{c}}^{j} \left( z \right) = \left\{ {\begin{array}{*{20}l} {V_{\text{c}}^{1} \left( z \right) = 0^{p} } \hfill & { - h/2 \le z \le - h/6} \hfill \\ {V_{\text{c}}^{2} \left( z \right) = \left( {\frac{{z - h_{2} }}{{h_{3} - h_{2} }}} \right)^{p} } \hfill & { - h/6 \le z \le h/6} \hfill \\ {V_{\text{c}}^{3} \left( z \right) = 1} \hfill & {h/6 \le z \le h/2} \hfill \\ \end{array} } \right.$$

(11)

In Eqs. (8)–(11), $h_{i}$ and $p$ are height from the center of the core of FGS cylindrical nanoshell and power function, respectively, the value of which is determined as follows:

$$h_{1} = - h/2,\quad h_{2} = - h/6,\quad h_{3} = h/6,\quad h_{4} = h/2, \,$$

(12)

2.2 Displacement field of the FGS cylindrical nanoshell

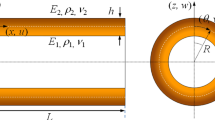
Figure 2 displays FGS cylindrical nanoshell. In this figure, $R$ and $h$ represent radius and height thickness of the FGS cylindrical nanoshell, respectively.

Fig. 2

Coordinates and displacements of a FGS cylindrical nanoshell

Based on the first shear deformable shell model, the displacement field is expressed as:

$$\begin{aligned} &u(x,\theta ,z,t) = U(x,\theta ,t) + z\psi_{x}(x,\theta ,t) \hfill \\ &{\text{v}}(x,\theta ,z,t) = V(x,\theta ,t) + z\psi_{\theta }(x,\theta ,t) \hfill \\ &w(x,\theta ,z,t) = W(x,\theta ,t) \hfill \\ \end{aligned}$$

(13)

where u, v, and w are the x-, y- and z-components of the displacement vector u of a point (x, y, z), respectively; also, $U$, $V$, and $W$ stand for the displacement vector in the middle surface of the cylindrical shell, respectively; and t represents time. Also, $\psi_{x}$ and $\psi_{\theta }$ are rotations around the x and $\theta$ axes.

2.3 Governing equations of motion and corresponding boundary conditions

In this section, equation of motion and boundary conditions of the FGS cylindrical nanoshell is developed using the couples stress theory. Figure (2) illustrates the coordinate system and displacement vector. By substituting Eq. (13) into Eq. (2), the nonzero strain components are expressed as:

$$\left( {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{\theta \theta } } \\ {\varepsilon_{x\theta } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } \\ {\varepsilon_{\theta \theta }^{0} } \\ {\varepsilon_{x\theta }^{0} } \\ \end{array} } \right) + z\left( {\begin{array}{*{20}c} {\varepsilon_{xx}^{1} } \\ {\varepsilon_{\theta \theta }^{1} } \\ {\varepsilon_{x\theta }^{1} } \\ \end{array} } \right),$$

(14)

And, in Eq. (14),

$$\left( {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } \\ {\varepsilon_{\theta \theta }^{0} } \\ {\varepsilon_{x\theta }^{0} } \\ {\varepsilon_{zx}^{0} } \\ {\varepsilon_{z\theta }^{0} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {\frac{\partial U}{\partial x}} \hfill \\ {\frac{1}{R}\left( {\frac{\partial V}{\partial \theta } + W} \right)} \hfill \\ {\frac{1}{2}\left( {\frac{1}{R}\frac{\partial U}{\partial \theta } + \frac{\partial V}{\partial x}} \right)} \hfill \\ {\frac{1}{2}\left( {\psi_{x} + \frac{\partial W}{\partial x}} \right)} \hfill \\ {\frac{1}{2}\left( {\psi_{\theta } + \frac{1}{R}\frac{\partial W}{\partial \theta } - \frac{V}{R}} \right)} \hfill \\ \end{array} } \right),\quad \left( {\begin{array}{*{20}c} {\varepsilon_{xx}^{1} } \\ {\varepsilon_{\theta \theta }^{1} } \\ {\varepsilon_{x\theta }^{1} } \\ {\varepsilon_{zx}^{1} } \\ {\varepsilon_{z\theta }^{1} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {\frac{{\partial \psi_{x} }}{\partial x}} \hfill \\ {\frac{{\partial \psi_{\theta } }}{\partial \theta }} \hfill \\ {\frac{1}{2}\left( {\frac{1}{R}\frac{{\partial \psi_{x} }}{\partial \theta } + \frac{{\partial \psi_{\theta } }}{\partial x}} \right)} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right)$$

(15)

$$\varepsilon_{x\theta } = \varepsilon_{\theta x} ,\quad \varepsilon_{xz} = \varepsilon_{zx} ,\quad \varepsilon_{z\theta } = \varepsilon_{\theta z}$$

(16)

By substituting Eq. (15) into Eq. (3), higher-order stress $\varvec{\chi}$ is expressed as [39]:

$$\left( {\begin{array}{*{20}c} {\chi_{xx} } \\ {\chi_{\theta \theta } } \\ {\chi_{zz} } \\ {\chi_{\theta x} } \\ {\chi_{\theta z} } \\ {\chi_{zx} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\chi_{xx}^{0} } \\ {\chi_{\theta \theta }^{0} } \\ {\chi_{zz}^{0} } \\ {\chi_{\theta x}^{0} } \\ {\chi_{\theta z}^{0} } \\ {\chi_{zx}^{0} } \\ \end{array} } \right) + z\left( {\begin{array}{*{20}c} {\chi_{xx}^{1} } \\ {\chi_{\theta \theta }^{1} } \\ {\chi_{zz}^{1} } \\ {\chi_{\theta x}^{1} } \\ {\chi_{\theta z}^{1} } \\ {\chi_{zx}^{1} } \\ \end{array} } \right), \,$$

(17)

And, in Eq. (17),

$$\left( {\begin{array}{*{20}c} {\chi_{xx}^{0} } \\ {\chi_{\theta \theta }^{0} } \\ {\chi_{zz}^{0} } \\ {\chi_{\theta x}^{0} } \\ {\chi_{\theta z}^{0} } \\ {\chi_{zx}^{0} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {\frac{1}{2R}\left( {\frac{{\partial^{2} W}}{\partial x\partial \theta } - \frac{\partial V}{\partial x} - R\frac{{\partial \psi_{\theta } }}{\partial x}} \right)} \hfill \\ {\frac{1}{2R}\left( {\frac{\partial V}{\partial x} - \frac{1}{R}\frac{\partial U}{\partial \theta } - \frac{{\partial^{2} W}}{\partial x\partial \theta } + \frac{{\partial \psi_{x} }}{\partial \theta }} \right)} \hfill \\ {\frac{1}{2}\left( {\frac{1}{{R^{2} }}\frac{\partial U}{\partial \theta } - \frac{1}{R}\frac{{\partial \psi_{x} }}{\partial \theta } + \frac{{\partial \psi_{\theta } }}{\partial x}} \right)} \hfill \\ {\frac{1}{4}\left( {\frac{1}{{R^{2} }}\left( {\frac{{\partial^{2} W}}{{\partial \theta^{2} }} - \frac{\partial V}{\partial \theta }} \right) - \frac{{\partial^{2} W}}{{\partial x^{2} }} - \frac{1}{R}\frac{{\partial \psi_{\theta } }}{\partial \theta } + \frac{{\partial \psi_{x} }}{\partial x}} \right)} \hfill \\ {\frac{1}{4R}\left( {\frac{\partial W}{\partial x} - \frac{1}{R}\frac{{\partial^{2} U}}{{\partial \theta^{2} }} + \frac{{\partial^{2} V}}{\partial x\partial \theta } - \psi_{x} } \right)} \hfill \\ {\frac{1}{4}\left( {\frac{V}{{R^{2} }} - \frac{1}{R}\frac{{\partial^{2} U}}{\partial x\partial \theta } + \frac{{\partial^{2} V}}{{\partial x^{2} }} - \frac{1}{{R^{2} }}\frac{\partial W}{\partial \theta } - \frac{{\psi_{\theta } }}{R}} \right)} \hfill \\ \end{array} } \right),\quad \left( {\begin{array}{*{20}c} {\chi_{xx}^{1} } \\ {\chi_{\theta \theta }^{1} } \\ {\chi_{zz}^{1} } \\ {\chi_{\theta x}^{1} } \\ {\chi_{\theta z}^{1} } \\ {\chi_{zx}^{1} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} 0 \hfill \\ {\frac{1}{2R}\left( {\frac{{\partial \psi_{\theta } }}{\partial x}} \right)} \hfill \\ 0 \hfill \\ 0 \hfill \\ {\frac{1}{4R}\left( {\frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } - \frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }}} \right)} \hfill \\ {\frac{1}{4}\left( {\frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta }} \right)} \hfill \\ \end{array} } \right)$$

(18)

$$\chi_{\theta x} = \chi_{x\theta } ,\quad \chi_{\theta z} = \chi_{z\theta } ,\quad \chi_{zx} = \chi_{zx}$$

(19)

By substituting classical and higher-order stresses and strains into Eq. (1), the strain energy of FGS cylindrical nanoshell is determined as:

$$\begin{aligned} \delta U_{\text{s}} = & \int_{0}^{2\pi } {\int_{0}^{L} {\left\{ {N_{xx} \delta \varepsilon_{xx}^{0} + M_{xx} \delta \varepsilon_{xx}^{1} + N_{\theta \theta } \delta \varepsilon_{\theta \theta }^{0} + M_{\theta \theta } \delta \varepsilon_{\theta \theta }^{1} } \right.} } + 2N_{x\theta } \delta \varepsilon_{x\theta }^{0} \\ + 2M_{x\theta } \delta \varepsilon_{x\theta }^{1} + 2N_{z\theta } \delta \varepsilon_{z\theta }^{0} + 2N_{xz} \delta \varepsilon_{xz}^{0} + Y_{xx} \delta \chi_{xx}^{0} + Y_{\theta \theta }^{{}} \delta \chi_{\theta \theta }^{0} + T_{\theta \theta }^{{}} \delta \chi_{\theta \theta }^{1} + Y_{zz}^{{}} \delta \chi_{zz}^{0} \\ + 2Y_{x\theta } \delta \chi_{x\theta }^{0} + 2Y_{z\theta }^{{}} \delta \chi_{z\theta }^{0} + 2T_{z\theta }^{{}} \delta \chi_{z\theta }^{1} \left. { + 2Y_{xz} \delta \chi_{xz}^{0} + 2T_{xz} \delta \chi_{xz}^{1} } \right\}Rdxd\theta \\ \end{aligned}$$

(20)

In the above equation, classical and non-classical forces and moments are written as follows:

$$N_{ij} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {\sigma_{ij}^{k} } {\text{d}}z} ,\quad M_{ij} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {\sigma_{ij}^{k} z} {\text{d}}z} ,$$

(21)

$$Y_{ij} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {m_{ij}^{k} } {\text{d}}z} ,\quad T_{ij} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {m_{ij}^{k} } z{\text{d}}z} ,$$

(22)

The kinetic energy for FGS cylindrical nanoshell is stated as follows:

$$T = \frac{1}{2}\rho \int_{0}^{2\pi } {\int_{0}^{L} {\int_{ - h/2}^{h/2} {\left\{ {\left( {\frac{\partial U}{\partial t} + z\frac{{\partial \psi_{x} }}{\partial t}} \right)^{2} + \left( {\frac{\partial V}{\partial t} + \frac{{\partial \psi_{\theta } }}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right\}R{\text{d}}z{\text{d}}x{\text{d}}\theta } } }$$

(23)

Now, using Hamilton’s principle

$$\int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta U_{\text{s}} - \delta T} \right){\text{d}}t = 0}$$

(24)

By substituting U _s and T values into Eq. (24), the equations of motion of the FGS cylindrical nanoshell are expressed as:

$$\begin{aligned} A_{1} \frac{{\partial^{2} U}}{{\partial x^{2} }} & + A_{2} \frac{{\partial^{2} U}}{{\partial \theta^{2} }} + A_{3} \frac{{\partial^{4} U}}{{\partial \theta^{4} }} + A_{4} \frac{{\partial^{4} U}}{{\partial x^{2} \partial \theta^{2} }} + A_{5} \frac{{\partial^{4} V}}{{\partial x^{3} \partial \theta }} + A_{6} \frac{{\partial^{4} V}}{{\partial x\partial \theta^{3} }} + A_{7} \frac{{\partial^{2} V}}{\partial x\partial \theta } \\ + A_{8} \frac{\partial W}{\partial x} + A_{9} \frac{{\partial^{3} W}}{{\partial x\partial \theta^{2} }} + A_{10} \frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + A_{11} \frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} + A_{12} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }} + A_{13} \frac{{\partial^{4} \psi_{x} }}{{\partial \theta^{4} }} + A_{14} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} \\ + A_{15} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }} + A_{16} \frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } + I_{0} \frac{{\partial^{2} U}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} = 0, \\ \end{aligned}$$

(25)

$$\begin{aligned} B_{1} \frac{{\partial^{2} U}}{\partial x\partial \theta } & + B_{2} \frac{{\partial^{4} U}}{{\partial x^{3} \partial \theta }} + B_{3} \frac{{\partial^{4} U}}{{\partial x\partial \theta^{3} }} + B_{4} \frac{{\partial^{2} V}}{{\partial x^{2} }} + B_{5} \frac{{\partial^{2} V}}{{\partial \theta^{2} }} + B_{6} \frac{{\partial^{4} V}}{{\partial x^{4} }} + B_{7} \frac{{\partial^{4} V}}{{\partial x^{2} \partial \theta^{2} }} + B_{8} V \\ + B_{9} \frac{\partial W}{\partial \theta } + B_{10} \frac{{\partial^{3} W}}{{\partial x^{2} \partial \theta }} + B_{11} \frac{{\partial^{3} W}}{{\partial \theta^{3} }} + B_{12} \frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } + B_{13} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} + B_{14} \frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }} + B_{15} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{4} }} \\ + B_{16} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }} + B_{17} \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} + B_{18} \frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} + B_{19} \psi_{\theta } + I_{0} \frac{{\partial^{2} V}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }} = 0, \\ \end{aligned}$$

(26)

$$\begin{aligned} C_{1} \frac{\partial U}{\partial x} & + C_{2} \frac{{\partial^{3} U}}{{\partial x\partial \theta^{2} }} + C_{3} \frac{\partial V}{\partial \theta } + C_{4} \frac{{\partial^{3} V}}{{\partial x^{2} \partial \theta }} + C_{5} \frac{{\partial^{3} V}}{{\partial \theta^{3} }} + C_{6} \frac{{\partial^{2} W}}{{\partial x^{2} }} + C_{7} \frac{{\partial^{4} W}}{{\partial x^{4} }} + C_{8} \frac{{\partial^{4} W}}{{\partial x^{2} \partial \theta^{2} }} \\ + C_{9} \frac{{\partial^{4} W}}{{\partial \theta^{4} }} + C_{10} \frac{{\partial^{2} W}}{{\partial \theta^{2} }} + C_{11} \frac{{\partial \psi_{x} }}{\partial x} + C_{12} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} + C_{13} \frac{{\partial^{3} \psi_{x} }}{{\partial x\partial \theta^{2} }} + C_{14} \frac{{\partial^{3} \psi_{\theta } }}{{\partial x^{2} \partial \theta }} + C_{15} \frac{{\partial^{3} \psi_{\theta } }}{{\partial \theta^{3} }} \\ + C_{16} \frac{{\partial \psi_{\theta } }}{\partial \theta } + I_{0} \frac{{\partial^{2} W}}{{\partial t^{2} }} = 0 \\ \end{aligned}$$

(27)

$$\begin{aligned} D_{1} \frac{{\partial^{2} U}}{{\partial x^{2} }} & + D_{2} \frac{{\partial^{2} U}}{{\partial \theta^{2} }} + D_{3} \frac{{\partial^{4} U}}{{\partial x^{2} \partial \theta^{2} }} + D_{4} \frac{{\partial^{4} U}}{{\partial \theta^{4} }} + D_{5} \frac{{\partial^{2} V}}{\partial x\partial \theta } + D_{6} \frac{{\partial^{4} V}}{{\partial x\partial \theta^{3} }} + D_{7} \frac{{\partial^{4} V}}{{\partial x^{3} \partial \theta }} \\ + D_{8} \frac{\partial W}{\partial x} + D_{9} \frac{{\partial^{3} W}}{{\partial x^{3} }} + D_{10} \frac{{\partial^{3} W}}{{\partial x\partial \theta^{2} }} + D_{11} \frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + D_{12} \frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} + D_{13} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }} + D_{14} \frac{{\partial^{4} \psi_{x} }}{{\partial \theta^{4} }} \\ + D_{15} \psi_{x} + D_{16} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} + D_{17} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }} + D_{18} \frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } + I_{1} \frac{{\partial^{2} U}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} = 0 \\ \end{aligned}$$

(28)

$$\begin{aligned} E_{1} \frac{{\partial^{2} U}}{\partial x\partial \theta } & + E_{2} \frac{{\partial^{4} U}}{{\partial x^{3} \partial \theta }} + E_{3} \frac{{\partial^{4} U}}{{\partial x\partial \theta^{3} }} + E_{4} \frac{{\partial^{2} V}}{{\partial x^{2} }} + E_{5} \frac{{\partial^{2} V}}{{\partial \theta^{2} }} + E_{6} V + E_{7} \frac{{\partial^{4} V}}{{\partial x^{4} }} + E_{8} \frac{{\partial^{4} V}}{{\partial x^{2} \partial \theta^{2} }} \\ + E_{9} \frac{{\partial^{3} W}}{{\partial x^{2} \partial \theta }} + E_{10} \frac{{\partial^{3} W}}{{\partial \theta^{3} }} + E_{11} \frac{\partial W}{\partial \theta } + E_{12} \frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } + E_{13} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} + E_{14} \frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }} + E_{15} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{4} }} \\ + E_{16} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }} + E_{17} \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} + E_{18} \frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} + E_{19} \psi_{\theta } + I_{1} \frac{{\partial^{2} V}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }} = 0 \\ \end{aligned}$$

(29)

The boundary conditions at the two ends of the FGS cylindrical nanoshell and for the simple support are as follows:

$$\begin{aligned} \left( {a_{1} \frac{\partial U}{\partial x}} \right. & + a_{2} \frac{{\partial^{3} U}}{{\partial x\partial \theta^{2} }} + a_{3} \frac{\partial V}{\partial \theta } + a_{4} \frac{{\partial^{3} V}}{{\partial x^{2} \partial \theta }} + a_{5} \frac{{\partial^{2} W}}{{\partial \theta^{2} }} + a_{6} W + a_{7} \frac{{\partial \psi_{x} }}{\partial x} + a_{9} \frac{{\partial^{3} \psi_{x} }}{{\partial x\partial \theta^{2} }} \\ + a_{10} \frac{{\partial^{3} \psi_{\theta } }}{{\partial x^{2} \partial \theta }} + \left. {\left. {a_{11} \frac{{\partial \psi_{\theta } }}{\partial \theta }} \right)} \right|_{x = 0,L} = 0,\quad \left( {\left. U \right|_{x = 0,L} \ne 0} \right) \\ \end{aligned}$$

(30)

$$\left. V \right|_{x = 0,L} = 0$$

(31)

$$\begin{aligned} &\left. {\left( {b_{1} \frac{{\partial^{2} U}}{\partial x\partial \theta } + b_{2} V + b_{3} \frac{{\partial^{2} V}}{{\partial x^{2} }} + b_{4} \frac{\partial W}{\partial \theta } + b_{5} \frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } + b_{6} \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} + b_{7} \psi_{\theta } } \right)} \right|_{x = 0,L} = 0, \, \hfill \\ &\, \left( {\left. {\frac{\partial V}{\partial x}} \right|_{x = 0,L} \ne 0} \right). \hfill \\ \end{aligned}$$

(32)

$$\left. W \right|_{x = 0,L} = 0,$$

(33)

$$\left( {c_{1} \frac{\partial V}{\partial \theta } + c_{2} \frac{{\partial \psi_{x} }}{\partial x} + c_{3} \frac{{\partial^{2} W}}{{\partial \theta^{2} }} + c_{4} \frac{{\partial^{2} W}}{{\partial x^{2} }} + c_{5} \frac{{\partial \psi_{\theta } }}{\partial \theta }} \right)_{x = 0,L} = 0,\quad \left( { \, \left. {\frac{\partial W}{\partial x}} \right|_{x = 0,L} \ne 0,} \right).$$

(34)

$$\begin{aligned} \left( {d_{1} \frac{\partial U}{\partial x}} \right. & + d_{2} \frac{{\partial^{3} U}}{{\partial x\partial \theta^{2} }} + d_{3} \frac{\partial V}{\partial \theta } + d_{4} \frac{{\partial^{3} V}}{{\partial x^{2} \partial \theta }} + d_{5} \frac{{\partial^{2} W}}{{\partial x^{2} }} + d_{6} \frac{{\partial^{2} W}}{{\partial \theta^{2} }} + d_{7} W \\ + d_{8} \frac{{\partial^{3} \psi_{x} }}{{\partial x\partial \theta^{2} }} + d_{9} \frac{{\partial \psi_{x} }}{\partial x} + d_{10} \frac{{\partial^{3} \psi_{\theta } }}{{\partial x^{2} \partial \theta }} + \left. {\left. {d_{11} \frac{{\partial \psi_{\theta } }}{\partial \theta }} \right)} \right|_{x = 0,L} = 0,\quad \left( { \, \left. {\psi_{x} } \right|_{x = 0,L} \ne 0,} \right). \\ \end{aligned}$$

(35)

$$\left. {\psi_{\theta } } \right|_{x = 0,L} = 0,$$

(36)

$$\begin{aligned} \left. {\left( {e_{1} \frac{{\partial^{2} U}}{\partial x\partial \theta } + e_{3} \frac{{\partial^{2} V}}{{\partial x^{2} }} + e_{2} V + e_{4} \frac{\partial W}{\partial \theta } + e_{6} \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} + e_{5} \frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } + e_{7} \psi_{\theta } } \right)} \right|_{x = 0,L} = 0, \, \hfill \\ \left( { \, \left. {\frac{{\partial \psi_{\theta } }}{\partial x}} \right|_{x = 0,L} \ne 0,} \right). \hfill \\ \end{aligned}$$

(37)

In order to solve Eqs. (25)–(27), given the fact that FGS cylindrical nanoshell is simply supported, the Navier solution with the assumption of the displacements is used as follows [42]:

$$\begin{aligned} U(x,\theta ,t) = \sum\limits_{n} {\sum\limits_{m} {U_{0} \cos \left( {\frac{m\pi x}{L}} \right)\cos (n\theta )} } , \hfill \\ V(x,\theta ,t) = \sum\limits_{n} {\sum\limits_{m} {V_{0} \sin \left( {\frac{m\pi x}{L}} \right)\sin (n\theta )} } , \hfill \\ W(x,\theta ,t) = \sum\limits_{n} {\sum\limits_{m} {W_{0} \sin \left( {\frac{m\pi x}{L}} \right)\cos (n\theta )} } , \hfill \\ \psi_{x} (x,\theta ,t) = \sum\limits_{n} {\sum\limits_{m} {\varPsi_{x} \cos \left( {\frac{m\pi x}{L}} \right)\cos (n\theta )} } , \hfill \\ \psi_{\theta } (x,\theta ,t) = \sum\limits_{n} {\sum\limits_{m} {\varPsi_{\theta } \sin \left( {\frac{m\pi x}{L}} \right)\sin (n\theta )} } , \hfill \\ \end{aligned}$$

(38)

where m and n are the axial half-wave and circumferential wave numbers, respectively.

By substituting Eq. (52) in Eqs. (23–27), the equations are rewritten in a matrix form as follows

$$[K]\left\{ d \right\} + [M]\left\{ {\ddot{d}} \right\} = 0$$

(39)

where $\left\{ d \right\}^{\text{T}} = \left\{ {U \, V \, W \, \varPsi_{x} \, \varPsi_{\theta } } \right\}^{\text{T}}$ is the displacement vector.

$$\left\{ d \right\} = \left\{ {d_{0} } \right\}e^{\omega t}$$

(40)

By substituting Eq. (40) in Eq. (39), the results are rewritten as follows:

$$\left( {[K] + \omega^{2} [M]} \right)\left\{ {d_{0} } \right\} = 0$$

(41)

where $\left\{ {d_{0} } \right\}^{\text{T}} = \left\{ {U_{0} \, V_{0} \, W_{0} \, \varPsi_{x} \, \varPsi_{\theta } } \right\}^{\text{T}}$ is the undetermined displacement amplitude vector and $\omega$ is the frequency. To obtain a non-trivial solution of Eq. (41), it is necessary to set the determinant of the coefficient matrix to zero.

3 Numerical results and discussions

In this section, the impact of MLS parameter, wavenumber and natural frequency of the FGS cylindrical nanoshell is investigated. Geometric dimensions and mechanical properties are as follows:

$$\begin{aligned} E_{m} = 70\,{\text{GPa}},\quad \upsilon_{m} = 0.3,\quad \rho_{m} = 2702\,{\text{kg}}/{\text{m}}^{3} , \hfill \\ E_{c} = 427\,{\text{GPa}},\quad \upsilon_{c} = 0.17,\quad \rho_{c} = \, 3100\,{\text{kg}}/{\text{m}}^{3} , \hfill \\ R = 5 \times 10^{ - 9} \,{\text{m}},\quad \, h = 0.5 \times 10^{ - 9} \,{\text{m}}. \hfill \\ \end{aligned}$$

(42)

In view of shortage of studies on FGS nanoshell vibration, in Table 1, the developed model is compared with Refs. [40, 43] in the case of isotropic cylindrical nanoshell. In Ref. [40], vibrational analysis of the FG cylindrical shell is investigated using first shear deformable shear theory and the Navier procedure. In Ref. [43], vibration of single-walled carbon nanotube (SWCNT) has been examined using the elasticity theory in three dimensions. Considering the results demonstrated in Table 1, in the classical case, the results of the present study have good consistency with the aforementioned references. Dimensionless natural frequency is $\varOmega = \omega R\sqrt {{\rho \mathord{\left/ {\vphantom {\rho E}} \right. \kern-0pt} E}}$, and the nanoshell mechanical and geometric characteristics are expressed as follows:

$$\, E = 1.06\,{\text{TPa}},\quad \upsilon = 0.3,\, \, \rho = 2300\,{\text{kg}}/{\text{m}}^{3} ,\quad L/R = 5,\quad R = 2.32\,{\text{nm}},\quad h = 0.34\,{\text{nm}}.$$

(43)

Table 1 Comparison of the dimensionless natural frequency for a cylindrical nanoshell based on classical theory

Due to a lack of experimental as well as MD results in connection with FGS cylindrical nanoshell vibration, the results of the present study are investigated using SWCNT vibration as demonstrated in Ref. [44]. In this reference, the MD method is used to compute SWCNT natural frequencies. The results obtained for the simply supported SWCNT are list in Table 2. Using couple stress theory, the MLS parameter for (10,10) SWCNT and (15,15) SWCNT was calculated as 0.0280 nm and 0.0178 nm, respectively. The parentheses in the Table 2 indicate the percentage of error of the results obtained using the two theories in comparison with the MD method. The degree of error in the couple stress theory is lower than that in the classical theory, indicating the efficiency of couple stress theory in investigating vibrations in nanodimensions. In this table, mechanical and geometric properties are used [44].

$$E = (3.19+3.15D^{-0.37})\,TPa ,\quad \rho = 11726 \,{\text{kg/m}}^{3} ,\quad h = 0.066\,{\text{nm}},\quad \upsilon = 0.19.$$

(44)

Table 2 Comparison of the natural frequency (THz) of couple stress shell model with MD simulation in different aspect ratios

Table 3 shows a comparison between the variation of natural frequency of FGS cylindrical nanoshell in different thicknesses and power-law indexes in the classical theory and couple stress theory. Besides, the natural frequency for three types of FGS cylindrical nanoshells has been determined. In this section, the assumption is that $\left( { \, L = 5R} \right)$ and $\left( {m = n = 1} \right)$. An increase in MLS parameter leads to an increase in natural frequency. Considering the fact that FGS cylindrical nanoshell stiffness in couple stress theory is dependent on MLS, it can be argued that the increase in the natural frequency of the FGS cylindrical nanoshell is due to the increase in FGS cylindrical nanoshell rigidity. Moreover, increase in power-law index leads to decrease in natural frequency, and increase in nanoshell thickness leads to increase in natural frequency. The MLS parameter has a stronger effect in higher nanoshell thicknesses. Furthermore, the FGS cylindrical nanoshell type ‘b’ and type ‘a’ have the highest and lowest natural frequency, respectively.

Table 3 Comparison of natural frequency (THz) of FGS cylindrical nanoshell with different thicknesses

The effects of MLS parameter and power-law index are displayed in Figs. 3, 4, 5. The natural frequency for the three types of FGS cylindrical nanoshells is determined, too. In this section, the assumption is that $\left( { \, L = 5R, \, h = 0.1R} \right)$ and $\left( {m = n = 1} \right)$. An increase in MLS parameter leads to an increase in natural frequency, which is indicative of higher prediction of stiffness by couple stress theory in comparison with the classical theory. Increase in power-law index leads to decrease in natural frequency. Moreover, the FGS cylindrical nanoshell type ‘b’ and type ‘a’ have the highest and lowest natural frequencies, respectively. In fact, type ‘b’ has more rigidity than the two other types. In type ‘c,’ in comparison with the other two types, in a certain MLS parameter, natural frequency variation in different power-law indexes is lower.

Fig. 3

Natural frequency based on MLS parameter and power-law indexes and for type ‘a’

Fig. 4

Natural frequency based on MLS parameter and power-law indexes and for type ‘b’

Fig. 5

Natural frequency based on MLS parameter and power-law indexes and for type ‘c’

Figures 6, 7, and 8 display the natural frequency of FGS cylindrical nanoshell based on nanoshell length, MLS parameter, and the three nanoshell types. In this section, the assumption is that $\left( {h = 0.1R} \right)$ and $\left( {m = n = 1} \right)$. As nanoshell length increases, natural frequency decreases. Besides, as nanoshell length increases, the effect of MLS parameter on natural frequency decreases. In FGS cylindrical nanoshell with couple stress theory, considering the fact that the size of MLS parameter is a dimension degree, variation of this parameter in FGS nanoshells with shorter lengths exerts a stronger effect on natural frequency. As displayed in Figs. 6, 7, and 8, FGS cylindrical nanoshell type ‘b’ and type ‘a’ undergo the highest and lowest variations in natural frequency, respectively.

Fig. 6

Natural frequency based on MLS parameter and L/R and for type ‘a’

Fig. 7

Natural frequency based on MLS parameter and L/R and for type ‘b’

Fig. 8

Natural frequency based on MLS parameter and L/R and for type ‘c’

Variations of the natural frequency of FGS cylindrical nanoshell based on MLS and circumferential wavenumber are displayed in Figs. 9, 10, and 11. In this section, the assumption is that $\left( {L = R} \right)$, $\left( {m = 1} \right)$, and $\left( {{l \mathord{\left/ {\vphantom {l h}} \right. \kern-0pt} h} = 1} \right)$. Increase in circumferential wavenumber in the couple stress theory is accompanied by increased natural frequency, with higher frequency increase in higher MLSs. In fact, increase in nanoshell rigidity leads to increased natural frequency. In fact, the rigidity of FGS cylindrical nanoshell type ‘b’ is more than that of types ‘a’ and ‘c.’ In addition, the size and degree of the variation of natural frequency in type b is greater than that in types a and c.

Fig. 9

Natural frequency based on MLS and circumferential wavenumber and for type ‘a’

Fig. 10

Natural frequency based on MLS and circumferential wavenumber and for type ‘b’

Fig. 11

Natural frequency based on MLS and circumferential wavenumber and for type ‘c’

4 Conclusion

In this paper, the vibration of FGS nanoshell was investigated using couple stress theory. For this purpose, the first shear deformable shell model was employed. Governing equations and boundary conditions were developed using Hamilton’s principle. Equations of FGS nanoshell in the special case were reduced to shell equations in the classical theory. By considering the simply supported FGS cylindrical nanoshell, the Navier solution was used to compute the natural frequency of the FGS cylindrical nanoshell. Afterward, the natural frequency was investigated based on different parameters such as MLS parameter, and axial and circumferential wavenumbers of the nanoshell. Results demonstrated that increase in MLS parameter and the consequent increase in rigidity leads to increase in natural frequency. Moreover, the MLS parameter has a considerable effect on natural frequency in different nanoshell lengths and wavenumbers.

Appendix

In equations of motion (25)–(29), the constant coefficients A _i , B _i , C _i , D _i and E _i are rewritten as follows:

$$\begin{aligned} A_{1} = - \tilde{A}_{11} , \, A_{2} = - \frac{{\tilde{A}_{33} }}{{R^{2} }} - \frac{{\tilde{A}_{66} l^{2} }}{{R^{4} }}, \, A_{3} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }}, \, A_{4} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, A_{5} = - \frac{{\tilde{A}_{66} l^{2} }}{4R}, \hfill \\ A_{6} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, A_{7} = - \frac{{\tilde{A}_{12} }}{R} - \frac{{\tilde{A}_{33} }}{R} + \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, A_{8} = - \frac{{\tilde{A}_{12} }}{R}, \, A_{9} = - \frac{{\tilde{A}_{66} l^{2} }}{{2R^{3} }}, \hfill \\ A_{10} = - \tilde{B}_{11} , \, A_{11} = - \frac{{\tilde{B}_{33} }}{{R^{2} }} + \frac{{5\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, A_{12} = \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }}, \, A_{13} = \frac{{\tilde{B}_{66} l^{2} }}{{4R^{4} }}, \, A_{14} = - \frac{{\tilde{B}_{66} l^{2} }}{4R}, \hfill \\ A_{15} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }}, \, A_{16} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }} - \frac{{\tilde{B}_{33} }}{R} - \frac{{\tilde{B}_{12} }}{R} + \frac{{\tilde{B}_{66} l^{2} }}{{2R^{3} }}. \hfill \\ \end{aligned}$$

(A.1)

$$\begin{aligned} B_{1} = - \frac{{\tilde{A}_{12} }}{R} - \frac{{\tilde{A}_{33} }}{R} + \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, B_{2} = - \frac{{\tilde{A}_{66} l^{2} }}{4R}, \, B_{3} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, B_{4} = - \tilde{A}_{33} - \frac{{\tilde{A}_{66} l^{2} }}{{2R^{2} }}, \hfill \\ B_{5} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }} - \frac{{\tilde{A}_{22} }}{{R^{2} }}, \, B_{6} = \frac{{\tilde{A}_{66} l^{2} }}{4}, \, B_{7} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, B_{8} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }} + \frac{{\tilde{A}_{55} k_{s} }}{{R^{2} }}, \hfill \\ B_{9} = - \frac{{\tilde{A}_{55} k_{s} }}{{R^{2} }} - \frac{{\tilde{A}_{22} }}{{R^{2} }} - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }}, \, B_{10} = \frac{{3\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, B_{11} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }}, \hfill \\ B_{12} = - \frac{{\tilde{A}_{66} l^{2} }}{{2R^{2} }} - \frac{{\tilde{B}_{12} }}{R} - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }} - \frac{{\tilde{B}_{33} }}{R}, \, B_{13} = - \frac{{\tilde{B}_{66} l^{2} }}{4R}, \, B_{14} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }}, \hfill \\ B_{15} = \frac{{\tilde{B}_{66} l^{2} }}{4}, \, B_{16} = \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }}, \, B_{17} = - \tilde{B}_{33} - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }} - \frac{{3\tilde{A}_{66} l^{2} }}{4R}, \hfill \\ B_{18} = - \frac{{\tilde{B}_{22} }}{{R^{2} }} - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, B_{19} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }} - \frac{{\tilde{A}_{55} ks}}{R}, \hfill \\ \end{aligned}$$

(A.2)

$$\begin{aligned} C_{1} = \frac{{\tilde{A}_{12} }}{R}, \, C_{2} = \frac{{\tilde{A}_{66} l^{2} }}{{2R^{3} }}, \, C_{3} = \, \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }} + \frac{{\tilde{A}_{55} k_{s} }}{{R^{2} }} + \frac{{\tilde{A}_{22} }}{{R^{2} }}, \, C_{4} = - \frac{{3\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \hfill \\ C_{5} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }}, \, C_{6} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }} - \tilde{A}_{44} k_{s} , \, C_{7} = \frac{{\tilde{A}_{66} l^{2} }}{4}, \, C_{8} = \frac{{\tilde{A}_{66} l^{2} }}{{2R^{2} }}, \, C_{9} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }}, \hfill \\ C_{10} = \frac{{\tilde{A}_{22} }}{{R^{2} }}, \, C_{11} = - \frac{{\tilde{A}_{55} k_{s} }}{{R^{2} }} - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }}, \, C_{11} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }} - \tilde{A}_{44} k_{s} + \frac{{\tilde{B}_{12} }}{R}, \hfill \\ C_{12} = - \frac{{\tilde{A}_{66} l^{2} }}{4}, \, C_{13} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, C_{14} = - \frac{{\tilde{A}_{66} l^{2} }}{4R} - \frac{{\tilde{B}_{66} l^{2} }}{{2R^{2} }}, \, C_{15} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \hfill \\ C_{15} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }} + \frac{{\tilde{B}_{22} }}{{R^{2} }} - \frac{{\tilde{A}_{55} k_{s} }}{R}, \hfill \\ \end{aligned}$$

(A.3)

$$\begin{aligned} D_{1} = - \tilde{B}_{11} , \, D_{2} = - \frac{{\tilde{B}_{33} }}{{R^{2} }} + \frac{{5\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, D_{3} = \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }}, \, D_{4} = \frac{{\tilde{B}_{66} l^{2} }}{{4R^{4} }}, \, \hfill \\ D_{5} = - \frac{{\tilde{A}_{66} l^{2} }}{{2R^{2} }} - \frac{{\tilde{B}_{12} }}{R} - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }} - \frac{{\tilde{B}_{33} }}{R}, \, D_{6} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }}, \, D_{7} = - \frac{{\tilde{B}_{66} l^{2} }}{4R}, \hfill \\ D_{8} = - \frac{{\tilde{B}_{12} }}{R} + \tilde{A}_{44} k_{s} - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, D_{9} = \frac{{\tilde{A}_{66} l^{2} }}{4}, \, D_{10} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }},D_{11} = - \frac{{\tilde{A}_{66} l^{2} }}{4} - \tilde{D}_{11} , \, \hfill \\ D_{12} = - \frac{{\tilde{A}_{66} l^{2} }}{{R^{2} }} + \frac{{\tilde{B}_{66} l^{2} }}{{2R^{3} }} - \frac{{\tilde{D}_{33} }}{{R^{2} }}, \, D_{13} = \frac{{\tilde{D}_{66} l^{2} }}{{4R^{2} }}, \, D_{14} = \frac{{\tilde{D}_{66} l^{2} }}{{4R^{4} }}, \, D_{15} = \tilde{A}_{44} k_{s} + \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, \hfill \\ D_{16} = \frac{{\tilde{D}_{66} l^{2} }}{4R}, \, D_{17} = - \frac{{\tilde{D}_{66} l^{2} }}{{4R^{3} }}, \, D_{18} = - \frac{{\tilde{B}_{66} l^{2} }}{{2R^{2} }} - \frac{{\tilde{D}_{33} }}{R} + \frac{{3\tilde{A}_{66} l^{2} }}{4R} - \frac{{\tilde{D}_{12} }}{R}, \hfill \\ \end{aligned}$$

(A.4)

$$\begin{aligned} E_{1} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }} - \frac{{\tilde{B}_{33} }}{R} - \frac{{\tilde{B}_{12} }}{R} + \frac{{\tilde{B}_{66} l^{2} }}{{2R^{3} }}, \, E_{2} = - \frac{{\tilde{B}_{66} l^{2} }}{4R}, \, E_{3} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }}, \hfill \\ E_{4} = - \tilde{B}_{33} - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }} - \frac{{3\tilde{A}_{66} l^{2} }}{4R}, \, E_{5} = - \frac{{\tilde{B}_{22} }}{{R^{2} }} - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, E_{6} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{4} }} - \frac{{\tilde{A}_{55} k_{s} }}{R}, \hfill \\ E_{7} = \frac{{\tilde{B}_{66} l^{2} }}{4}, \, E_{8} = \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }}, \, E_{9} = \frac{{\tilde{A}_{66} l^{2} }}{4R} + \frac{{\tilde{B}_{66} l^{2} }}{{2R^{2} }}, \, E_{10} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \hfill \\ E_{11} = - \frac{{\tilde{B}_{22} }}{{R^{2} }} + \frac{{\tilde{A}_{55} k_{s} }}{R} + \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, E_{12} = - \frac{{\tilde{B}_{66} l^{2} }}{{2R^{2} }} - \frac{{\tilde{D}_{33} }}{R} + \frac{{3\tilde{A}_{66} l^{2} }}{4R} - \frac{{\tilde{D}_{12} }}{R}, \hfill \\ E_{13} = - \frac{{\tilde{D}_{66} l^{2} }}{4R}, \, E_{14} = - \frac{{\tilde{D}_{66} l^{2} }}{{4R^{3} }}, \, E_{15} = \frac{{\tilde{D}_{66} l^{2} }}{4}, \, E_{16} = \frac{{\tilde{D}_{66} l^{2} }}{{4R^{2} }}, \, \hfill \\ E_{17} = - \frac{{\tilde{B}_{66} l^{2} }}{2R} - \tilde{A}_{66} l^{2} - \tilde{D}_{33} - \frac{{\tilde{D}_{66} l^{2} }}{{2R^{2} }}, \, E_{18} = - \frac{{\tilde{D}_{22} }}{{R^{2} }} - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, E_{19} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }} + \tilde{A}_{55} k_{s} , \, \hfill \\ \end{aligned}$$

(A.5)

In boundary conditions (30)–(37), the constant coefficients a _i , b _i , c _i , d _i and e _i are rewritten as follows:

$$\begin{aligned} a_{1} = - \tilde{A}_{11} , \, a_{2} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, a_{3} = \frac{{\tilde{A}_{12} }}{R} + \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \, a_{4} = \frac{{\tilde{A}_{66} l^{2} }}{4R}, \, a_{5} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{3} }}, \hfill \\ a_{6} = \frac{{\tilde{A}_{12} }}{R}, \, a_{7} = \tilde{B}_{11} , \, a_{8} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }}, \, a_{9} = \frac{{\tilde{B}_{66} l^{2} }}{4R}, \, a_{10} = \frac{{\tilde{B}_{12} }}{R} - \frac{{\tilde{A}_{66} l^{2} }}{{2R^{2} }} \hfill \\ \end{aligned}$$

(A.6)

$$\begin{aligned} b_{1} = - \frac{{\tilde{A}_{66} l^{2} }}{4R}, \, b_{2} = \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, b_{3} = \frac{{\tilde{A}_{66} l^{2} }}{4}, \, b_{4} = - \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, b_{5} = - \frac{{\tilde{B}_{66} l^{2} }}{4R}, \, \hfill \\ b_{6} = \frac{{\tilde{B}_{66} l^{2} }}{4}, \, b_{7} = - \frac{{\tilde{A}_{66} l^{2} }}{4R}, \, \hfill \\ \end{aligned}$$

(A.7)

$$c_{1} = - \frac{{\tilde{A}_{66} l^{2} }}{{2R^{2} }}, \, c_{2} = \frac{{\tilde{A}_{66} l^{2} }}{4}, \, c_{3} = \, \frac{{\tilde{A}_{66} l^{2} }}{{4R^{2} }}, \, c_{4} = - \frac{{\tilde{A}_{66} l^{2} }}{4}, \, c_{5} = - \frac{{\tilde{A}_{66} l^{2} }}{4R},$$

(A.8)

$$\begin{aligned} d_{1} = \tilde{B}_{11} , \, d_{2} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }}, \, d_{3} = \frac{{\tilde{B}_{12} }}{R} + \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }} - \frac{{\tilde{A}_{66} l^{2} }}{{2R^{2} }}, \, d_{4} = \frac{{\tilde{B}_{66} l^{2} }}{4R}, \, d_{5} = - \frac{{\tilde{A}_{66} l^{2} }}{4}, \, \hfill \\ d_{6} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }} + \frac{{\tilde{A}_{66} l^{2} }}{{2R^{2} }}, \, d_{7} = \frac{{\tilde{B}_{12} }}{R}, \, d_{8} = - \frac{{\tilde{D}_{66} l^{2} }}{{4R^{2} }}, \, d_{9} = \tilde{D}_{11} + \frac{{\tilde{A}_{66} l^{2} }}{4}, \, d_{10} = \frac{{\tilde{D}_{66} l^{2} }}{4R}, \hfill \\ d_{11} = \frac{{\tilde{D}_{12} }}{R} - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }} - \frac{{\tilde{A}_{66} l^{2} }}{4R}, \, \hfill \\ \end{aligned}$$

(A.9)

$$\begin{aligned} e_{1} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{3} }}, \, e_{2} = \frac{{\tilde{B}_{66} l^{2} }}{4}, \, e_{3} = \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }}, \, e_{4} = - \frac{{\tilde{B}_{66} l^{2} }}{{4R^{2} }}, \, e_{5} = \frac{{\tilde{D}_{66} l^{2} }}{4}, \, e_{6} = - \frac{{\tilde{D}_{66} l^{2} }}{4R}, \hfill \\ e_{7} = - \frac{{\tilde{B}_{66} l^{2} }}{4R}. \hfill \\ \end{aligned}$$

(A.10)

In equations (A.1)–(A.10), the constant coefficients $\tilde{A}_{ij}$, $\tilde{B}_{ij}$, and $\tilde{D}_{ij}$ are rewritten as follows:

$$\begin{aligned} \tilde{A}_{ij} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {C_{ij}^{k} } {\text{d}}z} , \, \tilde{B}_{ij} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {C_{ij}^{k} z} {\text{d}}z} , \, \tilde{D}_{ij} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {C_{ij}^{k} z^{2} } {\text{d}}z} , \hfill \\ \tilde{A}_{66} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {C_{33}^{k} } {\text{d}}z} , \, I_{i} = \sum\limits_{k = 1}^{n} {\int_{{h_{k} }}^{{h_{k + 1} }} {\rho z^{i} } {\text{d}}z} . \hfill \\ \end{aligned}$$

(A.12)