1 Introduction

Nowadays, dynamics analysis and mathematical modeling of nano-structures are important because of their industrial applications. Recently, by utilizing the physical features of the rotating CNT and the vacancy modified CNT, Tu et al. (2016) proposed a novel nanoscale fluidic device a rotating carbon nanotube membrane filter to resolve some of the critical issues in CNT-based membrane technology. This device can refine saltwater into the freshwater. Thus, because of the importance of this device, this study examined influences of rotational speed and velocity of viscous fluid flow on free vibration behavior of spinning single-walled carbon nanotube (SWCNT). Surprising mechanical properties of SWCNTs make them an appropriate choice to be used in chemistry, physics and nano-engineering applications, as well as their practical usages in electrical engineering, materials science and construction engineering. Therefore, it is vital to study mechanical behaviors of SWCNTs such as buckling and post-buckling (Eftekhari et al. 2013), vibration (Elishakoff and Pentaras 2009), thermal vibration (Zidour et al. 2012) and instability analysis (Yoon et al. 2005). Bringing some examples of SWCNT applications, drug delivery (Rao and Cheetham 2001), micro-/nano-electromechanical systems (MEMS/NEMS) (Li et al. 2015) and nano-pipes containing flowing fluid (Hummer et al. 2001) are notable. Rotating SWCNT has attracted attentions in recent years due to their promising future. These rotating nano-structures can be also used as MEMS gyroscope sensors (Yang et al. 2011) in the aerospace industry, military, automotive and consumer electronics markets including advanced automotive safety systems, high-performance navigation and guidance systems, ride stabilization, rollover detection and prevention, image stabilization in digital cameras and highly technological applications including nano-/micro-satellites, nano-/micro-robotics and even implantable devices to cure internal disorders. Lately, Tu et al. (2016) suggested rotating membrane filter built of carbon nanotubes for desalinating water which proves the preciousness of this study. The experiments and researches show that size effects play an important role in mechanical properties (Ghadiri et al. 2016). Thus, avoiding these effects may result wrong designs and unacceptable answers. It should be noted that the size effect is not considered in classical continuum theories, so this theory is not appropriate for micro- and nanoscales. One of the nonclassical theories that consider the effects of size is couple stress theory. Toupin, Koiter and Mindlin (Toupin 1962; Kolter 1964; Mindlin 1964) investigated the couple stress theory including higher-order rotational gradients which in fact it is the asymmetric part of the deformation gradient. According to this theory, it includes four material constants (two classical and two additional) for isotropic elastic materials. As an example of this theory, Asghari et al. (2011) presented the size effects in Timoshenko beams on the basis of the couple stress theory. It is difficult to determine the microstructure-related length scale parameters. Therefore, we are looking for the continuum theory which involves only one additional material length scale parameter. MCST is one of the best and most well-known continuum mechanics theories that include small-scale effects with reasonable accuracy in microscale devices. Yang et al. (2002) presented a modified couple stress theory, in which the couple stress tensor is symmetric and only one internal material length scale parameter is involved, unlike the classical couple stress theory mentioned above. Many researchers have used this theory to examine the dynamic and static behavior of micro-beams, micro-plates and micro-shells (Park and Gao 2006; Reddy 2011; Shaat et al. 2014; Ghadiri and SafarPour 2017). It is noted that nonlocal theory of Eringen is one of the best and most well-known continuum mechanics theories includes small-scale effects with good accuracy in nano-/microscale devices, but the results show that modified couple stress theory coincides with experimental results better than Eringen’s nonlocal elasticity and classical theories (Miandoab et al. 2014). Therefore, in this study, the modified couple stress theory is used. In classical shell theories, it is assumed that the stresses are constant along the thickness. Considering this assumption, the theories of classical shell cannot present precise results for thick and moderately thick shells. First-order shear deformation theory (FSDT) was presented by Reissner (1945) and Mindlin (1951) to compensate the defects of the classical theory. Researchers show that the dynamic behavior of carbon nanotubes is substantially similar to that of cylindrical shells (Torkaman-Asadi et al. 2015). Consequently, for a better comprehension of nanotubes rotational behavior, firstly, the rotational behavior of cylinder should be studied. In the field of rotating cylindrical shell structures, Hua and Lam (1998) presented frequency characteristic of a thin rotating cylindrical shell using GDQM. Also Liew et al. (2002) investigated the free vibration analysis of rotating cylindrical shells considering initial hoop tension effect using a mesh-free approach. Recently, Hosseini-Hashemi et al. (2013) presented an exact analytical solution for free vibration of a rotating circular functionally graded cylindrical shell based on FSDT shell theory. The whirling frequencies of rotating cylindrical shells surrounded by an elastic foundation with various boundary conditions were presented by Firouz-Abadi et al. (2013). In addition, stability of high rotational speed and free vibration analysis of carbon nanotubes partially resting on Winkler foundations were investigated by Torkaman-Asadi et al. (2015). All scopes of the above articles are dynamic analysis of cylindrical shell structures, but it should be noted that none of them have considered conveying fluid. In the field of vibration analysis of single-walled nanotube conveying fluid, Bahaadini and Hosseini (2016) presented the effects of slip condition and nonlocal elasticity on vibration and stability analysis of viscoelastic cantilever CNT conveying fluid. Arani et al. (2013) presented the effect of time discretization on nonlinear vibration of embedded single-walled boron nitride nanotube conveying viscous fluid based on the nonlocal piezoelasticity theory. Vibration analysis of fluid-conveying double-walled carbon nanotubes using MCST was presented by Zeighampour and Beni (2014). In this study, by increasing the fluid velocity, the natural frequency tends to decrease. Lee and Chang (2008) investigated the free transverse vibration of the fluid-conveying single-walled carbon nanotube using nonlocal elastic theory. Wave propagation in single- and double-walled carbon nanotubes filled with fluid was investigated by Natsuki et al. (2007). Also in other work, the effects of nonlocal elasticity and Knudsen number on fluid–structure interaction in carbon nanotube conveying fluid were presented by Mirramezani and Mirdamadi (2012). Zhang et al. (2016) investigated acoustic nano-wave absorption through clustered carbon nanotubes conveying fluid. Natural frequency and stability tuning of cantilevered CNTs conveying fluid in magnetic field were presented by Wang et al. (2016). Nonlinear vibration of fluid-conveying single-walled carbon nanotubes under harmonic excitation was presented by Zhen and Fang (2015). Also, size-dependent nonlinear vibration and instability of embedded fluid-conveying SWBNNT in thermal environment was investigated by Ansari et al. (2014). According to the theory of stress gradient, Zhang et al. (2014) presented free vibration analysis of the fluid-conveying carbon nanotube. They in this work investigated critical flow speed of carbon nanotube based on strain gradient theory. In the field of nonuniform CNTs, Rafiei et al. (2012) investigated the small-scale effect on the vibration of nonuniform carbon nanotubes conveying fluid and embedded in viscoelastic medium. In addition, in the field of vibration analysis of double-walled nanotubes conveying fluid, Kuang et al. (2009) presented analysis of nonlinear vibrations of double-walled carbon nanotubes conveying fluid. Nonlocal vibration and instability of embedded double-walled boron nitride nanotube conveying viscose fluid were presented by Maraghi et al. (2013). Also, nonlocal surface piezoelasticity theory for dynamic stability of double-walled boron nitride nanotube conveying viscose fluid was investigated by Arani et al. (2014). In the field of vibration analysis of micro-tubes conveying fluid, Wang (2010) presented size-dependent vibration characteristics of fluid-conveying micro-tubes. They in this work observed the micro-tube will become unstable by divergence at a critical flow velocity. In other work, Li et al. (2016) investigated size-dependent effects on critical flow velocity of fluid-conveying micro-tubes via nonlocal strain gradient theory. Tang et al. (2014) studied nonlinear modeling and size-dependent vibration analysis of curved micro-tubes conveying fluid based on modified couple stress theory. In the field of vibration analysis of micro-pipe conveying fluid, Wang et al. (2013) investigated flexural vibrations of microscale pipes conveying fluid by considering the size effects of micro-flow and microstructure. Stability analysis of a piezoelectrically actuated micro-pipe conveying fluid was presented by Abbasnejad et al. (2015). They in this work showed imposing voltage difference to piezoelectric layers can significantly suppress the effect of fluid flow on vibrational frequencies and thus extend the stable margins. Also, Hosseini and Bahaadini (2016) investigated size-dependent stability analysis of cantilever micro-pipes conveying fluid based on modified strain gradient theory. In other work, Hu et al. (2016) presented nonlinear and chaotic vibrations of cantilevered micro-pipes conveying fluid based on modified couple stress theory. Setoodeh and Afrahim (2014) investigated the size-dependent nonlinear vibration behavior of micro-pipes conveying fluid based on strain gradient theory. In the field of vibration analysis of nano-pipe conveying fluid, Mirramezani and Mirdamadi (2012) presented the effects of Knudsen-dependent flow velocity on vibrations of a nano-pipe conveying fluid. They in this work observed that, for passage of gas through nano-pipe with nonzero Knudsen number (Kn), the critical flow velocities decreased considerably as opposed to those for zero Kn. Recently, according to the Mindlin’s strain gradient theory, Ansari et al. (2016) investigated size-dependent thermo-mechanical vibration and instability of conveying fluid functionally graded nano-shells. Also, Ansari et al. (2016) studied geometrically nonlinear free vibration and instability of fluid-conveying nanoscale pipes including surface stress effects. It is worth mentioning none of the previous works have considered size effect, viscous fluid flow and initial hoop tension on a rotary SWCNT using MCST. The novelty of this work is considering the viscous fluid flow, rotation, initial hoop tension and size effect in addition to considering various boundary conditions on the SWCNT using MCST. Because of high accuracy and efficiency of the generalized differential quadrature method (GDQM), it is employed to solve the governing equations of the problem for all boundary conditions. The governing equations and boundary conditions have been developed using Hamilton principle which are solved with the aid of the GDQM. The results show that initial hoop tension, material length scale parameter, viscous fluid flow, angular velocity, length-to-radius ratio, radius-to-thickness ratio and boundary conditions play important roles on natural frequency of rotating SWCNT conveying viscous fluid.

2 Mathematical formulation

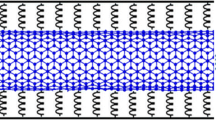
In order to have better understanding of the importance and applications of the proposed model, Fig. 1 demonstrates a rotating SWCNT conveying fluid flow which can turn saltwater into the freshwater (Tu et al. 2016). They have designed a rotating carbon nanotube membrane filter (RCNT-MF) for the reverse osmosis desalination that can refine saltwater into the freshwater.

Fig. 1
figure 1

One application of the rotating SWCNT model conveying fluid flow (Tu et al. 2016)

Full size image

2.1 Modified couple stress theory

Modified couple stress theory was presented by Yang et al. (2002) for the first time. In this theory, the strain energy expressed as a function of rotation tensor gradient and strain tensor; in addition, it includes one length scale parameter and two Lame parameters. According to this theory, the strain energy is expressed as:

$$U = \frac{1}{2}\iiint\limits_{V} {(\sigma_{ij} \varepsilon_{ij} + m_{ij}^{s} \chi_{ij}^{s} ){\text{d}}V}$$
(1)

In Eq. (1), \(\chi_{\text{ij}}^{\text{s}}\), ε ij , σ ij and m ij represent the components of symmetric rotation gradient tensor, strain tensor, stress tensor and higher-order stress tensor, respectively, which are expressed as:

$$\varepsilon_{ij} = \frac{1}{2}(u_{i,j} + u_{j,i} )$$
(2)
$$\chi_{ij}^{s} = \frac{1}{2}(\varphi_{i,j} + \varphi_{j,i} )$$
(3)
$$m_{ij}^{s} = 2l^{2} \mu (\hat{z})\chi_{ij}^{s} ,\quad \varphi_{i} = \frac{1}{2}\left[ {{\text{curl}}(u)} \right]_{i}$$
(4)

where u i and \(\varnothing_{i}\) represent the components of displacement vector and infinitesimal rotation vector, respectively. In Eq. (4), l is the parameter which denotes the additional independent material length scale parameter that is related to the symmetric rotation gradients. Note that the length scale parameter is assumed constant in FG cylindrical shell. In addition, the stress–strain relation can be expressed as follows:

$$\left\{ {\begin{array}{*{20}l} {\sigma_{xx} } \hfill \\ {\sigma_{\theta \theta } } \hfill \\ {\sigma_{x\theta } } \hfill \\ {\sigma_{\theta z} } \hfill \\ {\sigma_{xz} } \hfill \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {C_{11} } \hfill & {C_{12} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {C_{12} } \hfill & {C_{22} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {C_{66} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {C_{44} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {C_{55} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\varepsilon_{xx} } \hfill \\ {\varepsilon_{\theta \theta } } \hfill \\ {2\varepsilon_{x\theta } } \hfill \\ {2\varepsilon_{\theta z} } \hfill \\ {2\varepsilon_{xz} } \hfill \\ \end{array} } \right\}$$
(5)

where C ij is the elasticity matrix component. The stiffness coefficients are expressed as:

$$\begin{aligned} C_{11} & = \frac{E}{{1 - \nu^{2} }},\quad \,C_{12} = \nu C_{11} ,\quad \,C_{22} = C_{11} , \\ C_{44} & = C_{55} = C_{66} = \frac{E}{2(1 + \nu )} \\ \end{aligned}$$
(6)

2.2 Displacement field of cylindrical shell

Figure 2 shows a rotating SWCNT conveying viscous fluid flow in which x, θ and z denote the orthogonal curvilinear coordinates on the middle surface (z = 0). The thickness, length and the middle surface radius of cylindrical shell are denoted by h, L and R, respectively. According to the first-order shear deformation theory, the displacement field of cylindrical FG nano-shell along the three directions of x, θ and z is expressed as:

$$\begin{aligned} U(x,\theta ,z,t) & = u(x,\theta ,t) + z\psi_{x} (x,\theta ,t) \\ V(x,\theta ,z,t) & = v(x,\theta ,t) + z\psi_{\theta } (x,\theta ,t) \\ W(x,\theta ,z,t) & = w(x,\theta ,t) \\ \end{aligned}$$
(7)
Fig. 2
figure 2

Geometry of the rotating SWCNT conveying viscous flow

Full size image

In Eq. (7), u(x, θ, t), v(x, θ, t) and w(x, θ, t) are considered as neutral axis displacement, and ψ θ (x, θ, t) and ψ x (x, θ, t) as rotation of a transverse normal surface about the circumferential and axial directions.

2.3 Governing equations and boundary conditions

To derive equations of motion and boundary conditions for SWCNTs, using the modified couple stress theory and the first-order shear deformation shell model, one must insert the components of the displacement field into the strains. Now by substituting Eq. (7) into Eqs. (2)–(4), the components of the deviatory stretch gradient tensor and the strain tensor are obtained as follows:

$$\begin{aligned} \varepsilon_{xx} & = \frac{\partial u}{\partial x} + z\frac{{\partial \psi_{x} }}{\partial x} \\ \varepsilon_{\theta \theta } & = \frac{1}{R}\frac{\partial v}{\partial \theta } + z\frac{1}{R}\frac{{\partial \psi_{\theta } }}{\partial \theta } + \frac{w}{R} \\ \varepsilon_{xz} & = \frac{1}{2}\left( {\psi_{x} + \frac{\partial w}{\partial x}} \right) \\ \varepsilon_{x\theta } & = \frac{1}{2}\left( {\frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x}} \right) + \frac{z}{2}\left( {\frac{1}{R}\frac{{\partial \psi_{x} }}{\partial \theta } + \frac{{\partial \psi_{\theta } }}{\partial x}} \right) \\ \varepsilon_{\theta z} & = \frac{1}{2}\left( {\psi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R}} \right) \\ \end{aligned}$$
(8)

Moreover, the nonzero components of symmetric rotation gradient tensor are obtained as follows:

$$\begin{aligned} \chi_{xx}^{s} & = - \frac{1}{2}\left( {\frac{{\partial \psi_{\theta } }}{\partial x} + \frac{1}{R}\frac{\partial v}{\partial x} - \frac{1}{R}\frac{{\partial^{2} w}}{\partial x\partial \theta }} \right) \\ \chi_{\theta \theta }^{s} & = - \frac{1}{2R}\left( {\frac{1}{R}\frac{\partial u}{\partial \theta } - \frac{\partial v}{\partial x} - z\frac{{\partial \psi_{\theta } }}{\partial x}} \right) - \frac{1}{2}\left( {\frac{1}{R}\frac{{\partial^{2} w}}{\partial x\partial \theta } - \frac{1}{R}\frac{{\partial \psi_{x} }}{\partial \theta }} \right) \\ \chi_{zz}^{s} & = - \frac{1}{2}\left( {\frac{1}{R}\frac{{\partial \psi_{x} }}{\partial \theta } - \frac{{\partial \psi_{\theta } }}{\partial x} - \frac{1}{{R^{2} }}\frac{\partial u}{\partial \theta }} \right) \\ \chi_{x\theta }^{s} & = \, - \frac{1}{4}\left( {\frac{1}{{R^{2} }}\frac{\partial v}{\partial \theta } + \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \frac{{\partial \psi_{x} }}{\partial x} + \frac{1}{R}\frac{{\partial \psi_{\theta } }}{\partial \theta }} \right) \\ \chi_{xz}^{s} & = - \frac{1}{4}\left( {\frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } - \frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{v}{{R^{2} }} + \frac{1}{{R^{2} }}\frac{\partial w}{\partial \theta } + \frac{{\psi_{\theta } }}{R}} \right) - \frac{z}{4}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } - \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }}} \right) \\ \chi_{\theta z}^{s} & = - \frac{1}{4}\left( {\frac{1}{{R^{2} }}\frac{{\partial^{2} u}}{{\partial \theta^{2} }} - \frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta } - \frac{1}{R}\frac{\partial w}{\partial x} + \frac{{\psi_{x} }}{R}} \right) - \frac{z}{4}\left( {\frac{1}{{R^{2} }}\frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} - \frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta }} \right) \\ \end{aligned}$$
(9)

For the equations of the motion and boundary conditions, the principle of minimum potential energy states that (Tauchert 1974):

$$\int_{{t_{1} }}^{{t_{2} }} {(\delta T - \delta U + \delta W){\text{d}}t = 0}$$
(10)

Strain energy of cylindrical FG nano-shell based on the modified couple stress theory is expressed as follows:

$$\begin{aligned} \delta U & = \frac{1}{2}\iiint\limits_{V} {\left( {\sigma_{ij} \delta \varepsilon_{ij} + m_{ij}^{s} \delta \chi_{ij}^{s} } \right){\text{d}}V} = \delta U_{1} + \delta U_{2} \\ \delta U_{1} & = \frac{1}{2}\iiint\limits_{V} {(\sigma_{ij} \delta \varepsilon_{ij} )}{\text{d}}V = \iint\limits_{A} {\left\{ {\begin{array}{*{20}l} {\left( {N_{xx} \frac{\partial }{\partial x}\delta u + M_{xx} \frac{\partial }{\partial x}\delta \psi_{x} } \right) + N_{\theta \theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta v + \frac{\delta w}{R}} \right)} \hfill \\ {\quad + \,M_{\theta \theta } \frac{1}{R}\frac{\partial }{\partial \theta }\delta \psi_{\theta } + Q_{xz} \left( {\delta \psi_{x} + \frac{\partial }{\partial x}\delta w} \right)} \hfill \\ {\quad + \,N_{x\theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta u + \frac{\partial }{\partial x}\delta v} \right) + M_{x\theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta \psi_{x} + \frac{\partial }{\partial x}\delta \psi_{\theta } } \right)} \hfill \\ {\quad + \,Q_{z\theta } \left( {\delta \psi_{\theta } + \frac{1}{R}\frac{\partial }{\partial \theta }\delta w - \frac{\delta v}{R}} \right)} \hfill \\ \end{array} } \right\}}R{\text{d}}x{\text{d}}\theta \\ \delta U_{2} & = \frac{1}{2}\iiint\limits_{V} {(m_{ij}^{s} \delta \chi_{ij}^{s} )}{\text{d}}V = \iint\limits_{A} {\left\{ {\begin{array}{*{20}l} {\left( { - \frac{{Y_{\theta \theta } }}{{2R^{2} }} + \frac{{Y_{zz} }}{{2R^{2} }}} \right)\frac{\partial }{\partial \theta }\delta u - \left( {\frac{{Y_{\theta z} }}{{2R^{2} }}} \right)\frac{{\partial^{2} }}{{\partial \theta^{2} }}\delta u - \left( {\frac{{Y_{zx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \partial x}\delta u} \hfill \\ {\quad + \,\left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2R}} \right)\frac{\partial }{\partial x}\delta v + \left( {\frac{{Y_{xz} }}{2}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\delta v - \left( {\frac{{Y_{\theta x} }}{{2R^{2} }}} \right)\frac{\partial }{\partial \theta }\delta v} \hfill \\ {\quad + \,\left( {\frac{{Y_{\theta z} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \partial x}\delta v + \left( {\frac{{Y_{xz} }}{{2R^{2} }}} \right)\delta v + \left( {\frac{{Y_{\theta z} }}{2R}} \right)\frac{\partial }{\partial x}\delta w - \left( {\frac{{Y_{\theta x} }}{2}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\delta w} \hfill \\ {\quad - \,\left( {\frac{{Y_{zx} }}{{2R^{2} }}} \right)\frac{\partial }{\partial \theta }\delta w + \left( {\frac{{Y_{x\theta } }}{{2R^{2} }}} \right)\frac{{\partial^{2} }}{{\partial \theta^{2} }}\delta w + \left( { - \frac{{Y_{\theta \theta } }}{2R} + \frac{{Y_{xx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \partial x}\delta w} \hfill \\ {\quad + \,\left( {\frac{{Y_{x\theta } }}{2}} \right)\frac{\partial }{\partial x}\delta \psi_{x} + \left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2R}} \right)\frac{\partial }{\partial \theta }\delta \psi_{x} - \left( {\frac{{T_{zx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \partial x}\delta \psi_{x} } \hfill \\ {\quad - \,\left( {\frac{{Y_{z\theta } }}{2R}} \right)\delta \psi_{x} - \left( {\frac{{Y_{x\theta } }}{2R}} \right)\frac{\partial }{\partial \theta }\delta \psi_{\theta } + \left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2} + \frac{{Y_{zz} }}{2}} \right)\frac{\partial }{\partial x}\delta \psi_{\theta } } \hfill \\ {\quad + \,\left( {\frac{{T_{z\theta } }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \partial x}\delta \psi_{\theta } - \left( {\frac{{T_{z\theta } }}{{2R^{2} }}} \right)\frac{{\partial^{2} }}{{\partial \theta^{2} }}\delta \psi_{x} + \left( {\frac{{T_{xz} }}{2}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\delta \psi_{\theta } - \left( {\frac{{Y_{xz} }}{2R}} \right)\delta \psi_{\theta } } \hfill \\ \end{array} } \right\}}R{\text{d}}x{\text{d}}\theta \\ \end{aligned}$$
(11)

where the classical and nonclassical force and momentum are defined as follows:

$$\begin{aligned} & (N_{xx} ,N_{\theta \theta } ,N_{x\theta } ) = \int_{ - h/2}^{h/2} {(\sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } ){\text{d}}z,} \\ & (M_{xx} ,M_{\theta \theta } ,M_{x\theta } ) = \int_{ - h/2}^{h/2} {(\sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } )z{\text{d}}z} , \\ & (Q_{xz} ,Q_{z\theta } ) = \int_{ - h/2}^{h/2} {k_{s} (\sigma_{xz} ,\sigma_{z\theta } ){\text{d}}z} , \\ & (Y_{xx} ,Y_{\theta \theta } ,Y_{zz} ,Y_{x\theta } ,Y_{xz} ,Y_{z\theta } ) = \int_{ - h/2}^{h/2} {(m_{xx} ,m_{\theta \theta } ,m_{zz} ,m_{x\theta } ,m_{xz} ,m_{z\theta } ){\text{d}}z,} \\ & (T_{xx} ,T_{\theta \theta } ,T_{zz} ,T_{x\theta } ,T_{xz} ,T_{z\theta } ) = \int_{ - h/2}^{h/2} {(m_{xx} ,m_{\theta \theta } ,m_{zz} ,m_{x\theta } ,m_{xz} ,m_{z\theta } )z{\text{d}}z} \\ \end{aligned}$$
(12)

The velocity vector of any generic point on the rotating shell is expressed as:

$$V = \frac{\partial u}{\partial t}i + \left( {\frac{\partial v}{\partial t} + \varOmega w} \right)j + \left( {\frac{\partial w}{\partial t} - \varOmega v} \right)k$$
(13)

The first three terms represent linear velocities in axial, circumferential and lateral directions, respectively. The fourth and fifth terms are due to Coriolis and centrifugal effects; doted terms represent temporal derivatives; and i, j and k are unit vectors in the x, θ and z directions, respectively. Also, the kinetic energy of the cylindrical shell can be expressed as:

$$\delta T = \int\limits_{Z} {\iint\limits_{A} {\rho \left\{ {\begin{array}{*{20}l} {\left( {\frac{\partial u}{\partial t} + z\frac{{\partial \psi_{x} }}{\partial t}} \right)\left( {\frac{\partial }{\partial t}\delta u + z\frac{\partial }{\partial t}\delta \psi_{x} } \right) + \left( {\frac{\partial v}{\partial t} + z\frac{{\partial \psi_{\theta } }}{\partial t}} \right)\left( {\frac{\partial }{\partial t}\delta v + z\frac{\partial }{\partial t}\delta \psi_{\theta } } \right)} \hfill \\ {\quad + \,\left( {\frac{\partial w}{\partial t}} \right)\frac{\partial }{\partial t}\delta w + \varOmega \left[ {\begin{array}{*{20}l} {w\left( {\frac{\partial }{\partial t}\delta v + z\frac{\partial }{\partial t}\delta \psi_{\theta } } \right) - (v + z\psi_{\theta } )\left( {\frac{\partial }{\partial t}\delta w} \right)} \hfill \\ {\quad + \delta w\left( {\frac{\partial v}{\partial t} + z\frac{{\partial \psi_{\theta } }}{\partial t}} \right) - (\delta v + z\delta \psi_{\theta } )\left( {\frac{\partial }{\partial t}w} \right)} \hfill \\ \end{array} } \right]} \hfill \\ {\quad + \,\varOmega^{2} \left[ {(v + z\psi_{\theta } )(\delta v + z\delta \psi_{\theta } ) + w\delta w} \right]} \hfill \\ \end{array} } \right\}}} R{\text{d}}z{\text{d}}x{\text{d}}\theta$$
(14)

Centrifugal force of rotation produces initial hoop tension; this effect is considered in potential energy. Potential energy involves the nonlinear terms of thin sanders theory in strain relations as the theory recommends (Hosseini-Hashemi et al. 2013).

$$U_{h} = \frac{1}{2}\iint\limits_{A} {N_{h} \left\{ {\left( {\frac{\partial w}{R\partial \theta } - \frac{v}{R}} \right)^{2} + \frac{1}{4}\left( {\frac{\partial u}{R\partial \theta } - \frac{\partial v}{\partial x}} \right)^{2} } \right\}R{\text{d}}\theta {\text{d}}x}$$
(15)

In the above equation, N h  = ρhR 2Ω2. Consider the flow of fluid in a CNTRC cylindrical shell in which the flow is assumed to be axially symmetric, Newtonian and laminar (Rabani Bidgoli et al. 2016). By the well-known Navier–Stokes equation, the basic momentum governing equation of the flow is simplified to be expressed as:

$$\rho_{b} \frac{{{\text{d}}V_{R} }}{{{\text{d}}t}} = - \frac{\partial P}{\partial R} + \frac{1}{R}\frac{{\partial \tau_{R\theta } }}{\partial \theta } - \frac{{\tau_{\theta \theta } }}{R} + \frac{{\partial \tau_{Rx} }}{\partial x}$$
(16)

In Eq. (16), P and ρ b are flow fluid pressure and mass density of the fluid, respectively. The fluid force acted on the SWCNT can be calculated from Eq. (16). Since the acceleration and velocity of the SWCNT and fluid at the point of contact between them are equal (Rabani Bidgoli et al. 2016), we have:

$$v_{R} = \frac{{{\text{d}}w}}{{{\text{d}}t}},\quad \frac{\text{d}}{{{\text{d}}t}} = \frac{\partial }{\partial t} + v_{x} \frac{\partial }{\partial x}$$
(17)

where v x is the mean flow velocity. In Eq. (17), shear stress (τ) is dependent to viscosity (μ) which can be obtained as follows:

$$\tau_{R\theta } = \frac{\mu }{R}\frac{{\partial V_{R} }}{\partial \theta },\quad \tau_{\theta \theta } = 2\mu \frac{{V_{R} }}{R},\quad \tau_{Rx} = \mu \frac{{\partial V_{R} }}{\partial x}$$
(18)

Finally, using Eqs. (17) and (18) and their combination with Eq. (16), the pressure of fluid \(\left( {\frac{\partial P}{\partial R}} \right)\) will be obtained. Finally, the fluid flow work may be written as:

$$\delta W = \int_{0}^{2\pi } {\int_{0}^{L} {\frac{\partial P}{\partial R}} } R{\text{d}}x{\text{d}}\theta$$
(19)

The axial fluid velocity in above relation can be written as:

$$v_{x} = v_{{{\text{ave}},{\text{slip}}}} = {\text{VCF}} \times v_{{{\text{ave}},{\text{noslip}}}}$$
(20)

where the modified dimensionless coefficient VCF may be defined as (Fereidoon et al. 2016):

$${\text{VCF}} = (1 + aK_{n} ) \times \left[ {1 + 4\left( {\left( {\frac{{2 - \sigma_{v} }}{{\sigma_{v} }}} \right)\left( {\frac{{k_{n} }}{{1 + k_{n} }}} \right)} \right)} \right]$$
(21)

where the slip of flow from inner SWCNT through number of Knudsen (k n ) is considered; for practical purposes, it is σ v  = 0.7; in addition, other parameters are:

$$a = a_{0} \frac{2}{\pi }\left( {\tan^{ - 1} \left( {a_{1} k_{n}^{B} } \right)} \right),\quad a_{0} = \frac{64}{3\pi }\left( {1 - \frac{4}{b}} \right)^{ - 1} ,\quad \mu = \mu_{0} \left( {1 + ak_{n} } \right)^{ - 1}$$
(22)

In Eq. (22), μ and μ 0 are fluid viscosity and bulk viscosity, respectively. Now, substituting Eqs. (11), (14), (15) and (19) into (10) and integrating by parts, equations of motion and boundary conditions can be expressed as follows:

$$\begin{aligned} & \delta u:\frac{{\partial N_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial N_{x\theta } }}{\partial \theta } + \frac{1}{{2R^{2} }}\left( { - \frac{{\partial Y_{\theta \theta } }}{\partial \theta } + \frac{{\partial Y_{zz} }}{\partial \theta }} \right) + \frac{1}{2R}\frac{{\partial^{2} Y_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y_{\theta z} }}{{\partial \theta^{2} }} \\ & \quad - \,N_{h} \left( {\frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta } - \frac{1}{{R^{2} }}\frac{{\partial^{2} u}}{{\partial \theta^{2} }}} \right) = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} \\ & \delta v:\frac{{\partial N_{x\theta } }}{\partial x} + \frac{1}{R}\frac{\partial }{\partial \theta }N_{\theta \theta } + \frac{{Q_{z\theta } }}{R} + \frac{1}{2}\left\{ {\frac{1}{R}\frac{\partial }{\partial x}( - Y_{xx} + Y_{\theta \theta } ) - \frac{1}{{R^{2} }}\frac{{\partial Y_{\theta x} }}{\partial \theta } - \frac{{\partial^{2} Y_{xz} }}{{\partial x^{2} }} - \frac{{Y_{xz} }}{{R^{2} }} - \frac{1}{R}\frac{{\partial^{2} Y_{z\theta } }}{\partial \theta \partial x}} \right\} \\ & \quad - \,N_{h} \left( {\frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } - \frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{v}{{R^{2} }} - \frac{1}{{R^{2} }}\frac{\partial w}{\partial \theta }} \right) = I_{0} \left[ {\frac{{\partial^{2} v}}{{\partial t^{2} }} + 2\left( {\frac{\partial w}{\partial t}} \right)\varOmega - v\varOmega^{2} } \right] + I_{1} \left\{ {\frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }} - \psi_{\theta } \varOmega^{2} } \right\} \\ & \delta w:\frac{{\partial Q_{xz} }}{\partial x} + \frac{1}{R}\frac{{\partial Q_{z\theta } }}{\partial \theta } - \frac{{N_{\theta \theta } }}{R} - \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y_{\theta x} }}{{\partial \theta^{2} }} - \frac{1}{{2R^{2} }}\frac{{\partial Y_{zx} }}{\partial \theta } + \frac{1}{2R}\frac{{\partial Y_{\theta z} }}{\partial x} + \frac{{\partial^{2} Y_{x\theta } }}{{2\partial x^{2} }} \\ & \quad - \,\frac{1}{2R}\frac{{\partial^{2} }}{\partial \theta \partial x}(Y_{xx} - Y_{\theta \theta } ) - N_{h} \left( {\frac{1}{{R^{2} }}\frac{\partial v}{\partial \theta } - \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) - \varsigma_{1} v_{{_{x} }}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \varsigma_{2} v_{x} \frac{\partial w}{\partial x} \\ & \quad + \varsigma_{3} v_{x} \frac{{\partial^{3} w}}{{\partial x^{3} }} = I_{0} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - 2\varOmega \frac{\partial v}{\partial t} - \varOmega^{2} w} \right) - 2I_{1} \left\{ {\varOmega \frac{{\partial \psi_{\theta } }}{\partial t}} \right\} + \varsigma_{4} \frac{{\partial^{2} w}}{{\partial t^{2} }} \\ & \quad - \,\varsigma_{5} v_{x} \frac{{\partial^{2} w}}{\partial x\partial t} - \varsigma_{6} \frac{\partial w}{\partial t} + \varsigma_{7} \frac{{\partial^{3} w}}{{\partial t\partial x^{2} }} \\ & \delta \psi_{x} :\frac{{\partial M_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial M_{\theta \theta } }}{\partial \theta } - Q_{xz} + \frac{1}{2}\frac{{\partial Y_{\theta x} }}{\partial x} - \frac{1}{2R}\frac{\partial }{\partial \theta }(Y_{zz} - Y_{\theta \theta } ) + \frac{{Y_{zz} }}{R} + \frac{1}{2R}\frac{{\partial^{2} T_{zx} }}{\partial \theta \partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} T_{\theta z} }}{{\partial \theta^{2} }} \\ & \quad = \,I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} \\ & \delta \psi_{\theta } :\frac{1}{R}\frac{{\partial M_{\theta \theta } }}{\partial \theta } + \frac{{\partial M_{x\theta } }}{\partial x} - Q_{z\theta } + \frac{1}{2}\frac{\partial }{\partial x}\left( {Y_{zz} - Y_{xx} + \frac{{T_{\theta \theta } }}{R}} \right) - \frac{1}{2}\frac{{\partial Y_{\theta x} }}{\partial \theta } + \frac{{Y_{xz} }}{2R} - \frac{1}{2R}\frac{{\partial^{2} T_{\theta z} }}{\partial \theta \partial x} - \frac{1}{2}\frac{{\partial^{2} T_{zx} }}{{\partial x^{2} }} \\ & \quad = \,I_{1} \left( {\frac{{\partial^{2} v}}{{\partial t^{2} }} + 2\left( {\frac{\partial w}{\partial t}} \right)\varOmega - v\varOmega^{2} } \right) + I_{2} \left( {\frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }} - \psi_{\theta } \varOmega^{2} } \right)\, \\ \end{aligned}$$
(23)

Appendix describes the parameters used in Eq. (23). Nonclassical boundary conditions are as follows:

$$\begin{aligned} & \delta u = 0\quad {\text{or}}\quad \left( {N_{xx} + \frac{1}{4R}\frac{{\partial Y_{xz} }}{\partial \theta }} \right)n_{x} + \left( {N_{x\theta } - \frac{{Y_{\theta \theta } - Y_{zz} }}{2R} + \frac{1}{4}\frac{{\partial Y_{xz} }}{\partial x} + \frac{1}{2R}\frac{{\partial Y_{\theta z} }}{\partial \theta }} \right)n_{\theta } = 0, \\ & \delta u_{,x} = 0\quad {\text{or}}\quad \left( {\frac{{\partial Y_{xz} }}{4}} \right)n_{\theta } = 0, \\ & \delta u_{,\theta } = 0\quad {\text{or}}\quad \left( {\frac{{\partial Y_{xz} }}{4}} \right)n_{x} + \left( {\frac{{\partial Y_{\theta z} }}{2}} \right)n_{\theta } = 0, \\ & \delta v = 0\quad {\text{or}}\quad \left( {N_{x\theta } + \frac{{Y_{\theta \theta } - Y_{xx} }}{2R} - \frac{1}{2}\frac{{\partial Y_{xz} }}{\partial x} - \frac{1}{4R}\frac{{\partial Y_{\theta z} }}{\partial \theta }} \right)n_{x} + \left( {N_{\theta \theta } - \frac{1}{4R}\frac{{\partial Y_{\theta z} }}{\partial x} - \frac{{Y_{\theta x} }}{2R}} \right)n_{\theta } = 0, \\ & \delta v_{,x} = 0\quad {\text{or}}\quad \left( {\frac{{Y_{zx} }}{2}} \right)n_{x} + \left( {\frac{{Y_{z\theta } }}{4}} \right)n_{\theta } = 0, \\ & \delta v_{,\theta } = 0\quad {\text{or}}\quad \left( {\frac{{Y_{z\theta } }}{4}} \right)n_{x} = 0, \\ & \delta w = 0\quad {\text{or}}\quad \left( {Q_{xz} + \frac{{Y_{z\theta } }}{2R} + \frac{1}{2}\frac{{\partial Y_{x\theta } }}{\partial x} + \frac{1}{4R}\frac{{\partial (Y_{\theta \theta } - Y_{xx} )}}{\partial \theta }} \right)n_{x} + \left( {Q_{\theta z} - \frac{{Y_{zx} }}{2R} - \frac{1}{2R}\frac{{\partial Y_{x\theta } }}{\partial \theta } + \frac{1}{4}\frac{{\partial (Y_{\theta \theta } - Y_{xx} )}}{\partial x}} \right)n_{\theta } = 0, \\ & \delta w_{,x} = 0\quad {\text{or}}\quad \left( {\frac{{Y_{x\theta } }}{2}} \right)n_{x} + \frac{{(Y_{\theta \theta } - Y_{xx} )}}{4}n_{\theta } = 0, \\ & \delta w_{,\theta } = 0\quad {\text{or}}\quad \frac{{(Y_{\theta \theta } - Y_{xx} )}}{4}n_{x} + \left( {\frac{{Y_{x\theta } }}{2}} \right)n_{\theta } = 0, \\ & \delta \psi_{x} = 0\quad {\text{or}}\quad \left( {M_{xx} + \frac{1}{4R}\frac{{\partial T_{xz} }}{\partial \theta } + \frac{{Y_{x\theta } }}{2}} \right)n_{x} + \left( {M_{\theta x} + \frac{1}{4}\frac{{\partial T_{xz} }}{\partial x} + \frac{1}{2R}\frac{{\partial T_{\theta z} }}{\partial \theta } + \frac{{(Y_{\theta \theta } - Y_{zz} )}}{2}} \right)n_{\theta } = 0, \\ & \delta \psi_{x,x} = 0\quad {\text{or}}\quad \left( {\frac{{T_{xz} }}{4}} \right)n_{\theta } = 0, \\ & \delta \psi_{x,\theta } = 0\quad {\text{or}}\quad \left( {\frac{{T_{xz} }}{4}} \right)n_{x} + \left( {\frac{{T_{\theta z} }}{2}} \right)n_{\theta } = 0, \\ & \delta \psi_{\theta } = 0\quad {\text{or}}\quad \left( {M_{x\theta } - \frac{{(Y_{xx} - Y_{zz} )}}{2} - \frac{1}{4R}\frac{{\partial T_{\theta z} }}{\partial \theta } - \frac{1}{2}\frac{{\partial T_{xz} }}{\partial x} + \frac{{T_{\theta \theta } }}{2R}} \right)n_{x} + \left( {M_{\theta \theta } - \frac{{Y_{x\theta } }}{2} - \frac{1}{4}\frac{{\partial T_{\theta z} }}{\partial x}} \right)n_{\theta } = 0, \\ & \delta \psi_{\theta ,x} = 0\quad {\text{or}}\quad \left( {\frac{{T_{xz} }}{2}} \right)n_{x} + \left( {\frac{{T_{\theta z} }}{4}} \right)n_{\theta } = 0, \\ & \delta \psi_{\theta ,\theta } = 0\quad {\text{or}}\quad \left( {\frac{{T_{\theta z} }}{4}} \right)n_{x} = 0 \\ \end{aligned}$$
(24)

3 Solution procedure

In the past decade, Bellman et al. introduced differential quadrature (DQM) as a reliable and effective method (Bellman and Casti 1971; Bellman et al. 1972). In DQM preliminary formulations, weight coefficients were calculated using an algebraic equation system which limits the use of large grid numbers in DQM. So, for this defect, general quadrature method appeared. Shu (2012) devised an explicit formula for the weighting coefficients with infinite number of grid points leading to GDQM. Early applications of GDQ were applied mostly to regular domain problems; in addition, Shu and Richards (1992) developed a domain decomposition technique to be used in the multi-domain problems. By this method, the main domain is divided into a number of sub-domains or elements, before discretizing each sub-domain for using GDQ. The rth-order derivative of the function f(x i ) can be expressed as follows (Shu 2012):

$$\left. {\frac{{\partial^{r} f(x)}}{{\partial x^{r} }}} \right|_{{x = x_{p} }} = \sum\limits_{j = 1}^{n} {C_{ij}^{(r)} f(x_{i} )}$$
(25)

where “n” is the number of grid points along “x” direction. Also, “C ij ” is obtained as follows:

$$\begin{aligned} C_{ij}^{\left( 1 \right)} & = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}\quad i,j = 1,2, \ldots ,n\quad {\text{and}}\quad i \ne j \\ C_{ij}^{\left( 1 \right)} & = - \sum\limits_{j = 1,i \ne \,j}^{n} {C_{ij}^{\left( 1 \right)} } \quad i = j \\ \end{aligned}$$
(26)

M(x) is developed as:

$$M\left( {x_{i} } \right) = \prod\limits_{j = 1,j \ne i}^{n} {\left( {x_{i} - x_{j} } \right)}$$
(27)

Superscript “r” is the order of the derivative; also, C (r) is the weighing coefficient along x direction which is written as follows:

$$\begin{aligned} C_{ij}^{\left( r \right)} & = r\left[ {C_{ij}^{{\left( {r - 1} \right)}} C_{ij}^{\left( 1 \right)} - \frac{{C_{ij}^{{\left( {r - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right]\quad i,j = 1,2, \ldots ,n,\quad i \ne \,j\quad {\text{and}}\quad 2 \le r \le n - 1 \\ C_{ii}^{\left( r \right)} & = - \sum\limits_{j = 1,i \ne \,j}^{n} {C_{ij}^{\left( r \right)} } \quad i,j = 1,2, \ldots ,n\quad {\text{and}}\quad 1 \le r \le n - 1 \\ \end{aligned}$$
(28)

Owing to the geometrical periodicity of the cylindrical shell, the displacement vector for the free vibration analysis can be described as follows:

$$\left\{ {\begin{array}{*{20}l} {u(x,\theta ,t)} \hfill \\ {v(x,\theta ,t)} \hfill \\ {w(x,\theta ,t)} \hfill \\ {\psi_{x} (x,\theta ,t)} \hfill \\ {\psi_{\theta } (x,\theta ,t)} \hfill \\ \end{array} } \right\} = \sum\limits_{n = 1}^{\infty } {\left\{ {\begin{array}{*{20}l} {\bar{u}(x)\cos (n\theta )e^{i\omega t} } \hfill \\ {\bar{v}(x)\sin (n\theta )e^{i\omega t} } \hfill \\ {\bar{w}(x)\cos (n\theta )e^{i\omega t} } \hfill \\ {\bar{\psi }_{x\,} (x)\cos (n\theta )e^{i\omega t} } \hfill \\ {\bar{\psi }_{\theta } (x)\sin (n\theta )e^{i\omega t} } \hfill \\ \end{array} } \right\}}$$
(29)

A proper method to discretize the domain is applying Chebyshev polynomials as it is explained in Civalek (2004). Now the following equation is obtained by substituting Eq. (2) into equations Eqs. (23) and (24):

$$\left( {[M]\{ \omega^{2} \} + [C]\{ \omega \} + [K]} \right)\left( {\begin{array}{*{20}l} {d_{b} } \hfill \\ {d_{d} } \hfill \\ \end{array} } \right) = 0$$
(30)

Stiffness matrix [K], damping matrix [C] and mass matrix [M] are obtained by applying GDQ into the equations of motion and the boundary conditions. Also the d and b indexes denote the domain and boundary, respectively, and d is the mode shape. For solving Eq. (30) and reducing it to a standard form of eigenvalue problem, it is convenient to rewrite Eq. (30) as the following first-order variable as

$$\left\{ {\dot{Z}} \right\} = \left\{ A \right\}\left\{ Z \right\}$$
(31)

in which the state vector Z and state matrix [A] are defined as:

$$Z = \left\{ {\begin{array}{*{20}l} {d_{d} } \hfill \\ {\dot{d}_{d} } \hfill \\ \end{array} } \right\}\quad {\text{and}}\quad \left[ A \right] = \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} & {\left[ I \right]} \\ { - \left[ {M^{ - 1} K} \right]} & { - \left[ {M^{ - 1} C} \right]} \\ \end{array} } \right]$$
(32)

In Eq. (25), [0] and [I] are the zero and unitary matrices, respectively. Eventually the natural frequency and its mode shape are obtained.

4 Results

Here, the numerical results of the influence of the rotational speed and fluid flow velocity on the vibrational behavior of rotary SWCNT conveying viscous flow based on the FSD and MCS theories must be found to obtain accurate results for GDQ method. Table 1 shows that for getting convergent results, fifteen grid points are enough. The results are shown and analyzed in two sections. The first one verifies the proposed model with existing literatures. Second section shows the effect of length-to-radius ratio, radius-to-thickness ratio, initial hoop tension, fluid flow velocity, angular velocity, material length scale parameter and boundary conditions on critical rotational speed, critical velocity of viscous fluid flow and natural frequency of the rotating SWCNT conveying viscous flow (Table 2).

Table 1 Effect of the number of grid points on evaluating convergence of the dimensionless natural frequency of the rotating SWCNT conveying viscous flow with respect to the flow velocity, angular velocity and L/R = 10, h/R = 0.1, l = R/3
Full size table
Table 2 Material properties of single-walled carbon nanotubes for verification
Full size table

4.1 Results verification with other articles

Material properties of single-walled carbon nanotubes are presented in Table 2. Achieved results are compared with those of GDQ and an exact analytical method, moreover in Tables 3 and 4; it can be seen from the results that by setting L = h, the achieved results of classical cylindrical nano-shell theory are very close to results of Alibeigloo and Shaban (2013). Some researchers (Ghadiri and Safarpour 2016; Beni et al. 2015) show, as l = R/3, the results of the current research based on FSDT are very similar to those of MD simulation. In addition, dimensionless frequency in this article is approximated by equation \(\varOmega = \omega R\sqrt {\frac{\rho }{E}}\).

Table 3 Comparison of first dimensionless natural frequencies of nonrotating simply supported isotropic homogeneous nano-shells with different thicknesses
Full size table
Table 4 Comparison of first three dimensionless natural frequencies of simply supported isotropic homogeneous nano-shells, with different thicknesses
Full size table

4.2 Verification of achieved results by using the results of an analytical method

Table 5 demonstrates the GDQ results in comparison with analytical results for different length and material length scale parameters of SWCNT. It is noteworthy that in this table the effect of flow velocity and angular velocity is ignored and E = 1.06 Tpa and ρ = 2300 kg/m3. Table 5 shows that the GDQ results are in good agreement with analytical results, so the GDQ method with N = 15 can be used instead of the analytical solution. Also, Table 5 shows that, by increasing the material length scale parameter, the natural frequency increases. Comparison of the natural frequencies given in Table 5 shows that increase in shell length leads to decrease in stiffness and therefore decrease in natural frequency.

Table 5 Comparison of fundamental natural frequency (THz) of simply supported SWCNTs, with different length and material length scale parameters and L/R = 10, h = 0.2R
Full size table

4.3 Parametric results

The material for this paper is carbon which its properties are given in Table 6. Now, in this section presents the effect of different parameters on the critical rotational speed, critical velocity of viscous flow and natural frequency of a rotating SWCNT conveying viscous flow. Also, the effect of L/R ratio on the critical flow velocity for flutter instability of rotating SWCNT is studied.

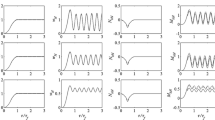
Table 6 Critical flow velocity for flutter instability of rotating SWCNT
Full size table

4.3.1 The effect of different length-to-radius ratios on natural frequency, critical flow velocity for flutter instability and critical speed rotation of SWCNT

According to Paidoussis and Denise (1972), the instability associated with n = 1 corresponds to beam flutter (lateral oscillations), while those associated with n = 2 correspond to “true” shell flutter. Also according to Yoon et al. (2006), the critical flow velocities for flutter instability occur as the second frequency (mode 2) is equal to zero. Table 6 gives a presentation of the critical flow velocity for flutter instability of rotating SWCNT under the various boundary conditions. Table 6 shows an increase in L/R ratio leads to a decrease in the critical flow velocity. This trend is observed under all types of boundary conditions. Clamp–free boundary condition has the lowest critical flow velocity because of its particular condition, and clamp–clamp boundary condition has the highest critical flow velocity. Figures 3, 4, 5 and 6 show the effect of the length-to-radius ratio on natural frequency and critical speed of SWCNT with different boundary conditions. Figures 4, 5, 6 and 7 show that the increase in L/R leads to the increase in critical rotational speed and consequently the increase in stability of the system. Also, by increasing the L/R parameter, the natural frequency in stability area decreases, because increase in the L/R parameter leads to the decrease in stiffness. The C–F boundary condition results in instability in lower critical speed; despite C–F boundary condition, C–C boundary condition leads to instability in higher critical speed.

Fig. 3
figure 3

Variation of fundamental frequency (THz) with angular velocity of a rotating simply–simply SWCNT conveying viscous flow with different length-to-radius ratios with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 4
figure 4

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–simply SWCNT conveying viscous flow with different length-to-radius ratios with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 5
figure 5

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–clamp SWCNT conveying viscous flow with different length-to-radius ratios with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 6
figure 6

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–free SWCNT conveying viscous flow with different length-to-radius ratios with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 7
figure 7

Variation of fundamental frequency (THz) with angular velocity of a rotating simply–simply SWCNT conveying viscous flow with different length scale parameters with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image

4.3.2 Effect of different material length scale parameters on natural frequency and critical rotational speed of SWCNT

Figures 7, 8, 9 and 10 demonstrate the effect of material length scale parameter on critical speed under different boundary conditions. These figures show that an increase in material length scale parameter leads to an increase in critical rotational speed value so that instability occurs in higher values of critical rotational speed. Therefore, the higher the length scale value is, more stable the system is. Also, C–F boundary condition results in instability in lower critical speed; in spite of C–F boundary condition, C–C boundary condition leads to instability in higher critical speeds.

Fig. 8
figure 8

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–simply SWCNT conveying viscous flow with different length scale parameters with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 9
figure 9

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–clamp SWCNT conveying viscous flow with different length scale parameters with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 10
figure 10

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–free SWCNT conveying viscous flow with different length scale parameters with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image

4.3.3 The effect of different velocities of viscous fluid flow on natural frequency and critical rotational speed of SWCNTs

Figures 11, 12, 13 and 14 present the influence of velocity of viscous fluid flow on frequency and critical rotational speed under different boundary conditions. It can be clearly seen that an increase in flow velocity results in a decrease in critical rotational speed, but it has higher tangible effect on the stability of cylindrical shell. It is worth to mention that increase in the angular velocity and flow velocity leads to decrease in natural frequency with more intensity and increase in unstable area.

Fig. 11
figure 11

Variation of fundamental frequency (THz) with angular velocity of a rotating simply–simply SWCNT conveying viscous flow with different velocities of viscous fluid flow with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 12
figure 12

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–simply SWCNT conveying viscous flow with different velocities of viscous fluid flow with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 13
figure 13

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–clamp SWCNT conveying viscous flow with different velocities of viscous fluid flow with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image
Fig. 14
figure 14

Variation of fundamental frequency (THz) with angular velocity of a rotating clamp–free SWCNT conveying viscous flow with different velocities of viscous fluid flow with h/R = 0.1, v x  = 500 m/s and L = 10 nm

Full size image

4.3.4 The effect of different length-to-radius ratios on natural frequency and critical velocity of viscous fluid flow of SWCNT

Figures 15, 16, 17 and 18 present the influence of length-to-radius ratios on frequency and critical flow velocities under different boundary conditions. It is shown that, as the length-to-radius ratio/flow velocity increases, the fundamental natural frequency decreases. It can also be concluded from Figs. 15, 16, 17 and 18 that as the length-to-radius ratio increases, the stiffness of the SWCNT decreases and leads to decrease in the natural frequency of the system. Also the C–F boundary condition results in instability in lower critical speed, and in spite of C–F boundary condition, C–C boundary condition leads to instability in higher critical speed.

Fig. 15
figure 15

Variation of fundamental frequency (THz) with flow velocity of a rotating simply–simply SWCNT conveying viscous flow with different length-to-radius ratios with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 16
figure 16

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–simply SWCNT conveying viscous flow with different length-to-radius ratios with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 17
figure 17

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–clamp SWCNT conveying viscous flow with different length-to-radius ratios with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 18
figure 18

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–free SWCNT conveying viscous flow with different length-to-radius ratios with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image

4.3.5 The effect of different material length scale parameters on natural frequency and critical velocity of viscous fluid flow of SWCNT

The effect of material length scale parameter on natural frequency and critical flow velocity is studied considering different boundary conditions as shown in Figs. 19, 20, 21 and 22. Results indicate that increasing length scale parameter enhances the natural frequency and the critical flow velocity. The results show that, in the clamp–clamp and clamp–simply boundary conditions, the critical flow velocity is very close and this boundary conditions have high critical flow velocity than simply–simply and clamp–free boundary conditions.

Fig. 19
figure 19

Variation of fundamental frequency (THz) with flow velocity of a rotating simply–simply SWCNT conveying viscous flow with different material length scale parameters with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 20
figure 20

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–simply SWCNT conveying viscous flow with different material length scale parameters with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 21
figure 21

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–clamp SWCNT conveying viscous flow with different material length scale parameters with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 22
figure 22

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–free SWCNT conveying viscous flow with different material length scale parameters with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image

4.3.6 The effect of different angular velocities on natural frequency and critical velocity of viscous fluid flow of SWCNT

Figures 23, 24, 25 and 26 illustrate the effect of angular velocity on the natural frequency and critical flow velocity of fluid-conveying rotating SWCNT. With the increase in angular velocity, the natural frequency and critical velocity of SWCNT decrease; hence, the region of stability of the SWCNT decreases, too. It is worth to mention that increase in the angular velocity and flow velocity leads to decreasing of natural frequency with more intensity and increasing of unstable area.

Fig. 23
figure 23

Variation of fundamental frequency (THz) with flow velocity of a rotating simply–simply SWCNT conveying viscous flow with different angular velocities with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 24
figure 24

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–simply SWCNT conveying viscous flow with different angular velocities with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 25
figure 25

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–clamp SWCNT conveying viscous flow with different angular velocities with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image
Fig. 26
figure 26

Variation of fundamental frequency (THz) with flow velocity of a rotating clamp–free SWCNT conveying viscous flow with different angular velocities with h/R = 0.1, Φ = 0.5 THz and L = 10 nm

Full size image

5 Conclusion

This article represents the analysis of size-dependent vibration of a rotating SWCNT conveying viscous flow to obtain the critical angular velocity and the critical viscous fluid flow velocity. Modified couple stress theory introduces the size-dependent effect. The equations of motion and nonclassical boundary conditions are derived using Hamilton’s principle. The natural frequency of the rotating SWCNT conveying viscous flow is investigated with respect to the material length scale parameter, velocity of viscous fluid flow, angular velocity, length, length-to-radius ratio, radius-to-thickness ratio and boundary conditions on critical speed, critical velocity of the SWCNT. The followings important results can be obtained from this study:

  1. 1.

    Increasing the length-to-radius ratio and material length scale parameter, the natural frequency tends to increase, while by increasing the flow velocity and angular velocity the natural frequency of the rotating SWCNT conveying viscous flow decreases.

  2. 2.

    Clamp–free boundary condition has the lowest natural frequency because of its particular condition, and clamp–clamp boundary condition has the highest natural frequency.

  3. 3.

    The results show that increasing the material length scale parameter leads to increase in the critical speed while increasing the length-to-radius ratio and flow velocity leads to decrease of critical rotational speed of the SWCNT conveying viscous flow.

  4. 4.

    By increasing the material length scale parameter, the flow velocity increases, while increasing the length-to-radius ratio and angular velocity leads to decrease in the flow velocity of the rotating SWCNT conveying viscous flow.