1 Introduction

Micro-beams play an important role in micro- and nano-electromechanical systems (MEMs and NEMs), e.g., biosensors, actuators, micro-pumps, atomic force microscopes (AFMs), micro-mirrors, and micro-resonators [1–4]. Some experimental observations resulted in the size-dependent mechanical behavior in micro-scale structures [5, 6]. Due to the weakness of the classical continuum theory to explain the experimentally detected small-scale effects in the size-dependent behavior of micro-scaled systems, various non-classical theories such as the nonlocal, strain gradient, and couple stress were introduced to eliminate the shortcoming in dealing with micron structures.

The couple stress theory is one of the non-classical theories introduced by some researchers, e.g., Toupin [7], in early 1960s in which higher-order stresses, known as the couple stress tensor, are taken into account, besides the classical force stress tensor. Yang et al. [8] suggested a modified couple stress theory in which a new higher-order equilibrium equation, i.e., the equilibrium equation of moments of couple stresses, was considered, as well as the classical equilibrium equations. This consideration causes the symmetry of the couple stress tensor.

On the other hand, the classical parabolic heat conduction theory is not capable of predicting reliable results in many practical situations, because it is based on Fourier law which implicitly postulates the propagation speed of thermal disturbances to be infinite in contrast with what is observed in reality. Of course, this law gives valid results in many practical situations. In small-scale systems, Fourier law is inaccurate, due to the fact that response time is in the picoseconds-order, and consequently the wave nature of thermal propagation becomes noticeable. In these applications, the results obtained by utilizing Fourier heat conduction model have significant differences with the experimental results [9, 10]. Tzou [11] developed a hyperbolic heat conduction model which is a special case of the dual-phase-lagging conduction equation. This model considers a finite propagation speed for thermal disturbances by applying thermal relaxation time as a material property.

In the last decade, numerous researches include the static, dynamic, and thermal analyses have been accomplished on micro-structures, using non-classical continuum mechanics theories, and hyperbolic heat conduction models (for instance, see these studies that are based on the nonlocal [12, 13], strain gradient [14, 15], modified couple stress [16, 17], theories, and non-Fourier heat conduction models [18, 19]). In what follows, investigations of mechanical and thermal behaviors of micro-beams are reviewed by means of modified couple stress theory, and hyperbolic heat conduction model. In this regard, Asghari et al. [20] presented the formulation of FG Timoshenko micro-beams and studied their static and free-vibration behaviors based on the modified couple stress theory. In addition, based on this theory Ke et al. [21, 22] investigated the size-effect on the dynamic stability of functionally graded micro-beams, and nonlinear vibration behaviors of micro-beams, respectively. Park and Gao [23], and Kong et al. [24] studied the static and dynamic problems of size-dependent Bernoulli–Euler beams. Taati et al. [17] developed a formulation for static behavior of the viscoelastic Euler–Bernoulli micro-beams. Ma et al. [25] presented a microstructure-dependent Timoshenko beam model, which can be used to obtain the static and free-vibration parameters of the simply supported micro-beams.

Researches on thermo-elastic vibration of beams have been widely developing. Landau and Lifshitz [26] obtained an exact solution for the attenuation coefficient of thermo-elastic vibration. Givoli and Rand [27] studied the thermo-elastic coupling effects on the dynamic behavior of rods. As the thermal excitation frequency is near the natural frequency of theory, they found that the natural response of the rod varies significantly. Massalas and Kalpakidis [28, 29] looked into the thermo-elastic vibration behaviors of a simply supported beam, using the Euler–Bernoulli and Timoshenko beam models, respectively. Manolis and Beskos [30] investigated the effect of thermal damping and axial loads on the vibration of beams imposed to fast heating at one of the ends. But, the coupling effect between the stress and temperature fields was ignored. Lifshitz and Roukes [31] achieved an analytical solution for the thermo-elasticity damping in micro-beams and explored the effect of different geometrical parameters on them.

For the first time, Taati et al. [32, 33] developed some size-dependent thermo-elasticity models which include effects of couple terms for dynamic analysis of Timoshenko micro-beams. These novel models are based on the combination of non-Fourier heat conduction model and one of the non-classical continuum mechanics theories (namely the modified couple stress [32], and strain gradient theories [33]). To the best of authors’ knowledge, vibrational frequencies of micro-beam resonators consisting of thermal coupling have not been derived by simultaneously considering the size-dependent effects on the thermal and mechanical behaviors of micro-beam resonators. This paper tries to fill the gap in the literature by finding an analytical solution for micro-beam resonators with two boundary condition cases, i.e., clamped and isothermal, and also simply supported and isothermal at the beam ends. For this purpose, the size-dependent generalized thermo-elasticity model, including a thermal relaxation time and a length scale parameter in heat conduction [32], and constitutive equations have been, respectively, utilized. Finally, the effects of end conditions, geometrical ratios, and length scale parameter on the vibrational frequencies are investigated.

2 Problem definition

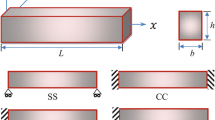
In most of MEMs, the micro-resonators can be modeled as elastic beams with rectangular cross-sections with either fully clamped or simply supported ends. Hence, a beam with length L, width b, and thickness h is considered to study the vibration behavior of micro-resonators, as shown in Fig. 1. The coordinate system is composed of the beam axis (the x coordinate), and axes correspond to the width and thickness (the y and z coordinates), respectively. Also, the origin is placed at the centroid of the cross section in the right hand side of the beam. In the initial equilibrium condition, the beam is unstrained, un-stressed, at a uniform temperature of \(T_{0}\). There is no heat flux across the top and bottom surfaces of the beam.

Fig. 1
figure 1

Beam configuration, coordinate system, geometric characteristics and boundary conditions

Full size image

2.1 Timoshenko beam model

On the basis of Timoshenko beam model, the transverse cross-sections of the beam remain planar after deformation, but are not restrained to be perpendicular to the bending axis. Hence, this model is capable of taking into account the shear effect on the transverse deflection, as well as the bending effect. The components of the displacement vector field, \({\mathbf{u}} = \left( {u_{x} , u_{y} ,u_{z} } \right)\) in a Timoshenko beam model can be defined as follows:

$$\begin{aligned} u_{x} & = u (x,t )+ z\,\psi (x,t ) ,\\ u_{y} & = 0 ,\\ u_{z} & = w (x,t ) ,\\ \end{aligned}$$
(1)

where the function \(u\left( {x,t} \right)\) denotes the axial displacement of points at the middle surface (\(z = 0\)), and the functions \(w\left( {x,t} \right)\) and \(\psi \left( {x,t} \right)\) stand for the rotation angle (about y axis) and transverse deflection of the beam cross-sections, respectively. Furthermore, parameter t denotes the time.

2.2 Modified couple stress theory

The modified couple stress theory developed by Yang et al. [8] is employed to in the present formulations. This theory is derived from the classical couple stress theory [7], which has been well established by some researchers. Based on the theory, an additional equilibrium equation is considered for the moments of couple, which causes the couple stress tensor to be symmetric. Moreover, the strain energy density function is only dependent on the strain and the symmetric part of the curvature tensor, and hence, only one length scale parameter is involved in the constitutive relations. According to the theory, the variation of the strain energy U for an anisotropic linear elastic material occupying region Ω can be written as [8]:

$$\delta U = \int\limits_{\varOmega } {\left( {\sigma_{ij} \delta \varepsilon_{ij} + m_{ij}^{{}} \delta \chi_{ij}^{{}} } \right)\text{d}\varOmega .}$$
(2)

In Eq. (2), ε ij and χ ij denote the components of the strain tensor \({\varvec{\upvarepsilon}}\) and the symmetric part of the curvature tensor \({\varvec{\upchi}}\), which are defined as:

$$\varepsilon_{ij} = \frac{1}{2}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right),$$
(3)
$$\chi_{ij} = \frac{1}{2}\left( {\frac{{\partial \theta_{i} }}{{\partial x_{j} }} + \frac{{\partial \theta_{j} }}{{\partial x_{i} }}} \right).$$
(4)

Also, the components of the infinitesimal rotation vector \({\varvec{\uptheta}} = \frac{1}{2}curl({\mathbf{u}})\) are introduced by θ i . For linear isotropic elastic materials, constitutive relations of the symmetric part of the force stress and the deviatoric part of the couple stress tensor with the kinematic parameters are given as [8]:

$$\sigma_{ij} = \lambda tr({\varvec{\upvarepsilon}})\delta_{ij} + 2\mu \varepsilon_{ij} ,$$
(5)
$$m_{ij}^{{}} = 2\mu l^{2} \chi_{ij} ,$$
(6)

where σ ij and m ij are called the force and higher-order stresses, respectively. Furthermore, the parameters λ and μ in the constitutive equation of the classical stress σ are Lame constants. The parameter l, which appears in the constitutive Eq. (6), is the material length scale parameter. It should be noted that the Lame constants can be represented in terms of the Young’s modulus E, and Poisson’s ratio v as \(\lambda = \frac{Ev}{{\left( {1 + v} \right)\left( {1 - 2v} \right)}}\) and \(\mu = \frac{E}{{2\left( {1 + v} \right)}}\).

2.3 Non-Fourier heat conduction model

Cattaneo [9] introduced a constitutive heat conduction relation as follows:

$$\tau \frac{{\partial {\varvec{q}}}}{\partial t} + {\varvec{q}} = - k\vec{\nabla }T,$$
(7)

where \(\varvec{q }\) is the heat flux vector, and \(k\) and τ are the thermal conductivity and thermal relaxation time, respectively. The function \(T\) represents the temperature distribution. As τ is equal to zero, the classic Fourier constitutive heat conduction relation can be obtained by neglecting term of thermal source, the energy equation can be shown as:

$$- \vec{\nabla } \cdot {\varvec{q}} = \rho c_{p} \frac{\partial T}{\partial t}.$$
(8)

In Eq. (8), \(\rho\) and \(c_{p}\) indicate the density and specific heat, respectively. Eliminating vector \(\varvec{q }\) between Eqs. (7) and (8) leads to a hyperbolic equation for temperature as:

$$k\nabla^{2} T = \rho c_{p} \left( {\frac{\partial T}{\partial t} + \tau \frac{{\partial^{2} T}}{{\partial t^{2} }}} \right),$$
(9)

in which \(\nabla^{2}\) is Laplace operator.

3 Theoretical formulation

In this section, the basic equations for the free-vibration analysis of micro-resonators including thermo-elastic coupling terms are derived. In order to do this, first the equations of motion associated with the boundary conditions are derived by considering the thermal effects. Then, the non-Fourier thermal conduction equation of a micro-beam containing the thermo-elastic coupling term is achieved. Finally, the normalized forms of the coupled thermo-elastic equations are expressed.

3.1 Dynamic equilibrium equations

Based on the displacement field assumed within the Timoshenko beam model, the strain and curvature components are obtained as the following:

$$\begin{aligned} \varepsilon_{xx} & = \frac{\partial u}{\partial x} + z\psi_{x,x} ,\quad \varepsilon_{xz} = \varepsilon_{zx} = \frac{1}{2}\left( {\psi_{x} + w_{,x} } \right), \\ \chi_{xy}^{s} & = \chi_{yx}^{s} = \frac{1}{4}\left( {\psi_{x,x} - w_{,xx} } \right). \\ \end{aligned}$$
(10)

Based on Eqs. (2) and (10), the strain energy variation of a micro-beam, considering the modified couple stress theory can be expressed as [32]:

$$\begin{aligned} \delta U & = \int\limits_{0}^{L} {\left[ {\left( { - EAu_{,xx} + \frac{1}{2}N_{,x}^{T} } \right)\delta u + \,\left( { - \left(EI + \frac{{\mu l^{2} A}}{4}\right)\,\psi_{x,xx} \, + \frac{1}{2}M_{,x}^{T} + \,\mu A\,\,(\psi_{x} + w_{,x} )} \right.} \right.\,\,} \\ & \left. {\quad \left. { + \frac{{\mu l^{2} A}}{4}w_{,xxx} } \right)\delta \psi_{x} - \mu A\,\left( {\psi_{x,x} + w_{,xx} + \frac{{l^{2} }}{4}(\psi_{x,xxx} - w_{,xxxx} )} \right)\delta w} \right]{\text{d}}x \\ & \quad + \left[ {\left( {EAu_{,x} - \frac{1}{2}N^{T} } \right)\delta u} \right]_{x = 0}^{x = L} + \left[ {\left( {\left(EI + \frac{{\mu l^{2} A}}{4}\right)\psi_{x,x} - \frac{1}{2}M^{T} - \frac{{\mu l^{2} A}}{4}w_{,xx} } \right)\delta \psi_{x} } \right]_{x = 0}^{x = L} \\ & \quad + \left[ {\mu A\left( {\psi_{x} + w_{,x} + \frac{{l^{2} }}{4}(\psi_{x,xx} - w_{,xxx} )} \right)\delta w} \right]_{x = 0}^{x = L} - \left[ {\frac{{\mu l^{2} A}}{4}(\psi_{x,x} - w_{,xx} )} \right]\delta w_{,x} \\ \end{aligned}$$
(11)

where

$$N^{T} = \int\limits_{A}^{{}} {\beta \theta {\text{d}}A = b} \int\limits_{ - h/2}^{h/2} {\beta \theta {\text{d}}z} ,\quad M^{T} = \int\limits_{A}^{{}} {\beta \theta z{\text{d}}A = b} \int\limits_{ - h/2}^{h/2} {\beta \theta z{\text{d}}z} .$$
(12)

\(\beta = E\alpha_{T} /\left( {1 - 2v} \right)\) is the thermal modulus, in which \(\alpha_{T }\) denotes the coefficient of linear thermal expansion. Furthermore, \(\theta = T - T_{0}\) is the temperature difference of any point of the beam from the reference temperature \(T_{0} .\)

On the other hand, the variation of the kinetic energy within the Timoshenko beam model can be computed from the following equation [32]:

$$\begin{aligned} \delta T & = \rho \int\limits_{0}^{L} {\left( {A\left( {u_{,t} \,\delta u_{,t} + w_{,t} \delta w_{,t} } \right) + I\psi_{x,t} \delta \psi_{x,t} } \right)} {\text{d}}x \\ & = - \rho \int\limits_{0}^{L} {\left( {A\left( {u_{,tt} \,\delta u + w_{,tt} \delta w} \right) + I\psi_{x,tt} \delta \psi_{x} } \right)} {\text{d}}x \\ & \quad + \rho \int\limits_{0}^{L} {\left( {A\left( {u_{,t} \,\delta u + w_{,t} \delta w} \right)_{,t} + I\left( {\psi_{x,t} \delta \psi_{x} } \right)_{,t} } \right)} {\text{d}}x. \\ \end{aligned}$$
(13)

On the basis of Eqs. (11) and (13), using the Hamilton principle, the dynamic equilibrium equations of a micro-beam, including thermal effects are as follows:

$$\begin{aligned} & \delta u :\quad EAu_{,xx} - \frac{1}{2}N_{,x}^{T} = \rho Au_{,tt} , \\ & \delta \psi_{x} :\quad \left( {EI + \frac{{\mu l^{2} A}}{4}} \right)\,\psi_{x,xx} \, - \frac{1}{2}M_{,x}^{T} - \mu A(\psi_{x} + w_{,x} ) - \frac{{\mu l^{2} A}}{4}w_{,xxx} = \rho I\psi_{x,tt} , \\ & \delta w :\quad \mu A\left( {\psi_{x,x} + w_{,xx} + \frac{{l^{2} }}{4}(\psi_{x,xxx} - w_{,xxxx} )} \right) = \rho Aw_{,tt} . \\ \end{aligned}$$
(14)

Moreover, the boundary conditions at the points located on the edges of the micro-beam, at \(x = 0\) and \(x = L\), can be obtained as:

$$\begin{aligned} & EAu_{,x} - \frac{1}{2}N^{T} = 0,\quad {\text{OR}}\quad \delta u = 0, \\ & \left( {EI + \frac{{\mu l^{2} A}}{4}} \right)\psi_{x,x} - \frac{1}{2}M^{T} - \frac{{\mu l^{2} A}}{4}w_{,xx} = 0,\quad {\text{OR}}\quad \delta \psi_{x} = 0, \\ & \psi_{x} + w_{,x} + \frac{{l^{2} }}{4}(\psi_{x,xx} - w_{,xxx} ) = 0,\quad {\text{OR}}\quad \delta w = 0, \\ & \psi_{x,x} - w_{,xx} = 0,\quad {\text{OR}}\quad \delta \left( {\frac{\partial w}{\partial x}} \right) = 0. \\ \end{aligned}$$
(15)

3.2 Thermal heat conduction equation

The non-Fourier thermal conduction equation, containing the thermo-elastic coupling terms, is:

$$k\frac{{\partial^{2} \theta }}{{\partial x_{i} \partial x_{i} }} = \rho c_{p} \left( {\frac{\partial \theta }{\partial t} + \tau \frac{{\partial^{2} \theta }}{{\partial t^{2} }}} \right) + \beta T_{0} \left( {\frac{{\partial^{2} u_{i} }}{{\partial t\partial x_{i} }} + \tau \frac{{\partial^{3} u_{i} }}{{\partial t^{2} \partial x_{i} }}} \right).$$
(16)

Substituting the displacement components from Eq. (1) into Eq. (16), results in:

$$k\left( {\theta_{,xx} + \theta_{,zz} } \right) = \rho c_{v} \left( {\theta_{,t} + \tau \theta_{,tt} } \right) + \beta T_{0} \left( {u_{,tx} + z\psi_{x,tx} + \tau \left( {u_{,ttx} + z\psi_{x,ttx} } \right)} \right).$$
(17)

Assuming that the temperature increment varies in terms of a \(\sin (pz)\) function thorough the thickness direction [31, 32], where \(p = \pi /h\), and by substituting this function into Eq. (17), one obtains the following result:

$$N_{T} = b\beta \int\limits_{ - h/2}^{ + h/2} {\theta {\text{d}}z} = 0.$$
(18)

Then, multiplying Eq. (18) by \(b\beta z\), and integration thorough the thickness, yields:

$$k\left( {M_{,xx}^{T} - p^{2} M_{T} } \right) = \rho c_{p} \left( {M_{,t}^{T} + \tau M_{,tt}^{T} } \right) + T_{0} \beta^{2} I\left( {\psi_{x,tx} + \tau \psi_{x,ttx} } \right).$$
(19)

3.3 Normalized coupled thermo-elastic equations

By substituting Eq. (18) into (14) and using Eq. (19), the coupled thermo-elastic equations of a micro-beam are expressed herein:

$$\begin{aligned} & \left( {EI + \frac{{\mu l^{2} A}}{4}} \right)\psi_{x,xx} - \frac{1}{2}M_{,x}^{T} - \mu A(\psi_{x} + w_{,x} ) - \frac{{\mu l^{2} A}}{4}w_{,xxx} - \rho I\psi_{x,tt} = 0, \\ & \mu A\,\left( {\psi_{x,x} + w_{,xx} + \frac{{l^{2} }}{4}(\psi_{x,xxx} - w_{,xxxx} )} \right) - \rho Aw_{,tt} = 0. \\ & k\left( {M_{,xx}^{T} - p^{2} M_{T} } \right) - \rho c_{p} \left( {M_{,t}^{T} + \tau M_{,tt}^{T} } \right) - T_{0} \beta^{2} I\left( {\psi_{x,tx} + \tau \psi_{x,ttx} } \right) = 0. \\ \end{aligned}$$
(20)

The clamped and simply supported end conditions are defined as:

$$\begin{aligned} & {\text{Clamped-Isothermal}}\,{\text{Ends:}} \\ & \psi_{x} = 0,\quad w = 0,\quad \psi_{x,x} - w_{,xx} = 0,\quad \theta = 0. \\ & {\text{Simple-Isothermal}}\,{\text{Ends:}} \\ & \left( {EI + \frac{{\mu l^{2} A}}{4}} \right)\,\psi_{x,x} - \frac{1}{2}M^{T} - \frac{{\mu l^{2} A}}{4}w_{,xx} = 0, \\ & w = 0,\quad \psi_{x,x} - w_{,xx} = 0,\quad \theta = 0. \\ \end{aligned}$$
(21)

The following dimensionless quantities are defined to transform the coupled thermo-elastic equations and the boundary conditions into the non-dimensional form:

$$\begin{aligned} \zeta = \frac{x}{L},\quad \tau = \frac{t}{L}C,\quad C = \sqrt {\frac{E}{\rho }} , \hfill \\ \tilde{\psi }_{\zeta } = \psi_{x} ,\quad \tilde{w} = \frac{w}{h},\quad \varPhi = \frac{{M_{T} }}{EAh}. \hfill \\ \end{aligned}$$
(22)

In Eq. (22), the parameters \(\tilde{\psi }_{\zeta }\), \(\tilde{w}\) and \(\varPhi\) indicate the dimensionless angle of rotation, deflection and thermal moment, respectively. Thus, the normalized forms of the governing Eqs. (20) are introduced as:

$$A_{1} \tilde{\psi }_{\zeta ,\zeta \zeta } - \tilde{\psi }_{\zeta ,\tau \tau } - A_{2} \tilde{\psi }_{\zeta } + A_{3} \tilde{w}_{,\zeta \zeta \zeta } - A_{4} \tilde{w}_{,\zeta } - A_{5} \varPhi_{,\zeta } = 0,$$
(23a)
$$A_{6} \tilde{\psi }_{\zeta ,\zeta \zeta \zeta } - A_{7} \,\tilde{\psi }_{\zeta ,\zeta } + A_{8} \tilde{w}_{,\zeta \zeta \zeta \zeta } - A_{9} \tilde{w}_{,\zeta \zeta } + \tilde{w}_{,\tau \tau } = 0,$$
(23b)
$$A_{10} \tilde{\psi }_{\zeta ,\tau \zeta } + A_{11} \tilde{\psi }_{\zeta ,\tau \tau \zeta } - \varPhi_{,\zeta \zeta } + A_{12} \varPhi_{,\tau \tau } + A_{13} \varPhi_{,\tau } + A_{14} \varPhi = 0.$$
(23c)

Also, the coefficients \(A_{i}\) in (23a–23c) are defined in the Appendix 1. Similarly, the normalized boundary conditions are as follows:

$$\begin{aligned} & {\text{Clamped-Isothermal}}\,{\text{Ends:}} \\ & \tilde{\psi }_{\zeta } = 0,\quad \tilde{w} = 0, \\ & A_{6} \tilde{\psi }_{\zeta ,\zeta } + A_{8} \tilde{w}_{,\zeta \zeta } = 0,\quad \varPhi = 0. \\ & {\text{Simple-Isothermal}}\,{\text{Ends:}} \\ & A_{1} \tilde{\psi }_{\zeta ,\zeta } + A_{3} \tilde{w}_{,\zeta \zeta } - A_{5} \varPhi = 0,\quad \tilde{w} = 0, \\ & A_{6} \tilde{\psi }_{\zeta ,\zeta } + A_{8} \tilde{w}_{,\zeta \zeta } = 0,\quad \varPhi = 0. \\ \end{aligned}$$
(24)

4 Exact solution and numerical results

4.1 Solution methodology

The normal mode analysis is employed to obtain the natural vibration frequencies, including thermo-elastic damping for two types of boundary conditions, including: the clamped-isothermal and the simply supported-isothermal, at the two ends of the micro-beams. It can be shown that the dimensionless kinematic parameters \(\tilde{\psi }_{\zeta }\) and \(\bar{w}\) as well as the thermal moment \(\varPhi\) change harmonically with the same frequency. Hence, all the quantities are assumed to be a harmonic function [34], i.e.:

$$\begin{aligned} \tilde{w} & = \tilde{w}(\zeta )e^{i\varOmega t} , \\ \tilde{\psi }_{\zeta } & = \tilde{\psi }_{\zeta } (\zeta )e^{i\varOmega t} , \\ \varPhi & = \varPhi (\zeta )e^{i\varOmega t} \\ \end{aligned}$$
(25)

By substituting Eq. (25) into Eq. (23a–23c), we obtain:

$$A_{1} \tilde{\psi }^{\prime\prime}_{\zeta } + \varOmega^{2} \tilde{\psi }_{\zeta } - A_{2} \tilde{\psi }_{\zeta } + A_{3} \tilde{w}^{\prime\prime\prime} - A_{4} \tilde{w}^{\prime} - A_{5} \varPhi^{\prime} = 0,$$
(26a)
$$A_{6} \tilde{\psi }_{\zeta }^{\prime \prime \prime } - A_{7} \tilde{\psi }_{\zeta }^{\prime } + A_{8} \tilde{w}^{\prime \prime \prime \prime } - A_{9} \tilde{w}^{\prime \prime } - \varOmega^{2} \tilde{w} = 0,$$
(26b)
$$i\varOmega A_{10} \tilde{\psi }^{\prime}_{\zeta } - \varOmega^{2} A_{11} \tilde{\psi }^{\prime}_{\zeta } - \varPhi^{\prime\prime} - \varOmega^{2} A_{12} \varPhi + i\varOmega A_{13} \varPhi + A_{14} \varPhi = 0.$$
(26c)

By differentiating Eq. (26c) with respect to \(\zeta\) and eliminating \(\varPhi^{\prime}\) between the resulting equation and Eq. (26a), one can obtain:

$$a_{1} (\tilde{\psi }_{\zeta } )^{{{\prime \prime \prime \prime }}} + a_{2} (\tilde{\psi }_{\zeta } )^{{{\prime \prime }}} + a_{3} \tilde{\psi }_{\zeta } + a_{4} \tilde{w}^{{{\prime \prime \prime \prime \prime }}} + a_{5} \tilde{w}^{{{\prime \prime \prime }}} + a_{6} \tilde{w}^{{\prime }} = 0 ,$$
(27)

where the coefficients \(a_{i}\) in Eq. (27) are introduced in Appendix 2. By using Eqs. (26b) and (27), the uncoupled equation is found to be:

$$p_{1} \frac{{d^{8} \tilde{w}}}{{d\zeta^{8} }} + p_{2} \frac{{d^{6} \tilde{w}}}{{d\zeta^{6} }} + p_{3} \frac{{d^{4} \tilde{w}}}{{d\zeta^{4} }} + p_{4} \frac{{d^{2} \tilde{w}}}{{d\zeta^{2} }} + p_{5} = 0 .$$
(28)

The coefficients \(p_{i}\) in Eq. (28) are given in Appendix 2. Then, the solution of the dimensionless deflection \(\tilde{w}\) is given by:

$$\tilde{w}(\zeta ) = \sum\limits_{i = 1}^{4} {\left( {B_{i} \sinh (\lambda_{i} \zeta ) + C_{i} \cosh (\lambda_{i} \zeta )} \right)} ,$$
(29)

where \(\pm \lambda_{i}\, \left( {{\text{for}}\,i = 1, \ldots ,4} \right)\) are the roots of the characteristic equation \(p_{1} \lambda^{8} + p_{2} \lambda^{6} + p_{3} \lambda^{4} + p_{4} \lambda^{2} + p_{5} = 0\) and \(B_{i}\) and \(C_{i}\) are constants.After calculating the deflection, we can substitute Eq. (29) into Eq. (27) to get the solution for the dimensionless rotation \(\tilde{\psi }_{\zeta }\):

$$\tilde{\psi }_{\zeta } (\zeta ) = \sum\limits_{i = 1}^{4} {d_{i} \left( {B_{i} \sinh (\lambda_{i} \zeta ) + C_{i} \cosh (\lambda_{i} \zeta )} \right)} ,$$
(30)

in which

$$d_{i} = - \frac{{a_{4} \lambda_{i}^{5} + a_{5} \lambda_{i}^{3} + a_{6} \lambda_{i}^{{}} }}{{a_{1} \lambda_{i}^{4} + a_{2} \lambda_{i}^{2} + a_{3} }}.$$
(31)

Similarly, by substituting the dimensionless rotation from Eq. (30) into (23c), one of the thermal moments \(\varPhi\) can be obtained as follows:

$$\varPhi (\zeta ) = \sum\limits_{i = 1}^{4} {e_{i} \left( {B_{i} \sinh (\lambda_{i} \zeta ) + C_{i} \cosh (\lambda_{i} \zeta )} \right)} ,$$
(32)

where

$$e_{i} = \frac{{\left( {i\varOmega A_{10} \, - \varOmega^{2} A_{11} } \right)\lambda_{i}^{{}} }}{{\lambda_{i}^{2} + \varOmega^{2} A_{12} - i\varOmega A_{13} - A_{14} }}.$$
(33)

By imposing the clamped-isothermal conditions from Eq. (24) in equations of the dimensionless kinematic parameters, introduced by Eqs. (29), (30) and (32), the following equations are derived:

$$\left\{ \begin{aligned} & \tilde{w}(\zeta = 0) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {C_{i} } = 0, \\ & \tilde{w}(\zeta = 1) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {\left( {B_{i} \sinh (\lambda_{i} ) + C_{i} \cosh (\lambda_{i} )} \right)} = 0, \\ & \tilde{\psi }_{\zeta } (\zeta = 0) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {d_{i} C_{i} = 0} , \\ & \tilde{\psi }_{\zeta } (\zeta = 1) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {d_{i} \left( {B_{i} \sinh (\lambda_{i} ) + C_{i} \cosh (\lambda_{i} )} \right)} = 0, \\ & (A_{6} \tilde{\psi }_{\zeta ,\zeta } + A_{8} \tilde{w}_{,\zeta \zeta } )(\zeta = 0) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {\lambda_{i} \left( {d_{i} A_{6} B_{i} + A_{8} \lambda_{i} C_{i} } \right)} = 0, \\ & (A_{6} \tilde{\psi }_{\zeta ,\zeta } + A_{8} \tilde{w}_{,\zeta \zeta } )(\zeta = 1) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {\lambda_{i} \left[ {\left( {d_{i} A_{6} \cos (\lambda_{i} ) + A_{8} \lambda_{i} \sinh (\lambda_{i} )} \right)B_{i} } \right.} \\ & \quad \quad \left. { + \left( {d_{i} A_{6} \sin (\lambda_{i} ) + A_{8} \lambda_{i} \cos (\lambda_{i} )} \right)C_{i} } \right] = 0, \\ & \varPhi (\zeta = 0) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {e_{i} C_{i} } = 0, \\ & \varPhi (\zeta = 1) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {e_{i} \left( {B_{i} \sinh (\lambda_{i} ) + C_{i} \cosh (\lambda_{i} )} \right)} = 0 \\ \end{aligned} \right.$$
(34)

For the simply supported conditions, the two following equations are replaced instead of the third and the fourth equations (\(\tilde{\psi }_{\zeta } (\zeta = 0) = \tilde{\psi }_{\zeta } (\zeta = 1) = 0\)) in Eq. (34) as:

$$\left\{ \begin{aligned} & \left( {A_{1} \tilde{\psi }_{\zeta ,\zeta } + A_{3} \tilde{w}_{,\zeta \zeta } - A_{5} \varPhi \,} \right)(\zeta = 0) = 0 \Rightarrow \left( {A_{1} \tilde{\psi }_{\zeta ,\zeta } + A_{3} \tilde{w}_{,\zeta \zeta } \,} \right)(\zeta = 0) = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{4} {\lambda_{i} \left( {d_{i} A_{1} B_{i} + A_{3} \lambda_{i} C_{i} } \right)} = 0, \\ & \left( {A_{1} \tilde{\psi }_{\zeta ,\zeta } + A_{3} \tilde{w}_{,\zeta \zeta } - A_{5} \varPhi \,} \right)(\zeta = 0) = 0 \Rightarrow \left( {A_{1} \tilde{\psi }_{\zeta ,\zeta } + A_{3} \tilde{w}_{,\zeta \zeta } \,} \right)(\zeta = 0) = 0 \\ & \sum\limits_{i = 1}^{4} {\lambda_{i} \left[ {\left( {d_{i} A_{1} \cos (\lambda_{i} ) + A_{3} \lambda_{i} \sinh (\lambda_{i} )} \right)B_{i} + \left( {d_{i} A_{1} \sin (\lambda_{i} ) + A_{3} \lambda_{i} \cos (\lambda_{i} )} \right)C_{i} } \right]} = 0 \\ \end{aligned} \right.$$
(35)

In order to obtain the non-trivial solution, the constants \(B_{i}\) and \(C_{i}\) must be non-zero. Therefore, the following frequency equation can be regarded as:

$$\left| {\begin{array}{*{20}c} {g_{11} } & {g_{12} } & {g_{13} } & {g_{14} } & {g_{15} } & {g_{16} } & {g_{17} } & {g_{18} } \\ {g_{21} } & {g_{22} } & {g_{23} } & {g_{24} } & {g_{25} } & {g_{26} } & {g_{27} } & {g_{28} } \\ {g_{31} } & {g_{32} } & {g_{33} } & {g_{34} } & {g_{35} } & {g_{36} } & {g_{37} } & {g_{38} } \\ {g_{41} } & {g_{42} } & {g_{43} } & {g_{44} } & {g_{45} } & {g_{46} } & {g_{47} } & {g_{48} } \\ {g_{51} } & {g_{52} } & {g_{53} } & {g_{54} } & {g_{55} } & {g_{56} } & {g_{57} } & {g_{58} } \\ {g_{61} } & {g_{62} } & {g_{63} } & {g_{64} } & {g_{65} } & {g_{66} } & {g_{67} } & {g_{68} } \\ {g_{71} } & {g_{72} } & {g_{73} } & {g_{74} } & {g_{75} } & {g_{76} } & {g_{77} } & {g_{78} } \\ {g_{81} } & {g_{82} } & {g_{83} } & {g_{84} } & {g_{85} } & {g_{86} } & {g_{87} } & {g_{88} } \\ \end{array} } \right| = 0$$
(36)

where \(g_{ij}\)s are expressed for both boundary conditions in Appendix 3. The dimensionless frequency \(\varOmega\) can be calculated by solving Eq. (36).

4.2 Numerical results

Let the material length scale parameters \(l\) and relaxation time \(\tau\) be equal to zero, then the size-dependent coupled thermo-elastic equations and the boundary conditions of a Timoshenko micro-beam can be obtained on the basis of the classical theory. Hence, corresponding results to each type of theory are obtained and compared. For obtaining numerical results, it is assumed that the micro-beam is made of silicon [31]:

$$\begin{aligned} E & = 169\,{\text{GPa}}, \quad \rho = 2330\,\frac{\text{kg}}{{{\text{m}}^{3} }}, \\ c_{v} & = 713\frac{\text{J}}{\text{kg}}{\text{K}}, \quad \alpha_{T} = 2.59 \times 10^{ - 6} \,\frac{1}{\text{K}},\quad v = 0.22\,\,{\text{and}}\,\,k = 156\,{\text{W/m}}\,{\text{K}}.\end{aligned}$$
(37)

Moreover, it is assumed that \(T_{0}\) = 293 K. There is a lack of experimental data for the value of the thermal relaxation time \(\tau\). However, a range of 10–50 μs have been reported for various materials [35]. In this study, \(\tau\) is set to be 16 μs for derivation of numerical results from the exact solution.

In Tables 1 and 2, the non-dimensional frequencies based on non-Fourier and Fourier heat conduction models for a micro-beam with the clamped and isothermal boundary conditions (case I) and the simply supported and isothermal boundary conditions (case II) at the two ends are presented. From Table 1, it is seen that real part of the frequencies and the complex magnitude of the pure imaginary frequencies, predicted by the modified couple stress theory, are larger than those of classical theory; whereas, the imaginary parts of the complex frequencies are smaller. Furthermore, two complex conjugate frequencies are identically calculated. It can be concluded from Table 2 that most of these non-dimensional frequencies are real numbers. Also, the modified couple stress theory predicts the non-dimensional frequencies equal to or smaller than the classical theory for the two cases of the boundary conditions considered. By making comparison between the numerical results in Tables 1 and 2, it can be concluded that values of vibrational frequencies and consequently the vibration behavior predicted by the non-Fourier and Fourier heat conduction models, differ significantly from each other. In Tables 3 and 4, the non-dimensional frequencies are given for different values of \(L/h\), based on the non-Fourier and Fourier heat conduction models, respectively. Taking a look at the results obtained in Table 3, it can be induced that unlike their imaginary part, the values of the real part of the non-dimensional frequencies for the non-Fourier heat conduction model are increased by rise in \(L/h\). The effect of aspect ratio \(\left( {L/h} \right)\) on the non-dimensional frequencies which are obtained based on Fourier heat conduction model is more drastic than those of the non-Fourier model.

Table 1 Comparison of non-dimensional frequencies based on different theories for the non-Fourier heat conduction model
Full size table
Table 2 Comparison of non-dimensional frequencies based on different theories for the Fourier heat conduction model
Full size table
Table 3 Comparison of non-dimensional frequencies for different L/h based on the non-Fourier heat conduction model
Full size table
Table 4 Comparison of non-dimensional frequencies for different L/h based on the Fourier heat conduction model
Full size table

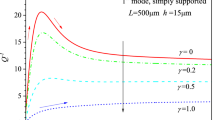
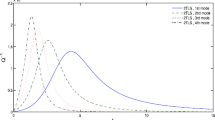
Since there are no results in the literature on the size-dependent coupled thermo-elastic behavior, in order to validate the results, some obtained results for the natural frequency in the special case of \(l = 0\), i.e., the results of the classical continuum theory, are compared with those presented by Sun et al. [36]. The variation of the minimum dimensionless frequency versus dimensionless thickness of the beam (\(h/h_{0}\)) is depicted in Fig. 2. The beam thickness varies from \(h/h_{0} = 0.1\) to \(h/h_{0}\) = 1.0, wherein \(h_{0}\) is equal to 20 μm. Figures 3 and 4 demonstrate the variation of the minimum dimensionless frequency by increasing \(h_{0} /l\) for the clamped-isothermal end conditions (case I) and the simply supported-isothermal end conditions (case II). From Figs. 3 and 4, it can be observed that the minimum values of the real part of dimensionless frequency are reduced continuously as the value of \(h_{0} /l\) increases. In addition, the difference between the values predicted for various values of aspect ratio \((L/h)\) becomes smaller with the decrease of \(h_{0} /l\).

Fig. 2
figure 2

Variation of the minimum dimensionless frequency versus dimensionless thickness based on the non-Fourier heat conduction model and classical theory for case I of boundary condition

Full size image
Fig. 3
figure 3

Variation of the minimum dimensionless frequency with the increase of \(h_{0} /l\) for the clamped-isothermal end conditions (case I)

Full size image
Fig. 4
figure 4

Variation of the minimum dimensionless frequency with the increase of \(h_{0} /l\) for the simply supported-isothermal end conditions (case II)

Full size image

5 Conclusion

In this paper, an exact solution for vibrational frequencies of micro-beam resonators was developed by employing the generalized thermo-elastic model presented by Taati et al. [32]. This size-dependent model is based on the modified couple stress and non-Fourier heat conduction theories, which have the capability of capturing the size-effect in micro-scaled structures. The uncoupled governing equations were obtained by performing mathematical operations. Then, the exact general solutions of dimensionless deflection, rotation and thermal moment were presented for any boundary conditions at beam ends [please see Eqs. (29), (30) and (32)]. Eventually, the frequency equation was acquired by imposing end conditions. The dimensionless frequencies were computed for two boundary condition cases, i.e., the clamped and isothermal, the simply supported and isothermal, which are widely used in most of MEMS. It can be readily concluded from numerical results that, values of vibrational frequencies, and so consequently the vibration behaviors predicted by the non-Fourier and Fourier heat conduction models, prove to be completely different from each other. As a result, the frequency response is extremely sensitive to values of the thermal relaxation time.