Approaches to multi-attribute decision-making based on picture fuzzy Aczel–Alsina average aggregation operators

Abstract

Picture fuzzy numbers (PFNs) are extremely reasonable to be utilized for delineating dubious or fuzzy data. In this article, we introduce the aggregation strategies of PFNs with assistance from Aczel–Alsina operations. We initially broaden the Aczel–Alsina t-norm and t-conorm to picture fuzzy (PF) situations and present a few new operations of PFNs; for example, Aczel–Alsina sum, Aczel–Alsina product, Aczel–Alsina scalar multiplication, and Aczel–Alsina exponentiation, in view of which we build up a few new PF aggregation operators; for instance, the PF Aczel–Alsina weighted average (PFAAWA) operator, PF Aczel–Alsina order weighted average (PFAAOWA) operator, and PF Aczel–Alsina hybrid average (PFAAHA) operator. We further build up various characteristics of those operators, keep several exceptional instances among themselves, and investigate the connections among such operators. Besides, we apply such operators to build up a methodology for managing multiple attribute decision-making (MADM) with PF data. A numerical example is stated to delineate the reasonableness, the viability of the created operators, and the approach. A comparative analysis is additionally introduced.

1 Introduction

Recently, there has been an increasing fascination with MADM-related studies. Speculations and ideas identified with MADM have already been effectively applied in taking care of various complex real-world issues. The fuzzy set (FS) theory proposed by Zadeh (1965) is one of the very popular hypotheses that usually connected to MADM, since the decision-making is constantly fitting to muddle, ambiguity, vulnerability, and abstract data. Regardless of its long achievement, the FS hypothesis which depicted the level of an individual from the set as membership function has a constraint, especially in portraying an individual from the set which has no membership. In this manner, Atanassov (1986) stretches out the FS hypothesis to the intuitionistic fuzzy set (IFS) by including a non-membership function. Practically like the FS, the hypothesis of IFS has been broadly placed on MADM studies. Be that as it may, FSs and IFSs cannot fulfill the circumstances where we face conclusions that include different sorts of answers, for example, yes, abstain, no, and refusal. To forestall this absence of data, Cuong (2013) presented PF sets (PFSs), which are able to use rather than FSs or IFSs. PFSs are portrayed by the degrees of positive membership, neutral membership, negative membership, and refusal membership, and the sum of such membership degrees should not exceed one. Clearly, utilizing PFS to explain the dubious data tends to be more reasonable and exact than FSs and IFSs.

After the invention of PFS, a huge number of researchers started working on PFS. Son together with colleagues (Son 2017; Son et al. 2017; Thong and Son 2016) have done a lot of works on PFS and PF clustering. Wei et al. (2018) introduced projection models for MADM issues with PF data. Wei together with colleagues (Wei and Gao 2018; Wei 2018) defined (Dice) similarity measures on PFSs. Wei (2017) investigated the MADM issues with picture 2-tuple linguistic data. Wei (2016) defined PF cross-entropy and employed it to supervise MCDM issues. On the basis of a new distance measure, Peng and Dai (2017) defined an algorithm for PF MADM issues. Peng (2017) examined undertaking hazard the executive’s evaluation dependent on PF MADM strategy. Zhang et al. (2018) proposed new working rules and aggregation operators of picture 2-tuple linguistic data for MADM issues. In accordance with 2-TLPPR, Nie et al. (2017) generalized a new group decision-making voting procedure to resolve the voting selection problem. Jana and Pal (2019) talked about the appraisal of big business execution in light of PF Hamacher aggregation operators. Ashraf et al. (2019) presented a progression of PF weighted geometric aggregation operators by utilizing t-norm and t-conorm. Ashraf et al. (2018) exhibited PF linguistic sets and implemented them in MAGDM problems. In view of Einstein operations, Khan together with colleagues Khan et al. (2019) intimated a few PF aggregation information and implemented it in MADM issues. Zeng together with colleagues Zeng et al. (2019) talked about the exponential Jensen PF divergence measure and applied it in decision-making problems. Qiyas et al. (2019) proposed linguistic PF Dombi aggregation operators and their application in the MAGDM problem. Khan et al. (2019) created a logarithmic decision-making strategy to manage uncertainty in the proper execution of a PFS. Wang et al. (2017) defined a few geometric aggregation operators dependent on PFS and discussed their implementation in MADM. Khalil and LI SG, Garg H, LI H, MA S, (2019) contemplated a new procedure on interval-valued PFS, interval-valued PF soft set. Wei (2018); Wei et al. (2018) considered PF Hamacher and Heronian mean aggregation operators to address MADM issues. Wei (2017) introduced a few cosine similarity measures for PFS and implemented them in strategic decision-making. By making use of the Dombi t-norm, Jana et al. (2019) studied new aggregation operators for PFS. To address the complex MCDM problems in practice, Wang et al. (2018a) offered the picture hesitant fuzzy set hypothesis. Recently, Senapati et al. (2021a) introduced Aczel–Alsina aggregation operators and utilized them in the intuitionistic fuzzy MADM process.

PF MADM has been extensively applied in numerous fields, for example, weather casting from satellite image (Son and Thong 2017), risk classification of energy efficiency planning projects (Wang et al. 2018a, b), selection of a project to modernize the energy efficiency of a hotel building (Wang et al. 2020), end-of-life vehicle management (Yang et al. 2019), image segmentation Wu and Chen (2020), choice of charging station for electric vehicles (Ju et al. 2019), financial investment risk management (Wang et al. 2019), technical innovation efficiency evaluation for high-tech industry (Song and Ding 2019), and safety assessment of construction projects (Wei et al. 2019). For other studies on PFS, the readers are referred to (Garg 2017; Khan et al. 2020; Khoshaim et al. 2021; Phuong et al. 2018; Qiyas et al. 2021).

Regrettably, along the way of handling PF data, we observe a short of suitable aggregation operators to combine PF data, that are an irrefutably imperative issue to incorporate PF data. Subsequently, the intention of such studies includes a few working rules of PFNs and builds up novel aggregation operators to incorporate PF data. Aczel–Alsina working laws are significant mathematical operations that are advantageously familiar with inaccurate and uncertain information. Inspired by these thoughts, we introduced Aczel–Alsina operations of PFNs and built up some PF Aczel–Alsina aggregation operators to solve PF MADM issues. The commitments of our technique are expressed in the following ways:

• (1) We built up a few Aczel–Alsina operations for PFNs, that may triumph over the deficiency of algebraic operations and capture the connection among diverse PFNs.

• (2) We prolonged Aczel–Alsina operators to PF Aczel–Alsina operators: PF Aczel–Alsina weighted averaging (PFAAWA) operator, PF Aczel–Alsina order weighted averaging (PFAAOWA) operator, PF Aczel–Alsina hybrid averaging (PFAAHA) operator in support of PF data, which can conquer the algebraic operator’s disadvantages.

• (3) We built up an algorithm to handle MADM issues utilizing PF data.

• (4) To exhibit the adequacy and unwavering quality of the suggested PF Aczel–Alsina aggregation operators, we carried out the suggested operator to a MADM issue.

• (5) The outcomes demonstrate that the suggested procedure is progressively powerful and gives an even more authentic output in comparison to current strategies.

The remaining portion of the paper is sorted out in the prescribed sequence: Some fundamental information associated with t-norms, t-conorms, Aczel–Alsina t-norms, PFSs, and several working rules in terms of PFNs are characterized in Sect. 2. The Aczel–Alsina working rules and the features of PFNs are discussed in Sect. 3. In Sect. 4, we interpret some PF Aczel–Alsina aggregation operators and look at several of their desirable properties. In the next section, we tackle the MADM issue, utilizing PF Aczel–Alsina aggregation operators. In the next section, we provide an illustrative instance. In Sect. 7, we look at how a parameter affects decision-making outcomes. Section 8 presents a comparative evaluation of the considered aggregation operators with the prevailing aggregation operators. Section 9 concludes the paper and elaborates on future studies.

2 Preliminaries

We’ll go over some basic concepts like t-norms, t-conorms, Aczel–Alsina t-norms, and PFSs in the sections below.

2.1 t-norms, t-conorms, and Aczel–Alsina t-norms

Definition 1

Menger (1942) A function $T:[0,1]^{2}\rightarrow [0,1]$ is a t-norm if the underlying axioms are hold for any $d, z, r \in [0, 1]$

• (i) Symmetry: $T(d,z) = T(z,d)$;

• (ii) Monotonicity: $T(d,z)\le T(d, r)$ if $z \le r$;

• (iii) Associativity: $T(d, T(z, r))= T(T(d,z), r)$;

• (iv) One identity: $T(d, 1) = d$.

Example 1

The following are common examples of t-norms:

• (i) Minimum t-norm: $T_{M}(d,z)=\min (d,z)$;

• (ii) Product t-norm: $T_{P}(d,z)=d.z$;

• (iii) Lukasiewicz t-norm: $T_{L}(d,z)=\max (d + z-1, 0)$;

• (iv) Drastic t-norm

  $$\begin{aligned} T_D(d,z) =\left\{ \begin{array}{ll} d, &{} \text{ if } z=1\\ z, &{} \text{ if } d=1\\ 0, &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

for any $d, z\in [0, 1]$.

Definition 2

Klement et al. (2000) A function $S:[0,1]^{2}\rightarrow [0,1]$ is a t-conorm if the underlying axioms are hold for any $d, z, r \in [0, 1]$

• (i) Symmetry: $S(d,z) = S(z,d)$;

• (ii) Monotonicity: $S (d,z)\le S (d, r)$ if $z\le r$;

• (iii) Associativity: $S(d, S(z, r))= S (S(d,z), r)$;

• (iv) Zero identity: $S (d, 0) = d$.

Example 2

The following are common examples of t-conorms:

• (i) Maximum t-conorm: $S_{M}(d,z)=\max (d,z)$;

• (ii) Probabilistic sum: $S_{P}(d,z)=d+z-d.z$;

• (iii) Lukasiewicz t-conorm: $S_{L}(d,z)=\min (d + z, 1)$;

• (iv) Drastic t-conorm

  $$\begin{aligned} S_D(d,z)=\left\{ \begin{array}{ll} d, &{} \text{ if } z=0\\ z, &{} \text{ if } d=0\\ 1, &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

for any $d, z \in [0, 1]$.

It also stated the fact Klement et al. (2000) that if T is a t-norm and S is a t-conorm, then $T(d,z)\le \min \{d, z\}$ and $S(d,z)\ge \max \{d, z\}$ for any $d, z \in [0, 1],$ respectively.

Definition 3

Aczel and Alsina (1982); Alsina et al. (2006)(Aczel–Alsina t-norm) Aczel–Alsina proposed this t-norm category in the early 1980s in the context of functional equations.

The category of Aczel–Alsina t-norms $(T_{A}^{\aleph })_{\aleph \in [0,\infty ]}$ is described by

$$\begin{aligned} T_{A}^{\aleph }(d,z)=\left\{ \begin{array}{ll} T_D(d,z), &{} \mathrm{if} \,\, \aleph =0\\ \min (d,z), &{} \mathrm{if} \,\, \aleph =\infty \\ e^{-((-\log d)^\aleph +(-\log z)^\aleph )^{1/\aleph }}, &{} \mathrm{otherwise}. \end{array}\right. \end{aligned}$$

The category of Aczel–Alsina t-conorms $(S_{A}^{\aleph })_{\aleph \in [0,\infty ]}$ is described by

$$\begin{aligned} S_{A}^{\aleph }(d,z)=\left\{ \begin{array}{ll} S_D(d,z), &{} \mathrm{if} \,\, \aleph =0\\ \max (d,z), &{} \mathrm{if} \,\, \aleph =\infty \\ 1-e^{-((-\log (1- d))^\aleph +(-\log (1-z))^\aleph )^{1/\aleph }}, &{} \mathrm{otherwise}. \end{array}\right. \end{aligned}$$

Limiting cases: $T_{A}^{0}=T_D$, $T_{A}^{1}=T_P$, $T_{A}^{\infty }=\min$, $S_{A}^{0}=S_D$, $S_{A}^{1}=S_P$, $S_{A}^{\infty }=\max$.

The t-norm $T_{A}^{\aleph }$ and the t-conorm $S_{A}^{\aleph }$ are dual to one another for each $\aleph \in [0,\infty ]$. The Aczel–Alsina t-norm category is strictly increasing, while the Aczel–Alsina t-conorm category is strictly decreasing.

2.2 PFSs

PFSs are general forms of FS and IFSs. Cuong (2013) was the first to introduce PFSs. Cuong (2014) provided additional information regarding PFSs. Let $\varUpsilon$ be a universal set. As demonstrated below, a PFS T can be described this way

$$\begin{aligned} T=\{\langle \hat{\wp }_T(\gamma ), \hat{\zeta }_T(\gamma ), \hat{\varrho }_T(\gamma )\rangle |\gamma \in \varUpsilon \}, \end{aligned}$$

$\hat{\wp }_T(\gamma ): \varUpsilon \rightarrow [0,1]$ (positive membership degree of element $\gamma$ in PFS T)

$\hat{\zeta }_T(\gamma ): \varUpsilon \rightarrow [0,1]$ (neutral membership degree of element $\gamma$ in PFS T)

$\hat{\varrho }_T(\gamma ): \varUpsilon \rightarrow [0,1]$ (negative membership degree of element $\gamma$ in PFS T)

$\pi _T(\gamma ): \varUpsilon \rightarrow [0,1]$ (degree of refusal memberships for element $\gamma$ in PFS T).

The sum of positive, neutral, and negative degree values lies on the interval [0, 1]. The pair $(\hat{\wp }_T,\hat{\zeta }_T,\hat{\varrho }_T)$ is named as PF number (PFN) or PF value (PFV). The refusal degree values could be computed utilizing the accompanying equation $\pi _T(\gamma )=1-\hat{\wp }_T(\gamma )-\hat{\zeta }_T(\gamma )-\hat{\varrho }_T(\gamma )$.

If $\pi _T(\gamma )=0$ for any element in the universal set, PFS comes back to an IFS. Whether either $\pi _T(\gamma )=0$ and $\hat{\zeta }_T(\gamma )=0$ for any element in the universal set, PFS comes back to a conventional FS. PFSs are clearly more comprehensive than fuzzy and IFSs. In the computing procedures, PFS gives extra data concerning our informational indexes, which is often reviewed as better inference results.

Motivated by the operations of Xu and Yager (2006), Cuong (2013) and Wei (2017) developed a few working rules for PFNs in the following way:

Definition 4

Cuong (2013); Wei (2017) Let $T=(\hat{\wp }_{T}, \hat{\zeta }_{T}, \hat{\varrho }_{T})$, $T_1=(\hat{\wp }_{T_1}, \hat{\zeta }_{T_1}, \hat{\varrho }_{T_1})$ and $T_2=(\hat{\wp }_{T_2}, \hat{\zeta }_{T_2},$ $\hat{\varrho }_{T_2})$ be three PFNs in the universe $\varUpsilon$, and then, succeeding operations are denominated as

• (1) $T_1\subseteq T_2$, if $\hat{\wp }_{T_1}(\gamma )\le \hat{\wp }_{T_2}(\gamma )$, $\hat{\zeta }_{T_1}(\gamma )\le \hat{\zeta }_{T_2}(\gamma )$ and $\hat{\varrho }_{T_1}(\gamma )\ge \hat{\varrho }_{T_2}(\gamma )$;

• (2) $T_1=T_2$ iff $T_1 \subseteq T_2$ and $T_2 \subseteq T_1$;

• (3) $T_1 \cup T_2=\langle \max \{\hat{\wp }_{T_1}(\gamma ),\hat{\wp }_{T_2}(\gamma )\}, \min \{\hat{\zeta }_{T_1}(\gamma ),\hat{\zeta }_{T_2}(\gamma )\}, \min \{\hat{\varrho }_{T_1}(\gamma ),\hat{\varrho }_{T_2}$ $(\gamma )\}\rangle$;

• (4) $T_1 \cap T_2=\langle \min \{\hat{\wp }_{T_1}(\gamma ),\hat{\wp }_{T_2}(\gamma )\}, \max \{\hat{\zeta }_{T_1}(\gamma ),\hat{\zeta }_{T_2}(\gamma )\}, \max \{\hat{\varrho }_{T_1}(\gamma ),\hat{\varrho }_{T_2}\}\rangle$;

• (5) $\overline{T}=\langle \hat{\varrho }_T(\gamma ), \hat{\zeta }_T(\gamma ), \hat{\wp }_T(\gamma )\rangle$;

• (6) $T_1 \bigoplus T_2=\big \langle \hat{\wp }_{T_1}(\gamma )+\hat{\wp }_{T_2}(\gamma )-\hat{\wp }_{T_1}(\gamma )\hat{\wp }_{T_2}(\gamma ),\hat{\zeta }_{T_1}(\gamma )\hat{\zeta }_{T_2}(\gamma ), \hat{\varrho }_{T_1}(\gamma )\hat{\varrho }_{T_2}(\gamma )\big \rangle$;

• (7) $T_1 \bigotimes T_2=\big \langle \hat{\wp }_{T_1}(\gamma )\hat{\wp }_{T_2}(\gamma ),\hat{\zeta }_{T_1}(\gamma )+\hat{\zeta }_{T_2}(\gamma )-\hat{\zeta }_{T_1}(\gamma )\hat{\zeta }_{T_2}(\gamma ), \hat{\varrho }_{T_1}(\gamma )+\hat{\varrho }_{T_2}(\gamma )-\hat{\varrho }_{T_1}(\gamma )$ $\hat{\varrho }_{T_2}(\gamma )\big \rangle$;

• (8) $\pounds T=\big \langle 1-(1-\hat{\wp }_T(\gamma ))^{\pounds }, \hat{\zeta }^{\pounds }_T(\gamma ), \hat{\varrho }^{\pounds }_T(\gamma )\big \rangle$;

• (9) $T^{\pounds }=\big \langle \hat{\wp }_T^{\pounds }(\gamma ), 1-(1-\hat{\zeta }_T(\gamma ))^{\pounds }, 1-(1-\hat{\varrho }_T(\gamma ))^{\pounds }\big \rangle$.

On the basis of Definition 4, Wei (2017) derived following operations in the following ways:

Definition 5

Let $T=(\hat{\wp }_{T}, \hat{\zeta }_{T}, \hat{\varrho }_{T})$, $T_1=(\hat{\wp }_{T_1}, \hat{\zeta }_{T_1}, \hat{\varrho }_{T_1})$ and $T_2=(\hat{\wp }_{T_2}, \hat{\zeta }_{T_2},$ $\hat{\varrho }_{T_2})$ be three PFNs over the universe $\varUpsilon$ and $\pounds ,\pounds _1,\pounds _2>0$, and then

• (i) $T_1 \bigoplus T_2= T_2 \bigoplus T_1$;

• (ii) $T_1 \bigotimes T_2= T_2 \bigotimes T_1$;

• (iii) $\pounds (T_1 \bigoplus T_2)=\pounds T_1 \bigoplus \pounds T_2$;

• (iv) $(T_1 \bigotimes T_2)^{\pounds }=T_{1}^{\pounds }\bigotimes T_{2}^{\pounds }$;

• (v) $\pounds _1T \bigoplus \pounds _2 T=(\pounds _1+\pounds _2)T$;

• (vi) $T^{\pounds _1}\bigotimes T^{\pounds _2}=T^{(\pounds _1+\pounds _2)}$;

• (vii) $(T^{\pounds _1})^{\pounds _2}=T^{\pounds _1\pounds _2}$.

Definition 6

Tian et al. (2019) Let $T_1=(\hat{\wp }_{T_1}, \hat{\zeta }_{T_1}, \hat{\varrho }_{T_1})$ and $T_2=(\hat{\wp }_{T_2}, \hat{\zeta }_{T_2}, \hat{\varrho }_{T_2})$ be a couple of PFNs, and the comparison technique of PFNs can be exhibited as

• (1) If $\hat{Y}(T_1)> \hat{Y}(T_2)$ or $\hat{Y}(T_1)= \hat{Y}(T_2)$ and $\hat{K}(T_1) > \hat{K}(T_2)$, then $T_1 \succ T_2$;

• (2) If $\hat{Y}(T_1)< \hat{Y}(T_2)$ or $\hat{Y}(T_1)= \hat{Y}(T_2)$ and $\hat{K}(T_1) < \hat{K}(T_2)$, then $T_1 \prec T_2$;

• (3) If $\hat{Y}(T_1)= \hat{Y}(T_2)$ and $\hat{K}(T_1) =\hat{K}(T_2)$, then $T_1=T_2$;

where $\hat{Y}(T_i)=\frac{1}{3}(\hat{\wp }_{T_i}+1-\hat{\zeta }_{T_i}+1-\hat{\varrho }_{T_i})$, $\hat{Y}(T_i)\in [0,1]$ and $\hat{K}(T_i)=\hat{\wp }_{T_i}- \hat{\varrho }_{T_i}$, $\hat{K}(T_i)\in [-1,1]$ $(i=1,2)$ represent score function, and accuracy function, respectively.

Wei (2017) prepared the PF aggregation operator portrayed in the succeeding definitions.

Definition 7

Let $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ $(q=1,2,\ldots h)$ be several PFNs. A PF weighted averaging (PFWA) operator of dimension h is a mapping ${\tilde{P}}^{h}\rightarrow {\tilde{P}}$ related to weight vector $\eth =(\eth _1,\eth _2,\ldots ,\eth _h)^{T}$, such that $\eth > 0$ and $\sum ^{h}_{q=1} \eth _q=1$, as $PFWA_{w}(\tilde{\delta }_1,\tilde{\delta }_2,\ldots , \tilde{\delta }_h)=\bigoplus \limits ^{h}_{q=1}(\eth _q\tilde{\delta }_q)$ $=\Big (1-\prod ^{h}_{q=1}{(1-\hat{\wp }_q)}^{\eth _q},$ $\prod ^{h}_{q=1}{\hat{\zeta }_q}^{\eth _q},$ $\prod ^{h}_{q=1}{\hat{\varrho }_q}^{\eth _q}\Big ).$

Definition 8

Let $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ $(q=1,2,\ldots h)$ be several PFNs. A PF ordered weighted averaging (PFOWA) operator of dimension h is a mapping ${\tilde{P}}^{h}\rightarrow {\tilde{P}}$ related to weight vector $\eth =(\eth _1,\eth _2,\ldots ,\eth _h)^{T}$ including $\eth > 0$ and $\sum ^{h}_{q=1} \eth _q=1$, as $PFOWA_{w}(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,$ $\tilde{\delta }_h)=\bigoplus \limits ^{h}_{q=1}\Big (\eth _q\tilde{\delta }_{(\varpi _q)}\Big )$ $=\Big (1-\prod ^{h}_{q=1}{\Big (1-\hat{\wp }_{\varpi (q)}\Big )}^{\eth _q},\prod ^{h}_{q=1}{\hat{\zeta }^{\eth _q}_{\varpi (q)}}, \prod ^{h}_{q=1}{\hat{\varrho }^{\eth _q}_{\varpi (q)}}\Big )$, where $(\varpi (1),$ $\varpi (2),\ldots ,\varpi (h))$ is a permutation of $(1,2,\ldots ,h)$, including $\tilde{\delta }_{\varpi (q-1)}\ge \tilde{\delta }_{\varpi (q)}$ for all $q=1,2,\ldots ,h$.

3 Aczel–Alsina operations of PFNs

In consideration of Aczel–Alsina t-norm and Aczel–Alsina t-conorm, we expounded Aczel–Alsina operations in connection with PFNs.

Definition 9

Let $\tilde{\delta }=(\hat{\wp }, \hat{\zeta }, \hat{\varrho })$, $\tilde{\delta }_1=(\hat{\wp }_1, \hat{\zeta }_1, \hat{\varrho }_1)$ and $\tilde{\delta }_2=(\hat{\wp }_2, \hat{\zeta }_2, \hat{\varrho }_2)$ be three PFNs, $\mathfrak {F} \ge 1$ and $\pounds >0$. Then, Aczel–Alsina T-norm and Aczel–Alsina T-conorm operations of PFNs are clarified as

• (i) $\tilde{\delta }_1 \oplus \tilde{\delta }_2= \Big \langle 1-e^{-((-\log (1- \hat{\wp }_1))^\mathfrak {F}+(-\log (1-\hat{\wp }_2))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-((-\log \hat{\zeta }_1)^\mathfrak {F}+(-\log \hat{\zeta }_2)^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-((-\log \hat{\varrho }_1)^\mathfrak {F}+(-\log \hat{\varrho }_2)^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$;

• (ii) $\tilde{\delta }_1 \otimes \tilde{\delta }_2= \Big \langle e^{-((-\log \hat{\wp }_1)^\mathfrak {F}+(-\log \hat{\wp }_2)^\mathfrak {F})^{1/\mathfrak {F}}}, 1- e^{-((-\log (1- \hat{\zeta }_1))^\mathfrak {F}+(-\log (1-\hat{\zeta }_2))^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-((-\log (1- \hat{\varrho }_1))^\mathfrak {F}+(-\log (1-\hat{\varrho }_2))^\mathfrak {F})^{1/\mathfrak {F}}} \Big \rangle$;

• (iii) $\pounds .\; \tilde{\delta }=\Big \langle 1-e^{-(\pounds (-\log (1- \hat{\wp }))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\pounds (-\log \hat{\zeta })^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\pounds (-\log \hat{\varrho })^\mathfrak {F})^{1/\mathfrak {F}}} \Big \rangle$;

• (iv) $\tilde{\delta }^{\pounds }=\Big \langle e^{-(\pounds (-\log \hat{\wp })^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-(\pounds (-\log (1- \hat{\zeta }))^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-(\pounds (-\log (1- \hat{\varrho }))^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$.

Example 3

Let $\tilde{\delta }=(0.48, 0.21,0.30)$, $\tilde{\delta }_1=(0.65, 0.15,0.20)$ and $\tilde{\delta }_2=(0.25,0.45,0.28)$ be three PFNs; at that point utilizing Aczel–Alsina operation on PFNs according to Definition 9 for $\mathfrak {F}=4$ and $\pounds =5$, we can get

• (i) $\tilde{\delta }_1 \oplus \tilde{\delta }_2 =\Big \langle 1-e^{-((-\log (1- 0.65))^4+(-\log (1-0.25))^4)^{1/4}}, e^{-((-\log 0.15)^4+(-\log 0.45)^4)^{1/4}}, e^{-((-\log 0.20)^4+(-\log 0.28)^4)^{1/4}}\Big \rangle =\langle 0.650516506, 0.147809098, 0.174127295 \rangle .$

• (ii) $\tilde{\delta }_1\otimes \tilde{\delta }_2= \Big \langle e^{-((-\log 0.65)^4+(-\log 0.25)^4)^{1/4}}, 1- e^{-((-\log (1- 0.15))^4+(-\log (1-0.45))^4)^{1/4}}, 1-e^{-((-\log (1- 0.20))^4+(-\log (1-0.28))^4)^{1/4}}\Big \rangle =\langle 0.249196223, 0.450447822, 0.291598446 \rangle .$

• (iii) $5 .\; \tilde{\delta }=\Big \langle 1-e^{-(5(-\log (1- 0.48))^4)^{1/4}}, e^{-(5(-\log 0.21)^4)^{1/4}}, e^{-(5(-\log 0.30)^4)^{1/4}}\Big \rangle =\langle 0.623880417, 0.096935186, 0.165239513 \rangle .$

• (iv) $\tilde{\delta }^{5}=\Big \langle e^{-(5(-\log 0.48)^4)^{1/4}}, 1-e^{-(5(-\log (1- 0.21))^4)^{1/4}}, 1-e^{-(5(-\log (1- 0.30))^4)^{1/4}} \Big \rangle =\langle 0.333690984, 0.297062365, 0.413365577 \rangle$.

Theorem 1

Let $\tilde{\delta }=(\hat{\wp }, \hat{\zeta }, \hat{\varrho })$, $\tilde{\delta }_1=(\hat{\wp }_1, \hat{\zeta }_1, \hat{\varrho }_1)$, $\tilde{\delta }_2=(\hat{\wp }_2, \hat{\zeta }_2, \hat{\varrho }_2)$ be three PFNs, and then, we get

(i):

$\tilde{\delta }_1 \oplus \tilde{\delta }_2=\tilde{\delta }_2 \oplus \tilde{\delta }_1$;

(ii):

$\tilde{\delta }_1 \otimes \tilde{\delta }_2=\tilde{\delta }_2 \otimes \tilde{\delta }_1$;

(iii):

$\pounds (\tilde{\delta }_1 \oplus \tilde{\delta }_2)=\pounds \tilde{\delta }_1 \oplus \pounds \tilde{\delta }_2$, $\pounds >0$;

(iv):

$(\pounds _1+\pounds _2 )\tilde{\delta }=\pounds _1 \tilde{\delta }\oplus \pounds _2 \tilde{\delta }$, $\pounds _1, \pounds _2 >0$;

(v):

$(\tilde{\delta }_1 \otimes \tilde{\delta }_2)^\pounds =\tilde{\delta }_1^\pounds \otimes \tilde{\delta }_2^\pounds$, $\pounds >0$;

(vi):

$\tilde{\delta }^{\pounds _1} \otimes \tilde{\delta }^{\pounds _2}=\tilde{\delta }^{(\pounds _1+\pounds _2 )}$, $\pounds _1, \pounds _2 >0$.

Proof

For the three PFNs $\tilde{\delta }$, $\tilde{\delta }_1$ and $\tilde{\delta }_2$, and $\pounds , \pounds _1, \pounds _2 > 0$, in accordance with Definition 9, we may get

(i):

$\tilde{\delta }_1\oplus \tilde{\delta }_2= \Big \langle 1-e^{-((-\log (1- \hat{\wp }_1))^\mathfrak {F}+(-\log (1-\hat{\wp }_2))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-((-\log \hat{\zeta }_1)^\mathfrak {F}+(-\log \hat{\zeta }_2)^\mathfrak {F})^{1/\mathfrak {F}}},$ $e^{-((-\log \hat{\varrho }_1)^\mathfrak {F}+(-\log \hat{\varrho }_2)^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle =\Big \langle 1-e^{-((-\log (1- \hat{\wp }_2))^\mathfrak {F}+(-\log (1-\hat{\wp }_1))^\mathfrak {F})^{1/\mathfrak {F}}},$ $e^{-((-\log \hat{\zeta }_2)^\mathfrak {F}+(-\log \hat{\zeta }_1)^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-((-\log \hat{\varrho }_2)^\mathfrak {F}+(-\log \hat{\varrho }_1)^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle =\tilde{\delta }_2 \oplus \tilde{\delta }_1$.

(ii):

It is obvious.

(iii):

Let $t= 1-e^{-((-\log (1- \hat{\wp }_1))^\mathfrak {F}+(-\log (1-\hat{\wp }_2))^\mathfrak {F})^{1/\mathfrak {F}}}$. Then, $\log (1-t)=-((-\log (1- \hat{\wp }_1))^\mathfrak {F}+(-\log (1-\hat{\wp }_2))^\mathfrak {F})^{1/\mathfrak {F}}$. Using this, we get $\pounds (\tilde{\delta }_1 \oplus \tilde{\delta }_2)=\pounds \Big \langle 1-e^{-((-\log (1- \hat{\wp }_1))^\mathfrak {F}+(-\log (1-\hat{\wp }_2))^\mathfrak {F})^{1/\mathfrak {F}}},$ $e^{-((-\log \hat{\zeta }_1)^\mathfrak {F}+(-\log \hat{\zeta }_2)^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-((-\log \hat{\varrho }_1)^\mathfrak {F}+(-\log \hat{\varrho }_2)^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$ $=\Big \langle 1-$ $e^{-(\pounds ((-\log (1- \hat{\wp }_1))^\mathfrak {F}+(-\log (1-\hat{\wp }_2))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\pounds ((-\log \hat{\zeta }_1)^\mathfrak {F}+(-\log \hat{\zeta }_2)^\mathfrak {F}))^{1/\mathfrak {F}}},$ $e^{-(\pounds ((-\log \hat{\varrho }_1)^\mathfrak {F}+(-\log \hat{\varrho }_2)^\mathfrak {F}))^{1/\mathfrak {F}}}\Big \rangle$ $=\Big \langle 1-e^{-(\pounds (-\log (1- \hat{\wp }_1))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\pounds (-\log \hat{\zeta }_1)^\mathfrak {F})^{1/\mathfrak {F}}},$ $e^{-(\pounds (-\log \hat{\varrho }_1)^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle \oplus \Big \langle 1-e^{-(\pounds (-\log (1- \hat{\wp }_2))^\mathfrak {F})^{1/\mathfrak {F}}},$ $e^{-(\pounds (-\log \hat{\zeta }_2)^\mathfrak {F})^{1/\mathfrak {F}}},$ $e^{-(\pounds (-\log \hat{\varrho }_2)^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$ $=\pounds \tilde{\delta }_1 \oplus \pounds \tilde{\delta }_2$.

(iv):

$\pounds _1 \tilde{\delta }\oplus \pounds _2 \tilde{\delta }=\Big \langle 1-e^{-(\pounds _1(-\log (1- \hat{\wp }))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\pounds _1(-\log \hat{\zeta })^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\pounds _1(-\log \hat{\varrho })^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$ $\oplus \Big \langle 1-e^{-(\pounds _2(-\log (1- \hat{\wp }))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\pounds _2(-\log \hat{\zeta })^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\pounds _2(-\log \hat{\varrho })^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$ $=\Big \langle 1-e^{-((\pounds _1+\pounds _2)(-\log (1- \hat{\wp }))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-((\pounds _1+\pounds _2)(-\log \hat{\zeta })^\mathfrak {F})^{1/\mathfrak {F}}},$ $e^{-((\pounds _1+\pounds _2)(-\log \hat{\varrho })^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$ $=(\pounds _1+\pounds _2 )\tilde{\delta }$.

(v):

$(\tilde{\delta }_1 \otimes \tilde{\delta }_2)^\pounds = \Big \langle e^{-((-\log \hat{\wp }_1)^\mathfrak {F}+(-\log \hat{\wp }_2)^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-((-\log (1- \hat{\zeta }_1))^\mathfrak {F}+(-\log (1-\hat{\zeta }_2))^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-((-\log (1- \hat{\varrho }_1))^\mathfrak {F}+(-\log (1-\hat{\varrho }_2))^\mathfrak {F})^{1/\mathfrak {F}}} \Big \rangle ^\pounds$ $=\Big \langle e^{-(\pounds ((-\log \hat{\wp }_1)^\mathfrak {F}+(-\log \hat{\wp }_2)^\mathfrak {F}))^{1/\mathfrak {F}}}, 1-e^{-(\pounds ((-\log (1- \hat{\zeta }_1))^\mathfrak {F}+(-\log (1-\hat{\zeta }_2))^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-(\pounds ((-\log (1- \hat{\varrho }_1))^\mathfrak {F}+(-\log (1-\hat{\varrho }_2))^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$ $=\Big \langle e^{-(\pounds (-\log \hat{\wp }_1)^\mathfrak {F})^{1/\mathfrak {F}}}, 1- e^{-(\pounds (-\log (1- \hat{\zeta }_1))^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-(\pounds (-\log (1- \hat{\varrho }_1))^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle \oplus \Big \langle e^{-(\pounds (-\log \hat{\wp }_2)^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-(\pounds (-\log (1- \hat{\zeta }_2))^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-(\pounds (-\log (1- \hat{\varrho }_2))^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$ $=\tilde{\delta }_1^\pounds \otimes \tilde{\delta }_2^\pounds$.

(vi):

$\tilde{\delta }^{\pounds _1} \otimes \tilde{\delta }^{\pounds _2} =\Big \langle e^{-(\pounds _1(-\log \hat{\wp })^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-(\pounds _1(-\log (1- \hat{\zeta }))^\mathfrak {F})^{1/\mathfrak {F}}}, 1- e^{-(\pounds _1(-\log (1- \hat{\varrho }))^\mathfrak {F})^{1/\mathfrak {F}}} \Big \rangle \otimes \Big \langle e^{-(\pounds _2(-\log \hat{\wp })^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-(\pounds _2(-\log (1- \hat{\zeta }))^\mathfrak {F})^{1/\mathfrak {F}}}, \!\! 1-e^{-(\pounds _2(-\log (1- \hat{\varrho }))^\mathfrak {F})^{1/\mathfrak {F}}} \Big \rangle$ $=\Big \langle e^{-((\pounds _1+\pounds _2)(-\log \hat{\wp })^\mathfrak {F})^{1/\mathfrak {F}}}, 1- e^{-((\pounds _1+\pounds _2)(-\log (1- \hat{\zeta }))^\mathfrak {F})^{1/\mathfrak {F}}}, 1-e^{-((\pounds _1+\pounds _2)(-\log (1- \hat{\varrho }))^\mathfrak {F})^{1/\mathfrak {F}}}\Big \rangle$ $=\tilde{\delta }^{(\pounds _1+\pounds _2 )}$. $\square$

4 PF Aczel–Alsina average aggregation operators

Using the Aczel–Alsina operations, we demonstrate a few PF average aggregation operators in this section.

Definition 10

Let $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ ($q=1,2,\ldots ,h)$ be several PFNs. Then, PF Aczel–Alsina weighted average (PFAAWA) operator is a mapping $P^{h}\rightarrow P$, such that

where $\eth =(\eth _1,\eth _2,\ldots ,\eth _h)^{T}$ is the weight vector of $\tilde{\delta }_q$ $(q=1,2,\ldots ,h)$ with $\eth _q> 0$ and .

Consequently, we obtain the succeeding theorem that is subsequent to the Aczel–Alsina operations concerning PFNs.

Theorem 2

Let $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ ($q=1,2,\ldots ,h)$ be several PFNs; at that point, aggregated value of them employing the PFAAWA operation is additionally PFNs, and

(1)

where $\eth =(\eth _1,\eth _2,\ldots ,\eth _h)$ is the weight vector of $\tilde{\delta }_q$ $(q=1,2,\ldots ,h)$, including $\eth _q> 0$ and .

Proof

We have implemented mathematical induction method to establish the Theorem 2 along the following lines: (i) When $h=2$ and the Aczel–Alsina operations of PFNs are taken into account, we get

$\eth _1 \tilde{\delta }=\Big \langle 1-e^{-(\eth _1(-\log (1- \hat{\wp _1}))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\eth _1(-\log \hat{\zeta _1})^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\eth _1(-\log \hat{\varrho _1})^\mathfrak {F})^{1/\mathfrak {F}}} \Big \rangle$,

$\eth _2 \tilde{\delta }=\Big \langle 1-e^{-(\eth _2(-\log (1- \hat{\wp _2}))^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\eth _2(-\log \hat{\zeta _2})^\mathfrak {F})^{1/\mathfrak {F}}}, e^{-(\eth _2(-\log \hat{\varrho _2})^\mathfrak {F})^{1/\mathfrak {F}}} \Big \rangle$. Based on Definition 9, we obtain $PFAAWA_{\eth }(\tilde{\delta }_1,\tilde{\delta }_2)=\eth _1 \tilde{\delta }_1 \bigoplus \eth _2 \tilde{\delta }_2$ As a result, (1) holds for $h=2$. (ii) Assuming that (1) holds for $h=k$, we obtain $IFAAWA_{\eth }(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,$ Now for $h=k+1$, then $IFAAWA_{\eth }(\tilde{\delta }_1, \tilde{\delta }_2,\ldots ,$

$\bigoplus \Bigg \langle 1-e^{-\Big (\eth _{k+1}(-\log (1- \hat{\wp }_{k+1}))^\mathfrak {F}\Big )^{1/\mathfrak {F}}}, e^{-\Big (\eth _{k+1}(-\log \hat{\zeta }_{k+1})^\mathfrak {F} \Big )^{1/\mathfrak {F}}},$

$e^{-\Big (\eth _{k+1}(-\log \hat{\varrho }_{k+1})^\mathfrak {F} \Big )^{1/\mathfrak {F}}} \Bigg \rangle$

.

Thus, (1) is correct for $h=k+1$. Consequently, on the basis of (i) and (ii), we draw a conclusion that (1) is true for all h. $\square$

Using the operator PFAAWA, we can efficiently show the following features. $\square$

Theorem 3

(Idempotency) In the event that $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ $(q=1,2,\ldots ,$ h) be several completely equivalent PFNs, i.e., $\tilde{\delta }_q=\tilde{\delta }$ for all q, then $PFAAWA_{\eth }$ $(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,\tilde{\delta }_h)=\tilde{\delta }.$

Proof

Since $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)=\tilde{\delta }$ $(q=1,2,\ldots , h)$. Then, we have by Eq. (1)

$=\Bigg \langle 1-e^{-\Big ((-\log (1- \hat{\wp }))^\mathfrak {F}\Big )^{1/\mathfrak {F}}},$

$e^{-\Big ((-\log \hat{\zeta })^\mathfrak {F} \Big )^{1/\mathfrak {F}}}, e^{-\Big ((-\log \hat{\varrho })^\mathfrak {F} \Big )^{1/\mathfrak {F}}}\Bigg \rangle$ $=\Bigg \langle 1-e^{\log (1- \hat{\wp })}, e^{\log \hat{\zeta }}, e^{\log \hat{\varrho }}\Bigg \rangle$ $=(\hat{\wp },\hat{\zeta },\hat{\varrho })$

$=\tilde{\delta }.$ Thus, $PFAAWA_{\eth }(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,\tilde{\delta }_h)=\tilde{\delta }$ holds. $\square$

Theorem 4

(Boundedness) Let $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ $(q=1,2,\ldots ,h)$ be an accumulation of PFNs. Let $\tilde{\delta }^{-}=\min (\tilde{\delta }_1,\tilde{\delta }_2,\ldots , \tilde{\delta }_h)$ and $\tilde{\delta }^{+}=\max (\tilde{\delta }_1,$ $\tilde{\delta }_2,\ldots ,$ $\tilde{\delta }_h)$. Then, $\tilde{\delta }^{-}\le PFAAWA_{\eth }(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,\tilde{\delta }_h)\le \tilde{\delta }^{+}.$

Proof

Let $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ $(q=1,2,\ldots ,h)$ be several PFNs. Let $\tilde{\delta }^{-}=\min (\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,$ $\tilde{\delta }_h)=\langle \hat{\wp }^{-},\hat{\zeta }^{-},\hat{\varrho }^{-}\rangle$ and $\tilde{\delta }^{+}=\max (\tilde{\delta }_1,\tilde{\delta }_2,\ldots , \tilde{\delta }_h)=\langle \hat{\wp }^{+},\hat{\zeta }^{+},\hat{\varrho }^{+}\rangle$. We have $\hat{\wp }^{-}=\min \limits _{q}\{\hat{\wp }_q\}$, $\hat{\zeta }^{-}=\max \limits _{q}\{\hat{\zeta }_q\}$, $\hat{\varrho }^{-}=\max \limits _{q}\{\hat{\varrho }_q\}$, $\hat{\wp }^{+}=\max \limits _{q}\{\hat{\wp }_q\}$, $\hat{\zeta }^{+}=\min \limits _{q}\{\hat{\zeta }_q\}$ and $\hat{\varrho }^{+}=\min \limits _{q}\{\hat{\varrho }_q\}$. Hence, there have the subsequent inequalities

Therefore, $\tilde{\delta }^{-}\le PFAAWA_{\eth }(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,\tilde{\delta }_h)\le \tilde{\delta }^{+}.$ $\square$

Theorem 5

(Monotonicity) Let $\tilde{\delta }_q$ and $\tilde{\delta }^{'}_q$ $(q=1,2,\ldots ,h)$ be a couple of PFNs; if $\tilde{\delta }_q\le \tilde{\delta }^{'}_q$ for all q, then $PFAAWA_{\eth }(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,\tilde{\delta }_h)\le PFAAWA_{\eth }(\tilde{\delta }^{'}_1,$ $\tilde{\delta }^{'}_2,\ldots ,\tilde{\delta }^{'}_h)$.

Now, we want to present PF Aczel–Alsina ordered weighted averaging (PFAAOWA) operator.

Definition 11

Let $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ $(q=1,2,\ldots ,h)$ be several PFNs. A PFAAOWA operator of dimension h is a mapping $PFAAOWA: {\tilde{P}}^{h}\rightarrow {\tilde{P}}$ with the corresponding vector $\varPhi =(\varPhi _1,\varPhi _2,\ldots ,\varPhi _h)^{T}$ including $\varPhi _q>0$ and , as

where $(\varpi (1),\varpi (2),\ldots ,\varpi (h))$ are the permutation of $(q=1,2,\ldots ,h)$, in such a way as $\tilde{\delta }_{\varpi (q-1)}\ge \tilde{\delta }_{\varpi (q)}$ for all $q=1,2,\ldots ,h$.

The accompanying theory is based on the Aczel–Alsina product operation on PFNs.

Theorem 6

Assume that $\tilde{\delta }_q=(\hat{\wp }_q,\hat{\zeta }_q,\hat{\varrho }_q)$ $(q=1,2,\ldots ,h)$ be several PFNs. A PF Aczel–Alsina ordered weighted average (PFAAOWA) operator of dimension h is a mapping PFAA $OWA: {\tilde{P}}^{h}\rightarrow {\tilde{P}}$ with the associated vector $\varPhi =(\varPhi _1,\varPhi _2,\ldots ,\varPhi _h)^{T}$, so that $\varPhi _q>0$ and . Then

(2)

where $(\varpi (1),\varpi (2),\ldots ,\varpi (h))$ are the permutation of $(q=1,2,\ldots ,h)$, in such a way as $\tilde{\delta }_{\varpi (q-1)}\ge \tilde{\delta }_{\varpi (q)}$ for any $q=1,2,\ldots ,h$.

Using the PFAAOWA operator, the following characteristics can be effectively shown.

Theorem 7

(Idempotency) In the event that $\tilde{\delta }_q$ $(q=1,2,\ldots ,h)$ are completely equivalent, i.e., $\tilde{\delta }_q=\tilde{\delta }$ for all q, then $PFAAOWA_{\varPhi }(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,\tilde{\delta }_h)=\tilde{\delta }.$

Theorem 8

(Boundedness) Let $\tilde{\delta }_q$ $(q=1,2,\ldots ,h)$ be several PFNs, and $\tilde{\delta }^{-}=\min \limits _{q}\tilde{\delta }_q$, $\tilde{\delta }^{+}=\max \limits _{q}\tilde{\delta }_q.$ Then, $\tilde{\delta }^{-}\le PFAAOWA_{\varPhi }(\tilde{\delta }_1,\tilde{\delta }_2,$ $\ldots ,\tilde{\delta }_h)\le \tilde{\delta }^{+}.$

Theorem 9

(Monotonicity) Let $\tilde{\delta }_q$ and $\tilde{\delta }^{'}_q$ $(q=1,2,\ldots ,h)$ be a couple of PFNs; if $\tilde{\delta }_q \le \tilde{\delta }^{'}_q$ for all q, then $PFAAOWA_{\varPhi }(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,\tilde{\delta }_h)\le PFAAOWA_{\varPhi }$ $(\tilde{\delta }^{'}_1,\tilde{\delta }^{'}_2,\ldots ,\tilde{\delta }^{'}_h).$

Theorem 10

(Commutativity) Let $\tilde{\delta }_q$ and $\tilde{\delta }^{'}_q$ $(q=1,2,\ldots ,h)$ be a couple of PFNs, and then, $PFAAOWA_{\varPhi }(\tilde{\delta }_1,\tilde{\delta }_2,\ldots ,\tilde{\delta }_h)= PFAAOWA_{\varPhi }(\tilde{\delta }^{'}_1,\tilde{\delta }^{'}_2,$ $\ldots ,\tilde{\delta }^{'}_h)$, where $\tilde{\delta }^{'}_q$ $(q=1,2,\ldots , h)$ is any permutation of $\tilde{\delta }_q$ $(q=1,2,\ldots , h)$.

In Definition 10, we realize that PFAAWA operator weights would be the most simple kind of the PFN itself, and in Definition 11, the PFAAOWA operator weights are the specific type of the arranged positions of the PFNs. In such a manner, the weights, stated in the operators PFAAWA and PFAAOWA, provide various circumstances that are against each other. In any case, these perspectives are viewed as the equivalent in a general methodology. Just to dispose of such inconvenience, in the following, we thusly present PF Aczel–Alsina hybrid averaging (PFAAHA) operator.

Definition 12

Let $\tilde{\delta }_q$ $(q= 1, 2, \ldots ,h)$ be a collection of PFNs. A PF Aczel–Alsina hybrid averaging (PFAAHA) operator of dimension h is a function $PFAAHA: {\tilde{P}}^{h}\rightarrow {\tilde{P}}$, such that

$$\begin{aligned} PFAAHA_{\eth ,\varPhi }(\tilde{\delta }_1, \tilde{\delta }_2, \ldots , \tilde{\delta }_h)= & {} \bigoplus ^{h}_{q=1}(\varPhi _q \dot{\tilde{\delta }}_{\varpi (q)})\\= & {} \varPhi _1 \dot{\tilde{\delta }}_{\varpi (1)} \bigoplus \varPhi _2 \dot{\tilde{\delta }}_{\varpi (2)} \bigoplus \cdots \bigoplus \varPhi _h \dot{\tilde{\delta }}_{\varpi (h)}, \end{aligned}$$

where $\varPhi =(\varPhi _1, \varPhi _2, \ldots , \varPhi _h)^T$ is the weighting vector associated with the PFAAHA operator, with $\varPhi _q \in [0, 1]$ $(q=1, 2, \ldots ,h)$ and $\sum \limits _{q=1}^{h}\varPhi _q=1$; $\dot{\tilde{\delta }}_q= h \eth _q \tilde{\delta }_q$, $q=1, 2, \ldots ,h$, $(\dot{\tilde{\delta }}_{\varpi (1)}, \dot{\tilde{\delta }}_{\varpi (2)}, \ldots , \dot{\tilde{\delta }}_{\varpi (h)})$ is any permutation of a group of the weighted PFNs $(\dot{\tilde{\delta }}_1, \dot{\tilde{\delta }}_2,$ $\ldots , \dot{\tilde{\delta }}_h)$, such that $\dot{\tilde{\delta }}_{\varpi (q-1)} \ge \dot{\tilde{\delta }}_{\varpi (q)}$ $(q=1, 2, \ldots ,h)$; $\eth = (\eth _1, \eth _2, \ldots , \eth _h)^T$ is the weighting vector of $\tilde{\delta }_q$, with $\eth _q \in [0, 1]$ and $\sum \limits _{q=1}^{h} \eth _q= 1$, and h is the balancing coefficient.

We can deduce the underlying two theorem based on Aczel–Alsina operations with PFNs.

Theorem 11

Let $\tilde{\delta }_q$ $(q= 1, 2, \ldots ,h)$ be several PFNs. Their aggregated value by PFAAHA operator is still a PFN, and

Proof

We can easily obtain Theorem 11 in the same way that we do in Theorem 2. $\square$

Theorem 12

The PFAAWA and PFAAOWA operators are particular instances of the PFAAHA operator.

Proof

(1) Assume that $\varPhi =(1/h, 1/h, \ldots , 1/h)^T$. Then

$$\begin{aligned} PFAAHA_{\eth ,\varPhi }(\tilde{\delta }_1, \tilde{\delta }_2, \ldots , \tilde{\delta }_h)= & {} \varPhi _1 \dot{\tilde{\delta }}_{\varpi (1)} \bigoplus \varPhi _2 \dot{\tilde{\delta }}_{\varpi (2)} \bigoplus \cdots \bigoplus \varPhi _h \dot{\tilde{\delta }}_{\varpi (h)}\\= & {} \frac{1}{h}(\dot{\tilde{\delta }}_{\varpi (1)} \bigoplus \dot{\tilde{\delta }}_{\varpi (2)} \bigoplus \cdots \bigoplus \dot{\tilde{\delta }}_{\varpi (h)})\\= & {} \eth _1 \tilde{\delta }_1 \bigoplus \eth _2 \tilde{\delta }_2 \bigoplus \cdots \bigoplus \eth _h \tilde{\delta }_h \\= & {} PFAAWA_{\eth }(\tilde{\delta }_1, \tilde{\delta }_2, \ldots , \tilde{\delta }_h). \end{aligned}$$

(2) Assume that $\eth =(1/h, 1/h, \ldots , 1/h)^T$. Then, $\dot{\tilde{\delta }}_q=\tilde{\delta }_q$ $(q= 1, 2, \ldots ,h)$ and

$$\begin{aligned} PFAAHA_{\eth ,\varPhi }(\tilde{\delta }_1, \tilde{\delta }_2, \ldots , \tilde{\delta }_h)= & {} \varPhi _1 \dot{\tilde{\delta }}_{\varpi (1)} \bigoplus \varPhi _2 \dot{\tilde{\delta }}_{\varpi (2)} \bigoplus \cdots \bigoplus \varPhi _h \dot{\tilde{\delta }}_{\varpi (h)}\\= & {} \varPhi _1 \tilde{\delta }_{\varpi (1)} \bigoplus \varPhi _2 \tilde{\delta }_{\varpi (2)} \bigoplus \cdots \bigoplus \varPhi _h \tilde{\delta }_{\varpi (h)}\\= & {} PFAAOWA_{\varPhi }(\tilde{\delta }_1, \tilde{\delta }_2, \ldots , \tilde{\delta }_h), \end{aligned}$$

which completes the proof. $\square$

5 Model for MADM using PF information

For the purposes of applying this, we may recommend an MADM strategy handling PF aggregation operators, where attribute values are PFNs and attribute weights, are real numbers. Let $\mathfrak {I}=\{\mathfrak {I}_1, \mathfrak {I}_2,\ldots , \mathfrak {I}_g\}$ and $\hslash =\{\hslash _1, \hslash _2, \ldots , \hslash _h\}$ be the set of choices and attributes, respectively. Let $\eth =(\eth _1,\eth _2,\ldots ,\eth _h)$ function as weight vector of the attribute $\eth _q$ $(q=1,2,\ldots ,h)$ is completely perceived to such an expand that $\eth _q>0$ and . We explicit the evaluation values of the choice $\mathfrak {I}_w$ $(w=1,2,\ldots ,g)$ regarding the criterion $\hslash _q$ $(q=1,2,\ldots ,h)$ by $\xi _{gh} =(\hat{\wp }_{gh},\hat{\zeta }_{gh},\hat{\varrho }_{gh})$. Assume that $R =\big (\xi _{gh}\big )_{g \times h}$ be the PF decision matrix, in which $\hat{\wp }_{gh}$ represents the positive membership degree with the property that choice $\mathfrak {I}_q$ fulfills the attribute $\hslash _q$ that has been supplied by the deciders, $\hat{\zeta }_{gh}$ imply the neutral membership degree in a way that choice $\mathfrak {I}_w$ does not fulfill the attribute $\hslash _q$, and $\hat{\varrho }_{gh}$ presented the degree that the choice $\mathfrak {I}_w$ does not address the attribute $\hslash _q$ which was specified by decider, where $\hat{\wp }_{gh}\subset [0,1]$, $\hat{\zeta }_{gh}\subset [0,1]$ and $\hat{\varrho }_{gh}\subset [0,1]$ allowing $0\le \hat{\wp }_{gh}+\hat{\zeta }_{gh}+\hat{\varrho }_{gh}\le 1$, $(w=1,2,\ldots ,g)$.

In the accompanying algorithm, we endeavor to take care of the MADM issue with the PF information by utilizing the PFAAWA operator.

Step 1. Change decision matrix $R =\big (\xi _{gh}\big )_{g \times h}$ into the normalization matrix $\overline{R} =\big (\overline{\xi }_{gh} \big )_{g \times h}$

$$\begin{aligned} \overline{\xi }_{gh}=\left\{ \begin{array}{ll} \xi _{gh} &{}\quad \text{ for } \text{ benefit } \text{ attribute } \hslash _q \\ (\xi _{gh})^c &{}\quad \text{ for } \text{ cost } \text{ attribute } \hslash _q\text{, } \end{array}\right. \end{aligned}$$

where $(\xi _{gh})^c$ is the complement of $\xi _{gh}$, so that $(\xi _{gh})^c=(\hat{\varrho }_{gh},\hat{\zeta }_{gh},\hat{\wp }_{gh})$.

Step 2. We handle the selected data expressed in matrix $\overline{R}$, and the operator PFAAWA

(3)

to achieve the standard desire values $\xi _w$ $(w=1,2,\ldots ,g)$ of the choices $\mathfrak {I}_w$.

Step 3. We compute the score function $\hat{Y}(\xi _w)$ $(w=1,2,\ldots , g)$ predicted on general PF information $\xi _w$ $(w=1,2,\ldots ,g)$ to list all the choice $\mathfrak {I}_w$ $(w=1,2,\ldots ,g)$ to select the best choice $\mathfrak {I}_w$. If there is no variation among score functions $\hat{Y}(\xi _w)$ and $\hat{Y}(\xi _q)$, at that point, we continue to figure accuracy degrees of $\hat{K}(\xi _w)$ and $\hat{K}(\xi _q)$ predicted on standard PF data of $\xi _w$ and $\xi _q$, and we rank the choices $\mathfrak {I}_w$ with regards to the accuracy degrees of $\hat{K}(\xi _w)$ and $\hat{K}(\xi _q)$.

Step 4. We rank all the choices $\mathfrak {I}_w$ $(w=1,2,\ldots ,g)$ to achieve the best possible one(s) according to $\hat{Y}(\xi _w)$ $(w=1,2,\ldots ,g)$.

Step 5. End.

6 Numerical example

So as to show the use of the created technique, we will consider a good example where there is a financing organization, which needs to put a whole of cash in the best choice (reorganized from Herrera and Herrera-Viedma (2000)). There is a board with five potential choices to put away the cash: $\mathfrak {I}_1$ is an automobile organization; $\mathfrak {I}_2$ is a nourishment organization; $\mathfrak {I}_3$ is a laptop organization; $\mathfrak {I}_4$ is a weapon organization; $\mathfrak {I}_5$ is a television organization. The financing organization must take a choice as indicated by the accompanying four attributes:

$\hslash _1$:

: Hazard investigation

$\hslash _2$:

: Growth investigation

$\hslash _3$:

: Social-political effect investigation

$\hslash _4$:

: Environmental effect investigation.

The attribute weight is allotted by decider as $\eth =(0.20, 0.10, 0.30,$ $0.40)^T$. The five available choices $\mathfrak {I}_w$ $(w=1,2,\ldots , 5)$ can be assessed utilizing the PF data by the decider under the above-mentioned four attributes, as listed in the consequent matrix:

Table 1 Picture fuzzy decision matrix

To be able to determine probably the most beneficial organization $\mathfrak {I}_w$ $(w=1,2,\ldots , 5)$, we employ PFAAWA operator to accumulate an MADM technique with PF information, which may be calculated like this:

Step 1.:

It is assumed that $\mathfrak {F}=1$. We take advantage of the PFAAWA operator to determine the standard desire values $\xi _w$ of the organizations $\mathfrak {I}_w$, $\widetilde{\xi }_1=(0.508241, 0.327308, 0.12153)$, $\widetilde{\xi }_2=(0.599384,$ 0.202459, 0.132463), $\widetilde{\xi }_3= (0.321599, 0.30760, 0.297106)$, $\widetilde{\xi }_4=(0.53198,$ 0.308900, 0.111022), $\widetilde{\xi }_5=(0.715012, 0.130896, 0.081355)$.

Step 2.:

By utilizing Definition 6, we calculate score values $\hat{Y}(\xi _w)$ $(w=1,2,\ldots ,5)$ of the PFNs $\xi _w$ $(w=1,2,\ldots ,5)$ as $\hat{Y}(\widetilde{\xi }_1)=0.686467$, $\hat{Y}(\widetilde{\xi }_2)=0.754821$, $\hat{Y}(\widetilde{\xi }_3)=0.572297$, $\hat{Y}(\widetilde{\xi }_4)=0.704018$, $\hat{Y}(\widetilde{\xi }_5)=0.834253$.

Step 3.:

Rank all the organizations $\mathfrak {I}_w$ $(w=1,2,\ldots ,5)$ according with the score values $\hat{Y}(\widetilde{\xi }_w)$ $(w=1,2,\ldots ,5)$ of the general PFNs as $\mathfrak {I}_5\succ \mathfrak {I}_2\succ \mathfrak {I}_4\succ \mathfrak {I}_1\succ \mathfrak {I}_3$.

Step 4.:

$\mathfrak {I}_5$ is chosen as the best preferable alternative.

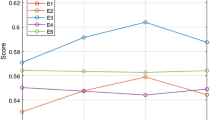
So as to review the impact of the working parameter on the preference order of alternatives in the PFAAWA operator, those are demonstrated in Table 2.

Table 2 Order of preference for different values of the working parameters in the aggregation procedure

Fig. 1

Score values of the alternatives for different values $\mathfrak {F}$ by PFAAWA operator

7 Investigation of the impact of working parameter $\mathfrak {F}$ upon decision-making outcomes

To spell out the impact of the working parameters $\mathfrak {F}$ on MADM outcomes, we will utilize various estimations of $\mathfrak {F}$ in accordance with rank the choices. The consequences of ordering the choices $\mathfrak {I}_w$ $(w=1,2,\ldots ,5)$ in view of the PFAAWA operator based on score values are shown in Table 2 and graphically illustrated in Fig. 1.

It is apparent that as the magnitude of $\mathfrak {F}$ for the IFAAWA operator increases, the score values for the alternatives gradually increase, but the relating ranking remains constant, $\mathfrak {I}_5\succ \mathfrak {I}_2\succ \mathfrak {I}_4\succ \mathfrak {I}_1\succ \mathfrak {I}_3$, indicating that the optimization approaches have the property of isotonicity, and the deciders can choose the appropriate value as indicated by their inclinations.

Furthermore, we can see from Fig. 1 that even when the values of F in the example are different, the ranking results of the alternatives are the same, demonstrating the uniformity of the suggested PFAAWA operators.

8 Comparative studies

In this section, we contrast our suggested techniques with current techniques as well as PF weighted averaging (PFWA) operator (Wei 2017), and PF Einstein weighted averaging ($PFWA^{\varepsilon }$) operator (Khan et al. 2019). Tables 3 and 4 give the comparison findings, which are visually illustrated in Fig. 2. Tables 2 and 3 show that the PFWA operator is a special instance of our suggested PFAAWA operator, and it acquires when $\mathfrak {F}=1$.

For this reason, our recommended techniques are likely to become more comprehensive and more adaptable than a few existing techniques to control PF MADM challenges.

Table 3 Comparative studies with a few of the currently exist techniques

Fig. 2

Comparison analysis with some of the currently exist techniques

Table 4 Comparison of attributes within a few currently exist techniques

9 Conclusions

In the present study, we have expanded the Aczel–Alsina t-norm and t-conorm in accordance with PF situations, defined a few novel working rules with regard to PFNs, and examined their properties and relationships. At that point, centered on such novel working rules, a few new aggregation operators, in particular, the PFAAWA operator, PFAAOWA operator, and PFAAHA operator, have now been constructed to fit the cases where in fact the given conflicts are PFNs. Different alluring features and some particular instances of those operators have now been examined in further detail, as well as the linkages between those operators. The suggested operators, along with PF data, were placed on MADM problems, and a mathematical formulation was presented to show the decision-making mechanism. The effect of parameter $\mathfrak {F}$ on decision-making outcomes has been examined.

The most favorable alternative can be acquired with PFAAWA operators by appropriately setting the parameter $\mathfrak {F}$. As a result, the suggested aggregation operators provide decision-makers with a new flexible method for reducing PF MADM difficulties. In other words, by providing a parameter, we can simply represent fuzzy information and make the information aggregation system more transparent than certain other current techniques. The existing aggregation operators (Wei 2017; Khan et al. 2019), on the other hand, do not make data aggregation more flexible. As a result, our proposed aggregation operators are more sophisticated and trustworthy in PF data decision-making.

We will apply the above operators and techniques to some realistic applications over time, such as hierarchical clustering, risk evaluation, behavioral economics, information processing, computer vision, and many domains in ambiguous contexts (Saha et al. 2021; Dey et al. 2020; Jana et al. 2019; Senapati and Yager 2019a, b, 2020; Senapati et al. 2021b).