1 Introduction

Inference is the process of formulating a nonlinear mapping from a given input space to output space, which provides a basis from which decisions can be made. The process of fuzzy inference involves all the membership functions, operators and if–then rules [30]. Fuzzy inference system (FIS) is also called as fuzzy rule based system, fuzzy expert system, fuzzy associative memory, fuzzy controller, fuzzy model or simply fuzzy system on the basis of the target for which the system is designed [7]. For instance, if the target of a system consists of temperature controlling tasks then the fuzzy system will be called as fuzzy controller and if the target is an expertise in medicine then the designed system is called fuzzy expert system [7].

Fuzzy inference systems are widely applicable in economic, scientific and engineering application areas due to the intuitive nature of the system and ability to analyze human judgments. For example, Khan, Daachi & Djouani [14] presented a fault detection for wireless sensor networks based on modeling a sensor node by Takagi–Sugeno–Kang (TSK) FIS, where a sensor measurement of a node is approximated by a function of the sensor measurements of the neighboring nodes. Nayak et al. [25] developed a FIS for predicting customer buying behavior where three different methods namely grid partitioning, fuzzy c-means and subtractive clustering were used to get the membership values during the fuzzification of inputs. Öztaysi et al. [26] described potential applications of FIS in disaster response, which is one of the critical stages of disaster management, which necessitates spontaneous decision making when a disaster occurs. There are numbers of FIS applications in various fields as shown in [31] ranging from computer networks design, diagnosis of prostate cancer, umbilical cord acid–base analysis, implementing onboard planning and scheduling for autonomous small satellite, to the applications in power systems.

A number of researchers in FIS have suggested how such systems can be tuned to enhance inference performance [2]. The first attempt involves the deterministic nature of the system. Cai, Hao & Yang [5] proposed an architecture for high-order fuzzy inference systems combining the kernel-based fuzzy c-means clustering and support vector machine. Chaudhari & Patil [7] proposed a multilayer system with defuzzification and weighted average, which can reduce the cost of defuzzification and lack of output expressivity that causes risk when used as a controller. Luo, Wang & Sun [20] introduced a novel adaptive stability scheme for a class of chaos system with uncertainties. Mieszkowicz-Rolka & Rolka [24] used a flow graph representation of a decision table with linguistic values. Pancho et al. [27] proposed visual representations of fuzzy rule-based inference for expert analysis of comprehensibility. Ton-That, Cao & Choi [24, 45] extended fuzzy associative memory, which can be viewed as the combination of associative memory and fuzzy logic. A series of works by Liu et al. in [8, 12, 16–19, 44] have presented some adaptive fuzzy controller designs for nonlinear systems. In [18], the systems are of the discrete-time form in a triangular structure and include the backlash and the external disturbance. A MIMO controller, composed of n subsystems nested lower triangular form and dead-zone nonlinearly inputs in non-symmetric nonlinear form was shown in [19]. Fuzzy logic systems were employed to approximate the unknown functions and the differential mean value theorem was used to separate dead-zone inputs herein [19].

It is obvious that learning capability is an influential factor to characterize efficient fuzzy rule based systems. Inference parameters include the central tendency and dispersion of the input and output fuzzy membership functions, the rule base, the cardinality of the fuzzy membership function sets, the shapes of the membership functions and the parameters of the fuzzy AND and OR operations [2]. Liu et al. [17, 44] designed controlled systems which are in a strict-feedback frame and contain unknown functions and non-symmetric dead-zone. A reinforcement learning algorithm based on the utility functions, the critic designs, and the back-stepping technique was used to develop an optimal control signal [17]. Likewise, evolutionary algorithms such as genetic algorithm, particle swarm optimization, differential evolution and bees algorithm have been used in [13, 15, 28]. Iman, Reza & Yashar [13] combined the Sugeno fuzzy inference system and glow worms algorithm for the diagnosis of diabetes. Khoobipour & Khaleghi [15] compared the capability of four evolutionary algorithms including genetic algorithm, particle swarm optimization, differential evolution and bees algorithms to improve the capability of a new strength fuzzy inference system for nonlinear function approximation. Rong, Huang & Liang [28] evaluated the learning ability of the batch version of Online Sequential Fuzzy Extreme Learning algorithm to train a class of fuzzy inference systems which cannot be represented by the Radial Basis Function networks. Fuzzy logic systems for the optimal tracking control problem were used to approximate the long-term utility function with the support of direct heuristic dynamic programming (DHDP) setting [12] and the fuzzy-neural networks and the back-stepping design technique [8, 16].

Despite having reasonable results in comparison with FIS, those relevant researches should be intensified on advanced fuzzy sets to achieve better performance [23]. Castillo, Martínez-Marroquín, Melin, Valdez & Soria [6] compared several bio-inspired algorithms applied to the optimization of type-1 and type-2 fuzzy controllers for an autonomous mobile robot. Maldonado, Castillo & Melin [21] used particle swarm optimization for average approximation of interval type-2 FIS. Melin [22, 23] implemented a new type-2 FIS method, which is a FIS on type-2 fuzzy set, for the detection of edges. It is indeed that extending FIS on advanced fuzzy sets has grasped a great attention [6, 22, 23]. Recently, a generalized fuzzy set namely picture fuzzy set (PFS) has been proposed in [9]. It is a generalization of fuzzy set (FS) of Zadeh [47] and intuitionistic fuzzy set (IFS) of Atanassov [3] with the debut of the positive, the negative, the neutral and the refusal degrees showing various possibilities of an element to a given set. PFS has a variety of applications in real contexts such as the confidence voting and personnel selection. Deploying fuzzy rule-based systems and soft computing methods on PFS would result in better accuracy [33]. Some preliminary researches on the soft computing methods on PFS have clearly demonstrated the usefulness of PFS in the modeling and performance improvement over traditional fuzzy tools [32–42, 46]. Thus, our objective in this research is to extend FIS on PFS in order to achieve better accuracy.

In this paper, a novel fuzzy inference system on PFS called picture inference system (PIS). In PIS, the positive, the neutral and the negative degrees of the picture fuzzy set are computed using the membership graph that is the combination of three Gaussian functions with a common center and different widths to express a visual view of degrees. Then, the positive and negative defuzzification values, synthesized from three degrees of the picture fuzzy set, are used to generate crisp outputs. Learning for PIS including training centers, widths, scales and defuzzification parameters is also discussed to build up a well-approximated model. The proposed method is empirically validated on the benchmark UCI Machine Learning Repository datasets [4].

The rests of the paper are organized as follows. Section 2 introduces the preliminary knowledge including the descriptions about the types of FIS and basic notions of PFS. Section 3 presents the new picture inference system including the design and the learning method. Section 4 shows the validation on both the Lorenz system and the Housing dataset. Section 5 gives the conclusions and delineates further works.

2 Preliminary

In this section, some types of FIS including the Mamdani, the Sugeno and the Tsukamoto fuzzy inferences are described in Section 2.1. Section 2.3 introduces the basic notions of PFS.

2.1 Types of fuzzy inference systems

There are three types of fuzzy inference systems [30] such as:

  • Mamdani fuzzy inference,

  • Sugeno (or Takagi-Sugeno) fuzzy inference,

  • Tsukamoto fuzzy inference.

A Mamdani fuzzy inference consists of two inputs x and y and a single output z. Each input x, y and output z has N, M and L membership functions, respectively. The system has R rules in the form:

$$ \text{k: If x is } A_{i}^{(k)} \text{ and y is } B_{j}^{(k)} \text{ then z is } C_{l}^{(k)} $$
(1)

where k = 1..R, i = 1..N, j = 1..M and l = 1..L. N, M and L are the numbers of membership functions for inputs and output, respectively. N, M, L can take any value depending on the model we construct, in this example: N =M =L =2. In this system, max/min is the most common rule of composition and the centre of method is used for defuzzification.

A Sugeno fuzzy inference has R rules in the form:

$$ \text{k: If x is } A_{i}^{(k)} \text{ and y is } B_{j}^{(k)} \text{ then z}^{\mathrm{(k)}} = \text{ f (x,y)} $$
(2)

where k = 1..R, i = 1..N and j = 1..M. N and M are the numbers of membership functions for inputs. This system uses the weighted average operator or the weighted sum operator for defuzzification.

In the Tsukamoto fuzzy inference, the consequent of each fuzzy if–then rule is represented by a monotonic membership function.

$$ \text{k: If x is } A_{i}^{(k)} \text{ and y is } B_{j}^{(k)} \text{ then z is } C_{l}^{(k)}, $$
(3)

The Tsukamoto fuzzy model aggregates each rule’s output by the method of weighted averages. Figure 1 illustrates a zero-order Sugeno inference.

Fig. 1
figure 1

Zero-order Sugeno fuzzy inference [30]

Full size image

Several researchers have compared the performances of those FIS systems in [10, 11, 29]. The results demonstrated the performance comparison of the three systems and the advantages of using Sugeno-type over Mamdani-type. Moreover, in fuzzy controllers, the root sum square inference engine is one of the most promising strategies and has better performance over the max-product and the max-min.

2.2 Picture fuzzy sets

Definition 1

A picture fuzzy set (PFS) [9] in a non-empty set X is,

$$ A=\left\{ {\left\langle {x,\mu_{A} \left(x \right),\eta_{A} \left(x \right),\gamma_{A} \left(x \right)} \right\rangle \vert x\in X} \right\}, $$
(4)

where μ A (x) is the positive degree of each element x∈X, η A (x) is the neutral degree and γ A (x) is the negative degree satisfying the constraints,

$$ \mu_{A} \left(x \right),\eta_{A} \left(x \right),\gamma_{A} \left(x \right)\in \left[ {0,1} \right], \quad \forall x\in X, $$
(5)
$$0\le \mu_{A} \left(x \right)+\eta_{A} \left(x \right)+\gamma_{A} \left(x \right)\le 1, \quad \forall x\in X. $$
(6)

The refusal degree of an element is calculated as ξ A (x)=1−(μ A (x)+η A (x)+γ A (x)), ∀x∈X. In cases ξ A (x)=0 PFS returns to the traditional IFS set. It is obvious that PFS is an extension of IFS where the refusal degree is appended to the definition.

Example 1

[36, 38, 39]. In a democratic election station, the council issues 500 voting papers for a candidate. The voting results are divided into four groups accompanied with the number of papers that are “vote for” (300), “abstain” (64), “vote against” (115) and “refusal of voting” (21). Group “abstain” means that the voting paper is a white paper rejecting both “agree” and “disagree” for the candidate but still takes the vote. Group “refusal of voting” is either invalid voting papers or did not take the vote. This example happened in reality and IFS could not handle it since the refusal degree (group “refusal of voting”) does not exist.

Now, some basic picture fuzzy operations, picture distance metrics and picture fuzzy relations are briefly presented [9]. Let P F S(X) denote the set of all PFS sets on universe X.

Definition 2

For A,B∈P F S(X), the union, intersection, complement and inclusion operations are defined as follows.

$$\begin{array}{@{}rcl@{}} A\!\cup\! B&\!=\!&\left\{ \left\langle x,\max \left\{ {\mu_{A} \left(x \right),\mu_{B} \left(x \right)} \right\},\min \left\{ {\eta_{A} \left(x \right),\eta_{B} \left(x \right)} \right\},\!\!\right.\right.\\ &&\left.\left.\min \left\{ {\gamma_{A} \left(x \right),\gamma_{B} \left(x \right)} \right\} \right\rangle \vert x\in X \right\}, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} A\cap B&=&\left\{ \left\langle x,\min \left\{ {\mu_{A} \left(x \right),\mu_{B} \left(x \right)} \right\},\min \left\{ {\eta_{A} \left(x \right),\eta_{B} \left(x \right)} \right\}\!,\!\!\!\!\right.\right.\\ &&\left.\left.\max \left\{ {\gamma_{A} \left(x \right),\gamma_{B} \left(x \right)} \right\} \right\rangle \vert x\in X \right\},\\ \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} \overline A =\left\{ {\left\langle {x,\gamma_{A} \left(x \right),\eta_{A} \left(x \right),\mu_{A} \left(x \right)} \right\rangle \vert x\in X} \right\}, \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} A&\subseteq& B \text{ iff } \forall x\in X:\mu_{A} \left(x \right)\le \mu_{B} \left(x \right)\! \text{ and } \eta_{A} \left(x \right)\le \eta_{B} \left(x \right)\!\\&&\text{and } \!\gamma_{A} \left(x \right)\ge \gamma_{B} \left(x \right), \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} A=B \text{ iff } A\subseteq B \text{ and } B\subseteq A. \end{array} $$
(11)

Definition 3

For A,B∈P F S(X), some operators on PFS are:

$$ A+B=\left\{ {\left\langle {x,\mu_{A} \left(x \right)+\mu_{B} \left(x \right)-\mu_{A} \left(x \right).\mu_{B} \left(x \right),\eta_{A} \left(x \right).\eta_{B} \left(x \right),\nu_{A} \left(x \right).\nu_{B} \left(x \right)} \right\rangle \vert x\in X} \right\} $$
(12)
$$ A.B=\left\{ {\left\langle {x,\mu_{A} \left(x \right).\mu_{B} \left(x \right),\eta_{A} \left(x \right).\eta_{B} \left(x \right),\nu_{A} \left(x \right)+\nu_{B} \left(x \right)-\nu_{A} \left(x \right).\nu_{B} \left(x \right)} \right\rangle \vert x\in X} \right\} $$
(13)
$$ A@B=\left\{ {\left\langle {x,\frac{1}{2}\left({\mu_{A} \left(x \right)+\mu_{B} \left(x \right)} \right),\frac{1}{2}\left({\eta_{A} \left(x \right)+\eta_{B} \left(x \right)} \right),\frac{1}{2}\left({\nu_{A} \left(x \right)+\nu_{B} \left(x \right)} \right)} \right\rangle \vert x\in X} \right\} $$
(14)
$$ A\$ B=\left\{ {\left\langle {x,\sqrt {\mu_{A} \left(x \right).\mu_{B} \left(x \right)} ,\sqrt {\eta_{A} \left(x \right).\eta_{B} \left(x \right)} ,\sqrt {\nu_{A} \left(x \right).\nu_{B} \left(x \right)} } \right\rangle \vert x\in X} \right\} $$
(15)
$$ A\# B=\left\{ {\left\langle {x,\frac{2\mu_{A} \left(x \right).\mu_{B} \left(x \right)}{\mu_{A} \left(x \right)+\mu_{B} \left(x \right)},\frac{2\eta_{A} \left(x \right).\eta_{B} \left(x \right)}{\eta_{A} \left(x \right)+\eta_{B} \left(x \right)},\frac{2\nu_{A} \left(x \right).\nu_{B} \left(x \right)}{\nu_{A} \left(x \right)+\nu_{B} \left(x \right)}} \right\rangle \vert x\in X} \right\} $$
(16)
$$ A\ast B=\left\{ {\left\langle {x,\frac{\mu_{A} \left(x \right)+\mu_{B} \left(x \right)}{2\left({\mu_{A} \left(x \right).\mu_{B} \left(x \right)+1} \right)},\frac{\eta_{A} \left(x \right)+\eta_{B} \left(x \right)}{2\left({\eta_{A} \left(x \right).\eta_{B} \left(x \right)+1} \right)},\frac{\nu_{A} \left(x \right)+\nu_{B} \left(x \right)}{2\left({\nu_{A} \left(x \right).\nu_{B} \left(x \right)+1} \right)}} \right\rangle \vert x\in X} \right\} $$
(17)

Remark 1

For a scalar c and a PFS A, the c×A is performed according to (13), for instance c=2:

$$\begin{array}{@{}rcl@{}} 2\times A&=&2.A\\ &=&A+A\\ &=&\left\{ {\left\langle {x,2\mu_{A} \left(x \right)-{\mu_{A}^{2}} \left(x \right),{\eta_{A}^{2}} \left(x \right),{\nu_{A}^{2}} \left(x \right)} \right\rangle } \right\} \end{array} $$
(18)

Definition 4

For A,B∈P F S(X), the Cartesian product of these PFS sets is,

$$\begin{array}{@{}rcl@{}} A\times_{1} B=\left\{ \left\langle \left({x,y} \right),\mu_{A} \left(x \right).\mu_{B} \left(y \right),\eta_{A} \left(x \right).\eta_{B} \left(y \right),\gamma_{A} \left(x \right).\gamma_{B} \left(y \right) \right\rangle \vert x\in A,y\in B \right\}, \end{array} $$
(19)
$$\begin{array}{@{}rcl@{}} A\times_{2} B=\left\{ \left\langle \left({x,y} \right),\mu_{A} \left(x \right)\wedge \mu_{B} \left(y \right),\eta_{A} \left(x \right)\wedge \eta_{B} \left(y \right),\gamma_{A} \left(x \right)\vee \gamma_{B} \left(y \right) \right\rangle \vert x\in A,y\in B \right\}. \end{array} $$
(20)

Definition 5

The distances between A,B∈P F S(X) are the normalized Hamming distance and the normalized Euclidean in formulae (22–23), respectively.

$$\begin{array}{@{}rcl@{}} d_{p} \left({A,B} \right)=\frac{1}{N}\sum \limits_{i=1}^{N} {\left({\left| {\mu_{A} \left({x_{i} } \right)-\mu_{B} \left({x_{i} } \right)} \right|+\left| {\eta_{A} \left({x_{i} } \right)-\eta_{B} \left({x_{i} } \right)} \right|+\left| {\gamma_{A} \left({x_{i} } \right)-\gamma_{B} \left({x_{i} } \right)} \right|} \right)} , \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} e_{p} \left({A,B} \right)=\sqrt {\frac{1}{N}\sum\limits_{i=1}^{N} {\left({\left({\mu_{A} \left({x_{i} } \right)-\mu_{B} \left({x_{i} } \right)} \right)^{2}+\left({\eta_{A} \left({x_{i} } \right)-\eta_{B} \left({x_{i} } \right)} \right)^{2}+\left({\gamma_{A} \left({x_{i} } \right)-\gamma_{B} \left({x_{i} } \right)} \right)^{2}} \right)} } . \end{array} $$
(22)

Definition 6

The picture fuzzy relation R is a picture fuzzy subset of A×B, given by

$$\begin{array}{@{}rcl@{}} R&=&\left\{ \left\langle {\left({x,y} \right),\mu_{R} \left({x,y} \right),\eta_{R} \left({x,y} \right),\gamma_{R} \left({x,y} \right)} \right\rangle \vert x\right.\\&&\left.\in A,y\in B \right\}, \end{array} $$
(23)
$$\begin{array}{@{}rcl@{}} \mu_{R} ,\eta_{R} ,\gamma_{R} :A\times B\to \left[ {0,1} \right], \end{array} $$
(24)
$$\begin{array}{@{}rcl@{}} \mu_{R} \left({x,y} \right)+\eta_{R} \left({x,y} \right)+\gamma_{R} \left({x,y} \right)\le 1, \end{array} $$
(25)
$$\begin{array}{@{}rcl@{}} \forall \left({x,y} \right)\in A\times B. \end{array} $$

P F R(A×B) is the set of all picture fuzzy subset on A×B.

Definition 7 (Zadeh extension principle for PFS)

For i=1,2,..,n, U i is a universe and V≠φ. Let f:U 1×2..×2 U n →V be a mapping, where y=f(z 1,..,z n ). Let z i is a linguistic variable on U i for i=1,2,..,n. Suppose, for all i, z i is A i where A i is a PFS on U i . Then, the output of the mapping f is B, which is a PFS on V defined for ∀y∈V by,

$$\begin{array}{@{}rcl@{}} B(y)=\left\{ \begin{array}{c} \left(\bigvee\limits_{D(y)} \left(\bigwedge\limits_{i=1}^{n} \mu_{A_{i}} (\mathrm{u}_{i})\right),\bigwedge\limits_{D(y)} \left(\bigwedge\limits_{i=1}^{n} \eta_{A_{i}} (\mathrm{u}_{i})\right),\bigwedge\limits_{D(y)} \left(\bigvee\limits_{i=1}^{n} \nu_{A_{i} } (\text{u}_{i})\right) \right)\textit{ if }f^{-1}(y)\ne 0 \\ (0,0,0)\textit{ if }f^{-1}(y)=0 \end{array}\right\} \end{array} $$
(26)
$$\begin{array}{@{}rcl@{}} D(y)=f^{-1}(y)=\{u=(u_{1} ,...,u_{n} ):f(u)=y\}. \end{array} $$
(27)

Remark 2

a) For some PFSs- A 1,..,A n and a function- f, the positive degree, neutral degree and negative degree of the PFS- f(A 1,..,A n ) are

$$\mu_{B} \left(y \right)=\left\{\begin{array}{l} \bigvee\limits_{D(y)} \left(\bigwedge\limits_{i=1}^{n} \mu_{A_{i}} (\mathrm{u}_{i})\right)\quad \textit{if } f^{-1}(y)\ne 0 \\ 0\quad \textit{if } f^{-1}(y)=0 \end{array}\right., $$
$$\eta_{B} \left(y \right)=\left\{ \begin{array}{l} \bigwedge\limits_{D(y)} \left(\bigwedge\limits_{i=1}^{n} \eta_{A_{i} } (\mathrm{u}_{i})\right)\quad \textit{if } f^{-1}(y)\ne 0 \\ 0\quad \textit{if } f^{-1}(y)=0 \end{array} \right., $$
$$\nu_{B} \left(y \right)=\left\{ \begin{array}{l} \bigwedge\limits_{D(y)} \left(\bigvee\limits_{i=1}^{n} \nu_{A_{i} } (\mathrm{u}_{i})\right)\quad \textit{if } f^{-1}(y)\ne 0 \\ 1\quad \textit{if } f^{-1}(y)=0 \end{array} \right., $$

where D(y)=f −1(y)={u=(u 1,...,u n ):f(u)=y}.

b) It is obvious that the product operations of the PFSs in Definition 4 are a special case of the Zadeh extension principle for PFS in Definition 7. We will prove this remark as follows.

Proof

Consider the Cartesian product in (21). For A,B∈P F S(X), assume that U 1=U 2=X, z 1=A,z 2=B and f is a bijective then,

$$\begin{array}{@{}rcl@{}} \mu_{f(A,B)} \left(y \right)&=&\mu_{A\times_{2} B} \left(y \right)\\ &=&\left\{ \begin{array}{l} \bigvee\limits_{D(y)} (\mu_{A} (\mathrm{u}_{1})\wedge \mu_{B} (\mathrm{u}_{2}))\quad \textit{if } f^{-1}(y)\ne 0 \\ 0\quad \textit{if } f^{-1}(y)=0 \end{array} \right.\\ &=&\mu_{A} (\mathrm{u}_{1})\wedge \mu_{B} (\mathrm{u}_{2}), \end{array} $$
$$\begin{array}{@{}rcl@{}} \nu_{f(A,B)} \left(y \right)&=&\nu_{A\times_{2} B} \left(y \right)=\gamma_{A} \left({u_{1} } \right)\vee \gamma_{B} \left({u_{2} } \right),\\ \eta_{f(A,B)} \left(y \right)&=&\eta_{A\times_{2} B} \left(y \right)=\eta_{A} \left({u_{1} } \right)\bigwedge \eta_{B} \left({u_{2} } \right), \end{array} $$

where D(y)=f −1(y)={u=(u 1,u 2):f(u)=y}. Thus, A×2 B is a special case of the Zadeh extension principle for PFS in Definition 7. Similarly, for A,B∈P F S(X), A×1 B is a special case of the Zadeh extension principle for PFS in Definition 7 with the product t-norm instead of the minimum t-norm.

3 Picture inference system

Picture inference system including design and learning phase is discussed in this section. The design of PIS is given in Section 3.1. Section 3.2 shows the learning method for PIS.

3.1 PFS design

According to Definition 1, PFS constitutes of three degrees of positive, neutral and negative memberships simulating different states of human’s feeling such as agree, neutral and disagree. Using the three degrees, it is convenient to estimate and make better approximation for FIS. In this section, a novel fuzzy inference system on PFS called picture inference system (PIS) including the design based on the membership graph and the general picture inference scheme is proposed. The advantage of the new system is that the set of rules can be reused without any change. The rule set is exactly the same, but the inference is more complex and requires more effort to deal with other degrees. Each rule generates a firing degree with three equivalent values namely positive, neutral and negative. There is no clear method to combine them or to use them for defuzzification or aggregation step so that in this section those steps are invoked to gain the crisp value.

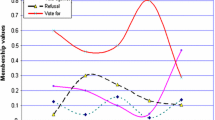
In a classic fuzzy system, each linguistic variable is represented by a membership function that generates a membership degree when the corresponding input variable is given a crisp value. In the new model, to be able to gain three values as mentioned above, a membership graph that is the combination of three lines giving a visual view of each degree is used. Figure 2 shows the membership graph where the lowest, the medium and the highest lines respectively expressed the positive, neutral and negative degree. For simplicity, it is assumed that these lines use the same form of function. In the other words, the Gaussian function with a common center and different widths is used for the lines. There are some reasons for us to construct such the graph. In real life as in Example 1, the graph could be a good approximation for elections where the number of people who vote for is the largest at the center and the number of people who abstain and vote against are quite low. In weather nowcasting, the membership graph is useful to demonstrate the main direction and the right and left expansion. Herein, the orientations in next hours are dependent on both the main direction and expansions of the current state with equivalent probabilities. In two sides of the center, the number of people who vote for decreases significantly, the number of people who abstain increases slightly and then decreases, and the number of people who vote against only increases as the opposite idea is getting sharp. Visually, the red area in Fig. 2 represents a normal membership degree.

Fig. 2
figure 2

The membership graph of PFS where (μ,η,ν) are the positive , neutral and negative degrees

Full size image

The formulae for the positive, neutral and negative degrees are expressed in (29–31) respectively.

$$ \mu_{A} (x)=\exp \left(-\frac{(x-c)^{2}}{2\sigma_{\mu }^{2} }\right), $$
(28)
$$ \eta_{A} (x)=\exp \left(-\frac{(x-c)^{2}}{2\sigma_{\eta }^{2} }\right)-\mu_{A} (x), $$
(29)
$$ \nu_{A} (x)=1-\exp \left(-\frac{(x-c)^{2}}{2\sigma_{\nu }^{2} }\right), $$
(30)

where c is the center of all three functions, σ μ (resp. σ η σ ν ) is the width value (i.e., the standard deviation) of positive (resp. neutral, negative ) function. From now on, for shorter denotation, the membership graph is denoted as set three functions - (f(x), g(x), h(x)) that describe three lines in the graph. It is clear that

$$ \mu_{A} (x)=f_{A} (x), $$
(31)
$$ \eta_{A} (x)=g_{A} (x)-f_{A} (x), $$
(32)
$$ \nu_{A} (x)=1-g_{A} (x). $$
(33)

The general picture inference scheme is described in Fig. 3

Fig. 3
figure 3

General picture inference scheme where (1..4) refer to steps

Full size image

Some steps are drawn as follows.

Step1: :

Compute the positive, the neutral and the negative degrees using the membership graph.

Obviously, with n crisp values of one vector input, each rule generates n sets of three degrees. To extract the firing strength of each rule, the following formulae (35–37) are used.

$$ \mu_{0}^{(r)} =\min\limits_{j} (\mu_{j}^{(r)} (x)), $$
(34)
$$ \eta_{0}^{(r)} =\min\limits_{j} (\eta_{j}^{(r)} (x)), $$
(35)
$$ \nu_{0}^{(r)} =\max\limits_{j} (\nu_{j}^{(r)} (x)). $$
(36)

In these formulae, r is the index of rule and j is the index of variable. Remember that the operations of three formulae are presented in [9], which guarantee the property (6).

Step 2: :

Distribute the neutral degree to the positive and negative degrees.

After extracting the firing strength, it is required to defuzzify them into a single crisp value. People who abstain do not either vote for or vote against; hence they are divided into half: one for the group of people who vote for, one for the group of people who vote again. As apply the idea in our model, we gain:

$$ \nu^{(r)}=\textit{v}_{0}^{(r)} +\frac{\eta_{0}^{(r)} }{2}, $$
(37)
$$ \mu^{(r)}=\mu_{0}^{(r)} +\frac{\eta_{0}^{(r)} }{2}. $$
(38)

In formulae (38–39), μ (r),ν (r) are the final positive and negative degrees. Next, those values are mixed and defuzzified by formula (40), which in essence is the weighted average method.

$$ y^{(r)}=\frac{\mu^{(r)}.C_{\mu }^{(r)} +\nu^{(r)}.C_{\nu }^{(r)} }{\mu^{(r)}+\nu^{(r)}}. $$
(39)
Step 3: :

Find the positive and negative defuzzification values.

In Fig. 3, \(C_{\mu }^{(r)} ,C_{\nu }^{(r)} \) are the defuzzification values associated with rule r-th. In the Mamdani model, \(C_{\mu }^{(r)} ,C_{\nu }^{(r)} \) are constants; in the Sugeno model, they can be constants or the values computed from defuzzification. Denote \(C_{\mu }^{r} \) (\(C_{\nu }^{r}\)) is the positive (negative) defuzzification value. It is clear that the power of fuzzy systems is from the parameters that make up the systems, but fuzzy systems are affected to the initial values of parameters. Therefore, picking up suitable defuzzification values should be taken into consideration. The process is presented for all architectures as follows.

  • In the Mamdani model:

$$ C_{\nu }^{(r)} =\frac{\sum\limits_{p,\textit{Label}(p)\ne \textit{Label}(r)} {C_{\mu }^{(p)} } }{L-1}, $$
(40)

where L is the number of labels of the output variable. Formula (41) means that \(C_{\nu }^{(r)} \) is set to the average of other \(C_{\mu }^{(p)} \) having different labels.

  • In the Sugeno model:

The recipe can be reused if many rules share the same label of defuzzification. If each rule has its own function, the following strategy is applied.

$$ f^{(r)}(x)=\frac{\sum\limits_{p\ne r} {f^{(p)}} (x)}{R-1}. $$
(41)

Again, the upper indices r and p are indexed of a rule. The positive and negative defuzzification values are calculated using defuzzification function. Picking up initial defuzzification parameters is not simple; fortunately, they can be adjusted easily in the learning phase.

  • In the Tsukamoto model:

The negative defuzzification functions are not needed to find because the classic model often consists of two opposite monotonic functions with respect to two terms of the linguistic output variable. For each rule, we can find the negative defuzzification value using the opposite function to the function of the current rule.

Step 4: :

Aggregate to find the crisp value of output.

What we have now is the crisp value for one rule only. To mix all these crisp values, the following formulae are used.

$$ y=\frac{\sum\limits_{r} {y^{(r)}(\mu^{(r)}+\nu^{(r)})} }{\sum\limits_{r} {(\mu^{(r)}+\nu^{(r)})} }. $$
(42)

Rewrite (43) as,

$$ y=\frac{\sum\limits_{r} {(\mu^{(r)}.C_{\mu }^{(r)} +\nu^{(r)}.C_{\nu }^{(r)} )} }{\sum\limits_{r} {(\mu^{(r)}+\nu^{(r)})} }. $$
(43)

3.2 Learning phase

In this section, the learning phase in PIS is discussed. Learning is an important process to adjust parameters to build up a well-approximated model. There are existing methods for learning in FIS such as the back-propagation, which is a powerful tool to train. However in our case, it is possible that constrain (6) is violated throughout the learning process. In Section 3.1, we use the membership graph with the following conditions being held to guarantee constraint (6).

$$ \sigma_{\mu } \le \sigma_{\eta } \le \sigma_{\nu } , $$
(44)

where σ μ ,σ η ,σ ν are the width values of positive, neutral, negative functions in formulae (29–31), respectively. These values follow the rule in formulae (46–47) where |α|,|β| are absolute values of numbers.

$$ \sigma_{\eta } =\sigma_{\mu } (1+\vert \alpha \vert ), $$
(45)
$$ \sigma_{\nu } =\sigma_{\eta } (1+\vert \beta \vert ). $$
(46)

It seems that the requirement is met but the system may not run smoothly since the derivatives in back-propagation must be computed. Thus, smooth functions like square values in formulae (48–49) should be used instead of absolute values.

$$ \sigma_{\eta } =\sigma_{\mu } (1+\alpha^{2}), $$
(47)
$$ \sigma_{\nu } =\sigma_{\eta } (1+\beta^{2}). $$
(48)

Finally, in learning process, some parameters such as the centers c, the width μ of positive degree and the scales α and β for each linguistic term have to be optimized. We now present here two main steps and formulae of learning. If denoting the index of input vector as i, the index of rule as r, the index of input variable as j and the input of membership function as k then \(\mu _{jk}^{(ir)} \) is the positive degree of variable j in input vector i with the rule- r and the index of membership function −k. Note that k is determined through r and j as in the formula (50).

$$ k=R(r,j). $$
(49)

R is a matrix that represents the rule set of the dataset implying relationship between three indices r, j, k.

3.2.1 Phase 1: learning centers, widths and scales

We start the learning phase with the definition of error of each input vector.

$$ e_{i} =y_{d}^{(i)} -y^{(i)}, $$
(50)

where \(y_{d}^{(i)} \) is the desired output and y (i) is the output calculated from system. The objective function is,

$$ \overline{E} =\frac{1}{2N}\sum\limits_{i} {{e_{i}^{2}}} . $$
(51)

N is the number of input vectors. Taking the derivative of (52), we have

$$ \frac{\partial \overline E }{\partial y^{(i)}}=\frac{-e_{i} }{N}. $$
(52)

The partial derivatives of y (i) with respect to μ (ir)and ν (ir) are,

$$\begin{array}{@{}rcl@{}} \frac{\partial y^{(i)}}{\partial \mu^{(ir)}}\!\!\!&=\!\!&\!\frac{\partial \frac{\sum\limits_{r} {(\mu^{(ir)}.C_{\mu }^{(ir)} +\nu^{(ir)}.C_{\nu }^{(ir)} )} }{\sum\limits_{r} {(\mu^{(ir)}+\nu^{(ir)})} }}{\partial \mu^{(ir)}} \\ &\!=\!\!&\!\!\frac{C_{\mu }^{(ir)}\! \sum\limits_{r} {\!(\mu^{(ir)}\!+\!\nu^{(ir)})} \!-\!\sum\limits_{r} {\!(\mu^{(ir)}\!.C_{\mu }^{(ir)} \!+\!\nu^{(ir)}.C_{\nu }^{(ir)} )} }{\left({\sum\limits_{r} {(\mu^{(ir)}+\nu^{(ir)})} } \right)^{2}} \\ &=&\!\!\frac{\frac{C_{\mu }^{(ir)} \sum\limits_{r} {(\mu^{(ir)}+\nu^{(ir)})} }{\sum\limits_{r} {(\mu^{(ir)}+\nu^{(ir)})} }-\frac{\sum\limits_{r} {(\mu^{(ir)}.C_{\mu }^{(ir)} +\nu^{(ir)}.C_{\nu }^{(ir)} )} }{\sum\limits_{r} {(\mu^{(ir)}+\nu^{(ir)})} }}{\sum\limits_{r} {(\mu^{(ir)}+\nu^{(ir)})} } \\ &=&\!\!\frac{C_{\mu }^{(ir)} -y^{(r)}}{\sum\limits_{r} {\mu^{(ir)}+\nu^{(ir)}} }, \end{array} $$
(53)

Analogously:

$$ \frac{\partial y^{(i)}}{\partial \nu^{(ir)}}=\frac{y^{(r)}-C_{\nu }^{(ir)} }{\sum\limits_{r} {\mu^{(ir)}+\nu^{(ir)}}}. $$
(54)

From formulae (38–39), it follows that

$$ \frac{\partial \mu^{(ir)}}{\partial \mu_{0}^{(ir)}}=1, $$
(55)
$$ \frac{\partial \nu^{(ir)}}{\partial \nu_{0}^{(ir)}}=1. $$
(56)

From (54–57), we have

$$\begin{array}{@{}rcl@{}} \frac{\partial \overline E }{\partial \mu_{0}^{(ir)} }&=&\frac{\partial \overline E }{\partial y^{(i)}}\frac{\partial y^{(i)}}{\partial \mu^{(ir)}}\frac{\partial \mu^{(ir)}}{\partial \mu_{0}^{(ir)} }\\ &=&\frac{-e_{i} }{N}\frac{y^{(r)}-C_{\mu }^{(ir)} }{\sum\limits_{r} {\mu^{(ir)}+\nu^{(ir)}} }, \end{array} $$
(57)

Analogously

$$ \frac{\partial \overline E }{\partial \nu_{0}^{(ir)} }=\frac{-e_{i} }{N}\frac{C_{\nu }^{(ir)} -y^{(r)}}{\sum\limits_{r} {\mu^{(ir)}+\nu^{(ir)}}}. $$
(58)

From formulae (38–39), we obtain

$$ \frac{\partial \overline E }{\partial \eta_{0}^{(ir)} }=\frac{1}{2}\left(\frac{\partial \overline E }{\partial \mu_{0}^{(ir)} }+\frac{\partial \overline E }{\partial \nu_{0}^{(ir)} }\right). $$
(59)

Note that

$$ \frac{\partial \mu_{0}^{(ir)}}{\partial \mu_{jk}^{(ir)} }=\left\{ \begin{array}{l} 1,\textit{if }\,\mu_{0}^{(ir)}=\min\limits_{j} (\,\mu_{jk}^{(ir)} ) \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\textit{otherwise} \end{array}\right., $$
(60)
$$ \frac{\partial \eta_{0}^{(ir)}}{\partial \eta_{jk}^{(ir)} }=\left\{ \begin{array}{l} 1,\textit{if }\,\eta_{0}^{(ir)}=\min\limits_{j} (\,\eta_{jk}^{(ir)} ) \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\textit{otherwise} \end{array} \right. $$
(61)
$$ \frac{\partial \nu_{0}^{(ir)}}{\partial \nu_{jk}^{(ir)} }=\left\{ \begin{array}{l} 1,\textit{if }\,\nu_{0}^{(ir)}=\max\limits_{j} (\,\nu_{jk}^{(ir)} )\\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\textit{otherwise} \end{array} \right.. $$
(62)

The partial derivatives with respect to center c j k are expressed in formulae (64–66). Note that the Gaussian functions are used where σ j k represents for the width of positive function.

$$\begin{array}{@{}rcl@{}} \frac{\partial \mu_{jk}^{(ir)} }{\partial c_{jk} }&=&\exp \left({-\frac{\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\sigma_{jk}^{2} }} \right)\frac{(x_{j}^{(i)} -c_{jk} )}{\sigma_{jk}^{2} }\\ &=&\mu_{jk}^{(ir)} \frac{(x_{j}^{(i)} -c_{jk} )}{\sigma_{jk}^{2} }, \end{array} $$
(63)
$$\begin{array}{@{}rcl@{}} \frac{\partial \eta_{jk}^{(ir)} }{\partial c_{jk} }\!&=&\!\frac{\partial \left({\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)-\exp \left({-\frac{\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\sigma_{jk}^{2} }} \right)} \right)}{\partial c_{jk} }\\ &=&\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)\frac{\left({x_{j}^{(i)} -c_{jk} } \right)}{\left({(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}\\&&-\frac{\partial \mu_{jk}^{(ir)} }{\partial c_{jk} }, \end{array} $$
(64)
$$\begin{array}{@{}rcl@{}} \frac{\partial \nu_{jk}^{(ir)} }{\partial c_{jk} }&=&\frac{\partial \left({1-\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)} \right)}{\partial c_{jk} }\\[-2pt] &=&-\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)\\[-2pt] &&\frac{(x_{j}^{(i)} -c_{jk} )}{\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}. \end{array} $$
(65)

The upgrade scheme for center c j k is,

$$\begin{array}{@{}rcl@{}} \Delta c_{jk} &=&-\eta \frac{\partial \overline E }{\partial c_{jk} }\\[-2pt] &=&-\eta \left(\sum\limits_{i,r} {\frac{\partial \overline E }{\partial \mu_{0}^{(ir)} }} \frac{\partial \mu_{0}^{(ir)} }{\partial c_{jk} }+\sum\limits_{i,r} {\frac{\partial \overline E }{\partial \eta_{0}^{(ir)} }} \frac{\partial \eta_{0}^{(ir)} }{\partial c_{jk} }\right.\\[-2pt] &&\left.+\sum\limits_{i,r} {\frac{\partial \overline E }{\partial \nu_{0}^{(ir)} }} \frac{\partial \nu_{0}^{(ir)} }{\partial c_{jk} } \right)\\[-2pt] &=&-\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \mu_{0}^{(ir)} }\frac{\partial \mu_{0}^{(ir)}}{\partial \mu_{jk}^{(ir)} }} \frac{\partial \mu_{jk}^{(ir)} }{\partial c_{jk} }\\[-2pt] &&+-\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \eta_{0}^{(ir)} }\frac{\partial \eta_{0}^{(ir)}}{\partial \eta_{jk}^{(ir)} }} \frac{\partial \eta_{jk}^{(ir)} }{\partial c_{jk} }\\[-2pt] &&+-\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \nu_{0}^{(ir)} }\frac{\partial \nu_{0}^{(ir)}}{\partial \nu_{jk}^{(ir)} }} \frac{\partial \nu_{jk}^{(ir)} }{\partial c_{jk} } \end{array} $$
(66)

where η is learning rate. Similarly, the partial derivatives of three types of degrees with respect to width σ j k are,

$$\begin{array}{@{}rcl@{}} \frac{\partial \mu_{jk}^{(ir)} }{\partial \sigma_{jk} }&=&\frac{\partial \exp \left({-\frac{\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\sigma_{jk}^{2} }} \right)}{\partial \sigma_{jk} } \\[-2pt] &=&\exp \left({-\frac{\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\sigma_{jk}^{2} }} \right).\frac{\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{\sigma_{jk}^{3} }\\[-2pt] &=&\mu_{jk}^{(ir)} \frac{(x_{j}^{(i)} -c_{jk} )^{2}}{\sigma_{jk}^{3} }, \end{array} $$
(67)
$$\begin{array}{@{}rcl@{}} \frac{\partial \eta_{jk}^{(ir)} }{\partial \sigma_{jk} }\!&=&\!\frac{\partial \left({\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)-\exp \left({-\frac{\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\sigma_{jk}^{2} }} \right)} \right)}{\partial \sigma_{jk} }\\[-2pt] &=&\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)\frac{\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{\left({(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{3}}\\[-2pt] &&(1+\alpha_{jk}^{2} )-\frac{\partial \mu_{jk}^{(ir)} }{\partial \sigma_{jk} }, \end{array} $$
(68)
$$\begin{array}{@{}rcl@{}} \frac{\partial \nu_{jk}^{(ir)} }{\partial \sigma_{jk} }\!\!&=&\!\!\frac{\partial \left({1-\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)} \right)}{\partial \sigma_{jk} }\\[-2pt] \!\!&=&\!\!-\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)\\[-2pt] &&\frac{(x_{j}^{(i)} -c_{jk} )^{2}}{\!\!\!\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{3}}(1+\alpha_{jk}^{2} )(1\!+\!\beta_{jk}^{2} ). \end{array} $$
(69)

Similar to formula (63), the upgrade scheme for width σ j k is,

$$\begin{array}{@{}rcl@{}} \Delta \sigma_{jk} =-\eta \frac{\partial \overline E }{\partial \sigma_{jk} }&=&-\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \mu_{0}^{(ir)} }\frac{\partial \mu_{0}^{(ir)}}{\partial \mu_{jk}^{(ir)} }} \frac{\partial \mu_{jk}^{(ir)} }{\partial \sigma_{jk} }\\[-2pt] &&+-\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \eta_{0}^{(ir)} }\frac{\partial \eta_{0}^{(ir)}}{\partial \eta_{jk}^{(ir)} }} \frac{\partial \eta_{jk}^{(ir)} }{\partial \sigma_{jk} }\\[-2pt] &&+-\,\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \nu_{0}^{(ir)} }\frac{\partial \nu_{0}^{(ir)}}{\partial \nu_{jk}^{(ir)} }} \frac{\partial \nu_{jk}^{(ir)} }{\partial \sigma_{jk} } \end{array} $$
(70)

The scale α appears in neutral and negative degrees only so that the positive degree can be ignored in this case.

$$\begin{array}{@{}rcl@{}} \frac{\partial \eta_{jk}^{(ir)} }{\alpha_{jk} }\!&=&\!\frac{\partial \left( {\exp \left( {\frac{-\left( {x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left( {(1+\alpha_{jk}^{2})\sigma_{jk} } \right)^{2}}} \right)-\exp \left( {-\frac{\left( {x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\sigma_{jk}^{2} }} \right)} \right)}{\partial \sigma_{jk} }\nonumber\\[-1pt] \!&=&\!\exp \left( {\frac{-\left( {x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left( {(1+\alpha_{jk}^{2})\sigma_{jk} } \right)^{2}}} \right)\frac{(x_{j}^{(i)} -c_{jk} )^{2}}\nonumber\\[-1pt] &&{\left( {(1+\alpha_{jk}^{2})\sigma_{jk} } \right)^{3}}\sigma_{jk} 2\alpha_{jk} , \end{array} $$
(71)
$$\begin{array}{@{}rcl@{}} \frac{\partial \nu_{jk}^{(ir)} }{\alpha_{jk} }\!&=&\!\frac{\partial \left({1-\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)} \right)}{\partial \alpha_{jk} }\\\!&=&\!-\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)\\&&\frac{(x_{j}^{(i)} -c_{jk} )^{2}}{\!\!\!\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{3}}\sigma_{jk} (1+\beta_{jk}^{2} )2\alpha_{jk} . \end{array} $$
(72)

Similarly to formula (71), the upgrade scheme of α j k is,

$$\begin{array}{@{}rcl@{}} \Delta \alpha_{jk} =-\eta \frac{\partial \overline E }{\partial \alpha_{jk} }&=&-\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \eta_{0}^{(ir)} }\frac{\partial \eta_{0}^{(ir)}}{\partial \eta_{jk}^{(ir)} }} \frac{\partial \eta_{jk}^{(ir)} }{\partial \alpha_{jk} }\\&&+-\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \nu_{0}^{(ir)} }\frac{\partial \nu_{0}^{(ir)}}{\partial \nu_{jk}^{(ir)} }} \frac{\partial \nu_{jk}^{(ir)} }{\partial \alpha_{jk} } \end{array} $$
(73)

Similarly, the partial derivative with respect to β j k is,

$$\begin{array}{@{}rcl@{}} \frac{\partial \nu_{jk}^{(ir)} }{\beta_{jk} }\!&=&\!\frac{\partial \left({1-\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)} \right)}{\partial \beta_{jk} }\\ \!&=&\!-\exp \left({\frac{-\left({x_{j}^{(i)} -c_{jk} } \right)^{2}}{2\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{2}}} \right)\\ &&\frac{(x_{j}^{(i)} -c_{jk} )^{2}}{\!\!\left({(1+\beta_{jk}^{2} )(1+\alpha_{jk}^{2} )\sigma_{jk} } \right)^{3}}\sigma_{jk} (1+\alpha_{jk}^{2} )2\beta_{jk} . \end{array} $$
(74)

Finally, we get the upgrade scheme for β j k which is similar to the upgrade scheme of α j k .

$$\begin{array}{@{}rcl@{}} \Delta \beta_{jk} =-\eta \frac{\partial \overline E }{\partial \beta_{jk} }=\eta \sum\limits_{i,r} {\frac{\partial \overline E }{\partial \nu_{0}^{(ir)} }\frac{\partial \nu_{0}^{(ir)}}{\partial \nu_{jk}^{(ir)} }} \frac{\partial \nu_{jk}^{(ir)} }{\partial \beta_{jk} }. \end{array} $$
(75)

3.2.2 Phase 2: Learning defuzzification parameters

It is infeasible if we ignore optimizing the positive and negative defuzzification parameters. This step is very simple, not time-consuming and quite trivial so that we do not mention here. The only thing has to be kept in mind is that optimizing can be different between the Mamdani and Sugano models in determining negative.

Being noted that initializing the parameter in FIS is much simpler than in PIS, a trick that could be used to improve the two-step learning phase above is to initialize parameters from trained FIS which means picking up a very small value of α and a very large value of β. The following steps describe such the improvement.

Step 1: :

Training positive functions.

In this step we actually train the center and width.

Step 2: :

Training defuzzification parameters corresponding to positive degrees.

Step 3: :

Training the height of each positive function.

In FIS, each membership function has the same height value, e.g. 1. A height value is added to the membership function as follows.

$$ \mu_{0} (x)=h_{\mu } \exp \left(-\frac{(x-c)^{2}}{2\sigma_{\mu }^{2}}\right), $$
(76)

where h μ is height of the positive function, c is center of all three functions and σ μ is width of the positive function. Each function should have its own height value, which aims to adjust the rule set and fixes the relation between rules.

Step 4: :

Initializing neutral degrees.

At first, neutral values are randomly set up and then repeated many times until a set of degrees that gives less error than that of the previous step is found. Neutral degrees do not need to be too small so that they are initialized with sizes of positive degrees. It is obvious that neutral degrees are equally distributed to positive and negative degrees so no matter how large neutral values are, positive (resp. negative) degrees still have large (resp. small) values. The neutral degree function is defined as follows,

$$ \eta_{0} (x)=h_{\eta } \mu_{0} (x), $$
(77)

where h η is height of neutral function.

Step 5: :

train neutral degrees.

This step trains the raw neutral degrees.

Step 6: :

Initialize and train the original negative degrees.

Since the minimum (resp. maximum) operator is used on positive (resp. negative) degrees, it is required to set up a very small value of the negative degree by some methods such as the triangular function as in formula (79).

$$ v_{0} (x)=h_{v} (1-f_{\Delta } (x,c,\sigma_{v} )), $$
(78)

where f Δ is a symmetric triangular membership function with center c and width σ ν .

$$ f_{\Delta } (x,c,\sigma_{v} )=\left\{\begin{array}{cl} 0 & \textit{if }\,x<c-\sigma_{v} \\ \dfrac{x-c+\sigma_{v} }{\sigma_{v} }& \textit{if }\,c-\sigma_{v} \le x<c\\ \dfrac{-x+c+\sigma_{v} }{\sigma_{v}}&\textit{if }\,c\le x<c+\sigma_{v} \\ 0&\textit{if }\,c+\sigma_{v} \le x \end{array}\right. $$
(79)

c is center of the three functions and σ ν is width of the negative function.

Step 7: :

Train the defuzzification parameter corresponding to negative degrees.

After having all degrees, the last defuzzification parameters are trained accordingly.

By these steps, we are able to train parameters of the PIS model. Note that after the learning phase, some membership values could be negative. We have to control this by checking the learning strictly, for example setting up the absolute values for those negative memberships after each round of height learning. The problem that the sum of memberships can be greater than 1 can be fixed by normalization.

3.3 Remarks

Although PIS is more advantages than FIS, there are some counter-examples showing the reverse. Consider an example: x 1+x 2=y with x 1,x 2∈[0,10] and 4 fuzzy rules:

$$\begin{array}{@{}rcl@{}} \text{R1:}&&\text{ If } x_{1} \text{ is small and } x_{2} \text{ is small then } y \text{ is small}.\\ \text{R2:}&&\text{ If } x_{1} \text{ is small and } x_{2} \text{ is large then } y \text{ is medium}.\\ \text{R3:}&&\text{ If } x_{1} \text{ is large and } x_{2} \text{ is small then } y \text{ is medium}.\\ \text{R4:}&&\text{ If } x_{1} \text{ is large and } x_{2} \text{ is large then } y \text{ is large}. \end{array} $$
(80)

Assume that the membership functions for those rules are:

$$\begin{array}{@{}rcl@{}} \mu_{SMALL} (x_{1} )\!&=&\!\mu_{SMALL} (x_{2} )\!=\!\left\{\begin{array}{ccc} 1 & \textit{if} & {x<0} \\ {1-0.1x} & \textit{if} & {0\le x\le 10} \\ 0 & \textit{if} & {10<x} \end{array}\right.\\ \!\!\mu_{LARGE} \!(x_{1} )\!&=&\!\mu_{LARGE} (x_{2} )\!=\!\left\{ \begin{array}{ccc} 0 & \textit{if} & {x<0} \\ \!{0.1x} & \textit{if} & {0\le x\le 10} \\ 1 & \textit{if} & {10<x} \end{array}\right.\!\!\!, \end{array} $$
(81)
$$\begin{array}{@{}rcl@{}} \mu_{SMALL} (y)&=&\left\{ \begin{array}{ccc} 1 & \textit{if} &{y<0} \\ {1-0.05y} & \textit{if} &{0\le y\le 20} \\ 0 & \textit{if} &{20<y} \end{array} \right.\\ \mu_{MEDIUM} (y)&=&\left\{\begin{array}{ccc} 0 & \textit{if} & {y<0} \\ {0.1y} & \textit{if} & {0\le y<10} \\ {2-0.1y} & \textit{if} & {10\le y<20} \\ 0 & \textit{if} & {20\le y} \end{array}\right.\\ \mu_{LARGE} (y)&==&\left\{ \begin{array}{ccc} 0 & \textit{if} & {y<0} \\ {0.05y} & \textit{if} & {0\le y\le 20} \\ 1 & \textit{if} & {20<y} \end{array} \right.. \end{array} $$
(82)

The defuzzification values for (44) are:

Rule

C μ

C ν

R1

0

20

R2

10

20

R3

10

0

R4

20

0

Assume that the negative degree:

$$ \gamma_{\dot{{A}}} \left(x \right)=1-\mu_{\dot{{A}}} \left(x \right), \quad \forall x\in X. $$
(83)

For a discrete case: x 1=3 and x 2=7, we calculate the outputs of each rule according to the Sugeno model as follows.

Rule

μ

ν

FIS

PIS

 

μ(x 1)

ν(x 1)

min

μ(x 2)

ν(x 2)

max

C μ ∗μ

C ν ∗ν

R1

0.7

0.3

0.3

0.3

0.7

0.7

0.3*0

0.7*20

R2

0.7

0.7

0.7

0.3

0.3

0.3

0.7*10

0.3*20

R3

0.3

0.3

0.3

0.7

0.7

0.7

0.3*10

0.7*0

R4

0.3

0.7

0.3

0.7

0.3

0.7

0.3*20

0.7*0

Then, the outputs calculated by FIS and PIS are:

$$ \text{FIS} = \frac{0.3\ast 0+0.7\ast 10+0.3\ast 10+0.3\ast 20}{0.3+0.7+0.3+0.3}=10 $$
(84)
$$ \text{PIS} \!=\! \frac{0.7\ast 20+0.3\ast 20+0.7\ast 0+0.7\ast 0}{0.7+0.3+0.7+0.7}=8.33 $$
(85)

The accurate result of this case is 10, which is identical to that of FIS. This clearly shows that FIS is better than PIS in this example. FIS performs better than PIS because it only uses the positive degree, which is well-oriented by the data. In real life situations where data may be variant and complex as shown in Example 1 and the weather nowcasting problem (the negative and neutral memberships appear therein), PIS is more effective than FIS because it can handle these membership degrees concurrently. In the next section, we will validate the performance of PIS through experiments.

4 Evaluation

4.1 An illustration on the Lorenz system

Control is a practical area and there are various investigations on solving the control problem using fuzzy systems. In this section, PIS is applied to solve a classic control problem - the Lorenz system defined below.

$$ \frac{dx}{dt}=\sigma (y-x), $$
(86)
$$ \frac{dy}{dt}=x(\rho -z)-y, $$
(88)
$$ \frac{dz}{dt}=xy-\beta z, $$
(89)

where σ, ρ, β are positive constants and often set as: σ=10, ρ=28, β=8/3 [1, 43]. It is noted that the system has an equilibrium point at the origin of coordinate. The component x with signal u is controlled. The change of x affects the whole system, which is proven to be asymptotically stable. Rewrite formula (87) as follow.

$$ \frac{dx}{dt}=\sigma (y-x)+u. $$
(90)

In formula (90), there are only variables x and y so that to construct the rule set we do not need to create the membership graph for z. In this part, to study and design the system that is stable under the control of signal u, the Lyapunov theory [43] is used. In that way, the system will be stable in Lyapunov sense. The dynamical system in the interval [ −40, 40] 3 is examined as well. Each variable (x or y) has 3 linguistic terms: N, Z and P.

Applying the algorithm in [43], the candidate function to design the controller is found.

$$ V(x,y,z)=\frac{1}{2}(x^{2}+y^{2}+z^{2}). $$
(91)

From the candidate function, the complete set of rules is described as follows.

$$ \text{If x is P and y is P then } u=-y(\rho +\sigma ) $$
(92)
$$ \text{If x is N and y is N then } u=-y(\rho +\sigma ) $$
(93)
$$ \text{If x is P and y is N then } u=-1 $$
(94)
$$ \text{If x is N and y is P then } u=1 $$
(95)
$$ \text{If x is P and y is Z then } u=\sigma x+\frac{y^{2}+\beta z^{2}}{x}-10(\sigma +\rho ) $$
(96)
$$ \text{If x is N and y is Z then } u=\sigma x+\frac{y^{2}+\beta z^{2}}{x}+10(\sigma +\rho ) $$
(97)
$$ \text{If x is Z and y is P then } u=-y(\rho +\sigma ) $$
(98)
$$ \text{If x is Z and y is N then } u=-y(\rho +\sigma ) $$
(99)
$$ \text{If x is Z and y is Z then } u=-y(\rho +\sigma ) $$
(100)

where N, Z, P are the negative, zero and the positive degrees respectively. The Gaussian function is used to make the membership graph and it does not change the rules above.

This function is dependent on center c and width σ so let us denote (σ, c) instead of writing a full exponential form of the function. x and y have the same membership graph as in Table 1. In this table, the short denotations for the membership graph and Gaussian function are used. The problem needed to solve is determining the defuzzification values. This could be a problem to picture fuzzy controller because in PIS, initial parameters are adjusted by training but cannot be done as in picture fuzzy controller. In order to calculate the defuzzification values, the formulae (41–42) are used. Note that some functions are the same but they have different meanings; this is the reason we should use the formulae (41–42).

Table 1 The membership graph of linguistic term
Full size table

Recall that we do not have any idea about the parameters so that random values for centers and widths of membership graphs were chosen and expressed in Table 1. There is no exact way to know how the system runs but we can use the Runge - Kutta (RK) method especially RK-4 to approximate the states of Lorenz system. Denote

$$ X=(x,y,z)^{T}. $$
(101)

The system is rewritten as,

$$ \frac{dX}{dt}=\overset{\cdot }{X} =f(X), $$
(102)

where \(\overset {\cdot }{X}\) is the partial derivative of width respect to time. We can estimate X(t) by

$$ X_{n+1} (t)=X_{n} (t)+\frac{h}{6}\left({k_{1} +2k_{2} +2k_{3} +k_{4} } \right), $$
(103)

where X n (t) is state of the system at n th iteration . k 1,k 2,k 3,k 4 are the functions of X n (t) with different intervals. Specifically, k 1 is the function on the slope at the beginning of interval. k 2 is the function at the midpoint of interval (h/2). Likewise, k 3 is at the midpoint but starting from k 2. Lastly, k 4 is the function at the end of interval.

$$ k_{1} =f\left({X_{n} (t)} \right), $$
(104)
$$ k_{2} =f\left({X_{n} (t)+\frac{h}{2}k_{1} } \right), $$
(105)
$$ k_{3} =f\left({X_{n} (t)+\frac{h}{2}k_{2} } \right), $$
(106)
$$ k_{4} =f\left({X_{n} (t)+hk_{3} } \right). $$
(107)

The step-size (h) is a positive constant. Pick h = 0.01 and examine the system in 10 seconds. The start points are x = 20, y = 20, z = 20.

Remind that design is very important and requires careful selection. For example, if the center for Z (zero) is not equal to zero, the controller may not be able to lead the system to the equilibrium point. Thus, the comparison of the effects of two controller systems especially on the bad selection should be investigated. The first controller uses fuzzy set with the parameters shown in Table 2. Note that each term has only one membership function associated with, and the same notations described in Table 1 are used. The bad design point is the center of the term being not zero.

Table 2 Bad parameter functions for classic fuzzy controllers
Full size table

As shown in Fig. 4, because the controller has the rule set designed by Lyapunov theory, the system converges to (x, y, z) = (0.0221, 0.6178, 0.0051) that is very near to the equilibrium point.

Fig. 4
figure 4

Radius versus time of bad fuzzy controller

Full size image

The second controller uses picture fuzzy set with the bad design shown in Table 3. The results are illustrated in Fig. 5. It is clear that the system finally converges to the origin even the bad parameters are selected. Since the neutral and negative degrees are utilized, they pull the convergence point back to the actual equilibrium point. This shows the advantages of using PFS to FIS.

Fig. 5
figure 5

Radius versus time of bad picture fuzzy controller

Full size image
Table 3 Bad membership graph for picture fuzzy controller
Full size table

We need to talk about the reason why the parameters in Table 1 are chosen. Intuitively, origin is the point at which the system is stable. Moreover, it is a crisp value to make the graph for Z (zero) thin. N and P do not show any difference in Lorenz system so that the symmetric across the zero is made. It is not necessary to make the graphs of x and y identical but in the example, we would like to simplify the computation. We now have the so-called “good design” parameters.

We have shown in this example the good parameters (in Table 1) and the bad ones (in Tables 2–3) to illustrate that using PIS would result in more accurate solutions than FIS. Starting from random initial parameters, by employing the membership graph with the learning strategy of PIS, good parameters can be achieved within small amount of time. The comparisons from Figs. 6, 7, 8 and 9 show that the convergence rate under control signal of PIS is fast with x coordinate being unstable in the few first seconds but quickly stable afterward (Fig. 6). Similar facts are found for y and z coordinates and time (Figs. 7–9). This depicts the advantage of PIS.

Fig. 6
figure 6

Variable x versus time

Full size image
Fig. 7
figure 7

Variable y versus time

Full size image
Fig. 8
figure 8

Variable z versus time

Full size image
Fig. 9
figure 9

Radius versus time

Full size image

4.2 The comparative results

In Section 2.1, we have discussed the Sugeno model, which is more general and has more advantages than Mamdani’s [10, 11, 29]. Sugeno model is not only general but also very flexible with the performance of defuzzification functions. Each rule may have its own function increasing the power of the model. Therefore, this section compares PIS and FIS on the Sugeno model. The experiments are taken on the benchmark UCI Machine Learning Repository namely Housing, Iris, Glass and Breast Cancer [4]. The rule set consists of 140 rules. Constant function is not linear or higher-order. Additionally, the same function is shared for each rule to avoid over-fitting. The cross-validation method is Hold-out.

The results of the first learning iteration of PIS and FIS on Housing dataset are shown in Figs. 10 & 11, respectively. It is clear that PIS has the same power as FIS does. Note that both models are strongly affected by the initial values of parameters. If the initial values are slightly changed, the result of PIS is better than that of FIS. It is clear from the figures that the error of PIS at the first time is higher than that of FIS (resp. 9.4 vs. 6.7). However, PIS quickly reduces the error and reaches the stable state after 600 seconds (sec) while FIS needs more than 2000 sec even though it starts from better parameters. The experimental results clearly show that PIS performance is better than that of FIS.

Fig. 10
figure 10

The first learning iteration of PIS on Housing dataset

Full size image
Fig. 11
figure 11

The first learning iteration of FIS on Housing dataset

Full size image

The results of the second learning iteration of PIS and FIS are shown in Figs. 12 & 13, respectively. It is indicated that PIS performance is better than that of FIS. It takes PIS few rounds of training to get the error of 4.8, then 8000 rounds to reduce the error down to 4.66. The error difference is small but valuable because the smaller the error is, the harder the optimizing step runs. Back to FIS, it takes FIS 30 rounds to get to the optimal value and the model cannot be optimized more. In this learning step, computational time is not the problem because each row consumes a little time but preciseness matters. This gives us a hint of when to stop learning for a given error value.

Fig. 12
figure 12

The second learning iteration of PIS on Housing dataset

Full size image
Fig. 13
figure 13

The second learning iteration of FIS on Housing dataset

Full size image

By similar processes with those learning iterations, we gain the final error values of PIS and FIS on testing datasets as in Table 4.

Table 4 RMSE values of PIS to FIS in various datasets
Full size table

The findings of experiments are as follows: PIS is better than FIS in term of RMSE. Table 4 shows the compared results of PIS and FIS. It is obvious that the values of PIS are smaller than those of FIS with the reduced percentages in comparison with FIS being 15.5 %, 10.5 %, 1.2 % and 3.2 %, respectively. This clearly shows the advantages of PIS over FIS.

5 Conclusions

In this paper, we proposed picture inference system (PIS) that integrates fuzzy inference system (FIS) with picture fuzzy sets. PIS was designed based on the membership graph and the general picture inference scheme. The proposed system is adapted for all architectures such as the Mamdani fuzzy inference, the Sugeno fuzzy inference and the Tsukamoto fuzzy inference. Learning for PIS including training centers, widths, scales and defuzzification parameters is also discussed to build up a well-approximated model. The novel contribution of this paper – PIS model including the design and the learning method on picture fuzzy set was attributed to have better performance than those of FIS model. In the evaluation, the new system was validated on a classic example in control theory - the Lorenz system and on the benchmark UCI Machine Learning datasets. The findings from experimental results are as follows: i) PIS is capable to effectively perform a classic controller like the Lorenz system; ii) PIS is better than FIS in term of RMSE as shown in the experiments.

Further works of this research can be investigated in the following ways:

Firstly, other strategies of learning in PIS should be investigated. As being observed from the paper, PIS used the gradient method to train the parameters. This method has the advantage of fast processing but produces local optimal solutions. In order to achieve (global) better solutions, evolutionary algorithms such as genetic algorithm, particle swarm optimization, differential evolution and bees algorithm can be applied to improve the inference performance. For instance, the learning of parameters for the membership graph in phase 1 namely the centers, width and scales can be done through particle swarm optimization. Therein, a particle is encoded as the combination of three parameters. The swarm of particles is gradually optimized until stopping conditions hold. Analogously, the defuzzification parameters in phase 2 can be trained using harmony search. However, this must cooperate with the previous training from phase 1 in order to utilize the optimal results. This strategy initiates the idea of a hybrid training for PIS in further works.

Secondly, we should take into account the high order PIS with picture fuzzy rules. From step 3 in the description of PIS in Section 3.1, the fuzzy rule is represented and used in first order which is quite simple. In order to handle with complex control processes, high order fuzzy rules should be utilized. But more than that, as we are working on the picture fuzzy set, picture fuzzy rules should be designed and used instead of the traditional fuzzy rules. Picture fuzzy rules are characterized by three membership degrees namely the positive, neutral and negative. It is indeed necessary to take into account those degrees simultaneously in the computation. In the current PIS method, the positive, negative and neutral degrees are combined to adapt with a single output of traditional fuzzy inferences. This should be ameliorated if we would like to not only enhance the inference performance but also provide more information to the control process. Even though the empirical results of PIS are better than FIS, the combination of high order and picture fuzzy rules is a good choice to help us significantly improve the performance.

Finally, since real-life applications are often complicated; therefore how to apply and adapt the proposed PIS system to those is in high demand. In this paper, we just applied PIS to a popular control problem - the Lorenz system. When applying PIS to other ones, we should make trial-and-test of appropriate parameters as well as find appropriate functions for the membership graph. For instance, we can use Bell function for three lines in the membership graph instead of Gaussian. Similarly, the trapezoid and triangular functions can be used also. The mix between those functions is possible for certain kinds of applications. It is very useful if we can compare the performance of various membership graphs using different functions above.