Multiple-attribute decision-making based on picture fuzzy Archimedean power Maclaurin symmetric mean operators

Abstract

In this paper, a novel multiple-attribute decision-making method based on a set of Archimedean power Maclaurin symmetric mean operators of picture fuzzy numbers is proposed. The Maclaurin symmetric mean operator, power average operator, and operational rules based on Archimedean T-norm and T-conorm are introduced into picture fuzzy environment to construct the aggregation operators. The formal definitions of the aggregation operators are presented. Their general and specific expressions are established. The properties and special cases of the aggregation operators are, respectively, explored and discussed. Using the presented aggregation operators, a method for solving the multiple-attribute decision-making problems based on picture fuzzy numbers is designed. The method is illustrated through example and experiments and validated by comparisons. The results of the comparisons show that the proposed method is feasible and effective that can provide the generality and flexibility in aggregation of values of attributes and consideration of interactions among attributes and the capability to lower the negative effect of biased attribute values on the result of aggregation.

1 Introduction

Multiple-attribute decision-making (MADM) is the process of finding the best option through comprehensively assessing the values of multiple attributes of all options. There are two essential tasks in this process. One task is to describe the values of attributes and the other task is to fuse the described values to determine the best option. One of the most important tools used in the first task is fuzzy set. Among the existing different types of fuzzy sets (Bustince et al. 2016), the fuzzy set (FS) presented by Zadeh (1965) is a classic type of fuzzy sets which leverages a degree of positive membership μ (0 ≤ µ ≤ 1) to describe the degree of satisfaction. It is sufficient for fuzzy information description in some practical applications (Chen et al. 2009, 2012; Chen and Niou 2011; Chen and Chen 2014; Chen and Adam 2017; Castillo et al. 2019). However, FS is insufficient to express the fuzzy information consisting of the degrees of satisfaction, dissatisfaction, and hesitancy.

In response to this limitation, Atanassov (1986) extended FS and presented the intuitionistic fuzzy set (IFS), which provides a degree of positive membership μ and a degree of negative membership ν (0 ≤ µ ≤ 1; 0 ≤ ν ≤ 1; 0 ≤ µ + ν ≤ 1). The two degrees can, respectively, quantify the degrees of satisfaction and dissatisfaction, and therefore, the degree of hesitancy is indirectly quantified by 1 − µ − ν. Due to such capability, IFSs have been widely applied to describe attribute values in MADM. Various research topics regarding IFSs in MADM, such as calculus for IFSs (Lei and Xu 2016, 2017; Ai and Xu 2018), intuitionistic preference relations (Liao and Xu 2014; Liao et al. 2015; Zhang and Pedrycz 2017a, Zhang and Pedrycz 2018; Zhang et al. 2020), operations for IFSs (Jamkhaneh and Garg 2018; Dutta 2019; Dutta and Saikia 2019), information measures for IFSs (Chen et al. 2016a; Garg and Kumar 2018, 2019; Song et al. 2019; Tan et al. 2020), aggregation operators (AOs) of intuitionistic fuzzy numbers (IFNs) for MADM (Xu and Yager 2011; Chen and Chang 2016; Liu and Chen 2017; Liu and Tang 2018; Zhang et al. 2019; Seikh and Mandal 2019; Liu et al. 2020), and MADM methods based on IFSs (Wang and Zhang 2013; Chen et al. 2016b; Garg 2017a; Zhang and Pedrycz 2017b; Kumar and Garg 2018; Rani et al. 2019; Zeng et al. 2019), have received widespread attention.

Even though IFS has showed great capability in MADM, it cannot be used to describe more complex fuzzy information. IFS does not provide an approach to express the fuzzy information including the degree of neutrality. Aiming at this shortcoming, Hinde et al. (2007) introduced the theory of picture fuzzy set (PFS). A PFS extends an IFS with a degree of neutral membership η. Obviously, PFS is the generalisation of FS and IFS, since a PFS will reduce to a FS when its η = ν = 0 and will become an IFS if its η = 0. It is obvious that PFSs have the greatest expressive capability compared to FSs and IFSs. Because of this, PFSs and their application in MADM have also received a lot of attention. A variety of related research topics, such as correlation coefficients of PFSs (Singh 2015), distance measure of PFSs (Son 2016), picture fuzzy clustering (Thong 2016), application of PFSs in decision-making (Wang et al. 2018a, b; Ju et al. 2019), AOs of picture fuzzy numbers (PFNs) for MADM (Garg 2017b; Wei 2017, 2018; Wei et al. 2018a; Zhang et al. 2018; Jana et al. 2019; Xu et al. 2019), MADM methods based on PFSs (Wang et al. 2018a; Liang et al. 2018), and extensions of PFSs (Wei et al. 2018b; Mahmood et al. 2019; Khalil et al. 2019) are gaining importance.

MADM problems are generally solved using traditional methods or AOs. AOs are capable of solving MADM problems in a more effective way since they can produce summary values and rankings of options, and traditional methods only output rankings (Liu and Liu 2018; Liu and Wang 2018; Qin et al. 2019a, 2020a). So far, a number of MADM methods based on AOs of PFNs have been presented, such as the methods presented by Wei (2017), Garg (2017b), Wei (2018), Jana et al. (2019), Wei et al. (2018a), Zhang et al. (2018), and Xu et al. (2019). The AOs of PFNs on which these methods are based are listed in Table 1. To the best of the knowledge, there is not yet a method that has flexibility in the aggregation of values of attributes and generality in the handling of interactions of attributes and, meanwhile, can lower the negative effect of biased values of attributes.

Table 1 The AOs of PFNs on Which the Seven MADM Methods Are Based

In practical MADM problems, the preferences of decision makers usually change dynamically and various interactions always exist among different considered attributes. To generate reasonable results for these problems, the used AOs should be general and flexible enough to capture the preferences and interactions when aggregating the values of attributes (Liu and Wang 2019). Among the existing AOs of PFNs, the Archimedean WA, Archimedean OWA, and Archimedean HA operators in (Garg 2017b) can provide flexibility in the aggregation of values of attributes. But they are only applicable for the situation where all of the considered attributes are independent of each other. The weighted Heronian mean operator in (Wei et al. 2018a) and the Dombi weighted Heronian mean and Dombi weighted dual Heronian mean operators in (Zhang et al. 2018) can work normally under the condition that there are no interactions among attributes or there are interactions between two attributes. But they could produce unreasonable results when there are interactions among multiple attributes. The weighted Muirhead mean and weighted dual Muirhead mean operators in (Xu et al. 2019) can make up for this deficiency. But they are not general and flexible enough for aggregating attribute values. Besides, the attribute values are mostly evaluated by experts. The absolute objectivity of this way is usually difficult to be ensured. This means that a few experts will provide some biased attribute values (Liu and Liu 2017). To obtain reasonable aggregation results under this circumstance, it is required to lower the negative impact of biased values of attributes. However, none of the existing AOs of PFNs have such capability. Based on the analysis above, the motivations of this paper are outlined as follows:

• 1 To construct a flexible AO of PFNs, Archimedean T-norm and T-conorm (ATT) (Klement et al. 2000; Xia et al. 2012) are introduced into PFSs. The ATT operations are important tools for generalising logical conjunction and disjunction to fuzzy logic. They can be used to develop versatile rules for the operations between fuzzy numbers. The AOs using such operational rules are flexible (Liu and Wang 2019; Zhong et al. 2019a; Qin et al. 2019b, 2020b).

• 2 To make the AO general in capturing the interactions of attributes, Maclaurin symmetric mean (MSM) operator (Maclaurin 1729) is chosen as its core component. The MSM operator, a generalisation of the arithmetic average (AA) operator, Bonferroni mean (BM) operator, and geometric average (GA) operator, is a general AO for describing the interactions of the aggregated arguments. It is applicable for the situations where there are no interactions among all arguments, where there are interactions between two arguments, and where there are interactions among multiple arguments.

• 3 To make the AO capable to reduce the negative effect of unduly high or unduly low attribute values on the aggregation result, power average (PA) operator (Yager 2001) is combined with the MSM operator of PFNs under the ATT operations. The PA operator is an AO which can assign weights to the aggregated arguments via computing the degrees of support between the arguments. This makes it capable to reduce the negative effect of unreasonable argument values (Liu et al. 2018; Teng et al. 2018; Zhong et al. 2019b; Qin et al. 2020c).

In a word, the objective of the paper is to present a set of Archimedean power MSM operators of PFNs for solving the MADM problems based on PFNs. This objective is achieved via combining the MSM operator and the PA operator under the ATT operations in the context of PFSs. The major contribution of the paper is the development of an MADM method based on picture fuzzy Archimedean power MSM operators. This method can provide the generality in aggregation of values of attributes, the flexibility in handling of interactions among attributes, and the capability to lower the negative impact of biased attribute values.

The rest of the paper is organised as follows. A brief introduction of some basic concepts is provided in Sect. 2. Section 3 describes the details of the presented operators. The specific process of the proposed method is described in Sect. 4. Section 5 demonstrates and evaluates the proposed method. Section 6 ends the paper with a conclusion.

2 Preliminaries

2.1 PFS theory

PFS can be seen as the generalisation of FS (Zadeh 1965) and IFS (Atanassov 1986). Its formal definition is given by Hinde et al. (2007):

Definition 1

APFS S in a finite domain of discourse X is S = {〈x, µ_S(x), η_S(x), ν_S(x)〉 | x∈X}, where µ_S: X → [0, 1] is the degree of positive membership of x∈X to S, η_S: X → [0, 1] is the degree of neutral membership of x∈X to S, and ν_S: X → [0, 1] is the degree of negative membership of x∈X to S, such that 0 ≤ µ_S(x) + η_S(x) + ν_S(x) ≤ 1. The degree of refusal membership of x∈X to S is π_S(x) = 1 − µ_S(x) − η_S(x) − ν_S(x).

A triple 〈µ_S(x), η_S(x), ν_S(x) 〉 is called a PFN and is usually denoted as 〈µ, η, ν 〉 . Two PFNs can be compared using their score values and accuracy values. Jana et al. (2019) introduced a function to calculate the score value of a PFN and Wei (2017) introduced a function to calculate the accuracy value of a PFN:

Definition 2

Suppose α = 〈µ, η, ν 〉 is a PFN, its score value can be calculated via S(α) = 0.5 × (1 + µ − ν).

Definition 3

Suppose α = 〈µ, η, ν 〉 is a PFN, its accuracy value can be calculated via A(α) = µ + η + ν.

Based on the score and accuracy values, Wei (2017) introduced the rules for comparing two PFNs:

Definition 4

Suppose α₁ = 〈µ₁, η₁, ν₁> and α₂ = 〈µ₂, η₂, ν₂〉 are two PFNs, S(α₁) and S(α₂) are their score values, and A(α₁) and A(α₂) are their accuracy values. Then: (1) α₁ > α₂ if S(α₁) > S(α₂); (2) α₁ > α₂ if S(α₁) = S(α₂) and A(α₁) > A(α₂); (3) α₁ = α₂ if S(αα₁) = S(α₂) and A(α₁) = A(α₂).

The distance of two PFNs can be calculated using a distance measure of PFNs. Cuong (2014) introduced a normalised Hamming distance measure of PFNs:

Definition 5

Suppose α₁ = 〈µ₁, η₁, ν₁〉 and α₂ = 〈µ₂, η₂, ν₂〉 are two PFNs. Their normalised Hamming distance is d(α₁, α₂) = 0.5(|µ₁ − µ₂| + |η₁ − η₂| + |ν₁ − ν₂|).

2.2 Operational rules

Based on ATT, Garg (2017b) introduced a set of operational rules of PFNs:

Definition 6

Suppose α = 〈μ, η, ν  〉 , α₁ = 〈μ₁, η₁, ν₁ 〉 , and α₂ = 〈μ₂, η₂, ν₂ 〉 are three PFNs, and c and d are two positive real numbers. The operations of PFNs based on T(x, y) = φ⁻¹(φ(x) + φ(y)) and T^C(x, y) = ψ⁻¹(ψ(x) + ψ(y)) are defined as follows:

$$\alpha_{ 1} \oplus \alpha_{ 2} = \, < T^{\text{C}} \left( {\mu_{ 1} ,\mu_{ 2} } \right),T\left( {\eta_{ 1} ,\eta_{ 2} } \right),T\left( {\nu_{ 1} ,\nu_{ 2} } \right) > \, = \, < \psi^{ - 1} (\psi \left( {\mu_{ 1} } \right) \, + \psi \left( {\mu_{ 2} } \right)),\varphi^{ - 1} (\varphi \left( {\eta_{ 1} } \right) \, + \varphi \left( {\eta_{ 2} } \right)),\varphi^{ - 1} (\varphi \left( {\nu_{ 1} } \right) \, + \varphi \left( {\nu_{ 2} } \right)) > ,$$

(1)

$$\alpha_{ 1} \otimes \alpha_{ 2} = \, < T\left( {\mu_{ 1} ,\mu_{ 2} } \right),T^{\text{C}} \left( {\eta_{ 1} ,\eta_{ 2} } \right),T^{\text{C}} \left( {\nu_{ 1} ,\nu_{ 2} } \right) > \, = \, < \varphi^{ - 1} (\varphi \left( {\mu_{ 1} } \right) \, + \varphi \left( {\mu_{ 2} } \right)),\psi^{ - 1} (\psi \left( {\eta_{ 1} } \right) \, + \psi \left( {\eta_{ 2} } \right)),\psi^{ - 1} (\psi \left( {\nu_{ 1} } \right) \, + \psi \left( {\nu_{ 2} } \right)) > ,$$

(2)

$$c\alpha \, = \, < \psi^{ - 1} (c\psi \left( \mu \right)),\varphi^{ - 1} \left( {c\varphi \left( \eta \right)} \right),\varphi^{ - 1} \left( {c\varphi \left( \nu \right)} \right) > ,$$

(3)

$$\alpha^{d} = \, < \varphi^{ - 1} (d\varphi \left( \mu \right)),\psi^{ - 1} (d\psi \left( \eta \right)),\psi^{ - 1} (d\psi \left( \nu \right)) > .$$

(4)

2.3 MSM operator

The MSM operator was introduced by Maclaurin (1729). This operator can be formally defined as:

Definition 7

Suppose a₁, a₂, ..., a_n are n crisp numbers and k is an integer such that 1 ≤ k ≤ n. If (i₁, i₂, ..., i_k) traverse all the k-tuple combinations of (1, 2, ..., n), then

$${\text{MSM}}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) = \left( {\frac{k!(n - k)!}{n!}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\prod\limits_{h = 1}^{k} {a_{{i_{h} }} } } } \right)^{1 /k}$$

(5)

is called the MSM operator.

2.4 PA operator

The PA operator was introduced by Yager (2001). This operator can be formally defined as:

Definition 8

Suppose a₁, a₂, ..., a_n are n crisp numbers, S(a_i, a_j) = 1 − d(a_i, a_j) (i, j = 1, 2, ..., n and j ≠ i; d(a_i, a_j) is the distance between a_i and a_j) is the degree of support for a_i from a_j which satisfies 0 ≤ S(a_i, a_j) ≤ 1, S(a_i, a_j) = S(a_j, a_i), and S(a_i, a_j) ≥ S(a_p, a_q) if |a_i, a_j| ≤ |a_p, a_q|, and

$$T(a_{i} ) = \sum\limits_{j = 1,j \ne i}^{n} {S(a_{i} , \, a_{j} )} ,$$

then

$${\text{PA}}(a_{1} ,a_{2} , \ldots ,a_{n} ) = {{\sum\limits_{i = 1}^{n} {\left( {\left( {1 + T(a_{i} )} \right)a_{i} } \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{n} {\left( {\left( {1 + T(a_{i} )} \right)a_{i} } \right)} } {\sum\limits_{i = 1}^{n} {\left( {1 + T(a_{i} )} \right)} }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{n} {\left( {1 + T(a_{i} )} \right)} }}$$

(6)

is called the PA operator.

3 Archimedean power MSM operators

3.1 PFAPMSM operator

A picture fuzzy Archimedean power MSM (PFAPMSM) operator is a power MSM operator of PFNs, in which the operations are carried out via the operational rules of PFNs based on ATT. This operator can be formally defined as:

Definition 9

Suppose α₁, α₂, ..., α_n (α_i = 〈μ_i, η_i, ν_i〉 , i = 1, 2, ..., n) are n PFNs, k is an integer which meets 1 ≤ k ≤ n, α_p $\oplus$ α_q and α_p $\otimes$ α_q (p, q = 1, 2, ..., n and p ≠ q) and cα_r and α ^d_s (r, s = 1, 2, ..., n and r ≠ s; c, d > 0) are the operations of PFNs based on ATT, and S(α_p, αα_q) = 1 − d(α_p, α_q) (d(α_p, α_q) is the distance between α_p and α_q) be the degree of support for α_p from α_q which satisfies 0 ≤ S(α_p, α_q) ≤ 1, S(α_p, α_q) = S(α_q, α_p), and S(α_p, α_q) ≥ S(α_r, α_s) if |α_p− α_q| ≤ |α_r− α_s|, and

$$T(\alpha_{p} ) = \sum\limits_{q = 1,q \ne p}^{n} {S(\alpha_{p} , \, \alpha_{q} )} .$$

If (i₁, i₂, ..., i_k) traverse all the k-tuple combinations of (1, 2, ..., n), then

$${\text{PFAPMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left( {\frac{1}{{C_{n}^{k} }}\mathop \oplus \limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} \mathop \otimes \limits_{h = 1}^{k} \left( {\frac{{n\left( {1 + T(\alpha_{{i_{h} }} )} \right)}}{{\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right)} }}\alpha_{{i_{h} }} } \right)} \right)^{1 /k}$$

(7)

is called the PFAPMSM operator.

The general expression of the PFAPMSM is constructed in the following theorem:

Theorem 1

Suppose α₁, α₂, ..., α_n (α_i = < μ_i, η_i, ν_i> , i = 1, 2, ..., n) are n PFNs. Then

$${\text{PFAPMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {\mu , \, \eta , \, \nu } \right\rangle ,$$

(8)

where

$$\begin{aligned} \mu = \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \hfill \\ \eta = \psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\eta_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \hfill \\ \nu = \psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\nu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \hfill \\ \omega_{{i_{h} }} = {{\left( {1 + T(\alpha_{{i_{h} }} )} \right)} \mathord{\left/ {\vphantom {{\left( {1 + T(\alpha_{{i_{h} }} )} \right)} {\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right)} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right)} }} \hfill \\ \end{aligned}$$

and PFAPMSM^(k)(α₁, α₂, ..., α_n) is still a PFN.

The proof of this theorem is provided in App. A. The properties of the PFAPMSM operator are stated in the following theorems:

Theorem 2

(Idempotency) Suppose α₁, α₂, ..., α_n (α_i = 〈μ_i, η_i, ν_i〉 , i = 1, 2, ..., n) are n PFNs. If α_i = α = < μ_α, η_α, ν_α > for all i = 1, 2, ..., n, then PFAPMSM^(k)(α₁, α₂, ..., α_n) = α = 〈μ_α, η_α, ν_α〉 .

Theorem 3

(Commutativity) Suppose α₁, α₂, ..., α_n (α_i = 〈μ_i, η_i, ν_i >}, i = 1, 2, ..., n) are n PFNs. If (β₁, β₂, ..., β_n) is any permutation of (α₁, α₂, ..., α_n), then PFAPMSM^(k)(β₁, β₂, ..., β_n) = PFAPMSM^(k)(α₁, α₂, ..., α_n).

Theorem 4

(Boundedness). Suppose α₁, α₂, ..., α_n (α_i = 〈μ_i, η_i, ν_i〉 , i = 1, 2, ..., n) are n PFNs, α⁺ = < max(μ_i), min(η_i), min(ν_i) > , and α⁻ = < min(μ_i), max(η_i), max(ν_i) > . Then α⁻ ≤ PFAPMSM^(k)(α₁, α₂, ..., α_n) ≤ α⁺.

The proofs of these theorems are, respectively, provided in App.es B, C, and D. Some special cases of the PFAPMSM operator are as follows:

• 1 If k = 1, the PFAPMSM operator will become

  $$\left\langle {\psi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {(n\omega_{i} )\psi (\mu_{i} )} \right)} } \right), \, \varphi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {(n\omega_{i} )\varphi (\eta_{i} )} \right)} } \right), \, \varphi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {(n\omega_{i} )\varphi (\nu_{i} )} \right)} } \right)} \right\rangle = {\text{PFAPAA}}(\alpha_{1} ,\alpha_{2} ,...,\alpha_{n} ),$$

  (9)

  which is a picture fuzzy Archimedean power AA (PFAPAA) operator.

• 2 If k = 2, the PFAPMSM operator will become

  $$\begin{aligned} \left\langle {\varphi^{ - 1} \left( {\frac{1}{2}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{n(n - 1)}\sum\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\psi \left( {\varphi^{ - 1} \left( {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{1} }} )\psi (\mu_{{i_{1} }} )} \right)} \right) + \varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{2} }} )\psi (\mu_{{i_{2} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right., \hfill \\ \, \psi^{ - 1} \left( {\frac{1}{2}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{n(n - 1)}\sum\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\varphi \left( {\psi^{ - 1} \left( {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{1} }} )\varphi (\eta_{{i_{1} }} )} \right)} \right) + \psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{2} }} )\varphi (\eta_{{i_{2} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right), \hfill \\ \, \left. {\psi^{ - 1} \left( {\frac{1}{2}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{n(n - 1)}\sum\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\varphi \left( {\psi^{ - 1} \left( {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{1} }} )\varphi (\nu_{{i_{1} }} )} \right)} \right) + \psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{2} }} )\varphi (\nu_{{i_{2} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right\rangle \hfill \\ ={\text{PFAPBM}}^{(1,1)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ), \hfill \\ \end{aligned}$$

  (10)

  which is a picture fuzzy Archimedean power BM (PFAPBM) operator.

• 3 If k = n, the PFAPMSM operator will become

  $$\begin{aligned} \left\langle {\varphi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{i} )\psi (\mu_{i} )} \right)} \right)} } \right), \, \psi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{i} )\varphi (\eta_{i} )} \right)} \right)} } \right), \, \psi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{i} )\varphi (\nu_{i} )} \right)} \right)} } \right)} \right\rangle , \hfill \\ = {\text{PFAPGA}}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \hfill \\ \end{aligned}$$

  (11)

  which is a picture fuzzy Archimedean power GA (PFAPGA) operator.

The specific expressions of the PFAPMSM operator are constructed as follows:

• 1 If Algebraic T-norm and T-conorm are applied to Eq. (8), a picture fuzzy Archimedean Algebraic power MSM (PFAAPMSM) operator can be obtained as:

  $$\begin{aligned} {\text{PFAAPMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {1 - \prod\limits_{h = 1}^{k} {\left( {1 - (1 - \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} } \right)} } \right)} } \right)^{{1 /C_{n}^{k} }} } \right)^{1 /k} } \right., \hfill \\ 1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {1 - \prod\limits_{h = 1}^{k} {(1 - \eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} )} } \right)} } \right)^{{1 /C_{n}^{k} }} } \right)^{1 /k} , \, \left. {1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {1 - \prod\limits_{h = 1}^{k} {(1 - \nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} )} } \right)} } \right)^{{1 /C_{n}^{k} }} } \right)^{1 /k} } \right\rangle . \hfill \\ \end{aligned}$$

  (12)

  Some special cases of this operator are as follows:

  • (a) If k = 1, the PFAAPMSM operator will become

    $$\left\langle {1 - \prod\limits_{i = 1}^{n} {(1 - \mu_{i} )^{{\omega_{i} }} } , \, \prod\limits_{i = 1}^{n} {\eta_{i}^{{\omega_{i} }} } , \, \prod\limits_{i = 1}^{n} {\nu_{i}^{{\omega_{i} }} } } \right\rangle = {\text{PFPAA}}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ),$$

    (13)

    which is a picture fuzzy power AA (PFPAA) operator.

  • (b) If k = 2, the PFAAPMSM operator will become

    $$\begin{aligned} \left\langle {\left( {1 - \prod\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\left( {1 - \left( {1 - (1 - \mu_{{i_{1} }} )^{{n\omega_{{i_{1} }} }} } \right)\left( {1 - (1 - \mu_{{i_{2} }} )^{{n\omega_{{i_{2} }} }} } \right)} \right)}^{{\frac{1}{n(n - 1)}}} } \right)^{1 / 2} } \right., \, 1 - \left( {1 - \prod\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\left( {1 - (1 - \eta_{{i_{1} }}^{{n\omega_{{i_{1} }} }} )(1 - \eta_{{i_{2} }}^{{n\omega_{{i_{2} }} }} )} \right)}^{{\frac{1}{n(n - 1)}}} } \right)^{1 /2} , \hfill \\ \, \left. {1 - \left( {1 - \prod\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\left( {1 - (1 - \nu_{{i_{1} }}^{{n\omega_{{i_{1} }} }} )(1 - \nu_{{i_{2} }}^{{n\omega_{{i_{2} }} }} )} \right)}^{{\frac{1}{n(n - 1)}}} } \right)^{1 /2} } \right\rangle = {\text{PFPBM}}^{(1,1)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ), \hfill \\ \end{aligned}$$

    (14)

    which is a picture fuzzy power BM (PFPBM) operator.

  • (c) If k = n, the PFAAPMSM operator will become

    $$\left\langle {\prod\limits_{i = 1}^{n} {\left( {1 - (1 - \mu_{i} )^{{n\omega_{i} }} } \right)}^{1/n} , \, 1 - \prod\limits_{i = 1}^{n} {(1 - \eta_{i}^{{n\omega_{i} }} )^{1/n} ,} \, 1 - \prod\limits_{i = 1}^{n} {(1 - \nu_{i}^{{n\omega_{i} }} )^{1/n} } } \right\rangle = {\text{PFPGA}}(\alpha_{1} ,\alpha_{2} ,...,\alpha_{n} ),$$

    (15)

    which is a picture fuzzy power GA (PFPGA) operator.

• 2 If Einstein T-norm and T-conorm are applied to Eq. (8), a picture fuzzy Archimedean Einstein power MSM (PFAEPMSM) operator can be obtained as:

  $$\begin{aligned} {\text{PFAEPMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {{{\left( {2(\mu^{\prime \prime } - 1)^{1 /k} } \right)} \mathord{\left/ {\vphantom {{\left( {2(\mu^{\prime \prime } - 1)^{1 /k} } \right)} {\left( {(\mu^{\prime \prime } + 3)^{1 /k} + (\mu^{\prime \prime } - 1)^{1 /k} } \right)}}} \right. \kern-0pt} {\left( {(\mu^{\prime \prime } + 3)^{1 /k} + (\mu^{\prime \prime } - 1)^{1 /k} } \right)}}} \right., \hfill \\ {{\left( {(\eta^{\prime \prime } + 3)^{1 /k} - (\eta^{\prime \prime } - 1)^{1 /k} } \right)} \mathord{\left/ {\vphantom {{\left( {(\eta^{\prime \prime } + 3)^{1 /k} - (\eta^{\prime \prime } - 1)^{1 /k} } \right)} {\left( {(\eta^{\prime \prime } + 3)^{1 /k} + (\eta^{\prime \prime } - 1)^{1 /k} } \right)}}} \right. \kern-0pt} {\left( {(\eta^{\prime \prime } + 3)^{1 /k} + (\eta^{\prime \prime } - 1)^{1 /k} } \right)}}, \, \left. {{{\left( {(\nu^{\prime \prime } + 3)^{1 /k} - (\nu^{\prime \prime } - 1)^{1 /k} } \right)} \mathord{\left/ {\vphantom {{\left( {(\nu^{\prime \prime } + 3)^{1 /k} - (\nu^{\prime \prime } - 1)^{1 /k} } \right)} {\left( {(\nu^{\prime \prime } + 3)^{1 /k} + (\nu^{\prime \prime } - 1)^{1 /k} } \right)}}} \right. \kern-0pt} {\left( {(\nu^{\prime \prime } + 3)^{1 /k} + (\nu^{\prime \prime } - 1)^{1 /k} } \right)}}} \right\rangle , \hfill \\ \end{aligned}$$

  (16)

  where

  $$\begin{aligned} \mu^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\mu^{\prime } + 3)} \mathord{\left/ {\vphantom {{(\mu^{\prime } + 3)} {(\mu^{\prime } - 1)}}} \right. \kern-0pt} {(\mu^{\prime } - 1)}}} \right)^{{1 /C_{n}^{k} }} } ,\;\mu^{\prime } = \prod\limits_{h = 1}^{k} {\left( {{{\left( {(1 + \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} + 3(1 - \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} } \right)} \mathord{\left/ {\vphantom {{\left( {(1 + \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} + 3(1 - \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} } \right)} {\left( {(1 + \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} - (1 - \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} } \right)}}} \right. \kern-0pt} {\left( {(1 + \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} - (1 - \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} } \right)}}} \right)} , \hfill \\ \eta^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\eta^{\prime } + 3)} \mathord{\left/ {\vphantom {{(\eta^{\prime } + 3)} {(\eta^{\prime } - 1)}}} \right. \kern-0pt} {(\eta^{\prime } - 1)}}} \right)^{{1 /C_{n}^{k} }} } ,\;\eta^{\prime } = \prod\limits_{h = 1}^{k} {\left( {{{\left( {(2 - \eta_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} + 3\eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)} \mathord{\left/ {\vphantom {{\left( {(2 - \eta_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} + 3\eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)} {\left( {(2 - \eta_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} - \eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)}}} \right. \kern-0pt} {\left( {(2 - \eta_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} - \eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)}}} \right)} , \hfill \\ \nu^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\nu^{\prime } + 3)} \mathord{\left/ {\vphantom {{(\nu^{\prime } + 3)} {(\nu^{\prime } - 1)}}} \right. \kern-0pt} {(\nu^{\prime } - 1)}}} \right)^{{1 /C_{n}^{k} }} } ,\;\nu^{\prime } = \prod\limits_{h = 1}^{k} {\left( {{{\left( {(2 - \nu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} + 3\nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)} \mathord{\left/ {\vphantom {{\left( {(2 - \nu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} + 3\nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)} {\left( {(2 - \nu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} - \nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)}}} \right. \kern-0pt} {\left( {(2 - \nu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} - \nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)}}} \right).} \hfill \\ \end{aligned}$$

• 3 If Hamacher T-norm and T-conorm are applied to Eq. (8), a picture fuzzy Archimedean Hamacher power MSM (PFAHPMSM) operator can be obtained as:

  $$\begin{aligned} {\text{PFAHPMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) && = \left\langle {{{\left( {\lambda (\mu^{\prime\prime} - 1)^{1/k} } \right)} / {\left( {(\mu^{\prime\prime} + \lambda^{2} - 1)^{1/k} + (\lambda - 1)(\mu^{\prime\prime} - 1)^{1/k} } \right)}},} \right. \\ && {{\left( {(\eta^{\prime\prime} + \lambda^{2} - 1)^{1/k} - (\eta^{\prime\prime} - 1)^{1/k} } \right)}/ {\left( {(\eta^{\prime\prime} + \lambda^{2} - 1)^{1/k} + (\lambda - 1)(\eta^{\prime\prime} - 1)^{1/k} } \right)}}, \\ && \left. \left( {(\nu^{\prime\prime} + \lambda^{2} - 1)^{1/k} - (\nu^{\prime\prime} - 1)^{1/k} } \right)/ {\left( {(\nu^{\prime\prime} + \lambda^{2} - 1)^{1/k} + (\lambda - 1)(\nu^{\prime\prime} - 1)^{1/k} } \right)} \right\rangle , \\ \end{aligned}$$

  (17)

  where λ > 0 and

  $$\begin{aligned} \mu^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\mu^{\prime } + \lambda^{2} - 1)} \mathord{\left/ {\vphantom {{(\mu^{\prime } + \lambda^{2} - 1)} {(\mu^{\prime } - 1)}}} \right. \kern-0pt} {(\mu^{\prime } - 1)}}} \right)^{{1/C_{n}^{k} }} } ,\;\mu^{\prime } = \prod\limits_{h = 1}^{k} {\frac{{\left( {\lambda + (1 - \lambda )(1 - \mu_{{i_{h} }} )} \right)^{{n\omega_{{i_{h} }} }} + (\lambda^{2} - 1)(1 - \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} }}{{\left( {\lambda + (1 - \lambda )(1 - \mu_{{i_{h} }} )} \right)^{{n\omega_{{i_{h} }} }} - (1 - \mu_{{i_{h} }} )^{{n\omega_{{i_{h} }} }} }}} , \hfill \\ \eta^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\eta^{\prime } + \lambda^{2} - 1)} \mathord{\left/ {\vphantom {{(\eta^{\prime } + \lambda^{2} - 1)} {(\eta^{\prime } - 1)}}} \right. \kern-0pt} {(\eta^{\prime } - 1)}}} \right)^{{1/C_{n}^{k} }} } ,\;\eta^{\prime } = \prod\limits_{h = 1}^{k} {\left( {{{\left( {\left( {\lambda + (1 - \lambda )\eta_{{i_{h} }} } \right)^{{n\omega_{{i_{h} }} }} + (\lambda^{2} - 1)\eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)} \mathord{\left/ {\vphantom {{\left( {\left( {\lambda + (1 - \lambda )\eta_{{i_{h} }} } \right)^{{n\omega_{{i_{h} }} }} + (\lambda^{2} - 1)\eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)} {\left( {\left( {\lambda + (1 - \lambda )\eta_{{i_{h} }} } \right)^{{n\omega_{{i_{h} }} }} - \eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)}}} \right. \kern-0pt} {\left( {\left( {\lambda + (1 - \lambda )\eta_{{i_{h} }} } \right)^{{n\omega_{{i_{h} }} }} - \eta_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)}}} \right)} , \hfill \\ \nu^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\nu^{\prime } + \lambda^{2} - 1)} \mathord{\left/ {\vphantom {{(\nu^{\prime } + \lambda^{2} - 1)} {(\nu^{\prime } - 1)}}} \right. \kern-0pt} {(\nu^{\prime } - 1)}}} \right)^{{1/C_{n}^{k} }} } ,\;\nu^{\prime } = \prod\limits_{h = 1}^{k} {\left( {{{\left( {\left( {\lambda + (1 - \lambda )\nu_{{i_{h} }} } \right)^{{n\omega_{{i_{h} }} }} + (\lambda^{2} - 1)\nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)} \mathord{\left/ {\vphantom {{\left( {\left( {\lambda + (1 - \lambda )\nu_{{i_{h} }} } \right)^{{n\omega_{{i_{h} }} }} + (\lambda^{2} - 1)\nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)} {\left( {\left( {\lambda + (1 - \lambda )\nu_{{i_{h} }} } \right)^{{n\omega_{{i_{h} }} }} - \nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)}}} \right. \kern-0pt} {\left( {\left( {\lambda + (1 - \lambda )\nu_{{i_{h} }} } \right)^{{n\omega_{{i_{h} }} }} - \nu_{{i_{h} }}^{{n\omega_{{i_{h} }} }} } \right)}}} \right).} \hfill \\ \end{aligned}$$

• 4 If Frank T-norm and T-conorm are applied to Eq. (8), a picture fuzzy Archimedean Frank power MSM (PFAFPMSM) operator can be obtained as:

  $$\begin{aligned} {\text{PFAFPMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} ,...,\alpha_{n} ) & = \left\langle {\log_{\varepsilon } \left( {1 + {{(\varepsilon^{{\mu^{\prime\prime\prime}}} - 1)^{1/k} } / {(\varepsilon - 1)^{1/k - 1} }}} \right)} \right., \, 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon^{1 - {\eta^{\prime\prime\prime}}} - 1)^{1/k} }/ {(\varepsilon - 1)^{1/k - 1} }}} \right), \\ & \left. { \quad 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon^{{1 - \nu^{\prime\prime\prime}}} - 1)^{1/k} }/ {(\varepsilon - 1)^{1/k - 1} }}} \right)} \right\rangle , \\ \end{aligned}$$

  (18)

  where ε > 1 and

  $$\begin{aligned} \mu^{\prime\prime\prime} = 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \mu^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \mu^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right. \kern-0pt} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \mu^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \mu^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right),\;\mu^{\prime \prime } = \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\mu^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\mu^{\prime } }} - 1)}}} \right)} }}} \right. \kern-0pt} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\mu^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\mu^{\prime } }} - 1)}}} \right)} }}} \right), \hfill \\ \mu^{\prime } = 1 - \log_{\varepsilon } \left( {1 + \left( {{{(\varepsilon^{{1 - \mu_{{i_{h} }} }} - 1)^{{n\omega_{{i_{h} }} }} } \mathord{\left/ {\vphantom {{(\varepsilon^{{1 - \mu_{{i_{h} }} }} - 1)^{{n\omega_{{i_{h} }} }} } {(\varepsilon - 1)^{{n\omega_{{i_{h} }} - 1}} }}} \right. \kern-0pt} {(\varepsilon - 1)^{{n\omega_{{i_{h} }} - 1}} }}} \right)} \right), \hfill \\ \eta^{\prime\prime\prime} = \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\eta^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\eta^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right. \kern-0pt} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\eta^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\eta^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right),\;\eta^{\prime \prime } = 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \eta^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \eta^{\prime } }} - 1)}}} \right)} }}} \right. \kern-0pt} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \eta^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \eta^{\prime } }} - 1)}}} \right)} }}} \right), \hfill \\ \eta^{\prime } = \log_{\varepsilon } \left( {1 + {{(\varepsilon^{{\eta_{{i_{h} }} }} - 1)^{{n\omega_{{i_{h} }} }} } \mathord{\left/ {\vphantom {{(\varepsilon^{{\eta_{{i_{h} }} }} - 1)^{{n\omega_{{i_{h} }} }} } {(\varepsilon - 1)^{{n\omega_{{i_{h} }} - 1}} }}} \right. \kern-0pt} {(\varepsilon - 1)^{{n\omega_{{i_{h} }} - 1}} }}} \right), \hfill \\ \nu^{\prime\prime\prime} = \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\nu^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\nu^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right. \kern-0pt} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\nu^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\nu^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right),\;\nu^{\prime \prime } = 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \nu^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \nu^{\prime } }} - 1)}}} \right)} }}} \right. \kern-0pt} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \nu^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \nu^{\prime } }} - 1)}}} \right)} }}} \right), \hfill \\ \nu^{\prime } = \log_{\varepsilon } \left( {1 + {{(\varepsilon^{{\nu_{{i_{h} }} }} - 1)^{{n\omega_{{i_{h} }} }} } \mathord{\left/ {\vphantom {{(\varepsilon^{{\nu_{{i_{h} }} }} - 1)^{{n\omega_{{i_{h} }} }} } {(\varepsilon - 1)^{{n\omega_{{i_{h} }} - 1}} }}} \right. \kern-0pt} {(\varepsilon - 1)^{{n\omega_{{i_{h} }} - 1}} }}} \right). \hfill \\ \end{aligned}$$

3.2 PFAPWMSM operator

To capture the relative importance of the aggregated PFNs, a picture fuzzy Archimedean power weighted MSM (PFAPWMSM) operator is presented. This operator can be formally defined as:

Definition 10

Suppose w₁, w₂, ..., w_n (0 ≤ w₁, w₂, ..., w_n ≤ 1 and w₁ + w₂ + ... + w_n = 1) are, respectively, the weights of α₁, α₂, ..., α_n that, respectively, denote the relative importance of α₁, α₂, ..., α_n. Then on the basis of Def. 9,

$${\text{PFAPWMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left( {\frac{1}{{C_{n}^{k} }}\mathop \oplus \limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} \mathop \otimes \limits_{h = 1}^{k} \left( {\frac{{nw_{{i_{h} }} \left( {1 + T(\alpha_{{i_{h} }} )} \right)}}{{\sum\limits_{j = 1}^{n} {\left( {w_{j} \left( {1 + T(\alpha_{j} )} \right)} \right)} }}\alpha_{{i_{h} }} } \right)} \right)^{1/k}$$

(19)

is called the PFAPWMSM operator.

The general expression of the PFAPWMSM is constructed in the following theorem:

Theorem 5

Suppose α₁, α₂, ..., α_n (α_i = 〈μ_i, η_i, ν_i〉 , i = 1, 2, ..., n) are n PFNs. Then

$${\text{PFAPWMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {\mu , \, \eta , \, \nu } \right\rangle ,$$

(20)

where

$$\begin{aligned} \mu = \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {\left( {{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right), \hfill \\ \eta = \psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {\left( {{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\varphi (\eta_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right), \hfill \\ \nu = \psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {\left( {{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\varphi (\nu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right), \hfill \\ \omega_{{i_{h} }} = {{\left( {1 + T(\alpha_{{i_{h} }} )} \right)} \mathord{\left/ {\vphantom {{\left( {1 + T(\alpha_{{i_{h} }} )} \right)} {\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right),} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right),} }} \hfill \\ \omega_{t} = {{\left( {1 + T(\alpha_{t} )} \right)} \mathord{\left/ {\vphantom {{\left( {1 + T(\alpha_{t} )} \right)} {\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right)} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right)} }}. \hfill \\ \end{aligned}$$

and PFAPWMSM^(k)(α₁, α₂, ..., α_n) is still a PFN.

This theorem can be proved like proof Theorem 1 in App. A. The properties of the PFAPWMSM operator are stated in the following theorems:

Theorem 6

(Commutativity) Suppose α₁, α₂, ..., α_n (α_i = < μ_i, η_i, ν_i> , i = 1, 2, ..., n) are n PFNs. If (β₁, β₂, ..., β_n) is any permutation of (α₁, α₂, ..., α_n), then PFAPWMSM^(k)(β₁, β₂, ..., β_n) = PFAPWMSM^(k)(α₁, α₂, ..., α_n).

Theorem 7

(Boundedness) Suppose α₁, α₂, ..., α_n (α_i = < μ_i, η_i, ν_i> , i = 1, 2, ..., n) are n PFNs, α⁺ = < max(μ_i), min(η_i), min(ν_i) > , and α⁻ = < min(μ_i), max(η_i), max(ν_i) > . Then α⁻ ≤ PFAPWMSM^(k)(α₁, α₂, ..., α_n) ≤ α⁺.

These theorems can be respectively proved like proof of Theorem 3 in App. C and proof of Theorem 4 in App. D. Some special cases of the PFAPWMSM operator are as follows:

• 1 If k = 1, the PFAPWMSM operator will become

  $$\begin{aligned} \left\langle {\psi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\left( {{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\psi (\mu_{i} )} \right)} } \right), \, \varphi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\left( {{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\varphi (\eta_{i} )} \right)} } \right),} \right. \hfill \\ \left. { \, \varphi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\left( {{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\varphi (\nu_{i} )} \right)} } \right)} \right\rangle = {\text{PFAPWAA}}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ), \hfill \\ \end{aligned}$$

  (21)

  which is a picture fuzzy Archimedean power weighted AA (PFAPWAA) operator.

• 2 If k = 2, the PFAPWMSM operator will become

  $$\begin{aligned} &\left\langle {\varphi^{ - 1} \left( {\frac{1}{2}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{n(n - 1)}\sum\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\psi \left( {\varphi^{ - 1} \left( {\varphi \left( {\psi^{ - 1} \left( {\frac{{nw_{{i_{1} }} \omega_{{i_{1} }} }}{{\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}\psi (\mu_{{i_{1} }} )} \right)} \right) + \varphi \left( {\psi^{ - 1} \left( {\frac{{nw_{{i_{2} }} \omega_{{i_{2} }} }}{{\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}\psi (\mu_{{i_{2} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right., \hfill \\ \, \psi^{ - 1} \left( {\frac{1}{2}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{n(n - 1)}\sum\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\varphi \left( {\psi^{ - 1} \left( {\psi \left( {\varphi^{ - 1} \left( {\frac{{nw_{{i_{1} }} \omega_{{i_{1} }} }}{{\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}\varphi (\eta_{{i_{1} }} )} \right)} \right) + \psi \left( {\varphi^{ - 1} \left( {\frac{{nw_{{i_{2} }} \omega_{{i_{2} }} }}{{\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}\varphi (\eta_{{i_{2} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right), \hfill \\ \, \left. {\psi^{ - 1} \left( {\frac{1}{2}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{n(n - 1)}\sum\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\varphi \left( {\psi^{ - 1} \left( {\psi \left( {\varphi^{ - 1} \left( {\frac{{nw_{{i_{1} }} \omega_{{i_{1} }} }}{{\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}\varphi (\nu_{{i_{1} }} )} \right)} \right) + \psi \left( {\varphi^{ - 1} \left( {\frac{{nw_{{i_{2} }} \omega_{{i_{2} }} }}{{\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}\varphi (\nu_{{i_{2} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right\rangle \hfill \\ & = {\text{PFAPWBM}}^{(1,1)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ), \hfill \\ \end{aligned}$$

  (22)

  which is a picture fuzzy Archimedean power weighted BM (PFAPWBM) operator.

• 3 If k = n, the PFAPWMSM operator will become

  $$\begin{aligned} \left\langle {\varphi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\varphi \left( {\psi^{ - 1} \left( {\left( {{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\psi (\mu_{i} )} \right)} \right)} } \right), \, \psi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\psi \left( {\varphi^{ - 1} \left( {\left( {{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\varphi (\eta_{i} )} \right)} \right)} } \right),} \right. \hfill \\ \, \left. {\psi^{ - 1} \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\psi \left( {\varphi^{ - 1} \left( {\left( {{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right)\varphi (\nu_{i} )} \right)} \right)} } \right)} \right\rangle = {\text{PFAPWGA}}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ), \hfill \\ \end{aligned}$$

  (23)

  which is a picture fuzzy Archimedean power weighted GA (PFAPWGA) operator.

  The specific expressions of the PFAPWMSM operator are constructed as follows:

• 4 If Algebraic T-norm and T-conorm are applied to Eq. (20), a picture fuzzy Archimedean Algebraic power weighted MSM (PFAAPWMSM) operator can be obtained as:

  $$\begin{aligned} {\text{PFAAPWMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) & = \left\langle {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {1 - \prod\limits_{h = 1}^{k} {\left( {1 - \left( {1 - \mu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} / {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)} } \right)} } \right)^{{1/C_{n}^{k} }} } \right)^{1/k} } \right., \\ & \quad 1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {1 - \prod\limits_{h = 1}^{k} {\left( {1 - \eta_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} / {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)} } \right)} } \right)^{{1/C_{n}^{k} }} } \right)^{1/k} , \\ & \left. { \quad 1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {1 - \prod\limits_{h = 1}^{k} {\left( {1 - \nu_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} / {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)} } \right)} } \right)^{{1/C_{n}^{k} }} } \right)^{1/k} } \right\rangle . \\ \end{aligned}$$

  (24)

  • (a) If k = 1, the PFAAPWMSM operator will become

    $$\left\langle {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i} } \right)^{{{{(w_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(w_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } , \, \prod\limits_{i = 1}^{n} {\eta_{i}^{{{{(w_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(w_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } , \, \prod\limits_{i = 1}^{n} {\nu_{i}^{{{{(w_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(w_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } } \right\rangle = {\text{PFPWAA(}}\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ),$$

    (25)

    which is a picture fuzzy power weighted AA (PFPWAA) operator.

  • (b) If k = 2, the PFAAPWMSM operator will become

    $$\begin{aligned} \left\langle {\left( {1 - \prod\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\left( {1 - \left( {1 - \left( {1 - \mu_{{i_{1} }} } \right)^{{{{(nw_{{i_{1} }} \omega_{{i_{1} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{1} }} \omega_{{i_{1} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)\left( {1 - \left( {1 - \mu_{{i_{2} }} } \right)^{{{{(nw_{{i_{2} }} \omega_{{i_{2} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{2} }} \omega_{{i_{2} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)} \right)}^{{\frac{1}{n(n - 1)}}} } \right)^{1 / 2} } \right., \, \hfill \\ \, 1 - \left( {1 - \prod\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\left( {1 - \left( {1 - \eta_{{i_{1} }}^{{{{(nw_{{i_{1} }} \omega_{{i_{1} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{1} }} \omega_{{i_{1} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)\left( {1 - \eta_{{i_{2} }}^{{{{(nw_{{i_{2} }} \omega_{{i_{2} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{2} }} \omega_{{i_{2} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)} \right)}^{{\frac{1}{n(n - 1)}}} } \right)^{1 /2} , \hfill \\ \, \left. {1 - \left( {1 - \prod\limits_{\begin{subarray}{l} i_{1} ,i_{2} = 1 \\ i_{2} \ne i_{1} \end{subarray} }^{n} {\left( {1 - \left( {1 - \nu_{{i_{1} }}^{{{{(nw_{{i_{1} }} \omega_{{i_{1} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{1} }} \omega_{{i_{1} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)\left( {1 - \nu_{{i_{2} }}^{{{{(nw_{{i_{2} }} \omega_{{i_{2} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{2} }} \omega_{{i_{2} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)} \right)}^{{\frac{1}{n(n - 1)}}} } \right)^{1 /2} } \right\rangle \hfill \\ = {\text{PFPWBM}}^{(1,1)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ), \hfill \\ \end{aligned}$$

    (26)

    which is a picture fuzzy power weighted BM (PFPWBM) operator.

  • (c) If k = n, the PFAAPWMSM operator will become

    $$\begin{aligned} &\left\langle {\prod\limits_{i = 1}^{n} {\left( {1 - \left( {1 - \mu_{i} } \right)^{{{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)}^{1/n} , \, 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \eta_{i}^{{{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)^{1/n} ,} \, 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \nu_{i}^{{{{(nw_{i} \omega_{i} )} \mathord{\left/ {\vphantom {{(nw_{i} \omega_{i} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \right)^{1/n} } } \right\rangle \hfill \\ &= {\text{PFPWGA}}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ), \hfill \\ \end{aligned}$$

    (27)

    which is a picture fuzzy power weighted GA (PFPWGA) operator.

• 5 If Einstein T-norm and T-conorm are applied to Eq. (20), a picture fuzzy Archimedean Einstein power weighted MSM (PFAEPWMSM) operator can be obtained as:

  $$\begin{aligned} {\text{PFAEPWMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {{{\left( {2(\mu^{\prime \prime } - 1)^{1/k} } \right)} \mathord{\left/ {\vphantom {{\left( {2(\mu^{\prime \prime } - 1)^{1/k} } \right)} {\left( {(\mu^{\prime \prime } + 3)^{1/k} + (\mu^{\prime \prime } - 1)^{1/k} } \right)}}} \right. \kern-0pt} {\left( {(\mu^{\prime \prime } + 3)^{1/k} + (\mu^{\prime \prime } - 1)^{1/k} } \right)}}} \right., \hfill \\ {{\left( {(\eta^{\prime \prime } + 3)^{1/k} - (\eta^{\prime \prime } - 1)^{1/k} } \right)} \mathord{\left/ {\vphantom {{\left( {(\eta^{\prime \prime } + 3)^{1/k} - (\eta^{\prime \prime } - 1)^{1/k} } \right)} {\left( {(\eta^{\prime \prime } + 3)^{1/k} + (\eta^{\prime \prime } - 1)^{1/k} } \right)}}} \right. \kern-0pt} {\left( {(\eta^{\prime \prime } + 3)^{1/k} + (\eta^{\prime \prime } - 1)^{1/k} } \right)}}, \, \left. {{{\left( {(\nu^{\prime \prime } + 3)^{1/k} - (\nu^{\prime \prime } - 1)^{1/k} } \right)} \mathord{\left/ {\vphantom {{\left( {(\nu^{\prime \prime } + 3)^{1/k} - (\nu^{\prime \prime } - 1)^{1/k} } \right)} {\left( {(\nu^{\prime \prime } + 3)^{1/k} + (\nu^{\prime \prime } - 1)^{1/k} } \right)}}} \right. \kern-0pt} {\left( {(\nu^{\prime \prime } + 3)^{1/k} + (\nu^{\prime \prime } - 1)^{1/k} } \right)}}} \right\rangle , \hfill \\ \end{aligned}$$

  (28)

  where

  $$\begin{aligned} \mu^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\mu^{\prime } + 3)} \mathord{\left/ {\vphantom {{(\mu^{\prime } + 3)} {(\mu^{\prime } - 1)}}} \right. \kern-0pt} {(\mu^{\prime } - 1)}}} \right)^{{1/C_{n}^{k} }} } ,\;\mu^{\prime } = \prod\limits_{h = 1}^{k} {\frac{{\left( {1 + \mu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} + 3\left( {1 - \mu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}{{\left( {1 + \mu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} - \left( {1 - \mu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}} , \hfill \\ \eta^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\eta^{\prime } + 3)} \mathord{\left/ {\vphantom {{(\eta^{\prime } + 3)} {(\eta^{\prime } - 1)}}} \right. \kern-0pt} {(\eta^{\prime } - 1)}}} \right)^{{1/C_{n}^{k} }} } ,\;\eta^{\prime } = \prod\limits_{h = 1}^{k} {\frac{{\left( {2 - \eta_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} + 3\eta_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}{{\left( {2 - \eta_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} - \eta_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}} , \hfill \\ \nu^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\nu^{\prime } + 3)} \mathord{\left/ {\vphantom {{(\nu^{\prime } + 3)} {(\nu^{\prime } - 1)}}} \right. \kern-0pt} {(\nu^{\prime } - 1)}}} \right)^{{1/C_{n}^{k} }} } ,\;\nu^{\prime } = \prod\limits_{h = 1}^{k} {\frac{{\left( {2 - \nu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} + 3\nu_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}{{\left( {2 - \nu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} - \nu_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}} . \hfill \\ \end{aligned}$$

• 6 If Hamacher T-norm and T-conorm are applied to Eq. (20), a picture fuzzy Archimedean Hamacher power weighted MSM (PFAHPWMSM) operator can be obtained as:

  $$\begin{aligned} {\text{PFAHPWMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) & = \left\langle {{{\left( {\lambda (\mu^{\prime \prime } - 1)^{1 /k} } \right)} / {\left( {(\mu^{\prime \prime } + \lambda^{2} - 1)^{1 /k} + (\lambda - 1)(\mu^{\prime \prime } - 1)^{1 /k} } \right)}}}\right., \\ & {{ \quad \left( {(\eta^{\prime \prime } + \lambda^{2} - 1)^{1 /k} - (\eta^{\prime \prime } - 1)^{1 /k} } \right)} / {\left( {(\eta^{\prime \prime } + \lambda^{2} - 1)^{1 /k} + (\lambda - 1)(\eta^{\prime \prime } - 1)^{1 /k} } \right)}}, \\ & \quad \left. {{{\left( {(\nu^{\prime \prime } + \lambda^{2} - 1)^{1 /k} - (\nu^{\prime \prime } - 1)^{1 /k} } \right)} / {\left( {(\nu^{\prime \prime } + \lambda^{2} - 1)^{1 /k} + (\lambda - 1)(\nu^{\prime \prime } - 1)^{1 /k} } \right)}}} \right\rangle , \\ \end{aligned}$$

  (29)

  where

  $$\begin{aligned} \mu^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {\frac{{\mu^{\prime } + \lambda^{2} - 1}}{{\mu^{\prime } - 1}}} \right)^{{1 /C_{n}^{k} }} } ,\;\mu^{\prime } = \prod\limits_{h = 1}^{k} {\frac{{\left( {\lambda + (1 - \lambda )(1 - \mu_{{i_{h} }} )} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} + (\lambda^{2} - 1)(1 - \mu_{{i_{h} }} )^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}{{\left( {\lambda + (1 - \lambda )(1 - \mu_{{i_{h} }} )} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} - (1 - \mu_{{i_{h} }} )^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}} , \hfill \\ \eta^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {\frac{{\eta^{\prime } + \lambda^{2} - 1}}{{\eta^{\prime } - 1}}} \right)^{{1 /C_{n}^{k} }} } ,\;\eta^{\prime } = \prod\limits_{h = 1}^{k} {\frac{{\left( {\lambda + (1 - \lambda )\eta_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} + (\lambda^{2} - 1)\eta_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}{{\left( {\lambda + (1 - \lambda )\eta_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} - \eta_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}} , \hfill \\ \nu^{\prime \prime } = \prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {\frac{{\nu^{\prime } + \lambda^{2} - 1}}{{\nu^{\prime } - 1}}} \right)^{{1 /C_{n}^{k} }} } ,\;\nu^{\prime } = \prod\limits_{h = 1}^{k} {\frac{{\left( {\lambda + (1 - \lambda )\nu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} + (\lambda^{2} - 1)\nu_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}{{\left( {\lambda + (1 - \lambda )\nu_{{i_{h} }} } \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} - \nu_{{i_{h} }}^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} }}} . \hfill \\ \end{aligned}$$

• 7 If Frank T-norm and T-conorm are applied to Eq. (20), a picture fuzzy Archimedean Frank power weighted MSM (PFAFPWMSM) operator can be obtained as:

  $$\begin{aligned} {\text{PFAFPWMSM}}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) & = \left\langle {\log_{\varepsilon } \left( {1 + {{(\varepsilon^{{\mu^{\prime\prime\prime}}} - 1)^{1 /k} } / {(\varepsilon - 1)^{1 /k - 1} }}} \right)} \right., \, 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon^{{1 - \eta^{\prime\prime\prime}}} - 1)^{1 /k} } / {(\varepsilon - 1)^{1 /k - 1} }}} \right), \\ & \left. { \quad 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon^{{1 - \nu^{\prime\prime\prime}}} - 1)^{1 /k} } / {(\varepsilon - 1)^{1 /k - 1} }}} \right)} \right\rangle , \\ \end{aligned}$$

  (30)

  where

  $$\begin{aligned} \mu^{\prime\prime\prime} = 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \mu^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \mu^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right. \kern-0pt} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \mu^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \mu^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right),\;\mu^{\prime \prime } = \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\mu^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\mu^{\prime } }} - 1)}}} \right)} }}} \right. \kern-0pt} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\mu^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\mu^{\prime } }} - 1)}}} \right)} }}} \right), \hfill \\ \mu^{\prime } = 1 - \log_{\varepsilon } \left( {1 + \left( {{{\left( {\varepsilon^{{1 - \mu_{{i_{h} }} }} - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{1 - \mu_{{i_{h} }} }} - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } {\left( {\varepsilon - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }} - 1}} }}} \right)} \right), \hfill \\ \eta^{\prime\prime\prime} = \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\eta^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\eta^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right. \kern-0pt} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\eta^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\eta^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right),\;\eta^{\prime \prime } = 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \eta^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \eta^{\prime } }} - 1)}}} \right)} }}} \right. \kern-0pt} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \eta^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \eta^{\prime } }} - 1)}}} \right)} }}} \right), \hfill \\ \eta^{\prime } = \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{\eta_{{i_{h} }} }} - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{\eta_{{i_{h} }} }} - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } {\left( {\varepsilon - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }} - 1}} }}} \right),\; \hfill \\ \nu^{\prime\prime\prime} = \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\nu^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\nu^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right. \kern-0pt} {\prod\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{\nu^{\prime \prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{\nu^{\prime \prime } }} - 1)}}} \right)^{{1/C_{n}^{k} }} } }}} \right),\;\nu^{\prime \prime } = 1 - \log_{\varepsilon } \left( {1 + {{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \nu^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \nu^{\prime } }} - 1)}}} \right)} }}} \right. \kern-0pt} {\prod\limits_{h = 1}^{k} {\left( {{{(\varepsilon - 1)} \mathord{\left/ {\vphantom {{(\varepsilon - 1)} {(\varepsilon^{{1 - \nu^{\prime } }} - 1)}}} \right. \kern-0pt} {(\varepsilon^{{1 - \nu^{\prime } }} - 1)}}} \right)} }}} \right), \hfill \\ \nu^{\prime } = \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{\nu_{{i_{h} }} }} - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{\nu_{{i_{h} }} }} - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}}} } {\left( {\varepsilon - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{{{(nw_{{i_{h} }} \omega_{{i_{h} }} )} \mathord{\left/ {\vphantom {{(nw_{{i_{h} }} \omega_{{i_{h} }} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }} - 1}} }}} \right). \hfill \\ \end{aligned}$$

4 MADM method

In an MADM problem based on PFNs, decision makers need to select the most appropriate option from a certain number of options. The selection criterion is usually based on a certain number of attributes, whose relative important is measured by weights. The values of the attributes of each option are given by PFNs. The basic components of an MADM problem based on PFNs include a set of options O = {O₁, O₂, ..., O_m}, a set of attributes A = {A₁, A₂, ..., A_n}, a vector of weights of attributes w = [w₁, w₂, ..., w_n] (0 ≤ w₁, w₂, ..., w_n ≤ 1, w₁ + w₂ + ... + w_n = 1), and a picture fuzzy decision matrix M = [α_i,j]_m×n (i = 1, 2,..., m; j = 1, 2,..., n; α_i,j = < μ_i,j, η_i,j, ν_i,j> is a PFN that is the evaluation value of A_j of O_i). The objective of the MADM problem is to determine the best option from the options in O on the basis of M and w. This objective can be achieved through the following steps:

Step 1:

Normalise the picture fuzzy decision matrix M. In general, an MADM problem may contain benefit and cost attributes, which have opposite influences on the aggregation result. To unify the influences, a complement rule is usually applied to normalise the PFNs expressing the values of cost attributes. Using this rule, the picture fuzzy decision matrix M = [α_i,j]_m×n is normalised according to the following equation:

$$\varvec{M}_{{\mathbf{N}}} = \left[ {\alpha_{i,j} } \right]_{m \times n} = \left\{ \begin{aligned} \left[ {\left\langle {\mu_{i,j} , \, \eta_{i,j} , \, \nu_{i,j} } \right\rangle } \right]_{m \times n} ,{\text{ if }}A_{j} {\text{ is a benefit attribute}} \hfill \\ \left[ {\left\langle {\nu_{i,j} , \, \eta_{i,j} , \, \mu_{i,j} } \right\rangle } \right]_{m \times n} ,{\text{ if }}A_{j} {\text{ is a cost attribute}} \hfill \\ \end{aligned} \right.$$

(31)

Step 2:

Compute the weights of α_i,j. Based on Def.s 9 and 10 and Theorem 5, the weights of α_i,j are calculated using

$$\varpi_{i,j} = {{(w_{j} \omega_{j} )} \mathord{\left/ {\vphantom {{(w_{j} \omega_{j} )} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \omega_{t} } \right)} }} = {{\left( {w_{j} \left( {1 + \sum\limits_{p = 1,p \ne j}^{n} {\left( {1 - d(\alpha_{i,j} , \, \alpha_{i,p} )} \right)} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w_{j} \left( {1 + \sum\limits_{p = 1,p \ne j}^{n} {\left( {1 - d(\alpha_{i,j} , \, \alpha_{i,p} )} \right)} } \right)} \right)} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \left( {1 + \sum\limits_{q = 1,q \ne t}^{n} {\left( {1 - d(\alpha_{i,t} , \, \alpha_{i,q} )} \right)} } \right)} \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \left( {1 + \sum\limits_{q = 1,q \ne t}^{n} {\left( {1 - d(\alpha_{i,t} , \, \alpha_{i,q} )} \right)} } \right)} \right)} }},$$

(32)

where d(α_i,j, α_i,p) and d(α_i,t, α_i,q) are, respectively, the normalised Hamming distances of α_i,j and α_i,p and α_i,t and α_i,q. They can be calculated according to Def. 5.

Step 3:

Compute the summary values of α_i,j. The summary values of α_i,j are calculated via

$$\alpha_{i} = \left\langle {\mu_{i} , \, \eta_{i} , \, \nu_{i} } \right\rangle = {\text{PFAPWMSM}}^{(k)} (\alpha_{i,1} ,\alpha_{i,2} ,...,\alpha_{i,n} )$$

(33)

where PFAPWMSM is a specific PFAPWMSM operator, such as the specific operators in Eqs. (24), (28), (29), and (30).

Step 4:

Compute the score and accuracy values of α_i. According to Defs. 2 and 3, the score and accuracy values of α_i are, respectively, calculated

Step 5:

Rank O_i. According to Def. 4 and the score and accuracy values of α_i, all O_i are ranked

Step 6:

Determine the best option. The best option is generally the option ranked first

5 Example, experiments, and comparisons

5.1 Example

An MADM example about selection of the best emerging technology enterprise from five viable enterprises (Jana et al. 2019) is introduced to illustrate the proposed MADM method. The five viable enterprises are E₁, E₂, E₃, E₄, and E₅. There are four attributes for decision-making, which are the technical advancement (A₁), the potential market (A₂), the industrialisation framework, human resources, and financial investments (A₃), and the employment formation and progress of science and technology (A₄). The weights of these attributes are given by w = [0.2, 0.1, 0.3, 0.4]. To provide enough freedom in the evaluation of attribute values, PFNs were used. The evaluation results form a picture fuzzy decision matrix M = [α_i,j]_5×4, whose elements are listed in Table 2.

Table 2 The elements of the picture fuzzy decision matrix M

According to the conditions above and the proposed MADM method, selection of the best emerging technology enterprise can be carried out as follows:

Step 1:

Normalise the picture fuzzy decision matrix M. Since all of the four attributes are benefit attributes, the normalised picture fuzzy decision matrix M_N = M = [αα_i,j]_5×4

Step 2:

Compute the weights of α_i,j. On the basis of Eq. (32), the weights of α_i,j are calculated as:

$$\left[ {\varpi_{i,j} } \right]_{5 \times 4} = \left[ \begin{aligned} \begin{array}{*{20}l} { 0. 2 2 9 6} & { 0. 0 9 2 1} & {\begin{array}{*{20}c} { 0. 3 3 4 2} & { 0. 3 4 4 1} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { 0. 2 0 3 1} & { 0. 1 0 0 0} & {\begin{array}{*{20}l} { 0. 2 8 7 4} & { 0. 4 0 9 5} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { 0. 1 9 7 9} & { 0. 1 0 9 4} & {\begin{array}{*{20}c} { 0. 2 5 4 9} & { 0. 4 3 7 8} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { 0. 1 9 0 5} & { 0. 1 0 0 6} & {\begin{array}{*{20}c} { 0. 2 9 6 8} & { 0. 4 1 2 1} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { 0. 1 8 9 4} & { 0. 0 9 9 4} & {\begin{array}{*{20}c} { 0. 2 9 1 7} & { 0. 4 1 9 5} \\ \end{array} } \\ \end{array} \hfill \\ \end{aligned} \right].$$

Step 3:

Compute the summary values of α_i,j. The summary values of α_i,j can be calculated via Eq. (33). Here the specific operator in Eq. (29) (λ = 3 and k = 3) is leveraged in Eq. (33). The calculated summary values are as follows:

α₁ = < 0.3965, 0.4461, 0.1450 > , α₂ = < .3205, 0.4746, 0.2026 > , α₃ = < 0.3366, 0.3767, 0.1287 > ,

α₄ = < 0.2318, 0.5861, 0.1435 > , α₅ = < 0.2895, 0.5283, 0.1641>

Step 4:

Compute the score and accuracy values of α_i. According to Def.s 2 and 3, the score and accuracy values of α_i are calculated as:

S(α₁) = 0.6258, S(α₂) = 0.5589, S(α₃) = 0.6039, S(α₄) = 0.5441, S(α₅) = 0.5627

A(α₁) = 0.9876, A(α₂) = 0.9978, A(α₃) = 0.8421, A(α₄) = 0.9614, A(α₅) = 0.9819

Step 5:

Rank E_i. On the basis of Def. 4, all E_i are ranked as:

E₁ ≻ E₃ ≻ E₅ ≻ E₂ ≻ E₄

Step 6:

Determine the best enterprise. The best enterprise is E₁ as it is ranked first

5.2 Experiments

To study the impact of different ATT operations and different argument values on the aggregation result, the following experiments were conducted:

• 1 Experiment 1. This experiment aims to study the impact of different ATT operations on the aggregation result. In this, the specific AOs using different ATT operations in Eqs. (24), (28), (29), and (30) with k = 3 and λ = ε = 3 were, respectively, used in the numerical example. The experiment results, as depicted in Fig. 1, are the score values of α_i and the rankings of E_i. As can been seen from Fig. 1, the generated rankings of E_i under different ATT operations just have difference at the fourth and fifth places, which indicates that different ATT operations have no obvious impact on the aggregation result for the numerical example. Please note that this does not mean that an arbitrary ATT operation can be used in all MADM problems based on PFNs. Whether an ATT operation is suitable for a specific problem should be judged according to the characteristics of the problem.

  Fig. 1

  

  The result of Experiment 1

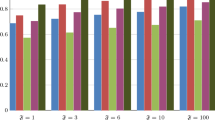
• 2 Experiment 2. This experiment aims to study the impact of different values of k on the aggregation result. In this, the presented specific AOs in Eqs. (24), (28), (29), and (30) with k = 1, 2, 3, 4 were, respectively, used in the numerical example. The experiment results, as listed in Table 3, are the score values of α_i and the rankings of E_i. From Table 3, the score value of each enterprise become smaller and smaller and the generated rankings and best enterprises are different from k = 1 to k = 4 for each AO. This indicates that the argument k in each AO reflects the risk attitude and the risk attitude changes from optimism to pessimism as k changes from 1 to 4. It is worth nothing that MSM will reduce to AA and all attributes are independent of each other when k = 1, MSM will reduce to BM and there are interactions between any two attributes when k = 2, and MSM will reduce to GA and there are interactions among the four attributes when k = 4. Thus the order of the optimism of AA, BM, MSM, and GA is AA ≻ BM ≻ MSM ≻ GA from the results of the experiment. In practical MADM problems, the value of k should be assigned on the basis of the interactions of attributes.

  Table 3 The results of Experiment 2

• 3 Experiment 3. This experiment aims to study the impact of different values of λ (ε) on the aggregation result. In this, the PFAHPWMSM operator in Eq. (29) with k = 3 and 0.01 ≤ λ ≤ 20.00 and the PFAFPWMSM operator in Eq. (30) with k = 3 and 1.01 ≤ ε ≤ 20.00 were, respectively, leveraged in the numerical example. The experiment results, as depicted in Figs. 2 and 3, are the score values of α_i and the rankings of E_i. From Figs. 2 and 3, the scores calculated by the two operators decrease or increase and the generated rankings have minor changes as the values of λ and ε gradually increase. This shows that there is no fixed rule for the influence of λ and ε on the aggregation result for the numerical example, although the two arguments can be used as risk attitude factors in other practical MADM problems. In general, an appropriate λ (ε) value (e.g. λ = 1, 2, 3; ε = 2, 3, 4) is recommended when the PFAHPWMSM (PFAFPWMSM) operator is used.

  Fig. 2

  

  The result of Experiment 3 when PFAHPWMSM is used

  Fig. 3

  

  The result of Experiment 3 when PFAFPWMSM is used

5.3 Comparisons

Representative MADM methods based on AOs of PFNs are the methods presented by Wei (2017), Garg (2017b), Wei (2018), Jana et al. (2019), Wei et al. (2018a), Zhang et al. (2018), and Xu et al. (2019). A qualitative comparison and a quantitative comparison between them and the proposed MADM method are, respectively, carried out to validate the proposed method:

• 1 Qualitative comparison. The qualitative comparison was made through comparing the features of the AOs. For the eight methods, the flexibility in the aggregation of attribute values, the generality in the consideration of attribute interactions, and the capability to reduce the negative impact of biased attribute values are used as the comparison characteristics. The comparison results are listed in Table 4:

  • (a) Flexibility in the aggregation of attribute values. The methods of Wei (2017), Wei et al. (2018a), and Xu et al. (2019) realise the aggregation through the operational rules based on Algebraic T-norm and T-conorm, their flexibility is relatively limited. The methods of Wei (2018), Jana et al. (2019), and Zhang et al. (2018) leverage the Hamacher, Dombi, and Dombi T-norms and T-conorms to carry out their aggregations, respectively. Their flexibility can be seen as moderate because each of the two T-norms and T-conorms can provide a flexible argument for aggregation. The flexibility of the method of Garg (2017b) and the proposed method are satisfying since their aggregations can be realised via the operational rules based on any family of ATTs.

  • (b) Generality in the consideration of attribute interactions. All of the comparison methods can handle the case where all attributes are independent of each other. The methods of Wei et al. (2018a) and Zhang et al. (2018) are applicable for the independence situation and the situation in which there are interactions between any two attributes because of the use of Heronian mean operator in them. The method of Xu et al. (2019) and the proposed method have the most desirable generality in the consideration of attribute interactions because of the use of two all-in-one AOs for capturing relationships, i.e. the Muirhead mean and MSM operators.

  • (c) Capability to reduce the negative impact of biased attribute values. Among all of the eight methods, the method of Wei (2018) and the proposed method have this capability since both of them combine the PA operator.

  Table 4 The results of the qualitative comparison

• 2 Quantitative comparison. The quantitative comparison was made leveraging the numerical examples in Ref. (Jana et al. 2019) (Example 1), Ref. (Wei 2017) (Example 2), and Ref. (Garg 2017b) (Example 3) as the benchmarks. The WA, Hamacher WA, Hamacher WA, Dombi WA, weighted Heronian mean, Dombi weighted Heronian mean, weighted Muirhead mean, and PFAHPWMSM operators were, respectively, used in the methods in Wei (2017), Garg (2017b), Wei (2018), Jana et al. (2019), Wei et al. (2018a), Zhang et al. (2018), Xu et al. (2019), and the present paper. In addition, the same function for calculating the score values was used in all of these methods for to unify the comparison. The comparison results are listed in Table 5.

  Table 5 The results of the quantitative comparison

From Table 5, the ranking of the proposed method has no significant difference with the rankings of the methods of Jana et al. (2019), Wei et al. (2018a), Zhang et al. (2018), and Xu et al. (2019) for Example 1, with the rankings of the methods of Wei et al. (2018a) and Xu et al. (2019) for Example 2, and with the rankings of all remaining methods for Example 3. This demonstrates that for practical MADM problems based on PFNs, the proposed method is feasible and effective. From Table 4, the method of Xu et al. (2019) and the proposed method are the most similar in characteristics. From Table 5, the rankings of the two methods are exactly identical or have no obvious difference with each other for all examples, which also validates the proposed method. As can also be seen from Table 5, the ranking and best option of the proposed method are fully different with the ranking and best option of the methods of Wei (2017), Garg (2017b), Wei (2018) for Example 1 and of the methods of Wei (2017), Garg (2017b), Wei (2018), Jana et al. (2019), and Zhang et al. (2018) for Example 2. This is because the specific AOs on which these methods are based are different from the specific AO in the proposed method, so do their mathematical properties.

It can be concluded from the results in Table 4 that the proposed MADM method can provide satisfying flexibility in the aggregation of attribute values and the consideration of attribute interactions and concurrently has the capability to reduce the negative impact of biased attribute values on aggregation result. The former characteristic is obvious. But the latter one is not intuitive. To show the difference between a method that has the capability to reduce negative impact and a method that does not have such capability, an additional quantitative comparison was carried out. In this comparison, the weighted Muirhead mean operator in the method of Xu et al. (2019) with P = (1, 1, 1, 0) and the PFAHPWMSM operator in Eq. (29) with λ = 1 and k = 3 were selected to solve the MADM problem in Example 1. Please note that the only difference of the two operators under such conditions is whether combines the PA operator (i.e. whether has the capability). Suppose the value of attribute A₂ of enterprise E₁ is a biased value. The degree of positive membership of this value was constantly reduced based on Table 6. It can be guessed that this adjustment will have influence on the ranking of E₁, which could be dropped from the first enterprise to the last one. To confirm this conjecture, Table 6 and Fig. 4 list the variation of the places of E₁ in the rankings generated by the method of Xu et al. (2019) and the proposed method.

Table 6 The results of the additional quantitative comparison

Fig. 4

The change of score value and ranking of E₁ in the additional quantitative comparison

From Table 6 and Fig. 4, the results of both methods fit the conjecture. This demonstrates the effectiveness of the proposed method indirectly. In addition, the place of E₁ in the rankings of the method of Xu et al. (2019) descends faster than the place of E₁ in the rankings of the proposed method, which shows the capability to reduce the negative impact of biased attribute values intuitively.

As can be summarised from the comparisons above, the main advantages of the proposed method over the existing methods are providing the flexibility in the aggregation of picture fuzzy information and the consideration of the interactions among attributes and the capability to reduce the negative impact of some biased attribute values.

6 Conclusion

In the present paper, a PFAPMSM operator and a PFAPWMSM operator have been proposed to address the MADM problems based on PFNs. The formal definitions and the general expressions of these AOs have been presented. Their properties and special cases have been explored. The specific expressions of the two AOs have been established applying the operational rules of PFNs based on four families of ATTs. Using the established specific PFAPWMSM operators, a method to solve the PFNs based MADM problems has been proposed. The paper has also introduced a numerical example to illustrate the proposed method and carried out a set of comparisons to demonstrate its features, feasibility, and effectiveness. The comparison results show that the method is feasible and effective that provides the flexibility in aggregation of values of attributes, the generality in consideration of interactions among attributes, and the capability to reduce the negative impact of extreme values of attributes. Future work will focus especially on extending the proposed method from the aspects of dealing with more complex interactions among attributes and applying the method in solving practical MADM problems based on PFNs.

Appendixes

1.1 A. Proof of Theorem 1

Proof

• 1 The following equations are successively derived from the operational rules in Eqs. (1), (2), (3), and (4)

  $$\begin{aligned}(n\omega_{{i_{h} }} )\alpha_{{i_{h} }} & = \left\langle {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right), \, \varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\eta_{{i_{h} }} )} \right), \, \varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\nu_{{i_{h} }} )} \right)} \right\rangle , \\ \mathop \otimes \limits_{h = 1}^{k} \left( {(n\omega_{{i_{h} }} )\alpha_{{i_{h} }} } \right) & = \left\langle {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right), \, \psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\eta_{{i_{h} }} )} \right)} \right)} } \right), \, \psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\nu_{{i_{h} }} )} \right)} \right)} } \right)} \right\rangle , \\ \mathop \oplus \limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} \mathop \otimes \limits_{h = 1}^{k} \left( {(n\omega_{{i_{h} }} )\alpha_{{i_{h} }} } \right) & = \left\langle {\psi^{ - 1} \left( {\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right),} \right. \\ & \quad \varphi^{ - 1} \left( {\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\eta_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right), \\ & \left. { \quad \varphi^{ - 1} \left( {\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\nu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right\rangle , \\ \frac{1}{{C_{n}^{k} }}\mathop \oplus \limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} \mathop \otimes \limits_{h = 1}^{k} \left( {(n\omega_{{i_{h} }} )\alpha_{{i_{h} }} } \right) & = \left\langle {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right., \\ & \quad \varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\eta_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right), \\ & \left. { \quad \varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\nu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right\rangle , \\ \left( {\frac{1}{{C_{n}^{k} }}\mathop \oplus \limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} \mathop \otimes \limits_{h = 1}^{k} \left( {(n\omega_{{i_{h} }} )\alpha_{{i_{h} }} } \right)} \right)^{1/k} & = \left\langle {\varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right),} \right. \\ & \quad \psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\eta_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right), \\ & \quad \left. {\psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\varphi (\nu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right)} \right\rangle . \\ \end{aligned}$$

• 2 The proof of “PFAPMSM^(k)(α₁, α₂, ..., α_n) is a PFN” is equivalent to the proof of “0 ≤ μ ≤ 1, 0 ≤ η ≤ 1, 0 ≤ ν ≤ 1, and 0 ≤ μ + η + ν ≤ 1”. The following is the proof of “0 ≤ μ ≤ 1”:

  • (i) According to the conditions 0 ≤ μ_ih ≤ 1, φ(t) and φ⁻¹(t) are monotonically decreasing, and ψ(t) and ψ⁻¹(t) are monotonically increasing, the following inequalities are successively derived

    $$\begin{aligned} (n\omega_{{i_{h} }} )\psi (0) & \le (n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} ) \le (n\omega_{{i_{h} }} )\psi (1), \\ \psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (0)} \right) & \le \psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right) \le \psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (1)} \right), \\ \sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (0)} \right)} \right)} & \ge \sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} \ge \sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (1)} \right)} \right)} , \\ \varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (0)} \right)} \right)} } \right) & \le \varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right) \le \varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (1)} \right)} \right)} } \right), \\ \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (0)} \right)} \right)} } \right)} \right)} & \le \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} \\ & \quad \le\,\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (1)} \right)} \right)} } \right)} \right)} . \\ \end{aligned}$$

    Since

    $$\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\sum\limits_{h = 1}^{k} {(n\omega_{{i_{h} }} ) = n\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\left( {\omega_{{i_{1} }} + \omega_{{i_{2} }} + \ldots + \omega_{{i_{k} }} } \right)} } } = n\frac{1}{n} = 1.$$

    The following inequalities are successively obtained

    $$\begin{aligned} \psi \left( {\varphi^{ - 1} \left( {k\varphi (0)} \right)} \right) \le \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} \le \psi \left( {\varphi^{ - 1} \left( {k\varphi (1)} \right)} \right), \hfill \\ \varphi^{ - 1} \left( {k\varphi (0)} \right) \le \psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right) \le \varphi^{ - 1} \left( {k\varphi (1)} \right), \hfill \\ \varphi (0) \ge \frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right) \ge \varphi (1), \hfill \\ 0 \le \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \le 1. \hfill \\ \end{aligned}$$

    That is 0 ≤ μ ≤ 1. “0 ≤ η ≤ 1” and “0 ≤ ν ≤ 1” can be proved in a similar way.

  • (ii) The following is the proof of “0 ≤ μ + η + ν ≤ 1”:

    Since 0 ≤ μ ≤ 1, 0 ≤ η ≤ 1, and 0 ≤ ν ≤ 1, it is obtained that 0 ≤ μ + η + ν ≤ 3. According to the definition of a PFN in Def. 1, it is further obtained that μ_ih + η_ih + ν_ih ≤ 1 and μ_ih ≤ 1 – (η_ih + ν_ih).

    According to the conditions φ(t) and φ⁻¹(t) are monotonically decreasing, ψ(t) and ψ⁻¹(t) are monotonically increasing, ψ(1 − t) = φ(t), ψ⁻¹(t) = 1 − φ⁻¹(t), φ(1 − t) = ψ(t), and φ⁻¹(t) = 1 − ψ⁻¹(t), the following inequalities are successively derived

    $$\begin{aligned} (n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} ) \le (n\omega_{{i_{h} }} )\psi \left( {1 - (\eta_{{i_{h} }} + \nu_{{i_{h} }} )} \right), \hfill \\ (n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} ) \le (n\omega_{{i_{h} }} )\varphi (\eta_{{i_{h} }} + \nu_{{i_{h} }} ), \hfill \\ \varphi (\eta_{{i_{h} }} + \nu_{{i_{h} }} ) \le 2\varphi (\eta_{{i_{h} }} + \nu_{{i_{h} }} ) \le \varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} ), \hfill \\ (n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} ) \le (n\omega_{{i_{h} }} )\varphi (\eta_{{i_{h} }} + \nu_{{i_{h} }} ) \le (n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right), \hfill \\ \psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right) \le \psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right), \hfill \\ \psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right) \le 1 - \varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right), \hfill \\ \sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} \ge \sum\limits_{h = 1}^{k} {\varphi \left( {1 - \varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} , \hfill \\ \sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} \ge \sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} , \hfill \\ \varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right) \le \varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right), \hfill \\ \varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right) \le 1 - \psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right), \hfill \\ \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} \le \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {1 - \psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} , \hfill \\ \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} \le \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} , \hfill \\ \psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right) \le \psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} } \right), \hfill \\ \psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right) \hfill \\ \le 1 - \varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} } \right), \hfill \\ \frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right) \hfill \\ \ge \frac{1}{k}\varphi \left( {1 - \varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} } \right)} \right), \hfill \\ \frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right) \hfill \\ \ge \frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} } \right)} \right), \hfill \\ \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \hfill \\ \le \varphi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} } \right)} \right)} \right), \hfill \\ \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \hfill \\ \le 1 - \psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} ) + \varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \hfill \\ \le 1 - \left( \begin{aligned} \psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\eta_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) + \hfill \\ \psi^{ - 1} \left( {\frac{1}{k}\psi \left( {\varphi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\varphi \left( {\psi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\psi \left( {\varphi^{ - 1} \left( {(n\omega_{{i_{h} }} )\left( {\varphi (\nu_{{i_{h} }} )} \right)} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \hfill \\ \end{aligned} \right). \hfill \\ \end{aligned}$$

    That is, μ + η + ν ≤ 1.

    Since 0 ≤ μ + η + ν ≤ 3 and μ + η + ν ≤ 1 have been proved, 0 ≤ μ + η + ν ≤ 1 can be obtained.

1.2 B. Proof of Theorem 2

Proof

Since α_i = α = < μ_α, η_α, ν_α > for all i = 1, 2, ..., n, d(α_i, α_j) = 0 for all j = 1, 2, ..., n and j ≠ i. Based on the expression of T(α_p) in Def. 9, it is obtained that

$$n\omega_{{i_{h} }} = n{{\left( {\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\sum\limits_{h = 1}^{k} {\left( {1 + T(\alpha_{{i_{h} }} )} \right)} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\sum\limits_{h = 1}^{k} {\left( {1 + T(\alpha_{{i_{h} }} )} \right)} } } \right)} {\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right)} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right)} }} = n{{\left( {1 + (n - 1)} \right)} \mathord{\left/ {\vphantom {{\left( {1 + (n - 1)} \right)} {\left( {n\left( {1 + (n - 1)} \right)} \right)}}} \right. \kern-0pt} {\left( {n\left( {1 + (n - 1)} \right)} \right)}} = 1.$$

Based on this and Theorem 1, it can be obtained that

$$\mu = \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi (\mu_{{i_{h} }} )} } \right)} \right)} } \right)} \right)} \right).$$

Since μ_i = μ_α, then

$$\sum\limits_{h = 1}^{k} {\varphi (\mu_{{i_{h} }} )} = \sum\limits_{h = 1}^{k} {\varphi (\mu_{\alpha } )} = k\varphi (\mu_{\alpha } )\;{\text{and }}\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi (\mu_{{i_{h} }} )} } \right) = \varphi^{ - 1} \left( {k\varphi (\mu_{\alpha } )} \right).$$

The following equations are successively obtained

$$\begin{aligned} \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi (\mu_{{i_{h} }} )} } \right)} \right)} = \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {k\varphi (\mu_{\alpha } )} \right)} \right)} = \psi \left( {\varphi^{ - 1} \left( {k\varphi (\mu_{\alpha } )} \right)} \right), \hfill \\ \psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi (\mu_{{i_{h} }} )} } \right)} \right)} } \right) = \psi^{ - 1} \left( {\psi \left( {\varphi^{ - 1} \left( {k\varphi (\mu_{\alpha } )} \right)} \right)} \right) = \varphi^{ - 1} \left( {k\varphi (\mu_{\alpha } )} \right), \hfill \\ \frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi (\mu_{{i_{h} }} )} } \right)} \right)} } \right)} \right) = \frac{1}{k}\varphi \left( {\varphi^{ - 1} \left( {k\varphi (\mu_{\alpha } )} \right)} \right) = \varphi (\mu_{\alpha } ), \hfill \\ \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi (\mu_{{i_{h} }} )} } \right)} \right)} } \right)} \right)} \right) = \varphi^{ - 1} \left( {\varphi (\mu_{\alpha } )} \right) = \mu_{\alpha } , \hfill \\ \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) = \mu_{\alpha } . \hfill \\ \end{aligned}$$

This is μ = μ_α. Similarly, it can be proved that η = η_α and ν = ν_α. Thus, PFAPMSM^(k)(α₁, α₂, ..., α_n) = < μ_α, η_α, ν_α > .

1.3 C. Proof of Theorem 3

Proof

It can be derived from the definition of the PFAPMSM operator that

$$\left( {\frac{1}{{C_{n}^{k} }}\mathop \oplus \limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} \mathop \otimes \limits_{h = 1}^{k} \left( {\frac{{n\left( {1 + T(\beta_{{i_{h} }} )} \right)}}{{\sum\limits_{j = 1}^{n} {\left( {1 + T(\beta_{j} )} \right)} }}\beta_{{i_{h} }} } \right)} \right)^{1/k} = \left( {\frac{1}{{C_{n}^{k} }}\mathop \oplus \limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} \mathop \otimes \limits_{h = 1}^{k} \left( {\frac{{n\left( {1 + T(\alpha_{{i_{h} }} )} \right)}}{{\sum\limits_{j = 1}^{n} {\left( {1 + T(\alpha_{j} )} \right)} }}\alpha_{{i_{h} }} } \right)} \right)^{1/k} .$$

According to Def. 9, it is obtained that PFAPMSM^(k)(β₁, β₂, ..., β_n) = PFAPMSM^(k)(α₁, α₂, ..., α_n).

1.4 D. Proof of Theorem 4

Proof

Based on Theorem 2, it can be obtained that PFAPMSM^(k)(α⁻, α⁻, ..., α⁻) = αα⁻, PFAPMSM^(k)(α⁺, α⁺, ..., α⁺) = α⁺, and nξ_ih = 1 for both PFAPMSM^(k)(α⁻, α⁻, ..., α⁻) and PFAPMSM^(k)(α⁺, α⁺, ..., α⁺). According to the conditions μ⁻ ≤ μ_ih ≤ μ⁺, φ(t) and φ⁻¹(t) are monotonically decreasing, and ψ(t) and ψ⁻¹(t) are monotonically increasing, the following inequalities are successively derived

$$\begin{aligned} \psi (\mu^{ - } ) \le (n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} ) \le \psi (\mu^{ + } ), \hfill \\ \mu^{ - } \le \psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right) \le \mu^{ + } , \hfill \\ k\varphi (\mu^{ - } ) \ge \sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} \ge k\varphi (\mu^{ + } ), \hfill \\ \varphi^{ - 1} \left( {k\varphi (\mu^{ - } )} \right) \le \varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right) \le \varphi^{ - 1} \left( {k\varphi (\mu^{ + } )} \right), \hfill \\ \psi \left( {\varphi^{ - 1} \left( {k\varphi (\mu^{ - } )} \right)} \right) \le \frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} \le \psi \left( {\varphi^{ - 1} \left( {k\varphi (\mu^{ + } )} \right)} \right), \hfill \\ \varphi^{ - 1} \left( {k\varphi (\mu^{ - } )} \right) \le \psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right) \le \varphi^{ - 1} \left( {k\varphi (\mu^{ + } )} \right), \hfill \\ \varphi (\mu^{ - } ) \ge \frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right) \ge \varphi (\mu^{ + } ), \hfill \\ \mu^{ - } \le \varphi^{ - 1} \left( {\frac{1}{k}\varphi \left( {\psi^{ - 1} \left( {\frac{1}{{C_{n}^{k} }}\sum\limits_{{1 \le i_{1} < \ldots < i_{k} \le n}} {\psi \left( {\varphi^{ - 1} \left( {\sum\limits_{h = 1}^{k} {\varphi \left( {\psi^{ - 1} \left( {(n\omega_{{i_{h} }} )\psi (\mu_{{i_{h} }} )} \right)} \right)} } \right)} \right)} } \right)} \right)} \right) \le \mu^{ + } . \hfill \\ \end{aligned}$$

That is μ⁻ ≤ μ ≤ μ⁺. Similarly, it can be proved that η⁻ ≥ η ≥ η⁺ and ν⁻ ≥ ν ≥ ν⁺.

According to Def. 2, it is obtained that

PFAPMSM^(k)(α⁻, α⁻, ..., α⁻) ≤ PFAPMSM^(k)(α₁, α₂, ..., α_n) ≤ PFAPMSM^(k)(α⁺, α⁺, ..., α⁺)

Therefore, α⁻ ≤ PFAPMSM^(k)(α₁, α₂, ..., α_n) ≤ α⁺.