Fermatean fuzzy sets

Abstract

In this paper, we propose Fermatean fuzzy sets. We compare Fermatean fuzzy sets with Pythagorean fuzzy sets and intuitionistic fuzzy sets. We focus on complement operator of Fermatean fuzzy sets. We find out the fundamental set of operations for the Fermatean fuzzy sets. We define score function and accuracy function for ranking of Fermatean fuzzy sets. In addition, we also study Euclidean distance between two Fermatean fuzzy sets. Later, we establish a Fermatean fuzzy TOPSIS method to fix multiple criteria decision-making problem. Ultimately, an interpretative example is stated in details to justify the elaborated method and to illustrate its viability and usefulness.

1 Introduction

Orthopair fuzzy sets are fuzzy sets in which the membership grades of an element x are pairs of values in the unit interval, $\langle \mu (x),\nu (x)\rangle$, one of which indicates support for membership in the fuzzy set and the other support against membership. Two examples of orthopair fuzzy sets are Atanass- ov’s classic intuitionistic fuzzy sets (Atanassov 1986, 2012; Atanassov et al. 2013) and a second kind of intuitionistic fuzzy sets (Atanassov 1983, 2016). This idea has been followed up in Atanassov et al. (2017), Atanassov and Vassilev (2018), Parvathi (2005), Parvathi et al. (2012), Vassilev et al. (2008), Vassilev (2012, 2013). It is noted that for classic intuitionistic fuzzy sets the sum of the support for and against is bounded by one, while for the second kind, Pythagorean fuzzy sets, the sum of the squares of the support for and against is bounded by one. Yager (2017) introduced a general class of these sets called q-rung orthopair fuzzy sets in which the sum of the qth power of the support for and the qth power of the support against is bonded by one. He noted that as q increases the space of acceptable orthopairs increases and thus gives the user more freedom in expressing their belief about membership grade. Liu and Wang (2018) proposed the q-rung orthopair fuzzy weighted averaging/geometric operators to deal with the decision information. Du (2018) presented the Minkowski-type distance measures for q-rung orthopair fuzzy sets.

When $q=2$, Yager (2014) have considered q-rung orthopair fuzzy sets as Pythagorean fuzzy sets. Yager presented juxtaposition of spaces of Pythagorean membership grades (PMGs) and intuitionistic membership grades (IMGs). The Pythagorean fuzzy sets provide a profitable human-focused reasoning apparatus for capturing and modelling deception and uncertainty in instinctive decision-making processes.

Yager (2014) established a variety of aggregation operators for Pythagorean fuzzy sets. He acknowledged MCDM problem on account the place the criteria fulfilment would be communicated utilizing PMGs. Zhang (2016) showed an MCDM problem by using the idea of the similarity measure. Ren et al. (2016) suggested Pythagorean fuzzy TODIM for MCDM problems. Yager and Abbasov (2013) showed that PMGs are special types of complex numbers referred to as ${\varPi }-\mathrm{i}$ numbers. They examined the difficulty of MCDM with satisfactions expressed as PMGs, ${\varPi }-\mathrm{i}$ numbers. Peng and Yang (2015) utilized Pythagorean fuzzy aggregation operators for assessing Internet stocks investment. Reformat and Yager (2014) implemented the PFNs to produce itemize nominated movies from the Netflix competition directory. Bustince et al. (2016) prepared a historical ledger of different types of FSs and their interconnections and specified that anyway, intuitionistic fuzzy sets are Pythagorean fuzzy sets. Regarding PFNs as variables, Gou et al. (2016) described the change values, the sequences, then analyzed the convergences concerning sequences on PFNs. They also discussed continuity and derivability of Pythagorean fuzzy functions.

In this paper, we define another extension of intuitionistic fuzzy sets. When $q=3$, we consider q-rung orthopair fuzzy sets as Fermatean fuzzy sets (FFSs). Here we look in details at FFS. We discuss some basic properties of FFSs. Furthermore, we expand the technique for order preference by the similarity to ideal solution (TOPSIS) method to control the MCDM issues with Fermatean fuzzy data. The TOPSIS method was first developed by Hwang and Yoon (1981) and ranks the alternatives in accordance after their distances out of the positive ideal solution (PIS) and the negative ideal solution (NIS), permanency, i.e. those best alternative need all the while the briefest separation starting with the PIS and the most distant separation from those NIS. To meet the specific requirements of real-world decision-making complications within a collection of various fuzzy frameworks in the past few decades, a few developed TOPSIS strategies need also been recognized, for instance, TOPSIS (Sattarpour et al. 2018), Fuzzy TOPSIS (Hadi-Vencheh and Mirjaberi 2014), TOPSIS with interval data (Li 2010; Niroomand et al. 2018), TOPSIS with intuitionistic fuzzy (Shen et al. 2018), interval-valued hesitant fuzzy TOPSIS (Zhang et al. 2018), Choquet based TOPSIS and TODIM (Lourenzutti et al. 2017), TOPSIS with hesitant fuzzy (Xu and Zhang 2013), TOPSIS with Pythagorean fuzzy (Liang and Xu 2017; Zhang and Xu 2014) etc. Nonetheless those TOPSIS systems furthermore its developments will be insufflated with illustrating the MCDM issues with Fermatean fuzzy data.

The contributions of this paper are the following: Sect. 2 gives formally the introductory consciousness of the paper. Then, in Sect. 3, we define Fermatean fuzzy sets and study their relationship with intuitionistic fuzzy set and Pythagorean fuzzy set. In Sect. 4, we focus on the complement operator. In next three sections, we define set operations, score function, accuracy function and Euclidean distance of FFSs. In Sect. 8, we stretch a Fermatean fuzzy TOPSIS strategy should elucidate those MCDM issues for FFSs. In Sect. 9, we outfit a useful decision-making issue will show those provision procedure of the suggested method. Finally, in Sect. 10, the conclusion and scope of future research are outlined and discussed.

2 Preliminaries

To assemble this work self-sufficient, we briefly introduce a few definitions engaged in the remaining work.

2.1 Intuitionistic fuzzy sets

Intuitionistic fuzzy set brought by Atanassov (1986) is a development of the traditional fuzzy set, which is an appropriate way to cope with vagueness. It is able to be defined as follows.

Definition 1

(Atanassov1986) The intuitionistic fuzzy sets defined on a non-empty set X as objects having the form $A=\{\langle x, \alpha _{A}(x), \beta _{A}(x)\rangle : x\in X\}$, where the functions $\alpha _{A}(x):X\rightarrow [0,1]$ and $\beta _{A}(x):X\rightarrow [0,1]$, denote the degree of membership and the degree of non-membership of each element $x \in X$ to the set A respectively, and $0\le \alpha _{A}(x)+ \beta _{A}(x)\le 1$ for all $x \in X$. Clearly, when $\beta _{A}(x)=1-\alpha _{A}(x)$ for every $x \in X$, the set A becomes a fuzzy set.

However, in practical decision-making problems the decision makers (or experts) may indicate their selections regarding the degree of an alternative about a criterion fulfilling the condition that the entirety of the assist (membership) degree and the oppose (nonmembership) degree may be bigger than 1. Noticeably, the expert’s selections are not appropriate to be represented by way of making use of the intuitionistic fuzzy set on this condition. For such instances, Yager (2013) launched a new notion of Pythagorean fuzzy set to manage this condition.

2.2 Pythagorean fuzzy sets

Currently, Yager (2013) acquainted a unique fuzzy set referred to as Pythagorean fuzzy set, whose illustration was once given as follows:

Definition 2

The Pythagorean fuzzy sets defined on a non-empty set X as objects having the form ${\mathcal {P}}=\{\langle x, \alpha _{P}(x)$, $\beta _{P}(x)\rangle : x\in X\}$, where the functions $\alpha _{P}(x): X\rightarrow [0,1]$ and $\beta _{P}(x): X \rightarrow [0,1]$, denote the degree of membership and the degree of non-membership of each element $x \in X$ to the set ${\mathcal {P}}$ respectively, and $0\le (\alpha _{P}(x))^2+ (\beta _{P}(x))^2 \le 1$, for all $x \in X$. For any Pythagorean fuzzy set ${\mathcal {P}}$ and $x \in X$, $\pi _{P}(x)=\sqrt{1-(\alpha _{P}(x))^2 - (\beta _{P}(x))^2}$ is called the degree of indeterminacy of x to ${\mathcal {P}}$.

3 Fermatean fuzzy sets

Definition 3

Let X be a universe of discourse. A Fermatean fuzzy set ${\mathcal {F}}$ in X is an object having the form

$$\begin{aligned} {\mathcal {F}}=\{\langle x, \alpha _{F}(x), \beta _{F}(x)\rangle : x\in X\}, \end{aligned}$$

where $\alpha _{F}(x):X\rightarrow [0,1]$ and $\beta _{F}(x):X\rightarrow [0,1]$, including the condition

$$\begin{aligned} 0\le (\alpha _{F}(x))^3+ (\beta _{F}(x))^3 \le 1, \end{aligned}$$

for all $x \in X$. The numbers $\alpha _{F}(x)$ and $\beta _{F}(x)$ denote, respectively, the degree of membership and the degree of non-membership of the element x in the set ${\mathcal {F}}$.

For any FFS ${\mathcal {F}}$ and $x \in X$,

$$\begin{aligned} \pi _{F}(x)=\root 3 \of {1-(\alpha _{F}(x))^3 - (\beta _{F}(x))^3} \end{aligned}$$

is identified as the degree of indeterminacy of x to ${\mathcal {F}}$.

In the interest of simplicity, we shall mention the symbol ${\mathcal {F}}=(\alpha _{F}, \beta _{F})$ for the FFS ${\mathcal {F}}=\{\langle x, \alpha _{F}(x), \beta _{F}(x)\rangle : x\in X\}$.

For simplicity, we consider the Fermatean fuzzy numbers (FFNs) be the components of the FFS.

For understanding the FFS better, we give an instance to illuminate the understandability of the FFS: the point when someone needs will plan as much craving for the level for an alternative $x_i$ on a criterion $C_j$, he might provide for the degree on which that alternative $x_i$ fulfils those criteria $C_j$ likewise 0.9, what’s more correspondingly the elective $x_i$ dissatisfies the criterion $C_j$ similarly as 0.6. We can definitely get $0.9+0.6>1$, and, therefore, it does not follow the condition of intuitionistic fuzzy sets. Also, we can get $(0.9)^2+(0.6)^2=0.81+0.36=1.17 >1$, which does not obey the constraint condition of Pythagorean fuzzy set. However, we can get $(0.9)^3+(0.6)^3=0.729+0.216=0.945 \le 1$, which is good enough to apply the FFS to control it.

We shall point out the membership grades related to Fermatean fuzzy sets as Fermatean membership grades (FMGs).

Theorem 1

The set of FMGs is larger than the set of PMGs and IMGs.

Proof

Any point (a, b) that is an IMG is also a PMG and an FMG. For any two numbers $a, b \in [0,1]$, we get $a^3 \le a^2 \le a$ and $b^3 \le b^2 \le b$. Thus $a+b \le 1 \, \Rightarrow \, a^2+b^2 \le 1 \, \Rightarrow \, a^3+b^3 \le 1$.

Yager showed that the space of PMGs is larger than the space of IMGs. There are FMGs that not PMGs and IMGs. Consider a point $\Big (\frac{\root 3 \of {7}}{2}, \frac{1}{2}\Big )$. We see that $\Big (\frac{\root 3 \of {7}}{2}\Big )^3+ \Big (\frac{1}{2}\Big )^3=1$, thus this is an FMG. Since $\Big (\frac{\root 3 \of {7}}{2}\Big )^2+ \Big (\frac{1}{2}\Big )^2=0.9148+0.25 \nleq 1$ and $\frac{\root 3 \of {7}}{2}+ \frac{1}{2}=0.9565+0.5\nleq 1$, therefore $\Big (\frac{\root 3 \of {7}}{2}, \frac{1}{2}\Big )$ is neither a PMG nor an IMG. $\square$

Fig. 1

Comparison of space of FMGs, PMGs and IMGs

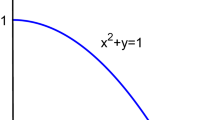
This development can be evidently recognized in Figure 1. Here we notice that IMGs are all points beneath the line $x + y \le 1$, the PMGs are all points with $x^2 + y^2 \le 1$ and the FMGs are all points with $x^3 + y^3 \le 1$. We see then that the FMGs enable for the presentation of a bigger body of nonstandard membership grades then IMGs and PMGs.

4 Complement operator

To have a firm observation on the complement operator, it is suggested that the reader may follow Klir and Yuan (1995). A comprehensive discussion on the aforesaid subject is nicely presented by Bustince et al. (2000) in the framework of intuitionistic fuzzy sets.

A complement operator N is a function $N: [0, 1] \rightarrow [0, 1]$ that fulfils:

• 1. Boundary Conditions: $N(0) = 1$ and $N(1) =0$;

• 2. Non-increasing: $N(x) \ge N(y)$ whenever $x \le y$, $\forall \, x, y \in [0,1]$;

• 3. Continuity, and;

• 4. Involution: $N(N(x)) = x$, $\forall \, x \in [0,1]$.

We notice as the function $N(x) = 1 - x$ stability is an example of a complement operator.

Sugeno (1977) and Yager (1979, 1980) each have launched the households of complement operators. The Sugeno category concerning complements is characterized as $N(x) = \frac{1 -x}{1 + \lambda x}$, for $\lambda \in (-1, \infty )$. The Yager category of complements is interpreted by $N(x) = (1 - x^P )^{1/P}$, where $P \in (0, \infty )$. We identify that to $p = 1$ it gets to be the excellent complement $N(x) = 1 - x$. We obtain $N(x) = (1 - x^2 )^{1/2}$ for $P = 2$. We note here $(N(x))^2 + x^2 = 1$. Yager indicated this as the Pythagorean complement. Yager (2014) indicated that $N(x) = (1 - x^P )^{1/P}$ is increasing with admiration to P. It will be intriguing will note that as $P \rightarrow \infty$ we get $N(x) = (1 - x^P )^{1/P}=1$ for $x \ne 1$ and $N(1) = 0$. If we put $P = 3$ in Yager class of complements, then we get $N(x) = (1 - x^3 )^{1/3}$, we note here $(N(x))^3 + x^3 = 1$. We might allude will this similarly as Fermatean complement.

5 Set operations on Fermatean fuzzy sets

Definition 4

Let ${\mathcal {F}}=(\alpha _{F}, \beta _{F})$, ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$ and ${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$ be three FFSs, then their operations are defined as follows:

(i):

${\mathcal {F}}_1 \cap {\mathcal {F}}_2=(\min \{\alpha _{F_1}, \alpha _{F_2}\}, \max \{ \beta _{F_1}, \beta _{F_2}\})$;

(ii):

${\mathcal {F}}_1 \cup {\mathcal {F}}_2=(\max \{\alpha _{F_1}, \alpha _{F_2}\}, \min \{ \beta _{F_1}, \beta _{F_2}\})$;

(iii):

${\mathcal {F}}^c=(\beta _{F}, \alpha _{F})$.

Definition 5

Let ${\mathcal {F}}=(\alpha _{F}, \beta _{F})$, ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$ and ${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$ be three FFSs and $\lambda >0$, then their operations are defined as follows:

(i):

${\mathcal {F}}_1 \boxplus {\mathcal {F}}_2=\bigg (\root 3 \of {\alpha _{F_1}^3 + \alpha _{F_2}^3-\alpha _{F_1}^3 \alpha _{F_2}^3}, \beta _{F_1}\beta _{F_2}\bigg )$;

(ii):

${\mathcal {F}}_1 \boxtimes {\mathcal {F}}_2=\bigg (\alpha _{F_1}\alpha _{F_2}, \root 3 \of {\beta _{F_1}^3 + \beta _{F_2}^3-\beta _{F_1}^3 \beta _{F_2}^3}\bigg )$;

(iii):

$\lambda {\mathcal {F}}=\bigg (\root 3 \of {1-{(1-\alpha _{F}^3)}^\lambda }, \beta _{F}^\lambda \bigg )$;

(iv):

${\mathcal {F}}^\lambda =\bigg (\alpha _{F}^\lambda , \root 3 \of {1-{(1-\beta _{F}^3 )}^\lambda }\bigg )$.

Theorem 2

For three FFSs${\mathcal {F}}=(\alpha _{F}, \beta _{F})$, ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$and${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$, the following ones are valid:

• (i) ${\mathcal {F}}_1 \boxplus {\mathcal {F}}_2={\mathcal {F}}_2 \boxplus {\mathcal {F}}_1$;

• (ii) ${\mathcal {F}}_1 \boxtimes {\mathcal {F}}_2={\mathcal {F}}_2 \boxtimes {\mathcal {F}}_1$;

• (iii) $\lambda ({\mathcal {F}}_1 \boxplus {\mathcal {F}}_2)=\lambda {\mathcal {F}}_1 \boxplus \lambda {\mathcal {F}}_2$, $\lambda >0$;

• (iv) $(\lambda _1+\lambda _2 ){\mathcal {F}}=\lambda _1 {\mathcal {F}}\boxplus \lambda _2 {\mathcal {F}}$, $\lambda _1, \lambda _2 >0$;

• (v) $({\mathcal {F}}_1 \boxtimes {\mathcal {F}}_2)^\lambda ={\mathcal {F}}_1^\lambda \boxtimes {\mathcal {F}}_2^\lambda$, $\lambda >0$;

• (vi) ${\mathcal {F}}^{\lambda _1} \boxtimes {\mathcal {F}}^{\lambda _2}={\mathcal {F}}^{(\lambda _1+\lambda _2 )}$, $\lambda _1, \lambda _2 >0$.

Proof

For the three FFSs ${\mathcal {F}}$, ${\mathcal {F}}_1$ and ${\mathcal {F}}_2$, and $\lambda , \lambda _1, \lambda _2 > 0$, according to Definition 5, we can obtain

$$\begin{aligned}&\mathrm{(i)} \, {\mathcal {F}}_1 \boxplus {\mathcal {F}}_2 =\bigg (\root 3 \of {\alpha _{F_1}^3 + \alpha _{F_2}^3-\alpha _{F_1}^3 \alpha _{F_2}^3}, \beta _{F_1}\beta _{F_2}\bigg )\\&\quad = \bigg (\root 3 \of {\alpha _{F_2}^3 + \alpha _{F_1}^3- \alpha _{F_2}^3 \alpha _{F_1}^3}, \beta _{F_2} \beta _{F_1}\bigg )= {\mathcal {F}}_2 \boxplus {\mathcal {F}}_1; \\&\mathrm{(ii)} \, {\mathcal {F}}_1 \boxtimes {\mathcal {F}}_2 =\bigg (\alpha _{F_1}\alpha _{F_2}, \root 3 \of {\beta _{F_1}^3 + \beta _{F_2}^3-\beta _{F_1}^3 \beta _{F_2}^3}\bigg ) \\& \quad =\bigg (\alpha _{F_2}\alpha _{F_1}, \root 3 \of { \beta _{F_2}^3+\beta _{F_1}^3- \beta _{F_2}^3\beta _{F_1}^3}\bigg )={\mathcal {F}}_2 \boxtimes {\mathcal {F}}_1; \\&\mathrm{(iii)} \, \lambda ({\mathcal {F}}_1 \boxplus {\mathcal {F}}_2) =\lambda \bigg (\root 3 \of {\alpha _{F_1}^3 + \alpha _{F_2}^3-\alpha _{F_1}^3 \alpha _{F_2}^3}, \beta _{F_1}\beta _{F_2}\bigg )\\&\quad =\Bigg (\root 3 \of {1-(1-\alpha _{F_1}^3 - \alpha _{F_2}^3+\alpha _{F_1}^3 \alpha _{F_2}^3)^\lambda }, (\beta _{F_1}\beta _{F_2})^\lambda \Bigg )\\&\quad =\Bigg (\root 3 \of {1-(1-\alpha _{F_1}^3)^\lambda (1 - \alpha _{F_2}^3)^\lambda }, \beta _{F_1}^\lambda \beta _{F_2}^\lambda \Bigg );\\&\lambda {\mathcal {F}}_1 \boxplus \lambda {\mathcal {F}}_2 = \bigg (\root 3 \of {1-{(1-\alpha _{F_1}^3 )}^\lambda }, \beta _{F_1}^\lambda \bigg ) \boxplus \bigg (\root 3 \of {1-{(1-\alpha _{F_2}^3 )}^\lambda }, \beta _{F_2}^\lambda \bigg ) \\&\quad =\Bigg (\root 3 \of {1-(1-\alpha _{F_1}^3)^\lambda (1 - \alpha _{F_2}^3)^\lambda }, \beta _{F_1}^\lambda \beta _{F_2}^\lambda \Bigg ) =\lambda ({\mathcal {F}}_1 \boxplus {\mathcal {F}}_2); \\&\mathrm{(iv)} \, (\lambda _1+\lambda _2 ){\mathcal {F}} = (\lambda _1+\lambda _2)(\alpha _{F}, \beta _{F}) =\bigg (\root 3 \of {1-{(1-\alpha _{F}^3 )}^{\lambda _1+\lambda _2}}, \beta _{F}^{\lambda _1+\lambda _2} \bigg )\\&\quad =\bigg (\root 3 \of {1-{(1-\alpha _{F}^3 )}^{\lambda _1} {(1-\alpha _{F}^3)}^{\lambda _2}}, \beta _{F}^{\lambda _1+\lambda _2} \bigg ) =\bigg (\root 3 \of {1-{(1-\alpha _{F}^3 )}^{\lambda _1}}, \beta _{F}^{\lambda _1}\bigg ) \\&\qquad \boxplus \bigg (\root 3 \of {1-{(1-\alpha _{F}^3)}^{\lambda _2}}, \beta _{F}^{\lambda _2}\bigg ) = \lambda _1 {\mathcal {F}}\boxplus \lambda _2 {\mathcal {F}}; \\&\mathrm{(v)} \, ({\mathcal {F}}_1 \boxtimes {\mathcal {F}}_2)^\lambda =\bigg (\alpha _{F_1}\alpha _{F_2}, \root 3 \of {\beta _{F_1}^3 + \beta _{F_2}^3-\beta _{F_1}^3 \beta _{F_2}^3}\bigg )^\lambda \\&\quad =\bigg ((\alpha _{F_1}\alpha _{F_2})^\lambda , \root 3 \of {1-(1-\beta _{F_1}^3 - \beta _{F_2}^3+\beta _{F_1}^3 \beta _{F_2}^3)^\lambda }\bigg )\\&\quad =\bigg (\alpha _{F_1}^\lambda \alpha _{F_2}^\lambda , \root 3 \of {1-(1-\beta _{F_1}^3)^\lambda (1-\beta _{F_2}^3)^\lambda }\bigg )\\&\quad =\bigg (\alpha _{F_1}^\lambda , \root 3 \of {1-{(1-\beta _{F_1}^3)}^\lambda }\bigg ) \boxtimes \bigg (\alpha _{F_2}^\lambda , \root 3 \of {1-{(1-\beta _{F_2}^3 )}^\lambda }\bigg ) ={\mathcal {F}}_1^\lambda \boxtimes {\mathcal {F}}_2^\lambda ; \\&\mathrm{(vi)} \, {\mathcal {F}}^{\lambda _1} \boxtimes {\mathcal {F}}^{\lambda _2} =\bigg (\alpha _{F}^{\lambda _1}, \root 3 \of {1-{(1-\beta _{F}^3)}^{\lambda _1}}\bigg ) \boxtimes \bigg (\alpha _{F}^{\lambda _2}, \root 3 \of {1-{(1-\beta _{F}^3 )}^{\lambda _2}}\bigg )\\&\quad =\bigg (\alpha _{F}^{\lambda _1+\lambda _2}, \root 3 \of {1-{(1-\beta _{F}^3 )}^{\lambda _1+\lambda _2}}\bigg ) ={\mathcal {F}}^{(\lambda _1+\lambda _2 )}. \end{aligned}$$

$\square$

Theorem 3

For three FFSs${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$, ${\mathcal {F}}_2=(\alpha _{F_2}$, $\beta _{F_2})$and${\mathcal {F}}_3=(\alpha _{F_3}, \beta _{F_3})$, the following ones are valid:

• (i) ${\mathcal {F}}_1 \cap {\mathcal {F}}_2={\mathcal {F}}_2 \cap {\mathcal {F}}_1$;

• (ii) ${\mathcal {F}}_1 \cup {\mathcal {F}}_2={\mathcal {F}}_2 \cup {\mathcal {F}}_1$;

• (iii) ${\mathcal {F}}_1 \cap ({\mathcal {F}}_2 \cap {\mathcal {F}}_3)=({\mathcal {F}}_1 \cap {\mathcal {F}}_2) \cap {\mathcal {F}}_3$;

• (iv) ${\mathcal {F}}_1 \cup ({\mathcal {F}}_2 \cup {\mathcal {F}}_3)=({\mathcal {F}}_1 \cup {\mathcal {F}}_2) \cup {\mathcal {F}}_3$;

• (v) $\lambda ({\mathcal {F}}_1 \cup {\mathcal {F}}_2)=\lambda {\mathcal {F}}_1 \cup \lambda {\mathcal {F}}_2$;

• (vi) $({\mathcal {F}}_1 \cup {\mathcal {F}}_2)^\lambda ={\mathcal {F}}_1^\lambda \cup {\mathcal {F}}_2^\lambda$.

Proof

We will present the proofs of (i), (iii) and (v). For the four FFSs ${\mathcal {F}}$, ${\mathcal {F}}_1$, ${\mathcal {F}}_2$ and ${\mathcal {F}}_3$, and $\lambda > 0$, according to Definitions 4 and 5, we can obtain

$$\begin{aligned}&\mathrm{(i)} \, {\mathcal {F}}_1 \cap {\mathcal {F}}_2 \\&\quad =(\min \{\alpha _{F_1}, \alpha _{F_2}\}, \max \{ \beta _{F_1}, \beta _{F_2}\})\\&\quad =(\min \{\alpha _{F_2}, \alpha _{F_1}\}, \max \{ \beta _{F_2}, \beta _{F_1}\})={\mathcal {F}}_2 \cap {\mathcal {F}}_1; \\&\mathrm{(iii)} \, {\mathcal {F}}_1 \cap ({\mathcal {F}}_2 \cap {\mathcal {F}}_3) \\&\quad =(\alpha _{F_1}, \beta _{F_1}) \\&\quad \cap (\min \{\alpha _{F_2},\alpha _{F_3}\}, \max \{ \beta _{F_2}, \beta _{F_3}\}) \\&\quad =(\min \{\alpha _{F_1},\min \{\alpha _{F_2}, \alpha _{F_3}\}\}, \max \{\beta _{F_1}, \max \{ \beta _{F_2}, \beta _{F_3}\}\}) \\&\quad =(\min \{\min \{\alpha _{F_1},\alpha _{F_2}\}, \alpha _{F_3}\}, \max \{\max \{\beta _{F_1}, \beta _{F_2}\}, \beta _{F_3}\}) \\&\quad = (\min \{\alpha _{F_1}, \alpha _{F_2}\}, \max \{ \beta _{F_1}, \beta _{F_2}\}) \cap (\alpha _{F_3}, \beta _{F_3}) \\&\quad =({\mathcal {F}}_1 \cap {\mathcal {F}}_2) \cap {\mathcal {F}}_3; \\&\mathrm{(v)} \, \lambda ({\mathcal {F}}_1 \cup {\mathcal {F}}_2) \\&\quad =\lambda (\max \{\alpha _{F_1}, \alpha _{F_2}\}, \min \{ \beta _{F_1}, \beta _{F_2}\})\\&\quad =\bigg (\root 3 \of {1-(1-\max \{\alpha _{F_1}^3, \alpha _{F_2}^3\})^\lambda }, \min \{ \beta _{F_1}^\lambda , \beta _{F_2}^\lambda \}\bigg );\\&\lambda {\mathcal {F}}_1 \cup \lambda {\mathcal {F}}_2 \\&\quad = \bigg (\root 3 \of {1-{(1-\alpha _{F_1}^3 )}^\lambda }, \beta _{F_1}^\lambda \bigg ) \\&\quad \cup \bigg (\root 3 \of {1-{(1-\alpha _{F_2}^3 )}^\lambda }, \beta _{F_2}^\lambda \bigg )\\&\quad =\bigg (\max \bigg \{\root 3 \of {1-{(1-\alpha _{F_1}^3)}^\lambda }, \root 3 \of {1-{(1-\alpha _{F_2}^3 )}^\lambda }\bigg \}, \\&\min \{\beta _{F_1}^\lambda , \beta _{F_2}^\lambda \}\bigg ) \\&\quad =\bigg (\root 3 \of {1-(1-\max \{\alpha _{F_1}^3, \alpha _{F_2}^3\})^\lambda },\\&\min \{ \beta _{F_1}^\lambda , \beta _{F_2}^\lambda \}\bigg ) \\&\quad =\lambda ({\mathcal {F}}_1 \cup {\mathcal {F}}_2). \end{aligned}$$

The other assertions are proved analogously. $\square$

Theorem 4

Let${\mathcal {F}}=(\alpha _{F}, \beta _{F})$, ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$and${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$be three FFSs, then

• (i) $({\mathcal {F}}_1 \cap {\mathcal {F}}_2)^c={\mathcal {F}}_1^c \cup {\mathcal {F}}_2^c$;

• (ii) $({\mathcal {F}}_1 \cup {\mathcal {F}}_2)^c={\mathcal {F}}_1^c \cap {\mathcal {F}}_2^c$;

• (iii) $({\mathcal {F}}_1 \boxplus {\mathcal {F}}_2)^c={\mathcal {F}}_1^c \boxtimes {\mathcal {F}}_2^c$;

• (iv) $({\mathcal {F}}_1 \boxtimes {\mathcal {F}}_2)^c={\mathcal {F}}_1^c \boxplus {\mathcal {F}}_2^c$;

• (v) $({\mathcal {F}}^c)^\lambda =(\lambda {\mathcal {F}})^c$;

• (vi) $\lambda ({\mathcal {F}}^c)=({\mathcal {F}}^\lambda )^c$.

Proof

We will present the proofs of (i), (iii) and (v). For the three FFSs ${\mathcal {F}}$, ${\mathcal {F}}_1$ and ${\mathcal {F}}_2$, and $\lambda > 0$, according to Definition 4 and Definition 5, we can obtain

$$\begin{aligned}&\mathrm{(i)} \, ({\mathcal {F}}_1 \cap {\mathcal {F}}_2)^c \\&\quad =(\min \{\alpha _{F_1}, \alpha _{F_2}\}, \max \{ \beta _{F_1}, \beta _{F_2}\})^c \\&\quad =(\max \{ \beta _{F_1}, \beta _{F_2}\}, \min \{\alpha _{F_1}, \alpha _{F_2}\}) \\&\quad =(\beta _{F_1}, \alpha _{F_1}) \cup (\beta _{F_2}, \alpha _{F_2})={\mathcal {F}}_1^c \cup {\mathcal {F}}_2^c; \\&\mathrm{(iii)} \, ({\mathcal {F}}_1 \boxplus {\mathcal {F}}_2)^c \\&\quad =\bigg (\root 3 \of {\alpha _{F_1}^3 + \alpha _{F_2}^3-\alpha _{F_1}^3 \alpha _{F_2}^3}, \beta _{F_1}\beta _{F_2}\bigg )^c \\&\quad =\bigg (\beta _{F_1}\beta _{F_2}, \root 3 \of {\alpha _{F_1}^3 + \alpha _{F_2}^3-\alpha _{F_1}^3 \alpha _{F_2}^3}\bigg ) \\&\quad =(\beta _{F_1}, \alpha _{F_1}) \boxtimes (\beta _{F_2}, \alpha _{F_2})={\mathcal {F}}_1^c \boxtimes {\mathcal {F}}_2^c; \\&\mathrm{(v)} \, ({\mathcal {F}}^c)^\lambda =(\beta _{F}, \alpha _{F})^\lambda \\&\quad =\bigg (\beta _{F}^\lambda , \root 3 \of {1-{(1-\alpha _{F}^3 )}^\lambda }\bigg ) =\bigg (\root 3 \of {1-{(1-\alpha _{F}^3 )}^\lambda }, \beta _{F}^\lambda \bigg )^c \\&\quad =(\lambda {\mathcal {F}})^c. \end{aligned}$$

The other assertions are proved analogously. $\square$

Theorem 5

Let${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$, ${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$and${\mathcal {F}}_3=(\alpha _{F_3}, \beta _{F_3})$be three FFSs, then

• (i) $({\mathcal {F}}_1 \cap {\mathcal {F}}_2) \boxplus {\mathcal {F}}_3=({\mathcal {F}}_1 \boxplus {\mathcal {F}}_3) \cap ({\mathcal {F}}_2 \boxplus {\mathcal {F}}_3)$;

• (ii) $({\mathcal {F}}_1 \cup {\mathcal {F}}_2) \boxplus {\mathcal {F}}_3=({\mathcal {F}}_1 \boxplus {\mathcal {F}}_3) \cup ({\mathcal {F}}_2 \boxplus {\mathcal {F}}_3)$;

• (iii) $({\mathcal {F}}_1 \cap {\mathcal {F}}_2) \boxtimes {\mathcal {F}}_3=({\mathcal {F}}_1 \boxtimes {\mathcal {F}}_3) \cap ({\mathcal {F}}_2 \boxtimes {\mathcal {F}}_3)$;

• (iv) $({\mathcal {F}}_1 \cup {\mathcal {F}}_2) \boxtimes {\mathcal {F}}_3=({\mathcal {F}}_1 \boxtimes {\mathcal {F}}_3) \cup ({\mathcal {F}}_2 \boxtimes {\mathcal {F}}_3)$.

Proof

We will present the proofs of (i) and (iii). For the three FFSs ${\mathcal {F}}_1$, ${\mathcal {F}}_2$ and ${\mathcal {F}}_3$, according to Definitions 4 and 5, we can obtain

$$\begin{aligned}&\mathrm{(i)} \, ({\mathcal {F}}_1 \cap {\mathcal {F}}_2) \boxplus {\mathcal {F}}_3 =(\min \{\alpha _{F_1}, \alpha _{F_2}\}, \max \{ \beta _{F_1}, \beta _{F_2}\}) \boxplus (\alpha _{F_3}, \beta _{F_3}) \\&\quad =\bigg (\root 3 \of {\min \{\alpha _{F_1}^3, \alpha _{F_2}^3\}+\alpha _{F_3}^3-\alpha _{F_3}^3\min \{\alpha _{F_1}^3, \alpha _{F_2}^3\}}, \max \{ \beta _{F_1}, \beta _{F_2}\}\beta _{F_3}\bigg ) \\&\quad =\bigg (\root 3 \of {(1-\alpha _{F_3}^3)\min \{\alpha _{F_1}^3, \alpha _{F_2}^3\}+\alpha _{F_3}^3}, \max \{ \beta _{F_1}\beta _{F_3}, \beta _{F_2}\beta _{F_3}\}\bigg ) ;\\&({\mathcal {F}}_1 \boxplus {\mathcal {F}}_3) \cap ({\mathcal {F}}_2 \boxplus {\mathcal {F}}_3) =\bigg (\root 3 \of {\alpha _{F_1}^3 + \alpha _{F_3}^3-\alpha _{F_1}^3 \alpha _{F_3}^3}, \beta _{F_1}\beta _{F_3}\bigg ) \\&\quad \cap \bigg (\root 3 \of {\alpha _{F_2}^3 + \alpha _{F_3}^3-\alpha _{F_2}^3 \alpha _{F_3}^3}, \beta _{F_2}\beta _{F_3}\bigg )\\&\quad =\bigg (\min \Big \{\root 3 \of {\alpha _{F_1}^3 + \alpha _{F_3}^3-\alpha _{F_1}^3 \alpha _{F_3}^3}, \\&\quad \qquad \root 3 \of {\alpha _{F_2}^3 + \alpha _{F_3}^3-\alpha _{F_2}^3 \alpha _{F_3}^3}\Big \}, \max \{\beta _{F_1}\beta _{F_3}, \beta _{F_2}\beta _{F_3}\}\bigg )\\&\quad =\bigg (\min \Big \{\root 3 \of {(1-\alpha _{F_3}^3)\alpha _{F_1}^3 + \alpha _{F_3}^3}, \\&\quad \qquad \root 3 \of {(1-\alpha _{F_3}^3)\alpha _{F_2}^3 + \alpha _{F_3}^3}\Big \}, \max \{\beta _{F_1}\beta _{F_3}, \beta _{F_2}\beta _{F_3}\}\bigg )\\&\quad =\bigg (\root 3 \of {(1-\alpha _{F_3}^3)\min \{\alpha _{F_1}^3, \alpha _{F_2}^3\}+\alpha _{F_3}^3}, \max \{\beta _{F_1}\beta _{F_3}, \beta _{F_2}\beta _{F_3}\}\bigg ). \\&\qquad \hbox {Hence} \, ({\mathcal {F}}_1 \cap {\mathcal {F}}_2) \boxplus {\mathcal {F}}_3=({\mathcal {F}}_1 \boxplus {\mathcal {F}}_3) \cap ({\mathcal {F}}_2 \boxplus {\mathcal {F}}_3). \\&\mathrm{(iii)} \, ({\mathcal {F}}_1 \cap {\mathcal {F}}_2) \boxtimes {\mathcal {F}}_3 =(\min \{\alpha _{F_1}, \alpha _{F_2}\}, \max \{ \beta _{F_1}, \beta _{F_2}\}) \boxtimes (\alpha _{F_3}, \beta _{F_3}) \\&\quad =\bigg (\min \{ \alpha _{F_1}, \alpha _{F_2}\}\alpha _{F_3}, \root 3 \of {\max \{\beta _{F_1}^3, \beta _{F_2}^3\}+\beta _{F_3}^3-\beta _{F_3}^3\max \{\beta _{F_1}^3, \beta _{F_2}^3\}}\bigg )\\&\quad =\Big (\min \{ \alpha _{F_1}\alpha _{F_3}, \alpha _{F_2}\alpha _{F_3}\}, \root 3 \of {(1-\beta _{F_3}^3)\max \{\beta _{F_1}^3, \beta _{F_2}^3\}+\beta _{F_3}^3}\Big ); \\&({\mathcal {F}}_1 \boxtimes {\mathcal {F}}_3) \cap ({\mathcal {F}}_2 \boxtimes {\mathcal {F}}_3) =\bigg (\alpha _{F_1}\alpha _{F_3}, \root 3 \of {\beta _{F_1}^3 + \beta _{F_3}^3-\beta _{F_1}^3 \beta _{F_3}^3}\bigg ) \\&\quad \cap \bigg (\alpha _{F_2}\alpha _{F_3}, \root 3 \of {\beta _{F_2}^3 + \beta _{F_3}^3-\beta _{F_2}^3 \beta _{F_3}^3}\bigg ) \\&\quad =\bigg (\alpha _{F_1}\alpha _{F_3}, \root 3 \of {(1-\beta _{F_3}^3)\beta _{F_1}^3 + \beta _{F_3}^3}\bigg )\\&\quad \cap \bigg (\alpha _{F_2}\alpha _{F_3}, \root 3 \of {(1-\beta _{F_3}^3)\beta _{F_2}^3 + \beta _{F_3}^3}\bigg ) \\&\quad =\bigg (\min \{\alpha _{F_1}\alpha _{F_3},\alpha _{F_2}\alpha _{F_3}\}, \max \Big \{ \root 3 \of {(1-\beta _{F_3}^3)\beta _{F_1}^3 + \beta _{F_3}^3}, \root 3 \of {(1-\beta _{F_3}^3)\beta _{F_2}^3 + \beta _{F_3}^3}\Big \}\bigg ) \\&\quad =\Big (\min \{ \alpha _{F_1}\alpha _{F_3}, \alpha _{F_2}\alpha _{F_3}\}, \root 3 \of {(1-\beta _{F_3}^3)\max \{\beta _{F_1}^3, \beta _{F_2}^3\}+\beta _{F_3}^3}\Big ). \\&\qquad \hbox {Hence} \, ({\mathcal {F}}_1 \cap {\mathcal {F}}_2) \boxtimes {\mathcal {F}}_3=({\mathcal {F}}_1 \boxtimes {\mathcal {F}}_3) \cap ({\mathcal {F}}_2 \boxtimes {\mathcal {F}}_3). \end{aligned}$$

The other assertions are proved analogously. $\square$

6 Ranking of Fermatean fuzzy sets

In order to rank FFSs, we define score function of the FFS:

Definition 6

Let ${\mathcal {F}}=(\alpha _{F}, \beta _{F})$ be a FFS, then the score function of ${\mathcal {F}}$ can be represented as

$$\begin{aligned} score({\mathcal {F}})=\alpha _{F}^3-\beta _{F}^3. \end{aligned}$$

Proposition 1

For any FFS${\mathcal {F}}=(\alpha _{F}, \beta _{F})$, the suggested score function$score({\mathcal {F}}) \in [-1,1]$.

Proof

We know that for FFS, $\alpha _{F}^3+\beta _{F}^3 \le 1$. Thus $\alpha _{F}^3-\beta _{F}^3 \le \alpha _{F}^3 \le 1$ and $\alpha _{F}^3-\beta _{F}^3 \ge -\beta _{F}^3 \ge -1$. Hence $-1 \le \alpha _{F}^3-\beta _{F}^3 \le 1$, namely $score({\mathcal {F}}) \in [-1,1]$. In particular, if ${\mathcal {F}}=(0, 1)$, then $score({\mathcal {F}})=-1$; if ${\mathcal {F}}=(1, 0)$, then $score({\mathcal {F}})=1$. $\square$

Definition 7

Let ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$ and ${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$ be two FFSs, a natural quasi-ordering concerning the FFSs as follows:

$$\begin{aligned} {\mathcal {F}}_1 \ge {\mathcal {F}}_2 \text{ if } \text{ and } \text{ only } \text{ if } \alpha _{F_1} \ge \alpha _{F_2} \text{ and } \beta _{F_1} \le \beta _{F_2}. \end{aligned}$$

In Definitions 8 and 9, we define a new relation between Fermatean fuzzy sets.

Definition 8

Let ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$ and ${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$ be two FFSs, $score({\mathcal {F}}_1)$ and $score({\mathcal {F}}_2)$ be the score function of ${\mathcal {F}}_1$ and ${\mathcal {F}}_2$ respectively, then

• 1. If $score({\mathcal {F}}_1) < score({\mathcal {F}}_2)$, then ${\mathcal {F}}_1 < {\mathcal {F}}_2$;

• 2. If $score({\mathcal {F}}_1) > score({\mathcal {F}}_2)$, then ${\mathcal {F}}_1 > {\mathcal {F}}_2$;

• 3. If $score({\mathcal {F}}_1) = score({\mathcal {F}}_2)$, then ${\mathcal {F}}_1 \sim {\mathcal {F}}_2$.

Example 1

Let ${\mathcal {F}}_1=(0.93, 0.60)$ and ${\mathcal {F}}_2=(0.85, 0.75)$, according to Definition 6, $score({\mathcal {F}}_1)=(0.93)^3-(0.60)^3=0.588357$ and $score({\mathcal {F}}_2)=(0.85)^3-(0.75)^3=0.19225$. Apparently, $score({\mathcal {F}}_1)>score({\mathcal {F}}_2)$. According to Definition 8, we have ${\mathcal {F}}_1 > {\mathcal {F}}_2$.

To provide a comparison of the majority of FFSs the efficiency of score function is accepted in this field. But in some cases, it cannot be applied to have a proper and appropriate notion in which the better FFS can be selected. For example, if ${\mathcal {F}}_1=\bigg (\frac{\root 3 \of {4}}{2}, \frac{\root 3 \of {4}}{2}\bigg )$ and ${\mathcal {F}}_2=(0.5,0.5)$, then $score({\mathcal {F}}_1)= score({\mathcal {F}}_2)=0$. More generally, if any FFS satisfies $\alpha _{F}=\beta _{F}$, then its score is 0. But we know that these FFSs may not match with each other. To rectify the definition of score function we define here accuracy function for FFS in the following way.

Definition 9

Let ${\mathcal {F}}=(\alpha _{F}, \beta _{F})$ be an FFS, then the accuracy function regarding ${\mathcal {F}}$ can be described as follows:

$$\begin{aligned} acc({\mathcal {F}})=\alpha _{F}^3+\beta _{F}^3. \end{aligned}$$

Clearly, $acc({\mathcal {F}}) \in [0,1]$. In fact $0 \le acc({\mathcal {F}})=\alpha _{F}^3+\beta _{F}^3 \le 1$. Bigger the value of $acc({\mathcal {F}})$, higher the accuracy of FFS ${\mathcal {F}}$ will be.

From Definitions  3 and 9, we can get $\pi _{F}^3+acc({\mathcal {F}})=1$. The lower degree of indeterminacy makes the higher accuracy of the FFS ${\mathcal {F}}=(\alpha _{F}, \beta _{F})$.

In light of those score function and accuracy function for FFSs, those positioning strategy to any two FFSs could make characterized as:

Definition 10

Let ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$ and ${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$ be two FFSs. $score({\mathcal {F}}_i)$ and $acc({\mathcal {F}}_i)$$(i=1,2)$ are the score values and accuracy values of ${\mathcal {F}}_1$ and ${\mathcal {F}}_2$ respectively, then

• 1. If $score({\mathcal {F}}_1) < score({\mathcal {F}}_2)$, then ${\mathcal {F}}_1 < {\mathcal {F}}_2$;

• 2. If $score({\mathcal {F}}_1) > score({\mathcal {F}}_2)$, then ${\mathcal {F}}_1 > {\mathcal {F}}_2$;

• 3. If $score({\mathcal {F}}_1) = score({\mathcal {F}}_2)$, then

  • (i) If $acc({\mathcal {F}}_1) < acc({\mathcal {F}}_2)$, then ${\mathcal {F}}_1 < {\mathcal {F}}_2$;

  • (ii) If $acc({\mathcal {F}}_1) > acc({\mathcal {F}}_2)$, then ${\mathcal {F}}_1 > {\mathcal {F}}_2$;

  • (iii) If $acc({\mathcal {F}}_1) = acc({\mathcal {F}}_2)$, then ${\mathcal {F}}_1 = {\mathcal {F}}_2$.

7 Euclidean distance of Fermatean fuzzy sets

In what follows, we define Euclidean distance of FFSs which will be helpful later.

Definition 11

Let ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$ and ${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$ be two FFSs. Then the Euclidean distance between ${\mathcal {F}}_1$ and ${\mathcal {F}}_2$ is:

$$\begin{aligned}&d({\mathcal {F}}_1, {\mathcal {F}}_2) \nonumber \\&\quad =\sqrt{\frac{1}{2}\big [(\alpha _{F_1}^3-\alpha _{F_2}^3)^2 +(\beta _{F_1}^3-\beta _{F_2}^3)^2+(\pi _{F_1}^3-\pi _{F_2}^3)^2\big ]}. \end{aligned}$$

(1)

We can use an example to illustrate the Euclidean distance measure. If ${\mathcal {F}}_1=(0.8,0.62)$ and ${\mathcal {F}}_2=(0.9,0.5)$ are two FFSs then degree of indeterminacy of ${\mathcal {F}}_1$ and ${\mathcal {F}}_2$ are $\pi _{F_1}=\root 3 \of {1-(0.8)^3-(0.62)^3}=\root 3 \of {0.249672}$ and $\pi _{F_2}=\root 3 \of {1-(0.9)^3-(0.5)^3}=\root 3 \of {0.146}$ respectively, and the Euclidean distance between ${\mathcal {F}}_1$ and ${\mathcal {F}}_2$ is $d({\mathcal {F}}_1, {\mathcal {F}}_2) = 0.18798952$ (Approx.).

Based on Definition 11, we can derive some properties of the Euclidean distance of two FFSs.

Theorem 6

Let ${\mathcal {F}}_1=(\alpha _{F_1}, \beta _{F_1})$ and ${\mathcal {F}}_2=(\alpha _{F_2}, \beta _{F_2})$ be two FFSs, then

• (i) $d({\mathcal {F}}_1, {\mathcal {F}}_2)=d({\mathcal {F}}_2, {\mathcal {F}}_1)$;

• (ii) $d({\mathcal {F}}_1, {\mathcal {F}}_2)=0$if and only if${\mathcal {F}}_1={\mathcal {F}}_2$;

• (iii) $0 \le d({\mathcal {F}}_1, {\mathcal {F}}_2) \le \sqrt{2}$.

Proof

From Definition 3, we can obtain $\alpha _{F_1}, \beta _{F_1}, \alpha _{F_2}, \beta _{F_2} \in [0,1]$, $0\le \alpha _{F_1}^3+ \beta _{F_1}^3 \le 1$ and $0\le \alpha _{F_2}^3+ \beta _{F_2}^3 \le 1$, then

$$\begin{aligned}&\mathrm{(i)} \, d({\mathcal {F}}_1, {\mathcal {F}}_2) \\&\quad =\sqrt{\frac{1}{2}\big [(\alpha _{F_1}^3-\alpha _{F_2}^3)^2 +(\beta _{F_1}^3-\beta _{F_2}^3)^2+(\pi _{F_1}^3-\pi _{F_2}^3)^2\big ]}\\&\quad =\sqrt{\frac{1}{2}\big [(\alpha _{F_2}^3-\alpha _{F_1}^3)^2 +(\beta _{F_2}^3-\beta _{F_1}^3)^2+(\pi _{F_2}^3-\pi _{F_1}^3)^2\big ]}\\&\quad =d({\mathcal {F}}_1, {\mathcal {F}}_2); \\&\mathrm{(ii)} \, \hbox {Let} \, d({\mathcal {F}}_1, {\mathcal {F}}_2)\\&\quad =\sqrt{\frac{1}{2}\big [(\alpha _{F_1}^3-\alpha _{F_2}^3)^2 +(\beta _{F_1}^3-\beta _{F_2}^3)^2+(\pi _{F_1}^3-\pi _{F_2}^3)^2\big ]} \\&\quad =0, \\&\qquad \hbox {then we get} \, (\alpha _{F_1}^3-\alpha _{F_2}^3)^2=0, (\beta _{F_1}^3-\beta _{F_2}^3)^2=0, \\&\qquad (\pi _{F_1}^3-\pi _{F_2}^3)^2=0, \\&\qquad \hbox {and thus} \, \alpha _{F_1}=\alpha _{F_2}, \beta _{F_1}=\beta _{F_2}, \\&\qquad \pi _{F_1}=\pi _{F_2} \, \hbox {i.e.}, \, {\mathcal {F}}_1={\mathcal {F}}_2; \\&\mathrm{(iii)} \, \hbox {See below}. \end{aligned}$$

Obviously $d({\mathcal {F}}_1, {\mathcal {F}}_2) \ge 0$. Now

$$\begin{aligned}&d({\mathcal {F}}_1, {\mathcal {F}}_2) \\&\quad = \sqrt{\frac{1}{2}\big [(\alpha _{F_1}^3-\alpha _{F_2}^3)^2 +(\beta _{F_1}^3-\beta _{F_2}^3)^2+(\pi _{F_1}^3-\pi _{F_2}^3)^2\big ]}\\&\quad = \sqrt{\frac{1}{2}\big [(\alpha _{F_1}^3-\alpha _{F_2}^3)^2 +(\beta _{F_1}^3-\beta _{F_2}^3)^2+ [(\alpha _{F_1}^3+\alpha _{F_2}^3) +(\beta _{F_1}^3+\beta _{F_2}^3)]^2\big ]}\\&\quad \le \sqrt{\frac{1}{2}\big [2\alpha _{F_1}^6+2\alpha _{F_2}^6 +2\beta _{F_1}^6+2\beta _{F_2}^6+ 4\alpha _{F_1}^3\beta _{F_1}^3+4\alpha _{F_2}^3\beta _{F_2}^3\big ]}\\&\quad = \sqrt{(\alpha _{F_1}^3+ \beta _{F_1}^3)^2+(\alpha _{F_2}^3+ \beta _{F_2}^3)^2}\\&\quad \le \sqrt{2}. \end{aligned}$$

Thus the proof is completed. $\square$

Theorem 7

Let${\mathcal {F}}_i=(\alpha _{F_i}, \beta _{F_i}) \, (i=1,2,3)$be three FFSs, if${\mathcal {F}}_1 \le {\mathcal {F}}_2 \le {\mathcal {F}}_3$, then$d({\mathcal {F}}_1, {\mathcal {F}}_2) \le d({\mathcal {F}}_1, {\mathcal {F}}_3)$and$d({\mathcal {F}}_2, {\mathcal {F}}_3) \le d({\mathcal {F}}_1, {\mathcal {F}}_3)$.

Proof

If ${\mathcal {F}}_1 \le {\mathcal {F}}_2 \le {\mathcal {F}}_3$ then $\alpha _{F_1} \le \alpha _{F_2} \le \alpha _{F_3}$ and $\beta _{F_1} \ge \beta _{F_2} \ge \beta _{F_3}$. According to Definition 11, we get,

$$\begin{aligned}&d({\mathcal {F}}_1, {\mathcal {F}}_2)\\&\quad =\sqrt{\frac{1}{2}\big [(\alpha _{F_1}^3-\alpha _{F_2}^3)^2 +(\beta _{F_1}^3-\beta _{F_2}^3)^2+(\pi _{F_1}^3-\pi _{F_2}^3)^2\big ]}\\&\quad \le \sqrt{\frac{1}{2}\big [(\alpha _{F_1}^3-\alpha _{F_3}^3)^2 +(\beta _{F_1}^3-\beta _{F_3}^3)^2+(\pi _{F_1}^3-\pi _{F_3}^3)^2\big ]}\\&\quad =d({\mathcal {F}}_1, {\mathcal {F}}_3) \quad \hbox {and}\quad d({\mathcal {F}}_2, {\mathcal {F}}_3)\\&\quad =\sqrt{\frac{1}{2}\big [(\alpha _{F_2}^3-\alpha _{F_3}^3)^2 +(\beta _{F_2}^3-\beta _{F_3}^3)^2+(\pi _{F_2}^3-\pi _{F_3}^3)^2\big ]}\\&\quad \le \sqrt{\frac{1}{2}\big [(\alpha _{F_1}^3-\alpha _{F_3}^3)^2 +(\beta _{F_1}^3-\beta _{F_3}^3)^2+(\pi _{F_1}^3-\pi _{F_3}^3)^2\big ]}\\&\quad =d({\mathcal {F}}_1, {\mathcal {F}}_3). \end{aligned}$$

$\square$

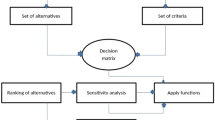
8 Fermatean fuzzy TOPSIS method to MCDM problem

In current section, we shall analyze how to employ the TOPSIS method to answer the MCDM problems where the ranking data is specified in FFNs. A PIS always wants maximum value of the benefit criteria and minimum value the cost criteria. On the other hand, a NIS always wants maximum value of the cost criteria and minimum value the benefit criteria.

8.1 Description of the MCDM problem with FFNs

The main work is done in most of the MCDM problem is to rank one or more alternatives from a collection of possible alternatives regarding multiple criteria. For a stated MCDM problem under Fermatean fuzzy domain, presume that there are m alternatives $S_i \, (i = 1, 2, \ldots , m)$ and n criterion $C_j \, (j = 1, 2, \ldots , n)$ with the criteria weight vector $w = (w_1,w_2,\ldots , w_n)^T$ certain up to expectation $0 \le w_j \le 1$, $j = 1, 2, \ldots , n$, and $\sum _{j=1}^{n}w_j = 1$. We express the assessment values of the alternative $S_i$ with respect to the criterion $C_j$ by $C_j(S_i ) =(u_{ij}, v_{ij})$, and $R =\big (C_j (S_i )\big )_{m \times n}$ is a Fermatean fuzzy decision matrix. Thus, the MCDM issue for FFNs might a chance to be acknowledged similarly as the resulting matrix form:

(2)

which implies that those degrees should which the alternative $S_i$ fulfils the attributes $C_j$ will be the value $u_{ij}$ and the degree should which the alternative $S_i$ disappoints the attributes $C_j$ may be the worth $v_{ij}$.

8.2 The proposed decision method

With successfully fathom the previously stated MCDM issue with FFNs, in the emulating, we present a Fermatean fuzzy TOPSIS system. The suggested systems need aid dependent upon the guideline that optimal alternative ought to need those briefest separations starting with the PIS and the most distant separation detachment starting with those NIS.

Thus, this method begins with the computation of Fermatean fuzzy PIS (FFPIS) and Fermatean fuzzy NIS (FFNIS). Recognizing up to expectation the choice data takes the structure of FFNs, we promote score function based totally evaluation method presented within Definition 6 in conformity with determining the FFPIS and the FFNIS. We symbolize the FFPIS via $S^+$, which may stay calculated by the use of the accordant equation:

$$\begin{aligned} S^+= & {} \left\{ \begin{array}{l} \max \limits _{i} \langle score(C_j(S_i))\rangle \ | \ j=1,2, \ldots , n, \\ \quad \text{ if } \, c_j \, \text{ is } \text{ a } \text{ benefit } \text{ criterion } \\ \min \limits _{i} \langle score(C_j(S_i))\rangle \ | \ j=1,2, \ldots , n, \\ \quad \text{ if } \, c_j \, \text{ is } \text{ a } \text{ cost } \text{ criterion } \end{array}\right. \nonumber \\= & {} \Big \{(u_1^+, v_1^+), (u_2^+, v_2^+), \ldots , (u_n^+, v_n^+)\Big \}. \end{aligned}$$

(3)

In the practical MCDM problem, there reliably subsist no FFPIS. That is looking into say, the individuals FFPIS $S^+$ will make regularly not the individuals attainable alternative, namely, $S^+ \notin X$. In any other case, the FFPIS $S^+$ is the most efficient alternative to the MCDM problem. Then, we carry on to focus the separation among every alternative and the FFPIS. To this case, we want to outline the hypothesis of distance measure for FFNs.

Thus, the distance between the alternative $S_i$ and the FFPIS $S^+$ might make ascertained toward utilizing Eq. (4) as takes after: see the first equation at the top of the next page.

$$\begin{aligned}&D(S_i, S^+) \nonumber \\&\quad = \sum \limits _{j=1}^n w_j \ d(C_j(S_i), C_j(S^+)) \nonumber \\&\quad = \frac{1}{2} \sum \limits _{j=1}^n w_j \sqrt{\frac{1}{2}\bigg [\Big (\alpha _{ij}^3-({\alpha _{j}^+})^3\Big )^2 +\Big (\beta _{ij}^3-({\beta _{j}^+})^3\Big )^2+\Big (\pi _{ij}^3- ({\pi _{j}^+})^3\Big )^2\bigg ]} \nonumber \\&\qquad i=1,2, \ldots , m \end{aligned}$$

(4)

Typically, the smaller $D(S_i, S^+)$ gives the superior alternative $S_i$, and assume

$$\begin{aligned} D_{\min }(S_i, S^+)= & {} \min \limits _{1 \le i \le m} D(S_i, S^+) \end{aligned}$$

(5)

However, those alternatives for the closest separation on FFPIS might a chance to be not those most distant from FFNIS. We indicate those FFNIS by $S^-$, which can be obtained by the accompanying formula:

$$\begin{aligned} S^-= & {} \left\{ \begin{array}{l} \min \limits _{i} \langle score(C_j(S_i))\rangle \ | \ j=1,2, \ldots , n, \\ \quad \text{ if } \, c_j \, \text{ is } \text{ a } \text{ benefit } \text{ criterion } \\ \max \limits _{i} \langle score(C_j(S_i))\rangle \ | \ j=1,2, \ldots , n, \\ \quad \text{ if } \, c_j \, \text{ is } \text{ a } \text{ cost } \text{ criterion } \end{array}\right. \nonumber \\= & {} \Big \{(u_1^-, v_1^-), (u_2^-, v_2^-), \ldots , (u_n^-, v_n^-)\Big \} \end{aligned}$$

(6)

It is effortlessly observed from Eq. (6) that the acquired esteem of FFNIS under every attribute is minimal among all of the alternatives. Normally, in the useful MCDM process, there might not exist those FFNIS. Particularly, the FFNIS $S^-$ is sometimes an unfeasible alternative, i.e., $S^- \notin X$. Otherwise, the FFNIS $S^-$ may be the most exceedingly bad alternative over the MCDM problem, which is a chance to be deleted in the preferred method.

The distance between the alternative $S_i$ and the FFNIS $S^-$ can be calculated from Eq. (7) in these ways:

$$\begin{aligned}&D(S_i, S^-) \nonumber \\&\quad = \sum \limits _{j=1}^n w_j \ d(C_j(S_i), C_j(S^-)) \nonumber \\&\quad = \frac{1}{2} \sum \limits _{j=1}^n w_j \sqrt{\frac{1}{2}\bigg [\Big (\alpha _{ij}^3-({\alpha _{j}^-})^3\Big )^2 -\Big (\beta _{ij}^3-({\beta _{j}^-})^3\Big )^2-\Big (\pi _{ij}^3- ({\pi _{j}^-})^3\Big )^2\bigg ]} \nonumber \\&\qquad i=1,2, \ldots , m \end{aligned}$$

(7)

Conventionally, the higher $D(S_i, S^-)$ produces the superior alternative $S_i$, and authorize

$$\begin{aligned} D_{\max }(S_i, S^-)= & {} \max \limits _{1 \le i \le m} D(S_i, S^-) \end{aligned}$$

(8)

In the established TOPSIS method, we, as a rule, have with ascertaining that relative closeness of the alternative $S_i$ with admiration to those FFPIS $S^+$ likewise below:

$$\begin{aligned} RC(S_i)= & {} \frac{D(S_i, S^-)}{D(S_i, S^-)+D(S_i, S^+)} \end{aligned}$$

(9)

Concerning illustration expressed by the closeness index $RC(S_i)$, those positioning requests of alternatives and the optimal alternatives could be decided. However, Hadi-Vencheh and Mirjaberi (2014) indicated that clinched alongside a portion situation, that relative closeness can’t attain the point that those optimal result ought to need the briefest separation from the PIS and the most distant separation from the NIS, all the while. Thus, they recommended that particular case might utilize the emulating equation as opposed to the relative closeness index (i.e., Eq. (9)):

$$\begin{aligned} \zeta (S_i)= & {} \frac{D(S_i, S^-)}{D_{\max }(S_i, S^-)}-\frac{D(S_i, S^+)}{D_{\min }(S_i, S^+)} \end{aligned}$$

(10)

which is denominated the revised closeness ancient to the measurement that degree will which the alternative $S_i$ may be close to those FFPIS $S^+$ and is significantly away from the FFNIS $S^-$, concurrently.

It can be easily seen that $\zeta (S_i) \le 0 \, (i = 1, 2, \ldots , m)$ and the larger $\zeta (S_i)$, the exceptional alternative $S_i$. If there occurs an alternative $S^*$ fulfilling the states that $D(S^*, S^-)=D_{\max }(S_i, S^-)$ and $D(S^*, S^+)=D_{\min }(S_i, S^+)$, simultaneously, afterward $\zeta (S^*) = 0$ and, glaringly, the alternative $S^*$ is the auspicious choice that is nearest to the FFPIS $S^+$ and farthest away from the FFNIS $S^-$, simultaneously.

8.3 Algorithms of the proposed method

In general, Fermatean fuzzy TOPSIS method entangles the consecutive steps:

Step I: For an MCDM problem with FFNs, we formulate the Fermatean fuzzy decision matrix $R =\big (C_j (S_i )\big )_{m \times n}$ where the elements $C_j(S_i) \, (j = 1, 2, \ldots , n, i = 1, 2, \ldots , m)$ are the appraisals of the alternative $S_i \in X$ regarding the criterion $C_j \in C$.

Step II: Utilize Eqs. (3) and (6) to distinguish the FFPIS $S^+=\{C_1(S^+),C_2(S^+), \ldots , C_n(S^+)\}$ and the FFNIS $S^-=\{C_1(S^-),C_2(S^-), \ldots ,$$C_n(S^-)\}$.

Step III: Compute the distances between the alternative $S_i$ and the FFPIS $S^+$ together with the FFNIS $S^-$, according to Eqs. (4) and (7) respectively.

Step IV: Utilize Eq. (10) to compute the revised closeness $\zeta (S_i)$ of the alternative $S_i \, (i = 1, 2, \ldots , m)$.

Step V: Decide the optimal ranking order of the alternatives and recognize the optimal alternative. On the backing of the revised closeness $\zeta (S_i)$ acquired from Step IV, we place the alternatives into sequences regarding the decreasing values of $\zeta (S_i) \, (i = 1, 2, \ldots , m)$, and the alternative with the largest revised closeness $\zeta (S_i)$ is the leading alternative, specifically,

$$\begin{aligned} S^*= & {} \left\{ S_i : (i : \zeta (S_i)=\max \limits _{1 \le l \le m} \zeta (x_l))\right\} . \end{aligned}$$

(11)

9 Practical example

Every man in this world dreams their own home/flat/ residential place. Suppose a group of Professors of Vidyasagar University wants to construct their home in a certain place. They construct a team named Senapati Construction Limited (SCL) among them. The SCL visit four places Ashoke Nagar $(S_1)$, Judge Court $(S_2)$, Patna Bazar $(S_3)$ and Kshudiram Nagar $(S_4)$ which are situated within 10 Kilometers of Vidyasagar University. They set five criteria for choosing a suitable land for home construction as follows

Lifestyle and neighbours$(C_1)$ While planning to have a new residential place one should think about the lifestyle in which one is accustomed to and the nature and character of the neighbours beside whom one is going to live for a long period of time. A good neighbour is always a source of pleasure and security of your life but there is opposite aspect also. At the initial stage of construction one should make sure that the neighbourhood is calm and quiet in nature, he knows his limit, he is conscious enough to secure one’s pleasing privacy, he is good at heart, he knows do’s and don’t’s etc. Not only neighbours but also neighbouring services like schools, colleges, hospitals etc. also important.

Soil type$(C_2)$ One of the most important thing in building larger constructions to have enormous knowledge about the condition of the soil on which the building will be erected. Nature of soil differs because of the difference in types and their compositions. The inactive soil is preferable than others as this kind of soil does not move in an accordance with the changing moisture in the climate. But if one wants to build construction on reactive soil, one should take some expensive measures like deep digging of the soil, consolidated foundation etc. To sum up, site classification is important enough to build a construction properly and with controlled expenditure.

Size, shape, orientation, and slope of the block of land$(C_3)$ If you have a particular design or particular style of building in your mind, you should also think about the graphical nature of the selected plot as it determines the shape of your dream construction. If you have a vast area for your construction, each and every design of your mind could be executed in the real scenario. Otherwise, you should restrict your plan according to the area of the plot you have. Actually, the problem in this subject arises when one wants to build a construction in suburban or urban areas. That’s why the selection of rural land may help you in this regard. Building construction on sloped land is expensive as well as reduces its attraction. Because if one wants to build on the sloped land, one must prepare the land as a flat area by filling the slopes with gravel or some other stipulated process. Not only that sunray may be obstructed on such a plot by its sloppiness and neighbour’s construction. That is why flat rural land should be selected for such purpose.

Existing roads and access to essential services$(C_4)$ Communication in its best phenomenon is highly desirable for new construction. It is not only for the carrying of goods but for the dwellers in future. Communication includes existing streets which connect the dwellers to the fast form of conveniences. Besides one should take brood over the matter that the newly constructed building may offer the inhabitants with water supply, gas connection, telephone line, cable connections, electricity supply, internet services etc. Moreover, good communication to a nearby hospital or nursing home is also important.

Cost$(C_5)$ Before choosing land for home construction, you should always know what your maximum budget is to spend on the entire build, including the registration fees and other charges at the time of registration.

9.1 Description

The SCL set the weight vector of the criteria as

$$\begin{aligned} w = (0.2, 0.2, 0.1, 0.3, 0.2)^T. \end{aligned}$$

They give less importance to criteria $(C_3)$ “Size, shape, orientation, and slope of the block of land” because it is a one time work. It’s not a permanent matter. After one-time labour and investment, the problem is over. They give more importance to the criteria $(C_4)$ “Existing roads and access to essential services” because it’s a lifetime matter. Professors have not enough time for these things.

Suppose that the evaluation values of the options with appreciate to every criterion furnished by using the committee are represented with the aid of FFNs as proven within the Fermatean fuzzy decision matrix inclined in Table 1. Those component $C_1(S_1) =(0.7, 0.3)$ to Table 1 could a chance to be demonstrated that the degree to which the alternative $S_1$ (Ashoke Nagar) fulfils those attribute $C_1$ (lifestyle and neighbours) is 0.7 and the level with which the alternative $S_1$ dissatisfies those attribute $C_1$ is 0. 3, and the others on Table 1 have those comparative implications.

Table 1 Fermatean fuzzy decission matrix

Using score functions we get (Table 2)

Table 2 Score values obtained by the score function

9.2 Decision process

In the following, we utilize the Fermatean fuzzy TOPSIS method to address the decision issue communicated over Sect. 9.1. First, we make use of Eqs. (3) and (6) to decide the FFPIS $S^+$ and the FFNIS $S^-$, correspondingly, and the outcomes are achieved as follows:

$$\begin{aligned} S^+ = \{(0.9, 0.6), (0.8, 0.1), (0.7, 0.2), (0.8, 0.2), (0.6, 0.5)\} \\ S^- = \{(0.5, 0.8), (0.4, 0.6), (0.4, 0.5), (0.5, 0.3), (0.9, 0.3)\} \end{aligned}$$

Then, we appoint Eqs. (4) and (7) in conformity with count the distances among the alternative $S_i$ and the FFPIS $S^+$ in conjunction with the FFNIS $S^-$, separately. The consequences are proven in Table 3. Furthermore, we take advantage of Eq. (10) in conformity with count the revised closeness $\zeta (S_i)$ over the alternative $S_i$, and the consequences also are additionally recorded in Table 3. Consistent with $\zeta (S_i)$, we are able to acquire the positioning of all alternatives as proven in Table 3.

Table 3 Decisions achieved by Fermatean Fuzzy TOPSIS Method

It is demonstrated in Table 3 that the optimal ranking order of the four places is $S_3 \succ S_2 \succ S_1 \succ S_4$, and thus the best alternative is $S_3$, namely, Patna Bazar.

10 Conclusions

In this article, we have initiated FFSs and FMGs. A relationship was shown between FFS, Pythagorean fuzzy set, and intuitionistic fuzzy set. We focused on the elementary set operations for the instance of FFSs. We then focused on the Fermatean complement. In view of the strong capability of FFS in illustrating the uncertain evaluation data, we have analyzed the augmentation of the TOPSIS process under Fermatean fuzzy contexts. Then, we have proposed the procedure of the Fermatean fuzzy TOPSIS method. To demonstrate the efficiency of Fermatean fuzzy TOPSIS method, a numerical example of the more common problem in human life has been taken and it has shown that our process is extremely fruitful in interpreting the MCDM problems with Fermatean fuzzy documentation. In the future, we will combine other methods like VIKOR method (Chen et al. 2018), Analytic hierarchy process (Abdel-Basset et al. 2018), Prioritized aggregation operators (Garg and Nancy 2018), Multi-level image compression method (Di Martino and Sessa 2018a), Bilinear fuzzy relation equation (Di Martino and Sessa 2018b), Graph partitioning methods (He et al. 2018), Robust and intelligent methods (Golshannavaz et al. 2018), with FFNs.