1 Introduction

Real physical systems show nonlinear and chaotic behaviors. Mathematical solutions of the differential equations for these systems are sometimes unmanageable and some special methods or techniques needed to be applied to reach the analytic solutions. One of these types of equations is called Gardner equation which can be written in the following form [1–5]

$$\begin{array}{@{}rcl@{}} U_{t}+a U U_{x}+b U^{2} U_{x}+p U_{xxx}=0, \end{array} $$
(1)

where U = U(x,t), \(U_{t}=\frac {\partial U}{\partial t}\), \(U_{x}=\frac {\partial U}{\partial x}\), and a, b and p are arbitrary constants. These parameters will be defined later depending on plasma parameters. Equation 1 contains U and U 2 which are related with well known K-dV (Korteweg-de Vries) and modified K-dV (mK-dV) equations. To study nonlinear properties of solitary waves, we focus on the derivation of the higher order nonlinear equation called Gardner equation for different physical plasmas [6–12].

There are so many effective methods defined in literature and some of them are really applicable to nonlinear differential equations to find the solitary type solutions in real physical systems. In this paper, we use the two-variable (1/G ′)- expansion and (G ′/G,1/G)-expansion methods, and direct integration to find the analytic solutions of the Gardner equation. The original (G ′/G)-expansion method is generalized to find (G ′/G,1/G)-expansion method [13]. Some applications of (G ′/G)-expansion method can be seen in [14–18]. As a pioneer work [19] has applied the two-variable (G ′/G,1/G)-expansion method and found the exact solutions of Zakharov equations. Some applications of (G ′/G,1/G)-expansion method can be seen in [16, 20–22]. The (1/G ′)-expansion method was firstly introduced by Ref. [23]. Then, [24] obtained some exact solutions by using the (1/G ′)-expansion method for the Boussinesq type equations. The direct integration is applied to some nonlinear differential equations to find the exact solutions. It is very effective and coincide with a method which is handled by doing some straightforward integrations [15].

The physical plasma is getting great deal of interest, and many efforts have been made during the last few decades to study the linear and nonlinear systems to find out the properties of shock waves and solitons in electron-acoustic and dusty plasmas [25–27]. They are very common cases in astrophysical and laboratory plasma environments. The linear properties of these cases are very well understood from theoretical and experimental points of view [28, 29]. During the last few years, there are many great efforts put forward in nonlinear systems to understand the dynamics of solitons, and shock waves and their strong correlation in dusty plasma for different plasma parameters, such as electron and proton number densities, electron, proton and ion temperatures, and the strength of the nonextensivity [30–32].

There are number of papers dealing with dynamical changes of the Gardner solitary and shock waves in unmagnetized plasma containing ions, negatively charged immobile dust, hot electrons and protons, as Refs. [6, 31, 33, 34] which investigated the electron-acoustic Gardner solitons in a nonextensive electron-positron-ion plasma system. They used the reductive perturbation method to derive the Gardner equation. The basic properties of the electron-acoustic Gardner solitons were studied depending on plasma parameters. The solitons which produce negative and positive hump were characterized depending on the critical values of nonextensive parameter q in [31]. The nonextensivities of the positrons and electrons play an important role in the modification of the behavior of the solitary structure. The theoretical determination of the nonextensivity on solitons was studied by taking nonextensive electrons and positrons in plasma system by [33]. In this paper, we will give the exact solutions of the Gardner equations by using the different methods and then apply these analytic solutions not only to find dynamical behavior of the solitons and shock waves in a wide range of plasma parameters but also to explain the traveling wave solutions of solitons.

The structure of the paper is as follows: Section 2 presents the main steps of (G ′/G,1/G)-expansion and (1/G ′)-expansion method to find the traveling wave solution of nonlinear differential equations. The traveling wave solutions of the Gardner equation by using the two dependent (G ′/G,1/G)-expansion and (1/G ′)-expansion methods and direct integration are given in Section 3. Section 4 covers applications of our analytic solutions to two different plasma systems. The dynamical behavior of the solitons and shock waves observed in these systems are analyzed using a wide range of plasma parameters. The numerical results are discussed and compared with the literature. Finally, our main conclusions are given in Section 5.

2 (G ′/G,1/G) and (1/G ′)-expansion Methods

2.1 (G ′/G,1/G)-expansion Method

The main steps of the (G ′/G,1/G)-expansion method are described for finding the traveling wave solutions of the nonlinear evolution equations. First of all, we consider the following second-order ordinary linear differential equation,

$$\begin{array}{@{}rcl@{}} G^{\prime\prime}(\eta)+\lambda G(\eta)=\mu, \end{array} $$
(2)

where G = G(η), \('=\frac {d}{d\eta }\) and we let

$$\begin{array}{@{}rcl@{}} \phi=G'/G, \quad \psi=1/G, \end{array} $$
(3)

Using (2) and (3), it yields

$$\begin{array}{@{}rcl@{}} \phi^{\prime}=-\phi^{2}+\mu\psi-\lambda, \quad \psi^{\prime}=-\phi\psi, \end{array} $$
(4)

From (2), we have the three cases of the general solutions which are,

Case I:

When λ<0,The general solutions of the (2) is

$$\begin{array}{@{}rcl@{}} G(\eta)=c_{1} sinh(\sqrt{-\lambda}\eta)+ c_{2}cosh(\sqrt{-\lambda}\eta)+\frac{\mu}{\lambda}, \end{array} $$
(5)

and we have

$$\psi^{2}=-\frac{\lambda}{\lambda^{2}\nu+\mu^{2}}(\phi^{2}-2\mu\psi+\lambda),$$

where \(\nu ={c_{1}^{2}}-{c_{2}^{2}}\), and c 1 and c 2 are arbitrary integration constants.

Case II:

When λ>0,

The general solutions of the (2) is

$$\begin{array}{@{}rcl@{}} G(\eta)=c_{1} sin(\sqrt{\lambda}\eta)+ c_{2}cos(\sqrt{\lambda}\eta)+\frac{\mu}{\lambda}, \end{array} $$
(6)

and we have

$$\psi^{2}=\frac{\lambda}{\lambda^{2}\nu-\mu^{2}}(\phi^{2}-2\mu\psi+\lambda),$$

where \(\nu ={c_{1}^{2}}+{c_{2}^{2}}\), and c 1 and c 2 are arbitrary integration constants.

Case III:

When λ=0,The general solutions of the (2) is

$$\begin{array}{@{}rcl@{}} G(\eta)=\frac{\mu}{2}\eta^{2}+c_{1}\eta+c_{2}, \end{array} $$
(7)

and we have

$$\psi^{2}=\frac{1}{{c_{1}^{2}}-2\mu c_{2}}(\phi^{2}-2\mu\psi),$$

where c 1 and c 2 are arbitrary constants.

The main steps of the (G ′/G,1/G)-expansion method are summarized as follows. The general form of the partial differential equation (PDE) is given as

$$\begin{array}{@{}rcl@{}} P(u,u_{t},u_{x},u_{tt},u_{xt},u_{xx}, . . .)= 0, \end{array} $$
(8)

where u = u(x,t) is an unknown function, P is a polynomial depending on u. By using transformation u(x,t) = u(η),η = x−V p t in (8), we obtain an ordinary differential equation (ODE) which is

$$\begin{array}{@{}rcl@{}} P(u,-V_{p}u^{\prime},u^{\prime},{V_{p}^{2}}u^{\prime\prime},-V_{p}u^{\prime\prime}, u^{\prime\prime},...)=0, \end{array} $$
(9)

where \(u^{\prime }=\frac {du}{d \eta }\). Suppose that the solution of (9) can be expressed in terms of ϕ and ψ and it is given as

$$\begin{array}{@{}rcl@{}} u(\eta)=\sum\limits_{i=0}^{N}a_{i} \phi^{i}+\sum\limits_{i=1} ^{N}b_{i}\phi^{i-1}\psi, \end{array} $$
(10)

where G = G(η) satisfies the (2), a i (i=1,...,N), b i (i=1,...,N), and the constants V p , λ and μ will be determined later. The positive integer N is determined by using homogeneous balance between the highest order derivatives and the nonlinear terms appearing in (9). Substituting (10) into (9), using (4) and (5) (or using (4), (6), and (4), (7)) the left-hand side of (9) can be converted into a polynomial in ϕ and ψ, in which the degree of ψ is not larger than 1. Equating each coefficient of the polynomial to zero yields a system of algebraic equations in a i (i=1,...,N), b i (i=1,...,N),V p , λ(λ<0), μ,c 1 and c 2. Solving the algebraic solutions and then substituting the values of a i (i=1,...,N), b i (i=1,...,N), λ(λ<0), μ,c 1 and c 2 obtained into (10), one can obtain the traveling wave solutions expressed by the hyperbolic, trigonometric, or rational functions of (9).

2.2 (1/G ′)-expansion Method

In this subsection, we identify the main steps of the (1/G ′)-expansion method to find the traveling wave solutions of nonlinear differential equations. The partial differential equation (PDE) given in (8) can be converted into the ordinary ones, same as given in (9). Suppose that the solution of (9) can be expressed in term of the polynomial (1/G ′),

$$\begin{array}{@{}rcl@{}} u(\eta)=\sum\limits_{i=0}^{N}a_{i}\left( \frac{1}{G^{\prime}}\right)^{i}, \end{array} $$
(11)

where G = G(η) and satisfies the following linear ordinary differential equation which is

$$\begin{array}{@{}rcl@{}} G^{\prime\prime}(\eta)+\lambda G^{\prime}(\eta)+\mu=0, \end{array} $$
(12)

where a i (i=1,...,N), λ and μ are constants to be determined. The positive integer N can be obtained by using the homogeneous balance between the highest order derivatives and the nonlinear terms appearing in (9). Additionally, the solution of the differential equation given in (12) is

$$\begin{array}{@{}rcl@{}} G(\eta)=c_{1}e^{-\lambda \eta}-\frac{\mu}{\lambda}\eta +c_{2}, \end{array} $$
(13)

where c 1 and c 2 arbitrary integration constants. (1/G ′) can be expressed as

$$\begin{array}{@{}rcl@{}} \left( \frac{1}{G^{\prime}}\right)= \frac{\lambda}{-\mu+\lambda c_{1}[cosh(\lambda\eta)-sinh(\lambda\eta)]}. \end{array} $$
(14)

By substituting (11) into (9) and using (12), the left-hand side of (9) can be converted into a polynomial in term of (1/G ′). Equating each coefficient of the polynomial to zero yields a system of algebraic equations. By solving the algebraic equations with symbolic computation, we define a i (i=1,...,N), λ and μ.

3 Traveling Wave Solution of Gardner Equation

3.1 Application of (G ′/G,1/G)-expansion Method

Gardner equation given in (1) can be converted into the following ordinary differential equation by using the transformation of η = x−V p t, U = U(η),

$$\begin{array}{@{}rcl@{}} p U^{\prime\prime\prime}-V_{p}U^{\prime}+a U U^{\prime}+b U^{2} U^{\prime}=0, \end{array} $$
(15)

where \(U'=\frac {dU}{d\eta }\). (15) is integrated and we find,

$$\begin{array}{@{}rcl@{}} p U^{\prime\prime}-V_{p} U+\frac{a}{2}U^{2}+\frac{b}{3}U^{3}+c=0, \end{array} $$
(16)

where c is an arbitrary integration constant. Balancing the terms U 3 and U ″ in (16), we have the following form of the solution

$$\begin{array}{@{}rcl@{}} U(\eta)=a_{1}\phi+a_{0}+b_{1}\psi. \end{array} $$
(17)

Substituting (17) and its derivatives into (16) and using the (4) and (5), we have the set of algebraic equations for a 1,a 0,b 0,p,a,b,c,V p ,λ,μ, and ν and then by solving the algebraic equations, we get

Case I:

λ<0

$$\begin{array}{@{}rcl@{}} a_{1}&=&\pm\sqrt{-\frac{3p}{2b}}, \quad a_{0}=-\frac{a}{2b}, \\ b_{1}&=&\pm\frac{1}{2b}\sqrt{\frac{3a^{4}\nu+24a^{2} b V_{p}\nu+12b^{2}p^{2}\mu^{2}+48b^{2}{V_{p}^{2}}\nu}{a^{2}+4bV_{p}}}, \\ \lambda& =&\frac{a^{2}+4bV_{p}}{2bp}, \quad c=-\frac{a(a^{2}+6bV_{p})}{12b^{2}}. \end{array} $$

Substituting (18) into (17), we have the solution of the (16) which is

$$\begin{array}{@{}rcl@{}} U&=&\pm\sqrt{-\frac{3p}{2b}}\phi \pm \frac{1}{2b} \\ &&\sqrt{\frac{3a^{4}\nu+24a^{2} b V_{p}\nu+12b^{2}p^{2}\mu^{2}+48b^{2}{V_{p}^{2}}\nu}{a^{2}+4bV_{p}}}\psi -\frac{a}{2b}.\\ \end{array} $$
(18)

Similarly, substituting the (17) and its derivatives in (16) and using the (4) and (6) yield a set of simultaneous algebraic equations for a 1,a 0,b 0,k,a,b,c,e,λ,μ and ν and then by solving the algebraic equations, we have,

Case II:

λ>0

$$\begin{array}{@{}rcl@{}} a_{1}&=&\pm\sqrt{-\frac{3p}{2b}},\quad a_{0}=-\frac{a}{2b}, \\ b_{1}&=&\pm\frac{1}{2b}\sqrt{\frac{-3a^{4}\nu-24a^{2}bV_{p}\nu+12b^{2}p^{2}\mu^{2}-48b^{2}{V_{p}^{2}}\nu}{a^{2}+4bV_{p}}}, \\ \lambda &=&\frac{a^{2}+4bV_{p}}{2bp},\quad c=-\frac{a(a^{2}+6bV_{p})}{12b^{2}}. \end{array} $$

Substituting (19) into (17), we have the following solution for the (16)

$$\begin{array}{@{}rcl@{}} U&=&\pm\sqrt{-\frac{3p}{2b}}\phi\pm\frac{1}{2b} \\ &&\sqrt{\frac{-3a^{4}\nu- 24a^{2}bV_{p}\nu+12b^{2}p^{2}\mu^{2}-48b^{2}{V_{p}^{2}}\nu}{a^{2}+4bV_{p}}}\psi -\frac{a}{2b}.\\ \end{array} $$
(19)

Finally, substituting the (17) and its derivatives in (16) and using the (4) and (7), we get algebraic equations for a 1,a 0,b 0,k,a,b,c,e,μ,c 1 and c 2, and then by solving the algebraic equations we reach the following solution

Case III:

λ=0

$$\begin{array}{@{}rcl@{}} &&a_{1}=\pm\sqrt{-\frac{3p}{2b}}, \quad b_{1}=\pm\sqrt{\frac{6c_{2} p \mu-3{c_{1}^{2}}p}{2b}},\quad a_{0}=\mp\frac{\sqrt{-bV_{p}}}{b},\\&& a=\pm 2\sqrt{-bV_{P}}\quad c=\mp\frac{\sqrt{-bV_{p}}V_{p}}{3b}\quad \lambda =0.\end{array} $$
(20)

Substituting (20) into (17), we have the solution of the (16) which is

$$\begin{array}{@{}rcl@{}} U=\pm\sqrt{-\frac{3p}{2b}}\phi\pm\sqrt{\frac{6c_{2} p \mu-3{c_{1}^{2}}p}{2b}}\psi \mp\frac{\sqrt{-bV_{p}}}{b}. \end{array} $$
(21)

where \(a=\pm 2\sqrt {-bV_{p}}, c=\mp \frac {\sqrt {-bV_{p}}V_{p}}{3b}, \lambda =0\).

3.2 Application of (1/G ′)-expansion Method

We use the balance N=1 for the solution of the (16) and then we get the following type solution

$$\begin{array}{@{}rcl@{}} U=a_{0}+a_{1}\left( \frac{1}{G^{\prime}}\right). \end{array} $$
(22)

Substituting (22) in (16) then collecting all the coefficients with respect to (1/G ′) and equating to zero, we get the following system of equations

$$\begin{array}{@{}rcl@{}} &&\left( \frac{1}{G^{\prime}}\right)^{0}:\quad 2{a_{0}^{3}}b+3{a_{0}^{2}}a-6a_{0}V_{p}+6c,\\ &&\left( \frac{1}{G^{\prime}}\right)^{1}:\quad a_{1}\left( {a_{0}^{2}}b+a_{0}a+ p\lambda^{2}-V_{p}\right),\\ &&\left( \frac{1}{G^{\prime}}\right)^{2}:\quad a_{1}\left( 2a_{1} a_{0} b+a_{1} a+6p\lambda\mu\right),\\ &&\left( \frac{1}{G^{\prime}}\right)^{3}:\quad a_{1}\left( {a_{1}^{2}}b+6p\mu^{2}\right). \end{array} $$

Solving the system of equations given above, we get

$$\begin{array}{@{}rcl@{}} &&a_{1}=\pm\sqrt{-\frac{6p}{b}}\mu,\quad a_{0}=\frac{-a\pm \sqrt{\frac{-a^{2}-4bV_{p}}{2bp}}\sqrt{-\frac{6p}{b}}b}{2b},\\ &&\lambda=\sqrt{-\frac{a^{2}+4bV_{p}}{2bp}},\quad c=-\frac{a(a^{2}+6bV_{p})}{12 b^{2}}. \end{array} $$

Substituting these solutions into (22), we obtain the following solution

$$\begin{array}{@{}rcl@{}} U=\pm\sqrt{-\frac{6p}{b}}\mu \left( \frac{1}{G^{\prime}}\right) +\frac{-a\pm \sqrt{\frac{-a^{2}-4bV_{p}}{2bp}}\sqrt{-\frac{6p}{b}}b}{2b} \end{array} $$
(23)

where \(\left (\frac {1}{G^{\prime }}\right )=\frac {\lambda }{-\mu +\lambda c_{1}[cosh(\lambda \eta )-sinh(\lambda \eta )]}\), \(\lambda =\sqrt {-\frac {a^{2}+4bV_{p}}{2bp}}\), \(c=-\frac {a(a^{2}+6bV_{p})}{12 b^{2}}\) and c 1 is the arbitrary integration constant.

3.3 Exact Solutions of the Gardner Equation by using the Direct Integration

The exact solution of Gardner equation is obtained by taking the direct integral of (16). For this purpose, let us multiply the right hand side of (16) with U ′. Hence, we have

$$\begin{array}{@{}rcl@{}} p U^{\prime} U^{\prime\prime}-V_{p} U U^{\prime}+\frac{a}{2}U^{2} U^{\prime}+\frac{b}{3}U^{3} U^{\prime}+c U^{\prime}=0. \end{array} $$
(24)

Equation 24 is an integrable equation. We have obtained the following first-order equation after integrating it once.

$$\begin{array}{@{}rcl@{}} U^{\prime}=\pm\sqrt{-(\frac{b}{6p})U^{4}-(\frac{a}{3p})U^{3}+(\frac{V_{p}}{p})U^{2}- (\frac{2c}{p})U-(\frac{2d}{p})}, \end{array} $$
(25)

where d is an arbitrary integration constant. Equation (25) can be written as \(\pm \int \frac {dU}{\sqrt {-(\frac {b}{6p})U^{4}-(\frac {a}{3p})U^{3}+(\frac {V_{p}}{p})U^{2}- (\frac {2c}{p})U-(\frac {2d}{p})}} =\int d\eta .\)

By integration of the right side of this equation, we get

$$\begin{array}{@{}rcl@{}} \pm\int\frac{dU}{\sqrt{-(\frac{b}{6p})U^{4}-(\frac{a}{3p})U^{3}+(\frac{V_{p}}{p})U^{2}- (\frac{2c}{p})U-(\frac{2d}{p})}}=\eta+e,\\ \end{array} $$
(26)

where e is a new arbitrary integration constant.

By integrating the left side of this equation and choosing the integration constants c = d = e=0 (otherwise it can not be integrable), (26) is written as

$$\begin{array}{@{}rcl@{}} \pm\int\frac{dU}{|U|\sqrt{-(\frac{b}{6p})U^{2}-(\frac{a}{3p})U+(\frac{V_{p}}{p})}}=\eta. \end{array} $$
(27)

Choosing U>0 (similar calculation can be also done for U<0). After using the transformation \(U=\frac {1}{S}\) and rearrangement, we get,

$$\mp\sqrt{\frac{p}{V_{p}}}\int\frac{dS}{\sqrt{S^{2}- (\frac{a}{3V_{p}})S-(\frac{b}{6V_{p}})}}=\eta.$$

This equation can be written as

$$\mp\sqrt{\frac{p}{V_{p}}}\int \frac{dS}{\sqrt{\left( S-\frac{a}{6V_{p}}\right)^{2}- \left( \frac{a^{2}+6bV_{p}}{36{V_{p}^{2}}}\right)}}=\eta.$$

Integrating this equation, we have

$$\begin{array}{@{}rcl@{}} \mp\sqrt{\frac{p}{V_{p}}} \ln \left[ (S-\frac{a}{6V_{p}})+\sqrt{\left( S-\frac{a}{6V_{p}}\right)^{2}-\left( \frac{a^{2}+6bV_{p}}{36{V_{p}^{2}}}\right)}\right]=\eta.\\ \end{array} $$
(28)

Solving the (28) for S and then using the transformation given above, we obtain the exact solutions of the Gardner equation as follows,

$$\begin{array}{@{}rcl@{}} U(\eta)=\frac{2A}{Ae^{\mp\sqrt{\frac{V_{p}}{p}}\eta}+ B e^{\pm\sqrt {\frac{V_{p}}{p}}\eta}+C}, \end{array} $$
(29)

where \(A=36{V_{p}^{2}} , B=a^{2}+6bV_{p}, C=12aV_{p}\) and η = x−V p t.

Equation 29 can be written in terms of the hyperbolic and trigonometric functions for the case of \(\frac {V_{p}}{p}>0\) and \(\frac {V_{p}}{p}<0\), respectively. Hence, the general solutions of Gardner equations are

$$\begin{array}{@{}rcl@{}} U_{1}(\eta)=\frac{2A}{(A+B)\cosh{\sqrt{\frac{V_{p}} {p}}\eta}\pm(B-A) \sinh{\sqrt{\frac{V_{p}}{p}}\eta}+C},\\ \end{array} $$
(30)
$$\begin{array}{@{}rcl@{}} U_{2}(\eta)=\frac{2A}{(A+B)\cos{\sqrt{\frac{V_{p}} {p}}\eta}\pm i(B-A) \sin{\sqrt{\frac{V_{p}}{p}}\eta}+C},\\ \end{array} $$
(31)

where \(A=36{V_{p}^{2}} , B=a^{2}+6bV_{p}, C=12aV_{p}\) and η = x−V p t.

4 Numerical Analysis

In this paper, we apply our analytic solutions to two different plasmas to understand the parameter dependencies of the solitary waves and to explain the dynamical behavior of the solitons and shock waves observed in these systems. The detailed study of the analytical solution can often tell us a great detail about dynamical features of the shock wave and the soliton.

4.1 The Electron Acoustic Waves in a Nonextensive Positron-electron-ion

The four-component plasma system which consists of cold electrons, nonextensive hot protons and electrons, and immobile positive ions has been studied, and the well known KdV and Gardner equations have been derived, depending on the the plasma parameters [34]. In this section, the analytic solutions of Gardner equation found by using the (G ′/G,1/G)-expansion method and direct integration are applied to the physical plasma which consists of electron acoustic waves in a nonextensive positron-electron-ion. These analytic solutions are given in Subsections 3.1 and 3.3, and they are very important to understand the dynamical behavior of solitons and shock waves in various astrophysical plasma systems. The analytic solutions of the Gardner equations introduced in this paper give more detailed knowledge about the electron-acoustic solitons.

4.1.1 Model Equation and Definition of Corresponding Parameters

The Gardner equation given in (1) was derived by [34] for unmagnetized plasma system, and they have found the corresponding parameters a, b and p depending on plasma parameters. The plasma parameters are the strength of q, the ratio of hot and cold electrons normalized densities at their equilibrium μ 1, the temperature ratio of hot electron and ion σ, the ratio of hot and cold protons normalized densities at their equilibrium μ 2, and phase velocity V p . q can vary and clarify the properties of the plasma. q>1 and q<1 identify the cases of subextensivity and superextensivity, respectively [35]. μ 1 represents the ratio of hot and cold electrons normalized densities at their equilibrium and is given as μ 1 = n h0/n c0. Here, n h0 and n c0 are the hot and cold electron number densities in the equilibrium case, respectively. The temperature ratio is σ = T h /T p , where T h and T p are the hot electron and ion temperatures.

The constant parameters given in (1) for this plasma can be defined as [34]

$$\begin{array}{@{}rcl@{}} a &=& sX_{1}Y \\ b &=& X_{2}Y \\ p &=& Y \end{array} $$
(32)

where s can be equal to 1 or −1, \(X_{1} = \frac {(q+1)(q-3)}{4}\), \(X_{2}= \frac {15}{2{V_{p}^{6}}} - \frac {(q+1)(q-3)(3q-5)(\mu _{1}-\mu _{2}\sigma )}{16}\), \(Y= \frac {{V_{p}^{3}}}{2}\). The phase velocity is given as

$$\begin{array}{@{}rcl@{}} V_{p}=\sqrt{\frac{2}{(q+1)(\mu_{1}+\sigma\mu_{2})}}. \end{array} $$
(33)

4.1.2 Numerical Results from the (G ′/G,1/G)-expansion Method

We have used the analytic solution of Gardner equation given in (18), (19), and (21) to understand the properties of the unmagnetized four-component electron-proton-ion plasma system consisting of inertial cold electron, immobile positive ions, and nonextensive hot electrons and positrons. We have found the behavior of the solitary shock waves depending on plasma parameters, and they are given in Figs. 1, 2, 3, and 4. All the range of parameters seen in the analytic solutions have been used to search for solitons, but they could not be found. We have only found the shock waves, and the variation of amplitudes totally depend not only on the plasma parameters, but also on the integration constants (c 1,c 2,c) and on the source term μ given in (2).

Fig. 1
figure 1

The variations of the shock waves along the η = x−V p τ are given for different values of the strength of nonextensivity q. The plasma parameters s=1, μ 1=0.1, μ 2=0.4, and σ=1, integration constants c 1=1 and c 2=0, and the source variable μ=1 are used in the each case of q

Full size image
Fig. 2
figure 2

Same as Fig. 1 but it is plotted for different values of plasma parameter μ 1 which refers to the ratio of the hot and cold electron number density

Full size image
Fig. 3
figure 3

Same as Figs. 1 and 2 but it is for different values of source term identified in Eq. 2

Full size image
Fig. 4
figure 4

Variation of the solution, produced from analytic solution of Gardner equation derived from (G ′/G,1/G)-expansion method, depending on the integration constants which are given. Integration constants play an important role to identify the type of solutions given in Section 3.1

Full size image

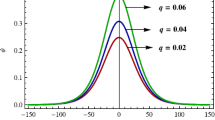
The strength of nonextensivity parameter q plays an important role to define the amplitude of the solitary shock waves. It is seen in Fig. 1 that the increase in q increases the amplitude of solitary shock waves for fixed plasma parameters s=1, μ 1=0.1, μ 2=0.4, σ=1, integration constants c 1=1 and c 2=0, and the source term μ=1. But it is observed in Fig. 2 that we find the opposite behavior for the values of μ 1. The ratio of hot and cold electrons normalized densities at their equilibrium can cause decreasing in amplitude when it is increasing.

On the other hand, the dynamic of solitary shock waves is depending not only on the plasma parameters, but also on the integration constants (c 1,c 2,c) and source term (μ) defined in the general definition of (G ′/G,1/G)-expansion method. It is noted in Fig. 3 that the source term μ plays a role in the shifting of the discontinuity location of the shock wave. Higher source term can cause the solitary wave to shift along the negative η. But the amplitude of shock wave and its basic features, which are amplitude, width, and polarity, do not change with changing μ. Furthermore, it is worth stressing that the results from different integration constants (c 1,c 2) are helpful to investigate the nonlinear features and different types of solutions of the Gardner equation in dusty and space plasmas. It is seen in Fig. 4 that, depending on the integration constants, the analytic solution of Gardner equations can go from the finite amplitude shock wave to the infinite one. The polarity, amplitude, and width of these shocks strongly depend on plasma parameters and the source term, as seen in Figs. 1, 2, and 3.

4.1.3 Numerical Results from the Direct Integration

The unmagnetized four-components plasma system is numerically analyzed by using the analytic solution of Gardner equation derived by using the direct integration. The analytic solutions are given in (30) and (31). We have observed and found that the constants A and B given in solutions play a significant role to define parametric limitations. The Gardner equation produces a solitary wave type solution when |A + B|>|B−A|. The variation of the amplitude of the soliton also changes for the different values of \(|(A+B)-(B-A)|=2A=72{V_{p}^{2}}\). The amplitude of soliton increases with increasing of \(72{V_{p}^{2}}\). On the other hand, the amplitude of solitary wave decreases with increasing the ratio of hot and cold electrons normalized densities at their equilibrium called μ 1 (Fig 5).

Fig. 5
figure 5

Variation of amplitude, width and position of maximum amplitude of the soliton as a function of η with μ 1. The other plasma parameters are q=0.8, s=−1, μ 2=0.5, and σ=1

Full size image

The variation of maximum amplitudes of solitons and their locations on η are extensively studied for μ 1 and μ 2, and numerical results are given in Figs. 6 and 7. Reference [34] found the solitary waves from Gardner equation only if μ 1≃μ c . In contrast to results obtained from [34], it is found that Gardner equation gives the solitons when μ 1≥μ c with different values of the strength of nonextensivity parameter q. For q=0.5 and μ c =0.0176, the variation of maximum amplitude of the soliton is given in Fig. 6 and it gets the biggest value U(η)=1.581 at μ 1=0.17455. For every data sets, the magnitude of soliton increases initially, produces a peak value, and starts to decrease exponentially with μ 1. It is also noted in the right part of the Fig. 6 that the location of the maximum amplitude moves back and forth between η=−2 and η=2.

Fig. 6
figure 6

The maximum values of the solitary wave amplitudes and their location at η are plotted with respect to plasma parameter μ 1 for different values of q with σ=1, s=−1, and μ 2=0.5. The left part of the plot indicates that the maximum amplitude occurs while μ 1 is less than 1, and gets higher as μ 1 gets close to the critical value for the strength of nonextensivity. The location of the maximum amplitude oscillates depending on μ 1, as seen in the panel at the right of the figure.

Full size image
Fig. 7
figure 7

Same as Fig. 6 but it is for different values of μ 2

Full size image

In Fig. 7, we explore the effect of the ratio of hot and cold protons normalized densities at their equilibrium, called μ 2, on the maximum amplitude of the solitons as a function of μ 1. It is seen that the amplitudes of solitary waves are strongly affected by plasma parameters, and that the amplitude decreases with increasing μ 2. The highest peak values 1.3, 1.41, 1.6, and 1.86 are produced for μ 1=−0.54, μ 1=−0.2, μ 1=0.129, and μ 1=0.37, respectively, with the different sets of plasma parameters given in left part of Fig. 7. The right part of Fig. 7 indicates that the locations of the highest amplitudes also show the same type of behavior. It is deduced from the Figs. 6 and 7 that q (μ 2) has positive (negative) effect on the amplitude of the solitons found from Gardner solutions.

The solitons propagate without changing dynamics (amplitude and width). One of the reason for this important conclusion may be a result of self-attraction of the wave itself [36]. We numerically investigate the time variations of the solitary waves of the Gardner solitons given in (30). Figure 8 shows propagation of solitary waves for given plasma parameters q=0.8, μ 2=0.5, σ=1, and s=1. We note that the solitons move along the positive η axis with positive phase velocity and a constant period. The amplitude and phase of the solitons do not change during the evolution.

Fig. 8
figure 8

The propagating solitary wave with constant velocity along η, at time t=0,3.6,7.2,10.8, and 14.4 with q=0.8, μ 2=0.5, σ=1, and s=1

Full size image

4.2 Investigating the Effect of Two-temperature Thermal Electrons on Dust-ion Acoustic Solitary Waves

Dust-ion acoustic waves are studied numerically and analytically for an unmagnetized plasma which consists of negatively charged immobile dust, inertial ions, and superthermal electrons [32]. This type of system may be seen in some of the astrophysical environments. Hence, we apply the exact solution of Gardner equation, found by using the direct integration and given in (30), to understand the dynamical behavior of the solitons in various parametric regimes.

The Gardner equation given in (1) is solved analytically and the constants which appear in the nonlinear terms can be defined as [32],

$$\begin{array}{@{}rcl@{}} a &=& sX_{3}Z, \\ b &=& X_{4}Z, \\ p &=& Z . \end{array} $$
(34)

The parameters X 3, X 4, and Z are defined depending on plasma parameters and given as [32]

$$\begin{array}{@{}rcl@{}} X_{3} & = &\frac{6{P_{2}^{2}}\mu_{e1}{\sigma_{1}^{2}}}{{P_{3}^{2}}} + \frac{6P_{2}P_{5}\mu_{e2}\sigma_{1}\sigma_{2}}{P_{3}P_{6}} - \frac{P_{1}P_{2}{\sigma_{1}^{2}}}{{P_{3}^{2}}}, \\ X_{4} &=& \frac{15}{2{V_{p}^{6}}} + \mu_{e1}\frac{P_{1}P_{2}P_{3}{\sigma_{1}^{3}}}{2{P_{3}^{3}}} + \mu_{e2}\frac{P_{4}P_{5}P_{6}{\sigma_{2}^{3}}}{2{P_{6}^{3}}},\\ Z &=& \frac{{V_{p}^{3}}}{2} , \end{array} $$
(35)

where \(P_{1}=-\frac {1}{2}-\kappa _{e1}\), \(P_{2}=\frac {1}{2}-\kappa _{e1}\), \(P_{3}=-\frac {3}{2}+\kappa _{e1}\), \(P_{4}=-\frac {1}{2}-\kappa _{e2}\), \(P_{5}=\frac {1}{2}-\kappa _{e2}\) and \(P_{6}=-\frac {3}{2}+\kappa _{e2}\) [32]. The phase velocity is given as [32]

$$\begin{array}{@{}rcl@{}} V_{p} = \sqrt{\frac{1}{\frac{\mu_{e1}(\kappa_{e1} -\frac{1}{2})\sigma_{1}}{\kappa_{e1}-\frac{3}{2}} + \frac{\mu_{e2}(\kappa_{e2} -\frac{1}{2})\sigma_{2}}{\kappa_{e2}-\frac{3}{2}}}} \end{array} $$
(36)

So the Gardner equation is represented depending on the plasma parameters. These parameters are σ 1 = T e f /T e1, σ 2 = T e f /T e2, μ 1e = n e10/n i0, μ 2e = n e20/n i0. κ e1 and κ e2 are the spectral index parameters which measure the slope of the thermal particles. T 1e and T 2e are the lower and higher electron temperatures, and T e f is the effective temperature of two electrons [32].

It is important to understand the space and laboratory dust plasmas by using the wide variety of plasma parameters [37]. It is found that the amplitudes of the solitary waves strongly depend on the plasma parameters, μ 1 and σ 1. The various values of these parameters increase or decrease the amplitude and width of the solitons seen in Fig. 9. It is deduced from this figure that the smaller or higher values of both parameters μ 1 and σ 1 create solitons with smaller amplitudes. On the other hand, the higher or smaller values of one of these parameters can cause the bigger amplitude solitons.

Fig. 9
figure 9

Showing the variation of soliton dynamics for different values of plasma parameters. Group 1: μ 1=0.1, μ 2=0.1→0.5, K 1=18→21, K 2=1→3, σ 1=1, and σ 2=1→3. Group 2: Same variables as in group 1, except σ 1=3. Group 3: Same variables as in group 1, except μ 1=0.5. Group 4: Same variables as in group 1, except μ 1=0.5 and σ 1=0.3

Full size image

Now, we can compute the maximum value of amplitude of each soliton with its position at η. As it is seen in Fig. 10, the maximum amplitudes of the solitary waves and their positions along η increase for different plasma parameters, but create three different arms depending on the lower electron temperature and initial ratio of electron particle density to ion particle density. We note that, depending on the values of μ 1 and σ 1, four different regions are observed and the analytic solution of Gardner equation produces solitary waves in similar amplitudes, polarity, and widths in the same region. But these properties of solitary waves change at different regions defined in Fig. 10. As a final word, it is numerically proved that every value of μ 1 or σ 1, with the other sets of plasma parameters, creates a region where the solutions have similar physical properties.

Fig. 10
figure 10

Variation of maximum amplitude of the solitons, U(η) m a x versus η for different values of plasma parameters, as given in Fig.9. The maximum amplitudes of the solitons and their locations increase with different plasma parameters, but are divided into three paths depending on the lower electron temperature and the initial ratio of electron density to ion density

Full size image

5 Conclusion

Gardner equation is analytically solved by using the two dependent (G ′/G,1/G)-expansion and (1/G ′)-expansion methods, and direct integration. The exact solutions are obtained, and they are used to find the solitary waves and understand their nonlinear behavior and their parametric dependences, observed in two different plasmas. We have considered two types of plasmas: one includes the electron acoustic waves in a nonextensive positron-electron-ion system, and the other has dust-ion acoustic waves produced by two-temperature thermal electrons.

First of all, we have obtained that the analytic solutions of the Gardner equation found from (G ′/G,1/G)-expansion and (1/G ′)-expansion methods do not produce the solitons. We observe only shock waves and the amplitudes of these shock waves not only change with the plasma parameters but also depend on the integration constants and source terms derived in analytic solutions. The strength of nonextensivity parameter q has a positive effect on the strength of the shock wave while it is reduced by increasing μ 1. The source term μ defined in (G ′/G,1/G)-expansion method slightly shifts the location of the shock wave but the amplitude of the shock wave keeps the same with increasing μ. Depending on values of c 1 and c 2, the analytic solutions go from one type of solution to the other.

Later, we derive the analytic solutions of the Gardner equation by using the direct integration. We have found the solitary waves for two different plasma systems and defined the deep internal structure of solitons, their maximum amplitudes and locations along η depending on plasma parameters. It is found that many solitons are produced in different parameter ranges. These ranges are more extensive than the one obtained from the analysis given in [32, 34]. The amplitudes, widths, and the locations of solitons along η vary significantly with the plasma parameters μ 1, q, the critical value of μ 1, μ 2, and σ 1. On the other hand, the maximum amplitudes of the solitary waves and their position along η separate into three different arms depending on the lower electron temperature and initial ratio of electron particle density to ion particle density. The time-dependent behavior of the soliton is also studied and a periodic motion of soliton along η is found during theevaluation.

Finally, it is important to mention here that the analytic solutions found from (G ′/G,1/G)-expansion and (1/G ′)-expansion methods and direct integration can be used to understand the dynamics of the solitary waves and their nonlinear features produced in different physical and astrophysical plasmas, such as hadronic matter, quark gluon plasma, neutron stars, and interstellar medium [38–40].