1 Introduction

Both solitary (Abdelsalam 2010; Abdelsalam et al. 2011; Malfliet 1992) and shock (Alinejad 2010; Abdou and Soliman 2005) waves are nonlinear waves in characteristics and are found from the solutions of KdV (Korteweg and de Vries 1895; Russell 1844) and Burgers’ (Burger 1948; Abdou and Soliman 2005; Alinejad 2010) equations. And there are already lots of works on those nonlinear waves using the solution of KdV and Burgers’ equations derived from reductive perturbation method (Abdelsalam and Selim 2013; Abdou and Soliman 2005; Moslem 1999; Moslem et al. 2010). Researchers have also found interest in nonlinear wave dynamics (Davidson 1972; Malfliet 1992; Wang et al. 2008) in presence of negative and positive ions in plasma (Merlino and Kim 2006; Intrator et al. 1983), electron degeneracy (Abdelsalam et al. 2008a, b, c, 2012; Abdelsalam and Selim 2013) with relativistic limits as non-relativistic limit and ultra-relativistic limits, (Chandrasekhar 1931, 1934, 1935), as well as in astrophysics and space science (Shukla 2002; Abdelsalam et al. 2008c, 2011, 2012; Alinejad 2010) to make more studies on astro compact objects. Very recently, the traveling waves (Samanta et al. 2013; Kazmierczak 1997; Wang et al. 2008) have taken the place of interest as a new topic in plasma research (Davidson 1972), as in space the waves could not form pure solitary or shock wave structure to travel but as a sine wave. Traveling waves are found to be more realistic to consider in space known as solitary or shock waves (Samanta et al. 2013; Kazmierczak 1997; Davidson 1972; Shukla 2002) where the waves form as a sine wave to propagate through the dense medium in free space because of presence of electric filed (Abdelsalam et al. 2008b, c, 2012) or magnetic filed (Samanta et al. 2013; Abdelsalam and Selim 2013) or both electric and magnetic fileds (Abdelsalam et al. 2008a; Moslem et al. 2010).

One of the most challenging facts of a mathematical model is to choose the correct method to derive an acceptable solution. There are many internationally recognized methods for solving nonlinear wave equations from a different type of mathematical modeling with physical problems, which are successfully proved to pride the exact solution. Among those methods, general expansion method (Moslem et al. 2010), extended homogeneous balance method (Abdelsalam et al. 2016a) and ‘\(G'/G\)’ method (Wang et al. 2008; Abdelsalam and Selim 2013) are used in this work with reductive perturbation method (Abdelsalam 2010; Abdelsalam and Selim 2013; Alinejad 2010; Abdou and Soliman 2005; Moslem 1999) mostly used methos to derive the solutions of stationary solitary and shock waves from well-known KdV (Korteweg and de Vries 1895; Russell 1844; Abdelsalam 2010; Abdelsalam et al. 2011) and Burgers’ (Burger 1948; Abdou and Soliman 2005; Alinejad 2010) equations. Comparing other methods, it is proved that, for the computation of exact traveling wave solutions, ‘\(G'/G\)’ (Wang et al. 2008; Abdelsalam and Selim 2013) is a direct and effective algebraic method.

In our current model where we consider one-dimensional, collisionless, unmagnetized plasma consists of both positive and negative ions, degenerate electrons, and stationary charged dust impurities which could be positive or negative or both. Effects of q-parameter for non-extensive electron distribution have been discussed in (Abdelsalam et al. 2016b), but degenerate electrons (Abdelsalam et al. 2008a, b, c, 2012) are found to as an important properties in astrophysical compact objects (Abdelsalam et al. 2008c, 2011; Alinejad 2010; Chandrasekhar 1931, 1935) such as black holes, neutron star, and white dwarfs. So we use degenerate electrons for both ultra-relativistic and non-relativistic limits to study high-dense plasma case, and we use ‘\(G'/G\)’ (Wang et al. 2008; Abdelsalam and Selim 2013; Zhang et al. 2008; Selim and Abdelsalam 2014) method with reductive perturbation method to solve the further modified Korteweg–de Vries (fmKdV) equation (Moslem 1999) in case of travelling wave (Abdelsalam et al. 2016b; Davidson 1972) and to obtain a solution describing the possible nonlinear waves in our plasma model.

This paper is organized as follows: in Sect. 2, we present the governing equations for our plasma model. In Sect. 3 the reductive perturbation method is employed to derive further modified KdV (fmKdV) equation describing the system and we apply \(G'/G\) method to solve fmKdV equation in Sect. 4. The numerical results are presented in Sect. 5. Finally, the results are summarized in Sect. 6.

2 Basic Equations

We consider unmagnetized, and collisionless three-component plasma consisting of negative ions, positive ions, electrons and stationary dust, a system of fluid equations for the negative and positive ion fluids, respectively distinguished using the index “−” and “+”. We consider continuity equation for both ions:

$$\begin{aligned} \frac{\partial n_{-,+}}{\partial t}+{\nabla } \cdot (n_{-,+}u_{-,+})=0, \end{aligned}$$
(1)

and the momentum equation for both ions,

$$\begin{aligned} m_{+}n_{+}\left( \frac{\partial }{\partial t}+\mathbf {u}_{+} \frac{\partial }{\partial x} \right) \mathbf {u}_{+}+\frac{\partial P_{+}}{\partial x}+ e Z_{+}n_{+}\frac{\partial \phi }{\partial x}=0, \end{aligned}$$
(2)

and

$$\begin{aligned} m_{-}n_{-}\left( \frac{\partial }{\partial t}+\mathbf {u}_{-} \frac{\partial }{\partial x}\right) \mathbf {u}_{-}+\frac{\partial P_{-}}{\partial x}- e Z_{-}n_{-}\frac{\partial \phi }{\partial x}=0, \end{aligned}$$
(3)

For electrons:

$$\begin{aligned} -e \frac{\partial \phi }{\partial x}+\frac{1}{n_{e}}\frac{\partial P_{e}}{\partial x}= 0, \end{aligned}$$
(4)

The Poisson equation reads

$$\begin{aligned} \nabla ^{2}\phi =4\pi e \biggl (Z_{+}n_{+} - Z_{-}n_{-}- n_{e} +\rho Z_d n_{d} \biggr ). \end{aligned}$$
(5)

In Eqs. (1)–(5), \(n_{-,+}\) is the negative (positive) ion number density, while \(n_{d}\) is the dust density. Furthermore, \(u_{-,+}\) is the negative (positive) ion fluid velocity, \(\phi \) is the electrostatic wave potential, e is charge of electrons, Z is the magnitude of charge for dust(d), negative (−) and positive (\(+\)) ions, \(m_{\pm }\) is the mass of positive and negative ions, \(\rho =\pm \). The ion pressure is assumed to be adiabatic and is expressed by \(P_{s}=n_{s}^{(0)}k_{\rm B}T_{s}n_{s}^{3}~(s=+,-)\). The degenerate electron pressure \(P_{e}=Kn_{e}^{5/3}~\)and \(K\simeq \frac{3}{4} \hbar c~,~\)where \(n_{s}^{(0)}~\)are the equilibrium densities for the positive ions, the negative ions, respectively, \(k_{\rm B}~\)is the Boltzmann constant, \(T_{s}~\)the positive (negative) ions temperature, \(\hbar \ \)is the Plank cons\(\tan \)t \({\text {div}}\)ided by \(2\pi \), and c is the speed of light in vacuum.

Equations (1)–(4) may be cast in a reduced (non-dimensional) form, for convenience in manipulation. For positive ion fluid, we have

$$\begin{aligned} \frac{\partial \overline{n}_{+}}{\partial \overline{t}}+\frac{\partial \overline{n}_{+}\overline{u}_{+}}{\partial \overline{x}}=0 \, , \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial \overline{u}_{+}}{\partial \overline{t}}+ \overline{u}_{+}\frac{\partial {u}_{+}}{\partial \overline{x}}+\sigma _{+}\overline{n}_{+}\frac{\partial \overline{n}_{+}}{\partial \overline{x}}+ \frac{\partial \overline{\phi }}{\partial \overline{x}}=0. \end{aligned}$$
(7)

In the same way, for the negative ion, we have

$$\begin{aligned} \frac{\partial \overline{n}_{-}}{\partial \overline{t}}+\frac{\partial \overline{n}_{-}\overline{u}_{-}}{\partial \overline{x}}=0 \, , \end{aligned}$$
(8)
$$\begin{aligned} \frac{\partial \overline{u}_{-}}{\partial \overline{t}}+ \overline{u}_{-}\frac{\partial {u}_{-}}{\partial \overline{x}}+\sigma _{-} Q_{-}\overline{n}_{-}\frac{\partial \overline{n}_{-}}{\partial \overline{x}}-Q_{-} \Delta _{-}\frac{\partial \overline{\phi }}{\partial \overline{x}}=0. \end{aligned}$$
(9)

For electrons:

$$\begin{aligned} \frac{\partial \overline{\phi }}{\partial \overline{x}}-\delta n^{-1/3}_{e}\frac{\partial \overline{n}_{e}}{\partial \overline{x}}=0. \end{aligned}$$
(10)

Finally, the Poisson equation becomes:

$$\begin{aligned} \frac{\partial ^{2}\overline{\phi }}{\partial \overline{x^{2}}}=\overline{n}_{+}-\alpha \Delta _{-}\overline{n} _{-}-\gamma \Delta _{+} \overline{n}_{e}-\rho \beta , \end{aligned}$$
(11)

where the mass ratio \(Q_{-}=m_{+}/m_{-}\) (\(m_{+}\) and \(m_{-}\) are the positive and negative ion mass, respectively), \(\sigma _{+,-}=3\frac{T_{+,-}}{T_{e}}\), \(\delta =\frac{5k n^{(0)}_{e}}{k_{\rm B} T_{ef}}\), \(\Delta _{-}=Z_{-}/Z_{+}\), and \(\Delta _{+}=1/Z_{+}\) and the upper bar in Eqs. (6)–(11) will henceforth be omitted (Abdelsalam and Selim 2013; Moslem et al. 2010).

The neutrality condition implies

$$\begin{aligned} 1=\Delta _{-}\alpha +\Delta _{+}\gamma -\rho \beta , \end{aligned}$$
(12)

where \(\alpha =n^{(0)}_{-}/n^{(0)}_{+}, \gamma =n^{(0)}_{e}/n^{(0)}_{+}\) and \(\beta =Z_{d}n^{(0)}_{d}/n^{(0)}_{+}\) (the index ‘(0)’ denotes the unperturbed density states).

3 Derivation of the Modified Korteweg–de Vries (mKdV) Equation

The independent variables can be stretched as:

$$\begin{aligned} X=\epsilon (x-\lambda t) , \quad {\rm and} \quad \tau =\epsilon ^{3}t, \end{aligned}$$
(13)

where \(\epsilon \) is a small dimensionless (real) parameter measuring the weakness of the dispersion and nonlinearity (Alinejad 2010; Abdelsalam and Selim 2013; Moslem et al. 2010; Malfliet 1992; Davidson 1972) and \(\lambda \) is the wave propagation speed. The dependent variables are expanded as

$$\begin{aligned} \Psi =\Psi ^{(0)}+\sum _{n=1}^{\infty }\epsilon ^{n}\Psi ^{(n)}, \end{aligned}$$
(14)

where

$$\begin{aligned} \Psi = \{n_{+},n_{-},n_{e},u_{+},u_{-},\phi \}^{\rm T}, \end{aligned}$$
(15)

and

$$\begin{aligned} \Psi ^{(0)}=\{1, \beta ,\alpha , 0, 0, 0\}^{\rm T} . \end{aligned}$$
(16)

Employing the variable stretching in Eq. (13) and the expansion of Eqs. (14)–(16) into Eqs. (6)–(11), we may now isolate distinct orders in \(\epsilon \) and derive the corresponding variable contributions. The lowest-order equations in \(\epsilon \) read

$$\begin{aligned} n_{e1}=\frac{1}{\delta }\phi _{1}, \quad n_{-}^{(1)}=\frac{-Q_{-}\Delta _{-}}{(\lambda ^{2}-\sigma _{-}Q_{-})}\phi ^{(1)}, \quad u_{-}^{(1)}= \frac{-Q_{-}\Delta _{-}\lambda }{(\lambda ^{2}-\sigma _{-}Q_{-})}\phi ^{(1)} , \end{aligned}$$
(17)

and

$$\begin{aligned} n_{+}^{(1)}=\frac{1}{(\lambda ^{2}-\sigma _{+}) }\phi ^{(1)} , \quad u_{+}^{(1)}=\frac{\lambda }{(\lambda ^{2}-\sigma _{+})}\phi ^{(1)} . \end{aligned}$$
(18)

The Poisson equation provides the compatibility condition.

$$\begin{aligned} \frac{1}{(\lambda ^{2}-\sigma _{+})}+\frac{\alpha Q_{-}\Delta _{-}^{2}}{(\lambda ^{2}-\sigma _{-}Q_{-})}-\frac{\gamma \Delta _{+}}{\delta }=0. \end{aligned}$$
(19)

The next order in \(\epsilon \) yields:

$$\begin{aligned} n_{+}^{(2)}=\frac{1}{(\lambda ^{2}-\sigma _{+})}\left[ \phi ^{(2)} +\frac{(3\lambda ^{2}+\sigma _{+})}{2(\lambda ^{2}-\sigma _{+})^{2}}\phi ^{(1)2}\right] \, , \end{aligned}$$
(20)
$$\begin{aligned} n_{-}^{(2)}=\frac{Q_{-}\Delta _{-}}{(\lambda ^{2}-\sigma _{-}Q_{-})}\left[ -\phi ^{(2)}+\frac{Q_{-}\Delta _{-}(3\lambda ^{2}+\sigma _{-}Q_{-})}{2(\lambda ^{2}-\sigma _{-}Q_{-})^{2}}\phi ^{(1)2}\right] \, , \end{aligned}$$
(21)
$$\begin{aligned} n_{e}^{(2)}=\frac{1}{\delta }\left[ \phi ^{(2)}+\frac{1}{6\delta }\phi ^{(1)2}\right] \, , \end{aligned}$$
(22)

the Poisson’s equation gives:

$$\begin{aligned} \left[ \frac{1}{(\lambda ^{2}-\sigma _{+})}+\frac{\alpha Q_{-}\Delta _{-}^{2} }{(\lambda ^{2}-\sigma _{-}Q_{-})}-\frac{\gamma \Delta _{+}}{\delta }\right] \phi ^{(2)}+B\phi ^{(1)2}=0, \end{aligned}$$
(23)

where

$$\begin{aligned} B=\frac{1}{2}\left[ \frac{(3\lambda ^{2}+\sigma _{+})}{(\lambda ^{2}-\sigma _{+})^{3}}-\frac{\alpha Q_{-}^{2}\Delta _{-}^{3}(3\lambda ^{2}+\sigma _{-}Q_{-} )}{(\lambda ^{2}-\sigma _{-}Q_{-})^{3}}-\frac{\gamma \Delta _{+}}{3\delta ^{2} }\right] . \end{aligned}$$
(24)

If we consider the third-order in \(\epsilon \), we obtain:

$$\begin{aligned} \frac{\partial n_{e}^{(3)}}{\partial \xi }=\frac{1}{\delta }\left[ \frac{\partial \phi ^{(3)}}{\partial \xi }+\frac{1}{3\delta }\frac{\partial (\phi ^{(1)}\phi ^{(2)})}{\partial \xi }-\frac{1}{18\delta ^{2}}\phi ^{(1)2} \frac{\partial \phi ^{(1)}}{\partial \xi }\right] . \end{aligned}$$
(25)

The Poisson’s equation in this order becomes:

$$\begin{aligned} \frac{\partial ^{2}\phi ^{(1)}}{\partial \xi ^{2}}= ( n_{+}^{(3)}-n_{+} ^{(2)} ) -\alpha \Delta _{-} ( n_{-}^{(3)}-n_{-}^{(2)} ) -\gamma \Delta _{+} ( n_{e}^{(3)}-n_{e}^{(2)} ) . \end{aligned}$$
(26)

Using the last equations, we obtain the fmKdV equation

$$\begin{aligned} \frac{\partial \phi }{\partial \tau }+AB\phi \frac{\partial \phi }{\partial \xi }+AC\phi ^{^{2}}\frac{\partial \phi }{\partial \xi }+\frac{A}{2}\frac{\partial ^{3}\phi }{\partial \xi ^{3}}=0. \end{aligned}$$
(27)

where we replace \(\phi ^{(1)}~\)by \(\phi ~\) for simplicity. The coefficients A and C are given as:

$$\begin{aligned} A=-\frac{1}{\lambda }\left[ \frac{1}{(\lambda ^{2}-\sigma _{+})^{2}} +\frac{\alpha Q_{-}\Delta _{-}^{2}}{(\lambda ^{2}-\sigma _{-}Q_{-})^{2}}\right] ^{-1}, \end{aligned}$$
(28)
$$\begin{aligned} C =-\frac{3}{2(\lambda ^{2}-\sigma _{+})^{5}}\left[ \lambda ^{2}(\lambda ^{2}+3\sigma _{+})+\frac{1}{2}(\lambda ^{2}+\sigma _{+})(3\lambda ^{2}+\sigma _{+})\right] - \end{aligned}$$
$$\begin{aligned} \frac{3\alpha Q_{-}^{3}\Delta _{-}^{4}}{2(\lambda ^{2}-\sigma _{-}Q_{-})^{5} }\left[ \lambda ^{2}(\lambda ^{2}+3\sigma _{-}Q_{-})+\frac{1}{2}(\lambda ^{2}+\sigma _{-}Q_{-})(3\lambda ^{2}+\sigma _{-}Q_{-})\right] - \frac{\gamma \Delta _{+}}{36\delta ^{3}}. \end{aligned}$$
(29)

4 Solution of the Further Modified Korteweg–de Vries fmKdV Equation via \(G'/G\)-Expansion Method

Now, we go beyond the “ traditional” solution of the further modified Korteweg–de Vries fmKdV Eq. (27) by quadrature (see in the previous Section) by adopting an alternative method, namely, the \(G'/G\)-expansion method introduced in Wang et al. (2008) and Abdelsalam and Selim (2013) (see for more details).

According to \(G'/G\)-expansion method, we anticipate that Eq. (27) has the following solution:

$$\begin{aligned} u(\zeta )=\sum ^{n}_{i=0}a_{i}\left( \frac{G'(\zeta )}{G(\zeta )}\right) ^{i}, \end{aligned}$$
(30)

where \(a_{i}\) are real constants with \(a_{n}\ne 0\) to be determined, and n is a positive integer to be determined. The function \(G(\zeta )\) is the solution of the auxiliary linear ordinary differential equation

$$\begin{aligned} G''+\nu G'+\mu G=0, \end{aligned}$$
(31)

where \(\nu \) and \(\mu \) are real constants to be determined.

Consider fmKdV Eq. (27) in the form

$$\begin{aligned} \frac{\partial u}{\partial \tau }+\Gamma u\frac{\partial u}{\partial \xi }+\Lambda u^{^{2} }\frac{\partial u}{\partial \xi }+\Omega \frac{\partial ^{3}u}{\partial \xi ^{3}}=0. \end{aligned}$$
(32)

where \(\Gamma =AB\), \(\Lambda =AC\), \(\Omega =\frac{A}{2}\).

We seek for the special solution of Eq. (32), traveling wave solution, in the form

$$\begin{aligned} u(\xi ,\tau )=u(\zeta ), \quad \zeta = \xi -\vartheta \,\tau , \end{aligned}$$
(33)

where \(\vartheta \) is a constant to be determined later. Using the transformation (33), Eq. (32) reduces to a nonlinear ordinary differential equation (ODE) Davidson (1972):

$$\begin{aligned} -\lambda U^{\prime }+\Gamma U U^{\prime }+\Lambda U^{2} U^{\prime }+\Omega U^{\prime \prime \prime }=0, \end{aligned}$$
(34)

Integrating Eq. (34) once,

$$\begin{aligned} -\vartheta u+\frac{1}{2}\Gamma u^{2}+\frac{1}{3}\Lambda u^{3}+C u^{\prime \prime }=0, \end{aligned}$$
(35)

where the balance between the highest order derivatives and the nonlinear term gives \(n=1\), so (30) reduced to

$$\begin{aligned} u(\zeta )=a_{0}+a_{1}\left( \frac{G'(\zeta )}{G(\zeta )}\right) , \end{aligned}$$
(36)

It is well known that exact solutions of Eq. (31) are as follows:

  1. (i)

    for \(k=\nu ^{2}-4 \ \mu >0\)

    $$\begin{aligned} \left( \frac{G'(\zeta )}{G(\zeta )}\right) = \frac{\sqrt{k}}{2} \left( \frac{c_{1}\cosh \left(\frac{\sqrt{k}}{2} \zeta \right)+c_{2}\sinh \left(\frac{\sqrt{k}}{2} \zeta \right)}{c_{1}\sinh \left(\frac{\sqrt{k}}{2} \zeta \right)+c_{2}\cosh \left(\frac{\sqrt{k}}{2} \zeta \right)}\right) -\frac{\nu }{2}, \end{aligned}$$
    (37)
  2. (ii)

    for \(k=\nu ^{2}-4\mu <0\)

    $$\begin{aligned} \left( \frac{G'(\zeta )}{G(\zeta )}\right) = \frac{\sqrt{-k}}{2} \left( \frac{c_{1}\cos \left(\frac{\sqrt{-k}}{2} \zeta \right)-c_{2}\sin \left(\frac{\sqrt{-k}}{2} \zeta \right)}{c_{1}\sin \left(\frac{\sqrt{-k}}{2} \zeta \right)+c_{2}\cos \left(\frac{\sqrt{-k}}{2} \zeta \right)}\right) -\frac{\nu }{2}, \end{aligned}$$
    (38)
  1. (i)

    for \(k=\nu ^{2}-4\mu =0\)

    $$\begin{aligned} \left( \frac{G'(\zeta )}{G(\zeta )}\right) = \left( \frac{c_{2}}{c_{1}+c_{2} \zeta }\right) -\frac{\nu }{2}, \end{aligned}$$
    (39)

Substituting Eq. (36) in Eq. (35) and making use of Eq. (31), we obtain a polynomial equation in \(\left( \frac{G'(\zeta )}{G(\zeta )}\right) \). Equating the coefficients of \(\left( \frac{G'(\zeta )}{G(\zeta )}\right) \) to zero will result in an overdetermined system of algebraic equations with respect to \(a_{0}\), \(a_{1}\), \(\mu \), \(\lambda \) and \(\vartheta \). We obtain a complete new set of solutions, which will be presented in the following.

For \(k>0\),

$$\begin{aligned} u_{1}(\zeta )=\frac{-\Gamma }{2\Lambda }\left( 1-\coth \left( \sqrt{\frac{-\Lambda }{6\Omega }}\frac{-\Gamma }{2\Lambda }\zeta \right) \right) , \end{aligned}$$
(40)
$$\begin{aligned} u_{2}(\zeta )=\frac{-\Gamma }{2\Lambda }\left( 1-\tanh \left( \sqrt{\frac{-\Lambda }{6\Omega }}\frac{-\Gamma }{2\Lambda }\zeta \right) \right) , \end{aligned}$$
(41)
$$\begin{aligned} u_{3}(\zeta )=\frac{-\Gamma }{2\Lambda }\left( 1+\coth \left( \sqrt{\frac{-\Lambda }{6\Omega }}\frac{-\Gamma }{2\Lambda }\zeta \right) \right) , \end{aligned}$$
(42)
$$\begin{aligned} u_{4}(\zeta )=\frac{-\Gamma }{2\Lambda }\left( 1+\tanh \left( \sqrt{\frac{-\Lambda }{6\Omega }}\frac{-\Gamma }{2\Lambda }\zeta \right) \right) . \end{aligned}$$
(43)

For \(k=0\),

$$\begin{aligned} u_{5}(\zeta )=\frac{-\Gamma }{2\Lambda } , \end{aligned}$$
(44)
$$\begin{aligned} u_{6}(\zeta )=\frac{-\Gamma }{2\Lambda }+\sqrt{\frac{-6\Omega }{\Lambda }}\zeta . \end{aligned}$$
(45)

For \(k<0\),

$$\begin{aligned} u_{7}(\zeta )=\frac{-\Gamma }{2\Lambda }\left( 1-\tan \left( \sqrt{\frac{\Lambda }{6\Omega }}\frac{-\Gamma }{2\Lambda }\zeta \right) \right) , \end{aligned}$$
(46)
$$\begin{aligned} u_{8}(\zeta )=\frac{-\Gamma }{2\Lambda }\left( 1-\cot \left( \sqrt{\frac{\Lambda }{6\Omega }}\frac{-\Gamma }{2\Lambda }\zeta \right) \right) , \end{aligned}$$
(47)
$$\begin{aligned} u_{9}(\zeta )=\frac{-\Gamma }{2\Lambda }\left( 1+\tan \left( \sqrt{\frac{-\Lambda }{6\Omega }}\frac{-\Gamma }{2\Lambda }\zeta \right) \right) , \end{aligned}$$
(48)
$$\begin{aligned} u_{10}(\zeta )=\frac{-\Gamma }{2\Lambda }\left( 1+\cot \left( \sqrt{\frac{-\Lambda }{6\Omega }}\frac{-\Gamma }{2\Lambda }\zeta \right) \right) . \end{aligned}$$
(49)

5 Results and Discussion

fmKdV equation has been derived for multicomponent plasma consisting of negative ions, positive ions, electrons and stationary dust, and the electrons are supposed to be degenerate. A lot of papers studied the KdV equation and its soliton solutions, and the KdV equation was derived for similar models of plasmas with various types of electron distribution (see Abdelsalam 2010; Abdelsalam et al. 2011; Abdelsalam 2013). We can see that the soliton solution was studied for a similar model of plasma in Abdelsalam (2010), in which the dust ion acoustic waves were studied in a similar dense plasma, and the author derived KdV equation to study the soliton waves and the affect of the many some physical parameters on these waves. The KdV equation and the soliton waves were studied for similar models but with nonextensive electrons in Abdelsalam et al. (2011), and with superthermal electrons, ion beam in Abdelsalam (2013). However, to study the shock waves we derived the fmKdV equation in the present paper, and by solving this equation we can get the kink or shock wave solution. To investigate the nonlinear properties of solitary waves represented by Eq. (27), we express the solution from Eq. (41) in the following form:

$$\begin{aligned} \phi (\zeta )=\frac{1}{2}\phi _{m}\left[ 1-\tanh \left( \frac{2\zeta }{W}\right) \right] , \end{aligned}$$
(50)

which represents a shock wave, where \(\phi _{m}~\) and W are the amplitude and width of the double layers, respectively, and are given by:

$$\begin{aligned} \phi _{m}=-\frac{B}{C} \quad {\rm and} \quad W =2\frac{\sqrt{-12/C}}{\left| \phi _{m}\right| }. \end{aligned}$$
(51)

It is noted that the amplitude and width depend on the electron density \(n^{(0)}_{e}\), negative-to-positive ion density ratio \(\alpha \left( =n^{(0)}_{-}/n^{(0)}_{+}\right) \), and the positive (negative) ion-to-electron temperature ratio \(\sigma _{+,-}=3\frac{T_{+,-}}{T_{\rm Fe}} \).

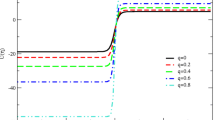
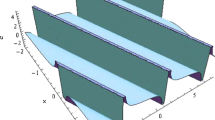
Figure 1 is the representation of amplitudes (u) of nonlinear waves that how u varies with x and t. It gives a pure 3D view to change the variations, but little complicated to make a quick assumption from this point of view. So Fig. 2 is comparatively easier than Fig. 1 to explain that with increasing time there is no such a change in u, but at the initial state, u increases with increasing the value of x. At a certain value of x, the value of u suddenly decreases as shown in the figure. And again, the value of u increases with the increasing value of x. The value of x, where u suddenly drops its value is called the critical point of x. We make a sharp view from the critical point of x, then we find something different from opposite polarity. At the opposite polarity of X axis, the value of amplitudes (u) increases slowly with x. And this is true before and after the critical value of x. So from Figs. 1 and 2, we can make a statement that our, in dusty plasma model, amplitudes increase with x before and after the critical value of x when \(\alpha \), \(\beta \), \(\sigma _{-}\), and \(\sigma {+}\) are fixed in value, but the rate of increasing value of u is not same for both polarity of x, from 3D point of view which is never observed in 2D plot.

Fig. 1
figure 1

Three-dimensional profile of the periodic solution [given by Eq. (46)] for fixed values of \(\alpha =0.7,\) \(\beta =0.2\), \(\sigma _{-}=0.6\) and \(\sigma _{+}=0.5\)

Full size image
Fig. 2
figure 2

Three-dimensional profile of the explosive/blowup pulse [given by Eq. (40)] for the same parameters as in Fig. 1

Full size image

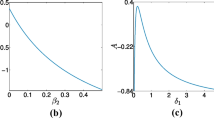
Now from Figs. 3, 4 and 5, we can make some analysis about the outcomes of our present work with some discussion. For example, the value of amplitudes (u) increases slowly for the higher electron number density (\(n_{e}^{(0)}\)) but it increases sharply with lower electron number density. But after passing a certain distance, the value of \(\zeta \), and u is same for all values of \(n_{e}^{(0)}\), when other parameters are fixed as shown in Fig. 3. In other word, it is obvious from Fig. 3 that increasing the parameter \(n_{e}^{(0)}~\) would lead to a decrease in the amplitude of the shock wave.

Fig. 3
figure 3

The shock wave profile for different values of \(n^{(0)}_{e}\) where \(n^{(0)}_{e}=2.31x10^{21}\) (solid line), \(n^{(0)}_{e}=3.7x10^{21}\) (dotted line), \(n^{(0)}_{e}=5.2x10^{21}\) (dashes line). Here, \(\alpha =0.9,\) \(\beta =0.1,\) \(T_{1}=9000,\) \(T_{2}=8000,\) and \(Q=0.8\)

Full size image
Fig. 4
figure 4

The shock wave profile for different values of \(\sigma _{+}\) and \(\sigma _{-}\) where \(\sigma _{+}=\sigma _{-}=0.6\) (solid line), \(\sigma _{+}=0.65,\) \(\sigma _{-}=0.6\) (dotted line), \(\sigma _{+}=0.6,\) \(\sigma _{-}=0.65\) (dashes line). Here, \(\alpha =0.9,\) \(\beta =0.1,\) and \(Q=0.8\)

Full size image
Fig. 5
figure 5

The shock wave profile for different values of \(\alpha \) where \(\alpha =0.4,\) (solid line), \(\alpha =0.6,\) (dotted line), \(\alpha =0.8,\) (dashes line). Here, \(\sigma _{+}=\) \(\sigma _{-}=0.6,\) and \(Q=0.8\)

Full size image

Figure 4 is the example to show the effect of \(\sigma \), which is a combination of \(\sigma _{+,-}\), on amplitude (u). When in such a combination, the value of \(\sigma _{+}\) is greater than \(\sigma _{-}\), then the value of u increases slowly with \(\zeta \). But u increases sharply against \(\zeta \) for \(\sigma \), where \(\sigma _{-}\) is greater than \(\sigma _{+}\). And when the values of \(\sigma _{-}\) and \(\sigma _{+}\) are same, then the effects of \(\sigma \) on u is between two conditions, just previously mentioned. We can also explain this in another way with simple analysis like, Fig. 4 clears that the increase of positive ion-to-electron temperature ratio would lead to make the shock amplitude taller but the negative ion-to-electron temperature ratio make the shock shorter. On the other hand, the ion temperature accelerate the particles due to generation of high potential shock wave.

And the effects of \(\alpha \) on amplitudes is shown in Fig. 5. The value of u increases slowly and sharply for lower and higher values of \(\alpha \). So it is obvious from Fig. 5 that the excess of negative-to-positive ion density ratio would lead to increase the shock amplitude. But the most interesting point to note from Figs. 3, 4 and 5 is that for the effects of different parameters (when some other parameters are fixed in values) the amplitudes of shock waves always negative in value, and the highest value of u is 0 in all conditions (Figs. 3, 4, 5). In addition, the amplitude for different values of \(\sigma _{+}\) and \(\sigma _{-}\) is 10 times smaller shown in Fig. 4 than \(n_e^{(0)}\) (in Fig. 3) and \(\alpha \) (in Fig. 5). So one conclusion could be established from this point that our dusty plasma model for nonlinear wave equations only negates negative values of amplitudes for shock wave profiles. And the main reasons could be: (1) we consider both positive and negative ions with stationary (positive/negative) charged dust impurities and (2) presence of electron degeneracy pressure. If we consider no dust particles or highly charged either positive or negative dust grains, then there could be some change in amplitudes of nonlinear shock waves. So, it needs to justify what makes the main effect to provide positive and negative shock wave profile, but this is beyond our present model.

6 Conclusion

In this paper, we consider a nonlinear propagation of traveling waves using the fluid model for ions (both positively and negatively charged) and electrons (with electron degenerate pressure), and a reductive perturbation technique. We derive further modified KdV equation (fmKdV) for the investigation of small but finite amplitude waves.

The solutions of fmKdV equation are obtained using \(G'/G\) method (Zhang et al. 2008; Selim and Abdelsalam 2014). \(G'/G\) method successfully proves different classes of solutions of the fmKdV equation (Davidson 1972; Fan 2000; Wang et al. 2008). Basically, different nonlinear wave equations are derived using \(G'/G\) method with new solutions and then those solutions are used to compare with the solutions (Yusufoglu and Bekir 2008; Fan 2003). The transformation formula is used in our nonlinear wave equations to show that our analysis of fmKdV is applicable for any nonlinear problems. So in this paper, \(G'/G\) method (Davidson 1972; Selim and Abdelsalam 2014; Fan 2000; Wang et al. 2008) is used with a computation of periodic traveling wave solutions for our model corresponding to nonlinear wave equations, and to understand the effects electron degeneracy pressure has on astrophysical compact objects as well as their wave characteristics.

In summary, we would like to say that our model is developed with multicomponent in dust plasma to derive the exact traveling solution of nonlinear shock waves from further modified Korteweg–de Vries equation using \(G'/G\) method (Zhang et al. 2008; Selim and Abdelsalam 2014). A mathematical derivation of nonlinear (Davidson 1972; Selim and Abdelsalam 2014; Fan 2000; Wang et al. 2008) wave equations with solutions justifies that our model is valid in such a limited case. There are still some facts to consider such as coupling parameter, degeneracy pressures for ions and neutrons, and magnetic field to observe the same phenomena in solitary and double layers waves. If we could consider all facts in one model, then it will be highly complicated to derive and solve, which could be critical to all researchers other than the strong mathematical background.

So for the future work, we hope there could be some works using our model with Gardner equations to analyze the nonlinear solitons. And we also hope for future laboratory work to justify our model with further validity and limitations.