1 Introduction

Bachmann (1964) introduced an important axiom in the foundation of geometry, stating that “Every quadrilateral with three right angles closes” (or “If a, b, c and d are lines such that a is orthogonal to b, b is orthogonal to c, and c is orthogonal to d, then a and d must intersect.”) He called it the Lotschnittaxiom (to be referred to as \(\mathbf{A}_1\)) and provided two equivalent statements for it, the equivalence holding over Hilbert’s plane absolute geometry \({\mathcal A}\) (whose axioms are the plane axioms of groups I, II, and III of Hilbert’s Grundlagen der Geometrie, being equivalent to the axioms A1–A9 in Schwabhäuser et al. (1983), the models of which are referred to as Hilbert planes). One of those equivalent statements is \(\mathbf{A_2}\), which states that: “If l and m are two lines which form a half-right angle (i.e., such that the reflection of l in m is orthogonal to l), then every line perpendicular to l must intersect m.” The other statement that is equivalent to \(\mathbf{A}_1\) is one indicative of the fact that the Lotschnittaxiom is weaker than the Euclidean parallel postulate. It states that “Through any point in the interior of a right angle there is a line which intersects the sides of that angle” (\(\mathbf{A}_3\)). A like-minded statement equivalent with respect to \({\mathcal A}\) to the Euclidean parallel postulate was first stated by J. F. Lorenz in 1791: “Through every point in the interior of any given angle there is a line intersecting the sides of that angle.” An order-free variant of \(\mathbf{A}_3\), which is equivalent to \(\mathbf{A}_3\) with respect to \({\mathcal A}\), was stated as axiom (s) in (Knüppel (1977), p. 6): “If a and b are two orthogonal lines, then any line c must intersect one of a or b.”

The first time a statement equivalent to \(\mathbf{A}_1\) was presented was long before 1964. On February 3, 1806 by Lagrange used the following axiom, whose equivalence to \(\mathbf{A}_1\) was shown in Pambuccian (2009): “If a and b are two parallels from P to g, then the reflection of a in b is parallel to g as well.” As shown in Pambuccian (1994), \(\mathbf{A}_1\) is also equivalent, with respect to \({\mathcal A}\), to the universal statement “The altitude to the base in an isosceles triangle with base angles of \(45^{\circ }\) is less than the base.”

The Lotschnittaxiom is essential for a geometric understanding of Pejas’s (Pejas 1961) algebraic characterization of the models of \({\mathcal A}\). A Hilbert plane \({\mathfrak H}\) can be embedded in a projective-metric plane over a Pythagorean ordered field K, in such a way that no point in it lies on the line [0, 0, 1] (written in homogeneous coordinates), so all its points can be written as (a, b, 1). The set \(M = \{a\in K:\, (a,0,1) \in {\mathfrak H}\}\) is called the set of abscissae of \({\mathfrak H}\). If M is a submodule of K (i.e. if M is a subgroup of the additive group of K), then \({\mathfrak H}\) is called modular. According to Bachmann (1964, Satz 2), a Hilbert plane embedded in a projective-metric plane is modular precisely if it satisfies \(\mathbf{A}_1\).

More general absolute geometries satisfying the Lotschnittaxiom have been investigated in Dress (1966) and Knüppel (1977).

The aim of this note is to show that the Lotschnittaxiom is equivalent to yet another statement of geometric interest. In Euclidean geometry, given a non-incident pair of point P and line l, the locus of all points Q equidistant from P and l is a parabola. The locus of all the points Q for which the distance to l is greater than the distance to P is the open convex region determined by that parabola. That region does not contain any (complete) line. Which absolute geometries, i.e. models of \({\mathcal A}\), have this property? We can state this property as

P For any non-incident pair (P, l) and any line h, there is a point Q on h whose distance to l is less than or equal to its distance to P.

The somewhat surprising answer is that those are precisely the absolute geometries satisfying the Lotschnittaxiom.

Theorem 1

\({\mathcal A}\vdash \mathbf{A}_2\leftrightarrow \mathbf{P}\).

2 Proving the equivalence

Suppose \({\mathfrak M}\) is a model of \({\mathcal A}\) in which \(\mathbf{A}_2\) holds, and let (P, l) be a non-incident pair consisting of a point P and a line l. Let O denote the foot of the perpendicular from P to l, and let m denote the line OP. Let b and \(b'\) denote the angle bisectors of the right angle formed by the lines m and l.

Suppose now that g is a line, such that all points Q on g have the property that their distance to l exceeds their distance to P. We want to show that g and b (or g and \(b'\)) must intersect (see Fig. 1).

Let G be an arbitrary point on g that is not on m (there must be such points, as g cannot be m). If G is incident with b or \(b'\), then there is nothing left to prove. Suppose G lies in the quadrant determined by l and m in which a half-line of b lies (the proof proceeds analogously were G to lie in the quadrant determined by l and m in which a half-line of \(b'\) lies). Let X and Y denote the feet of the perpendiculars from G to l and to m respectively. Notice that no point of g can lie on l, so that G is not on l. By the Crossbar Theorem [see Greenberg (2008), p. 116] and the Pasch axiom, the half-line of b that lies in the same quadrant determined by l and m in which G lies intersects one of the sides GX or GY of the quadrilateral OXGY. By \(\mathbf{A}_2\), the line GX, being a perpendicular to l, intersects b in some point B, and the line GY, being perpendicular to OP, intersects b in some point S. Thus either B belongs to the segment GX or S belongs to the segment GY.

Fig. 1
figure 1

\(\mathbf{A_2}\rightarrow \mathbf{P}\)

Full size image

If S belongs to the segment GY, then let \(S'\) be the foot of the perpendicular from S to l. Since orthogonal projection preserves betweenness and S lies between G and Y, point \(S'\) must lie between O and X, thus S must lie between O and B, and finally G must lie between X and B. Applying the Pasch axiom to triangle OXB and line g, and bearing in mind that g cannot intersect l, we conclude that g must intersect b.

If B belongs to the segment GX, then let \(B'\) be the foot of the perpendicular from B to OP. Since B lies between X and G and orthogonal projection preserves betweenness, \(B'\) lies between O and Y, thus B lies between O and S, and finally G lies between Y and S. Let R be the reflection of S in OP. Notice that R lies on \(b'\). Since G lies between Y and S, it lies between S and R as well. Unless g is YS, in which case we are done, as g and b intersect, we can apply the Pasch axiom to triangle ROS with secant g to conclude that g intersects one of the sides SO or RO, thus b or \(b'\).

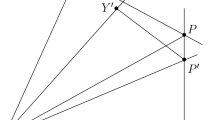
Let Z be the point of intersection of g and b. Let \(X'\) and \(Y'\) denote the feet of the perpendiculars from Z to l and OP respectively. Then \(ZY'\) is congruent to \(ZX'\), and \(ZP\ge ZY'\), so \(ZP\ge ZX'\), a contradiction, as Z was on g. Thus \(\mathbf{A_2}\rightarrow \mathbf{P}\).

Fig. 2
figure 2

\(\mathbf{P}\rightarrow \mathbf{A_2}\)

Full size image

Suppose now \({\mathfrak M}\) is a model of \({\mathcal A}\) in which \(\mathbf{P}\) holds. Let l be a line, O a point on it, m the perpendicular in O on l, and b and \(b'\) be the two angle bisectors of the angle formed by l and m. Let P be an arbitrary point on m. We will show that n, the perpendicular in P on m intersects b and \(b'\), and thus that \(\mathbf{A_2}\) must hold (see Fig. 2). By \(\mathbf{P}\), there is a point Q on n such that \(QQ'<QP\), where \(Q'\) is the foot of the perpendicular from Q to l. Now Q lies either in the quadrant determined by l and m in which a ray from b lies or in the quadrant in which a ray from \(b'\) lies. We can assume w. l. o. g. that it lies in the quadrant visited by b. The line b divides the plane into two half-planes: one containing P and one containing \(Q'\). If Q were in the same half-plane in which P lies, then the segment \(QQ'\) would have to intersect b in a point Z. Being on the bisector, Z has the property that \(ZQ'\) is congruent to ZX, where X is the foot of the perpendicular from Z to m. Thus \(QQ'=QZ+ZQ'=ZQ+ZX>QX>QP\), the first inequality being the triangle inequality and the second one stemming from the hypotenuse being greater than the side, contradicting the fact that \(QQ'<QP\). Thus P and Q must lie on different sides of b, so the segment PQ must intersect b, thus n must intersect b. Thus \(\mathbf{P}\rightarrow \mathbf{A_2}\).