A Refined Energy Bound for Distinct Perpendicular Bisectors

Abstract

Let ${\mathcal {P}}$ be a set of n points in the Euclidean plane. We prove that, for any $\varepsilon > 0$, either a single line or circle contains n/2 points of ${\mathcal {P}}$, or the number of distinct perpendicular bisectors determined by pairs of points in ${\mathcal {P}}$ is $\Omega (n^{52/35 - \varepsilon })$, where the constant implied by the $\Omega$ notation depends on $\varepsilon$. This is progress toward a conjecture of Lund, Sheffer, and de Zeeuw, that either a single line or circle contains n/2 points of ${\mathcal {P}}$, or the number of distinct perpendicular bisectors is $\Omega (n^2)$. The proof relies bounding the size of a carefully selected subset of the quadruples $(a,b,c,d) \in {\mathcal {P}}^4$ such that the perpendicular bisector of a and b is the same as the perpendicular bisector of c and d.

1 Introduction

Many classic problems in discrete geometry ask for the minimum number of distinct equivalence classes of subsets of a fixed set of points under some geometrically defined equivalence relation. The seminal example is the Erdős distinct distance problem [4]: How few distinct distances can be determined by a set of n points in the Euclidean plane? Guth and Katz have nearly resolved the Erdős distinct distance question [6], but many questions of this type remain wide open.

In this paper, we investigate the question: How few distinct perpendicular bisectors can be determined by a set of n points in the Euclidean plane? Distinct perpendicular bisectors were previously investigated by the author, Sheffer, and de Zeeuw [9], and a finite field analog was studied by Hanson, the author, and Roche-Newton [7].

Without any additional assumption, it is not too hard to give a complete answer to this question. The vertices of a regular n-gon determine n distinct perpendicular bisectors. Each point of an arbitrary point set ${\mathcal {P}}$ of n points determines $n-1$ distinct bisectors with the remaining points of ${\mathcal {P}}$, so the only question is whether it is possible that n points determine only $n-1$ bisectors. A set of two points determines only a single perpendicular bisector, and in Sect. 2.1, we give a simple geometric argument showing that n points determine at least n bisectors when $n>2$.

Assume that ${\mathcal {P}}$ is a set of n points such that no circle or line contains more than K points of ${\mathcal {P}}$.

The author, Sheffer, and de Zeeuw [9] proved the following lower bound on $|{\mathcal {B}}|$, the number of distinct bisectors determined by ${\mathcal {P}}$. For any $\varepsilon > 0$,

$$\begin{aligned} |{\mathcal {B}}| = \Omega \left( \min \left\{ K^{-{2}/{5}}n^{{8}/{5}-\varepsilon }, K^{-1} n^2\right\} \right) , \end{aligned}$$

(1)

where the implied constant depends on $\varepsilon$. The same paper proposes the following conjecture.

Conjecture 1

For any $\delta >0$, there is a constant $c>0$ depending on $\delta$ such that either a single line or circle contains $(1 - \delta )n$ points of P, or $|{\mathcal {B}}| \ge c n^2$.

In this paper, we prove the following.

Theorem 2

For any $\delta ,\varepsilon > 0$, there is a constant $c > 0$ depending on $\delta$ and $\varepsilon$ such that either a single circle or line contains $(1-\delta )n$ points of ${\mathcal {P}}$, or $|{\mathcal {B}}| \ge c n^{52/35 - \varepsilon })$.

This improves on the earlier result (1) of the author, Sheffer, and de Zeeuw in the case that some line or circle contains $\Omega (n^{2/7+\varepsilon })$ points of ${\mathcal {P}}$ and gives the first non-trivial result on Conjecture 1 in the case that a single line or circle contains a constant fraction of the points of ${\mathcal {P}}$.

The proof (in [9]) of inequality (1) uses the, now standard, method of bounding the “energy”¹ of the quantity in question. Specifically, we write ${B}(a,b)$ for the perpendicular bisector of distinct points a, b, and define the bisector energy to be the size of the set

$$\begin{aligned} {\mathcal {Q}}= \{(a,b,c,d) \in {\mathcal {P}}^4:a \ne b, c\ne d, {B}(a,b) = {B}(c,d)\}. \end{aligned}$$

It is easy to see that $|{\mathcal {Q}}| \le n^2(n-1)$, since each element of ${\mathcal {Q}}$ is determined by (a, b, c). Taking ${\mathcal {P}}$ to be the vertices of a regular n-gon shows that this bound is tight. In [9], it is shown that

$$\begin{aligned} |{\mathcal {Q}}| = O\left( K^{{2}/{5}}n^{{12}/{5}+\varepsilon } + Kn^2\right) , \end{aligned}$$

(2)

where K is the largest number of points of ${\mathcal {P}}$ contained in any line or circle. The same paper includes the conjecture that the strongest possible bound is $|{\mathcal {Q}}| = O(Kn^2)$. By the Cauchy–Schwarz inequality (see, for example, the proof of Lemma 12),

$$\begin{aligned} |{\mathcal {B}}| \ge n^2(n-1)^2/|{\mathcal {Q}}|. \end{aligned}$$

From here, a simple substitution gives (1).

Following this argument, even a tight bound of $|{\mathcal {Q}}| = O(Kn^2)$ would only give $|{\mathcal {B}}| \ge \Omega (n^2K^{-1})$. This only meets the bound of Conjecture 1 when K is a constant not depending on n, and does not give any non-trivial bound for $K = \Omega (n)$. Hence, it initially seems hopeless to use an energy bound to make substantial progress toward Conjecture 1 in the case that a single line or circle contains many points of ${\mathcal {P}}$.

The main new idea in this paper is to apply an energy bound to a refined subset of the pairs of points of ${\mathcal {P}}$. We show that there is a large set $\Pi \subset {\mathcal {P}}\times {\mathcal {P}}$ of pairs of points, such that

$$\begin{aligned} {\mathcal {Q}}^* = \{(a,b,c,d) \in {\mathcal {P}}^4: (a,b), (c,d) \in \Pi , {B}(a,b) = {B}(c,d)\} \end{aligned}$$

is small. In particular, we define $\Pi$ to be the set of pairs of points of ${\mathcal {P}}$ that are not contained in any circle or line that contains too many points of ${\mathcal {P}}$. We use a point–circle incidence bound, proved in [1, 2, 10], to show that $\Pi$ must be large. We use a slightly modified version of the argument used to bound ${\mathcal {Q}}$ in [9] to show that ${\mathcal {Q}}^*$ must be small. An application of the Cauchy–Schwarz inequality then shows that there must be many distinct bisectors determined by pairs of points in $\Pi$, which of course implies that there must be many bisectors in total.

2 Proofs

Throughout this section, ${\mathcal {P}}$ is a set of n points in the plane, and ${\mathcal {B}}$ is the set of distinct perpendicular bisectors determined by the pairs of points of ${\mathcal {P}}$. For any two distinct points a, b, we use B(a, b) to denote the perpendicular bisector of a and b, and use |ab| to denote the distance between a and b.

We rely on the connection between perpendicular bisectors and reflections. This is that, for any two distinct points a, b in the plane, b is the reflection of a over B(a, b).

2.1 There Are At Least n Bisectors

We give the best possible general lower bound on $|{\mathcal {B}}|$.

Proposition 3

If $n > 2$, then $|{\mathcal {B}}| \ge n.$

Proof

Since any point $a \in {\mathcal {P}}$ determines $n-1$ distinct bisectors with the remaining points ${\mathcal {P}}\setminus \{a\}$, it is sufficient to show that there are three points a, b, c such that ${B}(b,c)$ is distinct from ${B}(a,x)$ for any $x \in {\mathcal {P}}$.

Suppose that there is a line $\ell$ containing at least three points of ${\mathcal {P}}$. Order the points along $\ell$, let the first two points of ${\mathcal {P}}\cap \ell$ be b, c, and let a be any other point of ${\mathcal {P}}\cap \ell$. The point x such that $B(a,x) = B(b,c)$ lies in $\ell$ and precedes b, c, and hence cannot be in ${\mathcal {P}}$.

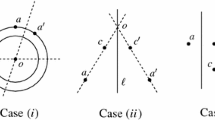
Now suppose that no three points are collinear. Let $a,b \in {\mathcal {P}}$ so that |ab| is minimal, and let $c \in {\mathcal {P}}$ so that the angle $\angle abc$ is minimal. If a is on the same side of ${B}(b,c)$ as c, then $|ac| \le |ab|$, which is a contradiction. If a is on the line ${B}(b,c)$, then there is no point x such that ${B}(a,x) = {B}(b,c)$, and we have accomplished our goal. Hence, we may suppose that a and b are on the same side of ${B}(b,c)$—see Fig. 1.

Let x be the reflection of a over ${B}(b,c)$. Since x is in the interior of the cone defined by $\angle abc$, we have that $\angle abx$ is less than $\angle abc$—see Fig. 2. Since c was chosen so that $\angle abc$ is minimal, $x \notin {\mathcal {P}}$, which completes the proof. $\square$

Fig. 1

Since $|ab| < |bc|$, both a and b must lie on the same side of B(b, c)

Fig. 2

If $B(a,x) = B(b,c)$, and a and c are on opposite sides of $\overline{ax}$, then $\angle abx < \angle abc$

2.2 Proof of Theorem 2

The proof of Theorem 2 has three main parts. First, we show that, for any $\varepsilon >0$, if a single circle or line contains at least $\varepsilon n$ points of ${\mathcal {P}}$, then $\Omega (n^2)$ distinct bisectors are determined, with the implied constant depending on $\varepsilon$. Second, we show that, for suitably chosen constants $c_1,c_2 > 0$, if no circle or line contains at least $c_2 n$ points of ${\mathcal {P}}$, then there is a set $\Pi$ of $\Omega (n^2)$ pairs of points such that no pair of points in $\Pi$ is contained in any circle that contains more than $M=c_1 n^{2/7} \log ^{2/7}n$ points of ${\mathcal {P}}$. Third, we apply an energy argument (as in [9]) to show that, for any $\varepsilon > 0$, there are $O(M^{2/5}n^{12/5+\varepsilon } + M n^2)$ quadruples (a, b, c, d) of points in ${\mathcal {P}}$ such that $B(a,b) = B(c,d)$ and $(a,b),(c,d) \in \Pi$, with the implied constant depending on $\varepsilon$. From there, a straightforward application of the Cauchy–Schwarz inequality finishes the proof.

Handling heavy circles. First, a geometric lemma.

Lemma 4

Let C be a circle or a line, and let $p,q \notin C$ with $p\ne q$. Then,

$$\begin{aligned} |\{(r,s) \in C \times C : {B}(p,r) = {B}(q,s)\}| \le 2. \end{aligned}$$

Proof

If $r,s \in C$ such that $B(p,r) = B(q,s)$, then p, q is contained in the reflection of C over B(p, r)—see Fig. 3. Since $p\ne q$, there are at most two reflections of C that contain (p, q) if C is a circle, and at most one such reflection of C if C is a line. Since we can recover r, s uniquely given one of these reflections, there are at most two choices for the pair (r, s). $\square$

Fig. 3

Illustration for Lemma 4. Both choices of r, s are shown for the given p, q and C. The dashed circle is the reflection of C over the dashed line $B(p,r) = B(q,s)$, and the dotted circle is the reflection of C over the dotted line $B(p,r') = B(q,s')$

Combining Lemma 4 with a combinatorial argument gives the result.

Lemma 5

For any $\varepsilon > 0$, if a single line or circle contains exactly $\varepsilon n$ points of ${\mathcal {P}}$, then

$$\begin{aligned} |{\mathcal {B}}| > \min (\varepsilon /2, 1-\varepsilon ) \cdot \varepsilon n^2/2. \end{aligned}$$

Proof

Let C be a circle or line that contains $\varepsilon n$ points of ${\mathcal {P}}$. Let ${\mathcal {P}}' \subset {\mathcal {P}}$ be a set of $k = \min (\varepsilon /2, 1-\varepsilon )n$ points that are not in C. Let $p_1, p_2, \dots p_k$ be an arbitrary ordering of the points of ${\mathcal {P}}'$. Then, by Lemma 4, $p_i$ determines a set ${\mathcal {B}}(p_i)$ of at least $\varepsilon n - 2(i-1)$ distinct perpendicular bisectors with the points of ${\mathcal {P}}\cap C$, such that no element of ${\mathcal {B}}(p_i)$ is an element of ${\mathcal {B}}(p_j)$ for any $j<i$. Summing over i, we have

$$\begin{aligned} \sum _{i =1}^{k}|{\mathcal {B}}(p_i)| \ge \sum _{i =1}^{ k} (\varepsilon n - 2(i-1)) = \varepsilon k n - k^2 + k > \varepsilon n k/2, \end{aligned}$$

which proves the lemma. $\square$

We will apply Lemma 5 for some $\varepsilon < 2/3$. In this range, the bound is $|{\mathcal {B}}| > \varepsilon ^2n^2/4$.

Refining the pairs of points. Let $c_1, c_2 > 0$, with specific values to be fixed in the proof of Lemma 7. Let $\Pi \subseteq {\mathcal {P}}\times {\mathcal {P}}$ be the set of ordered pairs of distinct points of ${\mathcal {P}}$ such that no pair in $\Pi$ is contained in a line or a circle that contains more than $c_1 n^{2/7}\log ^{2/7}n$ points of ${\mathcal {P}}$. We use a point–circle incidence bound to show that, under the assumption that no circle contains $c_2 n$ points, $|\Pi | = \Omega (n^2)$.

Denote by $s_k$ the number of lines and circles that each contain at least k points of ${\mathcal {P}}$, denote by $s_{=k}$ the number of lines and circles that each contain exactly k points of ${\mathcal {P}}$.

The strongest known point–circle incidence bound is derived using a combination of the papers by Agarwal, Nevo, Pach, Pinchasi, Sharir, and Smorodinsky [1] and by Marcos and Tardos [10]. A slightly weaker bound was proved earlier by Aronov and Sharir [2]. Combining the strongest known point–circle incidence bound with the point–line incidence bound proved by Szemerédi and Trotter [11] gives the following bound on $s_k$.

Lemma 6

$$\begin{aligned} s_k = O(n^{3} k^{-11/2} \log n + n^2 k ^{-3} + nk^{-1}). \end{aligned}$$

Recall that the definition of $\Pi$ depends on $c_1$, which we fix in the next Lemma.

Lemma 7

There are constants $c_1,c_2 > 0$ such that either a single line or circle contains $c_2 n$ points of ${\mathcal {P}}$, or $|\Pi | = \Omega (n^2)$.

Proof

Let $M = c_1 n^{2/7}\log ^{2/7}n$, and let $U = c_2 n$. Assume that no circle or line contains U points of ${\mathcal {P}}$, since otherwise we are done.

Let T be the number of triples (p, q, C) of two points p, q and a line or circle C such that $p,q \in C \cap {\mathcal {P}}$ and $M \le |C \cap {\mathcal {P}}| \le U$. Then,

$$\begin{aligned} T = \sum _{k = M}^U k^2 s_{=k} = \sum _{k = M}^U k^2(s_k - s_{k+1}) \le \sum _{k = M+1}^U 2k s_k + M^2 s_M. \end{aligned}$$

We use Lemma 6 to bound $s_k$. Since the term $n^3 k^{-11/2} \log n$ is dominant for $k=M$, this gives

$$\begin{aligned} T \le O \left( \sum _{k \ge M} n^{3}k^{-9/2}\log n + \sum _{k \ge M} n^2 k^{-2} + \sum _{k \le U} n + n^3M^{-7/2}\log n \right) . \end{aligned}$$

If we take $c_1$ to be sufficiently large depending on the implied constant in Lemma 6, then the first and fourth terms will each be bounded by $n^2/10$, and the second term will be bounded by $O(n^{9/7}\log ^{-5/7}n)$. If we take $c_2$ to be sufficiently small, again depending on the implied constant in Lemma 6, then the third term will be bounded by $n^2/10$. Adding these contributions together shows that $T < n^2/2$.

Since T counts each pair of points that is contained in a circle that contains at least M points of ${\mathcal {P}}$ (possibly more than once), $|\Pi | \ge n(n-1) - T = \Omega (n^2)$. $\square$

Bounding the energy. Next, we bound a refinement of the bisector energy depending on $\Pi$. Our argument is essentially identical to proof of the analogous bound in [9], and in fact we refer to [9] for many of the key facts used.

Let ${\mathcal {P}}^{2*} \subset {\mathcal {P}}^{2}$ be the set of pairs of distinct points of ${\mathcal {P}}$. For each pair $(a,b) \in P^{2*}$, let C(a, b) be the maximum number of points on any circle or line that contains a, b. Let

$$\begin{aligned} \Pi _K&= \{(a,b) \in P^2 : a \ne b, \, C(a,b) \le K\}, \\ {\mathcal {Q}}_K&= \{(a,b,c,d) \in P^4 : (a,b),(c,d) \in \Pi _K, \, {B}(a,b) = {B}(c,d)\}. \end{aligned}$$

Our goal is to prove an upper bound on ${\mathcal {Q}}_K$. Note that, if $B(a,b) = B(c,d)$, then

$$\begin{aligned} (a+b-c-d) \cdot (a-b)&= 0, \end{aligned}$$

(3)

$$\begin{aligned} (a+b-c-d) \cdot (c-d)&=0. \end{aligned}$$

(4)

Indeed, $(a+b-c-d)$ is parallel to the line through the midpoints of (a, b) and (c, d), hence (3) requires that this line be perpendicular to the line through a and b, and (4) that this line be perpendicular to the line through c and d. Hence, any quadruple that contributes to ${\mathcal {Q}}$ satisfies (3) and (4). There are some quadruples (a, b, c, d) that satisfy (3) and (4), but do not contribute to ${\mathcal {Q}}$. However, these cases only occur if $a=b$ or $c=d$; see [9, Lemma 3.1].

For any pair (a, c) of distinct points, let $S_{ac}$ be the set of pairs (b, d) satisfying (3) and (4). Let G be the incidence graph between varieties $\{S_{ac}:(a,c) \in P^{2*}\}$ and pairs of points $(b,d) \in P^{2*}$. Let $G_K$ be the subgraph of G so that an edge $(S_{ac}, (b,d)) \in G$ is in $G_K$ if and only if $(a,b),(c,d) \in \Pi _K$. Note that the edges of $G_K$ correspond exactly to the elements of ${\mathcal {Q}}_K$.

In [9], the authors used a geometric incidence argument to bound the number of edges in G. We will use the same argument to bound the number of edges in $G_K$; the only difficulty is in identifying the property of $G_K$ that enables us to run the argument of [9].

We need a couple of geometric facts from [9]. First, if $(S_{ac}, (b,d)) \in G$, then $|ac| = |bd|$. This is easy to derive from Eqs. (3) and (4): expand the products and subtract (4) from (3). Also see Fig. 4.

Fig. 4

Since $B(a,b) = B(c,d)$, the pair (b, d) is the reflection of (a, c) over the line B(a, b), and so $|ac| = |bd|$

Next, we have the following lemma, which gives a constraint on pairs (b, d) such that $B(a,b) = B(c,d)$ and $B(a',b) = B(c',d)$ for fixed points $a,c,a',c'$.

Lemma 8

[9, Lemma 3.2]. Let $a,c,a',c' \in \mathbb {R}^2$ such that $(a,c)\ne (a',c')$, and $|ac| = |a'c'| = \delta \ne 0$. There exist curves $C_1,C_2\subset {\mathbb {R}}^2$ depending on $a,c,a',c'$, which are either two concentric circles or two parallel lines, such that, if $B(a,b) = B(c,d)$ and $B(a',b) = B(c',d)$, then $a,a',b \in C_1$ and $c,c',d \in C_1$.

Now, we can establish the property we need from $G_K$.

Lemma 9

If ${S}_{ac}$ and ${S}_{a'c'}$ more than $K+2$ common neighbors in G, then they have no common neighbors in $G_K$.

Proof

We first show that, if $c \ne c'$, then $S_{ac}$ and $S_{ac'}$ have no common neighbors in $G_K$. Let $(b,d) \in S_{ac}$. If $b \ne a$ and $d \ne c$, then a, b, c, d are the vertices of an isosceles trapezoid. Hence, c is determined uniquely by a, b, d, and $(b,d) \notin S_{ac'}$ If $b = a$, then $(a,b) \notin \Pi _K$, so $(S_{ac},(b,d)) \notin G_K$, and similarly for the case $d=c$. By the same reasoning, $S_{ac}$ and $S_{a'c}$ have no common neighbors in $G_K$ for $a \ne a'$.

Assume that $a \ne a'$ and $c \ne c'$, and let $(b,d) \in S_{ac} \cap S_{a'c'}$. By Lemma 8, if $d \ne c$ and $d \ne c'$, then b is contained in a line or circle $C_1$ depending on $a,a',c,c'$. If $d = c$, then the location of b is uniquely determined by $a',c',c$, and similarly if $d = c'$. Hence, if $S_{ac} \cap S_{a'c'} > K+2$, then $C_1$ contains more than K points of ${\mathcal {P}}$. In this case, none of the pairs (a, b) with $a,b \in C_1$ are in $\Pi _K$, so the corresponding edges are missing in $G_K$. $\square$

The following is the general incidence bound we use to control the size of $G_K$. It is a slight generalization of a bound in [9], which is in turn a generalization of a bound in [5]. See [5] for definitions of the algebraic terms used.

Theorem 10

Let ${\mathcal {S}}$ be a set of n constant-degree varieties, and let ${\mathcal {P}}$ be a set of m points, both in ${\mathbb {R}}^d$, where $d \ge 2$. Let $s \ge 2$ be a constant, and $t \ge 2$ be a function of m, n. Let G be the incidence graph of ${\mathcal {P}}\times {\mathcal {S}}$. Let $G' \subseteq G$ such that, if a set L of s left vertices has a common neighborhood of size t or more in G, then no pair of vertices in L has a common neighbor in $G'$. Moreover, suppose that ${\mathcal {P}}\subset V$, where V is an irreducible constant-degree variety of dimension e. Then, for any $\varepsilon > 0$,

$$\begin{aligned} |G'| = O\left( m^{\frac{s(e-1)}{es-1}+\varepsilon }n^{\frac{e(s-1)}{es-1}}t^{\frac{e-1}{es-1}} +tm+n\right) , \end{aligned}$$

with the implied constant depending on $\varepsilon$.

The proof of Theorem 10 is nearly identical to the proof of [9, Theorem 2.5]. Instead of reproducing the full proof here, we briefly state how to modify the proof of [9, Theorem 2.5] to obtain the more general Theorem 10; the remainder of this paragraph refers to the notation from the proof of [9, Theorem 2.5]. We partition $G_K$ into $I_1, I_2,$ and $I_3$ as in the proof of [9, Theorem 2.5]. Bounding $|I_2|$ and $|I_3|$ requires no change at all; these bounds only depend on the fact that $G_K$ is $K_{s,t}$-free. Any incidence in $I_1$ occurs in some irreducible component W of $V \cap Z(f)$, where Z(f) is the zero set of our partitioning polynomial, such that W is fully contained in some variety $S \in {\mathcal {S}}$. In bounding $I_1$, we need to make use of the observation that if there are at least t varieties of ${\mathcal {S}}$ that fully contain W, then, by Lemma 9, no pair of vertices corresponding to the points contained in W has a common neighbor in $G_K$ among the varieties that contain W.

We now have all of the tools in place to bound $|{\mathcal {Q}}_K|$.

Lemma 11

For any $2 \le K \le n$ and $\varepsilon > 0$,

$$\begin{aligned} |{\mathcal {Q}}_K| = O\left( K^{{2}/{5}}n^{{12}/{5}+\varepsilon } + K n^2 \right) , \end{aligned}$$

with the implied constant depending on $\varepsilon$.

Proof

Let $\delta _1, \ldots , \delta _D$ denote the distinct non-zero distances determined by pairs of distinct points in ${\mathcal {P}}$. Let

$$\begin{aligned} {\mathcal {P}}^2_i&= \{(b,d) \in {\mathcal {P}}^{2*} : |bd| = \delta _i\},\\ {\mathcal {S}}_i&= \{S_{ac} \in {\mathcal {S}}: |ac| = \delta _i\}, \\ G'_i&= \{(S_{ac},(b,d)) \in G_K : |ac| = |bd| = \delta _i\}. \end{aligned}$$

Let

$$\begin{aligned} m_i = |{\mathcal {P}}^2_i| = |{\mathcal {S}}_i|. \end{aligned}$$

As observed above, each quadruple $(a,b,c,d) \in Q$ satisfies $|ac| = |bd|$. Hence, it suffices to study each $G'_i$ separately. That is, we have

$$\begin{aligned} |Q_K| = |G_K| = \sum _{i=1}^D |G'_i|. \end{aligned}$$

For each $i \in [D]$, we apply Theorem 10 with: $m=n=m_i$, $d=4$, ${\mathcal {S}}= {\mathcal {S}}_i$, ${\mathcal {P}}= {\mathcal {P}}^2_i$, $s = 2$, $t=K+3$, and $V = \{(a,b):|ab| = \delta _i \}$, and $e=3$. This gives, for any $\varepsilon > 0$,

$$\begin{aligned} |G'_i| = O(K^{2/5}m_i^{7/5+\varepsilon } + Km_i), \end{aligned}$$

(5)

with the implied constant depending on $\varepsilon$.

Let J be the set of indexes $1\le j\le D$ for which the bound in (5) is dominated by the term $K^{{2}/{5}} m_j^{{7}/{5}+\varepsilon }$. By recalling that $\sum _{j=1}^D m_j = n(n-1)$, we get

$$\begin{aligned} \sum _{j\not \in J}|G_j'| = O\left( Kn^2\right) . \end{aligned}$$

Next, we consider $\sum _{j\in J}|G'_j| = \sum _{j\in J} O(K^{2/5} m_j^{7/5+\varepsilon } )$. By Hölder’s inequality,

$$\begin{aligned} \sum _{j \in J} m_j^{7/5} = \sum _{j \in J} m_j^{3/5}(m_j^2)^{2/5} \le \left( \sum _{j \in J} m_j \right) ^{3/5} \left( \sum _{j \in J}m_j^2 \right) ^{2/5}. \end{aligned}$$

Guth and Katz [6, Proposition 2.2] proved a tight bound on $\sum m_j^2$:

$$\begin{aligned} \sum m_j^2 = O(n^3\log n). \end{aligned}$$

Combining these estimates, for any $\varepsilon > 0$,

$$\begin{aligned} \sum _{j \in J} |G_j'| = O_\varepsilon (K^{2/5}n^{12/5 + \varepsilon }). \end{aligned}$$

$\square$

Finishing the Proof. Lemma 7 is that $|\Pi _M| = \Omega (n^2)$, where $M = c_1 n^{2/7} \log ^{2/7}n$. The following standard application of the Cauchy–Schwarz inequality shows that the upper bound ${\mathcal {Q}}_M$ given in Lemma 11 implies a lower bound on $|{\mathcal {B}}|$.

Lemma 12

$$\begin{aligned} |{\mathcal {B}}| = \Omega \left( n^4|{\mathcal {Q}}_M|^{-1}\right) . \end{aligned}$$

Proof

Let

$$\begin{aligned} {\mathcal {B}}_M = \{{B}(a,b) : (a,b) \in \Pi _M \}. \end{aligned}$$

For a line $\ell$, denote by $w(\ell )$ the number of pairs $(a,b) \in \Pi$ such that ${B}(a,b) = \ell$. By the Cauchy–Schwarz inequality,

$$\begin{aligned} |{\mathcal {Q}}_M| = \sum _{\ell \in {\mathcal {B}}_M} w(\ell )^2 \ge \left( \sum _{\ell \in {\mathcal {B}}_M} w(\ell ) \right) ^2|{\mathcal {B}}_M|^{-1} = |\Pi |^2|{\mathcal {B}}_M|^{-1}. \end{aligned}$$

Hence,

$$\begin{aligned} |{\mathcal {B}}| \ge |{\mathcal {B}}_M| \ge |\Pi |^2|{\mathcal {Q}}_M|^{-1} = \Omega \left( n^4|{\mathcal {Q}}_M|^{-1}\right) . \end{aligned}$$

$\square$

Lemma 11 gives

$$\begin{aligned} |{\mathcal {Q}}_M| = O(n^{88/35 + \varepsilon }). \end{aligned}$$

Combining this with Lemma 12, we have

$$\begin{aligned} |{\mathcal {B}}| = \Omega (n^{52/35 - \varepsilon }), \end{aligned}$$

which is Theorem 2.