Lippmann’s axiom and Lebesgue’s axiom are equivalent to the Lotschnittaxiom

Abstract

We prove that both Lippmann’s axiom of 1906, stating that for any circle there exists a triangle circumscribing it, and Lebesgue’s axiom of 1936, stating that for every quadrilateral there exists a triangle containing it, are equivalent, with respect to Hilbert’s plane absolute geometry, to Bachmann’s Lotschnittaxiom, which states that perpendiculars raised on the two legs of a right angle meet. We also show that, in the presence of the Circle Axiom, the statement “There is an angle such that the perpendiculars raised on its legs at equal distances from the vertex meet” is equivalent to the negation of Hilbert’s hyperbolic parallel postulate.

1 Introduction

In a letter to Wolfgang Bolyai, Gauss wrote on December 16, 1799 from Helmstedt that

if one could prove that a straight triangle is possible, whose area would be larger than [that] of any given surface, then I would be able to prove the entire geometry completely rigorously.¹

In this paper we will determine what such a supposition would entail when expressed in the form that any figure of a special kind—such as a circle, or a quadrilateral—can be contained in a triangle, or in Gauss’s words, what “the entire geometry” is that one can “prove completely rigorously” in the presence of such an assumption.

Among those who tried, long after the matter had been settled, to prove that Euclid’s parallel postulate can be obtained from “facts of experience”, is the otherwise unknown Lippmann, whose only other publication reviewed by the Jahrbuch für die Fortschritte der Mathematik, is the first part of an introduction to aeronautics of 1911. In Lippmann (1907), a booklet reviewed by Max Dehn for the Jahrbuch and by “G. K.” for Monatshefte für Mathematik und Physik, he claims to have deduced, in the presence of the Archimedean axiom, the Euclidean parallel postulate from the following statement, considered a “fact of experience”

Lipp 1

For every circle ${{\mathcal {C}}}$ there exists a triangle which has ${{\mathcal {C}}}$ as its inscribed circle.

It is easy to see that it makes no difference if the triangle is asked just to contain the circle ${{\mathcal {C}}}$ in its interior or to have its sides tangent to ${{\mathcal {C}}}$. For, if ABC is a triangle containing ${{\mathcal {C}}}$ in its interior, then from O, the center of ${{\mathcal {C}}}$, we drop perpendiculars to AB, BC, and CA, which intersect ${{\mathcal {C}}}$ in the points $C'$, $A'$, and $B'$, respectively. The perpendiculars in $A'$ on $OA'$, in $B'$ to $OB'$, in $C'$ to $OC'$ are the sides of a triangle which is circumscribed to ${{\mathcal {C}}}$.

While some may just shrugg the episode off as one more case of stubborn denial of non-Euclidean geometry, we will handle this axiom in the manner put forth in Pambuccian (2009) with Lagrange’s attempt to prove the Euclidean parallel postulate, to ask what better known statement $\mathbf{Lipp}$ 1 is equivalent to, with Hilbert’s plane absoute geometry ${{\mathcal {A}}}$ as background.

First, let us observe that $\mathbf{Lipp}$ 1 is equivalent to the following apparently stronger statement

Lipp 2

For every circle ${{\mathcal {C}}}$ there exists an equilateral triangle which has ${{\mathcal {C}}}$ as its inscribed circle.

To show this, we first introduce the notion of an angle that is n-positive and the notion of an angle that is n-away from a straight angle.² Given an angle $\widehat{XOY}$, let $Y_1=Y_1'=Y$, let $X'$ denote the reflection of X in O, $Y_{i+1}$ denote the reflection of X into $OY_{i}$, for $i\in \{1, \ldots , n-1\}$, and $Y_{i+1}'$ the reflection of $X'$ into $OY_{i}'$. The angle $\widehat{XOY}$ is said to be n-positive if at least one of $\widehat{XOY_i}$ with $i\in \{1, \ldots , n\}$ is not acute, and it is said to be n-away from a straight angle if at least one of $\widehat{X'OY_i'}$, with $i\in \{1, \ldots , n\}$, is not an acute angle (i. e. is $\ge 90^{\circ }$).

We will not only show that $\mathbf{Lipp}$ 1 and $\mathbf{Lipp}$ 2 are equivalent, but also that they are equivalent, for any positive integer n, to

$\mathbf{L}_n$   If the angle$\widehat{XOY}$is not acute and isn-away from a straight angle, then every perpendicular to its side${\mathop {OX}\limits ^{\longrightarrow }}$intersects every perpendicular to its side${\mathop {OY}\limits ^{\longrightarrow }}$.

The connection between $\mathbf{L}_n$ and $\mathbf{Lipp}$ 2 is best established by observing that $\mathbf{L}_n$ is equivalent to

$\mathbf{L}_n'$   If$\widehat{XOY}$isn-away from a straight angle, such that$OX\equiv OY$, then the perpendicular raised inXtoOXintersects the perpendicular raised inYtoOY.

While $\mathbf{L}_n'$ states a certain property for all angles that are not “too obtuse,” it can be replaced by statements of the same nature for just one very obtuse but not too obtuse angle (the angle is such that $180^{\circ }-\frac{90^{\circ }}{2^{n-2}}< \widehat{XOY}\le 180^{\circ }-\frac{90^{\circ }}{2^{n-1}}$) or for just one very acute but not too acute angle (the angle is such that $\frac{90^{\circ }}{2^{n}}\le \widehat{XOY}<\frac{90^{\circ }}{2^{n-1}}$). The exact statements are:

$\mathbf{L}^{\lambda }_n$    There exists an angle$\widehat{XOY}$, which isn-away, but not$(n-1)$-away from a straight angle, such that, for allAandB, withAon${\mathop {OX}\limits ^{\longrightarrow }}$andBon${\mathop {OY}\limits ^{\longrightarrow }}$, with$OA\equiv OB$, the perpendicular raised inAtoOAintersects the perpendicular raised inBtoOB.

$\mathbf{L}^{\sigma }_n$   There exists an angle$\widehat{XOY}$, which is$(n+1)$-positive, but notn-positive, such that for allAandB, withAon${\mathop {OX}\limits ^{\longrightarrow }}$andBon${\mathop {OY}\limits ^{\longrightarrow }}$, with$OA\equiv OB$, the perpendicular raised inAtoOAintersects the perpendicular raised inBtoOB.

We also consider the following axiom:

$\mathbf{L}(\alpha ^{\circ })$   If$\widehat{XOY}$is an angle of measure$\alpha ^{\circ }$and$OX\equiv OY$, then the perpendicular raised inXtoOXintersects the perpendicular raised inYtoOY.

It is easy to see that $\mathbf{Lipp}$ 2 is equivalent to $\mathbf{L}(120^{\circ })$.

Friedrich Bachmann introduced in Bachmann (1964) an important axiom in the foundation of geometry, stating that “Every quadrilateral with three right angles closes,” which is none else than $\mathbf{L}_1$, and it is plain that it is also equivalent to $\mathbf{L}(90^{\circ })$. He called it the Lotschnittaxiom and provided two equivalent statements for it, the equivalence holding over Hilbert’s plane absolute geometry ${{\mathcal {A}}}$ (whose axioms are the plane axioms of groups I, II, and III of Hilbert’s (1977), being equivalent to the axioms A1–A9 in Schwabhäuser et al. (1983), the models of which are referred to as Hilbert planes). The first time a statement equivalent to the Lotschnittaxiom was presented was on February 3, 1806 by Lagrange (the equivalence was shown in Pambuccian (2009)). It has been signaled in Flye Sainte-Marie (1870, pp. 12–13) and Flye Sainte-Marie (1871, p. 133) in the same form that Bachmann chose, as an axiom (which Flye Sainte-Marie found to have a form which “se rapproche de celle qu’Euclide a choisie”) to critique an attempt to prove Euclid’s fifth Postulate by Jules Carton, a purported proof Joseph Bertrand was prevented from publishing in the Comptes Rendus of the Académie des Sciences only after the intervention of Darboux and others (see Henry and Nabonnand 2017 for more details on the matter). Various other equivalent statements can be found in Pambuccian (1994) and in Pambuccian (2017).

Without mentioning Lippmann [and very likely unaware of the existence of Lippmann (1907)], Lebesgue (1936) introduced an axiom similar to Lipp 1, stating that every quadrilateral can be enclosed in a triangle, as an equivalent, under the Archimedean axiom, to the Euclidean parallel postulate. Put differently, it states that

Leb

Given four points, there exists a triangle that contains the points in its interior or on its sides.

The purpose of this note is to show that, for any integer $n\ge 2$, the axioms $\mathbf{Lipp}$ 1, $\mathbf{Lipp}$ 2. $\mathbf{L}_n$, $\mathbf{L}_n'$, $\mathbf{L}(90^{\circ })$, $\mathbf{L}^{\lambda }_n$, and $\mathbf{L}^{\sigma }_n$, Leb, as well as several others, are equivalent with respect to ${{\mathcal {A}}}$. We will also show that an axiom, asking for just one angle for which it is true that any two perpendiculars raised on its legs at equal distances from its vertex intersect, is strictly weaker than the Lotschnittaxiom, and will determine its exact strength.

2 Main theorem on Lippmann’s axiom

For all integers n, with $n\ge 2$, we have

Theorem 1

${{\mathcal {A}}}\vdash \mathbf{Lipp}$ 1 $~\leftrightarrow \mathbf{Lipp}$ 2 $~\leftrightarrow \mathbf{L}_n\leftrightarrow \mathbf{L}_n' \leftrightarrow \mathbf{L}(90^{\circ })\leftrightarrow \mathbf{L}^{\lambda }_n\leftrightarrow \mathbf{L}^{\sigma }_n$

Proof

First, let us show that

$$\begin{aligned} {{\mathcal {A}}}\vdash \mathbf{L}_n\leftrightarrow \mathbf{L}_n' \end{aligned}$$

(1)

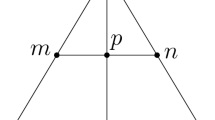
To see that $\mathbf{L}_n\rightarrow \mathbf{L}_n'$ holds in ${{\mathcal {A}}}$, first notice that, if $\widehat{XOY}$ is not acute, if we know that $\mathbf{L}_n$ holds and $OX\equiv OY$, then the perpendicular raised in X to OX intersects the perpendicular raised in Y to OY since the perpendicular in any point of ${\mathop {OX}\limits ^{\longrightarrow }}$ intersects the perpendicular in any point of ${\mathop {OY}\limits ^{\longrightarrow }}$. In particular, if $\mathbf{L}_n$ holds, we know that, if $\widehat{XOY}$ is a right angle and $OX\equiv OY$, then the perpendicular raised in X to OX intersects the perpendicular raised in Y to OY. Now notice that, if the conclusion of $\mathbf{L}_n'$ holds for a certain angle $\widehat{XOY}$, with $OX\equiv OY$, then it holds for any angle smaller than $\widehat{XOY}$. in other words,

$$\begin{aligned} \alpha ^{\circ }< \beta ^{\circ }\rightarrow (\mathbf{L}(\beta ^{\circ })\rightarrow \mathbf{L}(\alpha ^{\circ })). \end{aligned}$$

(2)

To see this, notice that, if $O, X, Y, Y'$ are such that no three are collinear, $OX\equiv OY$, $OX\equiv OY'$, the ray ${\mathop {OY'}\limits ^{\longrightarrow }}$ lies inside the angle $\widehat{XOY}$, and the perpendicular raised in X to OX intersects the perpendicular raised in Y to OY in P (see Fig. 1), then the perpendicular raised in X to OX intersects the perpendicular raised in $Y'$ to $OY'$ as well. This can be easily seen by noticing that ${\mathop {OP}\limits ^{\longrightarrow }}$ is the internal angle bisector of $\widehat{XOY}$, and that the internal bisector of $\widehat{XOY'}$ is a ray emanating from O and lying inside the angle $\widehat{XOP}$, and thus, by the Crossbar Theorem (see, Greenberg 2008, p. 116), it intersects the segment XP in a point $P'$, which is the point of intersection of the perpendicular raised in X to OX with the perpendicular raised in $Y'$ to $OY'$. Using this just proved fact, that if the conclusion of $\mathbf{L}_n'$ holds in a certain angle, then it holds in all smaller angles, and the fact that the conclusion of $\mathbf{L}_n'$ holds when $\widehat{XOY}$ is a right angle, we deduce that the conclusion of $\mathbf{L}_n'$ holds whenever $\widehat{XOY}$ is acute. This proves that $\mathbf{L}_n\rightarrow \mathbf{L}_n'$,

Fig. 1

$\alpha ^{\circ }< \beta ^{\circ }\rightarrow (\mathbf{L}(\beta ^{\circ })\rightarrow \mathbf{L}(\alpha ^{\circ }))$

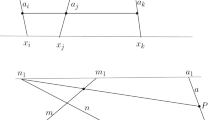
The converse, $\mathbf{L}_n'\rightarrow \mathbf{L}_n$ is also true in ${{\mathcal {A}}}$. For, if $\widehat{XOY}$ is a non-acute angle, which is n-away from a straight angle, and if $OX\ge OY$, then let $Y'$ denote the point on ${\mathop {OY}\limits ^{\longrightarrow }}$ for which $OY'\equiv OX$ (see Fig. 2). We know, by $\mathbf{L}_n'$, that the perpendiculars raised in X on OX and in $Y'$ to $OY'$ intersect in a point P. By Pasch’s axiom, the perpendicular $\pi$ in Y to OY must intersect one of the sides OP or $PY'$ of triangle $OPY'$ as well, and $\pi$ is parallel to $Y'P$ (as both are perpendicular ro OY), so $\pi$ intersects OP. Applying Pasch’s axiom again, with $\pi$ as transversal and OXP as the triangle, we conclude that $\pi$ intersects either side OX or side PX of triangle OPX. If it were to intersect the segment OX in a point Q, then triangle OYQ would have a right angle $\widehat{OYQ}$ and a non-acute angle $\widehat{QOY}$ (which is $\widehat{XOY}$), a contradiction, since a triangle can have at most one non-acute angle. Thus $\pi$ intersects side PX of triangle OPX in a point Q, so $\pi$ intersects the perpendicular raised in X on OX, so $\mathbf{L}_n$ holds. This proves (1).

Fig. 2

$\mathbf{L}_n'\rightarrow \mathbf{L}_n$

Let us now show that

$$\begin{aligned} {{\mathcal {A}}}\vdash \mathbf{Lipp}~\mathbf{1}\leftrightarrow \mathbf{Lipp}~\mathbf{2} \end{aligned}$$

(3)

Since the $\leftarrow$ implication is obvious, we turn to the $\rightarrow$ part of (3). Let ${{\mathcal {C}}}$ be a circle with center O and let ABC be its circumscribing triangle. Let $M_1, M_2,$ and $M_3$ be the points of tangency of ${{\mathcal {C}}}$ and triangle ABC. One of the angles $\widehat{M_iOM_{i+1}}$, with $i\in \{1,2,3\}$, and with addition modulo 3, i. e., $M_4$ stands for $M_1$, must be $\ge 120^{\circ }$. Given that an angle of $120^{\circ }$ exists in ${{\mathcal {A}}}$ (since there exists an equilateral triangle in ${{\mathcal {A}}}$, as proved in Pambuccian (1998)), by (2) we have that, $\mathbf{L}(\max _{i=1}^3 \widehat{M_iOM_{i+1}})\rightarrow \mathbf{L}(120^{\circ })$. Since $\mathbf{Lipp}$ 2 is equivalent to $\mathbf{L}(120^{\circ })$ and $\mathbf{Lipp}$ 1 is equivalent to $\mathbf{L}(\max _{i=1}^3\widehat{M_iOM_{i+1}})$, we have that ${{\mathcal {A}}}\vdash \mathbf{Lipp}$ 1$~\rightarrow \mathbf{Lipp}$ 2. This proves (3).

By (2) and bearing in mind that $\mathbf{Lipp}$ 2 is equivalent to $\mathbf{L}(120^{\circ })$, we have

$$\begin{aligned} {{\mathcal {A}}}\vdash \mathbf{L}^{\lambda }_n \rightarrow \mathbf{L}_n'\rightarrow \mathbf{Lipp}~\mathbf{2}\rightarrow \mathbf{L}(90^{\circ })\rightarrow \mathbf{L}^{\sigma }_n \end{aligned}$$

(4)

To prove that

$$\begin{aligned} {{\mathcal {A}}} \vdash \mathbf{L}^{\sigma }_n\rightarrow \mathbf{L}(90^{\circ }) \text{ and } {{\mathcal {A}}} \vdash \mathbf{L}(90^{\circ })\rightarrow \mathbf{L}^{\lambda }_n \end{aligned}$$

(5)

we will use their algebraic characterization, provided in Pejas (1961), as presented in Bachmann (1964).

Let K be an ordered field and k an element of K, to be referred to as the orthogonality constant (or the metric constant). By the affine-metric plane$\mathfrak {A}\,(K, k)$ (cf. Hessenberg and Diller 1967, p. 215) we mean the projective plane $\mathfrak {P}\,(K)$ over the field K from which the line [0, 0, 1], as well as all the points on it, have been removed (and we write $\mathfrak {A}\,(K)$  for the structure with the remaining point-set, the corresponding line-set, with their incidence and orthogonality relations), for whose points of the form (x, y, 1) we shall write (x, y) (which is incident with a line [u, v, w] if and only if $xu+yv+w=0$), together with a notion of orthogonality, the lines [u, v, w] and $[u', v', w']$ being orthogonal if and only if

$$\begin{aligned} uu' + vv' + kww' = 0. \end{aligned}$$

(6)

$\mathfrak {A}\,(K)$ is ordered in the usual way. The algebraic characterization of the Hilbert planes consists in specifying a point-set E of an affine-metric plane $\mathfrak {A}\,(K, k)$, which is the universe of the Hilbert plane (the set of lines of a Hilbert plane is the of lines of the affine-metric plane which are incident with at least one point of the Hilbert plane). The Hilbert plane will thus inherit the order relation Z from $\mathfrak {A}\,(K)$. We can also define a notion of congruence of two segments $\mathbf{ab}$ and $\mathbf{cd}$, which will be given, in case $E \subset \mathfrak {A}\,(K, 0)$, by the usual Euclidean formula

$$\begin{aligned} (a_{1} - b_{1})^{2} + (a_{2} - b_{2})^{2} = (c_{1} - d_{1})^{2} + (c_{2} - d_{2})^{2}, \end{aligned}$$

and, in case $E \subset \mathfrak {A}\,(K, k)$ with $k\ne 0$, by

$$\begin{aligned} \frac{F(\mathbf{a},\mathbf{b})^{2}}{Q(\mathbf{a})Q(\mathbf{b})} = \frac{F(\mathbf{c},\mathbf{d})^{2}}{Q(\mathbf{c})Q(\mathbf{d})}, \end{aligned}$$

(7)

where

$$\begin{aligned} F(\mathbf{x},\mathbf{y}) = k(x_{1}y_{1} + x_{2}y_{2}) + 1, Q(\mathbf{x}) = F(\mathbf{x},\mathbf{x}), \text{ and } \mathbf{x} = (x_{1}, x_{2}), \mathbf{y} = (y_{1}, y_{2}). \end{aligned}$$

Let now K be an ordered Pythagorean field, R the ring of finite elements, i.e., $R = \{ x \in K \, :\, (\exists n \in \mathbf{N})\, |x| < n \}$ and P the ideal of infinitely small elements of K, i.e., $P = \{ 0 \} \cup \{ x \in K \, :\, x^{-1} \not \in R \}$. All Hilbert planes are isomorphic to a plane of the following three types:

Type 1

$E = \{ (a,b)\, :\, a, b \in M\} \subset \mathfrak {A}\,(K, 0)$, where M is an R-module $\ne (0)$;

Type 2

$E = \{ (a,b)\, :\, a, b \in M\} \subset \mathfrak {A}\,(K, k)$ with $k \ne 0$, where M is an R-module $\ne (0)$ included in $\{ a \in K \mid ka^{2} \in P\}$, that satisfies the condition

$$\begin{aligned} a \in M \Rightarrow ka^{2} + 1 \in K^{2}; \end{aligned}$$

Type 3

$E = \{\mathbf{x} \, :\, Q(\mathbf{x}) > 0, Q(\mathbf{x}) \not \in J \} \subset \mathfrak {A}\,(K, k)$ with $k < 0$, where $J \subseteq P$ is a prime ideal of R that satisfies the condition

$$\begin{aligned} ka^2 +1 > 0, ka^2 +1 \not \in J \Rightarrow ka^2 +1 \in K^2, \end{aligned}$$

with K satisfying

$$\begin{aligned} \{a \in K \, :\, ka^2 \in R {\setminus } P \} \ne \emptyset . \end{aligned}$$

The meaning of k in this context can be best described by mentioning that its sign is the same as that of $\alpha +\beta +\gamma -180^{\circ }$, where $\alpha$, $\beta$, and $\gamma$ are the measures of the three angles of a triangle, and $180^{\circ }$ is the measure of two right angles.

As shown in Bachmann (1964), the Hilbert planes satisfying $\mathbf{L}(90^{\circ })$, are precisely those of Type 1 and Type 2. In other words, $\mathbf{L}(90^{\circ })$ holds in all models of Type 1 and Type 2 and does not hold in any model of Type 3. Given that we know that $\mathbf{L}(90^{\circ }) \rightarrow \mathbf{L}^{\sigma }_n$ holds in ${{\mathcal {A}}}$, to prove that $\mathbf{L}^{\sigma }_n\rightarrow \mathbf{L}(90^{\circ })$ holds as well, all we need to show is that $\mathbf{L}^{\sigma }_n$ does not hold in planes of Type 3. To prove that $\mathbf{L}(90^{\circ })\rightarrow \mathbf{L}^{\lambda }_n$ holds in ${{\mathcal {A}}}$ all we need to show is that $\mathbf{L}^{\lambda }_n$ holds in planes of Type 1 and Type 2 (that it does not hold in planes of Type 3 will follow from the fact that not even $\mathbf{L}^{\sigma }_n$ holds there, and we know that $\mathbf{L}^{\lambda }_n\rightarrow \mathbf{L}^{\sigma }_n$ holds in ${{\mathcal {A}}}$).

To show that $\mathbf{L}^{\sigma }_n$, with $n\ge 2$, does not hold in planes of Type 3, let ${{\mathfrak {M}}}$ be a model of Type 3. First we notice that if the angle with vertex $O=(0,0)$, whose legs are formed by the points with positive x-coordinates on [0, 1, 0] (the positive part of the x-axis) and by the points with positive x-coordinates on $[-m,1,0]$ (the positive x-part of the line $y=mx$) is to be $(n+1)$-positive, then $m\in R{\setminus } P$, since the formula for reflecting a line through O in another line through O is the same regardless of the value of the metric constant (and thus the same as in the case in which the metric is Euclidean). We will show that, for any $m\in R{\setminus } P$, with $0<m\le 1$, we can find points A and B on the angle with vertex $O=(0,0)$, whose legs are formed by the points with positive x-coordinates on [0, 1, 0] and by the points with positive x-coordinates on $[-m,1,0]$, such that the perpendiculars $\pi _A$ raised in A on OA and $\pi _B$ raised in B on OB do not meet.

First, let us note that, since there is an $a_0\in K$, with $ka_{0}^2\in R{\setminus } P$, there must be an $a_1\in K$ with $-1+\frac{m^4}{16}<ka_{1}^2\le -1+\frac{m^4}{8}$, as K is Pythagorean, and thus contains all $\sqrt{q}$ for $q\in {{\mathbb {Q}}}^{+}$, and $a_1$ can be chosen to be $a_0\sqrt{q}$, for some $q\in {{\mathbb {Q}}}^+$. Let $A=(a_1,0)$ and $B=\left( \frac{a_1}{\sqrt{m^2+1}}, \frac{ma_1}{\sqrt{m^2+1}}\right)$. We need to check that A (and thus B) belongs to ${{\mathfrak {M}}}$, which is plain, as $Q((a_1,0))=ka_{1}^2+1>\frac{m^4}{16}\not \in P$. We find that $\pi _A=[1,0,-a_1]$ and that $\pi _B=[1, m, -a_1\sqrt{m^2+1}]$, and that their point of intersection in the affine-metric plane $\mathfrak {A}\,(K, k)$ is

$$\begin{aligned} \mathbf{x}=\left( a_1, \frac{a_1(\sqrt{m^2+1}-1)}{m}\right) \end{aligned}$$

(8)

and

$$\begin{aligned} Q(\mathbf{x})=\frac{2ka_{1}^2(m^2+1-\sqrt{m^2+1})+m^2}{m^2} \end{aligned}$$

(9)

Using the fact that $ka_{1}^2\le -1+\frac{m^4}{8}$ and that $m^2+1-\sqrt{m^2+1}>0$, we get that

$$\begin{aligned} Q(\mathbf{x})\le \frac{\left( -2+\frac{m^4}{4}\right) \left( m^2+1-\sqrt{m^2+1}\right) +m^2}{m^2}. \end{aligned}$$

(10)

We claim that

$$\begin{aligned} \left( -2+\frac{m^4}{4}\right) \left( m^2+1-\sqrt{m^2+1}\right) +m^2<0. \end{aligned}$$

(11)

Now (11) can be rewritten as

$$\begin{aligned} \left( 2-\frac{m^4}{4}\right) \sqrt{m^2+1} <2-\frac{m^4+m^6}{4}+m^2. \end{aligned}$$

(12)

Squaring and simplifying, we get

$$\begin{aligned} \frac{m^6+m^8}{2} <m^4+\frac{m^{10}+m^{12}}{16}. \end{aligned}$$

(13)

Dividing by $m^4$, we get

$$\begin{aligned} \frac{m^2+m^4}{2} <1+\frac{m^{6}+m^{8}}{16}, \end{aligned}$$

(14)

which holds, since $m\le 1$, and so $\frac{m^2+m^4}{2}\le 1<1+\frac{m^{6}+m^{8}}{16}$, thus (13), (12), and (11) hold, so $Q(\mathbf{x})<0$, which means that $\mathbf{x}$ is not a point of ${{\mathfrak {M}}}$. Thus $\mathbf{L}^{\sigma }_n$, with $n\ge 2$, does not hold in planes of Type 3,

To show that $\mathbf{L}^{\lambda }_n$, with $n\ge 2$, holds in planes of Type 1 and of Type 2, we notice that, since the formula for reflecting a line through O in another line through O is the same regardless of the value of the metric constant (and thus the same as in the case in which the metric is Euclidean), the condition for the angle with vertex in $O=(0,0)$, with legs formed by the points with positive x-coordinates on [0, 1, 0] and by the points with positive y-coordinates on $[-m,1,0]$ to be n-away, but not $(n-1)$-away from a straight angle, implies that $m<0$ and $m\not \in P$. Now if $A=(a,0)$ is any point of a Hilbert plane ${{\mathfrak {M}}}$ of Type 1 or 2, then a is an element of an R-module M. If B is a point on $[-m,1,0]$, with positive y-coordinate, such that $OA\equiv OB$, then $B=(\frac{a}{\sqrt{m^2+1}}, \frac{ma}{\sqrt{m^2+1}})$. The perpendicular in A on OA is $[1,0,-a]$ while that in B on OB is $[1,m,-a\sqrt{1+m^2}]$, and their intersection point is $P=(a, \frac{a(\sqrt{m^2+1}-1)}{m})$. That it belongs to ${{\mathfrak {M}}}$ can be seen by the fact that $m^{-1}\in R$ (since $m\not \in P$), $\sqrt{m^2+1}\in R$ (there exists a natural number n such that $|m|<n$, since $m\in R$, and thus $\sqrt{m^2+1}<n+1$), so $\frac{\sqrt{m^2+1}-1}{m}\in R$, thus $\frac{a(\sqrt{m^2+1}-1)}{m}\in M$. We conclude that $\mathbf{L}^{\lambda }_n$, with $n\ge 2$, holds in planes of Type 1 and of Type 2, This proves (5). Together with (4), (3), and (1), this finishes the proof of the theorem. $\square$

Note that, given Theorem 1, even the following non-elementary form of Lippman’s axiom is equivalent to Lipp 1:

Lipp 3

For every circle ${{\mathcal {C}}}$ there exists a polygon which has ${{\mathcal {C}}}$ as its inscribed circle.

This means that, for some $n\ge 3$, there exists an n-gon, that is circumscribed to ${{\mathcal {C}}}$. One of the angles formed by the center O of ${{\mathcal {C}}}$ and the successive points of tangency of ${{\mathcal {C}}}$ with the n-gon must be $\ge \frac{360^{\circ }}{n}$ (the corresponding $\mathbf{L}$-type statement need not refer to $\frac{360^{\circ }}{n}$ at all (which may well not exist in ${{\mathcal {A}}}$), for one can state it as follows: there exists an angle $\widehat{X_1OX_2}$—with the property that, if $X_{i+1}$ denotes the reflection of $X_{i-1}$ into $OX_i$, then one of the $X_i$, with $i\in \{3, \ldots , n+1\}$ lies on the ray ${\mathop {OX_1}\limits ^{\longrightarrow }}$ or inside the angle $\widehat{X_1OX_2}$—such that, for all A on ${\mathop {OX_1}\limits ^{\longrightarrow }}$ and all B on ${\mathop {OX_2}\limits ^{\longrightarrow }}$ with $OA\equiv OB$, the perpendicular raised in A on OA intersects the perpendicular raised in B on OB). This, together with (2), implies $\mathbf{L}_{n}^{\sigma }$. Since $\mathbf{L}_{n}^{\lambda }$ implies that there exists an n-gon, that is circumscribed to ${{\mathcal {C}}}$, we have that Lipp 3 is equivalent to Lipp 1.

3 On the need to keep angles from being too acute or too obtuse

If we remove the condition that $\widehat{XOY}$ be n-away from a straight angle in $\mathbf{L}_n$ or $\mathbf{L}_n'$, that is, if the property that the perpendiculars intersect holds for any proper angle, then the resulting axioms $\mathbf{L}_{n}^+$ or $\mathbf{L}_n'^+$ are equivalent to the axiom stating that every triangle has a circumscribed circle, an axiom known to be equivalent to the Euclidean parallel postulate. Yet what if we remove from $\mathbf{L}^{\lambda }_n$ or $\mathbf{L}^{\sigma }_n$ any mention of the size of the angle $\widehat{XOY}$, except that it is a proper angle, which means that X, O,  and Y are not collinear? In other words, what is the strength of the axiom

$\mathbf{L}(\exists )$   There exist an angle$\widehat{XOY}$, such that, for allAandB, withAon${\mathop {OX}\limits ^{\longrightarrow }}$andBon${\mathop {OY}\limits ^{\longrightarrow }}$, with$OA\equiv OB$, the perpendicular raised inAtoOAintersects the perpendicular raised inBtoOB.

We will show that $\mathbf{L}(\exists )$ is weaker than the Lotschnittaxiom and thus than $\mathbf{L}^{\sigma }_n$, for any $n\ge 2$, and we will characterize those Hilbert planes of Type 3 that satisfy it.

Theorem 2

A Hilbert plane satisfies $\mathbf{L}(\exists )$ if and only if it is of Type 1 or of Type 2 or of Type 3 with either (i) $J\ne (0)$ or (ii) $J=(0)$ and there exists $u\in K$, $u>0$, such that, for all $a\in K$, if $ka^2+1>0$, then $ka^2+1>u$.

Proof

Since $\mathbf{L}(90^{\circ })$ holds in Hilbert’s planes of Types 1 and 2, $\mathbf{L}(\exists )$ holds in these models as well. Let ${{\mathfrak {M}}}$ be a Hilbert plane of Type 3 with $J\ne (0)$. Let $j\in J$, with $j>0$. We will choose the angle $\widehat{XOY}$, with $O=(0,0)$, with OX the line [0, 1, 0], and OY the line $[-j,1,0]$, such that the interior of $\widehat{XOY}$ is in the $x>0$ and $y>0$ quadrant. Let $A=(a,0)$ be any point on ${\mathop {OX}\limits ^{\longrightarrow }}$ and $B=(\frac{a}{\sqrt{j^2+1}}, \frac{ja}{\sqrt{j^2+1}})$ be the point on ${\mathop {OY}\limits ^{\longrightarrow }}$ for which $OA\equiv OB$. The perpendiculars $\pi _A=[1,0,-a]$ raised in A on OA and $\pi _B=[1, j, -a\sqrt{j^2+1}]$ raised in B on OB meet in $\mathfrak {A}\,(K, k)$ in

$$\begin{aligned} \mathbf{x}=\left( a, \frac{a(\sqrt{j^2+1}-1)}{j}\right) . \end{aligned}$$

(15)

We have

$$\begin{aligned} Q(\mathbf{x})=\frac{2ka^2(j^2+1-\sqrt{j^2+1})+j^2}{j^2}. \end{aligned}$$

(16)

Now, as can be easily seen by re-arranging, with the square root on one side, then squaring, and bearing in mind that j is infinitesimal (in fact, (17) even holds for $j\le \frac{1}{16}$, a fact that will be used later on),

$$\begin{aligned} \frac{j^2}{2}+j^5< j^2+1-\sqrt{j^2+1} < \frac{j^2}{2}+j^3 \end{aligned}$$

(17)

Multiplying by $\frac{2ka^2}{j^2}$, which is negative, and then adding 1, we get

$$\begin{aligned} ka^2+1+2j^3ka^2>\frac{2ka^2(j^2+1-\sqrt{j^2+1})+j^2}{j^2}> ka^2+1+2jka^2. \end{aligned}$$

(18)

This means that $Q(\mathbf{x})>ka^2+1+2jka^2$. We claim that $ka^2+1+2jka^2>0$ and $ka^2+1+2jka^2\not \in J$. Suppose $ka^2+1+2jka^2\le 0$. Then $ka^2+1\le -2jka^2$. Since $|ka^2|<1$, $2jka^2\in J$, so $0<ka^2+1\le -2jka^2$ implies $ka^2+1\in J$, a contradiction. Now suppose $ka^2+1+2jka^2=\epsilon \in J$. Then $ka^2+1= \epsilon - 2jka^2\in J$, a contradiction. Thus $\mathbf{x}$ is a point in ${{\mathfrak {M}}}$, which proves that Hilbert planes of Type 3 with $J\ne (0)$ satisfy $\mathbf{L}(\exists )$.

Suppose now that we are in the situation (ii), that ${{\mathfrak {M}}}$ is a Hilbert plane of Type 3, with $J=(0)$, and that there is $u\in K$, $u>0$, such that, for all $a\in K$, if $ka^2+1>0$, then $ka^2+1>u$. The existence of such a u ensures that $P\ne \emptyset$ (for if $P=\emptyset$, then there is an $a\in K$, with $-1<ka^2<-1+\frac{u}{2}$. since all $\sqrt{q}$, with $q\in {{\mathbb {Q}}}^+$, are in K). Let $j=\frac{u}{2}$. We will choose the angle $\widehat{XOY}$, with $O=(0,0)$, with OX the line [0, 1, 0], and OY the line $[-j,1,0]$, such that the interior of $\widehat{XOY}$ is in the $x>0$ and $y>0$ quadrant. Let $A=(a,0)$ be any point on ${\mathop {OX}\limits ^{\longrightarrow }}$ and $B=(\frac{a}{\sqrt{j^2+1}}, \frac{ja}{\sqrt{j^2+1}})$ be the point on ${\mathop {OY}\limits ^{\longrightarrow }}$ for which $OA\equiv OB$. The perpendiculars $\pi _A=[1,0,-a]$ raised in A on OA and $\pi _B=[1, j, -a\sqrt{j^2+1}]$ raised in B on OB meet in $\mathfrak {A}\,(K, k)$ in the point (15). By (18), $Q(\mathbf{x})>(ka^2+1)u>0$. Thus $\mathbf{x}\in {{\mathfrak {M}}}$, and so Hilbert planes of the kind described in (ii) also satisfy $\mathbf{L}(\exists )$.

Suppose now that ${{\mathfrak {M}}}$ is a Hilbert plane of Type 3, with $J=(0)$, and that for all $u\in K$, $u>0$, there exists $a\in K$, with $0<ka^2+1<u$. Then, for no angle $\widehat{XOY}$, with $O=(0,0)$, with OX the line [0, 1, 0], and OY the line $[-j,1,0]$, for some $j>0$, such that the interior of $\widehat{XOY}$ is in the $x>0$ and $y>0$ quadrant, is it true that for any $A=(a,0)$ on ${\mathop {OX}\limits ^{\longrightarrow }}$ and for the corresponding $B=(\frac{a}{\sqrt{j^2+1}}, \frac{ja}{\sqrt{j^2+1}})$ on ${\mathop {OY}\limits ^{\longrightarrow }}$ for which $OA\equiv OB$, the perpendiculars $\pi _A=[1,0,-a]$ raised in A on OA and $\pi _B=[1, j, -a\sqrt{j^2+1}]$ raised in B on OB meet. To see this, let a be such that $0<ka^2+1<j'^3$, where $j'$ stands for $\min \{j, \frac{1}{16}\}$. Then, by (18), with $\mathbf{x}$ denoting the intersection point of $\pi _A$ and $\pi _B$, determined in (15), we have $Q(\mathbf{x})< ka^2+1+2j^3ka^2<j'^3+2j^3(j'^3-1)<0$, which means that $\mathbf{x}$ is not a point of ${{\mathfrak {M}}}$. $\square$

An example of a Pythagorean field K, with $k\in K$, $k<0$, such that $\{a\in K: ka^2\in R{\setminus } P\}\ne \emptyset$, and such that there exists $u>0$ such that, for all $a\in K$, if $ka^2+1>0$, then $ka^2+1>u$, was communicated to us by Detlef Gröger. It can be constructed as follows: Let M be an Archimedean Pythagorean ordered field, which is not Euclidean, i.e., in which not all positive elements are squares. The first such field was constructed by Hilbert (1977, p. 120). Another option would be the Pythagorean hull of ${{\mathbb {Q}}}$ inside the field of real algebraic numbers, on which more can be found in Becker (1974) and Pambuccian (1990). Let $K=M((t))$ be the field of formal power series, whose elements are the formal power series

$$\begin{aligned} \alpha =t^r\left( \sum _{i=0}^{\infty } a_it^i\right) ,\, \text{ with } \, r\in {{\mathbb {Z}}}, a_0\ne 0,\, \text{ and } \, a_i\in M, \end{aligned}$$

(19)

with the usual way to add and multiply them, ordered by declaring $\alpha$ to be positive if and only of $a_0>0$. Under this order, t turns out to be infinitely small, i.e. $0<t<m$ for all positive $m\in M$. K is Pythagorean since M is Pythagorean, a fact that is easily seen by noticing (see Ribenboim 1974, 2(k), p. 180) that $\alpha$ is a square if and only if r is even and $a_0$ is a square in M. Let $k=-e^{-1}$ and $u=t$, where e is an element of M that is positive but not a square (such elements exists in M since it is not a Euclidean field). Since $1\in \{a\in K: -e^{-1}a^2\in R{\setminus } P\}$, the set is certainly nonempty. That if $-e^{-1}a^2+1>0$, then $-e^{-1}a^2+1>t$, can be seen by noticing that the assumption that $-e^{-1}a^2+1>0$ and $-e^{-1}a^2+1\le t$, would imply that

$$\begin{aligned} e-et\le a^2<e. \end{aligned}$$

(20)

Bearing in mind that $a^2$ can be written as in (19), with $a_0$ a square in M, we notice that r has to be 0. The two inequalities in (20) now force $a_0$ to be e, but $a_0$ is a square in M, while e is not a square in M, a contradiction.

Thus condition (ii) in Theorem 2 is not vacuous. However, if the Hilbert plane satisfies the Circle Axiom CA (“The segment joining a point inside a circle with one outside it intersects that circle”)³ and it is of Type 3, then K is a Euclidean ordered field and k can be chosen to be $-1$. In that situation, for all $u>0$, there is $a\in K$, such that $0<1-a^2<u$. Such an a is $1-\frac{u}{2}$. This means that, in Hilbert planes in which the Circle Axiom holds, the case (ii) in Theorem 2 cannot occur. This means that, in Hilbert planes satisfying CA, $\mathbf{L}(\exists )$ holds in all models except the Beltrami–Cayley–Klein inner-disc models of plane elementary hyperbolic geometry, a theory introduced by Hilbert (1903) by adding to the axioms of ${{\mathcal {A}}}$ the following elementary form of the hypebolic parallel axiom

HPA

From any point P not lying on a line l there are two rays $r_1$ and $r_2$ through P, not belonging to the same line, which do not intersect l, and such that every ray through P, contained in the angle formed by $r_1$ and $r_2$, does intersect l.

These observations together with Theorem 2 prove that

Theorem 3

$$\begin{aligned}&{{\mathcal {A}}} + \mathbf{CA} \vdash \mathbf{L}(\exists )\leftrightarrow \lnot \mathbf{HPA}\\&{{\mathcal {A}}}\vdash \mathbf{L}(\exists )\vee \mathbf{HPA}\\&{{\mathcal {A}}}\nvdash \lnot \mathbf{L}(\exists )\vee \lnot \mathbf{HPA}\\ \end{aligned}$$

4 Lebesgue’s axiom is equivalent to the Lotschnittaxiom

The purpose of this section is to prove the equivalence of Lebesgue’s axiom Leb with Bachmann’s Lotschnittaxiom. We will also show that a new class of statements, that bear some resemblance to the $\mathbf{L}$-axioms, are equivalent to the Lotschnittaxiom. These statements are:

$\mathbf{A}_n'$   If$\widehat{XOY}$isn-away from a straight angle, andPis any point inside it, then there exists a line throughPthat intersects both legs of the angle$\widehat{XOY}$.

$\mathbf{A}^{\lambda }_n$   There exists an angle$\widehat{XOY}$, which isn-away, but not$(n-1)$-away from a straight angle, such that, for any pointPinside it, there exists a line throughPthat intersects both legs of the angle$\widehat{XOY}$.

$\mathbf{A}^{\sigma }_n$   There exists an angle$\widehat{XOY}$, which is$(n+1)$-positive, but notn-positive, such that for any pointPinside it, there exists a line throughPthat intersects both legs of the angle$\widehat{XOY}$.

$\mathbf{A}(\alpha ^{\circ })$If$\widehat{XOY}$is an angle of measure$\alpha ^{\circ }$andPis any point inside it, then there exists a line throughPthat intersects both legs of the angle$\widehat{XOY}$.

That these are all equivalent to their $\mathbf{L}$ counterparts can be see by noticing that

Theorem 4

For any angle $\widehat{XOY},$ the following are equivalent with respect to ${{\mathcal {A}}}$:

• (a) for any M on ${\mathop {OX}\limits ^{\longrightarrow }}$ and for any N on ${\mathop {OY}\limits ^{\longrightarrow }}$ with $OM\equiv ON$, the perpendicular in M on OM intersects the perpendicular in N on ON

• (b) for any point P inside $\widehat{XOY}$, there exists a line through P that intersects both legs of the angle $\widehat{XOY}$.

• (c) the perpendicular raised in any point P on the internal angle bisector of $\widehat{XOY}$ intersects the sides of $\widehat{XOY}$.

Proof

The proof of this theorem, for the case in which $\widehat{XOY}$ is a right angle, can be found in Bachmann (1964, pp. 175–177). The proof for an arbitrary angle $\widehat{XOY}$ does not differ in any essential way from that presented there. We provide it here for the reader’s convenience. First, let us show that (b) is equivalent with (c). To prove this equivalence, suppose first that (b) holds, and let P be any point on the internal angle bisector of $\widehat{XOY}$. Since P is a point in the interior of $\widehat{XOY}$, by (b), there is a line g through P which interescts ${\mathop {OX}\limits ^{\longrightarrow }}$ in A and ${\mathop {OY}\limits ^{\longrightarrow }}$ in B. If g happens to be perpendicular to OP, we are done. If g is not perpendicular to OP, let h denote the perpendicular raised in P on OP. The line h does not pass through any of the vertices of triangle OAB and intersects one of its sides, namely AB. By the Pasch axiom it must also intersect one of the sides OA and OB of triangle OAB. Given that the angle $\widehat{XOY}$ is symmetric about OP, h intersects both ${\mathop {OX}\limits ^{\longrightarrow }}$ and ${\mathop {OY}\limits ^{\longrightarrow }}$. Thus (c) holds. Suppose now that (c) holds and let P be any point inside the angle $\widehat{XOY}$. Let r be the foot of the perpendicular from P to the internal angle bisector of $\widehat{XOY}$. By (c), the line RP intersects both ${\mathop {OX}\limits ^{\longrightarrow }}$ and ${\mathop {OY}\limits ^{\longrightarrow }}$, so RP is a line through R interescting the legs of $\widehat{XOY}$, so (b) holds.

Let us now show that (a) and (c) are equivalent. Suppose (a) holds and let P be any point on the internal angle bisector b of $\widehat{XOY}$. Let M be a point on ${\mathop {OX}\limits ^{\longrightarrow }}$ and N a point on ${\mathop {OY}\limits ^{\longrightarrow }}$, such that $OP\equiv OM$ and $OP\equiv ON$. Let R be the point of intersection of the perpendicular in M on OM with the perpendicular in N on ON. R lies on b, and if we now transport OR on ${\mathop {OX}\limits ^{\longrightarrow }}$ to get a point A on ${\mathop {OX}\limits ^{\longrightarrow }}$ with $OR\equiv OA$ and on ${\mathop {OY}\limits ^{\longrightarrow }}$ to get a point B on ${\mathop {OY}\limits ^{\longrightarrow }}$ with $OR\equiv OB$, then the line AB passes through P and intersects the sides of $\widehat{XOY}$, Suppose now that (c) holds. and let M and N be two points on ${\mathop {OX}\limits ^{\longrightarrow }}$ and on ${\mathop {OY}\limits ^{\longrightarrow }}$, respectively, such that $OM\equiv ON$. Let P be the point on the internal angle bisector b of $\widehat{XOY}$, for whoch $OP\equiv OM$. Let A be the point of intersection of the perpendicular in P on OP with ${\mathop {OX}\limits ^{\longrightarrow }}$. Let R be the point on b for which $OR\equiv OA$. Then R is the point of intersection of the perpendicular on M to OM with that on N to ON.

Corollary 1

${{\mathcal {A}}}\vdash \mathbf{A}_n'\leftrightarrow \mathbf{L}_n'$, $\mathbf{A}^{\lambda }_n\leftrightarrow \mathbf{L}^{\lambda }_n$, $\mathbf{A}^{\sigma }_n\leftrightarrow \mathbf{L}^{\sigma }_n$, $\mathbf{A}(\alpha ^{\circ })\leftrightarrow \mathbf{L}(\alpha ^{\circ })$, $\mathbf{A} (\exists )\leftrightarrow \mathbf{L}(\exists )$.

Here $\mathbf{A}(\exists )$ stands for

$\mathbf{A}(\exists )$   There exist an angle$\widehat{XOY}$, such that, for any pointPinside it, there exists a line throughPthat intersects both legs of the angle$\widehat{XOY}$.

It is worth mentioning that Legendre [1800, p. 23, Prop. XX, p. 280, Note II (6th ed.)]⁴ provided in 1800 a proof of the Euclidean parallel postulate in which he used the Archimedean axiom and what we by now recognize as an equiavent form of the Lotschnittaxiom:

$\mathbf{A}(\le 60^{\circ })$   If$\widehat{XOY}$is an angle$\le 60^{\circ }$andPis any point inside it, then there exists a line throughPthat intersects both legs of the angle$\widehat{XOY}$.

We are now ready to show that Leb is equivalent to A($120^{\circ })$, and thus, by Theorem 1 and Corollary 1, Leb is equivalent to the Lotschnittaxiom.

This can be seen by first noticing that, as proved by Legendre Greenberg (2008, p. 195), for any $\epsilon >0$, for which there exists a natural number n such that $n\epsilon >90^{\circ }$, the sum of the angles of a given triangle is $<180^{\circ }+\epsilon$, so that at least one angle of any convex quadrilateral must be $\le 120^{\circ }$. Suppose now A($120^{\circ }$) holds. Let ABCD be a convex quadrilatreal. One of its angles, say $\widehat{DAB}$, is $\le 120^{\circ }$, and since A($120^{\circ }$) holds, there exists a line g through C which intersects the sides ${\mathop {AB}\limits ^{\longrightarrow }}$ and ${\mathop {AD}\limits ^{\longrightarrow }}$ of the angle $\widehat{DAB}$ in X respectively Y. If X is such that B lies between A and X and Y is such that D lies between A and Y, then triangle AXY contains the quadrilateral ABCD and we are done. Suppose this is not the case and, one of X and Y is not in the desired position, say X is between A and B. In that case, the line CB intersects the side XY of triangle AXY and the extension of side AX, so it must intersect, by the Pasch axiom, side AY as well in a point P. Triangle ABP thus contains the quadrilateral ABCD and we are done. To prove that Leb$\rightarrow$A($120^{\circ }$), we will show that $\lnot$A($120^{\circ }$) $\rightarrow \lnot$Leb. Since $\lnot$A($120^{\circ }$) holds precisely in those models of ${{\mathcal {A}}}$ in which the negation of the Lotschnittaxiom holds, $\lnot$A($120^{\circ }$) holds precisely in Hilbert planes of Type 3. That Leb does not hold in Hilbert planes of Type 3 can be seen by noticing that, if $a\in K$ is such that $\frac{1}{2}<ka^2<1$ (such an a must exist in K since $\{a\in K: ka^2\in R{\setminus } P\}\ne \emptyset$), then the quadrilateral formed by $A=(-a,-a)$, $B=(-a,a)$, $C=(a,a)$, $D=(a, -a)$ cannot be included in a triangle. This can be seen by noticing that there is not even a triangle that circumscribes the circle with center (0, 0) passing through (a, 0) (that circle is inscribed in the quadrilateral ABCD). That this is so can be seen by noticing that the radius of the inscribed circle of the equilateral triangle inscribed in a circle of radius 1 is $\frac{1}{2}$. We conclude that:

Theorem 5

Lippmann’s axiom, Lebesgue’s axiom, and the Lotschnittaxiom are equivalent with respect to ${{\mathcal {A}}}$.

Leb is not just yet another equivalent of the Lotschnittaxiom. Among all the known equivalents, it is the only one that is expressed purely in terms of the betweenness relation, and thus a theorem of ordered geometry (see Pambuccian 2011 for the various axiomatizations of ordered geometries). One could certainly also express A$_n'$ in the following terms, to turn it into an axiom of ordered geometry

A

If O, A, B are three distinct points, such that O lies between A and B, if C is a point that does not lie on the line AB, if X is a point inside the angle $\widehat{AOC}$ and Y is a point inside the angle $\widehat{BOC}$, then there is a line l that (i) goes through X and intersects the rays ${\mathop {OA}\limits ^{\longrightarrow }}$ and ${\mathop {OC}\limits ^{\longrightarrow }}$ or (ii) goes through Y and intersects the rays ${\mathop {OB}\limits ^{\longrightarrow }}$ and ${\mathop {OC}\limits ^{\longrightarrow }}$.

If A($90^{\circ }$) holds, then A also holds, given that one of $\widehat{AOC}$ and $\widehat{BOC}$ is $\le 90^{\circ }$. If A is known to hold, then it holds in the case in which $CO\perp OA$ as well, and in that case it means A($90^{\circ }$).

Thus, of the three axioms that have a certain Euclidean flavor and are independent of ${{\mathcal {A}}}$, the Euclidean parallel postulate and the Lotschnittaxiom can both be stated as pure order axioms. Clairault’s Axiom R (see Greenberg 2008, p. 219), stating that there exists a rectangle, or equivalently that the perpendiculars raised on te two sides of a right angle are orthogonal—the axiom that postulates the Eucliddean nature of the metric, by forcing the sum of the angles of any triangle to be $180^{\circ }$ (or, in terms of the models of absolute geometry, stipulates that the orthogonality constant k is 0)—does not appear to be expressible in terms of the betweenness relation alone. Nor does L$(\exists )$ appear to be thus expressible. We leave these as open problems.

Open Problem

Is there a statement $\sigma$ expressed in terms of the betweenness predicate alone, such that ${{\mathcal {A}}}\vdash \mathbf{R}\leftrightarrow \sigma$? Is there a statement $\sigma$ expressed in terms of the betweenness predicate alone, such that ${{\mathcal {A}}}\vdash \mathbf{L}(\exists )\leftrightarrow \sigma$?