Artificial intelligence for suspended sediment load prediction: a review

Abstract

The estimation of sediment yield concentration is crucial for the development of stream ventures, watershed management, toxins estimation, soil disintegration, floods, and so on. In this study, we summarize various existing artificial intelligence (AI)-based suspended sediment load (SSL) estimation models to calculate the suspended sediment load, to our knowledge to date. The artificial neural network (ANN), generalized regression neural network (GRNN), neuro-fuzzy (NF), genetic algorithm (GA), gene expression programming (GEP), classification and regression tree (CART), linear regression (LR), multilinear regression (MLR), Chi-squared automatic interaction detection (CHAID), extreme learning machine (ELM), and support vector machine (SVM) are among the many AI-based models that have been successfully implemented for sediment load prediction. In this paper, we describe a few popular AI-based models that have been used for SSL prediction. ANN, SVM, and NF had overcome each other in different circumstances of prediction; and all three can be said as good predictors. Models using ANN with ELM or wavelet analysis in some ways are good predictors as their predicted values generally lie closer to the measured value. Performances of the algorithms are usually evaluated by applying various types of performance assessment methods most commonly RMSE, R², MAE, etc. This review is required to bear some significance to the researchers and hydrologists while seeking models that have been effectively actualized inSSLestimation or in hydrology related aspects, however, mainly focused on the researches between January 2015 and November 2020.

Definition and basic concepts

Sediment transport is a burning question in river management practices. It shows great variation in sediment deposition throughout the river bed. The intense seasonal rainfall, streamflow, tropical climate, and immature geology are some of the factors which influence sediment transport and its deposition. Generally, sediment transport predominantly occurs during the monsoon season which results in a notable amount of sediment deposit the downstream of the river. Mostly, the sediments are in the form of earth materials and finally get flushed into the sea in the magnificent amount due to the sediment transport by the river. Naidu (1999) stated that 20 billion tons of earth materials on the planet get conveyed to the oceans every year by waterways or streams of which Indian subcontinent alone contributes for 6 billion, due to a large number of rivers and intense rainfall presence. In storm-water, the sediment load particles could accumulate on the top of soil surface or could be trapped underground soil pores. The transportation of sediment frequently varies from one place to another place which affects greatly the process of sediment deposition. Hence, prediction of sediment load is essential for various civic development activities such as the dam designing, designing of reservoirs, watershed management and estimation of floods in flood-prone areas, etc. It is also essential to understand the sediment transport prediction during the development of Hydro-Power projects (Zarris et al. 2006, 2011). Hence, without a doubt, the precise estimation of suspended sediment load (SSL) plays a major part in hydraulic engineering as well as in civic development and river engineering practices(Brownlie 1981; Alonso et al., 1982).

Sediment transport mechanics is the study of fluid sediment motion laws and erosion, transport, and deposition processes. Various types of movement of sediments are found in nature, including the movement of sediments in rivers and canals, reservoirs, along the shore, and in the marine environment. The deserts and the pipelines are the results of flow, wind and waves of the stream. Stats indicate that 13 of the world's major rivers carry over 5.8 billion tones of annual sediment load (Chien and Wan 1998). There are peculiarities in a river that is heavily loaded with sediment that cause it to differ extensively from rivers that carry much less sediment. These differences have led to various engineering problems such as flood control, reservoir sedimentation, irrigation sedimentation of canals, and sedimentation problems in ports and estuaries (Duan and Takara 2020). According to Chien and Wan (1998), the mechanics of sediment transport should be a component of sediment science. In particular, this component should cover the following four aspects:

• 1. Sediment formation and its properties

• 2. Sediment transport mechanics

• 3. Field measurements and laboratory experiments

• 4. Applied science of sedimentation.

The sediment movement phenomenon is quite complicated. In general, sediment movement is a two-phase flow issue. Sediment moves under a flow's action, and its presence, in turn, influences the flow. In addition, practical problems arise when direct measurements are taken (Rezapour et al. 2010). Sediment transport is an intricate and non-linear process. Hence, it is a difficult task to model it (Kalteh et al., 2008). In the past, to perceive the mechanism for sediment transportation in rivers, great works have been enacted. As the evolution of river sediment science has taken place, the focus on sediment discharge estimation saw its growth. Sediment load in a river could be categorized into SSL and bed load (BL). The SSL corresponds to the major portion of the sediment load. BL depicts a particle in a flowing fluid that is transported along with the bed (Colby and Hembree 1955; Rijn 1984). A large number of researchers have studied the river SSL estimation and its simulation during the last few decades. Direct measurements or indirect measurement through algorithms have been used to calculate the SSL of a stream. Direct measurements are directly carried on the site which has been selected for the experiment for gaining data, but it is uneconomical to acquire data at all locations and is not a feasible way with respect of time as it requires an enormous amount of time to collect satisfactory data. These direct measurements are more trustworthy than indirect measurements, but are avoided due to their complex nature. In this work, we have reduced the range of review models to the ones that specifically take account of SSL.

Since the suspended load prediction is a complex process; a comprehensive model is required for prediction, which will be accurate and easy to use. Sediment load is dependent on flow conditions as well as climatic conditions like rainfall, temperature (in some special cases), as well as on river delta mouth characteristics; hence, suspended sediment load prediction is a non-linear phenomenon to understand thoroughly, because it includes a number of interconnected components. It was found that the traditional models, viz., Einstein approach (Einstein 1950), Brook’s approach (Brooks 1965), and SRC were used for suspended sediment load modeling (Kisi et al. 2006) before 1990. Furthermore, there was a tremendous turn of researchers toward the AI-based models like artificial neural network (ANN) (Tayfur and Gundal 2006) in various fields such as environmental engineering and water resource management. ANN algorithm is a very efficient and powerful computational machine learning algorithm utilized for simulating the complicated associations among variables which are non-linear (Gallantand Gallant 1993; Smithand Eli 1995; Yitianand Gu 2003). The application of ANN was performed in many areas other than river engineerings such as electrical engineering, image processing, financing, physics, neurophysiology, and others (Panagoulia et al. 2017).

In designing ANN models, some problems arise for high-value data and small value data; it does not provide satisfactory results in estimation compared to the actual value and converge to a local minimum. These ANN models for their better performance need a long duration training data, so that the over-fitting in the model could be avoided. To overcome these shortcomings, sometimes, it is inadequate to go for the ANN-based model. Hence, in this complex hydrological process, it would be better to use a tool which could provide a better solution to the problem taken. Vapnik and Cortes (1995) proposed a novel approach that uses the structural risk minimization principle, called SVM (Vapnik 1999, 2000). SVM is essentially implemented for solving problems concerned with classification and regression. The regression model is known as SVR (Drucker et al. 1997; Awad and Khanna 2015). They become popular because of their promising empirical performance. In several hydraulic engineering process and environmental problems, the SVM is effectively implemented in recent decades (Flood and Kartam 1994; Sivapragasam et al. 2001; Dibike and Solomatine 2001; Sivapragasamand Muttil 2005; Tripathi et al. 2006; Lin et al.2006; Hong 2008; Khan and Coulibaly 2006; Chen and Li 2010; Yunkai et al. 2010; Noori et al. 2011; Ch et al. 2013; Ji and Lu 2018). SVM is used in suspended sediment estimation through its different models to estimate the SSL of two water bodies (Cimen 2008). Sediment yield simulation was also done through SVM by Misra et al. (2009). It was reported by them that as compared to ANN, SVM furnish better outcomes in training, testing, and validation. Azamathulla et al. (2010) in their work applied SVM to validate its predictive capability. They finally found that SVM displayed superior performance in comparison with the other traditional models. Whenever the outputs gathered through the usage of datasets, it was seen that SVM provided better results as compared to ANN for SSL estimation (Jie and Yu 2011). Hazarika et al. (2020a) compared the prediction performance of SVR and ANN model and discovered that SVR outperforms the ANN model. Hassanpour et al. (2019) showed the applicability of fuzzy C-mean clustering-based SVR model for suspended sediment load prediction. A variation of SVM is also used in modeling is known as least square SVM (LSSVM). LSSVM was introduced for demonstrating SSL relationship and it was discovered that the LSSVM model could over-play the ANN model and the two models executed superior to the SRC model (Kisi 2012). Lafdani et al. (2013) described the two models, viz., ANN and SVM through gamma test for input selection might prompt preferable effectiveness over the regression combination. For solving non-linear classification, LSSVM is a powerful methodology. Mondal (2011) proposed a new model, viz., gamma geomorphologic instantaneous unit hydrograph (GGIUH) for the estimation of direct runoff for a river basin. This model yields satisfactory result in prediction. Yaseen et al. (2016) in his work introduced a new data-driven model for streamflow forecasting, known as ELM. It was contrasted with other data-driven models like SVR and GRNN and observed to be significantly more superior to them with RMSE value around 21.3% less than SVR and roughly 44.7% less compared to GRNN. Li and Cheng (2014) combined the ELM with WNN for better monthly water discharge estimation in the river. They compared it with SLFN-ELM and SVM and discovered that SLFN-ELM performs slightly better in the prediction of the peak discharge and the taken WNN-ELM model yields more précised estimation compared to the other two models. Gupta et al. (2020) applied two asymmetric Huber loss function-based ELM model to deal with the noisy nature of the river SSL data. Experimental results expose that the ELM-based models were able to deal with the SSL datasets with high accuracy. Sadeghpour et al. (2014) proposed a hybrid model called a wavelet SVM (WSVM), which was a conjunction of wavelet and SVM. It was found that WSVM could be used further as a prediction model for successful SSL prediction. Yadav et al. (2018) tried to forecast the SSL of Mahanadi River, India using a hybrid genetic algorithm-based artificial intelligence (GA-AI) model. In the comparison of this model with conventional models like MLR and SRC, it was found that the proposed GA-AI model yields better performance. Daneshvar and Bagherzadeh (2012) evaluated sediment yield using pacific southwest interagency committee (PSIAC) model and modified pacific southwest interagency committee (MPSIAC) model with the help of geographic information system (GIS) in Toroq watershed of Iran. Both models provided comparative outcomes and showed correlation coefficients with moderate level to the high level (R² = 0.436–0.996 to 0.893–0.998) for PSIAC as well as MPSIAC models, respectively. Rejaie-balf et al. (2017) applied a new parametric method called multivariate adaptive regression splines (MARS). It gave comparatively better performance compared to ANN, ANFIS, SVM, and M5 tree models. Choubin et al. (2018) used the CART model for modeling the SSL in a river. This model was compared with four common models: ANFIS, MLP neural network, radial basis function-SVM (RBF SVM), and proximal SVM (P-SVM). To evaluate the model capacities, various performance evaluation methods were used. As per the researcher, the CART model displayed the best results in estimating SSL, followed by RBF SVM. Kisi and Yassen (2019) implemented three ANFIS-based model to prove their usability in SSL estimation. Tarar et al. (2018) applied the Mann–Kendall test along with wavelet transform for SSL estimation in the upper Indus River and results show a very good R² value of 0.9. Gupta et al. (2018) tried to implement the KINEROS 2 model for forecasting streamflow and sediment load which yielded an average result. Very recent literature on SSL prediction using ANN includes Khan et al. (2019a, b), Nivesh et al. (2019), Yadav et al. (2020), Hazarika et al. (2020b), etc.

Predicting SSL through the GEP and ELM are some new techniques of artificial intelligence which had shown better performance over existing FFNN-BP technique. Notwithstanding when it is not feasible to create the mathematical function for the issue taken with the accessible soft computing methods, GEP could model it and thus wind up favorable during these circumstances over existing strategies. Another type of model known as SWAT was also implemented for calculating mean annual sediment precipitation. It showed an average result in SSL prediction (Oeurng et al., 2011). Morgan et al. (1998) applied a new model named the European soil erosion model (EUROSEM) for SSL estimation. However, it has a disadvantage that it is possible to be actualized only in smoothly incline railless planes, rilled surfaces, and crinkled surfaces. It was found by the researchers that EUROSEM overestimated the suspended sediment load concentration, but the dissimilarity was not large. Tabatabaei et al. (2019) proposed a non-dominated sorting algorithm for SSL prediction from the dataset of Ramian hydrometric station on Ghorichay River. The results obtained from various SRC models suggest that the sediment rating curve-genetic algorithm-II model using non-dominated sorting algorithm-II gives better efficacy than the other models. Nourani et al. (2019) in their work proposed a wavelet-based data mining approach called a wavelet-M5 model for predicting the SSL of two different rivers named Lighvanchai and Upper Rio Grande. The obtained results in the Upper Rio Grande river reveal that the proposed wavelet-M5 model showed better performance compared to ANN, M5, and Nash Sutcliffe efficiency. Sharghi et al. (2019) suggested a novel wavelet exponential smoothing algorithm for estimating the SSL in the Lighvanchai and Upper Rio Grande rivers. Experimental results reveal that combining wavelet transform with exponential smoothing algorithm yields more precise results compared to WANN, ARIMA, and seasonal ARIMA models. Samet et al. (2019) tried to compare the performance among ANN, ANFIS, and GA, and noticed that among these models, the ANFIS showed the least error while predicting the SSL. Sharghi et al. (2019) suggested a hybrid emotional ANN (EANN) and wavelet transform conjunction model called wavelet EANN (WEANN) for river SSL prediction. The obtained results suggest that the model gives a good performance in estimating the SSL of Lighvanchai and Upper Rio Grande rivers.

The main intent of this paper is to present a brief discussion of the different artificial intelligence (AI)-based model that has been successfully applied for sediment load prediction. However, the main focus in on the studies between January 2015 and November 2020. Furthermore, to reveal the quality works that have been published between January 2015 and November 2020, a list of SCI/SCIE and Scopus indexed publication is also presented.

The rest of the paper is organized as follows: “Existing AI-based SSL estimation models” focuses on the major artificial intelligence (AI)-based models that have been fruitfully implemented from January 2015 to November 2020. The papers are obtained using the two queries “sediment load prediction” and “suspended sediment load prediction” in Google Scholar. “Experimental analysis” shows experimental analysis on two different SSL datasets that are collected from two different rivers in India. The last section is the conclusion and the future projection of the work. The details of the work that has been performed for SSL predictions are shown in Table 1. To be more specific, we have shown only the works that are indexed only in SCI/SCIE and Scopus using the two queries “sediment load prediction” and “suspended sediment load prediction” in Google Scholar. However, we have omitted ResearchGate as the recent research suggests that ResearchGate cannot still challenge Google Scholar to provide early citation indicators. Moreover, although ResearchGate, in theory, allows automated data collection, unlike Google Scholar (except for Publish or Perish), its current maximum crawling speed is a major practical limitation on its use for large-scale data gathering (Thelwall and Kosha 2017). Moreover, Table 2 elaborates describes the performance evaluators that have been used by the researchers.

Table 1 List of contributions in SCI/SCIE and Scopus indexed journals from January 2015 to November 2020 using the queries “sediment load prediction” and “suspended sediment load prediction”

Table 2 Description of the performance indicators used in Table 1

Existing AI-based SSL estimation models

The ANN

The property of working of brain to learn is studied and checked if it can be applied to the machine learning and gave rise to a very strong learning model known as neural networks or ANNs. ANNs are distributed, adaptive, and generally non-linear in nature built from many different processing elements (PEs). Each PE receives connections from other PEs and/or itself. Interconnectivity defines the topology of the system. Signals flowing through the connections are scaled by adjustable parameters called weights. PEs add up all of these contributions and produce an output that is a non-linear function of the sum. Outputs of PEs are either system outputs or sent to the same or other PEs (Rojas 1996). The value of ANNs stems from their expressive power, their ability to approximate functions, starting with the famous “Universal Approximation Theorem” according to which ANNs with depth 2, depending on their activation function, can theoretically approximate any continuous function in a compact domain to any level of accuracy (Cybenko 1989; Funahashi 1989; Hornik et al. 1989; Debao 1993; Barron 1994). This is done by emulating a non-linear process without actual knowledge of the model (Sharma and Lie 2012) and is capable of auto-adjusting in case conditions change in a time-dependent way (Lodge and Yu 2014) and of handling same or similar patterns (Wang et al. 2004). ANN are computationally difficult to train. On the other hand, modern neural networks are trained efficiently using stochastic gradient descent, backpropagation (BP), conjugate gradient descent, radial basis function (RBF), cascade correlation algorithm, etc., and a variety of tricks, including various activation functions (Livni et al. 2014). Goodfellow et al. (2015) have shown, for seven different ANN models of practical interest, that there is a straight path from initialization to solution that reduces objective function smoothly and monotonically. Recently, Bastani et al. (2016), Zhang et al. (2018), and Mangal et al. (2019) proposed new matrices for measuring the robustness of ANN. The ANN network’s robustness is explicitly discussed in Bastani et al. (2016), Zhang et al. (2018), and Mangal et al. (2019). ANNs can easily become unstable in the presence of disturbances or unmodelled dynamics. A constrained stable background algorithm (CSBP) was proposed by Korkobi et al. (2008) to overcome this situation. Furthermore, Haber and Ruhetto (2017) developed new forward propagation techniques to overcome the numerical instabilities in vanishing gradient problems of deep neural networks. Few other structural learning (SL)-based ANN architectures are the Cascade-Correlation learning (Fahlman and Lebiere, 1989) and the SL via forgetting (SLF) (Ishikawa 1996).

In the field of pattern classification and pattern recognition, ANNs have been effectively implemented (Bishop 1995) and are progressively utilized as a part of the studies taken in hydrology (Aly and Peralta 1999; Dawson and Wilby 1998; Zhang and Stanley 1997; Behzad et al. 2009). The embodiment of numerical-water drive models in ANNs was done by Dibike et al.(1999) for the problem of flow forecasting with positive results. In watersheds, ANNs are widely applied for soil erosion problem and rainfall–runoff relationship (Zhu et al. 1994; Tokar and Johnson 1999). As the utilization of ANNs developed in hydrological resources, a review of its idea as well as implementations were done by ASCE (2000) and inferred that ANN’s execution is on a par with already operational models. By Freiwan and Cigizoglu (2005), it was applied in monthly river flow forecasting. Flood frequency analysis (1998), estimation of sanitary flows (1998), hydraulic characteristic of severe contraction (1998), and classification of river basins (2000) are some applications of ANN in other fields (Karunanithi et al. 1994; Grubert 1995; Venkatesan et al. 2009). Nagy et al. (2002) trained the ANN through deduced stream data for estimating the SSL in rivers. To calculate the output SSC (suspended sediment concentration), a network was established. This network has input variables like the Reynolds number, stream width ratio, Froude number (${F}_{r}$), mobility number, etc., which were applied to calculate the load concentration. The commonly used models were compared with the ANN model on the output data. For comparison, the information of observed total load concentration (TLC) and calculated TLC through the predictor was used by:

$$ D_{r} = {\raise0.7ex\hbox{${T_{o} }$} \!\mathord{\left/ {\vphantom {{T_{o} } {T_{c} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${T_{c} }$}}. $$

(1)

In (1)

$T_{o}$ = observed TLC and.

$T_{c}$ = calculated TLC through the predictor.

ANN showed much better results than the most frequently used models. The calculated discrepancy ratio for Engelundand Hansen (1967) approach (2.34) had shown much more variations between $T_{c}$ and $T_{o}$, whereas, for ANN (1.04), it was much closer. To predict the transportation rates of sediment load, an ANN-based method was introduced by Sarangi et al. (2005), which itself a data-driven model. Field data collected from several studies and published ravines having a high varying nature were taken to build or train the ANN model. The precision of estimation was observed to be superior to the models which were regularly utilized like Engelund and Hansen (1967). An ANN model was applied by Raghuwanshi et al. (2006) in Nagwan watershed for estimating the sediment load and overflow. Linear regression models were likewise produced for the examination of performance with the ANN. Here, every day and week by week drainage and sediment load was taken for prediction. The training data for both the models were of 5 years and the testing data were for 2 years. It was noticed that the ANN models outperformed the traditional methods like linear regression models. The ANN models for SSL prediction were also developed based on climate factors such as temperature, average rainfall, flow discharge, and the intensity of rainfall as these factors play a vital role in sediment depositions. Another ANN-based model was introduced by Zhu et al. (2007) based on these climate factors to simulate the monthly behavior of sediment depositions in Longchuanjiang River in China. The ANN model successfully simulated the monthly behavior of sediment depositions in Longchuanjiang River with nearly accurate results when proper variables were considered with the consideration of correlation of these variables with the suspended sediment depositions of the previous month. The conventional methods of prediction such as Multi Linear Regression (MLR) were also matched with the ANN models. In Alp and Cigizoglu’s research (2007), both these models were contrasted with each other based on their performance criteria. They took a couple of ANN models in which the BP learning algorithm and RBF algorithm were considered. The hydro-meteorological variables such as rainfall and flow and their relation with the daily SSL were examined by utilizing these two techniques of ANN by training it through the hydro-meteorological variables and SSL data taken from a catchment called Juniata in the United States. The outcomes implied that the performance given by ANN was much more accurate than MLR. To forecast the daily suspended sediment concentration, SRC, MLR, and ANN models were used by Rajaee et al. (2009) at a couple of gauging stations. The day-by-day waterway discharge and SSL information taken from these two stations utilized as the testing set for ANN. The outcomes generated from ANN model showed better results in comparison to the other models and the hysteresis phenomenon could be also simulated (Shiri and Kisi 2011). The conjunction of ANN with different approaches to make the predictions more precise to the measured value have also been done in the last decade. Geomorphology-based ANN (GANN) was modeled by Zhang and Govindaraju (2003), using morphological parameters to estimate the flow path probabilities for the prediction of runoff in a watershed. To estimate the flow path probabilities, a geomorphologic instantaneous unit hydrograph (GIUH) was applied. This graph could be developed through the engaged morphological parameters. To assign the synaptic, i.e., connection weights the path probabilities were applied to the hidden and the output layer. Hence, the application of other models along with the ANN showed that GANN performed more rationally and realistically. Soft computing tools were also used with the ANN to get more accuracy. According to Baskar et al. (2003), FFNN-BP performed better with five hidden layers with the use of GIS tools and ANN. Sarangi and Bhattacharya (2005) generated an ANN and a regression model using watershed-scale geomorphologic parameters for predicting sediment loss. While using the geomorphological based ANN, they found that the (coefficient of determination) R² values lying between 0.78 and 0.93 and efficiency factor (E) values in between 0.71 and 0.76, on the other hand, utilizing geomorphological based regression the R² numbers of 0.39–0.54 and E values of 0.53–0.46, and hence, it is concluded that ANN model was better concerning performance compared to regression models. Gharde et al. (2015) performed sediment yield modeling using the ANN model. The comparison of the performance of ANN with linear regression is done and they discovered that ANN concludes better accuracy compared to linear regression. Adib and Mahmoodi (2017), in his work, tried to predict ANN genetic algorithm (GA) and Markov chain hybrid model at flood conditions. Using GA, the various ANN parameters are optimized. The researchers found that the normalized mean square error (NMSE) can be deducted by GA to 80%, but it does not significantly increase R. The water discharge (Q) and the suspended sediment concentration (SSC) were taken and their relationship was modeled by Khan et al. (2019b), in Ramganga river using ANN for SSC calculation. They concluded that ANN algorithm is efficient to model the relation between Q and SSC of a river. Moeeni and Bonakdari (2018) for the first time applied autoregressive moving average with exogenous terms (ARMAX) in conjunction to ANN for sediment load prediction. The ARMAX-ANN conjunction model achieved better outcomes than each ANN and ARMAX model (Choubin et al. 2017).

The physics of ANN changes with its training data and as it is all carried through hidden layer hence is not known to the user. The definition of an optimal network architecture of ANN and the knowledge of the internal system conditions are rigid as the user is not aware of the working of the hidden layer and no defined physical principles are available due to non-linearity of the input data. Hence, researchers faced difficulty in determining the appropriate ANN structure; therefore, they used the trial-and-error methodology to find the unit quantity of neurons working in the hidden layers. These analyses were broad and an expansive number of trials must be done to get the correct number of units. Due to its time-consuming property with similar operations application the trial-and-error approach resulted in the need for the development of some new methodology. The hydrodynamics could be integrated into the ANN models, so that the disadvantages arose due to the trial-and-error approach could be avoided and the problem of selecting an optimum ANN structure could be solved.

ANN overview

ANN is not a new approach as its development began nearly in the 1940s by McCulloch and Pitts (1943), to imitate a brain’s way of functioning. It could be said that an ANN is a parallel-distributed information processing system. The information could be any raw data or a trained data. Its performance characteristic resembles the neural network formation inside the human brain.

Working of an ANN could be given in the following points:

• 1. The information is processed, at many single nodes, or elements or units known as neurons.

• 2. Connection links are established between nodes, and through them, signals are passed.

• 3. These connection links have weights assigned to them.

• 4. Non-linear transformations are implemented by the nodes to the aggregate input to get the aggregate yield (Jalalkamali et al., 2011).

A neural system is portrayed by its design that tends to the example of the links between the elements or neurons, its procedure for picking activation function, and the affiliated weights (Fausett 1994). Neural networks could be categorized based on layers: single, two-layer, and multi-layer, as well as on the basis of data flow. In multi-layer, the information flows from one layer to other layers, i.e., input for next layer are obtained from previous layer output and weights assigned to the connecting links, there is no relation between nodes in the same layer; whereas in recurrent ANN, the information runs in both ways from the input to the output as well as from output to the input side using the node (Bhattacharya et al. 2007; Ajmera and Goyal 2012; Barua et al. 2010).

The non-linear processes are mapped due to the use of SF in the network. SF is a non-decreasing, monotonic function. The simplicity of this function is obvious due to its derivative result; hence, it is easy to use during the testing procedure of ANN. The network of these above-defined nodes forms an ANN.

Training algorithms of ANN

The BP

At Harvard University, an algorithm was proposed by Werbos (1974) in his PhD thesis known as BP algorithm. However, it was popularized when Rumelhart et al. (1988) trained the hidden layer neurons for a complex non-linear mapping problem. To train the ANNs, BP is the most popular algorithm which was used by many researchers.

BP is an algorithm which minimizes the error function. There are two passes in this algorithm, viz., forward pass and backward pass. It comes in the category of gradient descent technique. Here, the initial step is the forward pass where the accessible diverse set of input patterns is given to the input layer and its output is passed forward through the neural network to the hidden layer or output layer. Hence, the outcome acquired from the output layer is compared with the target output in focus and error between both these outputs is calculated (Govindaraju 2000). Now in the second step, i.e., backward pass; this error propagated back to the network, passing through every node and the weighted connections are updated accordingly as per the given equation:

$$ \Delta w_{pq} (m) = - \eta^{\ell } \frac{\partial E}{{\partial w_{ij} }} + \kappa^{\ell } \Delta w_{pq} (m - 1), $$

(2)

where $\Delta w_{pq} (m)$ as well as $\Delta w_{pq} (m - 1)$ is the accretion in the weights between the nodes $i$ and $j$ in $m^{th}$ and $(m - 1)^{th}$ pass.

$\eta^{\ell }$ and $\kappa^{\ell }$ are learning rate as well as momentum, respectively.

A learning rate helps in reducing the likelihood of being caught in the local minima for the training procedure, and the momentum factor can accelerate the training procedure (Sahoo and Ray 2006; Freiwan and Cigizoglu 2005; Agarwal et al. 2009).

Even after the use of the learning rate the training process could be caught in local minima. The calculation to obtain minimum error is a slow training procedure as the solution traverses a zigzag path. Hence, a need for another training algorithm arose which could alleviate these factors.

The RBF

In the application of neural networks, Broomhead and Lowe (1988) introduced a new function called RBF that could be used for training then after some years, Leonard et al. (1992) introduced a new training method to train the ANN utilizing RBF instead of the sigmoid function. As in the nervous system, some neurons how the characteristic of locally tuned response bounded to small range input space. RBF’s working principle is also derived from the same concept.

This RBF neural network architecture is the same as normally used three-layer network models. In this model, a hidden layer is present and performing non-linear transformations without adjusting parameters. This hidden layer contains a parameter vector called ‘centre’. This center could be calculated in many ways, one of the simplest ways is to pick it randomly from the available training samples, or it could be determined through the k-means clustering method, i.e., selecting the center of the different group’s as the center or it could be adjusted through error correction training by considering it as a network parameter. For every node exist in the hidden layer, the Euclidean separation amongst center and the input vector is estimated and this Euclidean distance is changed via a non-linear function which decides the yield of concealed layer hubs, which are inputs to the output layer. At the output layer, these inputs are combined linearly to determine the ANN output for the ANN. Of an RBF-ANN, the output z could be calculated using the equation:

$$ z = f(v) = \sum\limits_{i = 1}^{n} {w_{i} R_{i} (x) + w_{0} } . $$

(3)

In Eq. (3) $w_{i}$ = weights assigned to the connections between neurons of the hidden layer and the output layer, $x$ = the input vector, $w_{0}$ = bias

$R_{i} :R^{n} \Rightarrow R$ is an RBF which could be given as:

$$ R_{i} (x) = \varphi \left\| {\left. {x - \varsigma_{i} } \right\|} \right.. $$

As it could be seen that the function $\varphi (.)$ will have the highest value at origin and decrease very quickly as its parameter goes to infinity, and it is also a requirement that $\varphi (.)$ should approach zero. Generally, the class of RBF is narrated by Gaussian function given as:

$$ R_{i} = - \exp \left( { - \sum\limits_{i = 1}^{n} {\frac{{\left\| {\left. {x - \varsigma_{i} } \right\|} \right.^{2} }}{{2\sigma_{ij}^{2} }}} } \right), $$

(5)

where $\varsigma_{i}^{T} = \left[ {\varsigma_{{i_{1} }} ,\varsigma_{{i_{2} }} ,...,\varsigma_{{i_{n} }} } \right]$ vector denotes the midpoint of the hidden layer, $\sigma_{ij}$ denotes the width needed for Gaussian function.

The main difference between BP and RBF is the function used to tackle the associated nonlinearity in the available problem. In error propagation, the fixed-function sigmoid is used to implement the non-linearity, whereas the RBF uses the training dataset to implement the non-linearity, where it tries to find all hidden layer basis functions by itself and then in linear fashion summing all of them at output layer to give output.

Other algorithms are also available such as the cascade correlation algorithm. However, due to the unavailability of their application to predict SSL, they are not discussed here.

Advantages of ANN

• 1. Ability to learn by themselves and produce the outputs that are not limited to the provided input.

• 2. Fault tolerance.

Disadvantages of ANN

• 1. Unexplained network behavior

• 2. Determination of appropriate network structure (Mijwel 2018).

The GRNN

GRNN is an ANN algorithm in which there is no requirement of the iterative training procedure and there is no problem of local minima as encountered in feedforward backpropagation (FFBP) (Yin et al. 2016). The physically implausible estimates are mainly not generated by GRNN. To model rainfall-runoff, Cigizoglu et al. (2004) used three neural networks out of which one was GRNN. To forecast and estimate the intermittent flow, Cigizoglu et al. (2004) applied the GRNN again to model river sediment yield. They applied the GRNN and compared its performance with MLR as well as SRC and showed that GRNN performance is the best among the three. Adnan et al. (2019) applied a novel dynamic evolving neural-fuzzy inference system (DENFIS) and proved its applicability in SSL prediction.

The model

Specht (1990) proposed a general regression neural system which does not need any iterative preparing method as in the BP model. In this model, an arbitrary function is approximated amid the input vectors and output vectors and is specifically evaluated from the training information. There is leverage appeared by GRNN that the error in estimation approaches to zero with the expansion in training set size by incorporating some mild limitations on the function. GRNN indicates predictable behavior and is fundamentally utilized in estimation issues of continuous variables as ordinarily standard regression strategies are utilized. GRNN follows the standard statistical methods. These methods are normally called kernel regression methods. Given a preparation set and the independent value $i$, it assesses the estimation of dependent variable $p$ which is most likely and diminishes the mean squared error. The GRNN calculates the joint probability density function of $i$ and $p$ for a given training set.

The regression of $p$ on $I$ could be expressed as

$$ E[p|I] = \frac{{\int\limits_{ - \infty }^{\infty } {yf\left( {I,p} \right)dp} }}{{\int\limits_{ - \infty }^{\infty } {f\left( {I,p} \right)dp} }}, $$

(6)

where $f(I,p)$ denotes the known joint pdf of vector $I$ and $p$;$I$ denotes the vector random variable; and $p$ denotes the sample random variable.

In case, when density function $f\left( {I,p} \right)$ is not known, then through the observations samples of $i$ and $o$, is estimated. A probability estimator $\hat{f}\left( {I,p} \right)$ could be computed based on sample values of $i$ and $p$ denoted by $I^{x}$ and $P^{x}$, respectively. It could be given as:

$$ \begin{gathered} \hat{f}\left( {I,p} \right) = \frac{1}{{(2\pi )^{{{\raise0.7ex\hbox{${(q + 1)}$} \!\mathord{\left/ {\vphantom {{(q + 1)} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \sigma^{(q + 1)} }}\frac{1}{N} \times \sum\limits_{i = 1}^{n} {\exp \left[ { - \frac{{(I - I^{i} )^{T} (I - I^{x} )}}{{2\sigma^{2} }}} \right]\exp \left[ { - \frac{{(P - P^{x} )^{2} }}{{2\sigma^{2} }}} \right]} \hfill \\ \sum\limits_{i = 1}^{n} {\exp \left[ { - \frac{{(I - I^{i} )^{T} (I - I^{x} )}}{{2\sigma^{2} }}} \right]\exp \left[ { - \frac{{(P - P^{x} )^{2} }}{{2\sigma^{2} }}} \right]} . \hfill \\ \end{gathered} $$

(7)

In (16) $q$ represents the dimension of the random vector variable $i$;

$N$ represents the number of inspections for samples.

Each sample $I^{x}$ and $P^{x}$ have the sample probability of width $\sigma$ which is assigned by the probability estimator $\hat{f}\left( {I,p} \right)$. The estimate for probability could be calculated as the aggregate of these probabilities (Specht 1990).

A scalar function ${\rm Z}_{i}^{2}$ could be written as:

$$ {\rm Z}_{i}^{2} = (I - I^{x} )^{T} (I - I^{x} ). $$

(8)

Hence, substituting the values of ${\rm Z}_{i}^{2}$ and performing the given integration, it yields the following expression:

$$ \hat{P}\left( X \right) = \frac{{\sum\nolimits_{i = 1}^{n} {P^{i} \exp \left( { - \frac{{{\rm Z}_{i}^{2} }}{{2\sigma^{2} }}} \right)} }}{{\sum\nolimits_{i = 1}^{n} {\exp \left( { - \frac{{{\rm Z}_{i}^{2} }}{{2\sigma^{2} }}} \right)} }}. $$

(9)

This equation could directly be applied to the available arithmetic data. The initial layer of GRNN is the input layer where input quantities present. However, in the next layer, the pattern units or neuron elements are present which pass its outputs to the additional units in the summation layer. This summation layer is the third layer. The outputs of the summation layer are passed to the final layer, i.e., output layer. Here, output units calculate the final output for the GRNN (Kisi 2008).

Advantages of GRNN

• 1. Ability to handle noisy datasets.

• 2. Single-pass learning, no backpropagation required.

Disadvantages of GRNN

• 1. Big size.

• 2. Computationally complex (Mareček 2016).

Wavelet transform

The conjunction of wavelet analysis with the soft computing techniques had seen a rise in its use in the last decade. Numbers of studies were carried out by applying wavelet analysis and ANN in environmental engineering problems. The wavelet transform was developed nearly in the 1980s, but its utilization spread in recent years. To deal with non-linear data, the existing conventional approaches were not as good as for linear data, and hence, the need for the conjunction of wavelet analysis with the traditional models arose. To predict droughts, Kim and Valdés (2003) introduced a wavelet ANN (WANN). Similarly, the conjunction of wavelet analysis with ANN in some other studies was studied by Tantanee et al. (2005) and Cannas et al. (2005) to predict annual rainfall and monthly rainfall–runoff, respectively in Italy. WANN models and ANN models were also compared in different studies based on their performance in prediction. In the estimation of monthly streamflow, the two models WANN and ANN were compared by Cigizoglu and Kisi (2006) and concluded that WANN over performs the ANN. The ANN model performance was checked and evaluated with pre-processed data and without pre-processed data by continuous and discrete wavelet transforms again by Cannas et al. (2006), and it was concluded that ANNs with pre-processed data performed much more efficient way than the raw data. To estimate the SSL in waterways, Partal and Cigizoglu (2008) proposed a model with the conjunction of wavelets and neural networks. The un-decomposed raw data were measured and decomposed into wavelet components through the use of discrete wavelet transform (DWT), now on these wavelets components sum is performed selectively to result in a wavelet series. This wavelet series acted as an input vector for the ANN. It was shown that WANN predictions conveyed much more accurate results in comparison to traditionally used models, i.e., ANN and SRC. A model with the conjunction of wavelet and ANN was proposed by Nourani et al. (2009) to estimate the precipitation for 1 month ahead in Lingvanchai watershed situated in Tabriz, Iran. In this study, first, primary rainfall time-series was taken and the time-series was decomposed through the utilization of the wavelet analysis. After decomposition, the time-series for primary rainfall was converted into several multi-frequency time-series and this multi-frequency time-series was taken as the input vector to the ANN model. It was shown that the prediction of precipitation events may be for long term or short term can be done successfully because of the usage of several multi-frequency time-series as an input vector. Wavelet analysis was also combined with approaches like neuro-fuzzy (NF) and it was portrayed that it performed significantly better than the conventional approach, i.e., NF model. Rajaee (2010) predicted the daily SSL at a hydrological station of gauging located in the United States by applying a model in which wavelet conjunction with NF model was taken and known as Wavelet NF (WNF) model, in which the daily river discharge and time-series generated through suspended sediment was decomposed into numbers of time-series through the DWT function at different scales. Again, it was shown that WNF outperformed NF (Adamowski 2008; Rajaee 2011) combined wavelet with NF and found that WNF is an effective approach for river SSL prediction. Li and Cheng (2014) suggested a hybrid model which is the conjunction of ELM and WANN. They discovered that ELM gives better performance compared to SVM and the proposed WANN-ELM gives a more precise prediction compared to ELM and SVM.

A wavelet could be defined as a function in a mathematical form which is used to decompose the given continuous-time signal function into several scale components different to each other where for every single scale component, a frequency range could be assigned. Each scale component will have different frequency range implying corresponding different resolutions; hence, each component could be studied with corresponding different resolutions. An oscillating waveform which is fast decaying and is of finite length known as mother wavelet. The mother wavelet is translated into multiple copies or scaled into different wavelets which are called daughter wavelets, and when a function is represented by wavelets, this is known as wavelet transform process. In the representation of functions that have discontinuities in their form and sharp peaks, the wavelet transforms show advantages over the traditionally used Fourier Transforms in the case of suspended sediment load prediction and reconstruction or deconstruction of the varying signals, non-periodic, or of discrete nature. There are two types of wavelet transforms such as discrete wavelet transform (DWT) and continuous wavelet transform (CWT).

The CWT

It is a tool or an analytical formula used for dividing continuous-time signal or continuous-time function into daughter wavelets. Several wavelets can be reconstructed using the mother wavelet (MW). Let us consider $\chi (x)$ be the MW function which wavelet function can be obtained by the temporal translation $\tau$ and with dilation,$d.$ The CWT of a continuous-time signal $x(s)$ may be expressed as (Ateeq- Ur-Rahman et al. 2018; Antoine 1998):

$$ C(a,\tau ) = \;\frac{1}{\sqrt a }\int\limits_{ - \infty }^{\infty } {x(s)\chi^{*} \left( {\frac{s - \tau }{a}} \right)ds,\;\;\;\;a > 0} . $$

(10)

Here, * denotes the complex conjugate of $\chi (x)$ and $\chi (x)$ is the mother wavelet function. CWT seeks for correlation between the signal and wavelet.

To be classified as wavelet three criteria may be fulfilled by $\chi (x)$. They are:

• 1. $E = \;\int_{ - \infty }^{\infty } {\left| {\chi (s)} \right|^{2} ds < \infty } ,$

where “| |” indicates the modulus operator that gives the magnitude of $\chi (x)$. If $\hat{\chi }(f)$ indicates the Fourier transform of $\chi (f)$, then the following condition must satisfy

• 2. $T_{\psi } = \;\int_{ - \infty }^{\infty } {\frac{{\left| {\chi (f)} \right|^{2} }}{f}df < \infty } .$

$T_{\psi }$ is the admissibility constant. The value of $T_{\psi }$ depends on the chosen wavelet. To reconstruct the signal, the inverse CWT can be applied for the signal reconstruction as (Addison 2018; Zhang et al. 2020):

$$ x(s) = \frac{1}{{T{}_{\psi }}}\int_{ - \infty }^{\infty } {\int_{0}^{\infty } {C(a,\tau )\chi_{a,b} (s)\frac{da.d\tau }{{a \times a}}} } , $$

(11)

where $\tilde{\phi }(t)$ represents the dual function for $\varphi (t)$.

The DWT

In practical applications, the discrete-time signal is taken into account due to unavailability of the continuous-time signal. Here, the continuous-time signal is discretized with the use of the trapezoidal rule as mentioned above. If the data set of length is taken, then the DWT will produce coefficients. As the coefficients produced are square of the length of the taken dataset, it means that there is some redundant information present in the coefficients. Now, based on the problem, this redundant information could be utilized or may not be utilized. It is good to have redundant information, but sometimes it provides extra complexity. Occasionally, logarithmic uniform spacing (LUS) is used to tackle this redundant information problem. In this LUS, the resolution of $\beta$ considered is coarser as compared to $\alpha$ scale discretization which results in $N$ coefficients for length $N.$ The DWT could be represented as:

$$ \varphi_{r,s} (t) = \frac{1}{{\sqrt {\alpha_{0}^{r} } }}\varphi \left( {\frac{{t - n\beta_{0} a_{0}^{r} }}{{\alpha_{0}^{p} }}} \right), $$

(12)

where $r$ is an integer used to control the dilation in the wavelet, $s$ is an integer used to control the translation in the wavelet, $\beta_{0}$ denotes the location parameter which takes its value always greater than 0

$\alpha_{0}$ denotes a step finely dilated taking its value always greater than 1

Mainly, the values are taken in practice for $\alpha_{0}$ and $\beta_{0}$ are 2 and 1 , respectively. For both the steps i.e., dilation and translation, if we take the power of two logarithmic scales, then it could be represented as:

$$ \varphi_{r,s} (t) = 2^{{ - {\raise0.7ex\hbox{$r$} \!\mathord{\left/ {\vphantom {r 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \varphi \left( {2^{ - r} t - s} \right). $$

(13)

This is normally known as the ‘dyadic grid’ arrangement. Here, the above-mentioned equation for dyadic grid wavelet is taken in a compact form. Generally, the discrete dyadic wavelets are orthonormal to each other. There is no redundancy present in the signal which is regenerated from the wavelet transformed signal as the information stored in all the wavelet coefficients is not repeated. For a discrete-time-series,$\omega_{i}$, the articulation for the dyadic wavelet change could be given as:

$$ X(r,s) = 2^{{ - {\raise0.7ex\hbox{$m$} \!\mathord{\left/ {\vphantom {m 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \sum\limits_{i = 0}^{N - 1} {\psi (2^{ - m} i - s)\omega_{i} } . $$

(14)

For the wavelet of discrete scale $\alpha = 2^{r}$, here,$X(r,s)$ represents the wavelet coefficient. In Eq. (14), $x_{i}$ represents a finite time-series where $i = 0,\;1,\;2,\;....,\;n - 1$ and $n$ represents an integer power of 2, where $n = 2^{m}$. Hence, this displays the range for the variables $r$ and $s$ as $\beta_{0}$ and $1 < r < M$, respectively. It is enough and sufficient to use one wavelet to cover the time interval, and when the wavelet scale which is largest (i.e.,$2^{r}$ where $r = m$) and creation of only one coefficient is needed. Hence, the same condition is applicable $r = 1$. At $r = 1$_,$\alpha$ could take the value as $2^{1}$, this infers that to convey the signal creation, $2^{M - 1}$ or ${\raise0.7ex\hbox{$n$} \!\mathord{\left/ {\vphantom {n 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}$ coefficients will occur at the same scale. It implies that if a discrete-time-series for above function having its length $n = 2^{m} `$ is taken, and then, the summation of wavelet coefficients is given by $1 + 2 + 4 + 8 + ... + 2^{m - 1} = n - 1$.

A component $\overline{X}$ remains the known smoothed component of the signal, which could be denoted by the mean of the signal. Hence, a time-series having its length $r = m$ is taken and is decomposed into $r = m$ components having no redundant information present in them.

The inverse discrete wavelet transform could be formulated as:

$$ \omega_{i} = \overline{X} + \sum\limits_{r = 1}^{M} {\sum\limits_{s = 0}^{{2^{M - p} - 1}} {X_{r,s} 2^{{{\raise0.7ex\hbox{${ - r}$} \!\mathord{\left/ {\vphantom {{ - r} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \psi \left( {2^{ - m} i - s} \right)} } . $$

(15)

Or simply, it could be formulated as:

$$ \omega_{i} = \overline{X} \left( t \right) + \sum\limits_{r = 1}^{M} {W_{m} \left( t \right)} , $$

(16)

where $\overline{X} \left( t \right)$ represents the approximate value of a sub-signal at any level $m$.

$W_{m} \left( t \right)$ denotes the coefficients for wavelet where $m = 1,2,...,M$.

These wavelet coefficients offer the details for sub-signals. Now, with these sub-signal details have the property to capture the small or it can be said that fine features in the values of data interpreted.

Here,$\overline{X} \left( t \right)$ is a residual term providing the information of the background for the available data. Due to the easiness quality of the $W_{1} \left( t \right),W_{2} \left( t \right),....,\;W_{m} \left( t \right)$,$\overline{X} \left( t \right)$, the number of properties can be easily considered using these components.

Advantages of WT

• 1. Shows simultaneous localization in time and frequency domain.

• 2. Fast computation while using fast WT.

Disadvantages of WT

• 1. Shift sensitivity.

• 2. Lack of phase information (Fernandes et al. 2003).

The NF

Neural networks perform excellently in recognizing patterns, but could not convey how these neural networks are reaching their decision. On the other hand, systems with the application of fuzzy logic efficiently explain the decisions taken by them, but do not have the property to automatically gain the rules to reach the decisions. Then, there are complex problems where there could be the presence of reasoning task as well as processing task which could be accomplished with fuzzy logic and neural network respectively. Therefore, it is better to use the hybrid model which could reason as well as the process in one single model, so that the complex problem could be solved with less effort. Hence, the need fora hybrid model such as NF approach has flourished which has the advantage of both the neural networks for processing as well as the fuzzy logic for decision-making and conveying.

There are numerous investigations performed to develop artificial intelligence techniques to simulate the problems available with inadequate physical knowledge of the systems. During the last decade, the use of fuzzy logic gained growth in the application of simulation problems like environmental uncertainties, river engineering, etc. As it is already mentioned, the application of ANN models in these non-linear problems shows its success widely. Still, we could not always rely only on one model; there is always a need for a different model about the chances of more accurate results. Hence, fuzzy logic (FL) is used to combine with these neural network learning algorithms in different estimation problems. This application of neural network learning algorithms on fuzzy modeling is normally known as NF modeling (Brown and Harris 1994). This model was implemented in many problems belonging to different areas like environmental engineering, financial trading, medical diagnosis, etc. Ocampo et al. (2007) applied a fuzzy model to model the ecological status in surface waters. Studies had been conducted to employ the neural network models with FL to arrive at a single hybrid model to evaluate the estimation of the SSLs. The fuzzy inference system (FIS) model is also applied in modeling the suspended sediments. The forecast of SSL was done by Tayfur et al. (2003) with the use of FL on slope data and rainfall intensity from exposed soil surfaces. They concluded that the fuzzy approach provides better results over different slopes with various rainfall intensities and performed better for steep slopes. Lohani et al. (2007) compared the rating curve method with FIS for the performance in the simulation of a relationship for stage-discharge sediment concentration. The simulation was performed in a couple of gauging stations in a river called the Narmada in India. As expected, outcomes concluded that fuzzy method over performs the rating curve method. The accuracy in the estimation of monthly suspended sediments using different models was studied by Cigizoglu and Kisi (2006). The study was done in Salur, Koprusu, and Kuylus stations in Turkey. They compared ANN and SRC models with ANFIS for accuracy in estimation of suspended sediments, and the results exposed that NF System outperforms the other two models in estimation. Rajaee et al. (2009) compared MLR, ANN, NF, and SRC models for estimating the daily SSC. The examination was carried out in two hydrometer stations in USA. The data for sediment concentration and daily river discharge belonging to both stations had been implemented to train the models. The outputs showed that the NF model outperforms the other three models in predicting daily SSL.

Model

To model the fuzzy neural network in its computational process basically, these three steps are followed:

• 1. The fuzzy neural model is developed based on the working process of biological neurons.

• 2. The synaptic connections or the connection between neurons in each layer are modeled with fuzziness.

• 3. The adjustment of synaptic weights pertaining to the development of the needed learning algorithm.

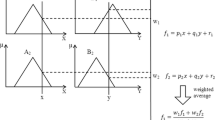
There are two models which could be considered for NF modeling. In the first one, the fuzzy interface responds to the linguistic statements given and as output provides a quantity having direction as well as the magnitude to the multi-layer neural network, as shown in Fig. 1. Then this neural network (NN) tries to adapt itself to achieve the desired results through a learning algorithm. In the second model, first, the NN tune the membership functions which are used by the fuzzy system in the decision-making process, as shown in Fig. 2. The FL itself tune the membership functions directly using the required rules with linguistic statements, but it is computationally expensive. Hence, the performance could be improved with the use of neural network learning algorithms which would automate the tuning process.

Fig. 1

The initial model of the fuzzy neural system (Fuller and Fullér 2000)

Fig. 2

The second model of the fuzzy neural system (Fuller and Fullér 2000)

In the above two figures.

FLI = fuzzy logic interface, NN = neural network, NI = neural input, NO/P = neural output, K based = knowledge-based, LA = learning algorithm, LS = linguistic statements.

The ANFIS and FL

Here, the model for adaptation of the second model (Fig. 2) is taken in a detailed manner which is also known by the name of ANFIS. This algorithm is an extraordinary instance of the second kind of modeling for NF-based models which were presented by Jang and Sun (1995). ANFIS follows the Sugeno-type fuzzy (SF) models. In this model, the reasoning mechanism attempts to determine the resultant function $f$ for the provided input vector [i, j].

Here, an FIS having two inputs $i$_,$j$ and $f$ as respective output is considered. In the initial order of the SF model, the knowledge used in the model has a form of if–then rules of FL, which can be shown as:

$$ {\text{Regulation }}1:{\text{If is }}X1{\text{ and }}j{\text{ is }}Y1,{\text{ then}}\,f_{1} = l_{1} i\; + m_{1} j\; + \;r_{1} $$

(17)

$$ {\text{Regulation }}2:{\text{If}}\,{\text{is }}X2\,{\text{and }}j{\text{ is }}Y2,{\text{ then}}\,f_{1} = l_{2} i\; + m_{2} j\; + \;r_{2} . $$

(18)

In (17) and (18),$X_{1}$,$X_{2}$ and $Y_{1\;} ,\;Y_{2}$ are the membership functions for inputs $i$ and $j,$ respectively;$l_{1} ,\;m_{1} ,n_{1}$ as well as $l_{2\;} ,\;m_{2} ,n_{2}$ are the parameters of the resultant function (Firatand Gungor 2008).

The ANFIS functions are given as:

Layer I: In this node, outputs are defined hence the output $OP_{x}^{l}$ could be given as

$$ OP_{x}^{l} \; = \;\mu_{{U_{x} }} (i)\;{\text{for}}\,x = 1,2\;{\text{or}} $$

(19)

$$ OP_{x}^{l} \; = \;\mu_{{V_{x} - 2}} (j)\;{\text{for}}\,x = 3,4, $$

(20)

where $i$ or $j$ are the input nodes.$U_{x}$ or $(V_{x} - 2)$ are the language statements or labels (high or low) which are associated with the given node. These labels to the node are characterized as the membership functions from which it is true for any continuous and piecewise differential function, viz., triangular-shaped functions, Gaussian functions, generalized bell-shaped or normal distribution function, and trapezoidal-shape. Generally, the membership functions are given by normal distributed or bell-shaped functions for A and B. The output $OP_{i}^{l}$, at the node, could be calculated as:

$$ {\rm O}{\rm P}_{x}^{1} = \mu_{{U_{x} }} (i)\; = \frac{1}{{1 + \;(i - \;{\raise0.7ex\hbox{${c_{x} }$} \!\mathord{\left/ {\vphantom {{c_{x} } {a_{x} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${a_{x} }$}})^{{2b_{x} }} }}. $$

(21)

In (21), $a_{x} ,b_{x} ,c_{x}$ is the set of parameters.

Layer II: Here, the incoming signal is multiplied at each node:

$$ {\rm OP}_{x}^{2} = \mu_{{U_{x} }} (i)\mu_{{V_{x} }} (j),\;\;\;\;x = 1,\;2. $$

(22)

Layer III: Here, the normalized firing strength is computed for the $i^{th}$ node which could be expressed as:

$$ {\rm OP}_{x}^{3} = \overline{w}_{x} \; = \;\frac{{w_{x} }}{{w_{1} + \;w_{2} }}. $$

(23)

Layer IV: Here, for every node I, the benefaction of $x^{th}$ rule is computed toward the output of the model:

$$ {\rm OP}_{x}^{4} = \sum\limits_{i} {\overline{w}_{x} f_{x} } = \overline{w}_{l} (p_{x} i\; + \;q_{x} j\; + r_{x} ). $$

(24)

In this equation,$\overline{w}_{l}$ is known as the output of layer III as well as $\{ p_{x} ,q_{x} ,r_{x} \}$ is the collection of parameters.

Layer V: There is only 1 node present in the layer which computes the total outcome of the ANFIS model (Jang and Sun 1995; Nayak et al. 2004; Aqil et al. 2007) which could be shown as

$$ {\rm OP}_{x}^{5} = \sum\limits_{x} {\overline{w}_{x} f_{x} } = \frac{{\sum\nolimits_{x} {w_{x} } f_{x} }}{{\sum\nolimits_{x} {w_{x} } }}. $$

(25)

The learning algorithm used in the model is a hybrid algorithm in which two approaches, such as gradient descent and least squares, are encompassed and combined. This model takes a premise and consequent optimization parameter. In the first phase, the consequent parameter is established through node outputs in forwarding pass till the layer IV by the use of the least square approach. In the second phase, the errors are propagated backwards in the backward pass, and hence, through the use of gradient descent, the basic parameters are established accordingly (Jang and Sun 1995; Aqil et al. 2007; Zounemat-Kermani and Teshnehlab 2008).

Advantages of ANFIS

• 1. Compared to ANN, more transparent to the user.

• 2. Causes low memorization errors.

Disadvantages of ANFIS

• 1. Curse of dimensionality.

• 2. High computational cost.

The SVM

In recent times, an advanced approach in regards to computerized reasoning, known as SVM, has numerous implementations in learning strategy machines. This technique effectively has been utilized as a part of data arrangement and lately in regression issues. Cortes and Vapnik (1995) introduced SVM for problems related to binary classifications, and later, it has been applied in regression problems. Most of the studies on SVM tried to optimize the dual optimization problem, and it is very effective on both linear and non-linear datasets. Few SVMs show great results even if the data size is very large. This model was utilized for water management initially by Sivapragasam et al. (2001), Dibike and Solomatine (2001), and Zhao et al. (2002), and the novel model is known as SVM (Cristianini and Shawe-Taylor 2000; Chapelle 2007; Fung and Mangasarian 2003).

The SVR

SVR is also known as SVM for regression which is a regression method based on the support vectors, introduced by Vladimir Vapnik and his team in AT&T labs (Drucker et al. 1997). Mainly, SVR tries to minimize the generalization error using the SRM principle.

Suppose, the calibrating data $\left\{ {\left( {i_{1} ,j_{1} } \right),......\left( {i_{l} ,j_{l} } \right)} \right\} \subset \lambda \times \Re ,$ where $\lambda$ denotes the input patterns count. The goal here lies in seeking a function $f\left( i \right)$ which has the highest $\varepsilon$ deviation. This model is also known as $\varepsilon$-support vector regression:

$$ f(i) = \left\langle {w,i} \right\rangle + z\,{\text{where}}\,w \in \lambda ,\;z \in \Re . $$

(26)

The primal problem of SVR may be stated as:

$$ \begin{gathered} \min \frac{1}{2}\left\| {\left. w \right\|} \right.^{2} \hfill \\ {\text{subject}}\;{\text{to}}\;\left\{ \begin{gathered} o_{l} - \left\langle {w,i_{x} } \right\rangle - z \le \in \hfill \\ \left\langle {w,i_{x} } \right\rangle + z - o_{x} \le \in \hfill \\ \end{gathered} \right.. \hfill \\ \end{gathered} $$

(27)

Sometimes errors are allowed, and therefore, slack variables $\xi$ and $\xi^{ * }$ are introduced:

$$ \begin{gathered} \min \frac{1}{2}\left\| {\left. w \right\|} \right.^{2} + z\sum\limits_{x = 1}^{l} {(\xi_{x} + \xi_{x}^{ * } )} \hfill \\ {\text{subject}}\;{\text{to}}\;\left\{ \begin{gathered} o_{x} - \left\langle {w,i_{x} } \right\rangle - z \le \in + \xi_{x} \hfill \\ \left\langle {w,i_{x} } \right\rangle + z - o_{x} \le \in + \xi_{x}^{ * } . \hfill \\ \xi_{x} ,\xi_{x}^{ * } \ge 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(28)

The constant $z > 0$ determines the flatness trade-off between $f$ and the maximum toleration of $\varepsilon$. This deals with $\left| \xi \right|_{ \in }$ is known as $\varepsilon$- insensitive loss function (Noori et al. 2015):

$$ \left| \xi \right|_{ \in } = \left\{ {\begin{array}{*{20}c} 0 & {if\left| \xi \right|\; \le \in } \\ {\left| \xi \right| - \; \in } & {{\text{otherwise}}} \\ \end{array} } \right.. $$

(29)

In practice, generally, the dual problem is solved rather than the primal problem. The dual formation can be inscribed as:

$$ L_{m} = \frac{1}{2}\left\| {\left. w \right\|} \right.^{2} + z\sum\limits_{x = 1}^{l} {(\xi_{x} + \xi_{x}^{ * } )} - \sum\limits_{x = 1}^{l} {(\eta_{x} \xi_{x} + \eta_{x}^{ * } \xi_{x}^{ * } )} - \sum\limits_{x = 1}^{l} {d_{x} ( \in + \xi_{i} - o_{x} + \left\langle {w,i_{x} } \right\rangle + z)} - \sum\limits_{x = 1}^{l} {d_{x}^{ * } ( \in + \xi_{x} - o_{x} + \left\langle {w,i_{x} } \right\rangle + z)} $$

(30)

subject to,$d_{x}^{\left( * \right)} ,\eta_{x}^{ * } \;\; \ge \;0$

Partially deriving with reference to the Lagrangian variables $\left( {w,z,\xi_{x} ,\xi_{x}^{*} } \right)$ and substituting them in (39) give the dual optimization problem:

$$ \begin{gathered} \max imize\;\left\{ \begin{gathered} - \frac{1}{2}\sum\limits_{x = 1}^{l} {\left( {d_{x} - d_{x}^{*} } \right)} \left( {d_{y} - d_{y}^{*} } \right)\left\langle {i_{x} ,i_{y} } \right\rangle \hfill \\ - \in \sum\limits_{x = 1}^{l} {\left( {d_{x} + d_{x}^{*} } \right)} + \sum\limits_{i = 1}^{l} {o_{x} \left( {d_{x} - d_{x}^{*} } \right)} \hfill \\ \end{gathered} \right. \hfill \\ subject\;to\;\sum\limits_{x = 1}^{l} {\left( {d_{x} - d_{x}^{*} } \right)} = 0\;\;and\;\;0 \le d_{x} ,d_{x}^{*} \le C. \hfill \\ \end{gathered} $$

(31)

Implementing the non-linear function using a kernel which is:

$$ k(i_{x} ,i_{x}^{ * } )\; = \;\phi (i_{x} )^{t} \phi (i_{x}^{*} ), $$

(32)

where $k(...)$ is a kernel function (Smolaand Schölkopf 2004). For any input space $\chi \in \Re$, its prediction is shown as:

$$ f(i) = \sum\limits_{x = 1}^{l} {\left( {d_{x} - d_{x}^{*} } \right)} \;k(x_{i} ,x_{i}^{ * } )\; + \;z. $$

(33)

Advantages of SVM/SVR

• 1. High generalization ability.

• 2. It scales relatively well with high dimensional data.

Disadvantages of SVM/SVR

• 1. Sensitive to noise and outliers.

• 2. High computational complexity (Hazarika and Gupta 2020).

The LSSVM

To take care of the non-linear classification and regression issues, SVM was updated and the new model was developed known as LSSVM. This model was first introduced by Suykens and Vandewale (1999) which has been vastly applied to the problems of work prediction and density prediction. The non-linear function of LSSVM could be written as:

$$ f(p) = w^{{\text{T}}} \phi {\text{(p) + }}v{,} $$

(34)

where f is the association between the streamflow and SSL, $w$ is called the weight vector with m dimension, and $v$ is the bias factor (Nourani et al. 2017).

Due to the complicated nature of function error as well as fitting error, the regression issue might be offered by the basic minimization guideline as:

$$ {\text{minJ(w,e)}} = \, \frac{{1}}{{2}}w^{T} w\; + \frac{\beta }{2}\sum\nolimits_{j = 1}^{m} {e_{j}^{2} } . $$

(35)

In (35), $\beta$ represents the margin parameter.

The equation has the constraints:

$$ Q_{{{j}}} = {{w}}^{{{t}}} \phi \left( {P_{j} } \right)\; + v\; + \;e_{j} (j = 1,2,.....,m). $$

(36)

In (36),$e_{j}$ represents the negligible variable for $P_{j}$. This equation represents the optimization problem but with the constraints. Hence, to get the solution to the problem, these constraints can be converted into unconstrained problems in the objective function with the use of the Lagrange multipliers $\alpha_{j}$ as (Nourani and Andalib 2015a, b):

$$ {\text{L(w,}}\;\;{\text{u,}}\;{\text{e,}}\;\alpha_{{\text{j}}} {)} = {\text{ J(w,}}\;\;{\text{e)}}\;{ - }\;\sum\limits_{j = 1}^{m} {\alpha_{j} \left\{ {w^{T} \phi (P_{j} )\; + \;v\; + \;e_{j} \; - \;Q_{j} } \right\}} . $$

(37)

$\phi$ denotes the mapping function. This function takes P and maps it into the m-dimensional feature vector. In Eq. (37), the partial derivatives could be taken with respect to $w,u,e\;$, and $\alpha_{j}$, respectively, to reach the optimal conditions (Suykensand Vandewale 1999). It could be given as:

$$ \left\{ \begin{gathered} w = \sum\limits_{j = 1}^{m} {\alpha_{j} \phi (P_{j} )} \hfill \\ \sum\limits_{j}^{m} {\alpha_{j} = \;0} \hfill \\ \alpha_{j} = \;\beta e_{j} \hfill \\ w^{T} \phi (P_{j} )\; + v\; + e_{j} \; - \;Q_{j} \hfill \\ \end{gathered} \right.. $$

(38)

Hence, the linear equations for (38) could be written as:

$$ \left[ {\begin{array}{*{20}c} 0 & { - Q^{T} } \\ Q & {ZZ^{T} \; + \;\frac{1}{\beta }} \\ \end{array} } \right]\;\left[ \begin{gathered} v \hfill \\ a \hfill \\ \end{gathered} \right]\; = \;\left[ \begin{gathered} 0 \hfill \\ 1 \hfill \\ \end{gathered} \right]. $$

(39)

In (39)

$$ \begin{gathered} Q\; = \;{\text{ Q}}_{{1}} {,}........{\text{,Q}}_{{{\text{ym}}}} {, } \hfill \\ R\; = \; \, \phi {\text{(P}}_{{1}} )^{T} Q_{1} ,..........,\phi (P_{m} )^{T} Q_{m} , \hfill \\ I = {[1,}.......{,1], } \hfill \\ \alpha = {[}\alpha_{{1}} {,}.......{,}\alpha_{{1}} {]}{\text{.}} \hfill \\ \end{gathered} $$

After using the kernel function,$K\left( {P,P_{j} } \right) = \; \, \phi {\text{(P}}_{{1}} )^{T} \phi (P_{j} ),\;\;j = \;1,..........,m,$ the LSSVM regressor becomes:

$$ f(p) = \sum\limits_{j = 1}^{m} {\alpha_{j} K(P,\;P_{j} )} \; + \;v. $$

(40)

The RBF is generally utilized as a part of regression issues. The RBF kernel function is utilized as a part of the study as:

$$ k(P,P_{j} ) = e^{{\left( { - \;\frac{{||P - P_{j} ||^{2} }}{{2\sigma^{2} }}} \right)}} ; $$

(41)

here, $\delta$ represents the parameter for RBF kernel. The estimation of this parameter is done through the network procedure itself. The universal architecture of LSSVM is illustrated in Fig. 3.

Fig. 3

Architecture of the LSSVM model (Suykensand Vandewalle 1999; Nourani and Andalib 2015a)

Here PV–Prediction vector, SV–Support vectors, KF–Kernel function, PR–Prediction results, NF–Non linear function.

Advantages of LSSVM

• 1. Good generalization performance.

• 2. Low computational cost.

Disadvantages of LSSVM

• 1. Sensitive to noise.

• 2. Sensitive to outliers.

The GA

Several new methodologies have been implemented to minimize the error rate in ANN, and eventually, they showed better performance. Among them, one of the most powerful methods is called the genetic algorithm. Although the algorithm consumes more time for training as compared to ANN, it achieves less erroneous results.

GAisthe types of computational models which are inspired by the functionality of genes. Though there are various applications of genetic algorithm, they are mainly viewed as function optimizers. GA provides different advantages to existing machine learning methods. For example, a GA.

• i. Can be utilized by data mining for the field/attribute choice, and

• ii. Can be attached with neural systems to decide ideal weights and design.

GA goes through three steps:

• i. Build a population (typically chromosomes) of solutions and maintain it.

• ii. Opt for better solutions for recombination among them.

• iii. Use their offspring for replacing poorer solutions.

The general genetic algorithm operates as:

• i. Initialization of a group of individual populations.

• ii. Calculation of the fitness of each individual.

• iii. Reproducing till a ceasing condition is not met.

Reproduction comprises of the following steps (Whitley 1994; Vankatesan et al. 2009):

• i. Take at least one parent to reproduce.

• ii. Make a mutation for selected individuals by making changes in a random bit of a string.

• iii. Creating a new population.

Finally, one can conclude that the GA-based models are very effective for predicting the SSL.

Advantages of GA

• 1. Ability to avoid being trapped in a local optimum.

• 2. Use probabilistic selection rules rather than deterministic rules.

Disadvantages of GA

• 1. Computationally expensive

• 2. Low convergence (Aljahdali et al. 2010).

The GEP

GEP analogous to GA utilizes the individual population. Ferreira (2002) developed GEP which utilizes major standards of GA and genetic programming. Initially, it was developed for computer program generation. GEP is an evolutionary approach that emulates natural headway progress for influencing the PC platform to program stage and further to create a model (Baylar et al. 2011). The issues are encrypted in straight chromosomes of the same length as a PC program. GEP utilizes a large portion of the GA operators to perform the emblematic operation. However, some distinguishable dissimilarity can be noticed between GEP and GA. In GA, any numerical formula involves a symbolic representation of similar length (chromosomes) or components of non-linear nature. These components vary in their shapes and sizes, which are represented in the form of parse trees. Furthermore, this mathematical expression is encoded and represented in the form of expression trees (ET) in GEP. These expression trees consist of very simple fixed-length strings and are of various shapes and sizes. The encoding is done on these strings present in the mathematical expression (Ferreira and Gepsoft 2008; Cevik 2007). The algorithm of GEP starts by taking five segments. These segments are based on the arrangement of the functions, terminals, fitness function, controlling parameters, and stopping condition. In the following steps of the algorithm, a comparison is performed for estimated values and the original values. When the coveted outcome is accomplished, i.e., the taken criterion for the error is achieved, GEP stops. Few chromosomes are mutated to get new chromosomes by utilizing roulette wheel sampling if the desired error criterion could not be accomplished. The program stops and the chromosomes are decoded to get the best outcomes when the desired outputs are achieved (Teodorescu and Sherwood 2008).

Usually, the principal components in a GEP algorithm are the symbolically fixed-length strings of a mathematical formula known as chromosomes and the ET which carries relevant information. This information could be translated using conclusive language (e.g., Karva language) into expression trees which are the valuable features that permit to accurately deduce the genotype (Kayadelen 2011).

Gene comprises of two components, viz., head and tail. These components are mathematically expressed using some parameters alternatively known as variables, present in the head of gene. However, these parameters fall short of encoding mathematically, which give rise to the parameters used in the tail. The tail is present with required variables or constants to determine the difficulties to encode expressions as it is present with extra terminal symbols that help in encoding. The head usually consists of the arithmetic functions like addition (+), subtraction (−), multiplication (×), and division ($\div$), etc., while the tail consists of the independent variables or the constants like ($1,2,3,...,a,b,c,x,y,....$). The length of the gene plays a vital role in the algorithm. Hence, it is decided at the starting of the analysis to define the total number of symbols present in both the head and tail. The ETs in the Karva language are read from left to right in a line and from top to bottom for whole of ET.

Advantages of GEP

• 1. Able to solve relatively complex problems using small population sizes.

• 2. Good generalization ability (Ferreira 2002).

Disadvantages of GEP

• 1. The conventional GA uses the method of fixed-length coding that performs poorly while facing complex problems (Cheng et al. 2018).

• 2. Low convergence.

The multiple regression (MLR and MNLR)

The MNLR

In MNLR, nonlinearity and multiple regression are the basic components for estimations of factual information. Linear regression (LR) in logarithmic space is generally used to decide the parameters of the derived equations:

$$ \ln \;Z = \;\ln \;K\; + \;a_{0} \ln \;I_{0} \; + a_{1} \ln \;I_{1} + a_{2} \ln \;I_{2} + ..... + a_{n} \ln \;I_{n} . $$

(42)

To make (42) non-linear in linear space, we can rewrite it as:

$$ Z = \;KI_{0}^{{a_{0} }} X_{1}^{{a_{1} }} I_{2}^{{a_{2} }} .............I_{n}^{{a_{n} }} . $$

(43)

Equation (43) does not consist of intercept and various components, i.e., $I_{0,} ...........I_{n}$(Tsykin 1984; Karim and Kennedy 1990). This method has been successfully implemented by a few researchers for SSL prediction.

The MLR

MLR models have influenced and controlled various fields for time-series estimation. MLR is generally utilized for modeling. For example, urban overflow toxin load, wash load silt concentrations, suspended sediment release, and the probability of swell capability of clayey soils. The main difference between MLR and simple LR (SLR) is that SLR has one predictor variables, whereas MLR has two or more predictor variables. In MLR, the dependent variables are dependent on $p$ independent variables. These variables are often called explanatory variables. The equation for MLR could be given as:

$$ y\; = \;\beta_{0} x_{0} + \;\beta_{1} x_{1} \; + \;....... + \beta_{p} x_{p} + \;\varepsilon . $$

(44)

In (44),$\beta_{0} ,\beta_{1} ,\beta_{2} ,.......,\beta_{p}$ are the coefficients for the $p$ independent variables representing the change in mean values (Rajaee et al. 2010; Toriman et al. 2018).

$x_{0} ,x_{1} ,x_{2} ,.......,x_{p}$ represent the $p$ explanatory variables or independent variables.$y$ explains the variable to be predicted or the dependent variable.$\varepsilon$ denotes the error. It follows the normal distribution with parameters $\mu = 0$ and $\sigma^{2} .$

The model fitting for MLR is considered with the addition of independent variables. The explained variance for the dependent variables will also increase when, i.e.,$R^{2}$ increases.

Hence, the model may lead to over-fitting. Least square error criterion is the simplest choice to calculate the deviation between the desired value and the observed value. Hence, the model of MLR is said to be fit, only when the least square error is minimum. Different values of the coefficient $\beta_{i}$ are taken to minimize the error.

This could also be represented in matrix form showing a more efficient structure of the model as there are a large number of predictor variables used in learning the model. Let us take a simple linear equation similar to Eq. (53), that is:

$$ y_{i} \; = \;\beta_{0} + \;\beta_{1} x_{i} \; + \;\varepsilon_{i} . $$

(45)

For $i = 1,2...........,n$, in (45), they could be written as:

$$ \begin{gathered} y_{1} \; = \;\beta_{0} + \;\beta_{1} x_{1} \; + \;\varepsilon_{1} \hfill \\ y_{2} \; = \;\beta_{0} + \;\beta_{1} x_{2} \; + \;\varepsilon_{2} \hfill \\ . \hfill \\ . \hfill \\ y_{n} \; = \;\beta_{0} + \;\beta_{1} x_{n} \; + \;\varepsilon_{n} . \hfill \\ \end{gathered} $$

These equations could be written in matrix form as:

(46)

Hence, $n$ number of equations in (45) could be represented by just a simple Eq. (46), which is given above. The modeling of MLR can be used for prediction of SSL.

Advantages of multiple regression (MLR/MNLR)

• 1. Ability to determine the relative impact of one or more predictor variables on the value of the criterion.

• 2. Ability to identify outliers.

Disadvantages of multiple regression (MLR/MNLR)

• 1. Poor prediction performance (Maxwell 1975).

• 2. Sensitive to design anomalies in data (Akkaya and Tiku 2008).

The CART

Model

In the past, decision trees were proposed to work on the empirical examples to understand their performance on SSL prediction. However, this approach became popular with no strong theoretical foundations, because the CART model that is much more sophisticated and offers technical proofs for the results obtained. The merit of the CART model is that it could process both continuous as well as nominal attributes in both forms of the target and predictor variables as compared to other DT algorithms. In machine learning, data mining, and non-parametric statistics problems, CART outperformed the other traditionally used algorithms for classification. The CART is applied in many domains such as medical science, marketing research, river engineering, and prediction problems. Besides, it is also applied in SSL prediction (Talebi et al. 2017).

The CART model applies a binary recursive partitioning procedure to the raw data. CART model was proposed by Breiman et al. (1984) to refer to both procedures, i.e., classification and regression. When the output to be predicted is a class, then it comes in classification category, and when the predicted output is any real number (like the price of a vehicle, age prediction), then it comes in the category of regression; it could be also said that if the predictor variable is of categorical form then CART gives classification and numerical form, then CART produces regression tree.

In this decision tree model, the tree initially grows without any stop to its maximum size and then pruning is performed split by split to the root, such that the model complexity could be minimized. The procedure of splitting and determining describes the procedure discrimination as classification and regression. In this model, as pruning is done split by split, hence the next split pruning will be the one which has the least complexity in tree performance for the available data for training. Trees produced will be invariant for any predictor attribute transformation. This model creates a grouping of nested trees. These all pruned trees are themselves candidate optimal trees. The calculation of predictive performance for each pruned tree is done and the tree with the best performance is taken as an honest tree. The tree selection is done based on independent test data depicting tree performance and not on any internal measurements. In case of unavailability of data or any cross-validation of data, the CART model would not give its fixed decision on the best tree selection. Instead, the CART model provides an automatic handle of missing values, balancing of class formation of dynamic features etc. (Breiman 2017). The split rule followed in CART is given by

where the CONDITION could be represented as $X_{i} < = C$ and for a nominal attribute for continuous attributes and it expresses the membership in a definite set of values for a nominal attribute.

The CART mainly follows the Gini rule of impurity for classification over miss classification error and entropy index are included symmetrised costs if extended. It forms a set a randomly chosen element is arbitrarily labeled; following the label distribution given in the subset the measure of Gini impurity tells how often this element is labeled mistakenly. If the target value is binary (i.e., 0/1), the Gini measure of impurity could be given as

$$ g(t) = 1 - \backslash c(t)^{2} - \left( {1 - c(t)} \right)^{2} . $$

(47)

For class 1,$c(t)$ represents the relative frequency inside the node in (47). And the gain produced due to the split of the parent node $C$ could be given as

$$ G(C) = g(C) - \alpha g(l) - (1 - \alpha )g(r). $$

(48)

In (48)

$l$ and $r$ represents the left and right children of $C$ respectively.

$\alpha$ represents the fraction of instances which are going to the left children node (Timofeev 2004).

Two common impurity calculations are least squares and least absolute deviations for regression trees (Moisen, 2008).

Advantages of CART

• 1. Data normalization not required.

• 2. Intuitive.

Disadvantages of CART

• 1. High computational cost.

• 2. The small change of data can cause a large change in a tree structure.

The M5 Model Tree

M5 Model Tree type models were actualized in different hydrological implementations (Bhattacharya et al. 2007; Shrestha and Solomatine 2006). Quinlan (1992) states that the methods involving model trees represent the data in a structured form for a class and give the piecewise linear fit. Hence, generalizing the regression trees having constant leave values. Their structure is similar to the traditionally used decision tree structure. These model trees use linear regression functions at the leaves in place of discrete labels for different classes. This makes it perform well even for continuous several numbers of attributes. As it is normally done in the learning of decision tree models, M5 also learns similarly by dividing the available data in a tree-structured form based on the values of the predictive attributes. As the dimensions of the data set increase the computations requirement grows at a rapid rate. However, M5 could tackle the problems of a very huge amount of computations involving a large number of attributes. These are much smaller than the conventional regression trees which have less number of variables with clear decision strength (Frank et al. 1998; Singh et al. 2010; Goyal and Ojha 2011).

M5 model does not choose its attributes by the information-theoretic metric; instead, it tries to choose those attributes which could reduce the intra subset difference in the values. These values are the class values of the instances, and each branch of the tree goes downwards. When these values going downwards from the root to the leaf node, at each node, the attribute values of that node are tested for the expected reduction in the error. Furthermore, the value which maximizes this error is selected to calculate the standard deviation (SD) in the values. This SD is the measurement of the variability of the values. This splitting or division of data is stopped if the instance values reaching node have a very slight difference or the number of instances remained is very less in number (Goyal 2014; Goyal et al. 2013; Witten and Frank 2016).

The standard deviation reduction (SDR) could be evaluated as expressed below:

$$ SDR\; = \;{\text{SD}}(T)\; - \;\sum\limits_{i} {\frac{{T_{i} }}{T}\; \times \;{\text{sd}}\left( {T_{x} } \right)} \;. $$

(49)

In (49) T represents the example set reaching the given node; $T_{x} \;$ represents the example set delivering the output for the given set (Rejaie-balf et al. 2017).

Sometimes, there could be the formation of over-elaborating structures which needs to be pruned back due to unrelenting structures. It could be done by placing a leaf instead of a subtree. At these leaves which created after pruning, there could emerge some sharp discontinuities between neighboring straight models in a model where less number of training examples are utilized. Subsequently, the smoothening is performed in the conclusive stage. The update of adjacent conditions (linear) is performed, so that the outputs which are anticipated for the input vectors in correspondence to various conditions turn out to be about same in terms of value.

Advantages of CART

• 1. Can handle both numerical and categorical data.

• 2. Intuitive and easy to visualize.

Disadvantages of CART

• 1. Constrained to make only binary splits.

• 2. A small change in the dataset can make the tree structure unstable.

The CHAID

CHAID is a white box decision tree-based model that is used to search for the algorithms between a categorical response variable and another categorical predictor variable. This model was proposed by Kass (1980). This creates a decision tree using Chi-square statistics. It has the capability of creating non-binary trees which implies that few splits achieve at least three branches, unlike the CART model. CHAID is successfully implemented in data mining, direct marketing, and medical diagnosis et cetera (Haughton and Oulabi 1997; Hill et al. 1997). Recently CHAID has been successfully implemented to predict the SSL along with SVM and ANN (Pektas and Dogan 2015). The obtained results revealed that the CHAID model was a better performer compared to SVM.

CHAID model proceeds stepwise:

• i. First, the most favorable subset is taken for each predictor available in the decision tree.

• ii. The second step follows with a comparison done between these predictors with their results, of which the best is taken.

• iii. In the third step, the available data are further divided into subsets as per the chosen predictor.

• iv. Finally, all these divided subsets are again analyzed without any dependency between them to get further subdivisions which are analyzed iteratively according to the above steps (Kass 1980).

Advantages of CHAID

• 1. Low computational cost.

• 2. Not constrained like CART to make binary splits.

Disadvantages of CHAID

• 1. To get reliable results, larger quantities of data are required.

• 2. Before analysis, real variables are forced into categorical bins (Nisbet et al. 2009).

The ELM

In machine learning, ANN is a great performer in terms of prediction as well as classification. It has been successfully applied in several fields that include hydrological forecasting. Compared to the traditional machine learning algorithm SLFN, ANN portrays satisfactory outcomes. However, ANN faces the problem of local minima and gives low generalization performance. The primary reason behind these issues is that moderate gradient descent algorithms are widely used and each parameter of the systems is tuned iteratively. Consequently, Huang et al. (2006) proposed another model called ELM to vanish these issues. Here, the weights and biases are arbitrarily relegated to the input layer and hidden layer separately. The output is estimated by utilizing the Moore Penrose generalized inverse of the hidden layer output network. ELM gives better generalization performance and is fundamentally quicker than the ANN.

Suppose, a set is considered for training samples $\left\{ {\left( {i_{x} ,o_{x} } \right)} \right\}_{x = 1,....,m}$, and for each input example $i_{x} = \left( {i_{x1\;} ,o_{xn} } \right)\;^{t} \in \;R^{n}$. Let $o_{x} \in \;\Re$ are the corresponding target values. For the arbitrarily allocated qualities of the learning parameters $a_{s} \in \;(a_{s1} ,a_{s2} ,...........a_{n} )\; \in \;R^{n}$ and $b_{s}$$\in \;R$ for the nodes present in the hidden layer, algorithm ELM computes its output function $f(.)$ as:

$$ f(i_{k} ) = \sum\limits_{{}}^{{}} {w_{s} E(a_{s} ,b_{s} ,i_{k} )} \; = \;o_{k} \,{\text{for}}\,k = 1,......,m. $$

(50)

In (50),$E(a, b, i )$ represents the output function of the hidden layer. This output function is a piecewise continuous function showing the non-linearity in its nature and fulfills the states for all the inclusive estimate ability theorems.

$w = \left( {w_{1} ,.......w_{l} } \right)\; \in \;\Re^{n}$ indicates the weight vector for the hidden layer connecting the nodes of the hidden layer to the output layer nodes. This vector is obscure in the knowledge of its working to the outer world, holding an ANN model property. The Eq. (50) can be modified to represent in matrix form as:

$$ H = \left[ \begin{gathered} E\left( {a_{1} ,b_{1} ,i_{n} } \right)\;\;\;.....\;\;\;E\left( {a_{n} ,b_{n} ,i_{n} } \right) \hfill \\ E\left( {a_{1} ,b_{1} ,i_{m} } \right)\;\;.....\;\;\;E\left( {a_{n} ,b_{n} ,i_{m} } \right) \hfill \\ \end{gathered} \right]_{m \times n} . $$

(51)

For hidden layer,$H$ represents the output matrix in the network as well as ${\text{o = }}\left( {o_{1} ,.......o_{m} } \right)^{t} \; \in \;\Re^{n}$ gives the output vector values which are observed. Various activation functions can be used in ELM viz. sigmoid, multiquadric, ReLU, RBFetc.

If the output function, $E\left( {a,b,i} \right)$ of the hidden layer, is defined already in advance and assignment of values to the parameters $a_{s} \; \in \;\Re^{n}$; $b_{s} \; \in \;\Re^{n}$ is done randomly, then, to train the SLFN will be same as it happens in a rectangular system to obtain the solution for the least squares, i.e., $w\; \in \;\Re^{l}$. Here, this rectangular system will be linear. The generation of $w\; \in \;\Re^{l}$ is done explicitly as the solution for $b_{s} \; \in \;\Re^{n}$, in the form of least norm least squares. In this generated solution,$w\; \in \;H^{ + } y$.$H^{ + }$ denotes the Moore–Penrose generalized matrix inverse of $H$(Balasundaramand Gupta 2014). Hence, the generated solution $w\; \in \;\Re^{l}$ will work as a fit model $f(.)$ for ELM regression. It could be expressed as

$$ f(i_{k} ) = \sum {w_{s} E(a_{s} ,b_{s} ,i_{k} )} . $$

(52)

Advantages of ELM

• 1. Fast and efficient.

• 2. Parameter tuning is not needed.

Disadvantages of ELM

• 1. Noise and outlier sensitivity.

• 2. Overfitting problem.

The RF

RF is one of the most potent ensemble-based learning models. Breiman (2001) suggested the RF algorithm by adding additional randomness layer to the bagging method. It functions by constructing multiple decision trees and final predictions are extracted from the averaged results.

The algorithm of RF starts by drawing $n_{tree}$ the bootstrap sample from the data. Afterward, an unpruned classification or regression tree is developed for each sample in the bootstrap (Ouedraogo et al. 2019). Subsequently, a random sample of the predictors is to be considered at each node and the best split from among those variables (predictors) is selected. Finally, new data are predicted by aggregating the prediction of $n_{tree}$ trees (Liaw and Wiener, 2002).

Advantages of RF

• 1. Good generalization performance.

• 2. Can handle nonlinearity.

Disadvantages of RF

• 1. No interpretability.

• 2. Overfitting problem.

The MARS

The MARS model was formulated in the early 1990s by Jerome H. Friedman. The MARS system fits an adaptive non-linear regression model using multiple piecewise linear basis functions hierarchically ordered in consecutive splits over the predictor variable space (Spline 2013). The generalized form of the MARS model can be expressed as:

$$ y = f(x) = c_{0} + \sum\limits_{n = 1}^{N} {c_{N} H_{kN} (x_{v(k,n)} )} \;, $$

(53)

where $y$ is the output parameter, and $c_{o}$ and $N$ are the constant and the number of basis functions, respectively.

The basis function $H_{kN} (x_{v(k,n)} )$ can be expressed as:

$$ H_{kN} (x_{v(k,n)} ) = \prod\limits_{k = 1}^{K} {H_{kN} } , $$

(54)

where $(x_{v(k,n)} )$ is the predictor of the $k^{th}$ of the $m^{th}$ product.

The ARMAX

The ARMAX model uses the linear input for prediction. The ARMAX model can be denoted as

$$ ARMAX(\eta_{a} ,\eta_{e} ,\eta_{m} ) = (1 - a_{1} d^{ - } ...{}^{ - }a_{{\eta_{a} }} d^{{\eta_{a} }} )S_{t} = (1 - b_{1} d^{ - } ... - b_{{\eta_{e} }} d^{{\eta_{e} }} ) + Q_{t - k} (1 - c_{1} d^{ - } ...{}^{ - }c_{{\eta_{m} }} d^{{\eta_{m} }} )\xi_{t} , $$

(55)

where $S_{t}$ and $Q_{t - k}$ are the predictor of the SSL and the discharge time-series, respectively.$(a_{1} ,a_{2} ....,a_{{\eta_{a} }} )$ are the exogeneous coefficient vector. The $\xi_{t}$ denotes the series of noise disturbance,$(c_{1} ,c_{2} ....,c_{{\eta_{a} }} )$ is the moving average coefficient.$\eta_{a} ,\eta_{e}$, and $\eta_{m}$ are the autoregressive, exogenous input, and moving average component, respectively.$d$ and $k$ are the predictor of the delay operator and the dead time in the system, respectively.

Advantages of ARMAX

• 1. Powerful model specially designed for time-series analysis.

• 2. Accurate and reliable forecast.

Disadvantages of ARMAX

• 1. Captures only linear relationships among variables.

• 2. Complex data pre-processing.

The fuzzy c-means clustering (FCM).

The FCM sections the dataset $X$ into $C$ clusters by minimizing the errors concerning the weighted distance of each data point $x_{i}$ toward all centroids of the $C$ clusters. Subsequently, the algorithm works as indicated by minimizing the objective function that is pigeonholed as:

$$ \begin{gathered} \min \;J_{FCM} \sum\limits_{c = 1}^{C} {\sum\limits_{i = 1}^{N} {w_{ic}^{e} \left\| {u_{i} - v_{c} } \right\|} } \hfill \\ subject\;\;to\;\sum\limits_{c = 1}^{C} {w_{ic} ,\;i = \;1,\;2,\;...,\;N} , \hfill \\ \end{gathered} $$

(56)

where $e$ represents the fuzzifier exponent $e > 1$, $N$ is the total number of data points, $w_{ic}$ represents the degree of belongings to the $i^{th}$ data point to the $c^{th}$ cluster which can be solved iteratively, $v$ and $u$ are the center of the cluster and the of data point that is provided as an input, respectively,

After initializing the center vectors, the centers can be recalculated until convergence as:

$$ v_{c} = \frac{{\sum\nolimits_{j = 1}^{N} {w_{jc}^{e} u_{j} } }}{{\sum\nolimits_{j = 1}^{N} {w_{jc}^{e} } }}\;for\;c = \;1,\;2,\;...,\;C\;and\;1 < e < N. $$

(57)

Advantages of FCM

• 1. Fast convergence.

• 2. Gives the best result for the overlapped data set.

Disadvantages of FCM

• 1. Computationally expensive.

• 2. Sensitivity to noise and outliers.

The LDMR

The primal problem of LDMR (Rastogi et al. 2020) can be expressed as:

$$ \begin{gathered} \mathop {\min }\limits_{{(w,b,\xi_{1} ,\xi_{2} )}} \frac{\upsilon }{2}||Y - (K(G,G^{t} )w + eb)||^{2} + \;\frac{1}{2}Ce^{t} \left( {\psi_{1} + \psi_{2} } \right) + \frac{{_{d} }}{2}||w||^{2} , \hfill \\ s.t.Y - (K(G,G^{t} )w + eb) \le e\varepsilon + \xi_{1} ,\,\xi_{1} \ge 0, \hfill \\ (K(G,G^{t} )w + eb) - Y \le e\varepsilon + \xi_{2} ,\xi_{2} \ge 0, \hfill \\ \end{gathered} $$

(58)

where $\varepsilon ,d,\upsilon > 0$ are the input parameters and $u = \left[ \begin{gathered} w \hfill \\ b \hfill \\ \end{gathered} \right]$; $||w||^{2} = u^{t} I_{0} u$ where $I_{0} = \left[ {\begin{array}{*{20}c} I & 0 \\ {} & . \\ {} & . \\ 0 & {...0} \\ \end{array} } \right]$;$I^{m \times m}$ is an identity matrix; $C > 0$ is the trade-off parameter; $\psi_{1}$ and $\psi_{2}$ are the slack variables. For obtaining the solutions from (58), Lagrange’s multipliers are introduced as:

$\alpha_{1} = (\alpha_{11} ,\alpha_{12} ,...,\alpha_{1m} )^{t}$ and $\alpha_{1} = (\alpha_{21} ,\alpha_{22} ,...,\alpha_{2m} )^{t} .$

The dual formulation of (58) may be expressed as:

$$ \begin{gathered} \mathop {\min }\limits_{{(\alpha_{1} ,\alpha_{2} )}} \frac{1}{2}\left( {\alpha_{1} - \alpha_{2} } \right)^{t} Z_{0} \left( {dI_{0} + \upsilon Z_{0}^{t} Z_{0} } \right)^{ - 1} Z_{0}^{t} \left( {\alpha_{1} - \alpha_{2} } \right) \hfill \\ + \;y^{t} Z_{0} \left( {dI_{0} + \upsilon Z_{0}^{t} Z_{0} } \right)^{ - 1} Z_{0}^{t} \left( {\alpha_{1} - \alpha_{2} } \right) \hfill \\ - Y^{t} (\alpha_{1} - \alpha_{2} ) + \varepsilon \;e^{t} (\alpha_{1} + \alpha_{2} ) \hfill \\ s.t.0 \le \alpha_{1} \le Ce\,{\text{and}}\,0 \le \alpha_{2} \le Ce, \hfill \\ \end{gathered} $$

(59)

where, $Z_{0} = [\begin{array}{*{20}c} {K(G,G^{t} )} & e \\ \end{array} ]$ and be an augmented matrix (Hazarika et al. 2020b).

For a new instance $x$, the decision function $\varphi (.)$ is achieved as follows:

$$ \varphi (x) = K(x^{t} ,G^{t} )w + b. $$

Advantages of LDMR

• 1. Insensitive to noise and outliers.

• 2. Handles non-linearity.

Disadvantages of LDMR

• 1. Computationally expensive.

In Table 3

Table 3 Statistics of the datasets (g/L)

N = Total samples

$$ f = \;{\text{predicted}}\;{\text{outcome}} $$

$$ \overline{f} = \;{\text{predicted}}\;{\text{outcome}}\;{\text{(mean)}} $$

$$ o = \;{\text{observed}}\;{\text{value}} $$

$$ \overline{o} = \;{\text{observed}}\;{\text{value}}\;{\text{(mean)}} $$

$$ \hat{o} = \;{\text{predicted}}\;{\text{value}}\;{\text{of}}\;o $$

$$ e = \;{\text{error}} $$

$$ \overline{e} = \;{\text{error}}\;{\text{(mean)}} $$

$$ K = \;{\text{the number of model parameters }} $$

$$ \log - {\text{likelihood}} = \;{\text{measure of model fit}}{\text{. The higher the number, the better the fit}}{. } $$

The year-wise publications in SCI/SCIE and Scopus indexed journals are portrayed in Fig. 4 from January 2015 to 2020 (November). It is noticeable from Fig. 4 that there is an increase in the number of good publications from 2018. Figure 5 shows the Pie-Chart for various prediction models that have been applied during the time range from January 2015 to November 2020. Figure 6 exhibits the various performance measures that have been used for evaluating the model performances. One can observe from Fig. 6 that R and R² are the most widely accepted performance measure for model evaluation which is followed by the RMSE. However, all these representations are approximate.

Fig. 4

Number of published journal papers regarding SSL prediction (indexed in SCI/SCIE and scopus) with respect to year of publication to best of our knowledge

Fig. 5

Pie-chart showing various implemented models for SSL prediction from 2015 to 2020 (November) (indexed in SCI/SCIE and Scopus)

Fig. 6

Doughnut chart showing the applied percentage of the various performance evaluators for SSL prediction from 2015 to 2020 (November)

Experimental analysis

The experiments are performed on a desktop computer system on MATLAB 2019a software with 32 GB RAM, 3.20Ghz Intel i-7 processor on Windows 7 operating system. The QPP problems of SVR, TSVR, OB-ELM, and LDMR models are solved using the quadprog function in MATLAB. The datasets are randomly split, such that 70% are used for training and the remaining 30% used for testing. The prediction errors based on RMSE and MAE are revealed in Tables 4 and 5, respectively. The optimum values of the regularization parameter,$C$ of the SVR, TSVR and ILTPISVR models are chosen from a range of parameters $\{ 10^{ - 5} ,10^{ - 4} ,..,10^{5} \} .$ Moreover, for the LDMR and the proposed MKLDMR and MHKLDMR models, the optimal regularization parameters $C,\;C_{1} = C_{2}$ are also chosen from $\{ 10^{ - 5} ,10^{ - 4} ,..,10^{5} \} .$ For all of the models, the value of the $\varepsilon$ parameter is chosen from a range of $\{ 0.05,0.1,0.5,1,1.5,2\} .$ For computational convenience, the $k$ parameter of the LDMR is fixed to 1. The optimum values of $L$ parameter is considered from $\{ 20,\;40,50,\;100,\;200,\;500\} .$ We have performed experiments using two SSL datasets that are collected from two different rivers in India, i.e., Pare river and Tawang Chu river. The Tawang Chu river dataset contains SSL data from January 1, 2015, to December 31, 2015, whereas the Pare river dataset contains SSL data from December 12, 2018, to 5 May 2019. The details of the datasets are expressed in Table 3.

Table 4 Obtained RMSE for a few models using the two SSL data from two different rivers

Table 5 Obtained MAE for a few models using the two SSL data from two different rivers

Few conventional AI models such as SVR, TSVR, ELM, OB-ELM, and LDMR has been applied on the two different SSL datasets. The results obtained based on RMSE and MAE are shown in Tables 4 and 5, respectively. It can be noticed that the AI model shows good prediction performance for the datasets. The observed SSL versus predicted SSL plots are shown in Fig. 7 for the reported models.

Fig. 7

Observed SSL (g/L) versus predicted SSL (g/L) plot of a few AI-based models on river SSL dataset collected from the Tawang Chu river. a SVR, b LSSVR, c TSVR, d ELM, e OB-ELM, and f LDMR

It can be observed from Fig. 7 that the R² value is low for the reported models. To improve the prediction performance of the reported models, different types of decomposition methods such as variational mode decomposition (VMD) (Dragomiretskiy and Zosso 2013) and ensemble empirical mode decomposition algorithms (EEMD) (Wu and Huang 2009) are suggested as a data pre-processing step. Also embedding the DWT to the conventional AI-based models can improve the prediction performance of the same (Zhu et al. 2016; Hazarika et al. 2020a, b, c).

Summary and future projections

Sediment load prediction is one of the prime issues in hydrology. The study of SSL characteristic is a very cumbersome process due to its non-linear nature. Models like MLR and MNLR have been used to tackle the non-linearity of the problem and succeeded in a great way. However, these models could not give great accuracy in prediction. However, these models could be tried in conjunction with other learning models and needs to be checked for their prediction accuracy. The different models applied for prediction of SSL cannot be compared strictly based on their performance. Since the different field conditions may alter the performance of the same model with accuracy in some condition and average in some other condition, it could give average accuracy. Therefore, it could be inferred that models like ANN, SVM, GEP, GA, ANFIS, and their hybrid models like ANFIS-ANN, WANN, etc., have their specialities and could perform better with the prevailing conditions. It is also noticed the application of wavelet transforms on the input available giving rise to daughter wavelets for different time-series. These daughter wavelets are also feasible to use.

The principal task of researchers has been to somehow study the non-linear nature of sediment loads using a simple learning algorithm, so that the learning process could be understandable to the outer world. However, it creates a paradoxical situation in models like ANN. Hence, to get better accuracy with a simplified learning process some other algorithms are also applied, viz., ELM, GEP, and so on. Out of these algorithms, ELM as well as wavelet-based models have been showing great potential and could be used by integrating it with different learning models. Also, the effectiveness of the random vector functional link (RVFL) could be tested for SSL prediction. These hybrid models perhaps could give better accuracy and could be tackled much more efficiently using different learning algorithms.