Introduction

Surface water quality impairment is one of the most prevalent environmental problems worldwide (Houser and Richardson 2010; Li and Zhang 2010; Morse and Wollheim 2014). In the last two decades, the increasing nutrients in the receiving water have been commonly attributed to non-point source (NPS) pollution from agricultural and human living systems (Wang et al. 2011). The excess nitrogen and phosphorus in rivers decrease the water quality, degrade aquatic ecosystem health, and induce anoxia and harmful algal blooms in several fresh water and coastal ecosystems (Bowes et al. 2010; Gao and Zhang 2010; Howarth et al. 2012; Ryusuke et al. 2002). The accurate nutrient load forecasts are particularly important to inform future policy and management decisions in terms of prioritizing water quality management and algal blooms control. But now, riverine total nitrogen (TN) load time series forecasting is still one of the most difficult and challenging issues for water resource managers and government agencies because riverine TN loads are closely related to anthropogenic activities as well as dynamic, non-linear, and complex natural processes involved in NPS pollution.

Complex mechanistic models such as Hydrological Simulation Program-Fortran (HSPF), Soil and Water Assessment Tool (SWAT), and Agricultural Non-Point Source Pollution Model (AGNPS) have been developed in the past few decades to obtain quantitative information of NPS pollution loads (Arnold and Fohrer 2005; Borah and Bera 2004; Donigian et al. 1984). These watershed scale models have been widely used for forecasting nutrient loads under various climate, management, and pollutant loads scenarios. For example, Shen et al. (2014) used SWAT model to simulate the spatial and temporal distribution of NPS pollution loads in the Three Gorges Reservoir Region (China). The results exhibited that the NPS pollution loads in the western area were the highest and an upward trend existed in recent years. Coffey and Line (1998) predicted nutrient loads export from dairies to Cane Creek Reservoir (USA) through AGNPS model, and the results indicated that annual TN and total phosphorus (TP) export from entire farms varied from 1.0 to 3.7 kg/ha and 0.7 to 1.8 kg/ha, respectively. Chou et al. (2007) employed HSPF model to estimate watershed pollutant loads from NPS in the Feitsui Reservoir watershed (China), and found that NPS pollution contributed ~ 85% of the annual average TP loads into the reservoir. However, these models are unable to provide defensible and quantifiable future nutrient loads which are required for developing early warning systems.

Traditionally, researchers have utilized statistical models on the basis of time series analysis (e.g., autoregressive, autoregressive moving average, and autoregressive integrated moving average) to cope with forecasting problems (Belayneh et al. 2014; Huang et al. 2004; Kothyari and Singh 1999; Mishra and Desai 2005; Wu et al. 2009a). Nevertheless, stochastic models have linear structures that prevent these models from dealing with highly non-linear processes. In the past two decades, artificial neural network (ANN) has gained significant attention and been widely used in various configuration to perform a range of tasks including forecasting, classification, pattern recognition, data mining, and non-linear process modeling (Chen and Chau 2016; Nabavi-Pelesaraei et al. 2017; Sefeedpari et al. 2016; Wang et al. 2014; Wu et al. 2009b; Yoon et al. 2011). It should be noted that ANN has shortcomings inherent in its architecture, like over-fitting, slow training speed, and vulnerability to being trapped in the local optimum (Chau 2017). The support vector regress (SVR) method, presented by Vapnik (1995, 1998), has been attracting a great deal of interest because of the following advantages: (1) simultaneous minimization of model complexity and prediction error since the use of kernel trick in building expert knowledge, (2) good generalization ability can be achieved due to the adoption of structural risk minimization (SRM) principle (Chau and Wu 2010), (3) good performance can be obtained with relatively small data sets, and (4) prevention of over-fitting problem which is the critical drawback of ANN. SVR model utilizes appropriate kernel function to map the original data sets from the input space into a higher dimensional space, from where the non-linear problem changed into linear problem. Consequently, SVR model is capable of modeling non-linear data. Recently, the SVR model has been widely applied to various scenarios, such as stream flow forecasting (Lin et al. 2006), water level prediction (Khan and Coulibaly 2006; Yoon et al. 2011), and water quality parameters modeling (Noori et al. 2015).

The aforementioned data-driven models are advantageous because they require less information, do not necessitate a full understanding of underlying processes in mathematical forms, and are easy to implement. Furthermore, they are capable of addressing forecasting problems. Yet, their ability is limited when dealing with non-stationary data (Adamowski and Sun 2010; Cannas et al. 2006). To overcome this drawback, some researchers explored wavelet analysis (WA) in hydrologic forecasting (Belayneh et al. 2014). WA is recognized as an effective tool for analyzing trends, periodicities, and variations in time series (Chou and Wang 2002; Lu 2002; Partal and Kucuk 2006; Simith et al. 1998). A non-stationary time series signal can be decomposed into several different resolution levels by WA to reveal the useful information involved in original time series. Because of this, WA has a significant advantage in handling non-stationary processes. In addition, the wavelet method is robust since any potentially parametric testing procedures or erroneous assumptions are included (Kisi and Cimen 2011). WA is often used as a data pre-processing tool for revealing hidden information and capturing both the periodic and chaotic behaviors of a time series otherwise not captured by other signal processing techniques (Adamowski and Sun 2010; Shoaib et al. 2014). In recent years, several studies have demonstrated the successful applications of WA combined with data-driven models (e.g., ANN and SVR) in hydrologic forecasting. For example, Wang and Ding (2003) first explored the ability of ANN model coupled with WA (WA-ANN) in short and long-term prediction of hydrological time series. They found that the suggested WA-ANN model absorbed several advantages of WA and ANN and was capable of forecasting daily river discharge with high accuracy. Similarly, Liu et al. (2013) proposed a WA-ANN model to predict suspended sediment concentration (SSC) in the Kuye River, a representative hyper-concentrated river in the middle Yellow River catchments of China. Results revealed that the proposed model obtained better SSC predicts than ANN model or sediment rating curve (SRC) model in a hyper-concentrated river setting, with highly non-linear and non-stationary time series. Olyaie et al. (2015) compared the accuracy of three different soft computing methods, namely ANN, adaptive neuro-fuzzy inference system (ANFIS), WA-ANN, and conventional SRC approach for estimating the daily SSC in two gauging stations in USA. Results indicated that the WA-ANN was the most accurate model in SSC estimation in comparison to other models. Kisi and Cimen (2011) used WA and SVR conjunction model (WA-SVR) to illustrate that the forecast accuracy was higher in monthly stream flow forecasting compared with the single SVR model. Kalteh (2013) applied two hybrid models (WA-ANN and WA-SVR) for monthly river flow prediction and investigated their accuracy, indicating the wavelet decomposition and artificial intelligence (AI) combination models could produce better efficiency than conventional forecasting models. Results also demonstrated that the WA-SVR model outperformed the WA-ANN model. Despite the applications of coupled WA-ANN or WA-SVR model to a multitude of hydrologic cases, no attempt has been performed on NPS load forecasting with the WA-ANN or WA-SVR model in highly agricultural watersheds for guiding NPS pollution remediation efforts and algal bloom control until now. Rather, only few mother wavelets were included in the abovementioned studies, which rarely consider the effect of different mother wavelets on accuracy of the combined models. Thus, forecasting of NPS loads by using WA-SVR model and investigation of the different mother wavelets’ impact on established model performance are required in terms of NPS pollution management.

NPS pollution processes are influenced by both natural and human factors; as such, riverine TN load time series often display highly stochastic, non-linear, and non-monotonic characteristics. Therefore, the supporting assumptions of TN load data cannot match well with the traditional stochastic and single ANN or SVR model. This might yield invalid results when these data-driven models are employed to forecast riverine TN loads. Through combining WA with SVR model, the WA-SVR model has the merits of both techniques and thus can effectively address the stochastic, non-linear, and non-stationary issues. For this reason, WA-SVR model was first proposed for pollutant load estimation in this study, with the purpose to overcome the difficulties associated with riverine TN load forecasting. Specifically, the main objectives of this study were to (1) obtain the riverine TN load time series in the ChangLe River from the years 2004 to 2012, (2) apply the WA-SVR hybrid model to forecast the short-term (daily) and long-term (monthly) riverine TN loads, (3) examine the effects of mother wavelets on the performance of constructed models, and (4) validate the performance of WA-SVR model by comparing it with that of single SVR model. It is expected that the results can provide accurate forecasts of riverine TN loads and early warning for water quality agencies and thus facilitate algal bloom control and water pollution remediation.

Study area and data collection

Study area

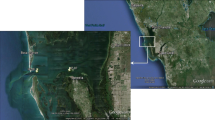
The ChangLe River watershed (29° 27′ 98″–29° 35′ 12″ N, 120° 35′ 56″–120° 49′ 03″ E) has a drainage area of 864 km2 in Zhejiang Province that lies in eastern China (Fig. 1). This region is characterized by subtropical monsoon climate, receiving 1228 mm of annual precipitation with 70% falls during summer (April–September). The average monthly air temperature ranges from 4 °C (in January) to 28 °C (in July). The river traverses a total distance of 70.5 km before merging with the Cao-E River, which ultimately drains into the East China Sea. The width of the river varies from 40 to 70 m, with an average value of 55 m. The ChangLe River watershed is located in the most intensive agricultural regions in China (Chen et al. 2011, 2013). The primary land use categories are woodland and farmland, accounting for around 48 and 42% of the entire watershed, respectively. Approximately 92% of the river water comes from catchment runoff, and the remainder originates as the headwater streams (Nanshan Reservoir) drainage. The ChangLe River watershed was selected because (1) this region represents a typically agricultural watershed in eastern China. The NPS pollution is the primary source of nitrogen in the river systems, and (2) the long period of observations for TN concentration and stream flow are available.

Fig. 1
figure 1

Location of ChangLe River watershed in China and Zhejiang Province and the river hydrology and water quality sampling site

Full size image

Data collection

River water quality samples were collected every month (n = 106 sampling times total) at Yazhi station (Fig. 1) from January 2004 to December 2012. Water samples were collected at a depth of ~ 20 cm in the middle of the river and stored in 0.5 L high-density polyethylene bottles. Subsequently, the samples were acidified with sulfuric acid (H2SO4) and immediately chilled by placing ice packs in the cold closet. The concentration of TN in water samples was determined within 24 h of sampling campaign by alkaline potassium persulfate method (State Environment Protection Bureau of China 2002). The continuous daily stream discharges at Yazhi station were obtained from the hydrological bureau of Zhejiang Province, China. The time series of stream flow and observed TN concentrations are illustrated in Fig. 2.

Fig. 2
figure 2

Stream flow and observed TN concentrations in the ChangLe River during 2004–2012

Full size image

Model development

Continuous time series data of riverine TN loads

Generally, river discharge is daily recorded by hydrology monitoring stations. Nevertheless, monthly or bimonthly sampling is often employed as the standard sampling frequency for water quality monitoring since the limitations of cost and time. Given this dilemma, the Load Estimator (LOADEST) model was presented to estimate daily nutrient loads over time from relatively infrequent discrete water quality samples and high frequency discharge measurements (Runkel et al. 2004). This method sufficiently considers the correlation between the pollutant loads and concentration, discharge, and time. It has many advantages such as low data dependency, stable result, and ease of operation. Therefore, LOADEST model software was adopted in this study. LOADEST has 11 regression models, and one of the most common models is listed as follows:

$$ {\displaystyle \begin{array}{l}\ln \left(\ \mathrm{Load}\right)={a}_o+{a}_1\ \left(\ln (Q)\ \ln {(Q)}_{\mathrm{c}}\right)+{a}_2\ {\left(\ln (Q)\hbox{--} \ln {(Q)}_{\mathrm{c}}\right)}^2+{a}_3\sin \left(2\pi\ \left(t\hbox{--} {t}_{\mathrm{c}}\right)\right)\\ {}\kern3.7em +{a}_4\cos \left(\ 2\pi\ \left(t\hbox{--} {t}_{\mathrm{c}}\right)\right)+{a}_5\left(t\hbox{--} {t}_{\mathrm{c}}\right)+{a}_6{\left(t\hbox{--} {t}_{\mathrm{c}}\right)}^2\end{array}} $$
(1)

where ln is the natural logarithm function; Load is the measured riverine TN loads (kg/day); Q is the measured daily average discharge (m3/s); ln(Q)c is a centering term of the study period (a constant) to ensure that the linear and quadratic discharge terms are independent (m3/s); t is time in decimal days; tc is a centering time of the study period (a constant) to ensure that the linear and quadratic time terms are independent; α0...α6 are the fitted parameters in the multiple regression model; α1 and α2 describe the relation between loads and discharge; α3 and α4 describe seasonal variation in loads data; α5 and α6 describe the relation between loads and time.

SVR model

The SVR model was chosen since it exhibited better results than the ANN model, as indicated by the results of previous works (He et al. 2014; Kalteh 2013; Kisi 2012; Mohammadpour et al. 2015). The SVR model, which employed the principle of SRM, was developed on the basis of machine-learning process (Mohammadpour et al. 2015). A more detailed information on SVR can be found in published literature (Cristianine and Taylor 2000; Raghavendra and Deka 2014; Vapnik 1998). Thereby, only a short explanation regarding SVR was given as below, and the network architecture of SVR model is shown in Fig. 3.

Fig. 3
figure 3

Network architecture of the SVR model for riverine TN flux forecasting

Full size image

Consider a data set {(xi, yi), i = 1,…,n}, where xi refers to the input vector, yi is the desired value, and n refers to the total number of data patterns, the regression function of SVR is formulated as follows:

$$ f\ (x)=w\cdot \phi (x)+b $$
(2)

where w and b denote the weight vector and bias, respectively, and φ(x) denotes the non-linear mapping function. Parameters w and b are estimated by solving the following optimization problem:

$$ \operatorname{Minimize}:\frac{1}{2}{\left\Vert w\right\Vert}^2+C\sum \limits_1^n\left({\xi}_i+{\xi}_i^{\ast}\right) $$
(3)
$$ {\displaystyle \begin{array}{l}\mathrm{Subject}\kern0.17em \mathrm{to}\kern0.5em {y}_i-w\cdot \phi (x)-b\le \varepsilon +{\xi}_i\\ {}\kern5em w\cdot \phi (x)+b-{y}_i\le \varepsilon +{\xi}_i^{\ast}\\ {}\kern5em {\xi}_i\ge 0,{\xi}_i^{\ast}\ge 0\end{array}} $$
(4)

where ξi and \( {\xi}_i^{\ast } \) are slack variables, and C is the penalty parameter.

Equation (3) can be solved by using Lagrangian theory and imposing Karush-Kuhn-Tucker optimality condition.

The final form of the SVR model can be expressed as the following:

$$ f(x)=\sum \limits_{i=1}^n\left({\alpha}_i-{\alpha}_i^{\ast}\right)\cdot K\left({x}_i,x\right)+b $$
(5)

There are four possible choices for the kernel function of SVR model, involved sigmoid, linear, polynomial, and radial basis function (RBF). RBF is by far the most popular kernel function (Zhang et al. 2008) due to the following reasons: (1) RBF has the ability to model non-linear relationships by mapping inputs vectors into a high-dimensional feature space in a non-linear fashion; (2) the number of tuning parameters in RBF is fewer than those in sigmoid and polynomial kernels, making RBF more easy-to-use (Keerthi and Lin 2001); and (3) the superior performances of RBF have been demonstrated in numerous studies (Dibike et al. 2001; Keerthi and Lin 2001). Thus, RBF was taken as the kernel function for riverine TN flux forecasting in this study. The RBF is defined as follows:

$$ K\left({x}_i,x\right)=\exp \left(-\gamma \left\Vert {x}_i-x\left\Vert {}^2\right.\right.\right) $$
(6)

where γ is the adjustable kernel parameter.

Data normalization is a common step prior to processing AI model for scaling raw data into a more usable form for the model to utilize. There are four commonly used methods for performing data normalization, such as min-max, median, logarithmic function, and z-score transformation (Antanasijević et al. 2014; Feng et al. 2015; He et al. 2014; Najah et al. 2014; Ravansalar et al. 2017). The four normalization techniques were tested using the single SVR model for daily TN load forecasting and the values of the performance metrics are illustrated in Fig. 11. Obviously, the model constructed using z-score normalized input values yielded the best performance; as such, the z-score normalization was selected to perform transformation on all time series data in this study. The mathematical formula for z-score method is the following:

$$ {x}_{\mathrm{n}}=\frac{x-{x}_{\mathrm{mean}}}{x_{\mathrm{SD}}} $$
(7)

where xn is the normalized value; x is the original value; xmean and xSD are the mean and standard deviation of the original data sets.

Wavelet analysis

WA is regarded as a powerful tool for extracting the useful information in stationary or non-stationary data (Nourani et al. 2014). Short intervals are generally used to capture high frequency information, whereas long intervals are typically used to capture low frequency information inherent to the time series during WA (Shoaib et al. 2014). The WA decomposes a time series into approximation (e.g., a3) and details (e.g., d1, d2, and d3) by translating, stretching, or squeezing the wavelet (Seo et al. 2015). It can provide good localization characteristics in both time and frequency domains. Additionally, the choice of the mother wavelet in wavelet decomposition is flexible in terms of the time series properties (Adamowski and Sun 2010). Two main wavelet transforms present, namely, the continuous wavelet transform (CWT) and discrete wavelet transform (DWT) (Wei et al. 2013). The CWT of signal x(t) can be expressed as the following:

$$ {\mathrm{CWT}}_x^{\psi}\left(\tau, s\right)=\frac{1}{\sqrt{\left|s\right|}}{\int}_{-\infty}^{+\infty }x(t){\psi}^{\ast}\left(\frac{t-\tau }{s}\right) dt $$
(8)

where ψ is the mother wavelet; s is the scale parameter; τ is the translation parameter; * is the complex conjugate. The mathematical formula for the DWT is listed in the following equation:

$$ {\psi}_{j,k}(t)=\frac{1}{\sqrt{\left|{s}_0^j\right|}}\psi \left(\frac{t-k{\tau}_0{s}_0^j}{s_0^j}\right) $$
(9)

where j and k are the integers that control the wavelet dilation and translation, respectively. s0 > 1 is the fixed dilation step, and τ0 is the location parameter. The CWT needs a significant amount of computation time since it calculates wavelet coefficients at every possible scale. In addition to time consuming, CWT might produce abundant and invalid data. Compare with CWT, DWT is simpler to implement and requires less computation time and resources (Kalteh 2013). Therefore, DWT was adopted to couple with SVR to develop the hybrid WA-SVR model. The decomposition result of the original signal(s) by DWT satisfies the following: s = d1 + a1 = d1 + d2 + a2 = d1 + d2 + d3 + a3 and so on (Shoaib et al. 2014).

WA-SVR model

The flowchart of the WA-SVR model for forecasting riverine TN loads is illustrated in Fig. 4. The hybrid model was completed in five steps that were listed as follows: (i) estimation of daily and monthly TN load time series, (ii) selection of suitable input variables and identification of the optimal lag times for the inputs, (iii) implementation of DWT to decompose original time series into approximation (ai) and details (d1, d2,…, di), where i is the number of decomposition level, (iv) SVR model training and testing wherein approximation and details are used as inputs, and (v) evaluation of the developed WA-SVR model performance.

Fig. 4
figure 4

Flowchart of the WA-SVR model for riverine TN load forecasting

Full size image

Model performance and execution

The performances of the established model can be evaluated using the following criteria: efficiency coefficient, determination coefficient (R2), agreement index, Nash-Sutcliffe model efficiency (NS), mean absolute error, mean square error (MSE), standard error of prediction, mean absolute relative error, and so on. A good examination of model performance should contain at least one absolute error measure (e.g., MSE) and at least one goodness-of-fit or relative error measure (e.g., NS) (Legates and McCabe Jr 1999). Additionally, R2, as the widely applied statistical score metric, is often used to estimate the model performance. A model can be adequately assessed by R2, NS, and MSE, and thus, the model performances in this study were evaluated using these performance indexes. R2 indicates the percentage of variability that can be explained by the model (Singh et al. 2011). NS, an indicator of the model fit, is typically used for assessing the performance of hydrological models (Adamowski et al. 2012; Shoaib et al. 2016). MSE measures the absolute error regarding dependent variable forecasting (Legates and McCabe Jr 1999). If the R2 = 1, NS = 1, and MSE = 0, the model presents the perfect performance. These criteria can be computed as the following:

$$ {R}^2={\left(\frac{\sum \limits_{i=1}^n\left({P}_i-\overline{P}\right)\left({O}_i-\overline{O}\right)}{\sqrt{\sum \limits_{i=1}^n{\left({P}_i-\overline{P}\right)}^2\sum \limits_{i=1}^n{\left({O}_i-\overline{O}\right)}^2}}\right)}^2 $$
(10)
$$ \mathrm{NS}=1-\frac{\sum \limits_{i=1}^n{\left({O}_i-{P}_i\right)}^2}{\sum \limits_{i=1}^n{\left({O}_i-\overline{O}\right)}^2} $$
(11)
$$ \mathrm{MSE}=\frac{1}{n}\sum \limits_{i=1}^n{\left({O}_i-{P}_i\right)}^2 $$
(12)

where n is the number of observations; Oi and Pi denote the observed and forecasted ith values of TN loads, respectively; O̅ and P̅ are the mean values of observed and forecasted TN loads, respectively.

In this study, LOADEST model software (United States Geological Survey 2004) was used to estimate the continuous daily riverine TN loads. Wave toolbox in MATLAB 2014a (Mathworks Inc., Natick, USA) was used to perform WA. The SVR model was constructed using the LIBSVM toolbox, which is a software package of support vector machine algorithms working in MATLAB environment (Chang and Lin 2011). All the other computations were also conducted in MATLAB.

Results and discussion

Estimation of daily riverine TN loads

LOADEST model was employed to estimate the continuous daily riverine TN loads in ChangLe River from 2004 to 2012 using the discrete monitoring data and continuous daily flow data. The available data for a period of 6 years from 2004 to 2009 was used for calibrating LOADEST model parameters (i.e., α0…α6), whereas the remaining data for a period of 3 years from 2010 to 2012 was used for validation purpose. The calibration and estimation procedures within LOADEST are based on the adjusted maximum likelihood estimation (AMLE), maximum likelihood estimation (MLE), and least absolute deviation (LAD) methods (Runkel et al. 2004). AMLE and MLE are appropriate when the calibration model residuals are normally distributed. Of the two, AMLE is the suitable method when the calibration data set contains censored data. If the censored data is not contained in calibration data set, MLE is equal to AMLE. LAD can be applied when the residuals are not normally distributed (Runkel et al. 2004). Therefore, the appropriate estimation method can be determined by evaluating the statistical distributions of residuals and the types of calibration data. The probability plot correlation coefficient (PPCC) was calculated to estimate the residual distribution. A PPCC of 1.00 represents a perfect normal probability of residuals (Helsel and Hirsch 2002). In this work, the PPCC value was 0.988 (Table 1), indicating the model residuals were normally distributed. For the above reasons, AMLE was adopted for the calibration and estimation procedures within LOADEST.

Table 1 The calibrated LOADEST parameters for riverine TN loads in the ChangLe River
Full size table

The plot of the modeled and observed daily riverine TN loads in the ChangLe River is illustrated in Fig. 5. High R2 and NS implied that the established LOADEST model can be successfully applied to estimate daily riverine TN loads in the ChangLe River. The monthly TN loads were calculated via summation of the corresponding daily TN loads.

Fig. 5
figure 5

Plot of the modeled and observed daily riverine TN loads in the ChangLe River in a 2004–2009 and b 2010–2012

Full size image

The performances of WA-SVR and single SVR models were examined on riverine TN loads. To achieve this, the available riverine TN loads data was divided into a training data set from 2004 to 2009 and testing data set from 2010 to 2012. All the models were first trained using the training data set to obtain the optimum values of the parameters (C and γ) and then tested using the testing data set. The statistical parameters of the riverine TN loads data are given in Table 2.

Table 2 The riverine TN loads statistical parameters of each data set
Full size table

Application of the WA-SVR model

Model inputs

The previous riverine TN loads were considered as input variables in this paper. Appropriate lag times must be determined in advance for developing WA-SVR model. This is because the response of a hydrological system is inherently relied upon their previous states, so the use of time lagged data is necessarily required with aim to encode temporal features of the input data (Shoaib et al. 2016). The optimal lag time for the inputs can be identified through the statistical analysis of data series such as auto-correlation function, partial auto-correlation function (PACF), cross-correlation function, and average mutual information. PACF has the capability for removing the dependence on intermediate elements (those within lags interpreted as a regression of time series against its past lagged value) and identifying the extent to which current TN loads is correlated to past days (Yaseen et al. 2016). At present, this approach has been successfully applied in many hydrological studies including He et al. (2014), Kalteh (2016), Seo et al. (2015), Shiri and Kisi (2010), Yaseen et al. (2016), etc. Hence, the PACF method was employed here to determine the numbers of lags. The PACF values, calculated for a lag range of 1–16, are presented in Fig. 6. It could be seen from the figure that first 4 lags and 10 lags had the most amount of information that could be used to forecast short-term and long-term riverine TN loads, respectively. Consequently, 4 and 10 previous lags for daily and monthly forecasting, respectively, were selected as inputs to the WA-SVR model. It may be argued that the selection of 4 lags and 10 lags was not optimum. Nevertheless, the aim of this paper was limited to evaluation of the WA-SVR model performance and examination of the effects of mother wavelets on developed model efficiency rather than the selection of optimal inputs. This might be a subject of another study.

Fig. 6
figure 6

Partial auto-correlation function of a daily and b monthly riverine TN load time series

Full size image

Wavelet analysis

The riverine TN load time series were decomposed into approximation (low frequency, large scale) and details (high frequency, small scale) by DWT, which requires less computational effort and simpler implementation than the CWT (Adamowski et al. 2012). The selection of the efficient mother wavelet and determination of the decomposition level are two important issues in WA (Nourani et al. 2014). Many types of wavelet families exist, including Haar wavelet (haar), Daubechies wavelet (dbN), Coiflet wavelet (coifN), Mexican hat wavelet, Gaussian wavelet, Morlet wavelet, and so on (Minu et al. 2010). Haar, which was invented by Haar (1910), is a single symmetry orthogonal and discontinuity wavelet (Stolojescu 2012) and the simplest of all available wavelets (Shoaib et al. 2014). The dbN was proposed by Ingrid Daubechies. It is one of the most commonly used wavelets. In dbN, N denotes the number of vanishing moments. Symmlet wavelet (SymN), which was also proposed by Ingrid Daubechies, is a modification to the dbN and has improved symmetry (Seo et al. 2015). The coifN was named after R. Coifman who demanded Ingrid Daubechies to construct this wavelet (Daubechies 1992). The wavelet and scaling functions both considered in coifN have vanishing moments. Moreover, the Coiflet is a continuous, compact supported, orthogonal, and nearly symmetric mother wavelet. Meyer wavelet, also called mey, was designed by Meyer (1985). The dmey denotes the discrete approximation of the Meyer wavelet. In order to cover maximum range of wavelets in the current study, we surveyed effects of 23 mother wavelets which are from the 5 most frequently used wavelet families on the performance of developed WA-SVR model. A summary of mathematical properties of these mother wavelets is presented in Table 3.

Table 3 Mathematical properties of selected mother wavelets
Full size table

Another important issue that should be considered in WA is the selection of suitable decomposition level. To the authors’ best knowledge, there is no standard method for determining the decomposition level. Partal and Kisi (2007), Adamowski and Sun (2010), and Kisi and Shiri (2011) used trial and error method to select decomposition level and employed level 10, level 8, and level 3 decomposition, respectively. According to regression analysis, Shoaib et al. (2014, 2016) favored the use of decomposition level 9. Yet, Kisi (2010) suggested that using a large number of inputs should be avoided in order to save computational time and effort. Furthermore, the higher level of decomposition, the less likely the transformed signals represent the original time series (Belayneh et al. 2014). At present, an effective and operable empirical formula has been used in many studies to choose suitable decomposition level (Adamowski and Chan 2011; Aussem et al. 1998; Nourani et al. 2009a, 2009b; Tiwari and Chatterjee 2010). Here, we also used the following empirical formula to obtain the decomposition level:

$$ L=\operatorname{int}\left[\log (N)\right] $$
(13)

where int is the integer-part function; L is the number of decomposition level; N is the number of time series data. According to the time series number, L was equal to 3 and 2 for daily and monthly riverine TN load forecasting, respectively. Consequently, daily and monthly riverine TN load time series were decomposed into sub-series at three and two resolution levels using DWT, respectively. The original riverine TN load time series, as well as the approximations and details are shown in Fig. 7. Considering that all sub-series contain information related to the original time series (Adamowski and Sun 2010), the new inputs to SVR for the WA-SVR model were set by using all wavelet components.

Fig. 7
figure 7

Original(s) and decomposed time series (a2, a3, d1, d2, and d3) of a daily and b monthly riverine TN loads using dmey wavelet

Full size image

Parameter optimization of the SVR model

The key step for constructing a high-performance SVR model is the determination and optimization of the penalty parameter (C) as well as adjustable kernel parameter (γ). Parameter C controls the empirical error in optimization problems (Singh et al. 2011). Too small value will lead to an under-fitting problem, whereas too large value will result in an over fit of training data (Wang et al. 2007). Parameter γ, which determines the amplitude of kernel function, is the only parameter in the RBF kernel function (Noori et al. 2011). The LIBSVM toolbox provides cross validation with grid search algorithm to find the optimal pairwise C and γ, and the MSE value is used as the criterion. In fivefold cross validation, the data points in the training set are divided into five equal size sub-sets. In the next stage, four sub-sets are used to train the model, and the rest one sub-set is used for the testing. All instances in the entire training set can be forecasted once (Singh et al. 2014). The advantage and characteristic of the cross validation method is that it avoids the over-fitting problem (Hsu and Chang 2003). The algorithm of grid search divides the search range to be optimized into grids. All grid points are then traversed to derive the best results. The parameter ranges along with interval size determine the accuracy of grid search optimization (Singh et al. 2011). A higher accuracy can be achieved by decreasing step size and increasing parameters range (Wang et al. 2007). In this work, the most appropriate C and γ were obtained through the grid search over a range from 2−10 to 210 with a step size of 21. The optimal parameters were subsequently employed to train the SVR model. Figure 8 illustrates an example of the optimization of pairwise C and γ during the grid search.

Fig. 8
figure 8

Three dimension view of the optimization results for parameters C and γ (take the WA-SVR with dmey for monthly riverine TN load forecasting for example, best C = 512, γ = 0.00097656)

Full size image

Mother wavelet selection

The performance of different combined WA-AI models, such as WA-SVR model, is extremely sensitive to the mother wavelet. In this regard, 23 selected mother wavelets, including haar, db2, db3, db4, db5, db6, db7, db8, db9, db10, sym2, sym3, sym4, sym5, sym6, sym7, sym8, coif1, coif2, coif3, coif4, coif5, and dmey, were utilized to examine their impacts on the performance of WA-SVR model. The values of the R2, NS, and MSE statistics of different mother wavelets during testing stage are listed in Table 4. It was clearly that the proposed WA-SVR model provided different accuracies for various mother wavelets. For short-term riverine TN load forecasting, the performance of the WA-SVR for the 23 mother wavelets followed the order of dmey > db10 > db9 > sym7 > coif5 > sym8 > coif4 > db7 > db8 > sym5 > coif3 > db6 > sym6 > coif2 > db3 = sym3 > db2 > sym4 > sym2 > db5 > db4 > coif1 > haar. Normally, if the NS is greater than 0.8, a model can be considered as accurate, if the NS is greater than 0.65, a model can be considered as satisfactory (Borah and Bera 2004; Shu and Ouarda 2008). According to the NS, all the selected mother wavelets provided excellent results (NS > 0.8), except for haar (NS = 0.7835). The WA-SVR model with dmey performed best among all tested mother wavelets, and the corresponding increase in NS and R2 were about 20%, whereas the decrease in MSE was over 80% relative to the worst performance mother wavelet (haar). A relatively weaker efficiency of the WA-SVR model was achieved for long-term forecasting. This phenomenon was likely due to previous monthly variations having smaller impacts on the current riverine TN loads compared to daily variation (Fig. 6). And besides that, it should be kept in mind that the monthly riverine TN load values in the training set did not cover the entire range in the testing set (Table 2), which had negative influences on the model efficiency. The performance of WA-SVR model for the 23 mother wavelets followed the order of dmey > coif5 > coif4 > coif3 > sym8 > db10 > db4 > db7 > sym6 > sym4 > coif2 > db6 > db5 > db3 = sym3 > sym7 > coif1 > db9 > db8 > sym5 > db2 > sym2 > haar. The NS value of WA-SVR model with dmey, coif5, coif4 coif3, sym8, db10, db4, db7, and sym6 wavelets were all greater than 0.8, indicating accurate performance, whereas with 7 of the 23 wavelets, the NS values were less than 0.65, demonstrating relatively inferior results. In this study, dmey mother wavelet was selected for further WA-SVR model performance validation as it outperformed other mother wavelets.

Table 4 Comparison of performance of the WA-SVR model with different mother wavelets during testing stage
Full size table

Comparison between the WA-SVR and single SVR

To assess and validate the effect of data pre-processing tool WA on the SVR model’s efficiency, the single SVR model without wavelet decomposition was adopted as the benchmark for comparison. The optimal WA-SVR model results were compared to that of the single SVR model. The generation of a single SVR model, including data partition and associated parameter optimization, was accomplished in exactly the same way as the WA-SVR model.

In fact, although the observed minimum riverine TN loads may be close to zero, they cannot be negative. Unfortunately, some negative values existed in the outputs of the established models (i.e., WA-SVR and SVR). These values are not unusual but serve no purpose with regard to riverine TN flux forecasting. Accordingly, all negative forecasts were adjusted to minimum values of observations in testing data set (i.e., 438.73 kg/day for daily and 24,675.72 kg/month for monthly riverine TN load forecasting). After changing the negative forecasts, the WA-SVR model performance improved slightly. For example, the R2 and NS of the optimal WA-SVR model for monthly riverine TN load forecasting were increased by 2.63% from 0.8928 to 0.9163 and 2.84% from 0.8906 to 0.9159, respectively.

A demonstration of the comparison between the observed daily riverine TN loads and the proposed WA-SVR as well as the SVR model results in testing period is provided in Fig. 9 via the hydrograph and scatter plots. The hydrograph demonstrated that the WA-SVR results were closer to the corresponding observed values than the SVR forecasts. The WA-SVR and SVR models both generally underestimated the corresponding peak daily riverine TN loads. In the field of stream flow forecasting, several previous research exhibited that black-box data-driven models failed to produce good forecasting accuracy for extremely high values of stream flow. The authors of these studies pointed out the reason behind this phenomenon could be lack of data in the high value region in training data set, as the black-box data-driven models’ training required large number of input-output data sets (Kasiviswanathan et al. 2016; Kisi and Cimen 2011; Ravansalar et al. 2017; Yaseen et al. 2016). Obviously, the WA-SVR or SVR model constructed here also cannot be sufficiently trained with only a small number of riverine TN load peaks and consequently compromised the model performance in forecasting peak values of riverine TN load. However, the WA-SVR model had greater improvement than single SVR. For example, the WA-SVR estimated the maximum peak value as 112,829 kg/d instead of the observed 140,100 kg/d with an underestimation of 19.47%, while the SVR result was 18,708 kg/d with an underestimation of 86.65%. In scatter plots, the 1:1 line represents perfect results, in which when the points are closer to it, the model yields the better results (Wu et al. 2015). As seen from the scatter plots, a standard deviation around 1:1 line for the WA-SVR model was lower than that of the single SVR model. The fit line equations, which assume that the mathematical equations expressed as y = ax + b, revealed that the coefficient of a and b for the WA-SVR model are close to 1 and 0, respectively. The comparison between the WA-SVR and SVR test results illustrated that the hybrid model provided better performance than the single SVR model with regard to TN load forecasting. The WA-SVR model yielded smaller MSE and higher R2 and NS. Concretely, the R2, NS, and MSE for the WA-SVR were 0.9699, 0.9658, and 0.4885 × 107 kg/day, respectively, while those of SVR were 0.5929, 0.5083, and 7.0324 × 107 kg/day, respectively.

Fig. 9
figure 9

Observed and forecasted daily riverine TN loads by the WA-SVR and SVR models in testing period

Full size image

Figure 10 demonstrates the observed and forecasted monthly riverine TN loads by the WA-SVR and SVR models in the testing phase. As shown in the hydrograph, the WA-SVR forecasts were closer to the corresponding observed values than those of the single SVR results. The SVR model failed to forecast riverine TN loads 1 month in advance. In contrast, the WA-SVR model performed much better as WA considerably improved the performance of the SVR model. The R2 and NS of the WA-SVR model increased from 0.0439 to 0.9163 and from −0.0779 to 0.9159, respectively. While the MSE decreased from 4.1474 × 1010 to 0.3237 × 1010 kg/month compared with that of the SVR model. For peaks, the hybrid model offered less error than the single SVR model. The WA-SVR estimated the maximum peak value (855,061 kg/month) as 759,221 kg/month with an underestimation of 11.21%, whereas the SVR result was 136,405 kg/month with an underestimation of 84.05%. The WA-SVR forecasted the second maximum peak value as 736,429 kg/month instead of the observed 757,419 kg/month with an underestimation of 2.77%, and the SVR forecasted as 195,138 kg/month with an underestimation of 74.24%. The WA-SVR and SVR computed the third maximum peak value (492,082 kg/month) as 468,663 and 135,960 kg/month, respectively, with underestimation of 4.76 and 72.37%. The scatter plots also demonstrated that the SVR model suffered more from scattering, which indicated lower accuracy, whereas the WA-SVR model had a better fitting effect between the forecasted and observed data considering that all of the data points clustered closely to the 1:1 line.

Fig. 10
figure 10

Observed and forecasted monthly riverine TN loads by the WA-SVR and SVR models in testing period

Full size image

In the light of these findings, the joint application of the SVR and WA methods seemed to be more adequate than the single SVR without WA for NPS load forecasting in agricultural river systems. This finding may be primarily attributed to the WA decomposing the complex original time series into several simple wavelet components, which in turn exhibits the features (such as periodically) more clearly than the original signal (Kisi and Cimen 2011). In addition, the wavelet transformed data improved the ability of the SVR model by capturing useful information on various resolutions (Adamowski and Sun 2010).

Conclusions

A combined WA and SVR model was developed and explored for riverine TN load forecasting in the ChangLe River watershed based on antecedent riverine TN load values. The riverine TN load time series obtained through the LOADEST model were decomposed into sub-series by DWT. These sub-series were then used as conjunction model inputs. In the WA-SVR, the effects of mother wavelet functions on the model efficiency were evaluated and the results revealed that the WA-SVR model was sensitive to the mother wavelets. For daily forecasting, all the selected mother wavelets could provide accurate performance, except haar. The model with the dmey mother wavelet function yielded the best results. For monthly forecasting, dmey, coif5, coif4 coif3, sym8, db10, db4, db7, and sym6 wavelets gave accurate results. Additionally, the models with sym4, coif2, db6, db5, db3, sym3, and sym7 yielded satisfactory results, whereas the other 7 wavelets performed weakly. The comparison between WA-SVR and single SVR models indicated that WA can significantly improve the efficiency of the SVR model. For daily riverine TN load forecasting, the R2, NS, and MSE in the testing period were 0.9699, 0.9658, and 0.4885 × 107 kg/day with WA-SVR, and 0.5929, 0.5083, and 7.0324 × 107 kg/day with the SVR model. For monthly riverine TN load forecasting, the R2, NS, and MSE in the testing period were 0.9163, 0.9159, and 0.3237 × 1010 kg/month with the WA-SVR, and 0.0439, −0.0779, and 4.1474 × 1010 kg/month with the SVR model.

This study, for the first time, explored the WA-SVR combination model for riverine TN load forecasting. The results highlighted that the WA-SVR model provided a promising and effective method to address the problem of riverine nutrient load forecasting. However, some unsolved problems require future investigations and improvements for reinforcing the conclusions in this study. First, negative values which served no purpose as forecasts occurred in the results of the proposed model. The attempt to present an appropriate method for dealing with negative values yielded by the WA-SVR model is recommended. Second, the NPS loads are affected by complex factors, e.g., flow velocity, temperature, precipitation, and fertilization. Nevertheless, for the WA-SVR model built in this research, only previous riverine TN load data was taken into account. In the future, other data regarding the riverine TN loads will be needed to reinforce the results drawn from this work. Third, the optimum decomposition level was selected by empirical equation, which could not guarantee obtaining the best performance. A comparative investigation on the impact of different decomposition level on the combined model can be also encouraged to improve the efficiency of the constructed model. Besides, the results exhibited the limitations in the use of WA-SVR model for forecasting peaks. Thereby, it is also suggested the future studies to integrate the WA-SVR model with physically based models or empirical relationships between influencing factors and peak values for enhancing forecasting of TN load peak values.