Introduction

Due to the fact that providing accurate and reliable future streamflow information plays an important role in water allocation, flood-control and disaster relief, developing excellent streamflow forecasting methods are significant and has attracted more and more attention of hydrology researchers in this field (Dehghani et al. 2015; Rahman et al. 2014; Wang et al. 2011). For daily or hourly run-off prediction, researchers have developed relatively mature methods such as distributed conceptual models with physical mechanisms. These models use rainfall forecasting as input to simulate the interception, infiltration and formation of run-off and achieve good run-off forecasting results. Compared with short-term run-off forecasting, reliable long-term run-off forecasting is much more difficult to accomplish for the lack of satisfying rainfall forecasting information. To solve this problem, researchers tend to use some data-based artificial intelligence models, which do not seek complex nature of run-off process and do not rely on high-precision rainfall forecasting to approach hydrological processes. Artificial neural network (ANN) and support vector regression (SVR) are very widely used artificial intelligence models. These models have the capacity of representing highly non-linear correlations of input and output, however, they are still found to be inadequate when dealing with non-stationary data (Sehgal et al. 2014).

Hydrological processes are non-stationary and random (Yarar 2014). When simply analyzing and simulating the original run-off series by these models, the details of change are ignored so that forecasting accuracy is reduced. Providing useful decompositions of original non-stationary time series on various resolution levels and extracting the significant information based on the series structure is a feasible way to make improvements in predictive ability of a model. For this reason, in the present investigation, time series decomposition has been combined with the artificial intelligence models for predicting monthly streamflow. Hence, the choices of time series decomposition methods and prediction models are the most important issues in this study.

The decomposition of time series is a statistical method that deconstructs a time series into notional components. Various decomposition techniques based on different principles are recommended for time series prediction. One of the widely used decomposition techniques is discrete wavelet transform (DWT), which is very helpful for non-stationary processes. Labat (2005) made a detailed description of the mechanism of wavelet transform. It decomposes time series into both time and frequency domains and can produce trend, periods, and random component of original series. Since DWT analyzes time series in different scales independently, it is possible to reveal change of run-off on multi-resolution level. Due to these attractive properties, Budu (2013) combined feed-forward neural networks with wavelets preprocessing techniques to predict the daily inflow proved that the wavelets hybrid ANN model performed better compared to artificial neural network. Sahay and Srivastava (2014) proposed a wavelet transform-genetic algorithm-neural network model (WAGANN) for forecasting one-day-ahead monsoon river-flows and WAGANN models are superior to models using original flow-time series (OFTS) for inputs. Tiwari and Adamowski (2014) developed two types of hybrid wavelet-artificial neural network (WANN) to forecast weekly and monthly water demand with limited data availability, the results showed that the proposed methods were able to improve the accuracy and reliability of water demand forecasting by incorporating the capability of wavelet transformation. Another decomposition approach used for dealing with non-linear and non-stationary time series is Empirical mode decomposition (EMD). EMD is a signal processing tool that decomposes a time series into intrinsic modes without fixing any a priori bounds (Huang et al. 1998). EMD method decomposes data from non-stationary and non-linear processes into simple oscillatory functions through the Hilbert transform, and that will yield a meaningful instantaneous frequency. Contrary to wavelet transform, EMD works in temporal space directly rather than in the corresponding frequency space, and it is based on the principle of local-scale separation and doesn’t need any predetermined basis functions (Huang et al. 1998; Lee and Ouarda 2010). Thus, it is empirical, intuitive, direct, and adaptive, with a posterioridefined basis derived from the data. Decomposing the data through EMD and then building hybrid models to forecast streamflow were explored by Napolitano et al. (2011), Huang et al. (2014) and Wang et al. (2015).

The foregoing research mainly focused on developing all kinds of forecasting models combined with preprocessing decomposed techniques to achieve better performance; it is hard to find comparative investigation of different decomposition methods. Karthikeyan and Kumar (2013) adopted ARMA model based DWT and EMD to predict non-stationary time series and then compared the performance of two kinds of decomposing methods, but the influence of the highest-frequency components of DWT and EMD is not involved in their work. Analysis of high-frequency components is important to find out if they are just noise or if they capture important aspects of the signal dynamics. Therefore, a relatively complete comparative investigation needs to be made to discuss the effect of decomposition methods as well as highest frequency components on streamflow forecasting.

Selection of prediction models is another key step. Artificial intelligence models have achieved success in hydrological applications (Chen et al. 2014; Kasiviswanathan and Sudheer 2013; Sattari et al. 2012). Artificial neural network (ANN) has been widely applied to rainfall–runoff forecast, flood estimation and drought forecast due to its characters of adaptivity, self-organization, and self-learning ability (Hsu et al. 1995; Sattari et al. 2012). In recent decades, a new machine learning method called support vector machine (SVM) has been developed for classification and simulation. The training objective of SVM is to simultaneously minimize both the empirical risk and the model complexity so that local minima and overfitting problems will be avoided and the training method of SVM is expressed as a convex quadratic programming problem on the high dimensional space which makes the training rapidly solved (Lin et al. 2009). Lin et al. (2009) used SVM to forecast reservoir inflow during typhoon-warning periods and the results indicated that SVM model performed better than back-propagation artificial neural network model. Guo et al. (2011) forecasted monthly streamflow based on improved SVM model and found that the SVM showed better generalization ability and higher prediction accuracy than ANN. Wei et al. (2013) adopted a dynamic particle filter-support vector regression method and obtained good predictions. Inspired by these attractive performances, support vector regression (SVR) is selected as prediction model in this investigation.

Therefore, in this study, time series decomposition techniques DWT and EMD are separately combined with the model of support vector regression (SVR). The effect of EMD and DWT on streamflow forecasting is compared and the influence of high frequency components on model performance is analyzed. Two kinds of models, i.e., EMD-SVR and DWT-SVR are developed. For the purpose of comparison, in addition to the above-mentioned decomposition-based models, stand-alone SVR model is also developed. The constructed models are evaluated for forecasting streamflow for one-month-lead-time in the upper reaches of Yangtze River, China.

Methodology

Discrete wavelet transform

Wavelet analysis can reveal localized time and frequency information of non-stationary time series, so it is suitable for streamflow process, which is highly non-linear and includes a lot of random factors. Discrete wavelet transform (DWT) produces a series of approximations (low-pass version) to the original signal and details (high-pass version) at different resolution levels. The principle of DWT is as follows:

Suppose that wavelet function ψ(t) is the mother wavelet satisfying \(\int_{ - \infty }^{ + \infty } {\psi (t){\text{d}}t = 0}\), then successive wavelets ψ a,b (t) can be obtained through compressing and expanding ψ(t) at scale a and location b:

$$\psi_{a,b} (t) = |a|^{ - 1/2} \psi \left( {\frac{t - b}{a}} \right)$$
(1)

For the discrete time series f(t) with integer time steps, DWT in the dyadic decomposition scheme is defined as:

$$W_{\psi } f(j,k) = 2^{ - j/2} \sum\limits_{t = 0}^{N - 1} {f(t)} \bar{\psi }(2^{ - j} t - k)$$
(2)

where W ψ f(j, k) is the wavelet coefficient of the discrete wavelet with a = 2j, b = 2j k, \(\bar{\psi }(t)\) is the complex conjugate functions of ψ(t).

W ψ f(j, k) reflects the characteristics of f(t) in frequency and time domain at the same time. When the frequency resolution of wavelet transform is low and the time domain resolution is high, j becomes small. When the time domain resolution is low and the frequency resolution is high, j becomes large (Wang and Ding 2003).

Empirical mode decomposition

Empirical mode decomposition (EMD) produces Hilbert–Huang transform (HHT) by coupling with Hilbert spectral analysis (HSA) (Huang and Wu 2008). HHT acts similar to wavelet analysis, while the differences are that HHT is a posteriori and its theoretical basis is empirical.

The essence of EMD is to analyze characteristic time scales and recognize the intrinsic oscillatory modes empirically and finally, decompose the time series into a sum of different time modes accordingly. Each of these oscillatory modes is represented by an Intrinsic Mode Function (IMF). HHT is consistent with physically meaningful definitions of instantaneous frequency and amplitude (Huang and Wu 2008), and it obtains the physical meaning related to the full non-linear system through individual components in the linear system rather than a physically linear expansion. In this way, HTT has the ability to acquire the important features of non-stationary and non-linear series (Lee and Ouarda 2011).

EMD is implemented through an adaptively iterative process called “sifting”, which is the core of the algorithm. The sifting process serves to not only eliminate riding waves but also smoothen uneven amplitudes. For certain series x(t), the sifting processes of EMD are described by Huang et al. (1998).

After decomposition, the original signal x(t) can be written as a sum of IMFs C i (t) and a residual r n (t):

$$X(t) = \sum\limits_{i = 1}^{N} {C_{i} (t) + r_{n} (t)}$$
(3)

Support vector regression (SVR)

Support vector machine, which is known as classification and then extended to regression, was proposed by Vapnik (1995). Support vector regression (SVR) is the method solving the problem of regression with SVM. Detail description of SVR can be found in many open literature (Lin et al. 2009). The following is a brief description of SVR.

Suppose N known data points for training are{(X i , d i )} N i , X i is m-dimensional input vector and d i is 1D desired output at sample point i. The aim of SVR is to find a regression function in the form of Eq. (4).

$$y_{i} = {\mathbf{W}}\varphi \left( {X_{i} } \right) + b\quad \forall i = 1,2, \ldots ,N$$
(4)

where φ(X) is a non-linear mapping, W is hyperplane, and b is offset.

It is worth mentioning that a penalty function is used in SVR (Guo et al. 2011):

$$\left\{ \begin{aligned} |d_{i} - y_{i} | \le \varepsilon ,\quad{\text{not}}\;{\text{allocating}}\;a\;{\text{penalty}} \hfill \\ |d_{i} - y_{i} | > \varepsilon ,\quad{\text{allocating}}\;a\;{\text{penalty}} \hfill \\ \end{aligned} \right.$$
(5)

When the estimated value is within the ε- insensitive tube, the loss value will be zero. Parameters of above regression function can be acquired by minimizing the following objective function:

$$\hbox{min} \left[ {\frac{1}{2}\left\| W \right\|^{2} + C\sum\limits_{i = 1}^{N} {L^{\varepsilon } (y_{i} ,d_{i} )} } \right]$$
(6)
$$L^{\varepsilon } (y_{i} ,d_{i} ) = \hbox{max} (0,|y_{i} - d_{i} | - \varepsilon )$$
(7)

where C represents the regularized constant that weighing the model complexity and the empirical error. A relative importance of the empirical risk will increase when the value of C increases.

Then the method of Lagrange multipliers is introduced to solve the above optimization problem in its dual form:

$$\hbox{max} \left[ {\sum\limits_{i = 1}^{N} {(\alpha_{i}^{ + } - \alpha_{i}^{ - } )y_{i} } - \varepsilon \sum\limits_{i = 1}^{N} {(\alpha_{i}^{ + } + \alpha_{i}^{ - } )} - \frac{1}{2}\sum\limits_{i = 1,j = 1}^{N} {(\alpha_{i}^{ + } - \alpha_{i}^{ - } )(\alpha_{j}^{ + } - \alpha_{j}^{ - } )K(X_{i} ,X_{j} )} } \right]$$
(8)

where α + i , α − i are the Lagrange multipliers and K(X i , X j )is a non-linear kernel function, which can map the lower dimension input into a higher dimension linear space.

Radial basis kernel function is used in this study:

$$K(X_{i} ,X_{j} ) = \exp \left( { - \frac{{||X_{i} - X_{j} ||^{2} }}{{2\sigma^{2} }}} \right),\;\;\sigma \in R$$
(9)

Hybrid decomposing- SVR model

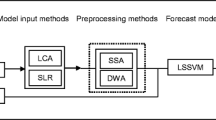
Decomposing-SVR model is a hybrid SVR model coupled with time series decomposition technique. Two types of decomposing technique i.e. DWT and EMD are adopted in this study. Construction of hybrid model is as follows. First, based on the auto-correlation function and the cross-correlation function of observed monthly streamflow and precipitation, appropriate inputs for models are chosen. Then observed streamflow and precipitation time series are decomposed into their sub-time series by DWT and EMD, respectively. For DWT, the sub-time series D1, D2 and D3 represent detail components corresponding to 2-, 4- and 8-months scale or periodicity, and A3 represents approximation component of 8-months scale. For EMD, the sub-time series IMF1 ~ IMF5 represent different oscillatory modes and r represents a residual after decomposition. Finally, hybrid models DWT-SVR and EMD-SVR are constructed by combining all the decomposed subseries with SVR models. D1 and IMF1 are called the ‘noise’ components, which are the most fluctuating and uncorrelated in original hydrology time series. To find out the influence of high-frequency components on streamflow forecasting, DWT*-SVR and EMD*-SVR models are established by removing D1 and IMF1 from the decomposed series. The working structures of DWT-SVR, DWT*SVR, EMD-SVR, EMD*-SVR and single SVR are given in Fig. 1.

Fig. 1
figure 1

Working structures of various models

Full size image

Application and results

Study area and data division

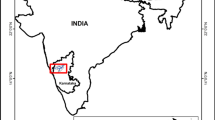
Jinsha River watershed is taken as the study area in this research. Jinsha River is in the upper reaches of Yangtze River and it originates in the northwest of Yunnan plateau. The total length is 2316 km and the water catchment area is 340,000 km2. Run-off volume of the river is abundant with an average annual flow of 149.8 billion m3. It features a big vertical drop of 3300 meters and hydropower resources of Jinsha River are rich, about 1.12 billion kW. 25 hydropower stations are in planning and 4 huge hydropower plants are already under construction. Monthly streamflow forecasting of Xiangjiaba, which is located in the basin outlet of Jinsha River, is researched in this study. Location of Jinsha River basin and Xiangjiaba station is shown in Fig. 2.

Fig. 2
figure 2

Location of Jinsha River basin and Xiangjiaba hydrologic station

Full size image

Data consist of run-off records from Xiangjiaba hydrometric station, and rainfall records from 32 meteorological stations in Jinsha River basin. To reduce the number of the model inputs and the complexity of the model structure, the rainfall used is the mean of the above 32 rainfall records. 48 years (January 1961 to December 2008) of the streamflow and rainfall data is plotted in Fig. 3. Data from the year of 1961–1997 (444 months) are used for model training and remaining data from 1998 to 2008 (132 months) are used for model validation.

Fig. 3
figure 3

Monthly streamflow and rainfall between January 1961 and December 2008

Full size image

Selection of model inputs

Selection of model inputs is an important phase in model calibration and it extremely affects the precision of the model. Generally, for the sake of simplicity, streamflow is the only input factor in many researches (Dehghani et al. 2015; Wu and Chau 2010; Yilmaz and Muttil 2013). In this paper, the influence of precipitation on the streamflow forecasting will be revealed by adding precipitation to the model. A result about the auto-correlation function and the cross-correlation function of streamflow and precipitation is shown in Fig. 4. Based on the analysis, the most correlated variables Q t-1, Q t-11, Q t-12 and P t-1, P t-2, P t-12 are selected as input variables of models, where Q t-1, Q t-11, Q t-12 stand for streamflow at 1, 11, 12 months ago, respectively; P t-1, P t-2, P t-12 stand for precipitation at 1, 11, 12 months ago, respectively.

Fig. 4
figure 4

a Auto-correlation coefficients for streamflow; b Cross-correlation coefficient for streamflow and rainfall

Full size image

Decomposition of the original data

The original data are, respectively, decomposed by DWT and EMD. EMD doesn’t need any predetermined basis functions, therefore five IMFs and one residual are generated directly from the initial series, which are displayed in Fig. 5. As for DWT decomposing procedures, subseries are obtained using fast Mallat algorithm on three decomposition levels, which is recommended by Aussem and Murtagh (1998) and Nourani et al. (2009). Selecting an appropriate mother wavelet is critical to obtain a better wavelet hybrid model. Maheswaran and Khosa (2012) pointed out that wavelets with wider support and higher vanishing moments are more suitable for irregular and oscillating hydrology series. Hence, an irregular mother wavelet, the Daubechies wavelet with five vanishing moments (db5), which has very high number of vanishing moments for a given support width, is selected. Three decomposition levels series of approximations (A) and details (D) through the high-pass and low-pass filter coefficients of the chosen db5 are displayed in Fig. 6, and each subseries may represent a special level of the temporal characteristics of the original time series. It can be seen from Figs. 5 and 6 that the high frequency decomposed components IMF1 and D1 are the most non-linear and disorder.

Fig. 5
figure 5

Sub-time series components decomposed by EMD

Full size image
Fig. 6
figure 6

Sub-time series components decomposed by DWT

Full size image

Model development

SVR, EMD-SVR, DWT-SVR, EMD*-SVR, DWT*-SVR discussed in “Methodology” section are evaluated for forecasting one-month-ahead streamflow in the Jinsha River of China. Based on different input combinations, eight models SVR-Q, SVR-QP, DWT-SVR-Q, DWT-SVR-QP, EMD-SVR-Q, EMD-SVR-QP, DWT*-SVR-QP and EMD*-SVR-QP are developed eventually in this research. SVR-Q has original streamflow with leading time of 1, 11, 12 months as inputs, DWT-SVR-Q has D1, D2, D3, A3 series (Fig. 5) produced by DWT decomposition of original streamflow as inputs. DWT-SVR-QP has D1, D2, D3, A3 series (Fig. 5) produced by DWT decomposition of original streamflow and precipitation as inputs. DWT*-SVR-QP has D2, D3, A3 series produced by DWT decomposition of original streamflow and precipitation as inputs. For EMD-SVR-Q, EMD-SVR-QP and EMD*-SVR-QP, the difference to above is that inputs are taken from subseries produced by EMD rather than DWT. The desired output of all models is one-month-ahead streamflow. All models and the corresponding inputs are provided in Table 1. In Table 1, Q t-1 and P t-1 denote original streamflow and precipitation at time t-1 respectively; Q t-1 (IMF1–IMF5, r) denote EMD components IMF1, IMF2, IMF3, IMF4, IMF5 and residue, and Qt-1 (D1–D3, A3) denote DWT components D1, D2, D3 and A3.

Table 1 Models and their corresponding inputs
Full size table

Based on the input–output pairs in training period, models will be separately optimized. When the optimization phase is done, all models will be applied to forecast monthly streamflow using the data from the historical series in validation period. The data are decomposed in advance by EMD or DWT based on different needs. For single SVR models, original series are directly used as inputs, for DWT-SVR hybrid models, original series will be decomposed by DWT and for EMD-SVR hybrid models, original series will be decomposed by EMD.

To improve the efficiency of training, model inputs and the desired output are conveniently standardized and scaled to the range [0, 1]. Model parameters are optimized by cross-validation (CV). CV is a standard technique for training SVR model. Typical fivefold cross-validation is adopted here.

Performance evaluation

The evaluation indicators of root mean square errors (RMSE), mean absolute errors (MAE), mean absolute percentage error (MAPE), correlation coefficient (R) and run time (RT) are employed to evaluate the accuracy and time cost of models. RMSE assesses the goodness of the fit related to high streamflow values whereas MAE measures a more balanced perspective of the fitness at moderate streamflows. R shows the degree which two variables are linearly related to. RT stands for time cost of model. RMSE, MAE and MAPE are defined as:

$${\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {Y_{i}^{\text{obs}} - Y_{i}^{\text{est}} } \right)^{2} } }$$
(10)
$${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {Y_{i}^{\text{obs}} - Y_{i}^{\text{est}} } \right|}$$
(11)
$${\text{MAPE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\frac{{Y_{i}^{\text{obs}} - Y_{i}^{\text{est}} }}{{Y_{i}^{\text{obs}} }}} \right|} \times 100\,\%$$
(12)

where N denotes the number of datasets, \(Y_{i}^{\text{obs}}\) represents the observed monthly streamflow. \(Y_{i}^{\text{est}}\) represents the estimated monthly streamflow.

Results analysis

Results of SVR models, SVR models combined with EMD and SVR models combined with DWT in validation period (January 1998 to December 2008) are shown in Figs. 7, 8 and 9, respectively. RMSE, MAE, MAPE, R and run time (RT) in the calibration and validation period are, respectively, given in Tables 2, 3 and 4. In view of indices RMSE, MAE, MAPE and R, Table 2 indicates that SVR-QP model, in which precipitation and streamflow as inputs, has a better accuracy than the SVR-Q model that only adopts streamflow as inputs. Table 3 shows that the performance of EMD-SVR-QP is superior to EMD-SVR-Q and proves again that the use of precipitation can improve modeling precision. Then EMD-SVR-QP and EMD*-SVR-QP are compared, it is found that removing the high frequency component IMF1 is inappropriate for a better accuracy. Results of DWT-SVR models are given in Table 4 and the same conclusions can be made for DWT-SVR models. In view of RT indices, it can be concluded from Tables 2, 3 and 4 that introducing precipitation data into model inputs will greatly influence the time cost in model calibration. Generally, more inputs lead to more cost of run time. However, once models have been calibrated, run time in model validation or forecast will be almost same.

Fig. 7
figure 7

Monthly streamflow estimations of single SVR models in the validation period

Full size image
Fig. 8
figure 8

Monthly streamflow estimations of SVR models combined with EMD in the validation period

Full size image
Fig. 9
figure 9

Monthly streamflow estimations of SVR models combined with DWT in the validation period

Full size image
Table 2 RMSE, MAE, MAPE, R and RT of the single SVR models
Full size table
Table 3 RMSE, MAE, MAPE, R and RT of the EMD-SVR based models
Full size table
Table 4 RMSE, MAE, MAPE, R and RT of the DWT-SVR based models
Full size table

Then a comprehensive analysis needs to be made to reveal the effect of different decomposing techniques on model accuracy based on Table 2, 3 and 4. Compare SVR-QP, EMD-SVR-QP and DWT-SVR-QP, all of which are optimum models in each group, it can be acquired that the models combined with decomposition techniques perform much better than single SVR model and DWT-SVR-QP improves the accuracy of prediction more highly than EMD-SVR-QP in both calibration and validation periods. Therefore, using time series decomposing techniques contributes to improving performance of forecasting, and decomposing technique DWT is more suitable than EMD for monthly streamflow modeling.

Furthermore, due to the reason that streamflow in flood season severely fluctuates, high-precision forecasting in that period is very challenging. An evaluation of the flood season (May–October) streamflow forecasting is discussed here. Results of SVR-QP, EMD-SVR-QP and EMD*-SVR-QP, DWT-SVR-QP and DWT*-SVR-QP in the validation period are illustrated in Fig. 10. It can be recognized that estimations of EMD-SVR-QP and DWT-SVR-QP approximate the observed streamflows better than single SVR model and hybrid models removing high frequency components. 20 % is considered as a reasonable and acceptable relative error in this study. Percentage of acceptable predictions, which is called qualified rate, is shown in Table 5. The results indicate that DWT-SVR-QP raises the qualified rate from 67 % of SVR-QP to 85 %. It can be seen from the table that DWT-SVR-QP achieves the greatest forecasting ability for flood season streamflow. Removing high-frequency components from original sub-series leads to an obvious reduction in forecast performance. The reason may be that streamflows in the flood season are extremely fluctuant and the high-frequency components contain the important information which is indispensable to estimate fluctuations.

Fig. 10
figure 10

Monthly streamflow estimations in the flood season

Full size image
Table 5 Qualified rate of forecasting in the flood season (May–October)
Full size table

Conclusions

Accuracy of monthly streamflow forecasting models coupled with different decomposition techniques was investigated in this paper. SVR, EMD-SVR, and DWT-SVR based models were, respectively, obtained by single support vector regression, SVR, combined with empirical mode decomposition, and SVR combined with discrete wavelet transform. To research the influence of precipitation on the forecast accuracy, all models were implemented with two kinds of inputs depending on whether antecedent precipitation was included. All models were applied to Xiangjiaba to perform one-month-ahead streamflow forecasting. Results can be summarized as follows:

  1. 1.

    All of the models that add antecedent precipitation in inputs exhibit a significant improvement, so a more excellent model can be built when precipitation information is taken into account.

  2. 2.

    Removing the high-frequency component from the subseries fails to improve the forecasting ability, especially for the forecasting in flood season. This is because sub-time series of first or second decomposition levels show major information on extreme flows. Therefore high-frequency component is indispensable to monthly streamflow forecasting.

  3. 3.

    Comparison results of SVR-QP, EMD-SVR-QP and DWT-SVR-QP models show that SVR-QP produces the worst performance, EMD and DWT both could significantly increase accuracy of monthly streamflow forecasting. Meanwhile, it can be acquired that DWT outperforms EMD in terms of the evaluation indices of RMSE, MAE, MAPE, R and RT.

  4. 4.

    For the flood season forecasting, SVR models combining EMD and DWT both raise the qualified rate based on the results from May to October. DWT-SVR-QP is superior to EMD-SVR-QP with a highest qualified rate of 85 %.

In conclusion, results in this paper indicate that models coupled with decomposition techniques perform better than the single models and decomposition technique DWT provides a superior alternative to EMD in monthly streamflow forecasting. Among all the developed models, DWT-SVR-QP which combining discrete wavelet transform and support vector regression, has the best performance and is recommended as an alternative to Xiangjiaba monthly streamflow forecasting.