Introduction

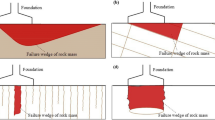
A major concern for foundation design of structures is to precisely estimate the bearing capacity of the underlying layer. The bearing capacity can be defined as the pressure required for causing failure through rupture of underlying soil or rock mass. Rock masses are commonly chosen as the underlying layer for important structures due to less settlement and high bearing capacity compared to soils. Figure 1 represents a typical sketch of a shallow foundation resting on a jointed rock mass. Bearing capacity failure in overloaded rock foundations is one of the common failure mechanisms in rocks (Sowers 1979). This failure mechanism mainly depends on the ratio of space between joints to foundation width (S/B), joint conditions (open or closed), the direction of joints, and rock type (Sowers 1979).

Fig. 1
figure 1

A typical sketch for a shallow foundation on jointed rock mass

Full size image

Direct determination of the ultimate bearing capacity using testing methods requires cumbersome and expensive laboratory or field tests. Therefore, several analytical and semi-empirical methods have been conducted to estimate the ultimate bearing capacity of rock beneath the foundations. Analytical methods such as finite element and limit equilibrium methods use initial assumptions for relating the bearing capacity to the footing geometry and rock properties (Terzaghi 1946; Bishoni 1968; Sowers 1979; Goodman 1989). The semi-empirical methods often propose a correlation between the bearing capacity and other properties of rock mass based on the empirical observations and experimental test results (Bowles 1996; Hoek and Brown 1988; Carter and Kulhawy 1988). One of the major drawbacks of the analytical methods is that they do not take into account the important role of the rock type and its qualitative mass parameters such as rock mass rating (RMR). On the other hand, the empirical methods often relate the bearing capacity to qualitative and rock mass classification parameters and do not account for the geometry of the foundations or space between joints. The limitations of the existing analytical and empirical methods imply the necessity of developing new models correlating the bearing capacity factor to both quantitative and qualitative parameters.

Soft computing techniques are considered as alternatives to traditional methods for tackling real-world problems. They automatically learn from data to determine the structure of a prediction model. Artificial neural network (ANN) is a well-known branch of soft computing (Alavi et al. 2010). This technique has been successfully employed to solve problems in civil engineering field (e.g., Kayadelen et al. 2009; Günaydın 2009; Kolay et al. 2010; Das et al. 2010; Yilmaz 2010a, b; Akgun and Türk 2010; Kaunda et al. 2010; Das et al. 2011a, b, c; Mert et al. 2011; Alavi and Gandomi 2011; Mollahasani et al. 2011; Yilmaz et al. 2012; Sattari et al. 2012; Tasdemir et al. 2013; Ocak and Seker 2012, 2013; Isik and Ozden 2013; Alkhasawneh et al. 2014; Wu et al. 2013; Maiti and Tiwari 2014; Park et al. 2013; Ceryan et al. 2013; Manouchehrian et al. 2014). Besides, ANN has been used to predict the bearing capacity of shallow foundations resting on soil layers (Soleimanbeigi and Hataf 2005; Padmini et al. 2008; Kuo et al. 2009; Kalinli et al. 2011).

This study is aimed at developing a new ANN model for the prediction of the bearing capacity of shallow foundations on rock masses. Despite the good performance of ANN in most cases, it is considered a black-box model. That is, it is not capable of generating practical prediction equations. To overcome this limitation, this study proposes an efficient approach to convert the derived ANN model into a relatively simple design equation through the interpretation of the fixed connection weights and bias factors of the best network structure. Multilayer perceptron (MLP), as one of the most popular ANN structures, is chosen for the analysis. A comparative database is used for the establishment of the models.

Artificial neural network

Artificial neural network is a computational simulated system that follows the neural networks of the human brain. The current interest in ANN is largely due to its ability to mimic natural intelligence in its learning from experience (Zurada 1992). ANN typically includes a series of processing elements, nodes or neurons, generally arranged in different layers such as input layer, output layer and one or more hidden layers between them. ANN and similar soft computing techniques are usually utilized to find the relationship or program between input and output variables. Unlike conventional methods, ANN has the ability to achieve acceptable results in less time and without need for predefined criteria, assumptions or rules. In the ANN process, inputs are adapted in hidden layer and after exit from output layer turn into the network’s results. ANN uses a learning rule to find a set of weights on training data. Then, the network produces new output with a particular accuracy. Thereafter, another data set is needed to validate the performance of training phase. This process is developed until the error reaches the minimum value (Alavi and Gandomi 2011).

Multilayer perceptron networks

Multilayer perceptron is one of the most widely used ANN structures utilizing feed-forward architecture. Rumelhart and McClelland (1986) and McClelland and Rumelhart (1988) developed back propagation (BP) or backward propagation of errors algorithm for training multilayer perceptrons. In MLP, each neuron of a layer is interconnected with weighted connections to all neurons of the next layer. Each layer may perform independent calculations on data that is received from the previous layer. In an artificial neuron, each input (x i ) from the previous layer is multiplied by an adaptive weight coefficient (w ij ) that connects two layers. Thereafter, the weighted inputs are summed (Summation Function) and a bias value (Bias j ) is added. This activity is then changed by a function (Transfer Function) to produce the output of the layer (y j ) or input of next layer. For nonlinear problems, the sigmoid functions (Hyperbolic tangent sigmoid or log-sigmoid) are usually selected as the transfer function (Alavi et al. 2010; Alavi and Gandomi 2011; Mollahasani et al. 2011). This process is typically shown by Eq. (1) and represented in Fig. 2.

$$ y_{j} = f\left( {\sum\limits_{i = 1}^{n} {w_{ij} .x_{i} + {\text{Bias}}_{j} } } \right) $$
(1)
Fig. 2
figure 2

Input–processing–output system in an artificial neuron

Full size image

The BP algorithm adjusts network weights by error propagation from the output to the input. In this algorithm, the process reverted and weight values changed to minimize the error (Alavi et al. 2010; Alavi and Gandomi 2011). Modifying the interconnections between layers will reduce the following error function (E):

$$ E = \frac{1}{2}\sum\limits_{n} {\sum\limits_{k} {(t_{k}^{n} - h_{k}^{n} )^{2} } } $$
(2)

where \( t_{k}^{n} \) and \( h_{k}^{n} \) are, respectively, the calculated output and the actual output value. n is the number of sample; and k is the number of output neurons.

Numerical simulation of bearing capacity

In order to reach reliable estimations of the bearing capacity of shallow foundations on rock masses, the impact of several parameters should be incorporated into the model development. The general forms of the existing prediction equations indicate that the ultimate bearing capacity of shallow foundations on rock mass mainly depends on the foundation width and properties of the rock beneath it (Terzaghi 1946; Bishoni 1968; Sowers 1979; Goodman 1989; Bowles 1996; Hoek and Brown 1988; Carter and Kulhawy 1988). The rock mass qualitative parameters such as rock quality designation (RQD) index and geological strength index (GSI) are widely used to develop empirical and semi-empirical equations for the evaluation of rock mass properties (Hoek and Brown 1988; Bowles 1996, 1988; Carter and Kulhawy 1988; AASHTO 2007; Paikowsky et al. 2010). The RMR index is another qualitative parameter that has found wide applications in various types of geological engineering projects. This parameter was introduced by Bieniawski (1978, 1989) to provide reliable estimation of rock mass properties. The RMR value represents different geologic parameters such as RQD index, joint or discontinuity spacing, joint condition, ground water condition, etc. Thus, the RMR parameter implicitly includes the effect of several important parameters for characterizing the rock mass behavior. The present study takes into account the effects of both these qualitative parameters, as well as other influencing quantitative parameters to predict the bearing capacity of shallow foundations on rock masses. It is notable that the rock mass is considered as a continuum equivalent medium. Consequently, the proposed model for the prediction of the ultimate bearing capacity (q ult) is considered to be a function of the following parameters:

$$ q_{\text{ult,ANN}} = f\left( {{\text{RMR}},{\mkern 1mu} q_{u} ,{\mkern 1mu} \frac{S}{B},{\mkern 1mu} \phi } \right) $$
(3)

where RMR is the rock mass rating, q u (MPa) the unconfined compressive strength of rock, S/B the ratio of joint spacing to foundation width (equivalent diameter), \( \phi \) (°) the angle of internal friction for rock mass.

Experimental database

The ANN-based models are developed using an extensive database including 102 elaborate experimental data obtained from different studies (Abu-Hejleh and Attwooll 2005; Baker 1985; Burland and Lord 1970; Carrubba 1997; Lord 1997; Glos and Briggs 1983; Goek and Hustad 1979; Hummert and Cooling 1988; Jubenville and Hepworth 1981; Lake and Simons 1970; Leung and Ko 1993; Maleki and Hollberg 1995; Mallard 1977; McVay et al. 2006; Nitta et al. 1995; Pellegrino 1974; Pells and Turner 1979, 1980; Radhakrishnan and Leung 1989; Spanovich and Garvin 1979; Thorne 1980; Ward and Burland 1968; Webb 1976; Williams 1980; Wilson 1976). The database contains results of 49 rock socket tests (6 centrifuge rock socket tests), 40 plate load tests and 13 load test on scaled model of footings. The database includes the results of experiments on circle and square footings of different sizes tested on various types of masses such as sandstone, claystone, shale, chalk, and basalt. The major bearing capacity values of rock mass is q ult, initially obtained or interpreted from load–displacement curves proposed by Hirany and Kulhawy (1988). Different parts of the employed database have been used by other researchers for the behavioral analysis of q ult (AASHTO 2007; Paikowsky et al. 2010). The descriptive statistics of the experimental results are given in Table 1. The complete list of the collected data is represented in Table 2.

Table 1 Descriptive statistics of parameters in database used to develop ANN-based model
Full size table
Table 2 The set of collected data incorporated in the ANN model and results
Full size table

Data preparation

Overfitting is one of the essential problems in generalization of ANN. Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations. A model which has been overfitted will generally have poor predictive performance, as it can exaggerate minor fluctuations in the data. An approach to avoid overfitting is to test individuals from the run on a validation set to find a better generalization. Then, another data set should be used at the end of the data analysis to verify the generalization performance of the model (Banzhaf et al. 1998; Gandomi et al. 2011). Accordingly, in the present study, the available data sets are randomly classified into three subsets: (1) learning, (2) validation (check), and (3) test subsets. The learning set is used to fit the models and the validation set is used to estimate the prediction error for model selection. Since both of the learning and validation data are involved in the modeling process, they can be categorized into one group, namely training data. Finally, the test set is employed for the evaluation of the generalization ability of the final chosen model. The learning, validation and test data are usually taken as 50–70, 15–25 and 15–25 % of all data, respectively (Shahin and Jaksa 2005; Alavi et al. 2011). In the present study, 85 % of the data sets are taken for the learning and validation processes (72 data vectors for the learning process and 15 data sets as the validation data). The remaining 15 % of the data sets are used for the testing of the obtained models.

Statistical criteria for measuring performance

The best ANN models are chosen on the basis of a multi-objective strategy as follows: (Alavi and Gandomi 2011; Gandomi et al. 2011):

  1. 1.

    The simplest model, although this is not a predominant factor.

  2. 2.

    The best fitness value on the learning data sets.

  3. 3.

    The best fitness value on the validation data sets.

In order to assess the performance of ANN model, correlation coefficient (R), root mean squared error (RMSE) and mean absolute error (MAE) are considered which are calculated using the following equations:

$$ R = \frac{{\sum\nolimits_{i = 1}^{n} {(h_{i} - \bar{h}_{i} )(t_{i} - \bar{t}_{i} )} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {(h_{i} - \bar{h}_{i} )^{2} \sum\nolimits_{i = 1}^{n} {(t_{i} - \bar{t}_{i} )^{2} } } } }} $$
(4)
$$ {\text{RMSE }}\left( {\text{MPa}} \right) = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {\left( {h_{i} - t_{i} } \right)^{2} } }}{n}} $$
(5)
$$ {\text{MAE }}\left( {\text{MPa}} \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {h_{i} - t_{i} } \right|} $$
(6)

in which h i and t i are, respectively, the actual and predicted output values for the ith output, \( \overline{{h_{i} }} \) and \( \overline{{t_{i} }} \) are the average of the actual and predicted outputs, and n is the number of sample.

Data normalization

An important step to optimize the learning process is data scaling or normalization. Normalization of data increases the speed of learning in neural networks and is especially efficient where the inputs are in widely different scales. More, it is recommended to normalize or standardize the inputs in order to reduce the chances of getting stuck in local optima or unchanged outputs (Alavi et al. 2010). The activation functions tangent sigmoid or log-sigmoid provide an output in the ranges [−1 1] and [0 1], respectively. There are several normalization methods (Swingler 1996; Mesbahi 2000). In this study, after controlling several normalization methods, the following method is used to normalize the variables to a range of [L, U]:

$$ X_{n} = \left( {U - L} \right)\frac{{X_{\hbox{min} } - X}}{{X_{\hbox{max} } - X_{\hbox{min} } }} + U, $$
(7)

where X max and X min are the maximum and minimum values of the variable and X n is the normalized value. In the present study, L = 0.05 and U = 0.95. Since the US Standard units are considered for the parameters in the original ANN modeling, the maximum and minimum values of the q u and q ult variables in Eq. (7) should be in kips per square foot (ksf). Consequently, q u,n and q ult,n , respectively, represent the normalized forms of q u and q ult, and can be readily determined using the following equations:

$$ q_{u,n} = \left( {U - L} \right)\frac{{5 - {\raise0.7ex\hbox{${q_{u} }$} \!\mathord{\left/ {\vphantom {{q_{u} } {0.0479}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${0.0479}$}}}}{1148.7-5} + U $$
(8)
$$ q_{{{\text{ult,}}\;n}} = \left( {U - L} \right)\frac{{5.22 - {\raise0.7ex\hbox{${q_{\text{ult}} }$} \!\mathord{\left/ {\vphantom {{q_{\text{ult}} } {0.0479}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${0.0479}$}}}}{1578.95 - 5.22} + U $$
(9)

in which, q u and q ult are in MPa. Evidently, the RMR, S/B, and ϕ parameters are not affected by this issue. These three parameters are normalized using Eq. (7) and their corresponding X max and X min values shown in Table 1.

Model development

The available database is used for establishing the ANN prediction models. After developing different models with different combinations of the input parameters, the final explanatory variables (RMR, q u , S/B, and \( \phi \)) are selected as the inputs of the optimal model. For the development of the ANN models, a script is written in the MATLAB environment using Neural Network Toolbox 5.1 (MathWorks 2007). The performance of an ANN model mainly depends on the network architecture and parameter settings. According to a universal approximation theorem (Cybenko 1989), a single hidden layer network is sufficient for the traditional MLP to uniformly approximate any continuous and nonlinear function. Choosing the number of the hidden layers, hidden nodes, learning rate, epochs, and activation function type plays an important role in the model construction (Alavi et al. 2010; Alavi and Gandomi 2011; Mollahasani et al. 2011). Hence, several MLP network models with different settings for the mentioned characters were trained to reach the optimal configurations with the desired precision (Eberhart and Dobbins 1990). The written program automatically tries various numbers of neurons in the hidden layer and reports the R, RMSE and MAE values for each model. The model that provided the highest R and lowest RMSE and MAE values on the learning and validation data sets is chosen as the optimal model. Various training algorithms are implemented for the training of the MLP network such as gradient descent (traingd), Levenberg–Marquardt (trainlm), quasi-Newton back-propagation (trainbfg), and resilient (trainrp) back-propagation algorithms. The best results are obtained by Levenberg–Marquardt method. Also, the transfer function between the input and hidden layer is log-sigmoid of form 1/(1 + e −x). A linear transfer function (purelin) is adopted between the hidden layer and output layer.

The weights and biases are randomly assigned for each run. These assignments considerably change the performance of a newly trained network even when all the previous parameter settings and the architecture are kept constant. This leads to extra difficulties in selection of optimal architecture and parameter settings. To overcome this difficulty, the weights and biases are frozen after the networks are well-trained. Thereafter, the following function is used to convert the optimal ANN model into mathematical equations relating the input parameters and the output parameter (h) (Goh et al. 2005; Alavi and Gandomi 2011):

$$ h = f_{\text{HO}} \left( {{\text{bias}}_{h} + \sum\limits_{k = 1}^{h} {V_{k} f_{\text{IH}} \left( {{\text{bias}}_{hk} + \sum\limits_{i = 1}^{m} {w_{ik} x_{i} } } \right)} } \right) $$
(10)

where bias h is the hidden layer bias, V k the weight connection between neuron k of the hidden layer and the single output neuron, bias hk the bias at neuron k of the hidden layer (k = 1, h), w ik the weight connection between the input variable (i = 1, m) and neuron k of the hidden layer, x i the input parameter i, f HO the transfer function between the hidden layer and output layer, and f IH is the transfer function between the input and hidden layer (Alavi and Gandomi 2011).

ANN-based formulation for q ult

The model architecture that gave the best results for the formulation of q ult is found to contain:

  • One invariant input layer, with 4 (n = 4) arguments (RMR, q u , S/B, and ϕ) and a bias term;

  • One invariant output layer with 1 node providing the value of q ult.

  • One hidden layer having 5 (m = 5) nodes.

Figure 3 shows a schematic illustration of the produced ANN network. The ANN model is built with a learning rate of 0.05 and trained for 1,000 epochs. After de-normalization of the output, the final ANN-based formulation of q ult (MPa) is as follows:

$$ q_{\text{ult}} \;({\text{Mpa}}) = 0.04788(5.22 - 1748.59(A - 0.95)) $$
(11)

where,

$$ A = \sum\limits_{k = 1}^{5} {\frac{{V_{k} }}{{1 + e^{{ - F_{j} }} }} + {\text{bias}}_{h} } $$
(12)
$$ F_{j} = {\text{RMR}}_{n} \; \times \;W_{1k} \; + \;q_{u,n} \; \times \;W_{2k} + \left( \frac{S}{B} \right)_{n} \; \times \;W_{3k} + \phi \; \times \;W_{4k} + {\text{bias}}_{k} $$
(13)

in which RMR n , q u,n , (S/B) n , and ϕ n , respectively, represent rock mass rating, unconfined compressive strength of rock, ratio of joint spacing to foundation width, and angle of internal friction for rock mass normalized using Eqs. (7) and (8). k is the number of the hidden layer neurons. The input layer weights (W k ), input layer biases (bias k ), hidden layer weights (V k ), and hidden layer biases (bias h ) of the optimum ANN model are presented in Tables 3 and 4. A comparison of the measured and predicted q ult values by ANN is shown in Fig. 4.

Fig. 3
figure 3

A schematic illustration of produced MLP network

Full size image
Table 3 Weight and bias values between the input and hidden layer
Full size table
Table 4 Weight and bias values between the hidden and output layer
Full size table
Fig. 4
figure 4

Measured versus predicted q ult values using the ANN model: a training (learning and validation) data, b testing data

Full size image

Calculation procedure: design example

A calculation procedure is proposed based on the fixed connection weights and bias factors of the best obtained ANN structure (Alavi and Gandomi 2011). The provided illustrative design example clearly explains the implementation of the ANN prediction equation. For this aim, one of the samples used for the testing of the models is taken. The RMR, q u , S/B, and ϕ values for this sample are equal to 50.00, 12.5 MPa, 1.35, and 34°, respectively, q ult is required. The calculation procedure can be divided into three sections: (1) normalization of the input data; (2) calculation of the hidden layers; and (3) prediction of the output (Alavi and Gandomi 2011). The calculation procedure is outlined in the following steps:

Step 1: Normalization of the input data (RMR, q u , S/B, and ϕ) to lie in a range of 0.05–0.95 and calculation of the input neurons (RMR n , q u,n , (S/B) n , and ϕ n ) for each input data vector using Eqs. (7) and (8). The input neurons are calculated as:

For RMR: the maximum and minimum values of the variable are 15 and 100, respectively. Thus:

$$ {\text{RMR}}_{n} \; = \;(0.95 - 0.05)\frac{{15 - {\text{RMR}}}}{100 - 15} + 0.95 = 0.579 $$

For q u : the q u,n value is obtained using Eq. (8). Thus:

$$ q_{u,n} = \left( {0.95 - 0.05} \right)\frac{{5 - {\raise0.7ex\hbox{${q_{u} }$} \!\mathord{\left/ {\vphantom {{q_{u} } { 0. 0 4 7 9}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${ 0. 0 4 7 9}$}}}}{1148.7 - 5} + 0.95 = 0. 7 4 8 $$

Similarly,

$$ (S/B)_{n} = \, 0.925\quad {\text{ and}}\quad f_{n} = \, 0.446. $$

Step 2: Calculation of the hidden layer. The input value of each neuron in the hidden layer is determined for five neurons using the input layer weights and biases shown in Table 3. Given the information provided, the input values of the neuron (F 1, …, F 5) are calculated using Eq. (13):

$$ {\text{F1}} = - 4. 3 6 60 \; \times \;0. 5 7 9 - 5. 9 3 9 2\; \times \;0. 7 4 8 + 4. 4 7 9 7\; \times \;0. 9 2 5 - 0. 8 7 7 8\; \times \;0. 4 4 6 - 2. 8 2 1 4 = - 6.0 3 9 6 $$

Similarly, \( F_{2} = \, 2.5286, \, F_{3} = \, 3.1551, \, F_{4} = \, - 4.0540,\quad{\text{and}}\quad F_{5} = \, 0.7077 \).

Step 3: Prediction of q ult. The input value of each output neuron is calculated using an activation function (log-sigmoid function). The calculated values are multiplied by the hidden layer connection weights (Table 4) and the summation is obtained:

$$ A = 6.3774f\left( {F_{1} } \right) \, + 9.4936f\left( {F_{2} } \right) - 2.8366f\left( {F_{3} } \right) - 0.8674f\left( {F_{4} } \right) - 1.3602f\left( {F_{5} } \right) - 4.3811 = \, 0.780 $$

where f(x) is the a log-sigmoid function of form 1/(1 + e −x). Using Eq. (11), the value of q ult is calculated as follows:

$$ q_{\text{ult}} = \, 0.0 4 7 8 8\; \times \;\left( { 5. 2 2- 1 7 4 8. 5 9\; \times \;\left( {0. 7 80 - 0. 9 5} \right)} \right) = { 14}. 4 8 {\text{ MPa}} $$

In this example, the results are in good agreement with the measured values (q ult = 14 MPa). The predicted q ult value is 3.4 % higher than the measured value.

Results and discussions

According to Smith (1986), if a model gives R > 0.8, and the error values (e.g., RMSE and MAE) are at the minimum, there is a strong correlation between the predicted and measured values. It can be observed from Fig. 4 that the ANN model with high R and low RMSE and MAE values is able to predict the target values with an acceptable degree of accuracy. The performance of the model on the training and testing data suggests that it has both good predictive abilities and generalization performance. Besides, new criteria recommended by Golbraikh and Tropsha (2002) are checked for external validation of the model on the testing data sets. It is suggested that at least one slope of regression lines (k or k′) through the origin should be close to 1. Also, the performance indexes of m and n should be lower than 0.1. Recently, Roy and Roy (2008) introduced a confirm indicator of the external predictability of models (R m ). For R m  > 0.5, the condition is satisfied. Either the squared correlation coefficient (through the origin) between predicted and experimental values (Ro 2), or the coefficient between experimental and predicted values (Ro′2) should be close to \( R_{\text{Test}}^{2} \), and close to 1. The considered validation criteria and the relevant results obtained by the models are presented in Table 5. As it is seen, the derived model satisfies the required conditions. The validation phase ensures the derived ANN model is strongly valid.

Table 5 Statistical parameters of the ANN model for the external validation
Full size table

In order to have an idea about the prediction performance of the proposed model against a classical model, a comparative study is conducted. For this aim, the obtained results are compared with those provided by the following well-known model developed by Goodman (1989) for the estimation of q ult of the non-fractured rocks:

$$ q_{\text{ult}} \; = \;q_{u} \left( {\frac{1}{{N_{\phi } - 1}}\left( {N_{\phi } \left( \frac{S}{B} \right)^{{{\raise0.7ex\hbox{${\left( {N_{\phi } - 1} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {N_{\phi } - 1} \right)} {N_{\phi } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${N_{\phi } }$}}}} - 1} \right)} \right),\;\quad N_{\phi } = \tan^{2} \left( {45 = \frac{\phi }{2}} \right) $$
(14)

where, q u is the unconfined compressive strength of rock, S/B the ratio of joint spacing to foundation width, ϕ the angle of internal friction for the rock mass, \( N_{\phi } \) the non-dimensional bearing capacity factor as a function of ϕ.

Figure 5 represents the prediction made by the Goodman’s and ANN models for the entire database. As can be observed, the proposed ANN model (R = 0.976, RMSE = 60.38, MAE = 32.97) model significantly outperforms the Goodman’s model (R = 0.880, RMSE = 443.22, MAE = 140.97). Note that another major advantage of the proposed model over the Goodman’s model is that it considers the important effect of rock mass classification through using RMR. It is worth mentioning that the most of the existing models are derived based on traditional statistical analyses (e.g., regression analysis). The major limitation of this type of analysis is that the structures of the models are designated after controlling only few equations established in advance. Thus, such models cannot efficiently consider the interactions between the dependent and independent variables. Conversely from the empirical and analytical methods, a distinction of ANN for determining the bearing capacity lies in its powerful ability to model the mechanical behavior without requesting a prior form of the existing relationships or any assumptions.

Fig. 5
figure 5

Experimental versus predicted q ult values using different models

Full size image

ANN sensitivity analysis of independent variables

It is known that the ANN weight values cannot be interpreted as regression coefficients nor can be used to compute the impact or response of variables. Considering the necessity of realizing the relative importance and output response, several approaches are proposed by various researchers to interpret the ANN weights (Garson 1991; Goh 1994; Olden et al. 2004). In this study, Garson (1991) approach is employed to obtain the relative importance of each variable. It is worth mentioning that the important role of RMR, q u , S/B and ϕ in the prediction of q ult is well-understood. Removing each of these parameters from the conducted analyses has resulted in decreasing the performance of the model. Thus, the sensitivity analysis is only performed to have a comparison between these important parameters.

However, according to the Garson’s approach, interconnection weights between layers of a trained neural network are partitioned and the absolute values of weights are taken to calculate the relative importance of each input variable. This approach has been implemented by several researchers (Das and Basudhar 2008; Alavi et al. 2010; Mollahasani et al. 2011). Figure 6 shows the procedure of this algorithm (Alavi et al. 2010). The relative importance contributions of RMR, q u , S/B and ϕ in the prediction of q ult obtained by ANN model are represented in Fig. 7. As represented in Fig. 6, the relative importance values for RMR, q u , S/B and ϕ are 19, 28, 35 and 19 %, respectively. These values indicate that the bearing capacity of shallow foundations on jointed (non-fractured) rock masses is more sensitive to q u and S/B compared to other input variables. The results generally conform to those noticed by Goodman (1989), Paikowsky et al. (2004, 2010).

Fig. 6
figure 6

The procedure Garson’s algorithm to determine the relative importance of each input variable

Full size image
Fig. 7
figure 7

The percentage relative importance histogram of each input variable for predicting q ult based on the Garson’s algorithm

Full size image

Parametric study

A comparative parametric study is performed to evaluate the response of the ANN model to the variation of each independent variable. The methodology is based on changing only one predictor variable at a time while the other variables are kept constant at the average values of their entire data sets. This procedure is repeated using another variable until the model response is obtained for all of the predictor variables (Alavi et al. 2011). In order to determine and compare the capability of the proposed model, the results of the parametric analysis of the Goodman’ model are also included. Figure 8 represents the parametric analysis results. The results for the ANN model indicate that q ult increases with increasing RMR, q u , S/B and ϕ. For S/B, the increasing trend for the ANN model is not as intense as that for the Goodman’ model. On the other hand, while q ult is remarkably increasing with increasing ϕ in the ANN model, the Goodman’ model seems not be very sensitive to the changes of this parameter.

Fig. 8
figure 8

The parametric analysis of q ult with different models

Full size image

Summary and conclusion

In the present study, a new model is proposed for the estimation of the q ult of shallow foundations on jointed rock masses using the ANN technique. For this aim, a comprehensive and reliable set of data including rock socket, centrifuge rock socket, plate load and large-scaled footing load test results is collected to develop the model. One of the major criticisms about ANN is that it usually does not provide practical prediction equations. To deal with this issue, the optimal ANN model is converted to a relatively simple equation. The tractable ANN-based design equation provides an analysis tool accessible to practicing engineers. The calculation procedure can readily be performed using a spreadsheet or hand calculations to provide precise predictions of q ult. Besides, the proposed model performs significantly better than the widely used Goodman’s model. Moreover, the derived model takes into account the important role of rock classification through using RMR. The results of the sensitivity and parametric analyses are generally expected cases from an engineering viewpoint. The sensitivity analysis indicates that q ult is more sensitive to q u and S/B compared to RMR and ϕ.