Introduction

Expansive soil and bedrock underlie more than one-third of world’s land surface. Each year, damage to buildings, roads, pipelines, and other structures by expansive soils is much higher than the damage caused by floods, hurricanes, tornadoes, and earthquakes combined (Jones and Holtz 1973). The estimated annual cost of damage due to expansive soils is $1,000 million in the USA, £150 million in the UK, and many billions of pounds worldwide (Gourley et al. 1993). However, as the hazards due to expansive soils develop gradually and seldom present a threat to life, they have received limited attention, despite their severe effects on the economy. Much of the damage related to expansive soils is not due to a lack of appropriate engineering solutions but to the non-recognition of expansive soils and expected magnitude of expansion early in land use and project planning. The damage to foundation on expansive soil can be avoided/minimized by proper identification, classification, quantification of swell pressure, and provision of an appropriate design procedure. Swelling potential of clayey soil is a measure of the ability and degree to which such a soil might swell if its environments were changed in a definite way. Hence, the expansive soil is classified based on its potential for swelling. However, there is not a definite expression of swell potential for classification of expansive soils (Nelson and Miller 1992). Holtz (1959) referred to swell potential as the volume change of air-dried undisturbed sample, whereas Seed et al. (1962) defined it as change in volume of a remolded sample. Though factors like clay content, Atterberg’s limits, and mineral types are found to affect the swelling potential, the available literature presents contradicting results. McCormack and Wilding (1975) found clay content to be reliable in predicting swelling potential for soil dominated by illite, whereas according to Yule and Ritchie (1980) and Gray and Allbrook (2002), there is no relationship between clay percentage and soil swelling. The cation exchange capacity (CEC), saturation moisture, and plasticity index (PI) are also important indices for estimation of swelling potential (Gill and Reaves 1957). Parker et al. (1977) concluded swell index and PI as superior to other indices for swelling potential. El-Sohby and El-Sayed (1981) observed that parameters like initial water content, type of clay mineral, initial dry density, clay content, and type of coarse grained fraction are major controlling factors for the swelling pressure of soil.

The swelling pressure depends upon various soil parameters such as mineralogy, clay content, Atterberg’s limits, dry density, moisture content, initial degree of saturation, etc. along with structural and environmental factors. The parameters are interrelated in a complex manner, and it is difficult to model and analyze effectively taking all the above aspects into consideration. However, it can be measured easily with relevant data pertaining to soil, structure, and environment. So various statistical/empirical methods have been attempted for predicting the swelling pressure based on index properties of soil (Mowafy and Bauer 1985; Mallikarjuna 1988; Das 2002). Recently, Erzin and Erol (2004) presented regression equation for prediction of swelling pressure of Bentonite–Kaolinte clay mixture. However, these regression methods are developed based on the total available data and have not been tested with new data set.

The ANNs are becoming more reliable than statistical method due to their special attributes of identifying complex system when the input and output are known from either laboratory or field experimentation. Kayadelen et al. (2009) presented a neuro-fuzzy model for prediction of swelling potential of compacted soil. The biggest challenge in successful application of ANN is when to stop training. If training is insufficient then the network will not be fully trained, whereas if training is excessive then it will memorize the training pattern or learn noise. When the numbers of data points are scanty the training set is driven to a very small value, but when new data are presented to the network the error is too large, which is known as overfitting. The network needs to be equally efficient for new data during testing or validation, which is called as generalization. There are different methods for generalization like early stopping and cross validation (Basheer 2001; Shahin et al. 2002; Das and Basudhar 2006). In case of early stopping criteria the error on the validation/testing set is monitored during the training process and the training is stopped when the error on the testing set begins to rise. In cross validation an independent test set is used to assess the performance of the model at various stages of learning. However, this method is not suitable if data points are scanty. The ‘learning’ or ‘training’ process in ANN, in general, is a nonlinear optimization of an error function. The aim of the training is to minimize the error function to get the optimized weight vectors. The most commonly used error function is the mean squared error (MSE) function. The error associated with weights and sigmoid function is a highly non-linear optimization with many local minima. Local and global optimization methods are carried out for finding out the weight vectors. The steepest descent algorithm and Levenberg–Marquardt (LM) algorithm which are gradient search algorithms are mostly used in ANNs applied to geotechnical engineering problems (Das 2005). As the characteristics of traditional nonlinear programming based optimization method are initial point dependent, the results obtained using backpropagation algorithm are sensitive to initial conditions (weight vectors) (Shahin et al. 2002). The use of global optimization algorithms like genetic algorithm (GA) and simulated annealing for training of ANN, though being widely used in other fields of engineering (Morshed and Kaluarachchi 1998), in geotechnical engineering use of GA for training ANN is limited (Goh 2002; Goh et al. 2005). In recent past another heuristic global optimization, called differential evolution (DE), introduced by Storn and Price (1995) is being used successfully in aerodynamic shape optimization and mechanical design.

The support vector machine (SVM) is an emerging machine learning technology where prediction error and model complexity are simultaneously minimized. It provides a new, efficient novel approach to improve the generalization performance due to which the method has received much attention compared to other artificial intelligence techniques. In many applications the results of SVMs are found to equally good if not better than ANN, but they are computationally efficient and produce an actual mathematical function. This has been used for classification problem and non-linear regression estimations to different engineering problems and also in some geotechnical engineering problems (Goh and Goh 2007; Pal 2006; Samui 2008).

With the above points in view, in the present study ANN models using DE algorithm and Bayesian regularization algorithm for training process are used for prediction of swelling pressure of soil from the inputs: natural moisture content (w n), dry density (γ d), liquid limit (LL), plasticity index (PI), and clay fraction (CF). Similarly, different SVM models are also developed based on different kernel functions. The statistical performance criteria like correlation coefficient (R 2), coefficient of efficiency (E), overfitting ratio, maximum absolute error (MAE), average absolute error (AAE), and root mean square error (RMSE) are used to evaluate different ANN and SVM models. The obtained ANN parameters (weights and biases) are interpreted to identify important input parameters.

Methodology

Artificial neural network (ANN)

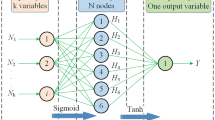
Artificial neural network is an artificial intelligence system/alterative statistical tool inspired by the behavior of human brain and nervous system. A typical structure of ANN consists of a number of processing elements or neurons that are usually arranged in layers: an input layer, an output layer, and one or more hidden layers. The input from each processing element in the previous layer is multiplied by an adjustable connection weight (w ji ). At each neuron, the weighted input signals are summed and a threshold value (bias) (b j ) is added. The combined input (I j ) is then passed through a nonlinear transfer function {f()} to produce the output of processing element. The adjustable connection weights and biases are obtained by ‘learning’ or ‘training’ process, which is nonlinear optimization of an error function. This is equivalent to the parameter estimation phase in conventional statistical models. In the present study, the ANN models are trained with differential evolution and Bayesian regularization method and are defined as DENN and BRNN, respectively. The use of DENN is not reported and use of BRNN is limited in geotechnical engineering (Goh et al. 2005; Das and Basudhar 2008). The results are compared with that obtained from commonly used Levenberg–Marquardt trained neural networks (LMNN) to discuss the prediction efficiency of the networks. The above neural network models have been developed using MATLAB tool boxes (MathWork 2001). A brief description of the Bayesian regularization and differential evolution neural network is presented here for completeness.

Bayesian regularization method

In case of back propagation neural network (BPNN) the error function considered for minimization is the mean square error (MSE). This may lead to overfitting due to unbounded values of weights. The other method, called as regularization, in which the performance function is changed by adding a term that consists of mean square error of weights and biases is given below.

$$ {\text{MSEREG}}\, = \,\gamma \,{\text{MSE}}\, + \,(1 - \gamma )\,\,{\text{MSW}} $$
(1)

where MSE is the mean square error of the network, γ is the performance ratio and

$$ {\text{MSW}}\, = \,{\frac{1}{n}}\sum\limits_{j\, = \,1}^{n} {w_{j}^{2} } .$$
(2)

This performance function will cause the network to have smaller weights and biases thereby forcing networks less likely to be overfit. The optimal regularization parameter γ is determined through Bayesian framework (Demuth and Beale 2000) as the low value of γ will not adequately fit the training data and high value of it may result in overfitting. The number of network parameters (weights and biases) that are being effectively used by the network can be found out by the above algorithm. The effective number of parameters remains the same irrespective of the total number of parameters in the network. In the present study it has been applied using MATLAB routine and it is a built-in function in MATLAB (Math Inc 2001). The above combination works best when the inputs and targets area scaled in the range [−1, 1] (Demuth and Beale 2000).

Differential evolution neural network

The training of the feed-forward neural network using differential evolution optimization is known as differential evolution neural network (DENN) (Ilonen et al. 2003). The DE optimization is a population-based heuristic global optimization method. Unlike other evolutionary optimizations, in DE the vectors in current populations are randomly sampled and combined to create vectors for next generation. The real-valued crossover factor and mutation factor govern the convergence of the search process. The details of DENN are available in Ilonen et al. (2003).

Support vector machine

Recently, SVM has been used to solve non-linear regression estimation and time series prediction by introducing ε-insensitive loss function (Mukherjee et al. 1997; Muller et al. 1997; Vapnik 1995, 1998). The SVM implements the structural risk minimization principle (SRMP), which has been shown to be superior to the more traditional empirical risk minimization principle (ERMP) employed by many of the other modeling techniques (Osuna et al. 1997; Gunn 1998). SRMP minimizes an upper bound of the generalization error, whereas ERMP minimizes the training error. In this way, it produces the better generalization than traditional techniques.

In this section, a brief introduction is presented on the construction process of SVM for regression problems. There are three distinct characteristics of SVM when it is used to estimate the regression function. First of all, SVM estimates the regression using a set of linear functions that are defined in a high-dimensional space. Second, SVM carries out the regression estimation by risk minimization where the risk is measured using Vapnik’s ε-insensitive loss function. Third, SVM uses a risk function consisting of the empirical error and a regularization term which are derived from the SRM principle. In SVM, high generalization performance is achieved by minimizing the sum of the training set error and a term that depends on the Vapnik–Chervonenkis (VC) dimension. This study uses the SVM as a regression technique by introducing a ε-insensitive loss function. The ε-insensitive loss function \( \left( {L_{\varepsilon } (y)} \right) \) can be described in the following way:

$$ \begin{aligned} & L_{\varepsilon } \left( y \right) = 0 \\ & \quad{\text{for }}\left| {f\left( x \right) - y} \right| \varepsilon\; {\text{otherwise}}\;L_{\varepsilon } \left( y \right) = \left| {f\left( x \right) - y} \right| - \varepsilon \end{aligned}$$
(3)

This defines a ε tube (Fig. 1) so that if the predicted value is within the tube, the loss is zero, while if the predicted point is outside the tube, the loss is the magnitude of the difference between the predicted value and the radius, ε, of the tube. Assume that the training dataset consists of l training sample \( \left\{ {\left( {x_{1} , y_{1} } \right), \ldots, \left( {x_{l} , y_{l} } \right)} \right\} \) where x is the input and y is the output. A problem with learning is related to choosing a function that predicts the actual response y as closely as possible, with a precision of ε. For this study, x = [w n, γ d, LL, PI, CF] and y = [SP]. Let us assume a linear function

$$ f\left( x \right) = \left( {w \cdot x} \right) + b $$
(4)

where \( w \in R^{n} \) and \( b \in r \); w = an adjustable weight vector; b = the scalar threshold; R n = n-dimensional vector space; and r = one-dimensional vector space.

Fig. 1
figure 1

Shows a typical architecture of SVM for swelling pressure (SP) prediction with pre-specified accuracy ε and slack variable ξ in support vector regression (Scholkopf 1997)

Full size image

The main aim of SVM is to find a function \( f\left( x \right) \) that gives a deviation ε from the actual output (y), which is, at the same time, as flat as possible. Flatness in the case of Eq. 4 means that one seeks a small w. One way of obtaining this is by minimizing the Euclidean norm\( \left\| w \right\|^{2} \) (Smola and Scholkopf 2004). The convex optimization problem thus involves

$$ \begin{aligned} & {\text{Minimize}}:{\frac{1}{2}}\left\| w \right\|^{2} \\& {\text{Subjected to}}:y_{i} - \left( {\left\langle {w \cdot x_{i} } \right\rangle + b} \right) \le \varepsilon \,,\;i \, = 1, 2, {\ldots} ,{\it{l}} \\& \quad\quad \left( {\left\langle {w \cdot x_{i} } \right\rangle + b} \right) - y_{i} \le \varepsilon \,,\,i \, = 1, 2, {\ldots} ,{\it{l}} \end{aligned}$$
(5)

The best regression line is defined by minimizing the following cost function:

$$\begin{aligned} & {\text{Minimize}}:{\frac{1}{2}}\left\| w \right\|^{2} + C\sum\limits_{i = 1}^{l} {\left( {\xi_{i} + \xi_{i}^{*} } \right)}\\& {\text{Subjected to}}: \, y_{i} - \left( {\left\langle {w \cdot x_{i} } \right\rangle + b} \right) \le \varepsilon + \xi_{i} , \,\, i = 1, 2, {\ldots} , {\it{l}} \\ & \quad\quad\quad\,\,\left( {\left\langle {w \cdot x_{i} } \right\rangle + b} \right) - y_{i} \le \varepsilon + \xi_{i}^{*}, \,\,i = 1, 2, {\ldots} , {\it{l}}\\ &\quad\quad\quad\,\,\xi_{i} \ge 0\,\,{\text{and}}\,\,\xi_{i}^{*} \ge \,\;0, \, i = 1, 2, \ldots ,{\it{l }} \end{aligned}$$
(6)

Hence, the Lagrangian function is constructed from both the objective function and corresponding constraints in Eq. 6 as follows:

$$ \begin{gathered} L\left( {w,\,\xi ,\xi^{ * } ,\alpha ,\alpha^{ * } ,\gamma ,\gamma^{ * } } \right) = {\frac{{\left\| w \right\|^{2} }}{2}} + C\left( {\sum\limits_{i - 1}^{l} {\left( {\xi_{i} + \xi_{i}^{ * } } \right)} } \right) - \sum\limits_{i = 1}^{l} {\alpha_{i} } \left[ {\varepsilon + \xi_{i} - y_{i} + \left\langle {w \cdot x_{i} } \right\rangle + b} \right] \hfill \\ - \sum\limits_{i = 1}^{1} {\alpha_{i}^{ * } \left[ {\varepsilon + \xi_{i}^{ * } + y_{i} - \left\langle {w \cdot x_{i} } \right\rangle - b} \right]} - \sum\limits_{i = 1}^{l} {\left( {\gamma_{i} \xi_{i} + \gamma_{i}^{ * } \xi_{i}^{ * } } \right)} \hfill \\ \end{gathered} $$
(7)

where L is the Lagrangian and α, α *, γ, and γ * are the Lagrangian multipliers. The partial derivative of L with respect to ω, b, ξ and ξ * need to be zero to satisfy the saddle point condition.

$$ \partial_{w} L = 0 \Rightarrow w = \sum\limits_{i\; = \;1}^{l} {x_{i} \left( {\alpha_{i} - \alpha_{i}^{*} } \right)} $$
$$ \partial_{b} L\; = 0 \Rightarrow \sum\limits_{i\; = \;1}^{l} {\alpha_{i} = \sum\limits_{i\; = \;1}^{l} {\alpha_{i}^{*} } } $$
$$ \partial_{\xi } L = 0 \Rightarrow \sum\limits_{i = 1}^{l} {\gamma_{i} = } \sum\limits_{i = 1}^{l} {\left( {C - \alpha_{i} } \right)} $$
$$ \partial_{{\xi^{*} }} L = 0 \Rightarrow \sum\limits_{i = 1}^{l} {\gamma_{i}^{*} = } \sum\limits_{i = 1}^{l} {\left( {C - \alpha_{i}^{*} } \right)} $$
(8)

Substituting (8) into (7) yields the dual optimization problem

$$ {\text{Maximize}}: - \varepsilon \sum\limits_{i\; = \;1}^{l} {\left( {\alpha_{i}^{*} + \alpha_{i} } \right) + \sum\limits_{i\; = \;1}^{l} {y_{i} \left( {\alpha_{i}^{*} - \alpha_{i} } \right) - {\frac{1}{2}}\sum\limits_{i\; = \;1}^{l} {\sum\limits_{j\; = \;1}^{l} {\left( {\alpha_{i}^{*} - \alpha_{i} } \right)\left( {\alpha_{j}^{*} - \alpha_{j} } \right)\left( {x_{i} \cdot x_{j} } \right)} } } } $$
$$ {\text{Subjected to}}:\sum\limits_{i\; = \;1}^{l} {\alpha_{i} = \sum\limits_{i\; = \;1}^{l} {\alpha_{i}^{*} } } \,;0 \le \alpha_{i}^{*} \le C\;\,{\text{and}}\;\,0 \le \alpha_{i} \le C $$
(9)

The coefficients α i and \( \alpha_{i}^{*} \)are determined by solving the above optimization problem (Eq. 9). An important aspect is that some Lagrange multipliers \( (\alpha_{i} ,\;\alpha_{i}^{*} ) \) will be zero, implying that these training objects are considered to be irrelevant for the final solution (sparseness). The training objects with nonzero Lagrangian multipliers are called support vectors. These are the objects with prediction errors larger than ±ε. In this way, the value of ε determines the amount of support vectors. Obviously, if ε is too large, too few support vectors are selected, which leads to a decrease in the final prediction performance. Furthermore, if the Lagrangian multipliers of the support vectors all have different values, it means that one support vector is considered to be more important than another one. So Eq. 4 can be written as

$$ f\left( x \right) = \sum\limits_{\rm(support\;vectors)} {\left( {\alpha_{i} - \alpha_{i}^{*} } \right)} \left( {x_{i} \cdot x} \right) + b $$

where

$$ b = - \left( {{\frac{1}{2}}} \right)w \cdot \left[ {x_{\text{r}} + x_{s} } \right].$$
(10)

From Eq. 10 it is clear that w has been completely described as a linear combination of training patterns. So, the complexity of a function represented by support vectors is independent of the dimensionality of input space and it depends only on the number of support vectors. The entry of the data in inner products is very important because (1) the dimension of the objects does not appear in the problem to be solved and (2) extension of this linear approach to nonlinear regression can be easily made.

When linear regression is not appropriate, then the input data must be mapped into a high-dimensional feature space through some nonlinear mapping (Boser et al. 1992) (see Fig. 2). In optimization problem expressed in Eq. 9, x has been replaced by the feature space, Φ(x). So, the optimization problem (Eq. 9) can be written as

$$ {\text{Maximize}}: - \varepsilon \sum\limits_{i\; = \;1}^{l} {\left( {\alpha_{i}^{*} + \alpha_{i} } \right) + \sum\limits_{i\; = \;1}^{l} {y_{i} \left( {\alpha_{i}^{*} - \alpha_{i} } \right) - {\frac{1}{2}}\sum\limits_{i\; = \;1}^{l} {\sum\limits_{j\; = \;1}^{l} {\left( {\alpha_{i}^{*} - \alpha_{i} } \right)\left( {\alpha_{j}^{*} - \alpha_{j} } \right)\left( {\Upphi \left( {x_{i} } \right) \cdot \Upphi \left( {x_{j} } \right)} \right)} } } } $$
$$ {\text{Subjected to}}:\sum\limits_{i\; = \;1}^{l} {\alpha_{i} = \sum\limits_{i\; = \;1}^{l} {\alpha_{i}^{*} } } \,;0 \le \alpha_{i}^{*} \le C\,{\text{and}}\,0 \le \alpha_{i} \le C $$
(11)
Fig. 2
figure 2

Concept of nonlinear regression

Full size image

The concept of a kernel function [\( K\left( {x_{i} , x_{j} } \right) = \Upphi \left( {x_{i} } \right) \cdot \Upphi \left( {x_{j} } \right) \)] has been introduced to reduce computational demand (Cristianini and Shwae-Taylor 2000; Cortes and Vapnik 1995). Hence, the optimization problem can be written as

$$ {\text{Maximize}}: - \varepsilon \sum\limits_{i\; = \;1}^{l} {\left( {\alpha_{i}^{*} + \alpha_{i} } \right) + \sum\limits_{i\; = \;1}^{l} {y_{i} \left( {\alpha_{i}^{*} - \alpha_{i} } \right) - {\frac{1}{2}}\sum\limits_{i\; = \;1}^{l} {\sum\limits_{j\; = \;1}^{l} {\left( {\alpha_{i}^{*} - \alpha_{i} } \right)\left( {\alpha_{j}^{*} - \alpha_{j} } \right)\left( {K\left( {x_{i} \cdot x_{j} } \right)} \right)} } } } $$
$$ {\text{Subjected to}}: \, \sum\limits_{i\; = \;1}^{l} {\alpha_{i} = \sum\limits_{i\; = \;1}^{l} {\alpha_{i}^{*} } } \;\;0 \le \alpha_{i}^{*} \le C\;\;{\text{and}}\;\;0 \le \alpha_{i} \le C $$
(12)

The introduction of kernels according to Mercer’s theorem (Vapnik 1995) avoids an explicit formation of the nonlinear mapping, makes the dimension of feature space even infinite, and reduces the computational load greatly by enabling the operation in low dimensional input space instead of high-dimensional feature space. Some common kernels, such as a polynomial (homogeneous), polynomial (nonhomogeneous), radial basis function, Gaussian function, and sigmoid functions have been used for non-linear cases. The regression function Eq. 4 has been obtained by applying the same procedure as in the linear case. Figure 3 shows the architecture of a SVM for prediction of swelling pressure. Three kernel functions used in this study are polynomial, radial basis, and spline functions. The SVM models developed using radial function, polynomial, and spline functions are named as SVM-R, SVM-P and SVM-S, respectively.

Fig. 3
figure 3

Architecture of SVM for swelling pressure (SP) prediction

Full size image

Results and discussion

The data from various sources available in literature (Aciroyd and Husain 1986; Abdujauwad 1994; Abdujauwad et al. 1998) are taken with input parameters are natural moisture content (w n), dry density (γ d), LL, PI, clay fraction (CF), and swelling pressure (SP) as output. The total number of data points considered is 230 out of which 167 are taken for training and 63 are taken for testing. The maximum, minimum, average, and standard deviation for the data used are shown in Table 1 and it can be seen that it covers a wide range of values. The successful application of a method depends upon the identification of suitable input parameters. Table 2 shows the cross correlation between the inputs and output; it can be seen that CF, LL, and PI are found to be important input parameters for predicting swelling pressure.

Table 1 Parameters of the data considered for the present study
Full size table
Table 2 Cross correlation between the inputs and output
Full size table

The results of different ANN models using the above parameters are shown in Table 3. The correlation coefficient (R 2) and root means square error (RMSE) are mostly for performance criteria evaluation of ANN models. However, R 2 is a biased parameter and sometimes, higher values of R 2 may not necessarily indicate better performance of the model because of the tendency of the model to be biased toward higher or lower values (Das and Basudhar 2006). The coefficient of efficiency (E) is also considered. The E is defined as

$$ E\,\,\, = \,\,\,{\frac{{E_{1} - \,E_{2} }}{{E_{1} }}} $$
(13)

where

$$ \begin{gathered} E_{1} \,\, = \,\,\sum\limits_{t\; = \;1}^{N} {({\text{SP}}_{\text{m}} - \mathop {{\text{SP}}_{\text{m}} }\limits^{\_\_\_\_} )}^{2} \hfill \\ E_{2} \,\, = \,\,\sum\limits_{t\; = \;1}^{N} {\left( {{\text{SP}}_{\text{p}} - {\text{SP}}_{\text{m}} } \right)}^{2} \hfill \\ \end{gathered} $$
(14)

and SPm, ŜPm and SPp are the measure, average, and predicted swelling pressure, respectively. The E value compares the modeled and measured values of the variable and evaluates how far the network is able to explain total variance in the data set. The overfitting ratio is defined as the ratio of RMSE for testing and training data, and it defines the generalization. A multilinear regression (MLR) analysis was also done considering input parameters as per Erzin and Erol (2004) and the results are presented in Table 3. The developed ANN models are found to be more efficient compared to MLR in terms R 2 and E values and have a strong correlation between predicted and observed values with |R| > 0.8 (Smith 1986). It can also be seen that comparing the values of R 2 and E values for training and testing data, BRNN is found to better than DENN and LMNN. However, DENN is having good generalization with small overfitting ratio, followed by LMNN and BRNN.

Table 3 General performance of different neural network models
Full size table

The RMSE value only defined the efficiency of a model overall; however, MAE can reveal the presence of regional areas of poor prediction. Figures 4 and 5 show the value of MAE, AAE, and RMSE for different ANN models for training and testing data, respectively. It can be seen that for training data, BRNN is having lowest values of MAE, AAE, and RMSE. However, for testing data, AAE is comparable for all the methods, but based on MAE and RMSE values BRNN performs better than DENN and LMNN. Hence, based on different statistical performance criteria for the present study it can be concluded that BRNN is better followed by DENN and LMNN. The weights and biases of the final network are presented in Table 4 for BRNN. The weights and biases can be utilized for selection of important input parameters based on its interpretation.

Fig. 4
figure 4

Comparison of prediction capabilities of ANN models for training data

Full size image
Fig. 5
figure 5

Comparison of prediction capabilities of ANN models for testing data

Full size image
Table 4 Weights and biases of BRNN for swelling pressure of soil
Full size table

The ANN is considered as a ‘Black box’ system due to insufficient explanations to the weight vectors, but methods like Garson’s algorithm and connection weight approach have been used utilizing the weight vector to identify the important input vectors (Das and Basudhar 2006). Such a study also made here to compare the above two methods in identifying the important parameters. Table 5 shows the ranking of important input parameters as calculated from Garson’s algorithm and connection weight approach with the weights obtained from DENN, BRNN, and LMNN. It can be seen from that the ranking of important input parameters as obtained by Garson’s algorithm and Connection weight approach is different for BRNN and LMNN, whereas for DENN the ranking of first and second parameters are same by both the methods.

Table 5 Relative importance of different input parameters
Full size table

The sucessful application of SVM models depends upon suitable paramters like type of kernel function and the parameters C and ε are obatined by trial and error. Table 6 presents the results of SVM models developed. Based on R 2 and E values SVM model with radial basis kernel function (SVM-R) found to be more efficient compared to models developed with other kernel functions (SVM-P and SVM-S). From Table 6, it is clear that SVM model employs 65–75% (radial basis function = 74.85%, polynomial kernel = 65.26% and spline kernel = 66.46%) of the training patterns as support vectors. So, SVM is remarkable in producing an excellent generalization level while maintaining the sparsest structure. Sparseness means that a significant number of the weights are zero (or effectively zero), which has the consequence of producing compact, computationally efficient models, which in addition are simple and therefore produce smooth functions. In SVM, support vectors represent prototypical examples. The prototypical examples exhibit the essential features of the information content of the data, and thus are able to transform the input data into the specified targets. Figures 6 and 7 show the value of MAE, AAE, and RMSE for different SVM models for training and testing data, respectively. It can be seen that for training data SVM-R is having lowest values of MAE, AAE, and RMSE. In comparison to ANN models SVM-R model is found to be better than all the ANN models. The use of the SRM principle in defining cost function provided more generalization capacity with the SVM compared to the ANN, which uses the empirical risk minimization principle. SVM uses only three parameters (radial basis function: σ, C, and ε; polynomial kernel: degree of polynomial, C, and ε). In ANN, there are a larger number of controlling parameters, including the number of hidden layers, number of hidden nodes, learning rate, momentum term, number of training epochs, transfer functions, and weight initialization methods. Obtaining an optimal combination of these parameters is a difficult task as well. Another major advantage of the SVM is its optimization algorithm, which includes solving a linearly constrained quadratic programming function leading to a unique, optimal, and global solution compared to the ANN. In SVM, the number of support vectors is determined by algorithm rather than by trial-and-error, which has been used by ANN for determining the number of hidden nodes.

Table 6 General performance of SVM for different kernels
Full size table
Fig. 6
figure 6

Comparison of prediction capabilities of SVM models for training data

Full size image
Fig. 7
figure 7

Comparison of prediction capabilities of SVM models and for testing data

Full size image

In this study, a sensitivity analysis has been carried out to extract the cause and effect relationship between the inputs and outputs of the SVM model. The basic idea is that each input of the model is offset slightly and the corresponding change in the output is reported. The procedure has been taken from the work of Liong et al. (2000). According to Liong et al. (2000), the sensitivity (S) of each input parameter has been calculated by the following formula:

$$ S_{\text{i}} = {\frac{1}{N}}\sum\limits_{i}^{N} {\left( {{\frac{{\% {\text{Change}}\;{\text{in}}\;{\text{output}}}}{{\% {\text{Change}}\;{\text{in}}\;{\text{input}}}}}} \right)} \times 100 $$
(15)

where N is the number of data points. The analysis has been carried out on the trained model by varying each of input parameter, one at a time, at a constant rate of 20%. The result of the above analysis is also presented in Table 5. According to the sensitivity analysis using SVM-model, PI is found to be more important parameters followed by γ d and w n, which is similar to ANN analysis using connection weight approach.

Conclusions

The different ANN techniques and SVM models examined here have shown the ability to build accurate models with high predictive capabilities for prediction of swelling pressure of soil from the inputs: natural moisture content (w n), dry density (γ d), liquid limit (LL), plasticity index (PI), and clay fraction (CF). The ANN and SVM models are found to be more efficient compared to MLR analysis. Based on different statistical performance criteria, the Bayesian regularization neural network (BRNN) model is found to be more efficient compared to DENN and LMNN. However, the DENN model is found to better in terms of generalization. The performance of the developed SVM model is better than the developed ANN models. The ranking of important input parameters is found to be consistent as per connection weight approach for the ANN model considered here. However, while using Garson’s algorithm the ranking is found to be different for different ANN models. Developed ANN and SVM models have the advantage that once the model is trained, it can be used as an accurate and quick tool for predicting swelling pressure without a need to perform any manual work such as using tables or charts. Comparison between the ANN and SVM model indicates that SVM model is superior to ANN model for predicting swelling pressure.