1 Introduction

It generally has been recognized that grain size is a fundamental independent variable controlling permeability in unconsolidated sediments. Previous theoretical and empirical investigations into the relationship between particle size and inter-granular permeability have resulted in the well-known formula (Eq. 1) for intrinsic permeability. In Eq. 1, d is particle diameter and c is dimensionless constant [1].

$$ k = cd^{ 2} $$
(1)

Since permeability is the measure of the ease with which water moves through aquifer material, certain relationships must exist between permeability and the statistical parameters that describe the grain-size distribution of the porous mediums.

Soft computing techniques—such as fuzzy logic, artificial neural networks, genetic algorithms, and neuro-fuzzy systems, which were first used in design of higher technology products—are now being used in many branches of sciences and technologies, and their popularities gradually increase.

Earth sciences aim to describe very complex processes and are in need of new technologies for data analyses. The number of researches in evolutionary algorithms and genetic programming, neural science and neural net systems, fuzzy set theory and fuzzy systems, fractal and chaos theory, and chaotic systems aiming the solution of problems in earth sciences (estimation of parameters; susceptibility, risk, vulnerability and hazard mapping; interpretation of geophysical measurement results; many kinds of mining applications; etc.) was especially increased in the last 5–10 years.

Correlations have been a significant part of scientific researches from earliest days. In some cases, it is essential as it is difficult to measure the amount directly, and in other cases it is desirable to ascertain the results with other tests through correlations. The correlations are generally semi-empirical based on some mechanics or purely empirical based on statistical analysis [2].

However, determination of permeability coefficient (k) of a soil is time-consuming, expensive, and involves destructive tests. If reliable predictive models could be obtained between k with quick, cheap, and nondestructive test results such as grain-size distribution parameters, it would be very valuable for the estimation of k.

The study presented herein aims to predict the permeability coefficient (k) of the coarse-grained soils due to grain-size distribution curves using a few soft computing techniques (artificial neural networks—ANN and adaptive neuro-fuzzy inference system—ANFIS) and to compare the models in prediction capability point of view. Soil samples have been collected from various locations of Ostrava (Czech Republic) and tested. The tests included grain-size distribution and permeability coefficient; and d 10, d 30, and d 60 were first correlated with k; and statistically significant models were selected. In order to establish predictive models, soft computing techniques such as artificial neural networks and neuro-fuzzy models were used, and prediction performances were then analyzed.

2 Perspective and purpose

Especially in water-bearing soils, permeability is one of the most important characteristics that significantly affect groundwater flow. Permeability represents the ability of a porous medium to transmit water through its interconnected voids. Accurate estimation of permeability is considered crucial for successful groundwater development and management practices. Grain-size distribution mainly controls the intrinsic permeability of medium, and increase in grain size increases the permeability due to the large pore openings. Moreover, sorting and uniformity of the grain size are also very important for permeability. Permeability decreases in poorly sorted soils because of the fine grains in pore spaces, while uniform soils have greater permeability coefficient than non-uniform soils.

Statistical grain-size distribution analyses are cheaper and lesser dependent on the geometry and hydraulic boundaries of the aquifer but reflect almost all the transmitting properties of the media [3]. That is why numerous attempts have been made to define the relationship between permeability and grain-size distribution of soil. Some well-known examples of these researches are as follows.

Hazen [4] first proposed a relationship (Eq. 1) between k and effective grain size (d 10). Shepherd [1] extended Hazen’s work by performing power regression analysis on 19 sets of published data for unconsolidated sediments. The data sets ranged in size from 8 to 66 data pairs. He found that the exponent in Eq. 1 varies from 1.11 to 2.05 with an average value of 1.72 and that the value of the constant c is most often between 0.05 and 1.18 but can reach a value of 9.85. Values for both c and the exponent are typically higher for well-sorted samples with uniformly sized particles and highly spherical grains. Uma et al. [5] suggested an equation to estimate the Ks and transmissivity of sandy aquifers of the same form as Eq. 1, with c values that depend on the nature of the geologic environment. Krumbein and Monk [6] proposed an equation based on experiments performed with sieved glacial outwash sands that were recombined to obtain various grain-size distributions. Kozeny [7] proposed an equation based on porosity and specific surface. Rawls and Brakensiek [8] used field data from 1,323 soils across the United States to develop a regression equation that relates porosity n, percentages of sand- and clay-sized particles in the sample. Jabro [9] estimated permeability from grain-size and bulk density data. Sperry and Peirce [10] developed a linear model to estimate permeability based on grain size, shape, and porosity. Lebron et al. [11] sought to improve upon permeability prediction methods by quantifying the characteristics of the pore spaces at a microscopic scale [12].

However, many attempts were done for the estimation of k; correlation coefficients (R 2) of the models were generally lower than ~0.80; and whole grain-size distribution curves were not included in the assessments.

Alyamani and Sen [3] included more information about the entire grain-size distribution curve by relating k to the initial slope and intercept of the curve for 32 sandy soil samples obtained in Saudi Arabia and Australia, and proposed the following equation:

$$ k = 1. 50 5*[I_{\text{o}} + 0.0 2 5*(d_{ 50} - d_{ 10} )]^{ 2} $$
(2)

in Eq. 2, k is expressed in cm/s, I o is x-intercept of the straight line formed by joining d 50 and d 10 of the grain-size distribution curve (mm). Alyamani and Sen [3] found that a log–log plot of k versus [I o + 0.025 * (d 50 − d 10] for their data set yielded a straight line having an R 2 = 0.94.

In the useful suggested method of Alyamani and Sen [3], an extra graph, which is plotted by calculated percentiles corresponding to increments of 5% starting from 5% (d 5, d 10, d 15, d 20,…,d 95), is needed. I o is then calculated from intercept of the straight-line drawn by joining d 50 and d 10 of this graph.

In order to predict the permeability coefficient from grain-size distribution curves directly, some neural computing models were constructed in this paper, and more information about the entire grain-size distribution curve relating to uniformity and sorting degree was included in the assessment of k. For grain-size distribution analyses and determination of permeability coefficient, selected 243 soil sample sets were first tested according to American Society for Testing and Materials (ASTM) guidelines [13, 14]. These analyses were performed on the samples collected from the various locations of Ostrava (Czech Republic). After drawing the grain-size distribution curves, as the parameters of uniformity and sorting degree, d 10 (grain-size diameter at which 10% by weight), d 30 (grain-size diameter at which 30% by weight), and d 60 (grain-size diameter at which 60% by weight) were then determined from the grain-size distribution curves. The results obtained from the experiments and their basic test statistics are tabulated in Table 1.

Table 1 Basic statistics of the results obtained from analyses
Full size table

3 Data sets used in the models

In order to establish relationships among the parameters obtained in this study, simple regression analyses were first performed, and relations between k with d 10 (grain-size diameter at which 10% by weight), d 30 (grain-size diameter at which 30% by weight), and d 60 (grain-size diameter at which 60% by weight) were analyzed employing linear, power, logarithmic, and exponential functions (Table 2). Regression equations were established among k with grain-size distribution analyses results (Table 3), and it was found that the relationships were not statistically enough strong to establish significant models by traditional statistical methods. Figure 1 shows the plot of the k versus d 10, d 30, and d 60. However, exponential regression models are relatively stronger than other models (Table 2). That is why some soft computing techniques were used for prediction of permeability coefficient from d 10, d 30, and d 60.

Table 2 Correlation coefficients (R 2) obtained from the simple regressions between k with d 10, d 30, d 60
Full size table
Table 3 Predictive models for the assessment of k
Full size table
Fig. 1
figure 1

k versus d 10, d 30, d 60 graphics

Full size image

Multiple regression analysis was also carried out to correlate the measured permeability to three grain-size parameters, namely, d 10, d 30, and d 60 (Table 4). Multiple regression model to predict permeability is given below.

$$ k = \left( {0.00 4} \right)d_{ 10} + \left( { 3. 4* 10^{ - 5} } \right)d_{ 30} + \left( { 8. 6* 10^{ - 6} } \right)d_{ 60} $$
(3)
Table 4 Model summaries of multiple regressions for prediction of k
Full size table

In fact, the coefficient of correlation between the measured and predicted values is a good indicator to check the prediction performance of the model. Figure 2 shows the relationships between measured and predicted values obtained from the MR model for S%, with a poor correlation coefficient (R 2 = 0.587).

Fig. 2
figure 2

Cross-correlation of predicted and observed values of k obtained from multiple regression analysis

Full size image

4 An overview of Artificial Neural Network (ANN) models

When the materials are natural materials, there will be faced many uncertainty and material will never be known with certainty. That is why some methodologies in artificial neural networks, fuzzy systems, and evolutionary computation have been successfully combined, and new techniques called soft computing or computational intelligence have been developed in recent years. These techniques are attracting more and more attention in several research fields because they tolerate a wide range of uncertainty [15].

Artificial neural networks are data processing systems devised via imitating brain activity and have performance characteristics like biological neural networks. ANN has a lot of important capabilities such as learning from data, generalization, working with unlimited number of variable [16]. Neural networks may be used as a direct substitute for auto correlation, multivariable regression, linear regression, trigonometric, and other statistical analysis and techniques [17]. Neural networks, with their remarkable ability to derive meaning from complicated or imprecise data, can be used to extract patterns and detect trends that are too complex to be noticed by either humans or other computer techniques [18, 19]. Rumelhart and McClelland [20] reported that the main characteristics of ANN include large-scale parallel distributed processing, continuous nonlinear dynamics, collective computation, high fault tolerance, self-organization, self-learning, and real-time treatment. A trained neural network can be thought of as an “expert” in the category of information it has been given to analyze. This expert can then be used to provide projections given new situations of interest and answer “what if” questions [21].

The most commonly used algorithms are multilayer feed-forward artificial neural network (multiple layer perceptron-MLP) and radial basis function network (RBFN). The radial basis function network (RBFN) is traditionally used for strict interpolation problem in multi-dimensional space and has similar capabilities with MLP neural network which solves any function approximation problem [22]. RBFs were first used in design of neural network by Broomhead and Lowe [23], who showed how a nonlinear relationship could be modeled by RBF neural network, and interpolation problems could be implemented [23]. The main two advantages of RBFN are

  1. (a)

    Training of networks in a short time than MLP [24],

  2. (b)

    Approximation of the best solution without dealing with local minimums [25].

Moreover, RBFN are local networks compared to the feed-forward networks which perform global mapping. Otherwise, RBFN uses a single set of processing units, and each of these units is most receptive to a local region of the input space [26]. That is why, RBFN are used as an alternative neural network model in applications of function approximation, time series forecasting as well as classifying task in recent years [27–35].

The structure of RBFN is composed of three layers (Fig. 3), and the main distinction between MLP and RBFN is the number of the hidden layer. RBFN has only one hidden layer, which contains nodes called RBF units, and radially symmetric basis function is used as activation functions of hidden nodes.

Fig. 3
figure 3

Architecture of radial basis function network (RBF)

Full size image

The input layer serves as an input distributor to the hidden layer. Different from MLP, the values in input layer are forwarded to hidden layer directly without being multiplied by weight values. The hidden layer unit measures the distance between an input vector with the center of its radial function and produces an output value depending on the distance. The center of radial basis function is called reference vector. The closer input vector is to the reference vector, the more the value is produced at the output of hidden node. However, a lot of radial basis functions are suggested for using in hidden layer (Gaussian, Multi-Quadric, Generalized Multi-Quadric, Thin Plate Spline), Gaussian function is the most widely used in applications. Chen et al. [27] indicate that the choice of radial basis function used in network does not significantly affect performance of network. The activation function of the individual hidden nodes defined by the Gaussian function is expressed as follows:

$$ \phi_{j} = e^{{\left[ { - {\frac{{\left\| {X - C_{j} } \right\|^{2} }}{{\sigma_{j}^{2} }}}} \right]}}\quad j = 1,2\,\ldots ,L $$
(4)

where ϕ j denotes the output of the jth node in hidden layer, \( \left\| . \right\| \)is Euclidian distance function which is generally used in applications, X is the input vector, C j is center of the jth Gaussian function, σ j is radius which shows the width of the Gaussian function of the jth node, and L denotes the number of hidden layer nodes.

In the next step, the neurons of the output layer perform a weighted sum using the hidden layer outputs and the weights which connect hidden layer to output layer. Output of network can be presented as a linear combination of the basis functions:

$$ y_{k} = \sum\limits_{j = 1}^{L} {\phi_{j} w_{kj} } + w_{k0} $$
(5)

where w kj is the weight that connects hidden neuron j and output neuron k,w k0 is bias for the output neuron.

5 Artificial neural network models for prediction of k

All data were first normalized and divided into three data sets, such as, training (1/2 of all data), test (1/4 of all data), and verification (1/4 of all data). In this study, Matlab 7.1 [36] software was used in neural network analyses having a three-layer feed-forward network, and models were constructed by MLP and RBF architectures.

5.1 MLP models for prediction of k

In this study, permeability coefficients of soils were first predicted indirectly by using the MLP algorithm. They consist of an input layer (3 neurons), one hidden layer (10 neurons), and one output layer (Fig. 4). In the analyses network parameters of learning parameters, momentum parameters, networks training function, and activation (transfer) function for all layer were respectively adjusted to 0.01, 0.9, trainLm, and tansig. As in many other network training methods, models and parameters were used to be able to reach minimum RMS values, and network goal was reached at the end of 437 iterations.

Fig. 4
figure 4

MLP model used in this study

Full size image

In fact, the coefficient of determination between the measured and predicted values is a good indicator to check the prediction performance of the model. Figure 5 shows the relationships between measured and predicted values obtained from the models for k, with good coefficient of determinations. In this study, variance account for (VAF) (Eq. 6) and root mean square error (RMSE) (Eq. 7) indices were also calculated to control the performance of the prediction capacity of predictive models developed in the study as employed by Alvarez and Babuska [37, Finol et al. [38], Yilmaz and Yüksek [39, 40]:

$$ {\text{VAF}} = \left[ {1 - {\frac{{\text{var} \left( {y - y^{'} } \right)}}{{\text{var} \left( y \right)}}}} \right] \times 100 $$
(6)
$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {y - y^{'} } \right)^{2} } } $$
(7)

where y and y′ are the measured and predicted values, respectively. If the VAF is 100 and RMSE is 0, then the model will be excellent. The obtained values of VAF and RMSE given in Table 5 indicated a high prediction performance.

Fig. 5
figure 5

Cross-correlation of predicted and observed values of k for MLP model

Full size image
Table 5 Performance indices (RMSE, VAF, and R 2) for models used
Full size table

5.2 RBF models for prediction of k

Training of RBF networks contains process of determination of center vector (C j ), radius value (σ j ), and linear weight values (w kj ). Two-stage hybrid learning algorithm is used to train RBF networks in general. In the first stage of hybrid learning algorithm, center and width of RBFs in hidden layer are determined by using unsupervised clustering algorithms or randomly selected from given input data set. Output weight is calculated in the second stage. A lot of methods are proposed in literature to determine the center and width of reference vector, and some of them are listed below.

Number of hidden neurons is set to the number of training examples, and all input vectors are also used as centers of RBFs. In other words, for each point in input space, one radial basis function is determined. This case is named as “Exact RBF”. There are two disadvantages of Exact RBF such as size problem and overtraining problem. Size problem causes calculation complexity when data set is too large. Network is over trained with these noisy data, so the performance of the system for test data will not as good as performance of training data. To reduce calculating complexity and to deal with overtraining problem, the number of neurons in hidden layer is reduced as smaller than the number of sample in input data set, and central vectors are chosen from input vectors randomly.

Pruning or growing methods start with a number of prespecified hidden neuron and iteratively, and continues by adding/removing hidden neurons to/from RBFN. The network structure that has minimum testing and training error is selected as a final model of RBFN. In this iterative process, parameters of hidden nodes are randomly selected from input vectors or determined by using clustering methods. In order to determine central vectors with clustering methods, input vectors are devoted to certain number of clusters by using clustering algorithms, such as, k means, Self-Organization Map (SOM), and cluster centers are then used as RBF centers.

In the analyses, three different algorithms of RBF such as Exact RBF, RBF trained with k means, and RBF trained with SOM were used in prediction of k. However, three models consist of 3 neurons in input layer and one output layer; the neuron numbers in the hidden layer of Exact RBF, RBF trained with k means, and RBF trained with SOM were, respectively, 26, 41, 37.

Cross-correlations between predicted and observed values (Figs. 6, 7, 8), RMSE, and VAF values indicated that the three models of RBF constructed are highly acceptable for prediction of k. RMSE, VAF, and R 2 values are also tabulated in Table 5.

Fig. 6
figure 6

Cross-correlation of predicted and observed values of k for Exact RBF model

Full size image
Fig. 7
figure 7

Cross-correlation of predicted and observed values of k for RBF (k means) model

Full size image
Fig. 8
figure 8

Cross-correlation of predicted and observed values of k for RBF (SOM) model

Full size image

6 Adaptive Neuro-Fuzzy Inference System model for prediction of k

In ANFIS, both of the learning capabilities of a neural network and reasoning capabilities of fuzzy logic were combined in order to give enhanced prediction capabilities, when compared to using a single methodology alone. The goal of ANFIS is to find a model or mapping that will correctly associate the inputs (initial values) with the target (predicted values). The fuzzy inference system (FIS) is a knowledge representation where each fuzzy rule describes a local behavior of the system. The network structure that implements FIS and employs hybrid learning rules to train is called ANFIS.

Let X be a space of objects and x be a generic element of X. A classical set A ⊆ X is defined as a collection of elements or objects x ∈ X such that each x can either belong or not belong to the set A. By defining a characteristic function for each element x in X, we can represent a classical set A by a set of ordered pairs (x, 0) or (x, 1), which indicates x /∉ A or x ∈ A, respectively. On the other hand, a fuzzy set expresses the degree to which an element belongs to a set. Hence, the characteristic function of a fuzzy set is allowed to have values between 0 and 1, which denotes the degree of membership of an element in a given set. So a fuzzy set A in X is defined as a set of ordered pairs:

$$ A = \{ (x,\,\mu A(x))|x \in X\} $$
(8)

where μA(x) is called the membership function (MF) for the fuzzy set A.

The MF maps each element of X to a membership grade (or a value) between 0 and 1. Usually, X is referred to as the universe of discourse or simply the universe. The most widely used MF is the generalized bell MF (or the bell MF), which is specified by three parameters {a, b, c} and defined as [41]

$$ {\text{bell}}\,(x;\,a,\,b,\,c) = 1/\left( { 1+ \left| {x - \left( {c/a} \right)} \right|^{ 2b} } \right) $$
(9)

Parameter b is usually positive. A desired bell MF can be obtained by a proper selection of the parameter set {a, b, c}. During the learning phase of ANFIS, these parameters are changing continuously in order to minimize the error function between the target output values and the calculated ones [42, 43].

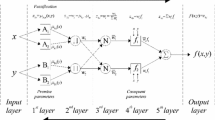
The proposed neuro-fuzzy model of ANFIS is a multilayer neural network-based fuzzy system. Its topology is shown in Fig. 9, and the system has a total of five layers. In this connected structure, the input and output nodes represent the training values and the predicted values, respectively, and in the hidden layers, there are nodes functioning as membership functions (MFs) and rules. This architecture has the benefit that it eliminates the disadvantage of a normal feed-forward multilayer network, where it is difficult for an observer to understand or modify the network.

Fig. 9
figure 9

Type- 3 fuzzy reasoning (a) and equivalent ANFIS (b)

Full size image

For simplicity, we assume that the examined fuzzy inference system has two inputs x and y and one output. For a first-order Sugeno fuzzy model, a common rule set with two fuzzy if–then rules are defined as

$$ {\text{Rule 1}}:\,{\text{If}}\,x\,{\text{is}}\,A_{ 1\,} \quad{\text{and}}\,y\,{\text{is}}\,B_{ 1} ,\quad{\text{then}}\quad f_{ 1} = p_{ 1} x + q_{ 1} y + r_{ 1} , $$
(10)
$$ {\text{Rule 2}}:{\text{If}}\,x\,{\text{is}}\,A_{ 2\,} \quad{\text{and}}\,y\,{\text{is}}\,B_{ 2} ,\quad{\text{then}} \quad f_{ 2} = p_{ 2} x + q_{ 2} y + r_{ 2} . $$
(11)

As seen from Fig. 9b, different layers of ANFIS have different nodes. Each node in a layer is either fixed or adaptive [44]. Different layers with their associated nodes are described below:

Layer 1 Every node I in this layer is an adaptive node. Parameters in this layer are called premise parameters.

Layer 2 Every node in this layer is a fixed node labeled Π, whose output is the product of all the incoming signals. Each node output represents the firing strength of a rule.

Layer 3 Every node in this layer is a fixed node labeled N. The ith node calculates the ratio of the ith rules’ firing strength. Thus, the outputs of this layer are called normalized firing strengths.

Layer 4 Every node i in this layer is an adaptive node. Parameters in this layer are referred to as consequent parameters.

Layer 5 The single node in this layer is a fixed node labeled Σ, which computes the overall output as the summation of all incoming signals.

The learning algorithm for ANFIS is a hybrid algorithm, which is a combination of gradient descent and the least-squares method. More specifically, in the forward pass of the hybrid learning algorithm, node outputs go forward until layer 4 and the consequent parameters are identified by the least-squares method [44]. In the backward pass, the error signals propagate backwards and the premise parameters are updated by gradient descent. Table 6 summarizes the activities in each pass.

Table 6 Forward and backward pass for ANFIS
Full size table

The consequent parameters are optimized under the condition that the premise parameters are fixed. The main benefit of the hybrid approach is that it converges much faster since it reduces the search space dimensions of the original pure back propagation method used in neural networks. The overall output can be expressed as a linear combination of the consequent parameters. The error measure to train the above-mentioned ANFIS is defined as [45]:

$$ E\, = \,\sum\limits_{k = 1}^{n} {(f_{k} - f'_{k} )^{2} } $$
(12)

where f k and f′ k are the kth desired and estimated output, respectively, and n is the total number of pairs (inputs–outputs) of data in the training set.

In this study, a hybrid intelligent system called ANFIS (the adaptive neuro-fuzzy inference system) (Table 7) for predicting k was also applied. ANFIS was trained with the help of Matlab version 7.1 [36], SPSS 10.0 [46] package was used for RMSE and statistical calculations. Different parameter types and their values used for training ANFIS can be seen in Table 7.

Table 7 Different parameter types and their values used for training ANFIS
Full size table

According to the RMSE, VAF, R 2 values (Table 5), and cross-correlation between predicted and observed values (Fig. 10), ANFIS model constructed to predict k has the highest prediction performance.

Fig. 10
figure 10

Cross-correlation of predicted and observed values of k for ANFIS model

Full size image

7 Results and conclusions

In this paper, use of some neural computing models—such as, artificial neural network (ANN) with different algorithms (MLP, Exact RBF, RBF trained with k means, and RBF trained with SOM) and artificial neuro-fuzzy inference system (ANFIS) models for prediction of permeability coefficient value of soils—was described and compared. It appears that there is a possibility of estimating k of coarse-grained soils from grain-size distribution curves by using the soft computing models.

The results of the present paper and their conclusions can be drawn as follows:

  1. (1)

    The result of the multiple regression analysis showed that the model performance is very low with the correlation coefficient of 0.587 obtained from cross-correlation between observed and predicted values of k.

  2. (2)

    In order to predict the permeability coefficient, ANN models having three inputs, one output were applied successfully and exhibited reliable predictions. However, all four different algorithms of ANN have almost the same prediction capability, and accuracy of MLP was relatively higher than RBF models.

  3. (3)

    The ANFIS model for prediction of permeability coefficient revealed the most reliable prediction when compared with the ANN models.

The comparison of VAF, RMSE indices, and coefficient of correlations (R2) for predicting k revealed that prediction performances of the artificial neuro-fuzzy inference system model are higher than those of four algorithms of artificial neural networks (MLP, Exact RBF, RBF trained with k means, RBF trained with SOM). In order to show the deviations from the observed values of k, the distances of the predicted values from the models constructed from the observed values were also calculated, and graphics were drawn (Fig. 11). The deviation intervals (will be multiplied by 10−6) (−0.000117 to +0.000111) of the predicted values from ANFIS are smaller than the deviation intervals of ANN models (in MLP −0.000271 to +0.000463, in Exact RBF −0.000336 to +0.000646, in RBF trained with k means −0.000560 to +0.000458, in RBF trained with SOM −0.000317 to +0.00011) (Fig. 12).

Fig. 11
figure 11

Graphics showing the variation of the values, predicted by ANN (Exact, k means, SOM) and ANFIS models, from the observed values

Full size image
Fig. 12
figure 12

Intervals of variations of predicted from observed values

Full size image

As is known, the potential benefits of soft computing models extend beyond the high computation rates. Higher performances of the soft computing models were sourced from greater degree of robustness and fault tolerance than traditional statistical models because there are many more processing neurons, each with primarily local connections.

The performance comparison also showed that the soft computing techniques are good tools for minimizing the uncertainties, and their use will also may provide new approaches and methodologies and minimize the potential inconsistency of correlations. The results of this paper will provide dissemination of important results of the use of soft computing technologies in soil sciences and serve as an example for engineering geologists, geotechnique and civil engineers engaged in this area of interest.