Introduction

Laser plasma interaction is a widely used phenomenon for producing various nonlinear effects like production of various radiations of desired frequency (THz generation [1,2,3,4,5,6,7,8,9,10] and harmonic generation [11,12,13,14,15,16,17]), controlling the intensity of propagating laser pulse (self-focusing [18,19,20,21,22,23]), particle acceleration (laser wakefield acceleration [24,25,26,27] and plasma wake field acceleration [28, 29]), etc. Particle acceleration, especially electron acceleration is one of the most important utilized nonlinear phenomena. Optimization of various laser and plasma parameters is required for the maximum energy efficient laser wakefield acceleration (LWFA). Askari et al. [30] have compared LWFA produced by Gaussian-like and rectangular–triangular pulse in magnetized plasma. In this study, they have investigated the role of pulse profile along with the role of external magnetic field. Abedi-Varaki et al. [31] have taken Gaussian, super-Gaussian, and Bessel–Gaussian profile for the comparative study of LWFA in magnetized plasma. Role of laser pulse profile on LWFA using different Gaussian-like laser pulses is investigated by Sharma et al. [32] and found that the laser pulse with broadest pulse profile is most suited for wakefield generation.

The role of frequency chirped laser pulse (both positive and negative) on electron acceleration is investigated by Ghotra [33], Pathak et al. [34], Zhang et al. [35], Sharma et al. [36, 37], Jain et al. [38] and Singh et al. [39]. Role of laser pulse polarization is investigated by Heydarzadeh et al. [40], Sharma et al. [41], and Zhang et al. [42]. Plasma density also plays a crucial role in electron acceleration process. Sharma et al. [43] have studied plasma with ripple density variation, and Pukhov et al. [44] and Gupta et al. [45] have investigated LWFA in density modulated plasma. Up-ramp density plasma has positive correlation with electron energy gain in LWFA [46].

Asymmetric laser pulse can significantly affect electron acceleration due to its specific pulse shape. Leemans et al. [47], Sharma et al. [48], Xie et al. [49], Gopal et al. [50], etc. have investigated this correlation. Sharma et al. [51] have studied the role of wiggler magnetic field, Abedi-Varaki [52] have selected periodic magnetic field, and Singh et al. [53] have used sheared magnetic field to investigate their role on laser wakefield acceleration. The effect of beating of laser pulses to enhance wakefield excitation is investigated by Sharma et al. [54].

In this study, we have chosen Sinh–Gaussian pulse profile with transverse static magnetic field to investigate the role of both chosen laser profile and magnetic field. Using this specific pulse profile, analytical solution for wake potential, wakefield and electron energy gain is derived in section II. By selecting feasible parameters, curves are drawn in result and discussion section III. Research outcomes based on these curves are discussed in conclusion section IV. The paper ends with references.

Derivation of formulas

A laser pulse with an electric field E and a magnetic field B that is traveling in the z-direction through a uniform plasma with a density n is analyzed. The rest mass of an electron is denoted as m_0. We introduce a new parameter, defined as \(\upxi ={\text{z}}- {v}_{g}t\), where \({v}_{g}\) represents the group velocity and t is the time. An external magnetic field, denoted as \({B}_{0}\), is applied in the y-direction. The expression for the wake potential (\(\Phi \)) created in the presence of an external transverse magnetic field is as follows: [32]

$$ \left( {\frac{{\partial^{2} \Phi }}{{\partial \xi^{2} }}} \right) + k_{P}^{2} \Phi - \left\{ {\frac{{e\left( {\beta^{2} - 1} \right)}}{{2m_{0} v_{g}^{2} }}} \right\}\left( {E^{2} + 2B_{0} Ev_{g} } \right) = 0 $$
(1)

Here, \(\beta\) is the ratio of speed of light in vacuum to group velocity. \(\beta = c/v_{g} , \) and \(k_{P} \times v_{g} = \omega_{P}\).

In this study, we have chosen a Sinh–Gaussian laser pulse with a pulse envelope expressed as

$$ E^{2} = E_{0}^{2} e^{{ - \frac{{2\left( {\xi - \frac{L}{2}} \right)^{2} }}{{w_{0}^{2} }}}} \left\{ {{\text{sinh}}\left( {\frac{{\left( {\xi - \frac{L}{2}} \right)}}{{w_{0} }}} \right)} \right\}^{2} \;,\;{ }0 \le {\upxi } \le {\text{L}} $$
(2)

Here, \({w}_{0}\) indicates the laser’s characteristics, \({E}_{0}\) represents the strength of the laser’s electric field, and L represents the length of the pulse.

By solving Eq. (1) for the laser profile described in Eq. (2), we derive the resulting wake potential:

$$ \begin{aligned} \Phi &= \frac{1}{{8k_{P} m_{0} v_{g} }}iee^{{\frac{1}{4}\left( {1 - k_{P}^{2} w_{0}^{2} - 2ik_{P} \left( {L + 2\xi + w_{0} } \right)} \right)}} \left( {e^{{iLk_{P} }} + e^{{2i\xi k_{P} }} } \right)\sqrt \pi \hfill \\ & \quad ( - 1 + \beta^{2} )\left( {e^{{ik_{P} w_{0} }} erf\left[ {\frac{1}{2}\left( { - 1 + \frac{L}{w_{0} } - ik_{P} w_{0} } \right)} \right] - erf\left[ {\frac{1}{2}\left( { - 1 + \frac{L}{{w_{0} }} + ik_{P} w_{0} } \right)} \right]} \right. \hfill \\ & \quad \left. { - erf\left[ {\frac{{L + w_{0} - ik_{P} w_{0}^{2} }}{{2w_{0} }}} \right] + e^{{ik_{P} w_{0} }} erf\left[ {\frac{{L + w_{0} + ik_{P} w_{0}^{2} }}{{2w_{0} }}} \right]} \right)B_{0} w_{0} {\mathbb{E}}_{0} \hfill \\ & \quad + \frac{1}{{32k_{P} m_{0} v_{g}^{2} }}ee^{{ - \frac{1}{8}k_{P} \left( {4i\left( {L + 2\xi } \right) + 4iw_{0} + k_{P} w_{0}^{2} } \right)}} \left( {e^{{iLk_{P} }} - e^{{2i\xi k_{P} }} } \right)\sqrt {\frac{\pi }{2}} \hfill \\ & \quad( - 1 + \beta^{2} )\left( {ie^{{\frac{1}{2} + ik_{P} w_{0} }} erf\left[ {\frac{{2L + 2w_{0} + ik_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}\left] { + 2e^{{\frac{1}{2}ik_{P} w_{0} }} erfi} \right[\frac{{ - 2iL + k_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}} \right] - 2e^{{\frac{1}{2}ik_{P} w_{0} }} erfi\left[ {\frac{{2iL + k_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}} \right]} \right. \hfill \\ & \quad + e^{{\frac{1}{2} + ik_{P} w_{0} }} erfi\left[ {\frac{{2iL - 2iw_{0} + k_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}} \right] - \sqrt e erfi\left[ {\frac{{ - 2iL + 2iw_{0} + k_{P} w_{0}^{2} }}{2\sqrt 2 w_{0} }} \right] \hfill \\ & \quad \left. { + \sqrt e erfi\left[ {\frac{{2iL + 2iw_{0} + k_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}} \right]} \right)w_{0} {\mathbb{E}}_{0}^{2} \hfill \\ \end{aligned} $$
(3)

The formula for generated longitudinal laser wakefield is \(E_{w} = - \frac{{\partial {\Phi }}}{{\partial {\text{z}}}}\)

$$ \begin{aligned} E_{w} = ~ & - \frac{1}{{64m_{0} v_{g}^{2} }}{\text{ee}}^{{ - \frac{1}{8}k_{P} \left( {8i\left( {L + 2\xi } \right) + w_{0} \left( {8i + 3k_{P} w_{0} } \right)} \right)}} \sqrt \pi \\ & \quad ( - 1 + \beta ^{2} )w_{0} \mathbb{E}_{0} \left( {8e^{{\frac{1}{8}\left( {2 + k_{P}^{2} w_{0}^{2} + 4ik_{P} \left( {L + 2\xi + w_{0} } \right)} \right)}} \left( {e^{{iLk_{P} }} - e^{{2i\xi k_{P} }} } \right)} \right. \\ & \quad \left( { - 2 + e^{{ik_{P} w_{0} }} \left( {{\text{erf}}\left[ {\frac{1}{2}\left( { - 1 + \frac{L}{{w_{0} }} - ik_{P} w_{0} } \right)} \right] + {\text{erf}}\left[ {\frac{1}{2}\left( {1 + \frac{L}{{w_{0} }} + ik_{P} w_{0} } \right)} \right]} \right)} \right. \\ & \quad \left. { + {\text{erfc}}\left[ {\frac{1}{2}\left( {1 + \frac{L}{{w_{0} }} - ik_{P} w_{0} } \right)} \right] + {\text{erfc}}\left[ {\frac{1}{2}\left( { - 1 + \frac{L}{{w_{0} }} + ik_{P} w_{0} } \right)} \right]} \right)B_{0} v_{g} \\ & \quad - \sqrt 2 e^{{\frac{1}{4}k_{P} \left( {2i\left( {L + 2\xi } \right) + w_{0} \left( {2i + k_{P} w_{0} } \right)} \right)}} (e^{{iLk_{P} }} + e^{{2i\xi k_{P} }} )\left( {2e^{{\frac{1}{2}ik_{P} w_{0} }} \left( {{\text{erf}}\left[ {\frac{{2L - ik_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}} \right] + {\text{erf}}\left[ {\frac{{2L + ik_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}} \right]} \right)} \right. \\ & \quad + \sqrt e \left( {{\text{erf}}\left[ {\frac{{ - 2L + w_{0} \left( {2 - ik_{P} w_{0} } \right)}}{{2\sqrt 2 w_{0} }}} \right] - {\text{erf}}\left[ {\frac{{2L + w_{0} \left( {2 - ik_{P} w_{0} } \right)}}{{2\sqrt 2 w_{0} }}} \right]} \right) \\ & \quad \left. { \left. { + e^{{\frac{1}{2} + ik_{P} w_{0} }} \left( {{\text{erf}}\left[ {\frac{{ - 2L + w_{0} \left( {2 + ik_{P} w_{0} } \right)}}{{2\sqrt 2 w_{0} }}} \right] - {\text{erf}}\left[ {\frac{{2L + w_{0} \left( {2 + ik_{P} w_{0} } \right)}}{{2\sqrt 2 w_{0} }}} \right]} \right)} \right)\mathbb{E}_{0} } \right) \\ \end{aligned} $$
(4)

For a new variable \(\eta = k_{p} \left( {{\upxi } - {\text{L}}/2} \right)\), the change in the relativistic factor (∆γ) is

$$ \Delta \gamma = \frac{ - e }{{k_{p} m_{0} c^{2} \left\{ {1 - \frac{1}{\beta }} \right\}}}\int {E_{w} {\text{d}}\eta } $$

By utilizing the formula, one can obtain the energy gained by an electron called electron energy gain. \(\Delta W = m_{0} c^{2} \Delta \gamma .\)

$$ \begin{aligned} \Delta W = & \frac{e}{{64\left( { - 1 + \beta } \right)k_{P} m_{0} v_{g}^{2} }}{\text{ie}}\left( { - 1 + e^{{i\xi k_{P} }} } \right)\sqrt \pi \beta \\ & \quad ( - 1 + \beta ^{2} )w_{0} \mathbb{E}_{0} \left( { - 8e^{{\frac{1}{4} - \frac{1}{4}k_{P}^{2} w_{0}^{2} - ik_{P} \left( {L + \xi + w_{0} } \right)}} \left( {e^{{\frac{1}{2}ik_{P} \left( {3L + w_{0} } \right)}} - e^{{\frac{1}{2}ik_{P} \left( {L + 2\xi + w_{0} } \right)}} } \right)} \right. \\ & \quad \left( { - 2 + e^{{ik_{P} w_{0} }} \left( {{\text{erf}}\left[ {\frac{1}{2}\left( { - 1 + \frac{L}{{w_{0} }} - ik_{P} w_{0} } \right)} \right] + {\text{erf}}\left[ {\frac{1}{2}\left( {1 + \frac{L}{{w_{0} }} + ik_{P} w_{0} } \right)} \right]} \right)} \right. \\ & \quad \left. { + {\text{erfc}}\left[ {\frac{1}{2}\left( {1 + \frac{L}{{w_{0} }} - ik_{P} w_{0} } \right)} \right] + {\text{erfc}}\left[ {\frac{1}{2}\left( { - 1 + \frac{L}{{w_{0} }} + ik_{P} w_{0} } \right)} \right]} \right)B_{0} v_{g} \\ & \quad + \sqrt 2 e^{{ - \frac{1}{8}k_{P} \left( {4i\left( {L + 2\xi } \right) + w_{0} \left( {4i + k_{P} w_{0} } \right)} \right)}} \left( {e^{{iLk_{P} }} + e^{{i\xi k_{P} }} } \right)\left( {2e^{{\frac{1}{2}ik_{P} w_{0} }} ({\text{erf}}\left[ {\frac{{2L - ik_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}} \right]} \right. \\ & \quad \left. { + {\text{erf}}\left[ {\frac{{2L + ik_{P} w_{0}^{2} }}{{2\sqrt 2 w_{0} }}} \right]} \right) + \sqrt e \left( {{\text{erf}}\left[ {\frac{{ - 2L + w_{0} \left( {2 - ik_{P} w_{0} } \right)}}{{2\sqrt 2 w_{0} }}} \right] - {\text{erf}}\left[ {\frac{{2L + w_{0} \left( {2 - ik_{P} w_{0} } \right)}}{{2\sqrt 2 w_{0} }}} \right]} \right) \\ & \quad \left. { \left. { + e^{{\frac{1}{2} + ik_{P} w_{0} }} \left( {{\text{erf}}\left[ {\frac{{ - 2L + w_{0} \left( {2 + ik_{P} w_{0} } \right)}}{{2\sqrt 2 w_{0} }}} \right] - {\text{erf}}\left[ {\frac{{2L + w_{0} \left( {2 + ik_{P} w_{0} } \right)}}{{2\sqrt 2 w_{0} }}} \right]} \right)} \right)\mathbb{E}_{0} } \right) \\ \end{aligned} $$
(5)

The error function (erf) and the imaginary error function (erfi) are defined in this context as follows: [55]

\({\text{erf }}\left[ {\text{Y}} \right] \, = \frac{2}{\sqrt \pi }\mathop \smallint \limits_{0}^{Y} e^{{ - q^{2} }} {\text{d}}q,\;\;{\text{erfc [Y]}} = { 1} - {\text{ erf}}[{\text{Y}}]\;\;{\text{and}}\;\;{\text{erfi }}\left[ {\text{Y}} \right] \, = \frac{2}{\sqrt \pi }\mathop \smallint \limits_{0}^{Y} e^{{q^{2} }} {\text{d}}q\), respectively.

Result and discussion

The current study utilized plasma with the following specifications: an electron density of\(4 \times 10^{22} \;{\text{m}}^{ - 3}\), a frequency of \(1.13 \times 10^{13} \;{\text{rad}}/{\text{s}}\), and plasma wavelength of 166 μm corresponding to selected plasma density. In the numerical investigation, a laser pulse was chosen with a wavelength of 10.6 μm (generated by CO2 laser source), a frequency of \(1.78 \times 10^{14} \; {\text{rad}}/{\text{s}}\), and a pulse duration of 83 μm. The selected amplitudes of the laser electric field (\(E_{0}\)) are\(3.85 \times 10^{11} \; {\text{V}}/{\text{m}}, \;4.04 \times 10^{11} \; {\text{V}}/{\text{m}}\), \(4.23 \times 10^{11} \;{\text{V}}/{\text{m}},\; 4.43 \times 10^{11} \; {\text{V}}/{\text{m}},\;4.61 \times 10^{11} \; {\text{V}}/{\text{m}},\) and\(4.81 \times 10^{11} \;{\text{V}}/{\text{m}}\). The numerical value of \(w_{0}\) is 16.87 µm. To assess the influence of the magnetic field on electron acceleration via the LWFA phenomenon, we employ external field intensities of 0, 10, 20, 30, and 40 T (1 T = 10 kilogauss).

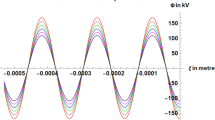
Figure 1 illustrates the variation of generated laser wake potential with propagation distance for different laser intensities. With the increase in laser intensity from \(3.85 \times 10^{11}\) to \(4.81 \times 10^{11} \; {\text{V}}/{\text{m}}\), amplitude of generated wake potential increases from 88.7471 to 138.581 kV for static magnetic field of 20 T. Curves are plotted to obtain peak values of generated wake potential for selected different laser pulse amplitude at external magnetic field strength 0 T, 10 T, 20 T, 30 T, and 40 T. The peak values of generated wake potential are noted in Table 1. Using these data, Fig. 2 is plotted to show the variation of generated wake potential with laser electric field amplitude of \(3.85 \times 10^{11} \;{\text{V}}/{\text{m}}\) and selected magnetic field. Curve represents a positive correlation of generated wake potential with external magnetic field.

Fig. 1
figure 1

Illustration of generated laser wake potential with propagation distance for laser electric field \(3.85 \times 10^{11} \;{\text{V}}/{\text{m}} \;\left( {{\text{black}}} \right)\;, 4.04 \times 10^{11} \;{\text{V}}/{\text{m}} \;\left( {{\text{magenta}}} \right)\), \(4.23 \times 10^{11} \; {\text{V}}/{\text{m }}\;\left( {{\text{blue}}} \right), 4.43 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{green}}} \right),4.61 \times 10^{11} \;{\text{V}}/{\text{m }}\left( {{\text{brown}}} \right),\) and \(4.81 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{red}}} \right).\) \(B_{0} = 20 \;T,\) \(w_{0}\)= 16.87 μm, L = 83 μm

Full size image
Table 1 Amplitude of generated wake potential (in kV) with laser field amplitude (\({E}_{0}\)) and external magnetic field strength (\({B}_{0}\))
Full size table
Fig. 2
figure 2

Illustration of generated laser wake potential amplitude for different magnetic field strength \(w_{0}\)= 16.87 μm, L = 83 μm and laser field amplitude \(3.85 \times 10^{11} \;{\text{ V}}/{\text{m}}\)

Full size image

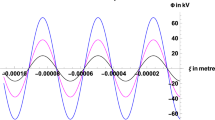
Figure 3 depicts the relationship between the laser intensities and the generated laser wakefield as the propagation distance changes. By increasing the laser intensity from \(3.85 \times 10^{11}\) to \(4.81 \times 10^{11} \;{\text{V}}/{\text{m}}\), the amplitude of the generated wakefield increases from 3.89 to 6.08 GV/m. This occurs when a static magnetic field of 20 T is applied. Laser wakefield graphs are generated for various laser pulse amplitudes and external magnetic field strengths of 0 T, 10 T, 20 T, 30 T, and 40 T. The maximum value of the generated wakefield is shown in Table 2. Based on the provided data, Fig. 4 illustrates the relationship between the generated wakefield and magnetic field for the laser electric field amplitude of \(3.85 \times 10^{11} \;{\text{ V}}/{\text{m}}\). The curve illustrates a direct relationship between the generated wakefield and the external magnetic field.

Fig. 3
figure 3

Illustration of generated laser wakefield with propagation distance for laser electric field \(3.85 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{black}}} \right), 4.04 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{magenta}}} \right)\), \(4.23 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{blue}}} \right), 4.43 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{green}}} \right),.61 \times 10^{11} \; {\text{V}}/{\text{m }}\left( {{\text{brown}}} \right),\) and \(4.81 \times 10^{11} \;{\text{V}}/{\text{m }}\left( {{\text{red}}} \right).\) \(B_{0} = 20 T,\) \(w_{0}\)= 16.87 μm, L = 83 μm

Full size image
Table 2 Amplitude of generated wakefield (in GV/m) with laser field amplitude (\({E}_{0}\)) and external magnetic field strength (\({B}_{0}\))
Full size table
Fig. 4
figure 4

Illustration of generated laser wakefield amplitude for different magnetic field strength \(w_{0}\)= 16.87 μm, L = 83 μm and laser field amplitude \(3.85 \times 10^{11} \;{\text{V}}/{\text{m}}\)

Full size image

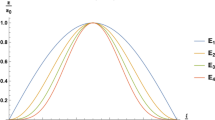
The relationship between the electron energy gain and propagation distance for various laser intensities is shown in Fig. 5. The maximum energy gain increases from 102.694 to 160.353 MeV as the laser intensity rises from \(3.85 \times 10^{11}\) to \(4.81 \times 10^{11}\) V/m in a static magnetic field of 20 T. Curves are generated to represent specific variations in electron energy gain in response to laser pulse amplitude and external magnetic field strengths of 0 T, 10 T, 20 T, 30 T, and 40 T. Table 3 presents the maximum value of the electron energy gain amplitude that was generated. Based on the provided data, Fig. 6 illustrates the correlation between the generated wake potential and the chosen magnetic field at constant laser electric field amplitude of \(3.85 \times 10^{11}\) V/m. The curve illustrates a positive correlation between the electron energy gain and the external magnetic field.

Fig. 5
figure 5

Illustration of electron energy gain with propagation distance for laser electric field \(3.85 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{black}}} \right), 4.04 \times 10^{11} \; {\text{V}}/{\text{m}} \left( {{\text{magenta}}} \right)\), \(4.23 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{blue}}} \right), 4.43 \times 10^{11} \;{\text{V}}/{\text{m}} \left( {{\text{green}}} \right),4.61 \times 10^{11} \; {\text{V}}/{\text{m}} \left( {{\text{brown}}} \right),\) and \(4.81 \times 10^{11} \; {\text{V}}/{\text{m}} \left( {{\text{red}}} \right).\) \(B_{0} = 20 T,\) \(w_{0}\)= 16.87 μm, L = 83 μm

Full size image
Table 3 Amplitude of electron energy gain (in MeV) with laser field amplitude (\({E}_{0}\)) and external magnetic field strength (\({B}_{0}\))
Full size table
Fig. 6
figure 6

Illustration of maximum electron energy gain for different magnetic field strength \(w_{0}\)= 16.87 μm, L = 83 μm and laser field amplitude \(3.85 \times 10^{11} \;{\text{V}}/{\text{m}}\)

Full size image

When an intense laser beam propagates through underdense plasma, nonlinear ponderomotive force and electrostatic force between electron and positive ions are responsible for periodic oscillation of electrons (plasma wave) about the axis of propagation of laser pulse. As a result, a wake potential and wakefield develops along the longitudinal axis called laser wake potential and laser wakefield, respectively, which can be utilized to accelerate electrons. With the increase in laser field amplitude or strength of external magnetic field, the phenomenon of electron acceleration becomes more effective. It can be seen through the curves obtained in our study.

Using Gaussian-like and rectangular–triangular pulses, Askari et al. [30] have studied the impact of magnetic field on wakefield generation and concluded that the use of external magnetic field enhances acceleration of electrons. They also used Gaussian laser pulse for the similar study [56].

Conclusion

Laser wakefield acceleration (LWFA) is a notable process that rapidly increases the energy of electrons over a short distance using laser-induced wakefield. For this investigation, we have selected a Sinh–Gaussian laser pulse that is accompanied by a static magnetic field positioned perpendicular to the pulse’s direction of propagation. The analytical solution for the selected electric field is derived from a generalized differential equation of the laser wake potential. Consequently, equations for the wakefield and the increase in electron energy are also derived. By varying the laser field amplitude within reasonable limits, it was found that increasing it from \(3.85 \times 10^{11}\) to \(4.81 \times 10^{11} \; {\text{V}}/{\text{m}}\) resulted in an increase in electron energy gain from 102.504 to 160.163 MeV when there was no external magnetic field. When an external magnetic field of 40 T was present, the electron energy gain increased from 103.258 to 160.918 MeV. The amplitude of the laser field and the strength of the magnetic field directly affect the increase in electron energy gain, resulting in an enhancement of energy gain. Out of electric and magnetic fields, the role of electric field is dominant as per the results of our study using selected parameters. An electric field of high amplitude can enhance the wakefield more effectively to generate a plasma wave of higher amplitude. This generated plasma wave is responsible for generating enhanced laser wakefield acceleration. Our findings will provide valuable insights for researchers seeking to enhance the efficiency of electron acceleration mechanisms for energy production.