Introduction

The terahertz (THz) frequency range is situated between the infrared and microwave regions, namely between the frequency range of 1011–1013 Hz. The THz gap exhibits significant promise in various domains such as THz spectroscopy, topography, communication, food production and quality control, hence offering substantial chances for scholars and scientists [1,2,3,4].Over the past three decades, there has been a significant increase in the development of systems for generating THz radiation [5,6,7,8,9,10,11,12,13,14,15].

Forlov et al. [16]conducted a theoretical investigation on the effects of p-polarised radiation on semi-bounded plasma. Strong THz amplification is observed when an ultra-short laser pulse is incident at or near the critical angle.The study conducted by Xie et al. [17] focuses on investigating the creation of THz waves by the utilisation of laser-induced air plasma. The findings demonstrate that efficient THz radiation production occurs when the incident laser possesses the same polarisation state.The chirped laser pulse with a hot inhomogeneous ripple density plasma was investigated by Hashemzadeh [18]. The individual conducts research on the impact of frequency chirp, laser intensity, electron temperature, and electron density inhomogeneity on THz wave production. The investigation conducted by Li et al. [19]examines the interaction between laser and solid materials using chirped laser pulses at relativistic intensity. This study investigates the generation of transit current through the nonlinear interaction between laser and plasma, specifically focusing on the copper foil material.The study conducted by Huang et al. [20] investigated the concurrent emission of THz and X-rays resulting from the interaction between an intense, brief laser pulse and a thin, unconfined water flow in air. They demonstrate the progression of material alteration.In their study, Liao et al. [21] provide a comprehensive analysis of the diverse techniques employed for the generation of THz radiation. These approaches encompass the utilisation of plasma waves, electron transport, and emission as means of THz generation.The study conducted by Zheng et al. [22] examined the utilisation of particle-in-simulations to investigate the creation of THz waves by laser interactions at the interface between a vacuum and plasma. The energy of induced THz waves is typically on the order of a few megawatts.The study conducted by Amouamouha et al. [23] focuses on the creation of THz radiation through the interaction of a super Gaussian laser beam with a plasma characterised by ripple density. The researchers employed the paraxial approximation approach in their investigation. The researchers tuned various laser plasma settings in order to achieve a THz efficiency of 6.5%.Hamsters [24] have the capability to generate sub-picosecond THz radiation by the use of laser-produced plasma. The author demonstrates that the creation of THz radiation is more pronounced when solid targets are employed as opposed to gas targets.In their study, Thakur et al. [25] investigate the phenomenon of second harmonic production induced by a chirped laser pulse in a plasma density ramp accompanied by a transverse magnetic field.In their research, Hashemzadeh [26] investigated the creation of THz radiation using Hermite-cosh-Gaussian and hollow Gaussian laser beams in a magnetised plasma with spatial variations. The researcher investigates the impact of a decentred parameter and an external magnetic field on the efficiency of THz generation.The study conducted by Jahangiri et al. [27] focuses on the development of powerful THz radiation within the range of 10–70 millijoules (mJ) from plasma formed by argon clusters. In this research, Sharma et al. [28] investigate the characteristics of the cosh-Gaussian laser beam within a wiggler magnetised plasma environment, with a specific focus on its potential for generating second harmonics.The results of argon gas are compared with those of argon clusters. The study conducted by Bakhtiari et al. [29] focuses on the creation of THz radiation by the utilisation of two Gaussian laser array beams. The researchers investigate the laser and array structure factors in order to optimise the creation of THz radiation for enhanced efficiency. In their study, Gurjar et al. [30] investigate the creation of THz waves in a spatially slanted density plasma profile through the beating of a chirped laser pulse. The maximum amplitude of THz waves occurs when the phase matching resonance condition is satisfied, namely at a specific slanting angle of plasma density. Thakur et al. [31] conducted a study on the phenomenon of self-focusing shown by Hermite-cosh-Gaussian laser pulses in a collisionless cold plasma characterised by an exponential density profile.

The work conducted by Mou et al. [32] investigates the impact of laser chirp on the polarisation of THz radiation. The findings demonstrate that positive and negative chirp has contrasting impacts on the polarisation state and phase difference of THz waves.The numerical investigation conducted by Nguyen et al. [33] examines the impact of chirp and time delay on the efficacy of THz generation. The researchers employ three-dimensional simulation techniques to achieve a conversion efficiency of \({10}^{-4}\) for THz radiation. Zhang et al. [34] employ the photocurrent model to theoretically investigate the creation of THz radiation through the interaction of a monochromatic chirped laser pulse with a gas plasma. The chirped and chirp-free laser pulses are compared in terms of their THz yield. In their research, Xing et al. [35] investigate the THz emission resulting from laser chirping in an air plasma. They employ the linear dipole array approach to analyse this phenomenon.In their study, Ghayemmoniri et al. [36] investigate the creation of THz pulses through the interaction of two chirped laser pulses with a carbon nanotube array in the presence of an external tapered magnetic field. The findings demonstrate that a tapered magnetic field has the ability to modulate the THz field.

Scientists and academics employ various laser and plasma characteristics to investigate distinct mechanisms, including self-focusing, Wakefield acceleration, harmonic creation, and THz generation [25, 31, 37,38,39,40,41,42].

In the present investigation, a pair of p-polarised chirped laser beams are directed towards a hot collisional plasma characterised by a slanting up density profile. The phenomenon of laser plasma interaction leads to the production of high-intensity THz waves. The optimisation of laser and plasma characteristics enables the attainment of an efficient source of THz radiation. Section "Analytical study of THz generation" of this work involves the analytical derivation of the ponderomotive force, equation of motion, nonlinear plasma current density, and the subsequent generation of THz fields. In this study, section "Result and discussion" investigates the correlation between the normalised THz electric field and various parameters, such as the normalised THz frequency, normalised slanting up density modulation, incidence angle, normalised collisional frequency, and chirp parameter. In the section "Conclusion", the Conclusions are presented. The document is concluded by incorporating references.

figure a

Analytical study of THz generation

Two p-polarised laser beams are propagating in x–z plane and interact with hot slanting up density plasma modulation having density profile \(n = n_{0} e^{{k_{z} z}}\) (where \(n_{0}\) is plasma density at \(z = 0\) and \(k_{z}\) is wave number of plasma density). Electric and magnetic fields of laser pulses are given by these equations. Electric field of two p-polarised laser beams is

$$ \overrightarrow {{E_{J} }} = \left( {\hat{z}\cos - \hat{x}\sin } \right) E_{0J} e^{{ - i\left( {\omega_{J} t - k_{J} \left( {z\sin + x\cos } \right)} \right)}} ,\quad {\text{where}}\quad J = 1,2 $$
(1)

In this context, \({E}_{0J}\) represents the amplitude of the laser beam, \(\theta \) denotes the angle of incidence, \(\omega_{J }\) signifies the angular frequency and \(k_{J}\) represents the propagation constantof incidental laser beam.

Corresponding magnetic field of laser beam is

$$ \overrightarrow {{B_{j} }} \left( {r,z} \right) = \frac{{\left( {\vec{k}_{j} \times \overrightarrow {{E_{j} }} \left( {r,z} \right)} \right)}}{{\omega_{j} }},\quad {\text{where}}\quad J = {1},{2} $$
(2)

Incident laser beam is positively chirped, and chirp is represented as

$$ \omega_{1} = \omega_{0} + b\omega_{0}^{2} \left( {t - \frac{{\left( {z\sin + x\cos } \right)}}{c}} \right), $$

where \(\omega_{0}\) is the frequency of incident laser beam in the absence of chirp, b is chirp parameter, c is velocity of light in vaccum. We choose \(\omega_{2}\) such as \(\omega_{1} - \omega_{2} = \omega\) lies in THz range.

So,

$$ \omega_{2} = \omega_{1} - \omega = \left\{ {\omega_{0} + b\omega_{0}^{2} \left( {t - \frac{{\left( {{\text{z sin}} + x \cos } \right)}}{c}} \right)} \right\} - \omega $$
(3)

During the initial stage, it can be assumed that electrons are in a state of rest, resulting in the absence of any magnetic force acting upon them. The oscillatory velocity of a plasma electron can be determined by using the equation of motion

$$ m\left( {\frac{{d\overrightarrow {{V_{J} }} }}{dt}} \right) = - e \overrightarrow {{E_{J} }} - m\overrightarrow {{V_{J} }} \nu_{en} $$

where \(\nu_{en}\) is collision frequency of collisional plasma.

By solving this equation, we get.

$$ \overrightarrow {{V_{1} }} = \frac{{e \overrightarrow {{E_{1} }} }}{{im\omega_{0} \left\{ {1 + b\omega_{0} \left( {2t - \frac{{\left( {{\text{z sin}} + x \cos } \right)}}{c}} \right)} \right\} - m\nu_{en} }} $$
(4)
$$ \overrightarrow {{V_{2} }} = \frac{{e \overrightarrow {{E_{2} }} }}{{im\omega_{0} \left\{ {1 + b\omega_{0} \left( {2t - \frac{{\left( {{\text{z sin}} + x \cos } \right)}}{c}} \right) - \frac{\omega }{{\omega_{0} }}} \right\} - m\nu_{en} }} $$
(5)

Here e, m, \(\nu\) is charge, rest mass and collisional frequency of the plasma electron, respectively.

This oscillatory velocity of plasma electron gives rise to nonlinear ponderomotive force.

Nonlinear ponderomotive force is

$$ \overrightarrow {{F_{P} }}^{NL} = - \frac{e}{2c}\left( {\overrightarrow {{V_{1} }} \times \overrightarrow {{B_{2} }}^{*} + \overrightarrow {{V_{2} }}^{*} \times \overrightarrow {{B_{1} }} } \right) - \frac{m}{2}\vec{\nabla }\left( {\overrightarrow {{V_{1} }} \overrightarrow {{V_{2} }}^{*} } \right) $$
(6)

Here, * represents the complex conjugate.

Solving this equation by putting values of \(\overrightarrow {{V_{1} }} ,\overrightarrow {{V_{2} }}^{*} , \overrightarrow {{B_{1} }} ,\;{\text{and}}\; \overrightarrow {{B_{2} }}^{*}\) and neglecting the higher order derivatives of second term, we get

$$ \overrightarrow {{F_{P} }}^{NL} = \left( {\widehat{x }\cos + \widehat{z }\sin } \right)\frac{{e^{2} E_{1} E_{2}^{*} }}{{2im\omega_{0} c}}\left( {\frac{{2\frac{\nu }{{i\omega_{0} }} - \frac{\omega }{{\omega_{0} }}}}{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{{\left( {z \sin + x \cos } \right)}}{c}} \right) - \frac{{\nu_{en} }}{{i\omega_{0} }}} \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{{\left( {z \sin + x \cos } \right)}}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{{\nu_{en} }}{{i\omega_{0} }}} \right\}}}} \right) $$
(7)

By solving the equation of motion \(\partial \vec{V}_{\omega }^{NL} /\partial t = \vec{F}_{P}^{NL} /m - \nu_{en} \vec{V}_{\omega }^{NL}\) and equation of continuity \(\partial n_{\omega }^{NL} /\partial t + \vec{\nabla } \cdot n\vec{V}_{\omega }^{NL} = 0\), For slanting up density profile \(n = n_{0} e^{{k_{z} z}}\), we get nonlinear oscillatory velocity and nonlinear density perturbation of plasma electron as per given equation.

$$ \vec{V}_{\omega }^{NL} = \frac{{i\omega \vec{F}_{P}^{NL} }}{{m\left( {\omega^{2} + i\omega \nu_{en} } \right)}} $$
(8)
$$ n_{\omega }^{NL} = \frac{{n_{0} \vec{\nabla }.\left( {e^{{k_{z} z}} } \right)\vec{F}_{P}^{NL} }}{{m\left( {\omega^{2} + i\omega \nu_{en} } \right)}} $$
(9)

In this derivation, we consider n \({\text{is constant with time}},{\text{ and is a function of zonly so }}\) \(\partial \left( n \right)/\partial t = 0.\)

This nonlinear density perturbation \(n_{\omega }^{NL}\) gives rise to self-consistent space charge potential \(\phi\) and field, because of separation of electrons from ions. This gives rise to linear density perturbation as \(n_{\omega }^{L} = - \chi_{P} \vec{\nabla } \cdot \left( {\vec{\nabla }\phi } \right)/4\pi e\) where \(\chi_{P} = - \omega_{P}^{2} /\left( {\omega^{2} + i\omega \nu_{en} - k^{2} V_{th}^{2} } \right)\) is electric susceptibility of collisional plasma.

Using Poisson’s equation \(\nabla^{2} \phi = 4\pi \left( {n_{\omega }^{L} + n_{\omega }^{NL} } \right)e\), we get linear force \(\vec{F}_{P}^{L}\) due to space charge field on electrons such as.

Linear force

$$ \vec{F}_{P}^{L} = {\text{e}}\vec{\nabla }\phi = \frac{{\omega_{P}^{2} e^{{k_{z} z}} \vec{F}_{P}^{NL} }}{{\left( {1 + \chi_{P} } \right)\left( {\omega^{2} + i\omega \gamma_{en} } \right)}} $$
(10)

as \(\omega_{P} = \sqrt {\left( {4\pi n_{0} e^{2} /m} \right)}\) is \({\text{plasma frequency}}\).

By solving the equation of motion \(\partial \vec{V}^{NL} /\partial t = \left( {\vec{F}_{P}^{NL} + \vec{F}_{P}^{L} } \right)/m - \nu_{en} \vec{V}^{NL}\), one may determine the nonlinear oscillatory velocity of electrons because of the linear and nonlinear ponderomotive forces as

$$ \vec{V}_{\omega }^{NL} = \frac{1}{m}\left\{ {\frac{{\omega^{2} + i\omega \nu_{en} - \omega_{P}^{2} + \omega_{P}^{2} \left( {e^{{k_{z} z}} } \right)}}{{\left( { - i\omega + \nu_{en} } \right)\left( {\omega^{2} + i\omega \nu_{en} - \omega_{P}^{2} } \right)}}} \right\}\vec{F}_{P}^{NL} $$
(11)

Here, we consider \(\omega_{1,} \omega_{2} \gg \omega_{P}\).

\(\vec{J}^{NL} = - \frac{1}{2}ne\vec{V}^{NL}\), where \(n = n_{0} e^{{k_{z} z}}\) is density perturbation which is much greater than the \(n_{0}\).

$$ \Rightarrow \vec{J}^{NL} = - \frac{{n_{0} e}}{2m}\left\{ {\frac{{\omega^{2} + i\omega \nu_{en} - \omega_{P}^{2} + \omega_{P}^{2} \left( {e^{{k_{z} z}} } \right)}}{{\left( { - i\omega + \nu_{en} } \right)\left( {\omega^{2} + i\omega \nu_{en} - \omega_{P}^{2} } \right)}}} \right\}\vec{F}_{P}^{NL} e^{{i\left( {kz - \omega t} \right)}} $$
(12)

where \(\left( {k_{1} - k_{2} } \right) = k\;{\text{ and}}\; \left( {\omega_{1} - \omega_{2} } \right) = \omega\).

This nonlinear current density is responsible for THz generation. By using III and IV Maxwell’s equation,\(\vec{\nabla } \times \vec{E} = - \frac{1}{c}\left( {\partial \vec{B}/\partial t} \right)\) and \(\vec{\nabla } \times \vec{B} = \left( {\varepsilon /c} \right)\left( {\partial \vec{E}/\partial t} \right) + \left( {4\pi /c} \right)\vec{J}^{NL}\), we can calculate the THz wave generation equation.

Equation for THz generation is

$$ \vec{\nabla } \cdot \left( {\vec{\nabla }\overrightarrow {{E_{THz} }} } \right) - \nabla^{2} \overrightarrow {{E_{THz} }} = \frac{{\omega^{2} }}{{c^{2} }}\varepsilon \overrightarrow {{E_{THz} }} + \frac{4\pi i\omega }{{c^{2} }}\vec{J}^{NL} $$
(13)

In order to neglect higher-order derivatives due to fast variation of THz field. So normalised THz amplitude is

$$ \frac{{E_{THz} }}{E} = \left[ {\frac{{\omega_{P}^{2} eE}}{{\varepsilon \omega m\omega_{0} c}}\left\{ {\frac{{\omega^{2} + i\omega \nu_{en} - \omega_{P}^{2} + \omega_{P}^{2} \left( {e^{{k_{z} z}} } \right)}}{{\left( { - i\omega + \nu_{en} } \right)\left( {\omega^{2} + i\omega \nu_{en} - \omega_{P}^{2} } \right)}}} \right\}e^{{i\left( {kz - \omega t} \right)}} \left( {\widehat{x }\cos + \widehat{z }\sin } \right)\left( {\frac{{\frac{\omega }{{\omega_{0} }} - 2\frac{{\nu_{en} }}{{i\omega_{0} }}}}{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{{\left( {z \sin + x \cos } \right)}}{c}} \right) - \frac{{\nu_{en} }}{{i\omega_{0} }}} \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{{\left( {z \sin + x \cos } \right)}}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{{\nu_{en} }}{{i\omega_{0} }}} \right\}}}} \right)} \right] $$
(14)

Here, we consider incidental beam has same electric field amplitude \(E_{01} = E_{02} = E\) is the amplitude of incident laser beam.

Result and discussion

In this investigation of THz generation, two p-polarised laser beams are positively chirped and propagating in hot collisional underdense plasma. For this study we choose suitable laser parameter such as femtosecond Ti–Sapphire laser with wave length of 800 nm having angular frequency \(2.35 \times 10^{15}\) rad/sec, chirp parameter of \(0.0011\), propagation distance (z) = propagation distance (x) = \(20\,{ \upmu \text{m}}\), time \(t = 50 fs\), incidence angle is \(\pi /6{\text{ radian }}\) and electric field amplitude of 1 × \(10^{12}\) V/m. Plasma parameters are optimised as plasma density is \(5 \times 10^{23} {\text{m}}^{ - 3}\). Here in the present study, we choose \(\omega = 1.025\omega { }_{P}\) where \(\omega_{1} ,\omega_{2} > \omega_{P}\) and \(\nu_{en} = 0.1\omega { }_{P}\).

Effect of normalised THz frequency (\(\omega /\omega_{P}\))

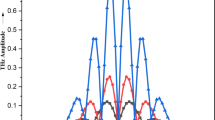
In this study variation of normalised THz amplitude is analysed with normalised THz frequency at \(k_{z} = 0.9{\text{ k}}\) for \({\text{chirp parameter }}b = 0.0011\left( {{\text{red}}} \right),{ }0.0044\left( {{\text{blue}}} \right),{ }0.0066\left( {{\text{green}}} \right),{ }0.0099\left( {{\text{black}}} \right)\).

For off-resonant condition, normalised THz amplitude decreases rapidly and approaches to zero for normalised THz frequency (\(\omega /\omega_{P}\)) greater than 1.2. Normalised THz amplitude approaches more than 0.8, as we decrease the chirp parameter from 0.0099 to 0.0011. The maximum normalised THz amplitude decreases from approximately 0.8–0.6. So, increase in chirp parameter decreases the THz conversion efficiency significantly (Fig. 1).

Fig. 1
figure 1

Variation of normalised THz amplitude with normalised THz frequency for \({\text{chirp parameter }}b = 0.0011\left( {{\text{red}}} \right),{ }0.0044\left( {{\text{blue}}} \right),{ }0.0066\left( {{\text{green}}} \right),{ }0.0099\left( {{\text{black}}} \right).{\text{ For }}k_{z} = 0.9{\text{ k}}.{ }\) Other parameters are same as mentioned above (colour figure online)

Full size image

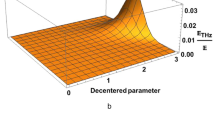
Effect of normalised slanting up density modulation parameter (\(k_{z} /k\))

This study aims to conduct a theoretical analysis of the relationship between the normalised amplitude of THz radiation and the wave propagation distance of THz waves. The analysis focuses on various values of the \({\text{chirp parameter }}b = 0.0011\left( {{\text{red}}} \right),{ }0.0044\left( {{\text{blue}}} \right),{ }0.0066\left( {{\text{green}}} \right),{ }0.0099\left( {{\text{black}}} \right)\).

This study shows that normalised THz amplitude increases with normalised slanting up density modulation parameter (\(k_{z} /k\)). With the increase in the chirp parameter from 0.0011 to 0.0099, the maximum value of normalised THz amplitude decreases from 0.8 to 0.2 approximately (Fig. 2).

Fig. 2
figure 2

Variation of normalised THz amplitude with normalised slanting up density parameter for chirp parameter b = 0.0011 (red), 0.0044 (blue), 0.0066 (green), 0.0099 (black). Other parameters are same as mentioned above (colour figure online)

Full size image

Effect of incidence angle (θ)

This study focus on examining the relationship between the normalised THz amplitude and the incident angle for chirp parameter b = 0.0011. In Fig. 3, normalised THz amplitude is shown along vertical axis while, oblique angle (normalised by π/12) is represented along horizontal axis. This examination shows that normalised THz amplitude changes in oscillatory manner with incidence oblique angle and the peak of the curve (maximum THz amplitude) is obtained at normalised oblique value 3. Corresponding oblique angle is 3*π/12 or 45° with selected parameters. It concludes that for effective THz generation, oblique angle also plays a crucial role, and this angle should be optimised to obtain energy-efficient THz generation.

Fig. 3
figure 3

Variation of normalised THz amplitude with normalised THz frequency for \({\text{chirp parameter }}b = 0.0011{\text{ and}}\;k_{z} = 0.9{\text{ k}}.\) Other parameters are same as mentioned above

Full size image

Normalised THz amplitude has maximum value is 0.86 for incidence angle 45° and minimum value is 0.4 for incidence angle 225°.

Effect of normalised collisional frequency (\(\nu_{en} /\omega_{P}\))

This study focuses on examining the relationship between the normalised THz amplitude and the normalised collisional frequency for b = 0.0011 and \(\theta = \pi /6\).

According to the findings of the investigation, the normalised THz amplitude experiences a precipitous drop as the normalised collisional frequency rises. Approximately 0.7 is the maximum value for the normalised THz amplitude. When the normalised collisional frequency is bigger than 0.8 value, the normalised THz amplitude gets closer and closer to zero. This indicates an increase in collisional properties of plasma, and there is corresponding decrease in generated THz amplitude (Fig. 4).

Fig. 4
figure 4

Variation of normalised THz amplitude with normalised collisional frequency for chirp parameter b = 0.0011 and kz = 0.9 k, λ = 800 nm, z = x = 20 μm, t = 50 fs. Other parameters are same as mentioned above

Full size image

This investigation's results are consistent with the findings documented by Hashemzadeh [18]. The conclusion drawn by the researchers is that the utilisation of a p-polarised chirped laser beam proves to be an efficacious approach in the generation of THz radiation. During the course of our investigation, we utilised a chirped p-polarised beam within a hot collisional slanting up plasma profile as a method for producing THz waves.

Conclusion

This study examines the propagation of two p-polarised chirped laser beams in a hot collisional underdense plasma medium. An analytical solution is derived to determine the efficiency of THz generation, considering various characteristics such as the normalised THz frequency, incidence angle, collisional frequency, normalised transverse distance, and frequency chirp. The resulting solution is then analysed to optimise these parameters, aiming to achieve a tuneable and energy-efficient THz source. The normalised THz amplitude exhibits significant values up to 0.8 for normalised THz frequency corresponding to chirp parameter b = 0.0011. The findings indicate that as the value of the chirp parameter increases from 0.0011 to 0.0099, there is a decrease in the normalised amplitude of the THz signal. The normalised THz amplitude changes in oscillating manner with change in incidence angle from zero to 2π and shows a maximum for incident oblique angle 45° and minima at 225°. This study aims to contribute to the existing body of information about the determination of optimal incident oblique angle, chirp parameter, and collisional frequency for the purpose of achieving an energy-efficient THz source.