1 Introduction

Surface plasma waves (SPW) are electromagnetic waves that are formed by the interaction of lasers with metals. These waves propagate along the interface of two different media and have amplitude larger than the amplitude of the laser [1, 2]. The nonlinear interaction of laser with the matter has gained much attention in the past few decades because of its unique applications like high harmonic generation, laser-driven plasma-based accelerators, sensors, photoelectron spectroscopy, etc. [3,4,5,6,7,8,9,10,11,12]. Harmonic generation on different materials and in the presence of external agents like the wiggler field has been studied by many researchers. Jha et al. [13] studied SHG with an intense laser beam in magnetized plasma and found high conversion efficiency in the presence of the transverse magnetic field. Rajput et al. [14] investigated the generation of third harmonic by a short pulse laser in plasma and observed that the presence of the wiggler magnetic field makes the generation process resonant accompanied by the increase in the efficiency of harmonic generation. Vinay et al. [15] investigated propagation of a laser pulse through plasma and found that the laser interacts nonlinearly with electrons exerting a ponderomotive force which in turn makes them to oscillates. It results in harmonic generation. Abedi-Varaki [16] investigated the acceleration of electrons of metal by SPW in the presence of a helical magnetostatic wiggler and observed that under the effect of both SPW and wiggler field, the electrons can travel more distance in the direction of propagation of the laser. Vij et al. [17] studied the production of terahertz (THz) radiation by carbon nanotubes in the presence of a wiggler magnetic field and observed that the presence of the wiggler field enhances the efficiency of the generation of THz radiation. Abedi-Varaki and Jafari [18] studied the generation of THz radiations by mixing two Cosh-Gaussian laser beams in the presence of a wiggler magnetic field and observed the increase in efficiency with the increase in wiggler frequency. Ghimire et al. [19] had investigated harmonic generation in solids and reported that terahertz or infrared fields are suitable for metals and semiconductors due to their small bandgap. The presence of external factors like the wiggler magnetic field helps to make the process resonant. Singh et al. [20] studied the acceleration of electrons by a laser pulse in the presence of a magnetic wiggler, in vacuum and plasma. Their work showed that the suitably tapered magnetic wiggler can maintain electron-laser resonance conditions for a longer time, and electrons can gain sufficient energy.

In the present manuscript, second harmonic generation induced by surface plasma wave at the metal–semiconductor interface in the presence of a wiggler magnetic field has been studied. The phase matching condition is fulfilled by the application of the wiggler magnetic field. Here, in Sect. 2, we have obtained the expression for normalized amplitude for second harmonic generation. Results are discussed and presented in graphical form in Sect. 3, and the conclusion is presented in Sect. 4.

2 Theoretical Considerations

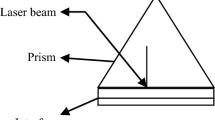
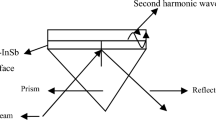
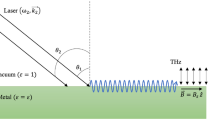
A thin metal layer over a glass prism with a thin layer of semiconductor has been considered in Kretschmann ATR configuration, as shown in Fig. 1, where laser light is incident at an acute angle on a metal-glass interface leading to SPW in the metal [21]. The EM fields of the laser interact with electrons of the metal and produce SPW of nearly the same frequency as that of the laser but with higher amplitude. The component of the wave vector of the laser along the surface matches with the wave number of surface plasma wave, leading to efficient coupling [22]. A thin layer of n-InSb with the thickness of a few nanometers is considered above the metal surface. The electromagnetic fields of SPW produced at the metal–semiconductor interface interact with electrons of n-InSb. The semiconductor can accumulate energetic electrons which can easily tunnel through plasmonic entities [23].

Fig. 1
figure 1

Kretschmann configuration with thin layer of a metal and a semiconductor

Full size image

Electric and magnetic fields of laser are considered as \(\overrightarrow E=\widehat xA(z,t)e^{-i(\omega t-k_1z)}\) and \(\overrightarrow B=\left({\overrightarrow k}_1\times\overrightarrow E\right)/\omega\) where A is the amplitude of the laser field, ω is the frequency of the laser, and k1 is the propagation constant. These fields interact with electrons of metal and produces surface plasma waves \({\overrightarrow E}_s=\widehat xA_se^{-i(\omega_st-k_sz)}\) where ks is the propagation constant such that \(k_{s} = (\omega_s/c)(\varepsilon_s\varepsilon_m/(\varepsilon_s+\varepsilon_m))^{^1/_2}\) with εm and εs as the permittivity of metal and semiconductor, respectively, and ωs is the frequency of the surface plasma wave. The frequency of SPW is nearly same as the frequency of the laser, so ωs = ω [16]. The amplitude of surface plasma wave As depends on the amplitude of incident laser A with As = f (A). Following [24], As / A can be considered as a normalized quantity with As = nA, where n is a positive real number. Fields of surface plasma waves interact with electrons of the semiconductor and accelerate them. Acceleration so produced is calculated using the equation of motion:

$$m\frac{d{\overrightarrow{v}}_{1}}{dt}=-e{\overrightarrow{E}}_{s}-e\overrightarrow{E}$$
(1)

The velocity gained by electrons is,

$${\overrightarrow v}_1=\left[\frac{-eAn'e^{-i\left(\omega t-k_sz\right)}}{m\left(-i\omega\right)}\right]\widehat x$$
(2)

As the wave vector increases more than linearly with incident frequency, the momentum is not conserved, i.e., the momentum of second harmonic is more than two times the momentum of incident photon. Here, n' = 1 + n which is a positive real number. Wiggler magnetic field is applied in transverse direction, given by \({\overrightarrow B}_w=B_0e^{ik_0z}\widehat y\) where B0 is the amplitude of wiggler field, and k0 is the wiggler wave number [25]. The presence of wiggler field helps to achieve the phase matching condition by providing additional momentum to the photons of second harmonic. The velocity \(\overrightarrow{v_1}\) beats with the wiggler magnetic field of the laser and generates ponderomotive force \(\overrightarrow {F}\), where \(\overrightarrow {F} = - e\left( {\overrightarrow {{v_{1} }} \times \overrightarrow {{B_{w} }} } \right)\) Due to this force the velocity of electrons changes, and it is taken as \(\overrightarrow{v_1^{'}}\) such that

$$\overrightarrow{v_1^{'}}=\left[\frac{-{e}^{2}{n'}{AB}_{0}{e}^{-i\left(\omega t-\left({k}_{1}+{k}_{0}\right)z\right)}}{{m}^{2}{\omega }^{2}}\right]\widehat{z}$$
(3)

It will induce density perturbation at \(\left( {\omega_{1} ,k_{1} + k_{0} } \right)\) in agreement with the equation of continuity:

$${n}_{1}=\left({\overrightarrow{k}}_{1}+{\overrightarrow{k}}_{0}\right){n}_{0}.\overrightarrow{v_1^{'}}/{\omega }_{1}$$
(4)

To exert ponderomotive force on electrons at \(\left( {2\omega ,2k_{1} + k_{0} } \right)\), \(\overrightarrow{v_1^{'}}\) beats with \({\overrightarrow B}_1\) and imparts velocity \(\overrightarrow v_2^{NL}\) to electrons, given as

$${\overrightarrow{v}}_{2}^{NL}=\left[\frac{-{ie}^{3}{n'}{{A}^{2}{k}_{1}B}_{0}{e}^{-i\left(2\omega t-\left({2k}_{1}+{k}_{0}\right)z\right)}}{2{m}^{3}{\omega }^{4}}\right]\widehat{x}$$
(5)

This gives rise to second harmonic nonlinear current density at metal-semiconductor interface,

$${\overrightarrow{J}}_{2}^{NL}=-{n}_{0}e{\overrightarrow{v}}_{2}^{NL}-{n}_{1}e{\overrightarrow{v}}_{1}$$
(6)

The linear current density due to self-consistent second harmonic field \({\overrightarrow E}_2=A_2e^{-i(2\omega t-k_2z)}\overrightarrow x\) at (2ω, k2) is \(\overrightarrow J_2^L=n_0{e\overrightarrow v}_2\) where \({\overrightarrow{v}}_{2}\) is obtained using equation of motion \(m({d\overrightarrow v}_2/dt)=-{e\overrightarrow E}_2.\) 

The amplitude \(A_2^{}\) for second harmonic is calculated by using equation:

$${{\nabla }^{2}\overrightarrow{E}}_{2}=\frac{4\pi \left({\varepsilon }_{m}+{\varepsilon }_{s}\right)\partial \overrightarrow{J}}{{c}^{2}\left({\varepsilon }_{m}{\varepsilon }_{s}\right)\partial t}+\frac{{\partial }^{2}{\overrightarrow{E}}_{2}}{{c}^{2}{\partial t}^{2}}$$
(7)

We take the laser profile to be Gaussian as \(A^2=\left[F\left(z-v_{g1}t\right)\right]^2\) and \(F\left(z-v_{g1}t\right)=A_0e^{-\left(\frac{z-v_{g1}t}{\tau v_{g1}}\right)^2}\) with \(v_{g1} = c\sqrt {1 - (\omega_{p}^{2} /\omega^{2} )}\), vg2 = k2 (\(c^{2}\)/ 2ω)\(\sqrt {1 - (1/4)(\omega_{p}^{2} /\omega^{2} )\left( {\varepsilon_{m} + \varepsilon_{s} } \right)/\varepsilon_{m} \varepsilon_{s} }\), and τ is laser pulse width. Using a new set of variables \(z-{v}_{\mathrm{g}1}t=\Omega\), z = η,\({\Omega }_{0}={\tau v}_{\mathrm{g}1}\), β' = (1 – vg1 / vg2), \(z^{'} = z\Omega_{0}\), and \(t^{'} = v_{g1} t/\Omega_{0}\), we get normalized second harmonic amplitude as:

$$\begin{aligned}\left|\frac{{A}_{2}}{{A}_{0}}\right|= &\left\{{\left(1-\frac{{\omega }_{p}^{2}}{{\omega }^{2}}\right)}^{1/2}\left(\frac{\it{a} \;{\omega }_{p}^{2}}{{\omega }^{2}}\right)\left(\frac{e{B}_{0}}{m\omega }\right)\left(\frac{e{A}_{0}}{mc\omega }\right)\right. \\ & \left. (d+b)\left[Erf\left({z}^{'}-{t}^{'}\right)-Erf\left\{\left(1-\beta{'}\right){z}^{'}-{t}^{'}\right\}\right]\right\}\end{aligned}$$
(8)

where \(a=\frac{\varepsilon_m+\varepsilon_s}{\varepsilon_m\varepsilon_s},\text{ d}=\frac{k_1\Omega_0\sqrt\pi n'}{8\beta'}\) and \(\text b=\frac{(k_1+k_0)\Omega_0\sqrt\pi n^{'2}}{4\beta'}\).

3 Results and Discussion

Equation (8) has been solved numerically for a Nd:YAG laser with wavelength 1064 nm and intensity \(I \approx 10^{12} {\text{ W/cm}}^{{2}}\). The refractive index of the prism lies in the range 1.5 – 2. The dielectric permittivity is taken as 57.909 for Ag, 49.58 for Cu, 106.82 for Al, and 19.5 for InSb at 1064 nm [26,27,28]. Here, the layers of metal and semiconductor are considered to be of few nanometers, and the doping level of n-InSb is adjusted to have \(\omega_{p} /\omega < 1\) for the semiconductor. The graphical relationship for normalized second harmonic amplitude with normalized propagation distance has been presented for different metal–semiconductor interfaces at different values of time and wiggler field. The other parameters of Eq. (8) are taken as ωp / ω1 = 0.9, n' = 2.5, eA0 / mcω1 = 0.09, (k1 + k0) \(\Omega_{0} \sqrt \pi\) / 8β' = 500, eB0 / mω = 0.006,0.012 and 0.018, \(k_{1} \Omega_{0} \sqrt \pi /8\beta ^{\prime} = 300\), and \(\beta ^{\prime} = 0.3.\)

Figure 2 shows the variation of normalized second harmonic amplitude \(A_{2} /A_{0}\) with normalized propagation distance \({\text{z}}^{\prime}\) for metals like Cu, Ag, and Al with thin layer of n-InSb, at time t' = 4, in the presence of a wiggler magnetic field. It has been observed that as the strength of magnetic field increases, the amplitude of second harmonic increases. In Fig. 2a, a sharp increase in amplitude has been observed at z' = 5 for all three metal–semiconductor interfaces at \(eB_{0} /m\omega = 0.006\), with larger increase in amplitude in the case of the Cu-InSb interface. The presence of the wiggler field helps to attain phase-matching conditions by providing additional momentum to the second harmonic photon. The electromagnetic fields of laser interact with electrons of metal and excite them. The excited electrons beat with the laser magnetic field and the wiggler field, leading to resonant SPW. These waves with high amplitude interact nonlinearly with electrons of n-InSb, leading to second harmonic. Figure 2b and c show the variation of normalized second harmonic amplitude \(A_{2} /A_{0}\) with normalized propagation distance z' for all three metal–semiconductor interfaces, at \(eB_{0} /m\omega = 0.012\) and \(eB_{0} /m\omega = 0.018\), respectively. The values of other parameters for Fig. 2b and c are the same as for Fig. 2a. As observed graphically under given conditions, increase in amplitude of SHG has been found more significant for Cu-InSb than for Ag-InSb and Al-InSb. The reason for this observation can be understood as the value of the density of conduction electrons in Cu is larger than in Ag and Al, therefore the fields of SPW in Cu are expected to be comparatively stronger and can efficiently interact with electrons of n-type semiconductor. As per the study by Takagi et al. [27], surface plasma waves in Kretschmann geometry show better agreement with bulk dielectric function for Cu than for Ag. Similarly, in our work, we have seen better enhancement in the amplitude of second harmonic for Cu. Hashemzadeh et al. [29] studied SHG of hollow Gaussian beam in inhomogeneous plasma and found the increase in amplitude of SHG with the increase in wiggler field. Sharma et al. [30] studied SHG of cosh-Gaussian laser beam in magnetized plasma and found enhancement in efficiency in the presence of wiggler field. Similarly, in the present work, good enhancement in amplitude of second harmonic has been observed in the presence of wiggler field.

Fig. 2
figure 2

Variation of normalized second harmonic amplitude A2 / A0 with normalized propagation distance \(z^{\prime}\), for metals Cu, Ag, and Al with layer of n-InSb, for different values of wiggler field eB0/mω at time t' = 4

Full size image

Figure 3 shows the variation of the normalized amplitude of second harmonic, A2 / A0, with normalized propagation distance z', at different values of wiggler field with \(eB_{0} /m\omega = 0.006,0.012{\text{ and }}0.018\), for Cu-InSb interface. The values of other parameters have been taken the same as those in Fig. 2. It is clear from Fig. 3 that with a slight increase in wiggler field strength, the amplitude of second harmonic enhances rapidly. Aggarwal et al. [31] studied second harmonic generation in atomic clusters in the presence of wiggler magnetic field, and they found increase in amplitude of second harmonic with the wiggler field strength. In their work the amplitude of second harmonic shows enhancement in the region where \(13 < {\text{z}}^{\prime} < 16\), for different values of wiggler frequency. In the present work, we have used the same values for wiggler frequency and have observed sharp increase in amplitude at \({\text{z}}^{\prime} = 5\), for the Cu-InSb interface. Figure 2 reveals that the enhancement in amplitude is larger for Cu-InSb, as compared to Ag-InSb and Al-InSb interfaces. Our work shows that a metallic surface like the Cu-InSb interface would be a better choice to study the second harmonic generation and its applications.

Fig. 3
figure 3

Variation of normalized second harmonic amplitude A2 / A0 with normalized propagation distance \(z^{\prime}\), for Cu-InSb interface, for different values of wiggler field at time t' = 4

Full size image

4 Conclusion

The electromagnetic fields of laser interact with electrons of the metal and generate SPW, which are electromagnetic waves with higher amplitude. The SPW of different metals like Cu, Ag, and Al interact nonlinearly with electrons of n-InSb, leading to second harmonic generation. The interaction has been studied in the presence of a wiggler field with different amplitudes. It has been observed that the amplitude increases sharply at the Cu-InSb interface, as compared to Ag-InSb and Al-InSb. The enhancement in second harmonic amplitude has been observed with the increase in wiggler field strength. The presence of the wiggler field helps in phase matching and resonates with the process of second harmonic generation.