Introduction

In the modern era, accelerated charged particles can be considered as back bone of scientific research and development. In the realm of materials science, accelerated electrons enable high-resolution imaging and characterization [1], facilitating breakthroughs in nanotechnology [2], catalysis, and material design [3]. In medical science, their application in radiation therapy has revolutionized cancer treatment, allowing for precise tumor targeting while minimizing damage to surrounding healthy tissues [4]. Furthermore, accelerated electrons play a pivotal role in particle physics research, aiding in the exploration of fundamental particles and their interactions, thus expanding our understanding of the universe's building blocks[5].The energy sector benefits from accelerated electrons through enhanced insights into materials for energy storage, conversion, and generation, fostering advancements in renewable energy technologies[6]. In environmental science, their utilization contributes to the development of novel pollution control methods and pollutant degradation processes [7]. Accelerated electrons also find their place in the preservation and restoration of cultural heritage artifacts, offering noninvasive analysis and cleaning techniques [8].

Due to such important applications, several energy efficient particle acceleration techniques have been developed and continuous efforts have been made to further improve these techniques. Tajima et al. [9] had proposed the mechanism to generate plasma waves with the help of intense laser pulse in underdense plasma. Tera hertz generation [10]–[16], second harmonic generation [17, 18], third harmonic generation[19, 20], self-focusing[21, 22] and electron acceleration[23, 24] are some of achievable phenomenon of plasma waves generated by laser–plasma interaction.

Recently, the use of electric field, magnetic field, and carbon nano-tubes has made a revolutionary change in nonlinear interaction phenomenon shown by laser–plasma interaction [15]–[13]. Under controlled conditions, this plasma wave can be utilized to accelerate electrons also. Laser pulse can carry energy with extremely high intensity in a controlled manner and plasma is an ultimate source of free electrons to be accelerated. Plasma provides a medium also, in which the collective behavior of charges can be utilized to accelerate electrons to a very high relativistic energy level.

Direct laser action (DLA), beat wave acceleration in vacuum and plasma (BWA), plasma wake field accelerator (PWFA) and laser wakefield acceleration (LWFA) are dominant acceleration techniques to obtain electrons of relativistic energy[25]. Fallah et al. [26] have used Bessel–Gaussian pulse to investigate electron acceleration and found that Bessel–Gaussian pulse produces effective electron acceleration. Sharma et al.[27, 28] have studied the effect of frequency chirp on LWFA and found that phenomenon of LWFA can be enhanced using positive chirp. Varaki et al. [29] have compared electron acceleration produced by Gaussian, Super-Gaussian, and Bessel–Gaussian pulse in the presence of wiggler magnetic field. Sharma et al.[33] have observed the enhancement in LWFA when oblique magnetic field is applied with a circular polarized pulse. Ghotra [31] has studied the combined effect of LWFA and direct laser acceleration on electron acceleration phenomenon.

Use of static or wiggler magnetic field, positive/negative or linear/quadratic frequency chirp, slanting or ripped plasma density, laser pulse profile, laser pulse length, laser strength are some of the important parameters which have direct impact on acceleration process[32]–[36].

In the present study, we have used Hermite–Gaussian laser pulse propagating through cold, collisionless, underdense homogeneous plasma. Homogeneous plasma refers to plasma with uniform density and composition. Such plasma improves acceleration consistency, reduces energy spread and minimizes plasma instabilities. It is easier to generate homogeneous plasma experimentally. These are some of the benefits of choosing homogeneous plasma as a medium for LWFA. Using equation of motion, continuity equation and Maxwell’s equation, solutions for wake potential, wakefield and energy gained by electrons are derived analytically. The effect of pulse length, laser intensity, plasma density, and Hermite–Gaussian mode index on LWFA is studied Curves are plotted to discuss and compare the results. Analytical solution is given in section II. Curves are plotted and outcomes are discussed in result and conclusion section III. Conclusions are given section IV of the paper. The paper ends with the references.

Analytical solution of LWFA

We explore the propagation of a laser pulse of an electric field (E) and a magnetic field (B) along the z-axis in homogeneous underdense collisionless plasma. The following fundamental equation of motion is used to create laser–plasma interaction.

$$\Rightarrow \frac{\partial \overrightarrow{P}}{\partial t}+\left(\overrightarrow{V}.\overrightarrow{\nabla }\right)\overrightarrow{P}=-e\left\{\overrightarrow{E}+\overrightarrow{V}\times \overrightarrow{B}\right\}$$
(1)

Here, e is electric charge, \(\overrightarrow{V}\) is velocity of electron, \(\overrightarrow{P}=\gamma {m}_{0}\overrightarrow{V}\) is relativistic momentum of electrons, \({m}_{0}\) is rest mass of electron, relativistic factor \(\gamma\) is given by

$$\gamma =\frac{1}{\sqrt{1-\frac{{V}^{2}}{{C}^{2}}}}= \sqrt{1+{\left(\frac{P}{mc}\right)}^{2}}$$
(2)

Here, c is speed of light. \(V_{\parallel }\) and \(V_{ \bot }\) are velocity components along (z-direction) and perpendicular (x-direction) to the laser propagation direction then,

$$\vec{V} = V_{ \bot } \hat{i} + V_{\parallel } \hat{k}$$
(3)
$${\text{z}} - {\text{ component of momentum }}P_{ \bot } = \frac{{m_{0} V_{ \bot } }}{{\sqrt {1 - \frac{{\left( {V_{\parallel }^{2} + V_{ \bot }^{2} } \right)}}{{c^{2} }}} }}{ } = { }\frac{{m_{0} V_{ \bot } }}{{\sqrt {1 - \frac{{V_{ \bot }^{2} }}{{c^{2} }}} }} \approx m_{0} V_{ \bot }$$
(4)
$${\text{x}} - {\text{ component of momentum }}P_{\parallel } = \frac{{m_{0} V_{\parallel } }}{{\sqrt {1 - \frac{{\left( {V_{\parallel }^{2} + V_{ \bot }^{2} } \right)}}{{c^{2} }}} }} = { }\frac{{m_{0} V_{\parallel } }}{{\sqrt {1 - \frac{{V_{ \bot }^{2} }}{{c^{2} }}} }} \approx m_{0} V_{\parallel }$$
(5)

Solving Eq. (1) using (3) to (5), we get

$$\frac{{{\text{d}}V_{\parallel } }}{{{\text{dt}}}}{ } + { }V_{\parallel } \frac{{\partial V_{\parallel } }}{\partial z}{ } = \frac{e}{{m_{0} }}\frac{\partial \Phi }{{\partial z}} - \frac{{eBV_{ \bot } }}{{m_{0} }}$$
(6)
$$\frac{{{\text{d}}V_{ \bot } }}{{{\text{dt}}}} + { }V_{\parallel } \frac{{\partial V_{ \bot } }}{\partial z}{ } = { } - \frac{{{\text{eE}}}}{{m_{0} }} + \frac{{ev_{\parallel } B}}{{m_{0} }}$$
(7)

let us define a new variable ‘ξ’ which depends on space and time as ξ = z \(-{v}_{g}t\)

So \(\frac{\partial }{\partial z}\equiv \frac{\partial }{\partial\upxi }\mathrm{ and}\frac{\partial }{\partial t}\equiv -{v}_{g}\frac{\partial }{\partial\upxi }\)

Here vg = c \(\sqrt{\left(1-\frac{{{\omega }_{P}}^{2}}{{\omega }^{2}}\right)}\) is group velocity &\({\omega }_{P}=\sqrt{\frac{n{e}^{2}}{m{\varepsilon }_{0}}}\) is plasma frequency.

$${\text{From continuity equation}}\frac{\partial n}{{\partial t}} + \vec{\nabla }.\left( {n\vec{V}} \right) = 0$$
(8)

here, n is plasma electron density.

If \({{n}_{e}}^{I}\) represents density perturbation caused by laser pulse propagation, then solving and rewriting Eqs. (6) to (8) yields

$$- v_{g} \frac{{\partial V_{ \bot } }}{{\partial {\upxi }}} + V_{\parallel } \frac{{\partial V_{ \bot } }}{{\partial {\upxi }}} = { } - \frac{{{\text{eE}}}}{{m_{0} }}{ } + { }\frac{{ev_{\parallel } B}}{{m_{0} }}$$
(9)
$$- v_{g} \frac{{\partial V_{\parallel } }}{\partial \xi } + V_{\parallel } \frac{{\partial V_{\parallel } }}{\partial \xi } = \frac{e}{{m_{0} }}\frac{\partial \phi }{{\partial \xi }} - \frac{{eV_{ \bot } B}}{{m_{0} }}$$
(10)
$$-{v}_{g}\frac{\partial {{n}_{e}}^{I}}{\partial\upxi }+{n}_{0}\frac{\partial {V}_{\parallel }}{\partial\upxi }+{V}_{\parallel }\frac{\partial {{n}_{e}}^{I}}{\partial\upxi }+ {{n}_{e}}^{I}\frac{\partial {V}_{\parallel }}{\partial\upxi }=0$$
(11)

By solving Eq. (9) to (11) under quasi-static approximation, we obtain general second-order differential equation for generated laser wake potential (\(\Phi\)) as

$$\left(\frac{{\partial }^{2}\Phi }{\partial {\upxi }^{2}}\right)+ {{k}_{P}}^{2}\Phi =\left\{\frac{e\left({\beta }^{2}-1\right)}{2{m}_{0}{{v}_{g}}^{2}}\right\}{E}^{2}$$
(12)

Generated laser wakefield is related to wake potential as

$${E}_{w}=-\frac{d\Phi }{d\upxi }$$
(13)

The electric field (E) of a plain polarized Hermite–Gaussian laser pulse propagating through homogeneous underdense plasma along z-axis is given by

$$E=\widehat{x}{E}_{0}{e}^{- \frac{{\left(\xi -\frac{L}{2}\right)}^{2}}{{r}_{0}^{2}}}{H}_{s}\left(\frac{\sqrt{2}\left(\xi -\frac{L}{2}\right)}{{r}_{0}}\right)0\le\upxi \le {\text{L}}$$
(14)

here, \({E}_{0}\) is amplitude of laser electric field, \({r}_{0}\) is laser beam waist, L is the laser pulse length, and s is mode index of Hermite polynomial. The value of Hermite polynomial depends on mode index (s).

Consider a new parameter η = \({k}_{p}\left(\upxi -\frac{{\text{L}}}{2}\right)\). In terms of η, the electron energy gain [36] is accomplished by using the relation

$$\Delta {\text{W}}=\frac{-e }{{k}_{p}\left\{1-\frac{1}{\beta }\right\}}{\int }_{-{k}_{p}L/2}^{\upeta }{E}_{w}d\upeta$$
(15)

Equation (12), (13) and (15) can be applied on this laser pulse profile E, to obtain generated laser wake potential (\(\Phi\)), laser wakefield (\({E}_{w}\)) and energy gain by electron (\(\Delta\) W).

For Hermite mode index s = 0

As per the definition of Hermite polynomial, for s = 0, \({H}_{0}\left(\frac{\sqrt{2}\left(\xi -\frac{L}{2}\right)}{{r}_{0}}\right)=1\). So, the solution of Eq. (12), (13) and (15), respectively, is

$${\Phi }_{0}=-\frac{1}{2}\left\{\frac{e\left({\beta }^{2}-1\right){{E}_{0}}^{2}}{2m{{v}_{g}}^{2}{k}_{P}}\right\}{e}^{-\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}\sqrt{\frac{\pi }{2}}({\text{Erf}}[\frac{2L-i{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]+{\text{Erf}}[\frac{2L+i{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){\text{Sin}}[\frac{1}{2}(L-2\xi ){k}_{P}]{r}_{0}$$
(16)
$${{\text{E}}}_{w0}=-\frac{1}{2}\left\{\frac{e\left({\beta }^{2}-1\right){{E}_{0}}^{2}}{2m{{v}_{g}}^{2}{k}_{P}}\right\}{k}_{P}{r}_{0}{e}^{-\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}\sqrt{\frac{\pi }{2}}{\text{Cos}}[\frac{1}{2}(L-2\xi ){k}_{P}]\left\{{\text{Erf}}[\frac{2L-i{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]+{\text{Erf}}[\frac{2L+i{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]\right\}$$
(17)
$$\Delta {{\text{W}}}_{0}=\frac{1}{2}\sqrt{\frac{\pi }{2}}[\frac{e{e}^{-\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(-1+{\beta }^{2}){\text{Cos}}[\frac{1}{2}(L-\xi ){k}_{P}]({\text{Erf}}[\frac{2L-i{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]+{\text{Erf}}[\frac{2L+i{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){\text{Sin}}[\frac{\xi {k}_{P}}{2}]{E}_{0}^{2}{r}_{0}}{(1-\frac{1}{\beta }){k}_{P}{m}_{0}{v}_{g}^{2}}]$$
(18)

Error function (Erf) and imaginary error function (Erfi) are defined [37] as.

Erf [Y] = \(\frac{2}{\sqrt{\pi }}{\int }_{0}^{Y}{e}^{-{q}^{2}}dq\) and Erfi [Y] = \(\frac{2}{\sqrt{\pi }}{\int }_{0}^{Y}{e}^{{q}^{2}}dq\), respectively.

For Hermite mode index s = 1

For s = 1, \({H}_{1}\left(\frac{\sqrt{2}\left(\xi -\frac{L}{2}\right)}{{r}_{0}}\right)=2\left(\frac{\sqrt{2}\left(\xi -\frac{L}{2}\right)}{{r}_{0}}\right)\). So, the solution of Eq. (12), (13) and (15), respectively, is

$${\Phi }_{1}=\frac{1}{16}\left\{\frac{e\left({\beta }^{2}-1\right){{E}_{0}}^{2}}{2m{{v}_{g}}^{2}{k}_{P}}\right\}{e}^{\frac{1}{8}\left(-4i\left(L+2\xi \right){k}_{P}-\frac{4{L}^{2}}{{r}_{0}^{2}}-{k}_{P}^{2}{r}_{0}^{2}\right)}\left({e}^{ iL{k}_{P}}-{e}^{2i\xi {k}_{P}}\right){r}_{0}^{2}\left\{-8i{e}^{\frac{1}{8}{k}_{P}\left(-4iL+{k}_{P}{r}_{0}^{2}\right)}\left(1+{e}^{iL{k}_{P}}\right)L-4{e}^{\frac{{L}^{2}}{2{r}_{0}^{2}}}\sqrt{2\pi }\left(Erf\left(\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}\right)-Erf\left(\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}\right){r}_{0}\right)+4{e}^{\frac{1}{8}{k}_{P}\left(-4iL+{k}_{P}{r}_{0}^{2}\right)}\left(-1+{e}^{ iL{k}_{P}}\right){k}_{P}{r}_{0}^{2}+{e}^{\frac{{L}^{2}}{2{r}_{0}^{2}}}\sqrt{2\pi }\left(Erfi\left(\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}\right)-Erfi\left(\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}\right){k}_{P}^{2}{r}_{0}^{3}\right)\right\}$$
(19)
$${{\text{E}}}_{w1}=\frac{1}{8}\left\{\frac{e\left({\beta }^{2}-1\right){{E}_{0}}^{2}}{2m{{v}_{g}}^{2}{k}_{P}}\right\}i{e}^{2i\xi {k}_{P}+\frac{1}{8}(-4i(L+2\xi ){k}_{P}-\frac{4{L}^{2}}{{r}_{0}^{2}}-{k}_{P}^{2}{r}_{0}^{2})}{k}_{P}(-8i{e}^{\frac{1}{8}{k}_{P}(-4iL+{k}_{P}{r}_{0}^{2})}(1+{e}^{iL{k}_{P}})L-4{e}^{\frac{{L}^{2}}{2{r}_{0}^{2}}}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){r}_{0}+4{e}^{\frac{1}{8}{k}_{P}(-4iL+{k}_{P}{r}_{0}^{2})}(-1+{e}^{iL{k}_{P}}){k}_{P}{r}_{0}^{2}+{e}^{\frac{{L}^{2}}{2{r}_{0}^{2}}}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{2}{r}_{0}^{3})+\frac{1}{16}i{e}^{\frac{1}{8}(-4i(L+2\xi ){k}_{P}-\frac{4{L}^{2}}{{r}_{0}^{2}}-{k}_{P}^{2}{r}_{0}^{2})}({e}^{iL{k}_{P}}-{e}^{2i\xi {k}_{P}}){k}_{P}(-8i{e}^{\frac{1}{8}{k}_{P}(-4iL+{k}_{P}{r}_{0}^{2})}(1+{e}^{iL{k}_{P}})L-4{e}^{\frac{{L}^{2}}{2{r}_{0}^{2}}}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){r}_{0}+4{e}^{\frac{1}{8}{k}_{P}(-4iL+{k}_{P}{r}_{0}^{2})}(-1+{e}^{iL{k}_{P}}){k}_{P}{r}_{0}^{2}+{e}^{\frac{{L}^{2}}{2{r}_{0}^{2}}}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{2}{r}_{0}^{3})$$
(20)
$$\Delta {{\text{W}}}_{1}=-\frac{1}{32}[\frac{1}{(1-\frac{1}{\beta }){k}_{P}{m}_{0}{v}_{g}^{2}}e{e}^{\frac{1}{8}(-4i(L+2\xi ){k}_{P}-\frac{4{L}^{2}}{{r}_{0}^{2}}-{k}_{P}^{2}{r}_{0}^{2})}(-1+{e}^{i\xi {k}_{P}})({e}^{iL{k}_{P}}+{e}^{i\xi {k}_{P}})(-1+{\beta }^{2}){E}_{0}^{2}(-8i{e}^{\frac{1}{8}{k}_{P}(-4iL+{k}_{P}{r}_{0}^{2})}(1+{e}^{iL{k}_{P}})L-4{e}^{\frac{{L}^{2}}{2{r}_{0}^{2}}}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){r}_{0}+4{e}^{\frac{1}{8}{k}_{P}(-4iL+{k}_{P}{r}_{0}^{2})}(-1+{e}^{iL{k}_{P}}){k}_{P}{r}_{0}^{2}+{e}^{\frac{{L}^{2}}{2{r}_{0}^{2}}}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{2}{r}_{0}^{3})]$$
(21)

For Hermite mode index s = 2

For s = 2, \({H}_{2}\left(\frac{\sqrt{2}\left(\xi -\frac{L}{2}\right)}{{r}_{0}}\right)=4{\left(\frac{\sqrt{2}\left(\xi -\frac{L}{2}\right)}{{r}_{0}}\right)}^{2}-2\). So, the solution of Eq. (12), (13) and (15), respectively, is

$${\Phi }_{2}=\left\{\frac{e\left({\beta }^{2}-1\right){{E}_{0}}^{2}}{2m{{v}_{g}}^{2}{k}_{P}}\right\}\frac{1}{32{r}_{0}^{2}}{e}^{-i(L+\xi ){k}_{P}-\frac{{L}^{2}}{2{r}_{0}^{2}}-\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}({e}^{iL{k}_{P}}-{e}^{2i\xi {k}_{P}})(-32i{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(1+{e}^{iL{k}_{P}}){L}^{3}+16{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}L(-2i(1+{e}^{iL{k}_{P}})+(-1+{e}^{iL{k}_{P}})L{k}_{P}){r}_{0}^{2}-32{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){r}_{0}^{3}+8{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}{k}_{P}(6(-1+{e}^{iL{k}_{P}})+i(1+{e}^{iL{k}_{P}})L{k}_{P}){r}_{0}^{4}+16{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{2}{r}_{0}^{5}-4{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(-1+{e}^{iL{k}_{P}}){k}_{P}^{3}{r}_{0}^{6}-{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{4}{r}_{0}^{7})$$
(22)
$${{\text{E}}}_{w2}=\left\{\frac{e\left({\beta }^{2}-1\right){{E}_{0}}^{2}}{2m{{v}_{g}}^{2}{k}_{P}}\right\}\frac{1}{16{r}_{0}^{2}}i{e}^{2i\xi {k}_{P}-i(L+\xi ){k}_{P}-\frac{{L}^{2}}{2{r}_{0}^{2}}-\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}{k}_{P}(-32i{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(1+{e}^{iL{k}_{P}}){L}^{3}+16{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}L(-2i(1+{e}^{iL{k}_{P}})+(-1+{e}^{iL{k}_{P}})L{k}_{P}){r}_{0}^{2}-32{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){r}_{0}^{3}+8{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}{k}_{P}(6(-1+{e}^{iL{k}_{P}})+i(1+{e}^{iL{k}_{P}})L{k}_{P}){r}_{0}^{4}+16{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{2}{r}_{0}^{5}-4{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(-1+{e}^{iL{k}_{P}}){k}_{P}^{3}{r}_{0}^{6}-{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{4}{r}_{0}^{7})+\frac{1}{32{r}_{0}^{2}}i{e}^{-i(L+\xi ){k}_{P}-\frac{{L}^{2}}{2{r}_{0}^{2}}-\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}({e}^{iL{k}_{P}}-{e}^{2i\xi {k}_{P}}){k}_{P}(-32i{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(1+{e}^{iL{k}_{P}}){L}^{3}+16{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}L(-2i(1+{e}^{iL{k}_{P}})+(-1+{e}^{iL{k}_{P}})L{k}_{P}){r}_{0}^{2}-32{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){r}_{0}^{3}+8{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}{k}_{P}(6(-1+{e}^{iL{k}_{P}})+i(1+{e}^{iL{k}_{P}})L{k}_{P}){r}_{0}^{4}+16{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{2}{r}_{0}^{5}-4{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(-1+{e}^{iL{k}_{P}}){k}_{P}^{3}{r}_{0}^{6}-{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{4}{r}_{0}^{7})$$
(23)
$$\Delta {{\text{W}}}_{2}=-\frac{1}{64}[\frac{1}{(1-\frac{1}{\beta }){k}_{P}{m}_{0}{r}_{0}^{2}{v}_{g}^{2}}e{e}^{-i(L+\xi ){k}_{P}-\frac{{L}^{2}}{2{r}_{0}^{2}}-\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(-1+{e}^{i\xi {k}_{P}})({e}^{iL{k}_{P}}+{e}^{i\xi {k}_{P}})(-1+{\beta }^{2}){E}_{0}^{2}(-32i{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(1+{e}^{iL{k}_{P}}){L}^{3}+16{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}L(-2i(1+{e}^{iL{k}_{P}})+(-1+{e}^{iL{k}_{P}})L{k}_{P}){r}_{0}^{2}-32{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){r}_{0}^{3}+8{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}{k}_{P}(6(-1+{e}^{iL{k}_{P}})+i(1+{e}^{iL{k}_{P}})L{k}_{P}){r}_{0}^{4}+16{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{2}{r}_{0}^{5}-4{e}^{\frac{1}{8}{k}_{P}^{2}{r}_{0}^{2}}(-1+{e}^{iL{k}_{P}}){k}_{P}^{3}{r}_{0}^{6}-{e}^{\frac{1}{2}L(i{k}_{P}+\frac{L}{{r}_{0}^{2}})}\sqrt{2\pi }({\text{Erfi}}[\frac{-2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]-{\text{Erfi}}[\frac{2iL+{k}_{P}{r}_{0}^{2}}{2\sqrt{2}{r}_{0}}]){k}_{P}^{4}{r}_{0}^{7})]$$
(24)

Equations (16) to(24) are the outcomes of LWFA effect for various Hermite–Gaussian pulse profiles, which depend on various factors like beam waist (\({r}_{0}\)), pulse length (L), propagation distance (\(\xi\)), mode index (s), plasma propagation constant (\({k}_{P}\)), laser field amplitude (\({E}_{0}\)), etc.

Results and discussion

In this paper, we have chosen plasma of electron density \(2\times {10}^{23}{m}^{-3},\) plasma frequency \(2.52\times {10}^{13}rad/s\). Laser pulse of wavelength \(10.6 \mu m\), laser frequency \(1.78\times {10}^{14} rad/s\), and pulse length \(48.10 \mu m\) are chosen for numerical investigation. Amplitude of laser electric field (\({E}_{0}\)) is chosen as \(2.15\times {10}^{11} V/m\), \(4.30\times {10}^{11} V/m\) and \(8.60\times {10}^{11} V/m\) to investigate LWFA effect.

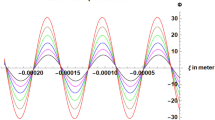
Figure 1 shows the variation of energy gain by electrons as a function of propagation distance for \({E}_{0}=4.30\times {10}^{11} V/m\). Peak of all 3 curves corresponding to Hermite mode indexed values s = 0, s = 1 and s = 2 in the figure lies at the same position (\(\xi =31.45 \mu m\)). Maximum energy gain is 470.10 MeV for s = 2 mode and minimum energy gain is 39.42 MeV for s = 1 mode. For s = 0, energy gain is 167.65 MeV for the same other parameters. So, it can be concluded that increment of energy gain depends on the mode of Hermite polynomial.

Fig. 1
figure 1

Variation of energy gain by electron with propagation distance for various Hermite mode indexes, s = 0 (\(\Delta {E}_{0}\)), s = 1 (\(\Delta {E}_{1}\)) and s = 2 (\(\Delta {E}_{2}\)) for \({E}_{0}=4.30\times {10}^{11} V/m, {r}_{0}=33.74 \mu m {\text{and}} L=48.10 \mu m .\) Other parameters are same as defined above

Full size image

Figure 2 shows the variation of maximum energy gain with beam waist for different laser field amplitudes (\({E}_{0}\)). For all Hermite polynomial mode indexes (s = 0, 1, 2), the maximum energy gain by electrons increases with increase in laser field amplitude as \({E}_{0}^{2}.\) For s = 0, energy gain increases rapidly with increase in beam waist up to a value of \(25.35 \mu m\), then attains its maximum value and becomes constant with further increase in beam waist. A maximum of 696 MeV energy gain is obtained for laser field amplitude \(8.60\times {10}^{11} V/m.\) For s = 1, electron energy gain increases rapidly till beam waist \(16.90 \mu m\), then decreases sharply with further increase in beam waist and becomes almost zero for beam waist greater than \(70 \mu m\). A maximum of 647.2 MeV energy gain is obtained for beam waist \(13.52 \mu m\) and laser field amplitude \(8.60\times {10}^{11} V/m.\) For s = 2, electron energy gain increases rapidly till beam waist \(10.14 \mu m\), then decreases till \(20.28 \mu m\), and finally increases with further increase in bream waist and becomes constant for beam waist greater than \(70 \mu m\). A maximum energy gain of 2652.54 MeV is obtained with selected parameters in this case. So, the effect of beam waist on energy gained by the electrons depends on the Hermite mode index of chosen pulse profile.

Fig. 2
figure 2

Variation of energy gain by electron with beam waist for various Hermite mode indexes, s = 0 a, s = 1 b and s = 2 c for \(L=48.10 \mu m\) Other parameters are same as defined above

Full size image

Hermite polynomial term \({H}_{s}\left(x\right)where x=\left(\frac{\sqrt{2}\left(\xi -\frac{L}{2}\right)}{{r}_{0}}\right)\) is a part of the selected laser pulse profile. With the variation in s value, Hermite polynomial and laser pulse profile also vary. Variation in laser pulse profile is responsible for energy enhancement.

Variation of energy gain by electrons with beam waist and laser pulse length is illustrated in Fig. 3. For s = 0 mode, energy gain becomes constant for higher values of beam waist if pulse length is small (< 0.0015 m). If the pulse length is increased further, periodic variation in energy gain with beam waist is obtained for smaller beam waist (\(0<{r}_{0}<50 \mu m\)) but energy gain becomes zero for higher values of beam waist. Similar variation can be seen for s = 1 mode, but the maximum energy gain is obtained for \(20 \mu m<{r}_{0}<70 \mu m\). Similarly, for s = 2 mode, the maximum energy gain is obtained for beam waist range\(40 \mu m<{r}_{0}<100 \mu m\). So, the range of beam waist corresponding to maximum energy gain depends on Hermite mode index as well as pulse length also and shifts toward higher beam waist with increase in Hermite mode index.

Fig. 3
figure 3

Variation of energy gain by electron with beam waist and pulse length for various Hermite mode indexes, s = 0 a, s = 1 b and s = 2 c for \({E}_{0}=4.30\times {10}^{11} V/m.\) Other parameters are same as defined above. \({r}_{0}\) and L are in meter and \(\Delta E\) is in MeV units

Full size image

Figure 4 illustrates the variation of energy gain by electrons with plasma density for different Hermite mode indexes. For s = 0 and s = 2 mode, energy gain oscillates with increasing amplitude till the condition of over dense plasma (\({\omega }_{p}>{\omega }_{L}\)) is achieved. But for s = 1 mode, the variation is just the opposite. Amplitude of oscillating energy gain decreases rapidly with increase in plasma density. Energy gain becomes almost zero for the plasma of higher plasma density for s = 1 mode but a maximum energy gain with higher plasma density is obtained for s = 0 and s = 0 mode. It is due to complex structure of Hermite–Gaussian laser pulse.

Fig. 4
figure 4

Variation of energy gain by electron with beam waist and pulse length for various Hermite mode indexes, s = 0 a, s = 1 b and s = 2 c for \({E}_{0}=4.30\times {10}^{11} V/m, {r}_{0}=10.12 \mu m and L=48.10 \mu m .\) Other parameters are same as defined above

Full size image

In this study, we have obtained a maximum energy gain of 2.65 GeV is obtained for \({E}_{0}=8.60\times {10}^{11} V/m\), \({r}_{0}= 70 \mu m, L=48.10 \mu m\) and plasma density \(2\times {10}^{23}{m}^{-3}\).

The outcomes of this study are consistent with the study of Ghotra et al. [38]. In their investigation, they used circular polarized Hermite–Gaussian laser pulse to accelerate electrons by direct laser acceleration (DLA) phenomenon for different Hermite mode indexes. They observed that enhanced electron energy gain can be obtained for even Hermite mode index as compared to odd Hermite mode indexes. In an experimental study done by Oumbarek et al. [39], it is observed that generated laser wakefield acceleration depends on laser profile. A complex laser pulse profile can develop a more effective, energy efficient acceleration scheme as compared to a simple Gaussian laser pulse.

Conclusion

Using Hermite–Gaussian laser pulses, the research studies the phenomena of laser wakefield acceleration in a collisionless underdense plasma. The research investigates the delicate interplay between the laser pulse's properties, the ensuing laser wakefield structure, and the electron energy gain using theoretical analysis. In our study, we observed that the electron energy gain grows as the amplitude of the laser pulse increases, regardless of the Hermite mode index. Under identical conditions, we observed enhanced energy gain for s = 0 and s = 2 mode indexes than for s = 1 mode. For a given Hermite mode index, electron energy gain varies with pulse length, plasma density, and beam waist. As a result, the optimized value of any one parameter for optimum energy gain swings together with the values of the other two parameters. With a certain combination of conditions, we were able to attain an energy increase of 2.65 GeV. The findings shed light on the ability of Hermite–Gaussian laser pulses to improve the performance of LWFA experimental setups, providing insights into optimizing the generation of high-energy particle beams for a variety of applications, including particle physics experiments and medical treatments.