Optimized ellipse packings in regular polygons

Abstract

We present model development and numerical solution approaches to the problem of packing a general set of ellipses without overlaps into an optimized polygon. Specifically, for a given set of ellipses, and a chosen integer m ≥ 3, we minimize the apothem of the regular m-polygon container. Our modeling and solution strategy is based on the concept of embedded Lagrange multipliers. To solve models with up to n ≤ 10 ellipses, we use the LGO solver suite for global–local nonlinear optimization. In order to reduce increasing runtimes, for model instances with 10 ≤ n ≤ 20 ellipses, we apply local search launching the Ipopt solver from selected random starting points. The numerical results demonstrate the applicability of our modeling and optimization approach to a broad class of highly non-convex ellipse packing problems, by consistently returning good quality feasible solutions in all (231) illustrative model instances considered here.

1 Introduction and motivation

Object packing problems (OPPs) arise in relation to a broad range of engineering and scientific applications. First, we present a concise review of some well-frequented as well as several less known OPPs, comment on solution approaches, and highlight various applications.

A finite circle packing is an optimized non-overlapping arrangement of n circles inside a container set such as a circle, square or a general rectangle. This problem—in particular, the case of packing identical circles—has received considerable attention in the literature. The object-symmetric structure of identical circle packings (ICPs) makes these problems easier, but finding optimal configurations for arbitrary values of n is still a difficult challenge. Studies of packing identical circles frequently aim at proving the optimality of the configurations found, either theoretically or with the help of rigorous computational approaches. As of today, provably optimal configurations are known only for tens of circles, with the exception of certain special cases; best known numerical results are available for packing up to 2600 circles in a circle, and 10,000 circles in a square. For further details and references, consult e.g., Szabó et al. [51] or Specht [47].

The general circle packing (GCP) problem defined for collections of n (in principle) arbitrary sized circles is a substantial generalization of the ICP case. Provably optimal GCP configurations can be found only to models with n ≤ 4. Therefore GCP studies frequently utilize generic or tailored global scope numerical solution strategies. Without going into further details related to circle packings, we refer to Castillo et al. [7] and to Hifi and M’Hallah [16] for reviews of both ICPs and GCPs and their applications, noting that Pintér et al. [41] present numerical results for generalized d-sphere packings in d = 2, 3, 4, 5 dimensions with up to 50 spheres.

Compared to ICPs and GCPs, ellipse packing problems (EPPs) have received relatively little attention in the literature so far. Finding globally optimized packings of ellipses with arbitrary size and orientation is a hard computational problem. The key challenge is the modeling and enforcement of the constraints to avoid ellipse overlaps, as a function of ellipse center locations and orientations.

To illustrate the difficulty of this class of problem, first we mention an exact result that deals with the densest packing of just two non-overlapping congruent ellipses in a square. For this very special case, Gensane and Honvault [14] analytically define the densest packing of two identical ellipses with aspect ratio r, for all real numbers r in $\left[ {0,1} \right]$. Honvault [18] analytically describes the densest packing of three non-overlapping congruent ellipses in a square.

Galiev and Lisafina [13] study the problem of packing identically sized and orthogonally oriented ellipses inside a rectangular container. Binary linear optimization models are proposed using a grid that approximates the container region, and then considering the nodes of the grid as potential positions for the ellipse centers. Two special cases regarding the orientation of the ellipses are considered: (i) the major axes of all ellipses are parallel to the x or y axis, and (ii) the major axes of some of the ellipses are parallel to the x axis, and for all others they are parallel to the y axis. A heuristic algorithm based on binary linear model formulations is proposed, with numerical results.

Litvinchev et al. [26] investigate optimized packings of so-called circular-like objects—including circles, ellipses, rhombuses, and octagons—in a rectangular container. Similarly to Galiev and Lisafina [13], they propose a binary linear optimization model formulation based on a grid that approximates the container. The resulting problem is then solved using the software package CPLEX. Numerical results related to packing identically sized and oriented circles, ellipses, rhombuses, and octagons are presented.

Uhler and Wright [54] study the problem of packing arbitrary size ellipsoids into an ellipsoidal container so as to minimize a measure of overlap between ellipsoids. A model formulation and two local scope solution approaches are discussed: one approach for the general case, and a simpler approach for the special case in which all ellipsoids are, in fact, spheres. The authors illustrate their approach applied to modeling chromosome organization in the human cell nucleus.

Kallrath and Rebennack [22] address the problem of packing ellipses of arbitrary size and orientation into an optimized rectangle. The packing model formulation is introduced as a cutting problem. Their key idea is to use separating lines to ensure that the ellipses do not overlap with each other, using hyperplanes and coordinate transformations. For problem instances with n ≤ 14 ellipses, the authors find globally optimal numerical solutions (considering the finite arithmetic precision of the global solvers used). At the same time, for their n > 14 ellipse-based model instances none of the (local or global) nonlinear optimization solvers tried by them in the GAMS modeling environment could compute even a feasible solution. Therefore, they propose heuristic approaches in which ellipses are added sequentially to find an approximately optimized rectangular container: this strategy allows the computation of high quality solutions for up to 100 ellipses. Kallrath [21] extends the work presented in Kallrath and Rebennack [22], to pack ellipsoids into optimized rectangular boxes.

Birgin et al. [3, 4] propose several model formulations for packing ellipsoids in a container. Specifically, they address various two- and three-dimensional EPPs with rectangular containers (for both identical and arbitrary sized ellipses), elliptical containers (for identical ellipses), spherical containers (for identical ellipsoids), and cuboid containers (for identical ellipsoids). The authors propose multi-start global scope optimization procedures that use starting guesses, followed by using local optimization solvers, in order to find good quality solutions with up to 1000 ellipsoids.

Stoyan et al. [49] further develop their phi-function technique (cf. Stoyan et al. [50]) to pack ellipses into rectangular containers of minimal area. These functions—referred to as quasi-phi-functions—support the packing of non-overlapping ellipses with arbitrary size and orientation. The authors develop an efficient solution algorithm based on local optimization combined with a feasible region transformation procedure. This procedure reduces the dimension of the problem instance, which allows the authors to use a local solver (Ipopt in their case) to find a high quality solution. Stoyan et al. [49] present computational results that compare favorably with those presented by Kallrath and Rebennack [22].

In addition to being an interesting model development and optimization challenge per se, ellipse and ellipsoid packings have important scientific and industrial applications. To illustrate this aspect, we mention studies related to the structure of liquids, crystals, and glasses (Bernal [2]); the flow and compression of granular materials (Edwards [12], Jaeger and Nagel [19], Jaeger et al. [20]); the design of high density ceramic materials, and the formation and growth of crystals (Cheng et al., [10], Rintoul and Torquato [44]); the thermodynamics of liquid to crystal transition (Alder and Wainwright [1], Chaikin [9], Pusey [43]); and chromosome organization in human cell nuclei (Uhler and Wright [54]).

In this article, we study the packing of ellipses with arbitrary size and orientation in regular m-polygons: our objective is to minimize the area of the container polygon. Packing ellipses into a regular polygon requires i) the determination of the maximal distance from the center of all polygon faces to each ellipse boundary, and ii) the finding of the minimal distance between all pairs of the ellipses. The first requirement is necessary to determine the length of the polygon’s apothem (the line segment from the center of the polygon to the midpoint of one of its sides, see Fig. 1), which is then to be minimized. The second requirement serves to prevent the ellipses from overlapping. Explicit analytical formulas for the first requirement can be directly derived, and used in our optimization strategy. However, for the second requirement explicit analytical formulas—even if they exist—would be complicated. Therefore, our modeling and solution approach is based on embedding optimization calculations, using Lagrange multipliers, into the overall optimization strategy. In this Lagrangian framework, optimization proceeds simultaneously considering both requirements.

Fig. 1

Apothem of a regular polygon (m = 8)

To summarize, we propose a modeling and optimization framework that uses embedded Lagrange multipliers to prevent the ellipses from overlapping. This allows us to solve the container minimization problem numerically with a single call to a suitable optimization procedure. Our model formulation for regular polygons allows the high quality approximations of a range of container shapes. This is particularly important in so called “open-field” or “green-field” situations where a set of regular polygonal containers can adequately approximate the field under consideration. Our model can also be extended to consider general (not necessarily regular) convex polygons: see Giachetti and Sanchez [15] for an interesting design application.

Our modeling and optimization strategy consistently provides high quality feasible solutions to non-trivial model instances. We are able to reproduce all previous related results considered here, improving some of the previously reported best numerical results. We also solve new problem instances for a range of model parameter choices.

2 Optimization model development

Our objective is to minimize the area of the regular m-polygon that contains, without overlaps, a given collection of n ellipses with arbitrary size and shape characteristics. The input data to these optimization problem instances are m, n, and the (semi-major and semi-minor) axes (a_i, b_i) of the ellipses to be packed for $i = 1, \ldots ,n$. The primary decision variables are the polygon’s apothem $d$, and the centre position $\left( {x_{i}^{c} ,y_{i}^{c} } \right)$ and orientation θ_i of the packed ellipses, i = 1, …, n. Secondary (induced) variables are the positions of the distance maximizing lines pointing from each ellipse boundary to the center of each of the polygon faces, and the positions of the points on one of each pair of ellipses which minimizes the value of the equation describing the other ellipse. Other secondary variables are the embedded Lagrange multipliers used to determine those points. All listed secondary variables are implicitly determined by the primary variables, as discussed below.

The model constraints belong to two groups. The first constraint group uses the secondary variables to keep the ellipses inside the container, and to prevent them from overlapping. The second constraint group represents the equations generated by the embedded Lagrange multiplier conditions. The calculations for optimizing the polygon and for preventing ellipse overlaps proceed simultaneously, rather than being performed to completion at each optimization step. Observe that since the area of the polygon equals $m \cdot d^{2} \cdot \tan \left( {\pi /m} \right),$m being an input parameter, finding the minimal apothem d is equivalent to minimizing the area of the regular polygon.

Omitting first the index $i$(for a simpler notation) equation $e\left( {a,b,x^{c} ,y^{c} ,\theta ;x,y} \right) = 0$ introduced by (1) defines the boundary of an ellipse with semi-major and semi-minor axes a and $b$, centered at $\left\{ {x^{c} ,y^{c} } \right\}$, and rotated counterclockwise by angle θ. The formula for $e\left( {a,b,x^{c} ,y^{c} ,\theta ;x,y} \right)$ is obtained by transforming the equation of a circle with radius 1, centered at (0, 0), as shown below.

$$ \begin{aligned} e\left( {a,b,x^{c} ,y^{c} ,\theta ;x,y} \right) & = \left( {\frac{{\cos \theta \left( {x - x^{c} } \right)}}{a} + \frac{{\sin \theta \left( {y - y^{c} } \right)}}{a}} \right)^{2} \\ & \quad + \left( {\frac{{\cos \theta \left( {y - y^{c} } \right)}}{b} - \frac{{\sin \theta \left( {x - x^{c} } \right)}}{b}} \right)^{2} - 1 = 0. \\ \end{aligned} $$

(1)

In (1) the coordinate system is rotated clockwise by an angle of −θ, which is equivalent to rotating the ellipse counterclockwise by $\theta$ around its centre. The value of $e\left( {a,b,x^{c} ,y^{c} ,\theta ;x,y} \right)$ is negative for all points $\left( {x,y} \right)$ located inside the ellipse, zero for all points on the ellipse boundary, and positive for all points outside the ellipse. Let us recall here that $\left( {x^{c} ,y^{c} } \right)$ and θ are primary decision variables for each ellipse i: in general, these variables will be denoted by $\left( {x_{i}^{c} ,y_{i}^{c} } \right)$ and θ_i for i = 1, …, n.

In order to standardize our model formulation, we assume that the optimized regular polygon container is centered at the origin. Consider now the line $\gamma_x x + \gamma_y y = \ell$ that embeds one of the polygon sides. The slope of this line is $- \gamma_{x} /\gamma_{y}$, and the distance from the origin to the line equals

$$ \sqrt {\frac{{\ell^{2} }}{{\gamma_{x}^{2} + \gamma_{y}^{2} }}} . $$

(2)

If $\left( {\gamma_{x} ,\gamma_{y} } \right)$ is a unit vector so that $\gamma_{x}^{2} + \gamma_{y}^{2} = 1$, then the point on the line closest to the origin is $\ell \left( {\gamma_{x} ,\gamma_{y} } \right)$, located at a distance $\ell$ from the origin. The slope of the line to that point is $\gamma_{y} /\gamma_{x}$: hence, the line from the origin to the closest point on $\gamma_{x} x + \gamma_{y} y = \ell$ is perpendicular to it. This fact will be used to determine the apothem d of the polygon.

Proceeding now towards the requirement to contain all ellipses inside the regular polygon, we find the maximum value of ℓ for which the side of the polygon intersects the ellipse. Our derivation for a polygon follows the first order Karush–Kuhn–Tucker conditions described by Kallrath and Rebennack [22] for a rectangular container.

For an ellipse to be contained inside the polygon, all sides $\gamma_{x} x + \gamma_{y} y$ must be less than or equal to this maximum value. Therefore we consider the following equation using $\lambda$ as the maximizing embedded Lagrange multiplier.

$$ \gamma_{x} x + \gamma_{y} y = \lambda \cdot e\left( {a,b,x^{c} ,y^{c} ,\theta ;x,y} \right). $$

(3)

Differentiating both sides of Eq. (3) with respect to x, y, and λ, we obtain

$$ \begin{aligned} & \gamma_{x} x^{c} + \gamma_{y} y^{c} - \sqrt \tau , \\ & \gamma_{x} x^{c} + \gamma_{y} y^{c} + \sqrt \tau , \\ \end{aligned} $$

(4)

where

$$ \begin{aligned} \tau & = \left( {a^{2} \gamma_{x}^{2} + b^{2} \gamma_{y}^{2} } \right){ \cos }^{2} \theta + \left( {b^{2} \gamma_{x}^{2} + a^{2} \gamma_{y}^{2} } \right){ \sin }^{2} \theta \\ & \quad + \left( {a - b} \right)\left( {a + b} \right)\gamma_{x} \gamma_{y} { \sin }\left( {2\theta } \right). \\ \end{aligned} $$

(5)

Notice that the Lagrange multiplier λ does not appear in (4). More importantly, the maximum value in the direction $\left( {\gamma_{x} ,\gamma_{y} } \right)$ is the result in (4) with the positive sign in front of $\sqrt \tau$. This explicit analytical result will be used in our optimization strategy for all sides of the regular polygon, which, of course, share the same apothem d.

Based on the above discussion, the condition of containing a given ellipse inside the polygon can be described by the relation

$$ d \ge p\left( {a,b,x^{c} ,y^{c} ,\theta ;x,y} \right): = \gamma_{x} x^{c} + \gamma_{y} y^{c} + \sqrt \tau . $$

(6)

In order to complete our analysis related to the sides of the container polygon, note that for a regular polygon with m sides, the points $\left( {\gamma_{{x_{k} }} ,\gamma_{{y_{k} }} } \right)$ that define the unit vectors for each apothem (i.e., for each side k of the polygon) are given by

$$ \left( {\gamma_{{x_{k} }} ,\gamma_{{y_{k} }} } \right) = \left( {\cos \left( {\frac{2 \cdot k \cdot \pi }{m} - \frac{\pi }{2}} \right),\sin \left( {\frac{2 \cdot k \cdot \pi }{m} - \frac{\pi }{2}} \right)} \right),k = 1, \ldots ,m. $$

(7)

Proceeding next towards preventing ellipse overlaps, it is useful to determine equations for the derivatives of the ellipse Eq. (1) with respect to x and y. For a given set of values $\left( {a,b,x^{c} ,y^{c} ,\theta } \right)$ we will denote $e\left( {a,b,x^{c} ,y^{c} ,\theta ;x,y} \right)$ simply as $e\left( {x,y} \right)$: then these derivatives are determined as

$$ \frac{{de\left( {x,y} \right)}}{dx} = \frac{2}{{a^{2} b^{2} }}\left( {b^{2} \left( {x - x^{c} } \right){ \cos }^{2} \theta - \left( {a^{2} - b^{2} } \right)\left( {y - y^{c} } \right)\cos \theta \sin \theta + a^{2} \left( {x - x^{c} } \right){ \sin }^{2} \theta } \right), $$

(8)

$$ \frac{{de\left( {x,y} \right)}}{dy} = \frac{2}{{a^{2} b^{2} }}\left( {a^{2} \left( {y - y^{c} } \right){ \cos }^{2} \theta - \left( {a^{2} - b^{2} } \right)\left( {x - x^{c} } \right)\cos \theta \sin \theta + b^{2} \left( {y - y^{c} } \right){ \sin }^{2} \theta } \right). $$

(9)

All pairs of packed ellipses are prevented from overlapping by requiring that the minimum value of the ellipse equation for the first ellipse (ellipse i) for any point on the second ellipse (ellipse j) has to be greater than a judiciously set, sufficiently small parameter ɛ ≥ 0. This requirement will be met using the embedded Lagrange multiplier method.

The next set of equations serves to determine the point on ellipse j that maximizes or minimizes the value of the function describing ellipse i. In the case considered here, λ must be negative to obtain the minimum. During optimization, this requirement with respect to the sign of λ will be enforced by setting its search bounds.

$$ \begin{aligned} & \frac{{de\left( {x,y} \right)}}{dx}\left( {a_{i} ,b_{i} ,x_{i}^{c} ,y_{i}^{c} ,\theta_{i} ;x,y} \right) = \lambda \cdot \frac{{de\left( {x,y} \right)}}{dx}\left( {a_{j} ,b_{j} ,x_{j}^{c} ,y_{j}^{c} ,\theta_{j} ;x,y} \right), \\ & \frac{{de\left( {x,y} \right)}}{dy}\left( {a_{i} ,b_{i} ,x_{i}^{c} ,y_{i}^{c} ,\theta_{i} ;x,y} \right) = \lambda \cdot \frac{{de\left( {x,y} \right)}}{dy}\left( {a_{j} ,b_{j} ,x_{j}^{c} ,y_{j}^{c} ,\theta_{j} ;x,y} \right), \\ & e\left( {a_{j} ,b_{j} ,x_{j}^{c} ,y_{j}^{c} ,\theta_{j} } \right)\left( {x,y} \right) = 0. \\ \end{aligned} $$

(10)

The last equation type introduced is the requirement that the minimizing point lies on ellipse j. Eliminating λ from the first two equations, we obtain

$$ \begin{aligned} & \frac{{de\left( {x,y} \right)}}{dy}\left( {a_{i} ,b_{i} ,x_{i}^{c} ,y_{i}^{c} ,\theta_{i} ;x,y} \right) \cdot \frac{{de\left( {x,y} \right)}}{dx}\left( {a_{j} ,b_{j} ,x_{j}^{c} ,y_{j}^{c} ,\theta_{j} ;x,y} \right) \\ & \quad = \frac{{de\left( {x,y} \right)}}{dy}\left( {a_{j} ,b_{j} ,x_{j}^{c} ,y_{j}^{c} ,\theta_{j} ;x,y} \right) \cdot \frac{{de\left( {x,y} \right)}}{dx}\left( {a_{i} ,b_{i} ,x_{i}^{c} ,y_{i}^{c} ,\theta_{i} ;x,y} \right). \\ \end{aligned} $$

(11)

Note that at the point on ellipse j that minimizes or maximizes the value of the function describing ellipse i, the slope of ellipse i equals the slope of ellipse j.

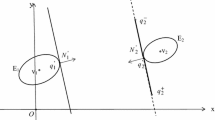
To illustrate the approach, consider the ellipses $e_{i} \left( {1.25,0.75,1,2,\pi /3;x,y} \right)$ and $e_{j} \left( {1.5,0.83, -\,0.5,1,\pi /4;x,y} \right)$. The overlapping value of Eq. (1) for ellipse i between the ellipses is − 0.886 with (x, y) = (0.701, 1.777): this value can be found by solving the set of Eq. (10). Figure 2 shows the ellipse configuration.

Fig. 2

Two overlapping ellipses

To give another example, consider two ellipses defined by $e_{i} \left( {1.25,0.75, -\,1, -\,2,\pi /3;x,y} \right)$ and $e_{j} \left( {1.5,0.83, -\,0.5,1,\pi /4;x,y} \right)$. The non-overlapping value between the ellipses is 1.84 with (x, y) = (− 0.758, − 0.141): again, this value can be found by solving the set of Eqs. (10) for x and y. Figure 3 shows the resulting non-overlapping ellipse configuration.

Fig. 3

Two non-overlapping ellipses

Constructing Lagrange multiplier Eqs. (10) for $e_{i} \left( {x,y} \right)$ and $e_{j} \left( {x,y} \right)$, as shown above, and requiring that the Lagrange multiplier be negative and the value of $e_{i} \left( {x,y} \right)$ be positive, guarantees that these two ellipses do not overlap. Note that requiring $e_{i} \left( {x,y} \right) 0$ allows the ellipses to touch. Consequently, the requirement that two ellipses do not overlap can be implemented by creating constraints from the Lagrange multiplier Eqs. (10). That is, we require five constraints for each pair of ellipses: $\lambda_{i,j} \le 0$(a bound constraint), $e_{i} \left( {x,y} \right) \ge 0$, $e_{j} \left( {x,y} \right) = 0$, and the two Lagrange multiplier equations generated by differentiating the equation $e_{i} \left( {x,y} \right) = \lambda_{i,j} \cdot e_{j} \left( {x,y} \right)$ with respect to x and y. In the optimization framework, $\lambda_{i,j} \le 0$ are the Lagrange multipliers appearing in the equations to find the point $\left( {x_{j,i} ,y_{j,i} } \right)$ on ellipse j that minimizes the value of the equation that describes ellipse i. Finally, we state constraints to prevent ellipse i from overlapping with ellipse j, by requiring that the minimal value of the equation describing ellipse i at the minimizing point on ellipse j has to be at least ɛ. We remark that the optimization solvers used in our study are not too sensitive to the choice of this parameter: for instance, values of ɛ = 0, 10⁻⁶, and 10⁻² have been all tested without leading to numerical issues.

Summarizing the model development steps, we obtain the following model-class for packing n general ellipses into an optimized regular m-polygon container.

$$ \begin{array}{*{20}l} {\text{minimize}} \hfill & d \hfill & {} \hfill \\ {{\text{subject}}\,{\text{to}}} \hfill & {d \ge p\left( {a_{i} ,b_{i} ,x_{i}^{c} ,y_{i}^{c} ,\theta_{i} ;\gamma_{{x_{k} }} ,\gamma_{{y_{k} }} } \right)} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n} \hfill \\ {} \hfill & {} \hfill & {\quad k = 1, \ldots ,m} \hfill \\ {} \hfill & {\frac{{de\left( {x,y} \right)}}{dx}\left( {a_{i} ,b_{i} ,x_{i}^{c} ,y_{i}^{c} ,\theta_{i} ;x_{j,i} ,y_{j,i} } \right) = \lambda_{j,i} \cdot \frac{{de\left( {x,y} \right)}}{dx}\left( {a_{j} ,b_{j} ,x_{j}^{c} ,y_{j}^{c} ,\theta_{j} ;x_{j,i} ,y_{j,i} } \right)} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n - 1} \hfill \\ {} \hfill & {} \hfill & {\quad j = i + 1, \ldots ,n} \hfill \\ {} \hfill & {\frac{{de\left( {x,y} \right)}}{dy}\left( {a_{i} ,b_{i} ,x_{i}^{c} ,y_{i}^{c} ,\theta_{i} ;x_{j,i} ,y_{j,i} } \right) = \lambda_{j,i} \cdot \frac{{de\left( {x,y} \right)}}{dy}\left( {a_{j} ,b_{j} ,x_{j}^{c} ,y_{j}^{c} ,\theta_{j} ;x_{j,i} ,y_{j,i} } \right)} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n - 1} \hfill \\ {} \hfill & {} \hfill & {\quad j = i + 1, \ldots ,n} \hfill \\ {} \hfill & {e\left( {a_{j} ,b_{j} ,x_{j}^{c} ,y_{j}^{c} ,\theta_{j} ;x_{j,i} ,y_{j,i} } \right) = 0} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n - 1} \hfill \\ {} \hfill & {} \hfill & {\quad j = i + 1, \ldots ,n} \hfill \\ {} \hfill & {e\left( {a_{i} ,b_{i} ,x_{i}^{c} ,y_{i}^{c} ,\theta_{i} } \right) \ge \varepsilon } \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n - 1} \hfill \\ {} \hfill & {} \hfill & {\quad j = i + 1, \ldots ,n} \hfill \\ {} \hfill & {l \le x_{i}^{c} \le u} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n} \hfill \\ {} \hfill & {l \le y_{i}^{c} \le u} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n} \hfill \\ {} \hfill & { - \pi \le \theta_{i} \le \pi } \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n} \hfill \\ {} \hfill & {l \le x_{j,i} \le u} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n - 1} \hfill \\ {} \hfill & {} \hfill & {\quad j = i + 1, \ldots ,n} \hfill \\ {} \hfill & {l \le y_{j,i} \le u} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n - 1} \hfill \\ {} \hfill & {} \hfill & {\quad j = i + 1, \ldots ,n} \hfill \\ {} \hfill & {2 \cdot l \le \lambda_{j,i} \le 0} \hfill &\quad {{\text{for}}\,i = 1, \ldots ,n - 1} \hfill \\ {} \hfill & {} \hfill & {\quad j = i + 1, \ldots ,n} \hfill \\ \end{array} $$

(12)

In the model (12) l and u denote lower and upper bounds for the ellipse center positions: these bounds can be defined appropriately for each ellipse packing instance studied, in order to facilitate the finding of feasible solutions.

The optimization model (12) has $1 + 3n + 3\left( {n - 1} \right)^{2}$ decision variables. In addition to the bound constraints imposed on all decision variables, the model has $m \cdot n + 4\left( {n - 1} \right)^{2}$ non-convex constraints. Considering also the formulas introduced earlier for the ellipses, model (12) represents a hard global optimization challenge: both the number of decision variables and the number of nonconvex constraints increase as a quadratic function of n, observing also the term m · n. For example, a problem instance with $n = 10$ ellipses inside a regular polygon with $m = 8$ sides leads to a model with 274 decision variables, corresponding bound constraints, and 404 non-convex constraints. Arguably, this rather small model instance can be already perceived as a computational global optimization challenge. Based on the above observations, we can expect that the computational difficulty of the model-class (12) rapidly increases as a function of n and m.

3 Numerical global optimization applied to ellipse packing problems

Considering even far less complicated object packing models than the model-class introduced here, one cannot expect to find general analytical solutions. Therefore we have been applying numerical global optimization to find high quality feasible numerical solutions to a range of challenging OPPs. Without going into details, we only refer here to some of our own related studies: consult e.g. Pintér [29], Stortelder et al. [48], Riskin et al. [46], Castillo and Sim [8], Pintér and Kampas [37, 38], Kampas and Pintér [23], Castillo et al. [7], Pintér and Kampas [39], Kampas et al. [24, 25], Pintér et al. [41]. Similarly to most of the works listed here, in the present study we utilize the Lipschitz Global Optimizer (LGO) solver system for global–local nonlinear optimization: here specifically, using its implementation linked to the computing system Mathematica [55], by Wolfram Research.

LGO (Pintér [34]) is aimed at finding the numerical global optimum of model instances from a very general class of global optimization problems. In order to use LGO within a theoretically rigorous framework, the key model assumptions are: bounded, non-empty feasible region; continuous or Lipschitz-continuous objective and constraint functions. These analytical conditions can be simply verified by inspection for model (12). LGO has been in use since the early 1990s, and it has been documented in detail elsewhere. In particular, Pintér [27] presents adaptive deterministic partition strategies and stochastic search methods, to solve global optimization problems under Lipschitz-continuity or mere continuity assumptions. The exhaustive search capability of these general algorithmic procedures guarantees their theoretical global convergence (correspondingly, in a deterministic sense or with probability 1).

The core solver system in LGO with implementations linked to various modeling platforms has been discussed e.g., by Pintér [27, 28, 30,31,32,33], and by Pintér et al. [42]. For more recent development work, benchmarking studies and real-world applications, consult e.g. Çaĝlayan and Pintér [6], Deschaine et al. [11], Pintér and Horváth [36], Pintér and Kampas [39], Pintér [35]. Current implementation details are described in the LGO manual [34], with reference to a broad range of further LGO applications. LGO integrates several derivative-free global and local optimization strategies, without requiring higher-order model function information. These strategies include a sampling procedure as a global pre-solver, a branch-and-bound global search method (BB), global adaptive random search (RS), multi-start based global random search (MS), and local search (LS). According to extensive numerical experience, in difficult GO models, MS with subsequent LS solver phases often finds the best numerical solution. For this reason, the recommended default LGO solver option is MS + LS: this has been utilized also in our present numerical study.

The implementation of LGO with a link to Mathematica—with the software product name MathOptimizer Professional (Pintér and Kampas [40])—has been extensively used in our benchmarking studies, and it has been used also here. MathOptimizer Professional users formulate their optimization model in Mathematica; this model is automatically translated into C or Fortran code; the converted model is solved by LGO; finally, the results are seamlessly returned to the calling Mathematica work document. The outlined structure supports the combination of Mathematica’s model development, visualization, and other capabilities with the robust performance and speed of the external LGO solver engine. LGO solver performance compares favorably not only to the related numerical optimization capabilities of Mathematica, but also to a broad range of other derivative-free nonlinear solvers. In support of the latter remark, consult e.g. the substantial benchmarking study of Rios and Sahinidis [45] in which, at the time of their study, a several years old LGO version has been one of the most efficient solvers. The current LGO release—as well as its MathOptimizer Professional implementation—supports the numerical solution of nonlinear optimization models with thousands of variables and general constraints. To illustrate this aspect, we present a substantial set of ellipse packing test results in the next section.

4 Illustrative results

Our numerical experiments were mostly performed on a PC running under Windows 7, with an Intel Core i5 processor running at 2.6 GHz, with 16 GBytes of RAM, using MathOptimizer Professional running in Mathematica (versions 10 and 11), and using the gcc compiler [53] to automatically generate the necessary model input files for LGO. While we cannot guarantee the theoretical optimality of the ellipse configurations found, our computational results lead to visibly high quality packings. Let us also point out that MathOptimizer Professional is used here with its default parameter settings, without any “tweaking.”

To our best knowledge, there are no previously studied model instances available for the ellipse packing problem-class considered in our present work. Thus we first proceed to dealing with the basic setting presented in Honvault [18] of packing three congruent ellipses in a square: n = 3, all ellipses sharing the same eccentricity, and m = 4. In order to reproduce the results presented in Honvault [18], we use the following input structure: a_i = 1, b_i = c for i = 1, …, 3, c = 0.01, 0.02, …, 1.00 is the eccentricity parameter of the ellipses. We note that Honvault [18] used a stochastic algorithm based on the so-called inflation formula presented in Honvault [17]. Figure 4 numerically captures the function between the packing fraction and the eccentricity input parameter c. In this set of examples, solving each problem took less than 2 s of CPU time. Honvault [18] has shown analytically that for congruent ellipses placed inside a square the function between the packing fraction and the eccentricity is continuous, reaching the maximal packing fraction at an eccentricity of 1/3, with optimum value of $\pi /4 \sim 0.7853981634$: this is comparable to the fraction 0.78089 obtained in our numerical results at c = 0.33, given our discretized eccentricity parameter structure. (We did not spend further effort on this rather simple illustrative example.)

Fig. 4

Packing fraction versus eccentricity c for n = 3 congruent ellipses

Evidently, a regular polygonal container approaches a circular container as the number of sides m increases. Following the same input structure, Fig. 4 captures the function between the packing fraction and the eccentricity for m = 40. In this case, the packing fraction reaches its approximate maximum of 0.86482 at eccentricity c = 0.58. For m = 40 solving each problem took less than 40 s.

Next, we consider packing ellipses into containers with a priori bounded size. The problem instances summarized in Table 1 are cited from Kallrath and Rebennack [22]. Table 2 includes computational results using the solver NMinimize, available in Mathematica and the solver BARON (Tawarmalani and Sahinidis [52]), available via the NEOS Server (https://neos-server.org/neos/). Specifically, for NMinimize we tested its Automatic, SimulatedAnnealing, and RandomSearch option settings. Among these, RandomSearch provided the most consistent results: hence, these results are reported in the table. Let us also note that BARON does not support trigonometric functions. In order to handle our model using BARON, we replaced function cosθ with the decision variable $\varPhi$, function sinθ with the decision variable $\varPsi$, and added the constraint $\varPhi^{2} + \varPsi^{2} = 1$ with the bounds $- 1 \le \varPhi ,\varPsi \le 1$. All model instances were solved for a square container (m = 4) with the same overall lower and upper bound values. Our optimization strategy consistently provided superior results, both in terms of higher quality packings found and (typically) much lower CPU times.

Table 1 Ellipse packing instances from Kallrath and Rebennack [22]

Table 2 Comparison of ellipse packing instances from Kallrath and Rebennack [22] with m = 4

Table 3 summarizes additional computational results, including those from Kallrath and Rebennack [22] and Stoyan et al. [49]: these works were aimed at packing ellipses in optimized rectangles. Since our model can be extended to consider general convex polygons, our results include optimized regular polygonal containers with m = 4 (square), general polygonal containers with m = 4 (rectangle), and regular polygonal containers with m = 8 (octagon). The configuration geometries, as mentioned, are rather different given the different optimized containers: however, we gain an overall impression regarding the packing densities that can be achieved for a range of model instances. In terms of the quality of the packings for a rectangular container, our modeling and optimization strategy often matches (within 0.1% accuracy) or improves the best results previously reported. It is interesting to note that for test cases TC5b and TC6, the packing fractions with a regular octagonal container (our results) approach the packing fractions obtained using a rectangular container.

Table 3 Additional computational results for different configuration geometries

Next, we proceed to packing ellipses of (in principle) arbitrary size and orientation. The ellipse packing problem instances summarized in Table 4 have been generated with the following input structure: $a_{i} = 1/\sqrt i$, $b_{i} = a_{i} /c$ for $i = 1, \ldots ,n$, where c again denotes the eccentricity of the ellipses. Note that with c = 1 this problem becomes a general circle packing problem for circles with radii $a_{i} = 1/\sqrt i$. This choice guarantees that for the total area $A\left( n \right)$ of the packed ellipses we have the relation $A\left( n \right) \to \infty$ as $n \to \infty$. In our opinion, this general property can make the corresponding packing model instances more difficult to handle, as opposed to packing objects into containers with a priori bounded size.

Table 4 Ellipse packing instances

Tables 5, 6, 7, 8, 9, 10 and 11 summarize the computational results, for a total of 210 ellipse packing problems solved. In these model instances, the number of ellipses n is chosen as 3, 4, 5, 6, 8, or 10; for each given n, the eccentricity parameter c is chosen as one of the values 1.00, 1.05, 1.15, 1.35, 1.50, 1.75, or 2.00; and for each fixed pair $\left( {n, c} \right)$ the number of regular polygon container sides m is chosen as one of 3, 4, 5, 6, or 8.

Table 5 Ellipse packing results for eccentricity c = 1.00

Table 6 Ellipse packing results for eccentricity c = 1.05

Table 7 Ellipse packing results for eccentricity c = 1.15

Table 8 Ellipse packing results for eccentricity c = 1.25

Table 9 Ellipse packing results for eccentricity c = 1.50

Table 10 Ellipse packing results for eccentricity c = 1.75

Table 11 Ellipse packing results for eccentricity c = 2.00

The CPU times are reasonable for the entire range of parameter choices, ranging from seconds to a few minutes. Note that these tables also include the packing fraction and the maximum constraint violation.

Two illustrative packing configurations are displayed by Figs. 5 and 6. The points shown on the ellipses (in light green color in the online version of this article) are the auxiliary points used for preventing ellipse overlap: note that for preventing the overlap of a pair of ellipses, there is a point on one of the two ellipses, not on both.

Fig. 5

Packing configurations found for n = 8, c = 1.25, and $m = 3, 4, 5, 6$

Fig. 6

Packing configurations found for n = 8, m = 8, for all c > 1.00

Figures 7, 8 and 9 capture the positive correlation between the packing fraction and the different input parameters: number of ellipses, eccentricity, and number of container sides. Multiple linear regression analysis indicates that the regression function for the packing fraction can be estimated as $0.5443 + 0.0068 \cdot n + 0.0893 \cdot c + 0.0104 \cdot m$, with p-values (i.e., observed significance levels, cf. Black et al. [5]) below 0.0001 for all input parameters. This finding indicates that we have very strong statistical evidence suggesting that the regression coefficients are different from zero. Figure 10 illustrates the quality of the regression equation by depicting actual versus predicted packing fractions.

Fig. 7

Packing fraction versus number of ellipses n (diamonds represent the problem instances)

Fig. 8

Packing fraction versus eccentricity c (diamonds represent the problem instances)

Fig. 9

Packing fraction versus number of container sides m (diamonds represent the problem instances)

Fig. 10

Actual (computed) versus predicted packing fractions

To conclude the discussion of numerical results, let us point out that—based on our current model formulation and the experiments conducted—it is apparent that our default global optimization strategy could become prohibitively expensive for arbitrarily increasing m and n. Therefore, also based on related earlier research experience, we believe that large-scale problem instances will benefit from exploiting suitable, problem-dependent heuristic approaches. As a proof-of-concept, in Table 12 we present illustrative results using the input structure $a_{i} = 1/\sqrt i$, $b_{i} = a_{i} /c$, based on a random starting solution used by a single call to the local nonlinear optimization solver Ipopt. Ipopt is developed and maintained as part of the COIN-OR Initiative; consult http://www.coin-or.org. Our admittedly very simple heuristic strategy already gives promising results which certainly could be improved by using more sophisticated solution strategies. Figure 11 shows some of the packing configurations found for n = 20 and m = 40, using various eccentricity parameters.

Table 12 Ellipse packing results obtained using a heuristic approach for m = 40

Fig. 11

Packing configurations for n = 20 and m = 40, for all c > 1.00

5 Summary and conclusions

In this work, we introduce the problem-class of packing, without overlap, n general ellipses into an optimized regular m-polygon. The packed ellipses can have arbitrary size, shape, and orientation. These packing problems lead to hard global optimization challenges: the number of model variables and general constraints are both rapidly increasing functions of m and n. The model formulation based on regular polygons also supports the approximation of different container shapes. Our model development approach can be directly extended to consider also general convex, but not necessarily regular, polygons.

The optimization strategy presented requires the determination of the maximal distance from the center of the polygon faces to each ellipse, in order to determine the size of the polygon’s apothem, which is then minimized. To meet this requirement, we present explicit analytical formulas. Our strategy also requires the finding of the minimal distance between all pairs of the ellipses, in order to prevent the ellipses from overlapping. To satisfy the latter requirement, we develop embedded optimization calculations using Lagrange multipliers. In this framework, the optimization strategy proceeds simultaneously to find the optimized area of the regular polygon and to prevent ellipse overlaps. The use of embedded Lagrange multipliers allows us to determine quantities that cannot be found by explicitly formulated relations. To illustrate this point, see Figs. 12 and 13 below with further object packing examples that are part of our closely related studies. These examples demonstrate the packing of circles, ellipses, and hyper-ellipses simultaneously into a regular polygon (Fig. 12), and packing ellipses into a non-regular, elongated container polygon (Fig. 13).

Fig. 12

Packing example with circles, ellipses, and hyper-ellipses

Fig. 13

Packing example with ellipses in a non-regular container polygon

To solve the resulting highly non-convex optimization problems, we use the LGO solver system in its implementation linked to Mathematica. Our numerical results—including both global optimization and a simple random start + local search based “naïve” approach—successfully reproduce or surpass all previously published analytical results, in all examples considered here. Compared to several other optimization approaches, our optimization strategy consistently provides high quality packings, typically at a fraction of the computational time required by all other software used in our tests. These facts demonstrate the viability and efficiency of our modeling and optimization approach, for a wide range of parameter choices.

As a closing remark, we conjecture that regression analysis based on the results obtained supports the determination of statistically established estimates of the packing fraction in new model-instances from given model-classes. This observation is also consistently supported by our results across all model-classes considered here.