Quasi-phi-functions and optimal packing of ellipses

Abstract

We further develop our phi-function technique for solving Cutting and Packing problems. Here we introduce quasi-phi-functions for an analytical description of non-overlapping and containment constraints for 2D- and 3D-objects which can be continuously rotated and translated. These new functions can work well for various types of objects, such as ellipses, for which ordinary phi-functions are too complicated or have not been constructed yet. We also define normalized quasi-phi-functions and pseudonormalized quasi-phi-functions for modeling distance constraints. To show the advantages of our new quasi-phi-functions we apply them to the problem of placing a given collection of ellipses into a rectangular container of minimal area. We use radical free quasi-phi-functions to reduce it to a nonlinear programming problem and develop an efficient solution algorithm. We present computational results that compare favourably with those published elsewhere recently.

1 Introduction

Optimal placement problem is a part of operational research and computational geometry. It is also known as Packing and Cutting problem [1–6]. It has multiple applications in modern biology, mineralogy, medicine, materials science, nanotechnology, robotics, coding, pattern recognition systems, control systems, space apparatus control systems, as well as in the chemical industry, power engineering, mechanical engineering, shipbuilding, aircraft construction, civil engineering, etc. At present, the interest in finding effective solutions for placement problems is growing rapidly. This is due to a large and growing number of applications (e.g. see http://smartimtech.com) and an extreme complexity of methods used to handle many of them.

Our approach is based on mathematical modeling of relations between geometric objects and thus reducing the Packing and Cutting problem to a nonlinear programming problem. To this end we have introduced phi-functions (see e.g. [7, 8]) that for the past 2–3 decades have been our working tool: we used them for analytic description of objects placed in a container taking into account their continuous rotations and translations. At present, a complete class of ready-to-use basic phi-functions is derived in [9], which allows us to construct radical free phi-functions for arbitrary shaped 2D-objects, bounded by circular arcs and line segments [8, 10]. Phi-functions for the simplest 3D-objects, such as parallelepipeds, convex polytopes and spheres are considered in [11, 12]. But our attempts to construct phi-functions for more general types of continuously rotated objects, such as ellipses, cylinders, cones have been futile. In addition some of phi-functions (especially for 3D-objects) happen to be rather complicated, analytically (involve a lot of radicals, operations of maximum), and difficult in practical use (to apply NLP-solvers, e.g. IPOPT). It seems that further progress requires conceptually new approaches.

In this paper we further develop the concept of phi-functions, extending their domains by including auxiliary variables. The new functions, called quasi-phi-functions, can be described by analytical formulas that are substantially simpler than those used for phi-functions, for some types of objects. They also are simple enough for some types of objects for which phi-functions could not be constructed. In particular, we find convenient quasi-phi-functions for ellipses and for certain 3D-objects. The use of quasi-phi-functions, instead of phi-functions, thus allows us to handle new types of objects, but there is a price to pay: now the optimization has to be performed over a larger set of parameters, including the extra variables used by our new functions, but this is a small price.

To demonstrate high efficiency of our quasi-phi-functions we consider a practical problem of placing a set of given non-identical ellipses into a rectangular container of minimal area. We construct quasi-phi-functions for ellipses and develop an efficient optimization algorithm that finds a nearly optimal solution.

We came to realize that the brilliant concept used for packing circles and convex polygons by Kallrath in [13], as well as its extension to ellipses by Kallrath and Rebennack [14], is the most powerful approach to the problems within the field of Packing and Cutting.

We applied our algorithm to several test cases studied in [14], and in each case it found a better solution than those published elsewhere.

The paper is organized as follows: Sect. 2 provides definitions of phi-functions, normalized and pseudonormalized phi-functions; in Sect. 3 we define our quasi-phi-functions for an analytical description of non-overlapping and containment constraints and discuss their general properties; we also introduce normalized and pseudonormalized quasi-phi-functions to describe the given minimal allowable distances between geometric objects. In Sect. 4 we construct quasi-phi-functions for certain types of 2D- and 3D-objects needed in applications. In Sect. 5 we formulate the ellipse packing problem taking into account distance constraints, propose a mathematical model as a nonlinear programming problem by means of quasi-phi-functions, and develop a new solution algorithm, which involves a fast starting point and efficient local optimization procedures. In Sect. 6 we present our computational results for some new instances and several instances studied in [14]. In Sect. 7 we give some conclusions.

2 The concept of phi-functions

Let $A\subset R^{d}$ and $B\subset R^{d}$ be closed phi-objects, $d=2,3$; see a precise definition of phi-objects in e.g. [7, 8]. We assume that at least one of these objects is bounded. Sizes of objects may change according to homothetic coefficients ${\uplambda }_A ,{\uplambda }_B >0$. Position of the object A is defined by vector of placement parameters $(v_A ,{\uptheta } _A )$, where: $v_A =(x_A ,y_A )$ is a translation vector and ${\uptheta } _A$ is a rotation angle for $d=2, v_A =(x_A ,y_A ,z_A )$ is a translation vector and ${\uptheta }_A =({\uptheta } _z ,{\uptheta } _x ,{\uptheta } _y)$ are rotation angles (from axis OX to OY, from axis OY to OZ and from axis OX to OZ) for $d=3$. We denote the vector of variables for the object A by $u_A =(v_A ,{\uptheta } _A ,{\uplambda }_A )$ and the vector of variables for the object B by $u_B =(v_B ,{\uptheta } _B ,{\uplambda }_B )$. The object A, rotated by angle ${\uptheta } _A$ (or angles ${\uptheta } _z ,{\uptheta } _x ,{\uptheta } _y$, in this order), translated by vector $v_A$, and rescaled by homothetic coefficient ${\uplambda }_A$, will be denoted by $A(u_A )$.

In order to describe non-overlapping and containment constraints in cutting and packing problems analytically we apply the concept of phi-functions [7, 8].

Definition 1

A continuous and everywhere defined function ${\Phi }^{AB}(u_A ,u_B )$ is called a phi-function for objects $A(u_A )$ and $B(u_B )$ if

$$\begin{aligned} \begin{array}{c} {\Phi }^{AB}<0,\quad \hbox {if int}\,A(u_A )\cap \hbox {int}\,B(u_B )\ne \varnothing ;\\ {\Phi }^{AB}=0,\quad \hbox {if int}\,A(u_A )\cap \hbox {int}\,B(u_B )=\varnothing \, \hbox {and} \,frA(u_A )\cap frB(u_B )\ne \varnothing ;\\ {\Phi }^{AB}>0,\quad \hbox {if}\,A(u_A )\cap B(u_B )=\varnothing , \end{array} \end{aligned}$$

provided that we fix the homothetic multipliers ${\uplambda }_A ={\uplambda }_A^0$ and ${\uplambda }_B ={\uplambda }_B^0$.

Here $fr(\cdot )$ means the boundary (frontier) and $\hbox {int}(\cdot )$ means the interior of object $(\cdot )$.

A phi-function ${\Phi }^{AB}$ must be defined for all position vectors and all rotation angles. The phi-function ${\Phi }^{AB}$ describes analytically the relation between the objects A and B in such a way that ${\Phi }^{AB}>0$ if the objects do not have common points; ${\Phi }^{AB}=0$ if the objects just touch each other, and ${\Phi }^{AB}<0$ if the objects have common interior points. Thus, ${\Phi }^{AB}\ge 0\Leftrightarrow \hbox {int}\,A(u_A )\cap \hbox {int}\,B(u_B )=\varnothing .$ We employ phi-functions for the description of the contaiment relation $A\subseteq B$ as follows: ${\Phi }_{AB^{*}} \ge 0$, where $B^{*}=R^{d}\backslash \hbox {int}\,B$, $d=2,3$. We emphasize that according to the definition 1, the phi-function ${\Phi }^{AB}$ for a pair of objects A and B can be constructed by many different formulas, and we can choose the most convenient ones for our optimization algorithms.

The concept of phi-functions is used for the purpose of modeling distance constraints. To this end we define normalized and pseudonormalized (adjusted) phi-functions (see e.g., [8]).

Let $\hbox {dist}(A,B)=\mathop {\min }\nolimits _{a\in A,b\in B} \hbox {dist}(a,b)$, where $\hbox {dist}(a,b)$ stands for the Euclidean distance between points $a,b\in R^{d}$, $d=2,3$, and let $\uprho ^{-}>0$ denote minimal allowable distances between objects $A(u_A )$ and $B(u_B )$.

Definition 2

A phi-function $\tilde{\Phi }^{AB}(u_A ,u_B )$ for objects $A(u_A )$ and $B(u_B )$ is said to be a normalized phi-function if

$$\begin{aligned}&\tilde{\Phi }^{AB}(u_A ,u_B )= \hbox {dist}(A,B)\quad \hbox {whenever int}\,A(u_A )\cap \hbox {int}\,B(u_B )=\varnothing .\\&\hbox {Thus},\, \tilde{\Phi }^{AB}\ge {\uprho }^{-}\Leftrightarrow \hbox {dist}(A,B)\ge {\uprho }^{-}. \end{aligned}$$

Definition 3

A continuous and everywhere defined function is called a pseudonormalized (adjusted) phi-function for objects $A(u_A )$ and $B(u_B )$, if

Thus, . The function may be derived as an ordinary phi-function for the equidistant object and the object B (or the object A and the equidistant object . Here $\oplus$ is a symbol of the Minkowski sum, $C({\rho } ^{-})$ is a circle of the radius ${\rho } ^{-}$ and the center point located at the origin of the local coordinate system of the object A (or the object B). “Appendix 1” provides the simplest examples of phi-functions.

3 Quasi-phi-functions and their properties

Now we extend domains of phi-functions by including auxiliary variables $u'$, which take values in some domain $U\subset R^{n}$ (it depends on the shapes of objects A and B), and introduce a function ${{\Phi }^{'}}^{AB} (u_A ,u_B ,u^{\prime })$. The function must be defined for all values of $u_{A }$ and $u_{B}$. It must be continuous in all its variables.

Definition 4

A function ${{\Phi }^{'}}^{AB} (u_A ,u_B ,u^{\prime })$ is called a quasi-phi-function for two phi-objects $A(u_A )$ and $B(u_B )$ if $\mathop {\max }\nolimits _{u^{\prime }\in U} {{\Phi }^{'}}^{AB} (u_A ,u_B ,u^{\prime })$ is a phi-function for the objects, provided that we fix the homothetic multipliers ${\uplambda }_A ={\uplambda }_A^0$ and ${\uplambda }_B ={\uplambda }_B^0$.

Our definition of quasi-phi-functions gives us additional “degrees of freedom”, as we can choose the auxiliary variables $u'$ as we please.

Next we discuss general properties of quasi-phi-functions. Let ${{\Phi }^{'}}^{AB} (u_A ,u_B ,u^{\prime })$ be a quasi-phi-function for two phi-objects $A(u_A )$ and $B(u_B )$.

Theorem 1

If ${{\Phi }^{'}}^{AB} (u_A ,u_B ,u^{\prime })\ge 0$ for some $u'$, then $\hbox {int}\,A(u_A )\cap \hbox {int}\,B(u_B )=\varnothing$.

Proof

Let us introduce two subsets $M_1 =\{(u_A ,u_B ,u^{\prime })\in R^{m}{:}\hbox {int}\,A(u_A )\cap \hbox {int}\,B(u_B )\ne \varnothing \}, M_2 =\{(u_A ,u_B ,u^{\prime })\in R^{m}{:}\hbox { int}\,A(u_A )\cap \hbox {int}\,B(u_B )=\varnothing \}$. It is clear that $M_1 \cup M_2 =R^{m}$, since ${{\Phi }^{'}}^{AB} (u_A ,u_B ,u^{\prime })$ is defined for all values of its variables. From definition 4 it follows that $\mathop {\max }\nolimits _{u^{\prime }\in U} {{\Phi }^{'}}^{AB} (u_A ,u_B ,u^{\prime })<0$ if $\hbox {int}\,A(u_A )\cap \hbox {int}\,B(u_B )\ne \varnothing$. It should be noted that a quasi-phi-function ${{\Phi }^{'}}^{AB} (u_A ,u_B ,u^{\prime })$ may take negative values not only on the subset $M_1$ but also at some points of the subset $M_2$. However, if $p^{0}=(u_A^0 ,u_B^0 ,{{u'}{}^0})\in M_1$ then ${{\Phi }^{'}}^{AB} (p^{0})<0$. Therefore, if ${{\Phi }^{'}}^{AB} (p^{0})\ge 0$ then $p^{0}\in M_2$. $\square$

Next, assume, that A and B are convex objects. In addition, we assume that ${\uplambda }_A$ and ${\uplambda }_B$ take values in $(0,+\infty )$.

Let $P(u_P )=\{(x,y,z){:}{\uppsi }_P ={\upalpha } \cdot x+{\upbeta } \cdot y+{\upgamma } \cdot z+{\upmu }_P \le 0\}$ be a half-space (for $t=2$ it will be a half-plane; see below); here $u_P =({\uptheta }_{xP} ,{\uptheta }_{yP} ,{\upmu }_P ), {\upalpha } =\sin {\uptheta } _{yP} , {\upbeta } =-\sin {\uptheta } _{xP} \cdot \cos {\uptheta } _{yP} , {\upgamma } =\cos {\uptheta } _{xP} \cdot \cos {\uptheta } _{yP}$ (note that ${\upalpha } ^{2}+{\upbeta } ^{2}+{\upgamma } ^{2}=1)$. If $A,B\subset R^{2}$, then $P(u_P )=\{(x,y){:}\,{\uppsi } _P ={\upalpha } \cdot x\, +\, {\upbeta } \cdot y\, +\, {\upmu }_P \le 0\}$, where $u_P =({\uptheta } _P ,{\upmu }_P ) {\upalpha } =\cos {\uptheta } _P , {\upbeta } =\sin {\uptheta } _P$. Suppose $\Phi ^{AP} (u_A ,u_P )$ is a phi-function for $A(u_A )$ and $P(u_P )$ and $\Phi ^{BP^{{*}}} (u_B ,u_P )$ is a phi-function for $B(u_B )$ and $P^{*}(u_P )=R^{d}\backslash \hbox {int}\,P(u_P ), d=2,3$.

Theorem 2

A function defined by

$$\begin{aligned} {{\Phi }^{'}}^{AB}(u_A ,u_B ,u_P )=\min \{\Phi ^{AP} (u_A ,u_P ),{\Phi }^{BP^{{*}}} (u_B ,u_P )\}, \end{aligned}$$

(1)

is a quasi-phi-function for the pair of bounded objects $A(u_A )$ and $B(u_B )$. Here $u^{\prime }=u_P$.

Proof

We need to show that the function (1) meets all the requirements of definition 4. First, the function ${{\Phi }^{'}}^{AB}$ is defined everywhere and is continuous in all its variables, since the phi-functions $\Phi ^{AP}$ and $\Phi ^{BP^{{*}}}$enjoy the same properties. Next we need to verify the following:

• (1) $\mathop {\max }\nolimits _{u^{\prime }\in U} {{\Phi }^{'}}^{AB} <0$,   if $\hbox {int}\,A(u_A )\cap \hbox {int}\,B(u_B )\ne \varnothing$;

• (2) $\mathop {\max }\nolimits _{u{\prime }\in U} {{\Phi }^{'}}^{AB} =0,$   if $\hbox {int}\,A(u_A )\cap \hbox {int}\,B(u_B )=\varnothing$ and $frA(u_A )\cap frB(u_B )\ne \varnothing$;

• (3) $\mathop {\max }\nolimits _{u^{\prime }\in U} {{\Phi }^{'}}^{AB} >0,$   if $A(u_A )\cap B(u_B )=\varnothing$.

Indeed, if $\hbox {int}\,A(u_A )\cap \hbox {int}\,B(u_B )\ne \varnothing$, then for each $u_P$ we have ${{\Phi }^{'}}^{AB} <0$, and therefore $\mathop {\max }\nolimits _{u_P \in U} {{\Phi }^{'}}^{AB} <0$. Now if $A(u_A )\cap B(u_B )=\varnothing$, then due to the convexity of our objects A and B there exists a separating hyperplane with parameters $u_P \in R^{2}$ or $u_P \in R^{3}$ (depending on whether our objects are in 2D or 3D); then we have $\Phi ^{AP} (u_A ,u_P )>0$ and $\Phi ^{BP^{{*}}} (u_B ,u_P )>0$, and therefore $\mathop {\max }\nolimits _{u_P \in U} {{\Phi }^{'}}^{AB} >0$. Lastly, if $\hbox {int}\,A(u_A )\cap \hbox {int}\,B(u_B )=\varnothing$ but $frA(u_A )\cap frB(u_B )\ne \varnothing$, then ${{\Phi }^{'}}^{AB} =0$, since $\Phi ^{AP} (u_A ,u_P )=0$ and $\Phi ^{BP^{{*}}} (u_B ,u_P )=0$. $\square$

Corollary 1

If ${{\Phi }^{'}}^{AP} (u_A ,u_P ,u_1^{\prime } )$ is a quasi-phi-function for $A(u_A )$ and $P(u_P ), {{\Phi }^{'}}^{BP^{{*}}} (u_B ,u_P ,u_2^{\prime } )$ is a quasi-phi-function for $B(u_B )$ and $P^{*}(u_P )$, then function

$$\begin{aligned} {{\Phi }^{'}}^{AB}(u_A ,u_B ,u^{\prime })=\min \left\{ {{\Phi }^{'}}^{AP} (u_A ,u_P ,u_1^{\prime } ),{{\Phi }^{'}}^{BP^{{*}}} (u_B ,u_P ,u_2^{\prime } )\right\} , \end{aligned}$$

(2)

is a quasi-phi-function for the pair of bounded objects $A(u_A )$ and $B(u_B )$. Here $u{\prime }=(u_P ,u_1^{\prime } ,u_2^{\prime } )$.

The concept of quasi-phi-functions may be adapted for the purpose of modeling distance constraints. To this end we define normalized and pseudonormalized quasi-phi-functions, based on similar terms for phi-functions.

Definition 5

A quasi-phi-function $\tilde{\Phi }^{{\prime }AB}(u_A ,u_B ,u^{\prime })$ is called a normalized quasi-phi-function for objects $A(u_A )$ and $B(u_B )$, if a function $\mathop {\max }\nolimits _{u^{\prime }\in U} \tilde{\Phi }^{{\prime }AB} (u_A ,u_B ,u^{\prime })$ is a normalized phi-function for the objects.

Thus, $\mathop {\max }\nolimits _{u^{\prime }\in U} \tilde{\Phi }^{{\prime }AB} \ge {\uprho } ^{-}\Leftrightarrow \hbox {dist}(A,B)\ge {\uprho } ^{-}$.

Definition 6

Function is called a pseudonormalized quasi-phi-function for objects $A(u_A )$ and $B(u_B )$, if function is a pseudonormalized (adjusted) phi-function for the objects.

Thus, .

Let a quasi-phi-function have a form

$$\begin{aligned} {{\Phi }^{'}}^{AB}(u_A ,u_B ,u_P )=\min \left\{ \tilde{\Phi }^{AP} (u_A ,u_P ),\tilde{\Phi }^{BP^{{*}}} (u_B ,u_P )\right\} , \end{aligned}$$

(3)

where $\tilde{\Phi }^{AB}(u_A ,u_P ), \tilde{\Phi }^{BP^{{*}}}(u_B ,u_P )$ are normalized phi-functions.

Then a quasi-phi-function

$$\begin{aligned} \tilde{\Phi }^{{\prime }AB}(u_A ,u_B ,u_P )=2{\Phi }'^{AB}(u_A ,u_B ,u_P ), \end{aligned}$$

is a normalized quasi-phi-function, and a quasi-phi-function

is a pseudonormalized quasi-phi-function.

Let $A(u_A )=\mathop {\bigcup }\nolimits _{i=1}^{n_A } {A_i (u_A )}$ and $B(u_B )=\mathop {\bigcup }\nolimits _{j=1}^{n_B } {B_j (u_B )}$ be non-convex phi-objects, and ${\Phi }'^{A_i B_j }(u_A ,u_B ,u_{ij}^{\prime } )$ be a quasi-phi-function for convex objects A$_{i}$(u$_{A})$ and $B_j (u_B )$, $i=1,2,\ldots ,n_A , \,j=1,2,\ldots ,n_B$.

Theorem 3

A function defined by

$$\begin{aligned} {\Phi }'^{AB}(u_A ,u_B ,u_P )\!=\!\min \left\{ {\Phi }'^{A_i B_j }(u_A ,u_B ,u_{ij}^{\prime } ),\quad i\!=\!1,2,\ldots ,n_A ,j\!=\!1,2,\ldots ,n_B \right\} ,\quad \end{aligned}$$

(4)

is a quasi-phi-function for $\hbox {A}(\hbox {u}_{A})$ and $B(u_B ), u_P =(u_{ij}^{\prime } ,\quad i=1,2,\ldots ,n_A ,j=1,2,\ldots ,n_B )$.

Proof

To justify our formula (4) we note that the auxiliary variables $u_{ij}^{\prime }$ for each pair of objects $A_i (u_A )$ and $B_j (u_B )$ are defined independently from other pairs of objects; therefore the domain of the whole auxiliary vector $u_P =(u_{ij}^{\prime } ,\quad i=1,2,\ldots ,n_A ,j=1,2,\ldots ,n_B )$ is a direct product of the domains of $u_{ij}^{\prime }$’s. This implies

$$\begin{aligned}&\mathop {\max }\limits _{u_P\in U} {\Phi }'^{AB}(u_A ,u_B ,u_P )\\&\quad =\mathop {\max }\limits _{u_P\in U} \left( \min \left\{ {\Phi }'^{A_i B_j }(u_A ,u_B ,u_{ij}^{\prime } ),\quad i=1,2,\ldots ,n_A ,j=1,2,\ldots ,n_B \right\} \right) \\&\quad = \min \left\{ \mathop {\max }\limits _{u_{ij}^{\prime } \in U} {\Phi }'^{A_i B_j }(u_A ,u_B ,u_{ij}^{\prime } ),\quad i=1,2,\ldots ,n_A ,\quad j=1,2,\ldots ,n_B \right\} . \end{aligned}$$

$\square$

Replacing quasi-phi-functions ${\Phi ^{'}}^{A_i B_j }$ in (4) by normalized $\tilde{\Phi }^{{\prime }A_i B_j }$ (or pseudonormalized quasi-phi-functions for $i=1,2,\ldots ,n_A ,j=1,2,\ldots ,n_B$, we get a normalized (resp., a pseudonormalized) quasi-phi-function for objects $A(u_{A})$ and $B(u_B )$.

4 Construction of quasi-phi-functions

Here we construct quasi-phi-functions for certain 2D- and 3D-objects, based on our general formulas (1)–(3).

A quasi-phi-function for convex polytopes. Let $K_1 (u_1 )$ and $K_2 (u_2 )$ be convex polytopes, given by their vertices ${\uplambda }_1 p_i^1 \,, i=1,\ldots .,m_1$, and ${\uplambda }_2 p_j^2 , \,j=1,\ldots ,m_2$, respectively. Then ${\Phi }^{K_1 P}(u_1 ,u_P )=\mathop {\min }\nolimits _{1\le i\le m_1 } {\uppsi } _P ({\uplambda }_1 p_i^1 )$ and $\Phi ^{K_2 P^{*}}(u_2 ,u_P )=\mathop {\min }\limits _{1\le j\le m_2 } (-{\uppsi } _P ({\uplambda }_2 p_j^2 ))$ are phi-functions for $K_1$ and $P(K_2$ and $P^{*})$, respectively.

Now the function

$$\begin{aligned} {\Phi }'^{K_1 K_2 }(u_1 ,u_2 ,u_P )=\min \left\{ \Phi ^{K_1 P} (u_1 ,u_P ),\Phi ^{K_2 P^{{*}}} (u_2 ,u_P )\right\} , \end{aligned}$$

(5)

is a quasi-phi-function for $K_1 (u_1 )$ and $K_2 (u_2 )$.

Note that the function $2{\Phi }'^{K_1 K_2 }(u_1 ,u_2 ,u_P )$ is a normalized quasi-phi-function.

A pseudonormalized quasi-phi-function for convex polytopes $K_1 (u_1 )$ and $K_2 (u_2 )$ is defined by

(6)

A quasi-phi-function for a convex polytope $K(u_1)$ and a sphere $C(u_2 )$. Let $K(u_1 )$ be a convex polytope given by its vertices ${\uplambda }_1 p_i ,i=1,\ldots .,m$. Let $p_C$ and ${\uplambda }_2 r_C$ be the center and radius of a sphere $C(u_2 )$. Then $\Phi ^{KP}(u_1 ,u_P )=\mathop {\min }\nolimits _{1\le i\le m} {\uppsi } _P ({\uplambda }_1 p_i )$ and ${\Phi }^{CP^{*}}(u_2 ,u_P )=-{\uppsi } _P (p_C )-{\uplambda }_2 r_C$ are phi-functions.

Now a quasi-phi-function for $\hbox {K}(\hbox {u}_{1})$ and $C(u_2 )$ may be defined in the form

$$\begin{aligned} {\Phi }'^{CK}(u_1 ,u_2 ,u_P )=\min \{\Phi ^{KP} (u_1 ,u_P ),\Phi ^{CP^{{*}}} (u_2 ,u_P )\}. \end{aligned}$$

(7)

It should be noted that the function $2{\Phi }'^{CK}(u_1 ,u_2 ,u_P)$ is a normalized quasi-phi-function.

Remark

Quasi-phi-functions defined by (5)–(7) can be easily adapted to convex polygons and circles.

A quasi-phi-function for circular segments $D_1 (u_1 )$ and $D_2 (u_2 )$. Let $D_1 (u_1 )=T_1 (u_1 )\cap C_1 (u_1 )$, $D_2 (u_2 )=T_2 (u_2 )\cap C_2 (u_2 )$ be two circular segments, where $T_1 (u_1 )$ ($T_2 (u_2 ))$ denotes a triangle given by its vertices ${\uplambda }_1 p_i^1 ({\uplambda }_2 p_i^2 )$, $i=1,2,3$, (we note that two sides of T have to be tangents to C and one side is a horde of C) and $p_C^1 =(x_1 ,y_1 )$ ($p_C^2 =(x_2 ,y_2 ))$ and ${\uplambda }_1 r_C^1$ (${\uplambda }_2 r_C^2 )$ denote the center and radius of $C_1 (u_1 )$ (resp., $C_2 (u_2 ))$.

Then, following (1), a quasi-phi-function for $D_1 (u_1 )$ and $D_2 (u_2 )$ may be defined by

$$\begin{aligned} {\Phi ^{'}}^{D_1 D_2 }(u_1 ,u_2 ,u_P )=\min \left\{ \Phi ^{D_1 P} (u_1 ,u_P ),\Phi ^{D_2 P^{{*}}} (u_2 ,u_P )\right\} , \end{aligned}$$

(8)

where ${\Phi }^{D_1 P}(u_1 ,u_P )=\max \{{\Phi }^{T_1 P},{\Phi }^{C_1 P}\},{\Phi }^{D_2 P^{*}}(u_2 ,u_P )=\max \{{\Phi }^{T_2 P^{*}},{\Phi }^{C_{2} P^{*}}\}$, are phi-functions, and ${\Phi }^{T_1 P}(u_1 ,u_P )=\mathop {\min }\nolimits _{i=1,2,3} {\uppsi } _P ({\uplambda }_1 p_i^1 ), \,{\Phi }^{C_1 P}(u_1 ,u_P )={\uppsi } _P (p_C^1 )-{\uplambda }_1 r_C^1 , {\Phi }^{C_{2}P^{*}}(u_2 ,u_P )=-{\uppsi } _P (p_C^2 )-{\uplambda }_2 r_C^2 ,{\Phi }^{T_2 P^{*}}(u_2 ,u_P )=\mathop {\min }\nolimits _{i=1,2,3} (-{\uppsi } _P ({\uplambda }_2 p_i^2 ))$.

We can also define a quasi-phi-function for $D_{1}(u_{1})$ and $D_2 (u_2 )$ using formula (2):

$$\begin{aligned} {\Phi ^{'}}^{D_1 D_2}(u_1 ,u_2 ,u{\prime })=\min \left\{ {\Phi ^{'}}^{D_1 P} (u_1 ,u_P ,u_1^{\prime } ),{\Phi ^{'}}^{D_2 P^{{*}}} (u_2 ,u_P ,u_2^{\prime } )\right\} , \end{aligned}$$

where $u{\prime }=(u_P ,u_1^{\prime } ,u_2^{\prime } ), u_1^{\prime } \in [0,1]\subset R^{1}, u_2^{\prime } \in [0,1]\subset R^{1}$.

To this end, first, we construct quasi-phi-functions ${\Phi ^{'}}^{D_1 P}(u_1 ,u_P ,u_1^{\prime } )$ and ${\Phi ^{'}}^{D_2 P^{*}}(u_2 ,u_P ,u_2^{\prime } )$. Let ${\Phi }^{C_1 P}(u_1 ,u_P )$ be a phi-function for $C_1 (u_1 )$ and $P(u_p )$. We introduce function

$$\begin{aligned}&{\Phi ^{'}}^{D_1 P}(u_1 ,u_P ,u_1^{\prime } )=\min \left\{ {\uppsi } _P ({\uplambda }_1 p_1^1 ),{\uppsi } _P ({\uplambda }_1 p_2^1 ),{\upchi }_1 (u_1 ,u_P ,u_1^{\prime } )\right\} ,\\&{\upchi } _1 (u_1 ,u_P ,u_1^{\prime } )= {\uppsi } _P ({\uplambda }_1 p_3^1 ) -u_1^{\prime } {\uppsi } _P ({\uplambda }_1 p_3^1 )+ u_1^{\prime } {\Phi }^{C_1 P}(u_1 ,u_P ), \end{aligned}$$

where $u_1^{\prime } \in [0,1]\subset R^{1}, {\uplambda }_1 p_i^1 , \,i=1,2$, are the endpoints of the chord of $D_1 (u_1 )$.

By analogy we have

$$\begin{aligned}&{\Phi ^{'}}^{D_2 P^{*}}(u_2 ,u_P ,u_2^{\prime } )=\min \left\{ -{\uppsi } _P ({\uplambda }_2 p_1^2 ),-{\uppsi } _P ({\uplambda }_2 p_2^2 ),{\upchi } _2 (u_2 ,u_P ,u_2^{\prime } )\right\} ,\\&{\upchi } _2 (u_2 ,u_P ,u_2^{\prime } )= -{\uppsi } _P ({\uplambda }_2 p_3^2 ) -u_2^{\prime } (-{\uppsi } _P ({\uplambda }_2 p_3^2 ))+ u_2^{\prime } {\Phi }^{C_2 P^{*}}(u_2 ,u_P ), \end{aligned}$$

where $u_2^{\prime } \in [0,1]\subset R^{1}$, ${\uplambda }_2 p_i^2 , \,i=1,2$, are the endpoints of the chord of $D_2 (u_2 )$.

Remark

The quasi-phi-function defined by (8) may be adapted to a pair of spherical segments defined as intersections of right circular $T_1 (u_1 )$ and $T_2 (u_2 )$ with solid spheres (3D balls) $C_1 (u_1 )$ and $C_2 (u_2 )$, respectively cones. (We note that a spherical segment D can be bisected into two equal halves by a plane $P_{z}$ passing through the center of the sphere; that plane would intersect D in a circular segment $D_{z}$, which itself is the intersection of a circle $C_z$ and a triangle $T_z$ lying in the plane $P_{z}$; now two sides of the triangle $T_z$ have to be tangent to the circle $C_z$ and the third side has to be a chord of $C_z$.) In that case we can use ${\Phi }^{T_1 P} ({\Phi }^{T_2 P^{*}})$, which is a phi-function for a right circular cone and a half space.

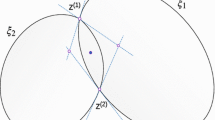
A quasi-phi-function for ellipses. Let $E_1 (u_1 )$ and $E_2 (u_2 )$ be two ellipses with semi-axes ${\uplambda }_i a_i$ and ${\uplambda }_i b_i , a_i >b_i \,i=1,2$.

Then, a quasi-phi-function for $E_1 (u_1 )$ and $E_2 (u_2 )$ may be defined as follows

$$\begin{aligned} {\Phi }'^{E_1 E_2 }(u_1 ,u_2 ,u^{\prime })=\min \left\{ {\upchi } ({\uptheta } _1 ,{\uptheta } _2 ,u^{\prime }),{\upchi } ^{+}(u_1 ,u_2 ,u^{\prime }),{\upchi } ^{-}(u_1 ,u_2 ,u^{\prime })\right\} , \end{aligned}$$

(9)

where ${\uptheta } _1$ and ${\uptheta } _2$ are rotation angles and $u^{{\prime }}=(t_1 ,t_2 )$ is a vector of auxiliary parameters, $0\le t_i \le 2{\uppi }$, $i=1,2$; functions ${\upchi } ,{\upchi } ^{+},{\upchi } ^{-}$ are defined below.

The parameter $t_i$ specifies a point on ellipse $E_i$. In the canonical coordinate system attached to ellipse $E_i$ that point is $(x_i^t ,y_i^t )=({\uplambda }_i a_i \cos t_i ,{\uplambda }_i b_i \sin t_i )$, and after rotation and translation its coordinates are $(x_i^{\prime } ,y_i^{\prime } )=v_i +M({\uptheta } _i )\cdot (x_i^t ,y_i^t )$, where $M({\uptheta } )$ denotes the standard rotation matrix, $v_i =(x_i ,y_i )$ is a translation vector of ellipse $E_i$.

Note that an outer normal vector to ellipse $E_i$ at point $(x_i^{\prime } ,y_i^{\prime } )$ can be defined by $N_i^{\prime } =({\upalpha } _i^{\prime } ,{\upbeta } _i^{\prime } )=M({\uptheta } _i )({\upalpha } _i ,{\upbeta } _i)$, ${\upalpha } _i =\frac{\cos t_i }{{\uplambda }_i a_i },{\upbeta } _i =\frac{\sin t_i }{{\uplambda }_i b_i }$. Note also that the equation of the tangent line to the ellipse $E_i (u_i )$ passing through the point $q_i^{\prime } =(x_i^{\prime } ,y_i^{\prime } )$ is ${\uppsi } _i (x,y)={\upalpha } _i^{\prime } x+{\upbeta } _i^{\prime } y-1=0$.We choose two points $q_2^\pm$ on the second tangent line, with coordinates $(x_2^\pm ,y_2^\pm )=(x_2^{\prime } ,y_2^{\prime } )\pm \upeta (-{\upbeta } _2^{\prime } ,{\upalpha } _2^{\prime } )$, where $\upeta =({\uplambda }_2 a_2 )^{2}$.

Now we define the three functions mentioned in (9):

$$\begin{aligned} {\upchi }= & {} -\left\langle {N_1^{\prime } ,N_2^{\prime } } \right\rangle =-{\upalpha } _1^{\prime } {\upalpha } _2^{\prime } -{\upbeta } _1^{\prime } {\upbeta } _2^{\prime } , {\upchi } ^{\pm }={\uppsi } _1 (x_2^\pm -x_1 ,y_2^\pm -y_1 )\\ {}= & {} {\upalpha } _1^{\prime } (x_2^\pm -x_1 )+{\upbeta } _1^{\prime } (y_2^\pm -y_1 )-1. \end{aligned}$$

Figure 1 illustrates the idea of our quasi-phi-function (9).

Fig. 1

The arrangement of non-overlapping ellipses $E_1$ and $E_2$

Alternatively, a quasi-phi-function for $E_1 (u_1 )$ and $E_2 (u_2)$ may be defined according to (2):

$$\begin{aligned} {\Phi ^{'}}^{E_1 E_2 }(u_1 ,u_2 ,u^{\prime })=\min \left\{ {\Phi ^{'}}^{E_1 P} (u_1 ,u_P ,u_1^{\prime } ),{\Phi ^{'}}^{E_2 P^{{*}}} (u_2 ,u_P ,u_2^{\prime } )\right\} . \end{aligned}$$

It remains to define a quasi-phi-function for an ellipse $E(u_E )$ and a halfplane $P(u_P )$. This can be done as follows:

$$\begin{aligned} {\Phi ^{'}}^{EP} (u_E ,u_P ,t)=\min \left\{ {\upchi } ({\uptheta } _E ,{\uptheta } _P ,t),{\uppsi } _P^+ (u_E ,u_P ,t),{\uppsi } _P^- (u_E ,u_P ,t)\right\} , \end{aligned}$$

(10)

where $u_P =({\uptheta } _P ,{\upmu }_P ), 0\le t\le 2{\uppi }$ is auxiliary parameter.

Here the half-plane is defined by ${\uppsi } _P (x,y)={\upalpha } _P x+{\upbeta } _P y+{\upmu }_P \le 0$, where ${\upalpha } =\cos {\uptheta } _P , {\upbeta } =\sin {\uptheta } _P$.

Note that $N_P =({\upalpha } _P ,{\upbeta } _P )$ is the corresponding outer normal vector for the half-plane. For ellipse $E(u_E )$ we adopt our previous formulas introduced for $E_2 (u_2 )$, such as $N_2^{\prime } =({\upalpha } _2^{\prime } ,{\upbeta } _2^{\prime } )$ and $(x_2^\pm ,y_2^\pm )$, we just replace the subscript 2 with E in those formulas.

Thus ${\uppsi } _P^\pm (x_E^\pm ,y_E^\pm )={\upalpha } _P x_E^\pm +{\upbeta } _P y_E^\pm +{\upmu }_P \le 0$.

Lastly we define ${\upchi } =-\left\langle {N_P ,N_E^{\prime } } \right\rangle$, which completes our construction of (10).

Now let a minimal allowable distance between two ellipses $E_1$ and $E_2$ be given, we denote it by ${\uprho } ^{-}$. Assume that are pseudonormalized quasi-phi-functions provided if $\hbox {dist}(E_1 ,P)\ge 0.5{\uprho } ^{-}$ and if $\hbox {dist}(E_2 ,P^{*})\ge 0.5{\uprho } ^{-}$. Then function

(11)

is a pseudonormalized quasi-phi-function for a distance constraint $\hbox {dist}(E_1 ,E_2 )\ge {\uprho } ^{-}$.

A quasi-phi-function for ellipse $E(u_1 )$ and the complement of the interior of a rectangular container $\Omega$. Let $E(u_1 )$ be an ellipse with variable parameters $u_1 =(x_1 ,y_1 ,{\uptheta } _1 ,{\uplambda }_1 )$, and let $\Omega$ be a rectangular container with appropriate vertices $p_1 =(0,0), p_2 =(l,0), p_3 =(l,w), p_4 =(0,w)$. Let $\Omega ^{*}=R^{2}\backslash \hbox {int}\,\Omega$.

We take an arbitrary parameter $t=t_{_1 }^{{\prime }1} , 0\le t_{_1 }^{{\prime }1} \le 2{\uppi }$, and consider the line $L_1 =\{(x,y)\in R^{2}{:}\ {\upvarphi } _1 =A_1 x+B_1 y+C_1 =0\}$ with $A_1 ={\upalpha } _1 \cdot \cos {\uptheta } _1 +{\upbeta } _1 \cdot \sin {\uptheta } _1$ and $B=-{\upalpha } _1 \cdot \sin {\uptheta } _1 +{\upbeta } _1 \cdot \cos {\uptheta } _1$, where ${\upalpha } _1 =\frac{\cos t_1^{1'}}{{\uplambda }_1 a},{\upbeta } _1 =\frac{\sin t_1^{1'}}{{\uplambda }_1 b}$. We put $C_1 =-A_1 x_1 -B_1 y_1$, so that the line $L_{1}$ passes though the center $v_1 =(x_1 ,y_1 )$ of the ellipse.

Now the two lines

$$\begin{aligned} L_{11}= & {} \left\{ (x,y)\in R^{2}{:}\ {\upvarphi } _{11} =A_1 x+B_1 y+C_1 -1=0\right\} ,\\ L_{12}= & {} \left\{ (x,y)\in R^{2}{:}\ {\upvarphi } _{12} =-A_1 x-B_1 y-C_1 -1=0\right\} , \end{aligned}$$

are parallel to $L_{1}$ and tangent lines to the ellipse E (see Fig. 2).

Fig. 2

The arrangement of $E(u_1 )$ within $\Omega$

Also, we take another arbitrary parameter $t=t_{_2 }^{{\prime }1}, 0\le t_{_2 }^{{\prime }1} \le 2{\uppi } , t_{_2 }^{{\prime }1} \ne t_{_1 }^{{\prime }1}$, and consider similar lines (see Fig. 2)

$$\begin{aligned}&L_2 =\left\{ (x,y)\in R^{2}{:}\ {\upvarphi } _2 =A_2 x+B_2 y+C_2 =0\right\} ,\\&L_{21} =\left\{ (x,y)\in R^{2}{:}\ {\upvarphi } _{21} =A_2 x+B_2 y+C_2 -1=0\right\} ,\\&L_{22} =\left\{ (x,y)\in R^{2}{:}\ {\upvarphi } _{22} =-A_2 x-B_2 y-C_2 -1=0\right\} . \end{aligned}$$

Now a quasi-phi-function for E and $\Omega ^{*}$ is defined by

$$\begin{aligned} {\Phi }^{E\Omega ^{*}}(u)= & {} \min \left\{ {\upvarphi } _{11} (p_1 ),{\upvarphi } _{11} (p_2 ),{\upvarphi } _{12} (p_3 ),{\upvarphi } _{12} (p_4 ),\right. \nonumber \\&\left. {\upvarphi } _{21} (p_2 ),{\upvarphi } _{21} (p_3 ),{\upvarphi } _{22} (p_1 ),{\upvarphi } _{22} (p_4 )\right\} , \end{aligned}$$

(12)

where $u=(x_1 ,y_1 ,{\uptheta } _1 ,{\uplambda }_1 ,t_1^{1{\prime }} ,t_2^{1{\prime }} )\in R^{6}$.

Let a minimal allowable distance ${\uprho } ^{-}$ between an ellipse $E(u_1 )$ and the frontier of the rectangle $\Omega$ be given. Then function

(13)

is a pseudonormalized quasi-phi-functions enforcing the distance constraint $\hbox {dist}(E_1 ,\Omega ^{*})\ge {\uprho } ^{-}$, where $p_{_i }^- ,i=1,2,3,4$, are vertices of region $\Omega ^{*}\oplus C({\uprho } ^{-}), C({\uprho } ^{-})$ is circle of radius ${\uprho } ^{-}$, i.e. $p_{_1 }^- =({\uprho } ^{-},{\uprho } ^{-}), p_{_2 }^- =(l-{\uprho } ^{-},{\uprho } ^{-}), p_{_3 }^- =(l-{\uprho } ^{-},w-{\uprho } ^{-}), p_{_4 }^- =({\uprho } ^{-},w-{\uprho } ^{-}), \oplus$ is a symbol of Minkowski sum.

5 Application of quasi-phi-functions for optimal packing of rotating ellipses

We consider here a packing problem in the following setting. Let $\Omega$ denote a rectangular domain of length l and width w. Both of these dimensions may be variable, or one may be fixed and the other variable. Suppose a set of ellipses $E_i , i\in \{1,2,\ldots ,n\}=I_n$, is given to be placed in $\Omega$ without overlaps. Each ellipse $E_i$ is defined by its semi-axes $a_i$ and $b_i$, whose values are fixed. With each ellipse $E_i$ we associate its eigen coordinate system whose origin coincides with the center of the ellipse and the coordinate axes are aligned with the ellipse’s axes. In that system the ellipse is described by parametric equations $x = a \,\hbox {cos }t,\, y = b\, \hbox {sin} \,t, 0 \le t \le 2{\uppi }$. We also use a fixed coordinate system attached to the container $\Omega$. The position of ellipse $E_i$ in the fixed coordinates is specified by the coordinates $(x_i,y_i)$ of its center and the rotation angle ${\theta }_{i}$. We call $(x_{i, }y_{i}, {\theta }_{i})$ the vector of placement parameters of $E_i$. Minimal allowable distances between ellipses $E_i$ and $E_j$, $j>i\in I_n$, as well as, between each ellipse $E_i , i\in I_n$, and the frontier (border) of $\Omega$ may be given.

Ellipse packing optimization problem. Place the set of ellipses $E_i , i\in I_n$, within a rectangular domain $\Omega =\{(x,y)\in R^{2}{:}\, 0\le x\le l,0\le y\le w\}$ of minimal area taking into account distance constraints. If one of the two dimensions (l or w) is fixed, we need to minimize the other one. If both are variable, it is natural to minimize the area $F=l\cdot w$ of the container.

One way to tackle the packing problem for ellipses is to approximate the latter with line segments and/or circular arcs [8] and then use the existing phi-functions described in [9]. However, the complexity of such a solution would depend on the number of lines/arcs used to approximate the ellipses, and it will grow fast if one tries to increase the accuracy of the approximation. In any case, this approach would only give an approximate solution.

Our approach, which is based on quasi-phi-functions, is capable of handling precise ellipses (without approximations) and thus finding an exact local optimal solution. The only other method of that sort was developed very recently by Josef Kallrath and Steffen Rebennack; see [14]. We learned about their remarkable paper after our work was completed and our manuscript was ready for submission. In view of similarities between [14] and our work, we postponed the submission of our manuscript and investigated the results of [14] more closely.

The paper [14] is entirely devoted to the problem of cutting ellipses from a rectangular plate of minimal area. Incidentally, it offers a good overview of related publications. The key idea of [14], just like ours, is to use separating lines to ensure that the ellipses do not overlap with each other. But their implementation of this idea is technically different. For a small number of ellipses they are able to compute a globally optimal solution subject to the finite arithmetic of global solvers at hand. However, for more than 14 ellipses none of the nonlinear programming (NLP) solvers available in GAMS can even compute a locally optimal solution. Therefore, the authors of [14] develop polylithic approaches, in which the ellipses are added sequentially in a strip-packing fashion to the rectangle restricted in width but unrestricted in length. The rectangle’s area is minimized at each step in a greedy fashion. The sequence in which they add ellipses is random; this adds some GRASP flavor to the approach. The polylithic algorithms allow the authors to compute good solutions for up to 100 ellipses. A number of examples are presented in the paper.

We believe our quasi-phi-functions (pseudonormalized quasi-phi-functions) and our optimization algorithm described below are more flexible and efficient than the techniques of [14]. In order to compare the performance of the two methods, we applied our algorithm to some instances of the ellipse packing problem as used in [14].

5.1 Mathematical model

First we assemble a complete set of variables for our optimization problem. At this stage we do not include the homothetic coefficients ${\lambda }_i$ for ellipses $E_i$ into our list of variables, we assume that they are fixed, in fact we assume that ${\lambda }_i =1$ for all $i=1,2,\ldots ,n$.

The vector $u\in R^{\sigma }$ of all our variables can be described as follows: $u=(l,w,u_1 ,u_2 ,\ldots ,u_n ,\tau )$, where (l, w) denote the variable dimensions (length and width) of the rectangular container $\Omega$ and $u_i =(x_i ,y_i ,{\theta } _i )$ is the vector of placement parameters for the ellipse $E_i ,\, i\in I_n$. Lastly, $\tau$ denotes the vector of additional variables, defined as follows: $\tau =t=(t_{_1 }^1 ,t_{_2 }^1 ,\ldots ,t_{_1 }^m ,t_{_2 }^m ,t_{_1 }^{{\prime }1} ,t_{_2 }^{{\prime }1} ,\ldots ,t_{_1 }^{{\prime }n} ,t_{_2 }^{{\prime }n} )$, if there are no distance constraints, where $t_{_1 }^k ,t_{_2 }^k$ are additional variables for the k-th pair of ellipses, according to (9), here $k=1,\ldots ,m, m=\frac{(n-1)n}{2}$, and $t_{_1 }^{{\prime }i} ,t_{_2 }^{{\prime }i}$ are additional variables for each ellipse $E_i, i\in I_n$, according to (12). If minimal allowable distances are specified, we have to use pseudonormalised quasi-phi-functions (11) and (13), instead of quasi-phi-functions (9) and (12). In that case $\tau =(t,u_P )$, where $u_P =(u_{_P }^1 ,\ldots ,u_{_P }^m ),u_{_P }^k =({\theta } _{_P }^k ,{\mu }_{_P }^k )$. Lastly, $R^{\sigma }$ denotes the $\sigma$-dimensional Euclidean space, where ${\sigma } =2 + 3n + n(n-1) + 2n=n^{2} + 4n + 2$ is the number of the problem variables if there are no distance constraints, and ${\sigma } =2+3n+2n(n-1)+2n=2n^{2}+3n+2$ if minimal allowable distances are given.

A mathematical model of the ellipse packing optimization problem may now be stated in the form:

$$\begin{aligned} \mathop {\min }\limits _{u\in W\subset R^{{\sigma } }} F(u), \end{aligned}$$

(14)

(15)

where $F(u)=l\cdot w$, is a radical free pseudonormalized quasi-phi-function (11) defined for the pair of ellipses $E_i$ and $E_j$, taking into account minimal allowable distance ${\rho } _{ij}^-$, is a pseudonormalized quasi-phi-function (13) defined for the ellipse $E_i$ and the object $\Omega ^{*}$ (to hold the containment constraint), also taking into account minimal allowable distance ${\rho } _i^-$.

If ${\uprho } _{ij}^- =0$ and ${\uprho } _i^- =0$ we replace a pseudonormalized quasi-phi-function by a radical free quasi-phi-function ${\Phi }_{ij}^{\prime }$ defined by (9) for each pair of ellipses to enforce the non-overlapping constraint and a quasi-phi-function with a radical free quasi-function ${\Phi }_i^{\prime }$ defined by (12) for each ellipse and the domain $\Omega ^{*}$ to enforce the containment constraint.

Our constrained optimization problem (14)–(15) is NP-hard nonlinear programming problem [15]. The feasible set W has a complicated structure: it is, in general, a disconnected set, the frontier of W is usually made of nonlinear surfaces containing valleys, ravines. A matrix of the inequality system which specifies W is strongly sparse and has a block structure.

Problem (14)–(15) is an exact formulation for the ellipse packing optimization problem. Our objective function is a quadratic; each quasi-phi-function inequality in (15) is described by a system of inequalities with infinitely differentiable functions. Our model is a different formulation for the ones presented in Section 2.2 of [14]. Both our models have in common that they are exact, non-convex and continuous.

5.2 A solution strategy

Our solution strategy consists of three major stages:

• (1) First we generate a number of starting points from the feasible set of the problem (14)–(15). We employ a new starting point algorithm (SPA). See Sect. 5.2.1.

• (2) Then starting from each point obtained at Step 1 we search for a local minimum of the objective function F(u) of problem (14)–(15). We employ a new Local Optimization with Feasible Region Transformation (LOFRT) procedure. See Sect. 5.2.2.

• (3) Lastly, we choose the best local minimum from those found at Step 2. This is our best approximation to the global solution of the problem (14)–(15).

An essential part of our local optimization scheme (Step 2) is the LOFRT procedure that reduces the dimension of the problem and computational time. It is due to this reduction that our strategy can process large sets of non-identical ellipses (100 and more, see examples below). The reduction scheme used by our LOFRT algorithm is described below. The actual search for a local minimum is performed by a standard IPOPT algorithm [16], which is available at an open access noncommercial software depository (https://projects.coin-or.org/Ipopt) .

5.2.1 Starting point algorithm (SPA)

In order to find a starting point $u^{0}$ that belongs to the feasible set W we apply the following algorithm based on homothetic transformation of ellipses. We assume here that homothetic coefficients ${\lambda }_i$ are variable provided that ${\lambda }_i ={\lambda }$, for $i=1,2,\ldots ,n$, and $0\le {\lambda }\le 1$.

The algorithm consists of the following steps:

• 1. First we choose starting dimensions (length and width) for the container $\Omega ^{0}$. They must be sufficiently large to allow for a placement of all our ellipses with required distance constraints within $\Omega ^{0}$. For example, we can choose

  $$\begin{aligned} l^{0}=w^{0}=2\sum _{i=1}^n {a_i } +(n-1){\rho } ^{-},\, {\rho } ^{-}=\mathop {\max }\limits _{i,j\in I_n } {\rho } _{ij}^- . \end{aligned}$$

• 2. Then we set ${\lambda }={\lambda }^0 =\frac{{\delta }}{\mathop {\max a_i }\nolimits _i }$, where ${\delta }=0.01(\mathop {\min }\nolimits _i b_i )$

• 3. Then we generate randomly, within $\Omega ^{0}$, a set of n non-overlapping equal circles of radius ${\delta }$ with randomly chosen centers $(x_i^0 ,y_i^0 ),\quad i=1,2,\ldots ,n$

• 4. Next we generate, randomly, a set of rotation parameters ${\theta } _i^0 \in [0,2{\pi } ),\quad i=1,2,\ldots ,n$

• 5. Then we find starting values for the additional variables $\tau ^{0}$ by a special optimization procedure that solves an auxiliary problem of finding (or ) and $\mathop {\max }\nolimits _{u_{ij}^{\prime } \in R^{2}} {\Phi ^{'}}_{ij} (u_i^0 ,u_j^0 ,u_{ij}^{\prime } )$ (or ) for each quasi-phi-function (or, respectively, pseudonormalised phi-function) that is involved in (15), under fixed parameters $u_i=(x_i^0 ,y_i^0 ,{\theta } _i^0 ,{\lambda }^0 )$ for each ellipse.

To solve the above auxiliary problem we use the following model:

$$\begin{aligned} \max {\mu },\;s.t. u^{\prime }\in W_{\mu }^{\prime } , \end{aligned}$$

where $W_{\mu }^{\prime } =\{(u^{\prime },{\mu }){:}{\Phi }'(u^0 ,u^{\prime } )\ge {\mu }\}, {\mu }\in R^{1}$ is a new auxiliary variable, function ${\Phi ^{'}}(u^0 ,u^{\prime } )$ may take form of ${\Phi ^{'}}_i(u_i^0 ,u_i^{\prime } )$ (or and ${\Phi ^{'}}_{ij}(u_i^0 ,u_j^0 ,u_{ij}^{\prime } )$ (or }), $u^{\prime }$ is the vector of auxiliary variables and $u^0$ is the vector of fixed parameters for our quasi-phi-functions (respectively, pseudonormalised phi-functions).

Thus all our quasi-phi-functions (or pseudonormalised quasi-phi-functions) at the point $u^{0}=(l^{0},w^{0},u_1^0 ,u_2^0 ,\ldots ,u_n^0 ,\tau ^{0})$ take non-negative values, where $\tau ^{0}=(t^{0})$ (or, respectively, $\tau ^{0}=(u_P^0 ,t^{0}))$.

• 6. Now we take the starting point $u^{0}$ under fixed $l=l^{0}$ and $w=w^{0}$, and solve the following auxiliary optimization problem:

$$\begin{aligned} \kappa ({u}'^{0})=\mathop {\max }\limits _{{u}'\in W{\prime }} \kappa ({u}'),\, \kappa ({u}')={\lambda }, \end{aligned}$$

(16)

(17)

where ${u}'=(u,{\lambda })$ denotes an extended vector of variables and u denotes the original vector of variables for the problem (14)–(15).

Remark

We note that if an optimal global solution is found, then ${\lambda }=1$. The solution automatically respects all the non-overlapping, containment and distance constraints.

Thus, the point $u^{{\prime }0}=(l^{0},w^{0},u_1^{{\prime }0} ,u_2^{{\prime }0} ,\ldots ,u_n^{{\prime }0} ,\tau ^{{\prime }0},1)$ of global maximum of the problem (16)–(17) guarantees that point $u^{0}=(l^{0},w^{0},u_1^{{\prime }0} ,u_2^{{\prime }0} ,\ldots ,u_n^{{\prime }0} ,\tau ^{{\prime }0})$ belongs to feasible set W of problem (14)–(15).

Our use of homothetic transformations of ellipses here is similar to the use of variable radii for optimal packing of n D-spheres, which was proposed in [17].

It should be noted that our algorithm by construction always finds the global solution of the problem (16)–(17). It is clear that the optimal solution to the above problem will automatically comply with all the non-overlapping, containment and distance constraints.

• 7. Lastly, our algorithm returns the vector $u^{0}=(l^{0},w^{0},u_1^{{\prime }0} ,u_2^{{\prime }0} ,\ldots ,u_n^{{\prime }0} ,\tau ^{{\prime }0})$ as a starting point for a subsequent search for a local minimum of the problem (14)–(15).

5.2.2 Algorithm of local optimization with feasible region transformation (LOFRT) in the ellipse packing problem

Let $u^{(0)}\in W$ be one of the starting points found by the previous method. The main idea of the subsequent LOFRT algorithm is as follows.

First we circumscribe a circle $C_i$ of radius $a_i$ around each ellipse $E_i, i=1,2,\ldots ,n$. Then for each circle we construct an “individual” rectangular container $\Omega _i \supset C_i \supset E_i$ with equal half-sides of length $a_i +{\varepsilon }$, $i=1,2,\ldots ,n$, so that $C_i$, $E_i$ and $\Omega _i$ have the same center $(x_i^0 ,y_i^0 )$ subject to the sides of $\Omega _i$ being parallel to those of $\Omega$ (see Fig. 3a). We take the fixed value of ${\varepsilon }$ of the LOFTR procedure as ${\varepsilon } =\mathop {\sum }\nolimits _{i=1}^n {b_i } /n$ (see “Appendix 2”). Further we fix the position of each individual container $\Omega _i$ and let the local optimization algorithm move the corresponding ellipse $E_i$ only within the container $\Omega _i$. It is clear that if two individual containers $\Omega _i$ and $\Omega _j$ do not have common interior points for ${\rho } _{ij}^- =0$, i.e. ${\Phi }^{\Omega _i \Omega _j }\ge 0$, (or dist($\Omega _i,\Omega _j)\ge {\rho } _{ij}^-$ for ${\rho } _{ij}^- >0$, i.e. , then we do not need to check the non-overlapping (or distance) constraint for the corresponding pair of ellipses $E_{i}$ and $E_{j}$ (see, e.g., the ellipses $E_1$ and $E_7, E_4$ and $E_8 , E_1$ and $E_8$ in Fig. 3b).

Fig. 3

Rectangular containers: a forming a rectangular container $\Omega _i \supset C_i \supset E_i$, b an initial placement of ellipses and their individual containers

The above key idea allows us to extract subsets of our feasible set W of the problem (14)–(15) at each step of our optimization procedure as follows.

We create an inequality system of additional constraints on the translation vector $v_i$ of each ellipse $E_i$ in the form: ${\Phi }^{C_i \Omega _{1i}^{*} }\ge 0, \quad i=1,2,\ldots ,n$, where

$$\begin{aligned} {\Phi }^{C_i \Omega _{1i}^{*} }=\min \left\{ -x_i +x_i^0 +{\varepsilon } ,-y_i +y_i^0 +{\varepsilon } ,x_i -x_i^0 +{\varepsilon } ,y_i -y_i^0 +{\varepsilon } \right\} , \end{aligned}$$

is the phi-function for the circle $C_{i}$ and $\Omega _{1i}^*=R^2 \backslash \hbox {int}\,\Omega _{1i}$.

The inequality $\Phi ^{C_{i}\Omega _i^{*}}\ge 0$ is equivalent to the system of four linear inequalities $-x_i +x_i^0 +{\varepsilon } \ge 0$, $-y_i +y_i^0 +{\varepsilon } \ge 0$, $x_i -x_i^0 +{\varepsilon } \ge 0$, $y_i -y_i^0 +{\varepsilon } \ge 0$.

Then we form a new subset defined by

where .

In other words, we delete from the system, which describes feasible set W, quasi-phi-function inequalities for all pairs of ellipses whose individual containers do not overlap for ${\rho } _{ij}^- =0$ (or dist($\Omega _i,\Omega _j)\ge {\rho } _{ij}^-$ for ${\rho } _{ij}^- >0)$ and we add additional inequalities ${\Phi }^{C_i \Omega _{1i}^{*} }\ge 0$, which describe the containment of the circles $C_i$ in their individual containers $\Omega _{1i}, i=1,2,\ldots ,n.$ Eo ipso we reduce the number of additional variables by ${\sigma } _1$. Then our algorithm searches for a point of local minimum $u_{w_1 }^*$ of the subproblem

$$\begin{aligned} \mathop {\min }\limits _{u_{w_1 } \in W_1 \subset R^{{\sigma } -{\sigma } _1 }} F(u_{w_1 } ). \end{aligned}$$

When the point $u_{w_1 }^*$ is found, it is used to construct a starting point $u^{(1)}$ for the second iteration of our optimization procedure (note that the ${\sigma } _1$ previously deleted additional variables $\tau _1$ have to be redefined by a special procedure used in SPA; see item 5, assuming $\lambda ^{0}=1)$.

At that iteration we again identify all the pairs of ellipses with non-overlapping individual containers, form the corresponding subset $W_2$ (analogously to $W_1)$ and let our algorithm search for a local minimum $u_{w_2 }^*\in W_2$. The resulting local minimum $u_{w_2 }^*$ is used to construct a starting point $u^{(2)}$ for the third iteration, etc.

Then we solve the k-th subproblem with starting point $u^{(k-1)}$ on a subset $W_k$:

If the point $u_{w_k }^*$ of local minimum of the k-th subproblem belongs to the frontier of an “artificial” subset

$$\begin{aligned} {\Pi }_k^{\varepsilon }= & {} \left\{ u\in R^{{\sigma } -{\sigma } _k }:-x_i +x_i^{(k-1)} +{\varepsilon } \ge 0,-y_i +y_i^{(k-1)} +{\varepsilon } \ge 0,\right. \\&\left. x_i -x_i^{(k-1)} +{\varepsilon } \ge 0,\quad y_i -y_i^{(k-1)} +{\varepsilon } \ge 0,\quad i=1,\ldots ,n\right\} , \end{aligned}$$

(i.e.$u_{w_k }^*\in fr{\Pi }_k^{\varepsilon } )$, we take the point $u_{w_k }^*=u^{(k)}$ as a center point for a new subset ${\Pi }_{k+1}^{\varepsilon }$ and continue our optimization procedure, otherwise (i.e. $u_{w_k }^*\in \hbox {int}{\Pi }_{\varepsilon } ^k )$ we stop our LOFRT procedure (see “Appendix 3”).

We note that dist($u_{w_k }^*,u_{w_{k+1} }^*)\ge {\varepsilon }$, if $u_{w_{k+1} }^*\in fr{\Pi }_{\varepsilon } ^k$, and the value of ${\varepsilon }$ is considerably greater than the accuracy of IPOPT ($10^{-8})$. Thus, we may conclude that the stopping condition of the LOFRT procedure is always reached in a finite number of iterations.

We claim that the point $u^*=u^{(k)*} =(u_{w_k }^*,\tau _k^*)\in R^{{\sigma } }$ is a point of local minimum of the problem (14)–(15), where $u_{w_k }^*\in R^{{\sigma } -{\sigma } _k }$ is the last point of our iterative procedure and $\tau _k^*$ is a vector of redefined values of the previously deleted additional variables $\tau _k \in R^{{\sigma } _k }$ (the values can be redefined by the special procedure used in SPA; see item 5). The assertion comes from the fact that any arrangement of each pair of ellipses $E_{i}$ and $E_{j}$ subject to $(i,j)\in \Xi \backslash \Xi _k$ guarantees that there always exists a vector $\tau _k$ of additional variables such that at the point $u^{(k)*}$. Here $\Xi =\{(i,j),i>j=1,2,\ldots ,n\}$. Therefore the values of additional variables of the vector $\tau _k$ have no effect on the value of our objective function, i.e $F(u_{w_k }^*)=F(u^{(k)*} )$. That is why, indeed, we do not need to redefine the deleted additional variables of the vector $\tau _k$ at the last step of our algorithm.

So, while there are O($n^{2})$ pairs of ellipses in the container, our algorithm may in most cases only actively controls O(n) pairs of ellipses (this depends on the sizes of ellipses and the value of ${\varepsilon } )$, because for each ellipse only its “${\varepsilon }$-neighbors” have to be monitored.

The parameter ${\varepsilon }$ provides a balance between the number of inequalities in each nonlinear programming subproblem and the number of the subproblems which we need to generate and solve in order to get a local optimal solution of problem (14)–(15). The LOFTR procedure allows us to reduce considerably computational costs (time and memory).

Thus our LOFRT algorithm allows us to reduce the problem (14)–(15) with $\hbox {O}(n^{2})$ inequalities and a $\hbox {O}(n^{2})$-dimensional feasible set W to a sequence of subproblems, each with $\hbox {O}(n)$ inequalities and a $\hbox {O}(n)$-dimensional solution subset $W_k$. This reduction is of a paramount importance, since we deal with nonlinear optimization problems.

6 Computational results

Here we present a number of examples to demonstrate the high efficiency of our methodology. We have run our experiments on an AMD Athlon 64 X2 5200+ computer, and for local optimization we used the IPOPT code (https://projects.coin-or.org/Ipopt) developed by [15]. Our web page https://app.box.com/s/yst9fuacyrscv85qdxrz provides more detailed descriptions of the instances presented below, as well as a number of other examples not included here.

We present two groups of instances: new instances (Examples 1–6 below) and those taken from the recent paper [14]. We set a time limit for each example to search for at least 10 local minima.

Example 1

Placing $n=32$ ellipses into a rectangular container of minimal area. The sizes of the ellipses are specified as follows: $\{(a_i ,b_i )=(222, 180), i=1,\ldots ,9\}, \{(a_i ,b_i )=(260, 170), i=10,\ldots ,18\}, \{(a_i ,b_i )=(360, 270), i=19,\ldots ,24\}, \{(a_i ,b_i )=(350, 70), i=25,\ldots ,32\}$. The local optimal placement is shown in Fig. 4, the container has dimensions $(l^{*},w^{*})$= (2406.3104, 2400.8160) and area $F(u^{*})=5777108.5092864$. Time limit is 12 h.

Example 2

Placing $n=33$ ellipses into a rectangular container of minimal area. The sizes of the ellipses are specified as follows: $\{(a_i ,b_i )=(222, 180), i=1,\ldots ,15\}, \{(a_i ,b_i )=(260, 170), i=16,\ldots ,30\}, \{(a_i ,b_i )=(360, 270), i=31,32,33\}$. The local optimal placement is shown in Fig. 5, the container has dimensions $(l^{*}\!,w^{*})\!=\! (2597.4554, 2212.6591)$ and area $F(u^{*})=5747283.32765414$. Time limit is 12 h.

Fig. 4

Local optimal placement of ellipses in Example 1

Fig. 5

Local optimal placement of ellipses in Example 2

Example 3

Now we set minimal allowable distances between ellipses, as well as between each ellipse and the object $\Omega ^{*}$: a) ${\uprho } _{ij}^- =0.1, {\uprho } _i^- =0$ and b) ${\uprho } _{ij}^- =0.1, {\uprho } _i^- =0.2$. Otherwise this example is similar to the previous ones: $n=20,\{(a_i ,b_i ),i=1,\ldots ,6\}=(2, 1.5, 1.5, 1, 1, 0.8, 0.9, 0.75, 0.8, 0.6, 0.7, 0.3), \{(a_i ,b_i )=(1, 0.8), i=7,\ldots ,20\}$. The local optimal packing is shown in Fig. 6, the container has dimensions: $(l^{*},w^{*})=(7.033623, 10.187241)$ and area $F(u^{*})=71.653212604143$ for case a) and $(l^{*},w^{*})=(9.179764 8.568622)$ and area $F(u^{*})=78.6579$ for case b). Time limit is 12 h.

Fig. 6

Local optimal placement of ellipses in Example 3 taking into account the given minimal allowable distance between ellipses: a ${\uprho } _{ij}^- =0.1, {\uprho } _i^- =0$, b ${\uprho } _{ij}^- =0.1, {\uprho } _i^- =0.2$

Fig. 7

Local optimal placement of ellipses in Example 4

Example 4

Placing a large set of n=120 ellipses into a rectangular container of minimal area. The sizes of the ellipses are specified as follows: $\{(a_i ,b_i ), i=1,\ldots ,6\}=(2, 1.5, 1.5, 1, 1, 0.8, 0.9, 0.75, 0.8, 0.6, 0.7, 0.3)$, $\{(a_i ,b_i ), i=7,\ldots ,12\}=(2, 1.5, 1.5, 1, 1, 0.8, 0.9, 0.75, 0.8, 0.6, 0.7, 0.3)$, $\{(a_i ,b_i ), i\!=\!13,\ldots ,18\}\!=\!(2, 1.5, 1.5, 1, 1, 0.8, 0.9, 0.75, 0.8, 0.6, 0.7, 0.3)$, $\{(a_i ,b_i )=(1, 0.8), i=19,\ldots ,120\}$. The local optimal placement is shown in Fig. 7, the container has dimensions $(l^{*},w^{*})=(18.880110, 20.085018)$ and area $F(u^{*})=379.2073492$. Time limit for this large example was set to 48 h.

Example 5

We apply our methodology for $n=5$ objects: a circle C of radius $r=3$; a polygon K with vertices $\{(0,0), (2,-3), (2,0)\}$; a circular segment D formed by a circle of radius $r=5$ with the center point (0,0), and the horde with the end points (5,0) and (0,5); two equal ellipses $E_1$ and $E_2$ of sizes $\{(a_1 ,b_1 ),(a_2 ,b_2 )\}=\{(2,1),(2,1)\}$, to pack into a rectangle $\Omega$ of the minimal area $l\cdot w$. For the problem we use: quasi-phi-functions to describe non-overlapping constraints for each pair of the objects; quasi-phi-functions to describe containment constraints for pairs of objects E and $\Omega ^{*}, D$ and $\Omega ^{*}$; ordinary phi-functions to describe containment constraints for pairs of objects C and $\Omega ^{*}, K$ and $\Omega ^{*}$. To describe distance constraints we use pseudonormalized quasi-phi-functions instead of quasi-phi-functions for the appropriate pairs of objects. In mathematical model (14)–(15) a vector of variables is defined as $u=(l,w,u_1 ,u_2 ,\ldots ,u_5 ,\tau )\in R^{56}$. Figure 8 shows the local optimal placement of the objects: (a) the container has dimensions $(l^{*},w^{*})=(8.562049, 7.234445)$ and area $F(u^{*})=61.943253$. Time limit is 1 hour; (b) the container has dimensions $(l^{*},w^{*})=(5.999999, 11.996817)$ and area $F(u^{*})=71.982703$ taking into acount minimal allowable distance ${\uprho } _{ij}^- =0.3$ between each pair of objects. Time limit is 1 hour.

Fig. 8

Local optimal placement of $n=5$ objects in Example 5: a without distance constraints; b ${\uprho } _{ij}^- =0.3, {\uprho } _i^- =0$

Example 6

We apply our methodology to pack $n=30$ convex polytopes into a box $\Omega =\{(x,y,z)\in R^{3}:0\le x\le l,0\le y\le w,0\le z\le h\}$ of the minimal volume $l\cdot w\cdot h$. For the problem we use a quasi-phi-function of the form (5) for describing non-overlapping constraints and an ordinary phi-function for object $\Omega ^{*}$ and a convex polytope for containment constraints. We set in mathematical model (14)–(15): $F=l\cdot w\cdot h$, $u=(l,w,h,u_1 ,u_2 ,\ldots ,u_n ,\tau )\in R^{{\sigma } }, u_i =(x_i ,y_i ,z_i ,{\theta } _i^1 ,{\theta } _i^2 ,{\theta } _i^3 ), i=1,2,\ldots ,30$, $\tau =(u_P ), u_P =(u_{_P }^1 ,\ldots ,u_{_P }^m ),u_{_P }^k =({\theta } _{xP}^k ,{\theta } _{yP}^k ,{\mu }_{P}^k ), k=1,\ldots ,m, m=\frac{(n-1)n}{2}=435, {\sigma } =3+6n+3m=1488$. Figure 9 shows the local optimal placement of $n=30$ convex polytopes, the container has dimensions $(l^{*},w^{*},h^{*})=(40.671324, 39.178921, 28.515067)$ and volume $F(u^{*})=\hbox {45437.578454475}$. Computational time is 216.671 sec

Fig. 9

Local optimal placement of polytopes in Example 6

Further we applied our method to some instances used in recent paper [14] by Kallrath and Rebennack and compare our local optimal solutions to theirs.

We set computational time for the group of instances: up to 20 objects—time limit 2 h, up to 50—time limit 5 h, 100 objects—time limit 12 h.

Table 1 lists some examples presented in [14]. For each the example the minimal area of the container found by our method (the middle column) happens to be smaller than the best solution reported in [14]. The improvement is not so big (1–2 %) for smaller sets of ellipses, but it becomes significant (8–9 %) for larger sets of ellipses. It should be noted that for examples TC02, TC03 and TC04 presented in [14] our method found the same results.

Table 1 Comparison of our results to those in [14]

Example “TC20” from [14]. Placing $n=20$ ellipses into a rectangular container of minimal area. The sizes of the ellipses are specified as follows: $\{(a_i ,b_i ), i=1,\ldots ,6\}=(2, 1.5, 1.5, 1, 1, 0.8, 0.9, 0.75, 0.8, 0.6, 0.7, 0.3), \{(a_i ,b_i )=(1, 0.8), i=7,\ldots ,20\}$. The local optimal placement is shown in Fig. 10, the container has dimensions $(l^{*},w^{*})=(9.2819628623, 7.1252676425)$ and area $F(u^{*})=66.136469641633$.

Fig. 10

Local optimal placement of ellipses in Example TC20

Example “TC50; from [14]. Placing $n=50$ ellipses into a rectangular container of minimal area. The sizes of the ellipses are specified as follows: $\{(a_i ,b_i ), i=1,\ldots ,6\}=(2, 1.5, 1.5, 1, 1, 0.8, 0.9, 0.75, 0.8, 0.6, 0.7, 0.3), \{(a_i ,b_i )=(1, 0.8), i=7,\ldots ,50\}$. The local optimal placement is shown in Fig. 11, the container has dimensions $(l^{*},w^{*})=(11.853222, 12.993055)$ and area $F(u^{*})=154.470487$.

Fig. 11

Local optimal placement of ellipses in Example TC50

Fig. 12

Local optimal placement of ellipses in Example “TC100”

Example “TC100” from [14]. Placing $n=100$ ellipses into a rectangular container of minimal area. The sizes of the ellipses are specified as follows: $\{(a_i ,b_i ),i=1,\ldots ,6\}=(2, 1.5, 1.5, 1, 1, 0.8, 0.9, 0.75, 0.8, 0.6, 0.7, 0.3), \{(a_i ,b_i )=(1,0.8), i=7,\ldots ,100\}$. The local optimal placement is shown in Fig. 12, the container has dimensions $(l^{*},w^{*})=(17.579199, 16.936948)$ and area $F(u^{*})=297.738$.

7 Concluding remarks

Here we introduce quasi-phi-functions for an analytical description of non-overlapping, containment and distance constraints for some types of 2D- and 3D-objects which can be continuosly rotated and translated. These new functions can work well: for new types of objects, such as ellipses, cones, cylinders for which phi-functions have not been constructed yet; for objects for which ordinary phi-functions are too complicated, e.g. for polytopes. Now, using our radical free quasi-phi-functions we can extend a class of packing and cutting problems for which we can develop exact nonlinear programming models and applied our methodology to search for “good” local optimal solutions. We may reasonably combine phi-functions and quasi-phi-functions in our models. We are constantly working on the improvement of our algorithms. The computational time reported in Sect. 6 for several examples is achieved presently, but we expect that it will be reduced in the future. We plan in the near future to solve a packing problem for ellipsoids, using quasi-phi-functions.

Appendices

Appendix 1: Examples of phi-functions

Example 7

We consider the simplest example of phi-functions for two circles $C_i$ of radii $r_i$ and center points $(x_{C_i } ,y_{C_i } )$, $i=1,2$. An ordinary phi-function, a normalized phi-function and a pseudonormalized phi-function for circles $C_1$ and $C_2$ may be defined in the following forms respectively:

Example 8

Let $p_i^1 =(x_i^{\prime },y_i^{\prime })$, $i=1,\ldots ,m_1$, be the vertices of $K_1 (u_1 )$, and $p_j^2 =(x_j{}^{\prime \prime },y_j{}^{\prime \prime }), j=1,\ldots ,m_2$, those of $K_2 (u_2 )$, and $K_1 (u_1 )=\{(x,y){:}{\upvarphi } _i \le 0,\;i=1,\ldots ,m_1 \}$, ${\upvarphi } _i ={\upalpha } _i^{\prime }x+{\upbeta } _i^{\prime }y+{\upgamma } _i ^{\prime }$, and $K_2 (u_2 )=\{(x,y){:}{\uppsi } _j \le 0,\;j=1,\ldots ,m_2 \}, \,{\uppsi } _j ={\upalpha } _j^{{\prime }'}x+{\upbeta } _j^{{\prime }'}y+{\upgamma } _j ^{{\prime }'}$, where $u_1 =(x_1 ,y_1 ,{\uptheta } _1 )$ and $u_2 =(x_2 ,y_2 ,{\uptheta } _2 )$ are placement parameters of polygons $K_1$ and $K_2$. It should be noted that each point $(\tilde{x},\tilde{y})\in K(0,0,0)$ in the local coordinate system of a convex polygon K is transformed into point (x, y):

$$\begin{aligned} x=\tilde{x}\cdot \cos {\uptheta } _K +\tilde{y}\cdot \sin {\uptheta } _K +x_K ,y=-\tilde{x}\cdot \sin {\uptheta } _K +\tilde{y}\cdot \cos {\uptheta } _K +y_K . \end{aligned}$$

A phi-function for two convex polygons $K_1$ and $K_2$ can be defined in the form

$$\begin{aligned} {\Phi }^{K_1 K_2 }=\max \left\{ \mathop {\max }\limits _{1\le i\le m_1 } \mathop {\min }\limits _{1\le j\le m_2 } {\upvarphi } _{ij} ,\mathop {\max }\limits _{1\le j\le m_2 } \mathop {\min }\limits _{1\le i\le m_1 } {\uppsi } _{ji} \right\} , \end{aligned}$$

(18)

where ${\upvarphi } _{ij} ={\upvarphi } _i (p_j^2 )={\upalpha } _i^{\prime }x_j^{\prime \prime }+{\upbeta } _i^{\prime }y_j^{\prime \prime }+{\upgamma } _i ^{\prime }$, ${\uppsi } _{ji} ={\uppsi } _j (p_i^1 )={\upalpha } _j^{\prime \prime }x_i ^{\prime }+{\upbeta } _j^{\prime \prime }y_i^ {\prime }+{\upgamma } _j^{\prime \prime }$.

In general, each of our phi-functions (ordinary, normalized, pseudonormalized) is formed by operations of minimum and maximum of continuous and everywhere defined functions. The more operations of maximum take part in forming of a phi-function the more nonlinear programming subproblems we need to solve.

For example, in order to reach the global minimum for the problem of packing of two convex polygons $K_1$ and $K_2$ in a rectangle of minimum area, using phi-function (18), we need to solve $m_1 +m_2$ nonlinear programming subproblems optimally. See details in [10].

Alternatively, in order to reach the global minimum of the latter problem, using quasi-phi-function (5), we need to solve only one nonlinear programming problem optimally. However, in the case the problem dimension is increased by two.

We may reasonably combine phi-functions and quasi-phi-functions in our models depending on types of our objects.

Appendix 2: The motivation of the epsilon parameter of the LOFTR procedure

We study the effect of the value of the parameter ${\varepsilon }$ on the computational time in our computational experiments. We take the value of ${\varepsilon }$ from the collection $\{0.1,0.2,0.4,0.6,\ldots ,3.8,4.0,\ldots ,{\varepsilon } ^{*}\}$, where ${\varepsilon } ^{*}=\max \{l^{0},w^{0}\}$, and apply our algorithm to our instances, starting from the same feasible point $u^{0}$ (point $u^{0}$ is obtaned by SPA algorithm).

Fig. 13

Dependence of the computational time on ${\upvarepsilon }$ for the instance “TC50”

From our computational experiments follows that there always exists an interval $[{\varepsilon } ^{-}, {\varepsilon } ^{+}]$, where the computational time reaches its “minimal” value and ${\varepsilon }$ weakly effects to the computational time. We take ${\varepsilon } =\frac{1}{n}\cdot \mathop {\sum }\nolimits _{i=1}^n {b_i }$ in our LOFRT algorithm since $\frac{1}{n}\cdot \mathop {\sum }\nolimits _{i=1}^n {b_i } \in [{\varepsilon } ^{-},{\varepsilon } ^{+}]$ for our computational experiments. It shold be noted that the value of ${\varepsilon }$ is taken significantly greater than the computational accuracy of IPOPT.

As an example we provide a diagram for the instance “TC50”. The diagram given in Figure 13 shows the dependence of the computational time on the value of ${\varepsilon }$, where $[{\varepsilon } ^{-}=0.6,{\varepsilon } ^{+}=1.6]$.

Fig. 14

A diagram of the LOFRT procedure

Appendix 3: A diagram of the LOFRT procedure

Figure 14 illustrates our LOFRT procedure. In fact on k-th step of the iterative procedure we solve the k-th subproblem on a subset $W_k =W\cap {\Pi }_k^{\varepsilon }$, provided that we ignore redundant inequalities , and fix variables of $\tau _k$, that have no effect on the value of our objective function in the “${\varepsilon }$-neighborhood” of point $u^{(k)*}$ by variables $x_i^k, y_i^k ,i=1,2,\ldots ,n$. If $u_{w_k }^*$ belongs to the frontier of the “artificial” subset ${\Pi }_k^{\varepsilon }$, then we take the point as a center point for a subset $\Pi ^{\varepsilon }_{k+1} \subset R^{\sigma }$ and continue our optimization procedure, otherwise we stop our LOFRT procedure. Figure 14 shows that each point of local minima $u_{w_k }^*$ is the frontier point of the appropriate “artificial” subset ${\Pi }_k^{\varepsilon }$ for $k=1,2,3,4,$ and the point $u_{w_5 }^*$ is the interior point of subset ${\Pi }_5^{\varepsilon }$. We note that $\hbox {dist}(u_{w_k }^*,u_{w_{k+1} }^*)\ge {\varepsilon }$ for $k=1,2,3$.