1 Introduction

In an extension of the work by Kallrath [11], we cut a set of ellipses with given semi-major and semi-minor axes from a rectangular plate. The ellipses are to be placed, free of any orientation restrictions, on a rectangular plate such that the area of the rectangle is minimized. The ellipses are not allowed to overlap; which poses the major challenge of this cutting problem together with the free rotation of the ellipses. Minimizing the area of the design rectangle is equivalent to minimizing trimloss.

Part of the motivation of this work is pure mathematical curiosity—ellipse cutting problems have a variety of real world applications. Color to be painted on walls is usually stored in paint buckets, which have an elliptical shape. This shape allows the painting rolls to be larger in length compared to a circular bucket having the same volume. The best area utilization is desired when transporting such buckets (differently or equally sized) on palettes. As described by Miller [20], ellipses can be used to approximate (irregular or non-convex) geometric objects via a cover. The obtained ellipse placements can then help to compute solutions to the original problem and provide safe bounds on optimal solutions, e.g., on the minimal area of the design rectangle.

The ellipse cutting problem falls into the class of two-dimensional cutting or packing problems of regular objects. This cutting problem comes close to the 2/V/D/F classification of Dyckhoff [4]; i.e., two-dimensional, V = a kind of assignment: a selection of objects and all items, D = an assortment of large objects: different figures, and F = an assortment of small items: few items of different figures. Packing and cutting problems differ in the following two aspects: (1) In cutting problems one tries to minimize trimloss or area, while in packing an area is given and one wants to fit as many objects as possible, and (2) while free objects are allowed in cutting problems, this might lead to stability problems in packing problems. Our ellipse problem falls into the category of a cutting problem.

The separation of ellipses by hyperplanes has been treated in a senior thesis by Miller [20]. His formulation starts from elementary geometry of ellipses from which he derives the hyperplane conditions. Confinement of the ellipses to the rectangle is modeled as a special hyperplane representing the boundaries of the rectangle. Our approach starts from a generic vector representation (to allow for its extension to the 3-D case in future work). At first, we compute the minimal and maximal extension of shifted and rotated ellipses. Second, we derive the hyperplane conditions from rotated coordinate systems. Miller reports in his thesis only on small examples with two ellipses. This is confirmed by his advisor Floudas [6].

Other than the unpublished work by Miller, it is hard to find published work on numerical approaches towards ellipse cutting and packing. However, the related problems of circle packing/cutting or orientation-free rectangle packing/cutting into one or multiple (design) rectangles have a rich body of literature, see Kallrath [11] and Rebennack et al. [24] and the references therein.

The technical report by Gensane and Honvault [8] establishes optimal packings for the case of two congruent ellipses in a square. Based on theoretical developments for sphere packings, the authors are able to derive the position for two congruent ellipses along with the minimal side length of a square hosting those two ellipses. Thus, their work is theoretical and not algorithmic, like ours.

The contributions of this paper are twofold: We develop

  1. 1.

    novel mathematical programming models for the ellipse cutting problems which allow us to solve larger instances to global optimality than previously reported in the literature.

  2. 2.

    two polylithicFootnote 1 approaches to compute good and near optimal cuttings for instances which cannot be handled by the current nonlinear and global solvers for the exact mathematical programming formulation developed. Both approaches sequentially solves ellipse cutting problems with fewer number of ellipses.

The remainder of this article is organized as follows. In Sect. 2, we develop (MI)NLP models for cutting ellipses from the design rectangle. We construct our polylithic approaches to compute good feasible, near optimal cuttings for instances which cannot be handled in the monolith formulation with the currently available solvers in Sect. 3. We present numerical experiments and results in Sect. 4. Section 5 concludes the paper.

At all places in this paper we use the term global optimum, or global optimality, in the sense of small relative gaps (difference between upper and lower bound divided by the lower bound) of the order of \(10^{-5}\). We are aware that the numeric solvers dealing with finite number arithmetic are subject to round-off errors. As such, all the presented results are only approximations, and although the small gaps hint on good/optimal results, due to the rounding errors, we do not obtain reliable results in the sense of interval analysis. For packing circles in a unit square, we find high precision guaranteed enclosures for both the global optimizer and the global optimum value and details of the interval arithmetic-based core elimination method in a series of publications by Markót and Csendes [19] and Markót [18].

2 Monolithic: non-convex (MI)NLP models

We describe ellipses by the coordinates of their center and an orientation angle to allow for their rotation. We need to model two types of constraints: (1) non-overlap of ellipses and (2) bounds placing the ellipses inside the rectangle.

While non-overlap of two circles can be enforced by one non-convex constraint, ensuring that their centers are apart no less than the sum of their radii, the case for ellipses is more involved (one reason is the possibility for rotation). We use the following key idea to ensure non-overlap: Because ellipses are convex objects, there must exist a hyperplane (i.e., a line) between any two pairs of ellipses, separating them from each other.

When the context allows, then we utilize a vector notation using the Euclidean norm scalar products to avoid the additional dimension index \(d\). The vector notation is indicated by bold symbols. We use lower case symbols for variables, and upper case symbols for input or derived data. The only exceptions are the semi-major and semi-minor axes \(a_i\) and \(b_i\), respectively, of the ellipses and the model indices.

Note that we provide lower and upper bounds in the model wherever possible and as tight as possible as these bounds help to solve the NLP and MINLP problems to global optimality.

We start with the modeling of the non-overlap and boundary constraints for ellipses in Sect. 2.1. This leads us to two equivalent NLP models, as summarized in Sect. 2.2. To enhance computational efficiency, we then present symmetry breaking constraints (Sect. 2.3), mixed-integer extensions (Sect. 2.4), and lower/upper bounding problems (Sect. 2.5).

2.1 Towards the NLP model formulations

The objective function minimizes the area, \(a\), of the design rectangle

$$\begin{aligned} \min \; a,\quad a=x_{1}^{\mathrm {R}} x_{2}^{\mathrm {R}}, \end{aligned}$$
(1)

where decision variable \(x_{d}^{\mathrm {R}}\) represents the extension of the design rectangle in dimension \(d;\, x_{1}^{\mathrm {R}}\) denotes the length and \(x_{2}^{\mathrm {R}}\) is the with of the rectangle.

Equivalently to (1), we could minimize waste, i.e.,

$$\begin{aligned} \min \; z,\quad z=a-\mathop {\displaystyle \sum }\limits _{i \in {\mathcal {I}}} A_{i}, \end{aligned}$$
(2)

where \(A_{i}\) denotes the area of ellipse \(i\); set \({\mathcal {I}}\) is the collection of ellipses to be packed.

The extensions \(x_{d}^{\mathrm {R}}\) of the rectangle are subject to pre-given bounds, \(S_{d}^{-}\) and \(S_{d}^{+}\)

$$\begin{aligned} S_{d}^{-}\le x_{d}^{\mathrm {R}}\le S_{d}^{+},\quad \forall d. \end{aligned}$$
(3)

The upper bound, \(S_{d}^{+}\), could be motivated by technical limitations; a lower bound, \(S_{d}^{+}\), is given by the maximum of all the minor ellipse axis lengths (maximum of \(2b_i\) over all \(i\)). Refinements of these bounds are described in Sect. 2.5, where we exploit circle cuttings.

2.1.1 Cutting circles

We start with the modeling of the circle cutting problem for two reasons: first, it was the starting point for our analysis of the ellipses cutting problem, and second, we use it to compute valid lower and upper bounds on the ellipse cutting problem (cf. Sect. 2.5).

The non-overlap constraints for circles \(i\) and \(j\) read

$$\begin{aligned} \big \Vert \mathbf{x}_{i}^0 -\mathbf{x}_{j}^0 \big \Vert _2 ^{2} := \sum \limits _{d=1}^2\left( x_{id}^0 - x_{jd}^0 \right) ^2 \ge \left( R_{i}+R_{j}\right) ^{2},\quad \forall \{ij:i<j\}, \end{aligned}$$
(4)

with radius \(R_i\) and (decision variable) \(x^0_{id}\) modeling the center of circle \(i\) in dimension \(d\). Constraints (4) are non-convex constraints (the left hand side constitutes a convex function). Note that for \(n\) circles we have \(n(n-1)/2\) inequalities of type (4).

Fitting the circles inside the enclosing rectangles requires

$$\begin{aligned} x_{id}^0 \ge R_{i}, \quad \forall \{id\} \quad \text {and} \quad x_{id}^0 + R_{i} \le x_{d}^{\mathrm {R}} ,\quad \forall \{id\}. \end{aligned}$$

2.1.2 Cutting ellipses

One might be tempted to follow the idea of the non-overlapping conditions (4) when treating ellipses. Unfortunately, the known radii \(R_i\) and \(R_j\) for the cases of circles become orientation-dependent variables. It turns out that this approach is not ideal, from the perspective of mathematical programming modeling. Thus, we follow a different idea.

Ellipse \(i\) is characterized by its semi-major and semi-minor axis \(a_{i}\) and \(b_{i}\), respectively. The ellipses \(i\) will be implicitly described by their centers, and their orientations; see Fig. 1.

Fig. 1
figure 1

Representation of ellipses \(i\): center \(\mathbf{x}_{i}^{0}\), semi-major axis \(a_i\), semi-minor axis \(b_i\), rotation angle \(\theta _i\) and extrema \(x_{i1}^{\mathrm {-}}, x_{i2}^{\mathrm {-}}, x_{i1}^{\mathrm {+}}\), and \(x_{i2}^{\mathrm {+}}\)

Full size image

The ellipses can be placed at a free “center” represented by the vector \(\mathbf{x}_{i}^{0}\) (with components \(x_{id}^{0}\)) with the semi-major axis \(a_{i}\) inclined by the angle \(\theta _{i}\). For \(\theta _{i}=0\), the ellipse is characterized by the equation

$$\begin{aligned} \frac{\left( x_1-x_{i1}^0\right) ^{2}}{a_i^{2}} + \frac{\left( x_2-x_{i2}^0\right) ^{2}}{b_i^{2}} = 1, \end{aligned}$$
(5)

i.e., all points \((x_1, x_2) \in {\mathbb {R}}^2\) satisfying constraint (5) lie on the perimeter of ellipse \(i\). For the rotated ellipse \(i\), we exploit the coordinate transformation

$$\begin{aligned} \left( \begin{array}{l} x_1^{\prime } \\ x_2^{\prime } \end{array} \right) = {\mathsf {R}}_{\theta i}\left( \begin{array}{l} x_1-x_{i1}^0 \\ x_2-x_{i2}^0 \end{array} \right) \quad \text {with} \quad {\mathsf {R}}_{\theta i}:=\left( \begin{array}{lc} \cos \theta _i \;\; &{} -\sin \theta _i \\ \sin \theta _i \;\; &{} \cos \theta _i \end{array} \right) \end{aligned}$$
(6)

or equivalently

$$\begin{aligned} x_1^{\prime }&= (\cos \theta _i )(x_1-x_{i1}^0)-(\sin \theta _i )(x_2-x_{i2}^0) \\ x_2^{\prime }&= (\sin \theta _i )(x_1-x_{i1}^0)+(\cos \theta _i )(x_2-x_{i2}^0). \end{aligned}$$

Now we can insert \(x_1^{\prime } \) and \(x_2^{\prime }\) into the ellipse equation (5).

More generally, an arbitrarily oriented ellipse \(i\), centered at \(\mathbf{x}_i^{0} \in {\mathbb {R}}^2\), is defined by the equation (quadratic form)

$$\begin{aligned} (\mathbf{x-x}_i^{0})^{\top } {\mathsf {A}}_i (\mathbf{x-x}_i^{0}) = 1 , \end{aligned}$$
(7)

where \({\mathsf {A}}_i\) is a positive definite matrix and \(\mathbf{x} \in {\mathbb {R}}^2\).

The eigenvectors of \({\mathsf {A}}_i\) define the principal directions of the ellipse (or, ellipsoid in 3-D) and the eigenvalues of \({\mathsf {A}}_i\) are the inverse squares of the semi-axes: \(a_i^{-2}\) and \(b_i^{-2}\). An invertible linear transformation applied to a circle (sphere) produces an ellipse (ellipsoid), which can be brought into the above standard form by a suitable rotation, a consequence of the polar decomposition (cf. Spectral Theorem). If the linear transformation is represented by a symmetric 2-by-2 (3-by-3) matrix, then the eigenvectors of the matrix are orthogonal (due to the Spectral Theorem) and represent the directions of the axes of the ellipse (ellipsoid): the lengths of the semi-axes are given by the eigenvalues. For ellipse \(i\) with semi-axes \(a_i\) and \(b_i\) rotated by \({\mathsf {R}}_{\theta i}\) as defined in (6), we have

$$\begin{aligned} {\mathsf {A}}_{\theta i} := {\mathsf {R}}_{\theta i}{\mathsf {D}}_i{\mathsf {R}}_{\theta i}^{\top } \quad \text {with} \quad {\mathsf {D}}_i := \left( \begin{array}{c@{\quad }c} \lambda _{i1} &{} 0 \\ 0 &{} \lambda _{i2} \end{array} \right) = \left( \begin{array}{c@{\quad }c} a_i^{-2} &{} 0 \\ 0 &{} b_i^{-2} \end{array} \right) . \end{aligned}$$

To avoid the occurrence of trigonometric terms in the optimization model, we use the following transformation into an equivalent (non-convex) quadratic model. We replace the decision variable \(\theta _i\) by the two decision variables

$$\begin{aligned} v_i := \cos \theta _i \quad \text {and} \quad w_i := \sin \theta _i. \end{aligned}$$

The new variables are subject to the bounds \(-1 \le v_i \le +1\) and \(-1 \le w_i \le +1\) and they are coupled by the Pythagorean Theorem

$$\begin{aligned} v_i^{2} + w_i^{2} = 1 . \end{aligned}$$
(8)

Note that for ellipses, due to their symmetry, it suffices to consider rotation angles, \(\theta _i\), in the range of \(\ 0^{\circ }\)–\(\ 180^{\circ }\), i.e., \(0 \le w_i \le 1\).

With this notation, we obtain

$$\begin{aligned} {\mathsf {A}}_{\theta i}&= \left( \begin{array}{cc} v_i \; &{} -w_i \\ w_i \; &{} v_i \end{array} \right) \left( \begin{array}{cc} \lambda _{i1} &{} 0 \\ 0 &{} \lambda _{i2} \end{array} \right) \left( \begin{array}{cc} v_i \;&{} w_i \\ -w_i \;&{} v_i \end{array} \right) =\left( \begin{array}{cc} v_i^{2}\lambda _{i1}+w_i^{2}\lambda _{i2} \;\; &{} v_iw_i\lambda _{i1}-v_iw_i\lambda _{i2} \\ v_iw_i\lambda _{i1}-v_iw_i\lambda _{i2} \;\; &{} v_i^{2}\lambda _{i2}+w_i^{2}\lambda _{i1} \end{array} \right) . \end{aligned}$$

Fitting the ellipses inside the enclosing design rectangle requires that

$$\begin{aligned} 0 \le x_{id}^{-} \le x_{id}^{\mathrm {+}} \le x_{d}^{\mathrm {R}}, \quad \forall \{id\}, \end{aligned}$$
(9)

where \(x_{id}^{-}\) and \(x_{id}^{\mathrm {+}}\) are the extreme extensions of ellipse \(i\) in dimension \(d\).

In Sect. 2.1.3, we show that

$$\begin{aligned} x_{i1}^{\pm }&= x_{i1}^0 \pm \sqrt{a_i^{2}\cos ^{2}\theta _{i}+b_i^{2}\sin ^{2}\theta _{i}} \quad \text {and} \quad x_{i2}^{\pm } = x_{i2}^0 \pm \sqrt{b_i^{2}\cos ^{2}\theta _{i}+a_i^{2}\sin ^{2}\theta _{i}}. \end{aligned}$$

For instance, \(\theta _i=0\) implies \(x_{i1}^\pm = x_{i1}^0 \pm a_i\) and \(x_{i2}^\pm = x_{i2}^0 \pm b_i\). Similarly, if the ellipses are circles (\(a_i = b_i = r_i\)), then for any angle \(\theta _i\) we obtain \(x_{i1}^\pm = x_{i2}^\pm = x_{i1}^0 \pm r_i\).

We continue with the derivation of these quantities in the following section; if you believe in the formulae above, then you can skip this section. The non-overlap conditions (discussed in Sect. 2.1.4) are then based on the ideas of extremal extensions of the ellipses.

2.1.3 Minimum and maximum extensions of ellipses

Let us compute \(x_{id}^{-}\) and \(x_{id}^{\mathrm {+}}\) for ellipse \(i\) with center \(x_{id}^0\) by solving the following optimization problems

$$\begin{aligned} x_{id}^{-} = \min \; \mathbf{c}^{\top } \mathbf{x} = \min \; x_{id} , \quad \forall d \quad \text {and} \quad x_{id}^{\mathrm {+}} = \max \; \mathbf{c}^{\top } \mathbf{x} = \max \; x_{id} , \quad \forall d , \end{aligned}$$

respectively, subject to the ellipse condition (7); for \(d=1\) we select \(\mathbf{c}^{\top }:= (1,0)\), while for \(d=2\) we have \(\mathbf{c}^{\top }:=(0,1)\). Instead of using (7), we can solve the simpler optimization problem

$$\begin{aligned} x_{id}^{-}&= \min \; \mathbf{c}^{\top }(\mathbf{x}+\mathbf{x}_{i}^0) = x_{id}^0 + \min \; x_{id},\quad \forall d \quad \text {and}\end{aligned}$$
(10)
$$\begin{aligned} x_{id}^{\mathrm {+}}&= \max \; \mathbf{c}^{\top }(\mathbf{x}+\mathbf{x}_{i}^0) = x_{id}^0 + \max \; x_{id},\quad \forall d , \end{aligned}$$
(11)

respectively, subject to

$$\begin{aligned} \mathbf{x}^{\top }{\mathsf {A}}_{\theta i}\mathbf{x}=1, \end{aligned}$$
(12)

which describes an ellipse centered at the origin. Note, however, that ellipse \(i\) cannot be centered at the origin, as the origin is identical to the left-bottom corner of the design rectangle.

The Lagrangian function of both optimization problems (10) and (11) reads

$$\begin{aligned} {\mathcal {L}}(\mathbf{x}, \bar{\lambda } )=\mathbf{c}^{\top }( \mathbf{x} + \mathbf{x}_i^0 ) + \bar{\lambda } \left( \mathbf{x}^{\top }{\mathsf {A}}_{\theta i}\mathbf{x} - 1 \right) \end{aligned}$$
(13)

for an (unrestricted) Lagrangian multiplier \(\bar{\lambda } \in {\mathbb {R}}\). The first order Karush–Kuhn–Tucker (KKT) conditions are derived as

$$\begin{aligned} \mathbf{c}+2\bar{\lambda } {\mathsf {A}}_{\theta i}^{\top }\mathbf{x} = \mathbf{0} \end{aligned}$$
(14)

together with (12). We multiply (14) by \(\mathbf{x}^{\top }\) from the left side, (this operation is safe, as the center of ellipse \(i\) cannot be an extremum) and exploit (12) to obtain \(x_{d} + 2\bar{\lambda } = 0\) for all \(d\). This allows us to eliminate the Lagrangian multiplier \(\bar{\lambda }\) from (14) yielding

$$\begin{aligned} \mathbf{c}-x_{d}{\mathsf {A}}_{\theta i}^{\top }\mathbf{x}=0 , \quad \forall d . \end{aligned}$$
(15)

For the first dimension (\(d=1\)) the two equations in (15) read

$$\begin{aligned} 1-x_{1}\left( A_{11}x_{1}+A_{21}x_{2}\right) =0 \quad \text {and} \quad x_{1}\left( A_{12}x_{1}+A_{22}x_{2}\right) =0 \end{aligned}$$

with

$$\begin{aligned} {\mathsf {A}}_{\theta i} = \left( \begin{array}{l@{\quad }l} A_{11} \;&{} A_{12} \\ A_{21} \;&{} A_{22} \end{array}\right) \!. \end{aligned}$$

As \(x_{1} \ne 0\) (the center cannot be a stationary point of these KKTs), we derive

$$\begin{aligned} x_{2} = -\frac{A_{12}}{A_{22}}x_{1} \end{aligned}$$
(16)

from which we further derive

$$\begin{aligned} x_{1}^{2}=\left( A_{11}-A_{21}\frac{A_{12}}{A_{22}}\right) ^{-1}=\frac{A_{22}}{\lambda _{i1}\lambda _{i2}}=A_{22}a_i^{2}b_i^{2}, \end{aligned}$$
(17)

where we exploit the fact that \(\det {\mathsf {A}}_{\theta i} = A_{11}A_{22} - A_{12}A_{21} = \lambda _{i1}\lambda _{i2} > 0\) (cf. Eigenvector Decomposition). From the geometry of the optimization problems (10) and (11), we know that each problem has a unique, global extremum. We further know that the global extrema satisfy the KKT conditions (12) and (14) (i.e., they are necessary). Because we have not excluded any global optima in our deviation to derive at (16) and (17) and they lead to exactly two points, we know that \(x_1\) and \(x_2\) in (16) and (17) define the global optimum for (11) and (10); one just needs to pick the correct one.

The minimum and maximum extensions of ellipse \(i\) in the first dimension, \((d=1)\), then reduce to

$$\begin{aligned} x_{i1}^{-}&= \min \; \mathbf{c}^{\top }(\mathbf{x}+\mathbf{x}_i^0) = x_{i1}^0 - \sqrt{x_{1}^{2}} = x_{i1}^0 - a_ib_i \sqrt{A_{22}} \nonumber \\&= x_{i1}^0 - \sqrt{a_i^{2}\cos ^{2}\theta _{i}+b_i^{2}\sin ^{2}\theta _{i}}\quad \end{aligned}$$
(18)

and

$$\begin{aligned} x_{i1}^{\mathrm {+}} =x_{i1}^0 + \sqrt{a_i^{2}\cos ^{2}\theta _{i}+b_i^{2}\sin ^{2}\theta _{i}},\quad \end{aligned}$$
(19)

respectively.

Similarly, for \(d=2\) we derive

$$\begin{aligned} -x_{2}\left( A_{11}x_{1}+A_{21}x_{2}\right) =0 \quad \text {and} \quad 1-x_{2}\left( A_{12}x_{1}+A_{22}x_{2}\right) =0 \end{aligned}$$

to obtain

$$\begin{aligned} x_{2}^{2}=\left( A_{22}-A_{12}\frac{A_{21}}{A_{11}}\right) ^{-1}=\frac{A_{11} }{\lambda _{i1}\lambda _{i2}}=A_{11}a_i^{2}b_i^{2}. \end{aligned}$$

This leads to

$$\begin{aligned} x_{i2}^{-}&= x_{i2}^0 - \sqrt{b_i^{2}\cos ^{2}\theta _{i}+a_i^{2}\sin ^{2}\theta _{i}}\quad \text {and} \quad \end{aligned}$$
(20)
$$\begin{aligned} x_{i2}^{\mathrm {+}}&= x_{i2}^0 + \sqrt{b_i^{2}\cos ^{2}\theta _{i}+a_i^{2}\sin ^{2}\theta _{i}}. \end{aligned}$$
(21)

2.1.4 Non-overlap condition for ellipses

One might have the following idea to model the non-overlap constraints for pairs of ellipses: We could enter a few points \(\mathbf{x}_{j}\) on the circumference of ellipse \(j\) into the equation defining ellipse \(i\). We would then ask that

$$\begin{aligned} (\mathbf{x}_{j}\mathbf{-x}_{i}^0)^{\top }{\mathsf {A}}_{\theta i}(\mathbf{x} _{j}\mathbf{-x}_{i}^0)\ge 1; \end{aligned}$$
(22)

the “\(\ge \)” forces the circumferences of ellipse \(j\) not to enter ellipse \(i\). However, to ensure non-overlap of the two ellipses \(i\) and \(j\) in this way, we would need to ensure that the (non-convex) constraints (22) hold for a continuum of points (not just a few), leading to a semi-infinite programming problem. One could resort to similar ideas of Rebennack and Kallrath [22, 23] or consult one of the various surveys about semi-infinite programming, for instance, by Hettich and Kortanek [9] or Lopez and Still [16]. We take a different route.

In Sect. 2.1.3, we derive the formulae to compute \(x_{id}^{-}\), the minimum value the ellipse extends to in coordinate axis direction \(d\). This computation can be extended by the following idea. Assume we are given a rotated ellipse \(i\) whose semi-major axis \(a_i\) has an angle \(\theta _i\) with the \(x\)-axis (the length of the rectangle). Furthermore, we have a separating line (or, hyperplane) parameterized by

$$\begin{aligned} \mathbf{G}(t) := \mathbf{g}^{0} + \mathbf{g} \cdot t, \quad t \in {\mathbb {R}} \end{aligned}$$
(23)

with footpoint \(\mathbf{g}^{0}\), and direction \(\mathbf{g}\) normalized to \(\left| \mathbf{g}\right| =1\). The footpoint \(\mathbf{g}^{0}\) is not uniquely defined, because it can lie anywhere on the separating hyperplane. As such, \(\mathbf{g}^0\) has two degrees of freedom. We eliminate one degree of freedom by requesting that that the footpoint lies on the intersection of the hyperplane and the line segment between the centers \(\mathbf{x}_i^{0}\) and \(\mathbf{x}_j^{0}\) of ellipses \(i\) and \(j\). Therefore, we introduce the non-negative variable \(\lambda , 0 \le \lambda _{ij} \le 1\), and represent the footpoint as the linear combination

$$\begin{aligned} \mathbf{g}^{0} = \lambda _{ij}\mathbf{x}_i^{0} + (1-\lambda _{ij})\mathbf{x}_j^{0} \end{aligned}$$
(24)

of the ellipse centers \(\mathbf{x}_i^{0}\) and \(\mathbf{x}_i^{0}\). With three decision variables (two for \(\mathbf{g}^{0}\) and one for \(\lambda _{ij}\)) and two constraints, we are left with one degree of freedom.

Can we provide a necessary condition for the ellipse being completely above \(\mathbf{G}(t)\), or just touching it? We can: \(\mathbf{G}(t)\) has an inclination angle \( \omega \) as derived from a scalar product of the unit vector \((1,0)^\top \) and \(\mathbf{g}\) as

$$\begin{aligned} \cos \omega :=(1,0) \cdot \mathbf{g} = g_{1} \end{aligned}$$
(25)

with the \(x_1\)-axis, and intersects with the \(x_1\)-axis at \(x_{h}\). Note that this intersection point only exists and necessary in our considerations, if \(\mathbf{g}\) is not parallel to the \(x_1\)-axis. The special parallel case does not depend on the coordinate transformation described below and allows us to compute the distance of the ellipse to the hyperplane directly. Note that for the moment we consider a generic hyperplane \(\mathbf{G}(t)\). Later, for separating two ellipses \(i\) and \(j, \mathbf{G}(t)\), and also \(\omega \), will become dependent on \(i\) and \(j\).

For ellipse \(i\) and hyperplane \(\mathbf{G}(t)\), we resort again to a coordinate transformation: We transform the coordinate system in such a way that (1) \((x_{h},0)\) becomes the origin of the new coordinate system and (2) \(\mathbf{G}(t)\) becomes identical to the new \(x\)-axis. If we then represent the ellipse in the new coordinate system (translation and rotation), we can apply the formulae of Sect. 2.1.3 to compute the minimum extension of ellipse \(i\) in dimension \(d=2\) in the new coordinate system: \(x_{i2}^{-\prime }\). Now, if \(x_{i2}^{-\prime }\ge 0\), ellipse \(i\) lies above the hyperplane; \( x_{i2}^{-\prime }\ge 0\) is also the necessary and sufficient condition for ellipse \(i\) to be above the hyperplane (or, just touching it).

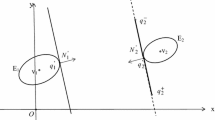
Before we algebraically derive the coordinate transformation and the non-overlap conditions for each pair of ellipses, we built some intuition with Fig. 2. Using geometry, \(d_{ij}^{ab}\) is the length of the projection of the vector \((\mathbf x _{i}^0 - \mathbf g _{ij}^0 )\) on the vector \((-g_{ij2},g_{ij1})\). Since \((-g_{ij2},g_{ij1})\) has unit length, the length of the projection is simply the inner product

$$\begin{aligned} d_{ij}^{ab} = -g_{ij2}\left( x_{i1}^0 - g_{ij1}^0\right) + g_{ij1} \left( x_{i2}^0 - g_{ij2}^0\right) . \end{aligned}$$

On the other hand, the length \(\delta _{ij}^{ab}\) is the maximum vertical extension of ellipse \(i\) if we consider the hyperplane as the horizontal axis. Now—relative to the hyperplane—the angle of the ellipse is \(\theta _i - \omega _{ij}\). So using Eq. (20), we obtain

$$\begin{aligned} \delta _{ij}^{ab} = \sqrt{b_i^2 \cos ^2(\theta _i - \omega _{ij}) +a_i^2 \sin ^2(\theta _i - \omega _{ij})}. \end{aligned}$$

For ellipse \(i\) to be “above” the hyperplane, we require \((d_{ij}^{ab})^2 \ge (\delta _{ij}^{ab})^2\).

Fig. 2
figure 2

Non-overlap of ellipses \(i\) and \(j\) via separating line. Notation ellipses: \(a_i,a_j\) semi-major axis; \(b_i,b_j\) semi-minor axis; \(\theta _i, \theta _j\) orientation angle; \(\mathbf{x}_{i}^{0}, \mathbf{x}_{j}^{0}\) center ; \(\delta _{ij}^\mathrm{ab}\) maximal vertical extension of ellipse \(i\) to the hyperplane; \(\delta _{ij}^{\mathrm{be}}\) maximal vertical extension of ellipse \(j\) to the hyperplane. Notation separating line: \(\mathbf{g}_{ij}^0\) footpoint; \(\omega _{ij}\) inclination angle; \((g_{ij1},g_{ij2})\) direction vector; \(d_{ij}^{\mathrm{ab}}, d_{ij}^{\mathrm{be}}\) distance to line

Full size image

Similarly, \(d_{ij}^{be}\) is the projection of the vector \((\mathbf x _{j}^0 - \mathbf g _{ij}^0 )\) on the vector \((-g_{ij2},g_{ij1})\); because \(\mathbf x _{j}^0\) is on the opposite side of the hyperplane—in the minus \((-g_{ij2},g_{ij1})\) direction—the inner product is negative. Moreover, from Fig. 2, it is clear that the absolute value of \(d_{ij}^{ab}\) and \(d_{ij}^{be}\) must be at least \(b_i\).

Using the trigonometric identities for the cosine of the differences of angles, we can further derive

$$\begin{aligned} \cos (\theta _i - \omega _{ij})&= \cos (\theta _i)\cos (\omega _{ij}) + \sin (\theta _i)\sin (\omega _{ij}) =g_{ij1} \cos (\theta _i) + g_{ij2} \sin (\theta _i) , \end{aligned}$$

which establishes the connection of the rotation angle \(\theta _i\) of ellipse \(i\) and the inclination angle \(\omega _{ij}\) of the hyperplane.

Now, let us derive the above equations algebraically. To establish the coordinate transformation for ellipse \(i\) and hyperplane \(\mathbf{G}(t)\), let \(t_{0}\) denote the value of \(t\), for which we obtain \(G_{2}(t)=0\), i.e., the separating line intersects with the original \(x\)-axis. In the new, shifted and rotated coordinate system the center of the ellipse \(i\) is given by

$$\begin{aligned} \mathbf{v}_{i}^0 := \left( \begin{array}{c} x_{i1}^0 - G_{1}(t^{0}) \\ d_i^{0} \end{array} \right) , \end{aligned}$$

where \(d_i\) is the distance of the ellipse center to \(\mathbf{G}(t)\), i.e.,

$$\begin{aligned} d_i := \frac{(-g_{2},g_{1})\cdot (\mathbf{x}_{i}^0 - \mathbf{g}^0)}{ \left| \mathbf{g}\right| } = \left( -g_{2},g_{1}\right) \cdot \left( \mathbf{x}_{i}^0 - \mathbf{g}^0\right) , \end{aligned}$$
(26)

where we constructed the vector \((-g_{2},g_{1})^{\top }\) orthogonal to \( \mathbf{g}\). The ellipse, in the new coordinate system, can be generated by

$$\begin{aligned} \mathbf{v}_i(\varphi _i) = \mathbf{v}_i^{0} + {\mathsf {R}}_{\theta - \omega ,i}\left( \begin{array}{l} a_i \cos \varphi _i \\ b_i \sin \varphi _i \end{array} \right) ,\quad 0 \le \varphi _i \le 2\pi . \end{aligned}$$

It fulfills the constraint

$$\begin{aligned} (\mathbf{v-v}_i^{0})^{\top } {\mathsf {E}}_{\theta -\omega ,i} (\mathbf{v-v}_{i}^0) = 1 \quad \text {with} \quad {\mathsf {E}}_{\theta -\omega ,i} := {\mathsf {A}}_{\theta -\omega ,i} = {\mathsf {R}}_{\theta -\omega ,i}{\mathsf {D}}_i\mathsf {R}_{\theta -\omega ,i }^{ \top }. \end{aligned}$$

The angle \(\theta _i - \omega \) for ellipse \(i\) satisfies the relation

$$\begin{aligned} \cos (\theta _i -\omega )=(\cos \theta _i ,\sin \theta _i ) \cdot \mathbf{g}, \end{aligned}$$
(27)

and is the angle between the semi-major axis and the separating line.

With formula (20), we obtain

$$\begin{aligned}&v_{i2}^{-} = v_{i2}^0 - \sqrt{v_{2}^{2}} \quad \text {with} \quad v_{2}^{2} = \left( E_{22}-E_{12}\frac{E_{21}}{E_{11}}\right) ^{-1} = \frac{E_{11}}{\lambda _{i1}\lambda _{i2}} = E_{11} a_i^{2} b_i^{2}, \\&\quad \text {or} \quad v_{i2}^{-} = v_{i2}^0 - a_i b_i \sqrt{E_{11}} = v_{i2}^0 - a_ib_i \sqrt{\cos ^{2}(\theta _i - \omega )\lambda _{i1}+\sin ^{2}(\theta _i -\omega )\lambda _{i2}}. \end{aligned}$$

The transformation (translation and rotation) leads, eventually, to the final constraint that ellipse \(i\) is “above” the hyperplane

$$\begin{aligned} v_{i2}^0 - a_{i}b_{i} \sqrt{\cos ^{2}(\theta _{i}-\omega )\lambda _{i1}+\sin ^{2}(\theta _{i}-\omega )\lambda _{i2}} \; \ge 0, \end{aligned}$$

or equivalently

$$\begin{aligned}&\left( v_{i2}^{0}\right) ^2 - \left[ b_{i}^{2}\cos ^{2}(\theta _{i}-\omega )+a_{i}^{2}\sin ^{2}(\theta _{i}-\omega )\right] \ge 0\quad \wedge \quad v_{i2}^0 \ge 0. \end{aligned}$$
(28)

Similarly, \(v_{i2}^0 + a_{i}b_{i} \sqrt{\cos ^{2}(\theta _{i} - \omega )\lambda _{i1} + \sin ^{2}(\theta _{i}-\omega )\lambda _{i2}} \; \le 0,\)

$$\begin{aligned}&\text {or} \quad \left( v_{i2}^{0}\right) ^2 - \left[ b_{i}^{2}\cos ^{2}(\theta _{i}-\omega )+a_{i}^{2}\sin ^{2}(\theta _{i}-\omega )\right] \ge 0\quad \wedge \quad v_{i2}^0 \le 0. \end{aligned}$$
(29)

enforce ellipse \(i\) to stay “below” the separating line.

Finally, we are able to put everything together to state the non-overlap conditions for a pair of ellipses \(i\) and \(j\). For each such pair, we require one separating line of type (23) and force ellipse \(i\) to stay above (recall, that touching is fine) that line via (28) and force ellipse \(j\) to stay below that line via (29). Recall that the decision variables (i.e., \(d_i, \omega , \mathbf{g}\) and \(\mathbf{g}^0\)) related to the separating line carry now the double index \(ij\). Especially, \(d_{i}\) becomes \(d_{ij}^{\mathrm {ab}}\), measuring the distance of ellipse \(i\) above the separating line, and \(-d_{ij}^{\mathrm {be}}\), measuring the distance of ellipse \(j\) below the separating line. We generate only hyperplanes for \(i<j\). This is illustrated in Fig. 2.

The case that ellipse \(j\) lies above ellipse \(i\) is covered by the reflected direction vector \(-\mathbf{g}\). As we do not restrict \(\mathbf{g}\), or its components, in sign, the direction is selected automatically when solving the problem. Thus, it is also automatically decided which ellipse lies above and which under the hyperplane.

The distances \(d_{ij}^{\mathrm {ab}}\) and \(-d_{ij}^{\mathrm {be}}\) of the centers of ellipse \(i\) and \(j\) to the hyperplane, indexed by \(ij\), separating the ellipses \(i\) and \(j\) are bounded by

$$\begin{aligned} b_i \le d_{ij}^{\mathrm {ab}} \le \overline{D}_{ij},\quad -\overline{D}_{ij} \le d_{ij}^{\mathrm {be}} \le -b_i,\quad \forall \{ij:i<j\} \end{aligned}$$
(30)

as follows from the geometry, for instance,

$$\begin{aligned} \overline{D}_{ij} = \tfrac{\sqrt{(S_{1}^{+})^2 + (S_{2}^{+})^2} - b_i - b_j}{2}, \quad \hbox {for all}\, \{ij:i<j\}. \end{aligned}$$

The model is completed by

$$\begin{aligned} 0 \le v_{i2}^0 = d_{ij}^{\mathrm {ab}} \quad \text {and}\quad 0 \ge v_{j2}^0 = d_{ij}^{\mathrm {be}},\quad \forall \{ij:i<j\} \end{aligned}$$
(31)

for each ellipse \(i\) and \(j\), and the computation of \(\omega _{ij}\) according to (25).

Let us conclude this section with a structural comment which illuminates the non-overlap constraints from a geometrical point of view and connects the non-overlap constraints to the non-convex character of the problem. The non-overlap constraints lead to a geometrical situation with a non-convex domain: Imagine the rectangle, from which to cut the \(n\) ellipses, and assume that ellipse \(i\) is fixed. The feasible area of the center coordinate of another ellipse \(j \ne i\) is a subset of the rectangle without the region covered by ellipse \(i\).

Similar to the case for circles, for \(n\) ellipses we have \(n(n-1)/2\) inequalities of type (28) and (29), each. However, there are the additional constraints to model the separating lines. We analyze the number of variables and constraints involved in the non-overlap constraints for ellipses in the following section.

2.2 The NLP formulations

Finally, we are able to state the resulting non-convex NLP formulations. However, before we start with the mathematical programming problem involving trigonometric terms, we define, for notational ease,

$$\begin{aligned} S_{id1} := \left\{ \begin{array}{ll} a_{i}^{2}\text {,} &{}\quad d=1 \\ b_{i}^{2}\text {,} &{}\quad d=2 \end{array} \right. \quad \; \text {and}\quad \; S_{id2} := \left\{ \begin{array}{ll} b_{i}^{2}\text {,} &{}\quad d=1 \\ a_{i}^{2}\text {,} &{}\quad d=2 \end{array} \right. ,\quad \forall \{id\}. \end{aligned}$$
(32)

The ellipse cutting problem (EP) is then summarized as follows

$$\begin{aligned} (\text {EP}_{\theta }): a^{*} = \min \; \prod \limits _{d=1}^{2}x_{d}^{\mathrm {R}}&\end{aligned}$$
(33)

subject to

(fit ellipses \(i\) into rectangle)

$$\begin{aligned}&S_{id1} \cos ^{2}\theta _{i} + S_{id2}\sin ^{2}\theta _{i} \le \left( x_{id}^0 \right) ^{2} \quad&\forall \{id\} \quad \end{aligned}$$
(34)
$$\begin{aligned}&S_{id1} \cos ^{2}\theta _{i} + S_{id2}\sin ^{2}\theta _{i} \le \left( x_{d}^{R}-x_{id}^0 \right) ^{2} \quad&\forall \{id\} \quad \end{aligned}$$
(35)
$$\begin{aligned}&x_{id}^0 \le x_{d}^{R} - b_{i} \quad&\forall \{id\} \quad \end{aligned}$$
(36)

(non-overlap of ellipses \(i\) and \(j\))

$$\begin{aligned}&\sum \limits _{d=1}^2 \big (g_{ijd}\big )^{2} =1\quad&\forall \{ij:i<j\} \quad \end{aligned}$$
(37)
$$\begin{aligned}&g_{ijd}^{0} = \lambda _{ij}x_{i d}^0 + (1-\lambda _{ij})x_{j d}^0 \quad&\forall \{ijd:i<j\}\quad \end{aligned}$$
(38)
$$\begin{aligned}&d_{ij}^\mathrm{ab} = -g_{ij2} \left( x_{i 1}^0-g_{ij1}^0\right) + g_{ij1}\left( x_{i 2}^0-g_{ij2}^0\right) \quad&\forall \{ij:i<j\} \quad \end{aligned}$$
(39)
$$\begin{aligned}&d_{ij}^\mathrm{be} = -g_{ij2} \left( x_{j 1}^0-g_{ij1}^0\right) + g_{ij1}\left( x_{j 2}^0-g_{ij2}^0\right) \quad&\forall \{ij:i<j\} \quad \end{aligned}$$
(40)
$$\begin{aligned}&\cos (\theta _{i}-\omega _{ij}) = g_{ij1}\cos \theta _{i} + g_{ij2} \sin \theta _{i} \quad&\forall \{ij:i<j\} \quad \end{aligned}$$
(41)
$$\begin{aligned}&\cos (\theta _{j}-\omega _{ij}) = g_{ij1}\cos \theta _{j} + g_{ij2} \sin \theta _{j} \quad&\forall \{ij:i<j\} \quad \end{aligned}$$
(42)
$$\begin{aligned}&\left( d_{ij}^\mathrm{ab}\right) ^2\ge b_{i}^{2}\cos ^2(\theta _{i}-\omega _{ij})+a_{i}^{2}\sin ^2(\theta _{i}-\omega _{ij})\quad&\forall \{ij:i<j\}\quad \end{aligned}$$
(43)
$$\begin{aligned}&\left( d_{ij}^\mathrm{be}\right) ^2\ge b_{j}^{2}\cos ^2(\theta _{j}-\omega _{ij})+a_{j}^{2}\sin ^2(\theta _{j}-\omega _{ij})\quad&\forall \{ij:i<j\}\quad \end{aligned}$$
(44)

(variable domain)

$$\begin{aligned} S_{d}^{-}&\le x_{d}^{\mathrm {R}}\;\,\le S_{d}^{+}&\forall d \quad \end{aligned}$$
(45)
$$\begin{aligned} b_i&\le x_{id}^0 \;\,\!\le S_{d}^{+} - b_i&\forall \{id\} \quad \end{aligned}$$
(46)
$$\begin{aligned} 0&\le \theta _{i} \;\;\,\le \pi&\forall i \quad \end{aligned}$$
(47)
$$\begin{aligned} 0&\le \lambda _{ij} \;\le 1&\forall \{ij:i<j\}\quad \end{aligned}$$
(48)
$$\begin{aligned} 0&\le g_{ijd}^0 \le S_{d}^{+}&\forall \{ijd:i<j\}\quad \end{aligned}$$
(49)
$$\begin{aligned} -1&\le g_{ijd} \le 1&\forall \{ijd:i<j\}\quad \end{aligned}$$
(50)
$$\begin{aligned} 0&\le \omega _{ij} \;\le 2\pi&\forall \{ij:i<j\} \quad \end{aligned}$$
(51)
$$\begin{aligned} b_i&\le d_{ij}^{ab} \,\,\!\le \overline{D}_{ij}&\forall \{ij:i<j\}\quad \end{aligned}$$
(52)
$$\begin{aligned} -\overline{D}_{ij} Z&\le d_{ij}^\mathrm{be} \,\,\!\le -b_i&\forall \{ij:i<j\}.\quad \end{aligned}$$
(53)

We start with the description of the decision variables involved in (EP\(_\theta \)). We have two variables for the design rectangle: its length and with, \(x_{d}^{\mathrm {R}}\). Each ellipse is modeled by three decision variables: the two center coordinates, \(x_{id}^0\), and the rotation angle, \(\theta _{i}\). For each pair of ellipses \(i\) and \(j\) with \(i<j\), we have one hyperplane \(ij\), modeled by five decision variables: the two footpoint coordinates, \(g_{ijd}^0\), the linear combination variable \(\lambda _{ij}\) and the two dimensional slope, \(g_{ijd}\). The coordinate transformation for ellipse \(i\) with respect to hyperplane \(ij\) requires the angles \(\omega _{ij}\). Finally, the distance of the two ellipses \(i\) and \(j\), in the new coordinate transform, involve the two decision variables \(d_{ij}^{\mathrm{ab}}\) and \(d_{ij}^{\mathrm{be}}\). Thus, for each pair of ellipses there are eight decision variables involved with the modeling of the non-overlap condition for ellipses.

We minimize with (33) the area of the design rectangle, i.e., objective function (1).

The first group of constraints, (34)–(36), enforces that all ellipses stay inside the design rectangle. Constraints (34) ensure that the minimum extension of each ellipse is non-negative; using constraints (9), (18), and (20). Similarly, constraints (35) and (36) ensure that the maximum extension of each ellipse is inside the rectangle; using constraints (9), (19), and (21).

The second group, (37)–(44), models the non-overlap of each pair of ellipses \(i\) and \(j\). Constraints (37) normalize the slope of the hyperplane \(ij\); constraints (38) place the footpoint of the hyperplane on the line segment of the two center coordinates of the corresponding ellipses; i.e., (24). The distance of the two ellipses \(i\) and \(j\) to their corresponding hyperplane \(ij\) is computed via (39) and (40); i.e., (26). The angle for the coordinate transformation with respect to the hyperplanes is given by (41) and (42); i.e., (27). Finally, the non-overlap of the two ellipses is given via (43) and (44); i.e., (28) and (29), respectively.

With the discussion above, for \(n \ge 2\) ellipses, (EP\(_\theta \)) involves \(2 - \frac{1}{2}n + \frac{7}{2}n^2\) continuous decision variables and \(\frac{3}{2} n + \frac{9}{2} n^2\) functional constraints, not counting the box constraints (45)–(53).

We formulated the ellipse cutting problem as the NLP problem (EP\(_\theta \)), with the non-convex objective function (33) and the non-convex constraints (34), (35), (37), (39)–(44), leading to a non-convex feasible region.

In Sect. 2.1.3, we indicate how to transform (EP\(_\theta \)) into an equivalent (and, thus, non-convex) quadratic model. Here it is:

$$\begin{aligned} (EP_\mathrm{QP}): a^* = \min \;&\prod \limits _{d=1}^{2}x_{d}^{\mathrm {R}}\nonumber \\ s.t. \;\;&(37), (38) {\hbox {--}} (41)\nonumber \\&v_i^{2} + w_i^{2} = 1&\forall i \quad \nonumber \\&S_{id1} v_i^{2} + S_{id2}\big ( 1- v_i^2 \big ) \le \left( x_{id}^0 \right) ^{2}&\forall \{id\} \quad \nonumber \\&S_{id1} v_i^{2} + S_{id2}\big ( 1- v_i^2 \big ) \le \left( x_{d}^{R}-x_{id}^0 \right) ^{2}&\forall \{id\} \quad \nonumber \\&p_{ij}^\mathrm{ab} = g_{ij1}v_i + g_{ij2} w_i \quad&\forall \{ij:i<j\} \quad \nonumber \\&p_{ij}^\mathrm{be} = g_{ij1}v_j + g_{ij2} w_j \quad&\forall \{ij:i<j\} \quad \nonumber \\&\left( d_{ij}^\mathrm{ab}\right) ^2\ge b_{i}^{2} \left( p_{ij}^\mathrm{ab}\right) ^2 + a_{i}^{2}\Big ( 1 - \left( p_{ij}^\mathrm{ab}\right) ^2 \Big )\quad&\forall \{ij:i<j\}\quad \nonumber \\&\left( d_{ij}^\mathrm{be}\right) ^2\le b_{j}^{2} \left( p_{ij}^\mathrm{be}\right) ^2 + a_{j}^{2}\Big ( 1 - \left( p_{ij}^\mathrm{be}\right) ^2 \Big )\quad&\forall \{ij:i<j\}\quad \nonumber \\&(46), (47), (50), (51), (53), (54)\nonumber \\&-1 \le v_i \le 1 \quad&\forall i \nonumber \\&0 \le w_i \le 1 \quad&\forall i \nonumber \\&-1 \le p_{ij}^\mathrm{ab},p_{ij}^\mathrm{be} \le 1&\forall \{ij:i<j\} \end{aligned}$$

We have re-formulated (EP\(_\theta \)) as a quadratic optimization problem in form of (EP\(_{\mathrm{QP}}\)) in order to utilize algorithms, specializing in bilinear and quadratic terms, which might be superior to general purpose algorithms and software packages.

The review by Floudas et al. [7] and the paper by Misener and Floudas [21] are good resources for further references and a description of various approaches to solve problems of the type of (EP\(_{\mathrm{QP}}\)); we avoid repeating the material here but list a few of the relevant references among them Androulakis et al. [3], Maranas and Floudas [17], Adjiman et al. [1, 2]. Algebraic reformulations and convex relaxation techniques as described in Liberti [13], and Liberti and Pantelides [14] are part of the global mixed-integer quadratic optimizer GloMIQO by Misener and Floudas [21].

In the remainder of the paper, we refer to the ellipse cutting problem as (EP) and mean either formulation (EP\(_\theta \)) or (EP\(_{\mathrm{QP}}\)); any discussion on (EP) applies for both formulations equally.

Next, we enhance (EP) by symmetry breaking constraints (Sect. 2.3) and extensions using binary decision variables (Sect. 2.4).

2.3 Symmetry breaking

The occurrence of symmetry in (any) mathematical programming problem can pose major challenges for global solvers for closing the optimality gap (this is also true for MILP solvers). Often, two symmetric solutions are “physically” identical (e.g., when cutting identical objects) or can be mapped to each other via a point or axis reflection. Thus, breaking symmetry does not exclude interesting optimal solutions but may help to solve the problem instance at hand faster (or even at all). In the following, we address three such symmetries for our ellipse cutting problem and how to break them.

Given any optimal (ellipse) cutting and the corresponding rectangle, we can obtain several alternative optimal solutions by horizontal and vertical reflections; the solver views them as different solutions. We break this symmetry by requesting that the center of one of the ellipses is placed into the first quadrant of the design rectangle. Let \(\iota \) be the index of that ellipse. Then, the symmetry breaking inequalities read \(x_{\iota d}^0 \le \frac{1}{2} x_{d}^{\mathrm {R}}\) for all \(d\).

If congruent (i.e., identical) ellipses are to be packed, then we break the resulting symmetry by sorting their center points with respect to the lower left corner of the rectangle. We collect all pairs \((i,j)\) of congruent ellipses in the set \({\mathcal {I}}^{\mathrm {co}}\) (we assume ordered pairs \(i < j\)) and apply the ordering inequalities

$$\begin{aligned} x_{i1}^0 + 5x_{i2}^0 \le x_{j1}^0 + 5x_{j2}^0 , \quad \forall (i,j) \in {\mathcal {I}}^{\mathrm {co}} . \end{aligned}$$
(54)

Constraints (54) can be strengthened via lexicographic sorting involving mixed-integer programming techniques (cf. Sect. 2.4).

Rather a matter of degeneracy than of symmetry are free ellipses, i.e., ellipses which can be moved locally without changing the objective function value (the area of the rectangle). In a cutting problem, free objects cause mainly degeneracy, however, in a packing problem, this poses major difficulties as they can freely “flow” around. We avoid free ellipses by adding a soft penalty term which moves the center coordinate towards the lower left corner of the rectangle.

2.4 MINLP extensions

The NLP models presented in Sect. 2.2 contain a combinatorial component: The ellipses can be placed in any order to each other. Actually, for \(n\) ellipses, there are \(n!\) many such orderings. This combinatorial nature is one of the reasons why the ellipse cutting problem turns out to be so computationally challenging to solve. We enhance the visibility of this combinatorial structure to the solvers via the following extension of the NLP models developed so far.

We partition the rectangle into a uniform grid of small rectangles. The size of the small rectangles depends on the problem instance and is governed by the “smallest” ellipses. It is chosen such that the center of each ellipse \(i\) can be uniquely assigned to one of these small rectangles. We denote by \((c_x,c_y)\) one such small rectangle (“cell”) and collect all cells in the set \({\mathcal {I}}^{\mathrm {ce}}\). We control the assignment of ellipses to cells by the binary variables \(\delta _{i c_x c_y}\). The following set of constraints assigns each ellipse to exactly one cell

$$\begin{aligned} \sum _{(c_x,c_y) \in {\mathcal {I}}^{\mathrm {ce}}} \delta _{i c_x c_y} = 1,\quad \forall i. \end{aligned}$$
(55)

The centers of the ellipses are then subject to the constraints

$$\begin{aligned} x_{id}^0&\ge C_{c_x c_y d}^- - S_d^+ ( 1 - \delta _{i c_x c_y} ) ,\quad \forall \left\{ \; i,d, (c_x,c_y) \in {\mathcal {I}}^{\mathrm {ce}} \; \right\} ,\end{aligned}$$
(56)
$$\begin{aligned} x_{id}^0&\le C_{c_x c_y d}^+ + S_d^+ ( 1 - \delta _{i c_x c_y} ),\quad \forall \left\{ \; i,d, (c_x,c_y) \in {\mathcal {I}}^{\mathrm {ce}} \; \right\} , \end{aligned}$$
(57)

where \(C_{c_x c_y d}^-\) and \(C_{c_x c_y d}^+\) are the lower and upper boundary coordinate of cell \((c_x, c_y)\), respectively. If \(\delta _{i c_x c_y} = 0\), then both constraints (56) and (57) (for each dimension) are dominated by the boundary conditions (9). However, \(\delta _{i c_x c_y} = 1\) forces the center of ellipse \(i\) not to be outside of cell \((c_x, c_y)\).

The ellipse cutting problem is now formulated via a MINLP problem. On paper, this MINLP looks even more difficult to solve than the NLP formulations. We might be surprised in Sect. 4.

The MINLP framework, and the presence of binary variables \(\delta _{i c_x c_y}\), allows us to develop an enhancement for the symmetry breaking constraints (54) for identical ellipses (cf. Sect. 2.3).

Let \(i\) and \(j\) be the indices of two identical ellipses with the indices ordered as \(i<j\), i.e., \((i,j) \in {\mathcal {I}}^{\mathrm {co}}\). We use a lexicographic ordering in the following sense: \(j\) is placed in a cell right of ellipse \(i\), or it is in the same column of cells and above ellipse \(i\) (or the same). This condition is modeled as

$$\begin{aligned} \nonumber \delta _{ic_{x}c_{y}}&\le \sum _{c_{x}^{\prime }: \; C_{ c_x^{\prime } c_y 1}>C_{ c_x c_y 1} } \;\; \sum _{c_{y}^{\prime }: \; (c_{x}^{\prime },c_{y}^{\prime }) \in {\mathcal {I}}^{\mathrm {ce}}}\delta _{jc_{x}^{\prime }c_{y}^{\prime }} \nonumber \\&+ \sum _{c_{y}^{\prime }: \; C_{ c_x c_y^{\prime } 2}>C_{ c_x c_y 2}}\delta _{jc_{x}c_{y}^{\prime }},\quad \forall \left\{ \; (i,j) \in {\mathcal {I}}^{\mathrm {co}}, (c_{x},c_{y}) \in {\mathcal {I}}^{\mathrm {ce}} \; \right\} . \end{aligned}$$
(58)

The first term models the “right” condition and the second term the “same column but higher” property.

2.5 Deriving lower and upper bounds via circle cuttings

(Tight) lower and upper bounds on the minimal area of the design rectangle translate directly to lower and upper bounds on the length and width of the design rectangle; because of (3). Good bounds are crucial for the performance of global solvers.

To compute a lower bound on the minimal area of the design rectangle, we replace all ellipses by their inner circles, i.e., \(R_i = b_i\). We then compute the area-minimizing rectangle hosting all these inner circles with the formulation described in Sect. 2.1.1. Solving the resulting circle cutting problem is computationally relative easy compared to the corresponding ellipsoid cutting problem (note that both problems are in fact NP-hard). The solution of the circle cutting problem provides only a tight bound on the minimal area, when the semi-minor axes are not significantly smaller than the semi-major axes of all ellipses to be packed.

We obtain an upper bound on the minimal area of the design rectangle by replacing all ellipses by their outer circles, i.e., \(R_i=a_i\). We then compute the optimal design rectangle by solving the resulting circle cutting problem. By placing the centers of the ellipses at the locations of the center of the corresponding circles in an optimal circle cutting yields in a feasible cutting.

Generally, we denote a lower bound (upper bound) on the minimal area of the design rectangle by \(A^-\) (\(A^{+}\)) and the lower bound (upper bound) obtained by the inner circle (outer circle) cutting by \(A^{\mathrm{ci,-}}\) (\(A^{\mathrm{ci,+}}\)).

We can now refine the lower and upper bounds on the rectangle length, \(L\), and width, \(W\), based on the cuttings we obtained for the inner and outer circle approximations. It is \(L \cdot W \le A^{\mathrm{ci,+}}\) and \(L \le A^{\mathrm{ci,+}}/W \le A^{\mathrm{ci,+}}/S_2^{-}\). The minimum width, \(S_2^{-}\), of the rectangle, could be the maximum of all the minor ellipse axis lengths, yielding an upper bound on the rectangles length. Similarly, by using \(A^{\mathrm{ci,-}}\), we obtain a lower bound on the rectangles length.

3 Polylithic: constructive heuristics

If the number of ellipses increases, it becomes more and more difficult to compute a feasible point. Therefore, we have developed two polylithic approaches.

Both heuristics share the same idea: We sequentially add ellipses in a strip-packing fashion to the rectangle plate; we restrict the width of the rectangle, but leave its length unrestricted. We start with the placement of \(n_1\) ellipses in the initial phase. Next, we use a greedy idea and add \(n_2\) ellipses. In each step, we minimize the rectangle’s area. The sequence, \(s \in {\mathcal {S}}\), in which we add the ellipses is random. This adds some GRASP flavor to our approach (cf. Feo and Resende [5]).

Some aspects of our heuristic may look similar to the tiling method introduced by Markót and Csendes [19], but these similarities are accidental—one of the referees pointed us to this method during the review process.

The pseudo-code of the first algorithm, H1, looks as follows:

figure a

The time limits for the (MI)NLP solves in steps H1_1.1, H1_1.2.4, and H1_1.2.5 make the algorithm a heuristic; typically the optimization problems are not solved to (proven) global optimality before the time limit is reached. We need to be careful to allow for enough CPU time (especially for steps H1_1.1 and H1_1.2.4) in order to find a feasible point for the given number of ellipses. If the ellipse cutting problem in step H1_1.2.5 can be solved to global optimality when all ellipses are present, then the ellipse cutting problem has been solved to global optimality as well. In most cases, however, the problem is not solved to global optimality in step H1_1.2.5—after all, this is why we use a polylithic approach. Rather, the idea is that the global solver is now getting the benefit of a good initial point and, like most solvers, it might start by doing local search from that point to improve upon the current point.

The idea of algorithm H1 is to aid the global solver by providing initial values for many of the decision variables, however, a few decision variables (e.g., related to the separating lines) need to be determined by the solver. It turns out that, as the problems grow in size, feasible point(s) cannot be computed anymore—we have developed a second approach. H2 reads in pseudo-code as follows:

figure b

Heuristics H1 and H2 differ mainly in steps 1.2.1 and 1.2.3; step H1_1.2.5 is entirely missing in H2. The idea (and advantage in the computational speed compared to H1) of H2 is to sequentially solve (EP) of the same size; they contain \(n_2 + n_3\) ellipses. However, a critical tuning parameter is \(X^{-}\) used to prevent new ellipses from being placed left of the front. Note that H2 does not deliver a lower bound on the ellipse cutting problem, because the ellipses fixed in step H2_1.2.1 never get unfixed (within the same sequence \(s\)) but are not further considered when a new front is determined.

4 Numerical experiments

We solve our non-convex MINLPs with the following global solvers available in GAMS: BARON [25], LindoGlobal [15] and GloMIQO [21]. All the instances used for the computations are summarized in Table 1. We used the following platforms for the computations.

Platform 1: :

Dual-six core machine with CPUs @ 2.93 GHz, 48 GB RAM and 1TB HDD running Ubuntu 10.04.4.

Platform 2: :

Dual core machine with CPUs @ 2.5 GHz (Intel booth technology) 48 GB RAM and 250 GB HDD running Windows 7.

Platform 3: :

Dual-six core machine with CPUs @ 3.3 GHz, 48 GB RAM and 1TB HDD running Win2008 Server.

All computations utilize only a single core of the platforms specified above.

Table 1 Ellipse cutting instances
Full size table

4.1 Proof-of-concept: treating circles as ellipses

We use the ellipse cutting formulation (EP\(_{\mathrm{QP}}\)) to demonstrate the correctness of the approach by solving (published) circle cutting instances; circles are special cases of ellipses. We use test instances by Kallrath [11]. Note that there are some typos regarding the instances 5a and 5b as reported in Table 3 in [11]; we provide the correct radii of the circles here.

Consider now Table 2. In the first two columns, we report on the problem instance; \(a^*\) is the globally minimal area of the design rectangle as computed via a circle cutting formulation, cf. Sect. 2.1.1. In the other columns, we summarize the lower bound, \(A^-\), and the upper bound, \(A^+\), on the minimal area of the design rectangle as well as the computational time for (EP\(_{\mathrm{QP}}\)) with three different global solvers available in GAMS. For these computations, for obvious reasons, we do not use the lower/upper bounds derived by the inner/outer circle cutting problems as described in Sect. 2.5. We observe that (1) the results computed with (EP\(_{\mathrm{QP}}\)) are consistent with the global optima computed with the circle cutting formulation, (2) global optimality can only be proven for the instances with 5 circles within the time limit, (3) the globally optimal cuttings are only found for the cases of 5 circles, and (4) the global solvers perform very differently in terms of lower bounds and the quality of computed feasible solutions.

Table 2 Cutting circles with (EP\(_{\mathrm{QP}}\))
Full size table

Two optimal circle cuttings are plotted in Fig. 3.

Fig. 3
figure 3

Feasible circle cuttings computed via (EP\(_\mathrm{QP}\)), including the separating lines. a Test case 5a, b test case 6

Full size image

4.2 Monolith

Table 3 summarizes the computational results for the monolith formulation (EP\(_{\mathrm{QP}}\)). We observe that (1) all three current state-of-the-art global optimization solvers have difficulties closing the gap for the tested instances with three or more ellipses (with the given computational framework) and (2) good cuttings are computed, cf. Fig. 4.

Fig. 4
figure 4

Ellipse cuttings computed via (EP\(_{\mathrm{QP}}\)). a TC05a: \(A^+=25.29557\). b TC5b: \(A^+=31.28873\)

Full size image
Table 3 Monolith: cutting ellipses with (EP\(_{\mathrm{QP}}\))
Full size table

For case TC03, the smallest relative gaps, \(\Delta \), are obtained on platform 3 using LindoGlobal with GAMS 24.0.2 (\(A^+=21.38577, A^-=21.17972, \Delta =0.00973\), 30 h) and using GloMIQO with GAMS 23.8.2 (\(A^+=21.38577, A^-=20.58535, \Delta =0.0388\), 63 h).

Figure 4a illustrates the difference between a packing and a cutting. The top right ellipse is not touching the ellipse centered at \((4.07, 1.27)\), which is allowed for cuttings but not for packings.

4.2.1 Inner and outer circles

Table 4 shows the lower bounds obtained by the area of ellipses (\(\sum _{i} A_i\)), the lower bounds obtained by the cutting computed for the inner circles (\(A^{\mathrm{ci, -}}\)) and an upper bound derived from a cutting using outer circles (\(A^{\mathrm{ci, +}}\)). The lower bounds obtained from the inner circle cuttings are slightly better than the sum of all areas of the ellipses when the majority of the ellipses has semi-minor axes not significantly smaller than their semi-major axes; otherwise, the sum of all areas of the ellipses exceeds \(A^{\mathrm{ci, -}}\). As the initial lower bounds obtained by the solvers for (EP) are significantly smaller, we use \(\max \{\sum _{i} A_i,A^{\mathrm{ci, -}}\}\) as the lower bound for (EP).

Table 4 Comparing area of ellipses, inner circles, outer circles and best solution found (taken from Tables 3 or 9)
Full size table

4.2.2 Tracking the gap as a function of the eccentricity ellipses

The more the ellipses deviate from circles, the more difficult it becomes to close the gap when solving (EP) to global optimality. To demonstrate this, we consider three ellipses with semi-major axes \(a_{1}=1.7, a_{2}=1.2\), and \(a_{3}=0.8\) and semi-minor axes \(b_{i}=\rho a_{i}\) with \(0\le \rho \le 1\), these are the test cases TE\(\rho \) of Table 1. The numerical eccentricity \(\varepsilon \), as a measure for the deviation of the ellipses from circles, is connected to \(\rho \) by

$$\begin{aligned} \varepsilon = \frac{\sqrt{a^{2}-b^{2}}}{a}=\sqrt{1-\rho ^{2}}\in [0,1 ]. \end{aligned}$$

Computational results for some values of \(\rho \) are summarized in Table 5 displaying the computed lower bound, \(A^-\), best solution found, \(A^+\), and relative gap \(\Delta = (A^+ - A^-)/ A^-\) versus \(\rho \) for the three global solvers BARON, LindoGlobal, GloMIQO. The last column computes the fraction of area of the design rectangle covered by the ellipses, which is the utilization of the cutting.

Table 5 Cutting ellipses with different eccentricity with (EP\(_{\mathrm{QP}}\))
Full size table

Consider now Table 5. Even for a mild eccentricity of \(\varepsilon =0.199\), or \(\rho =0.98\), respectively, the gap is already very difficult to close. For \(\rho \ge 0.7\), we observe that the lower bound, \(A^-\), remains close to the sum of the area of the three ellipses. We can see that the gap increases first linearly, then exponentially and then remains approximately stable, as \(\rho \) decreases from 1.0 to 0.1; cf. Fig. 5. Three ellipse cuttings for \(\rho =0.80, \rho =0.50\), and \(\rho =0.10\) are plotted in Fig. 6. Though we realize that the gaps are not closed (for \(\rho < 1\)), the ratio of the area of the rectangle to the areas of the ellipses appears to stay above 70% and peaks at approximately 80.5 % for \(\rho \approx 0.60\).

Fig. 5
figure 5

Gap for TE\(\rho \) instances for GloMIQO; see Table 5

Full size image
Fig. 6
figure 6

Feasible ellipse cuttings computed via (EP\(_\mathrm{QP}\)) for three ellipses with different eccentricities. a TE\(0.80:\, A^+=16.09992\). b TE\(0.50:\, A^+=9.74384\). c TE\(0.10:\, A^+=2.08193\)

Full size image

4.2.3 Identical ellipses

Before we report on our numerical results using our mathematical programming formulations to cut sets of identical ellipses, we derive quasi-analytic cutting configurations which we will call symmetric for simplicity. This allows us to test our formulations, benchmark the global solvers and compare the solution to unsymmetrical cuttings.

For identical ellipses, we can place the ellipses symmetrically, enabling us to compute feasible cuttings as follows. For the case of three ellipses, we place them as shown in Fig. 7a. The three ellipses are then centered and orientated at \((2,1;0^\circ ), (2,3;0^\circ )\) and (\(x_{31}^{0},2; 90^\circ )\) with nomenclature \((x_{i1}^\mathrm{0},x_{i2}^{0}; \theta _i\)). Let us refer to this configuration as \(2-\theta _i\) which means: two ellipses with \(\theta _i=0^\circ \), and one ellipse with rotation angle \(\theta _i=90^\circ \). The results we derive provide upper bounds as long the width of the rectangle is \(x^R_2\ge 4\). They are expected to be exact for \(x^R_2=4\).

Fig. 7
figure 7

Ellipse cuttings for identical ellipses. a “symmetric:” \(A^+=23.53419\). b “symmetric:” \(A^+=62.13676 = 15.53419 \cdot 4\). c “asymmetric:” \(A^+=61.62058 \approx 14.28642 \cdot 4.31323\). d “symmetric:” \(A^+=69.67096\)

Full size image

Ellipse 1 and 3 touch each other at point (\(x_{s},y_{s}\)) which can be obtained by solving the following optimization problem:

$$\begin{aligned}&\max \;\; x_{31}^{0} \nonumber \\&\text {s.t.} \;\; \frac{\left( x_{s}-2\right) ^{2}}{4}+\frac{\left( y_{s}-1\right) ^{2}}{1} = 1 \end{aligned}$$
(59)
$$\begin{aligned}&\frac{\left( x_{s}-x_{31}^{0}\right) ^{2}}{1}+\frac{\left( y_{s}-2\right) ^{2}}{4} =1 \\&x_{31}^{0} > x_{s} \nonumber \\&0.5 \le y_{s} \le 1.5 \nonumber \end{aligned}$$
(60)

Resolving (59) and (60) leads to equation

$$\begin{aligned} x_{s}=2\sqrt{2y_{s}-y_{s}^{2}}+2=x_{31}^{0}-\sqrt{1-\tfrac{1}{4}\left( y_{s}-2\right) ^{2}}, \end{aligned}$$

which allows us to write \(x_{31}^{0}\) as a function of \(y_{s}\)

$$\begin{aligned} x_{31}^{0}=x_{31}^{0}(y_{s})=2\sqrt{2y_{s}-y_{s}^{2}}+2+\sqrt{1-\tfrac{1}{4}\left( y_{s}-2\right) ^{2}}. \end{aligned}$$

Its maximum is obtained by equating the first derivative to zero

$$\begin{aligned} \frac{2-2y_{s}}{\sqrt{2y_{s}-y_{s}^{2}}}+\frac{2-y_{s}}{4\sqrt{1-\tfrac{1}{4} \left( y_{s}-2\right) ^{2}}}=0, \end{aligned}$$
(61)

and yields the numerical values \( (y_{s}, x_{31}^{0}) \approx (1.121357,4.88355)\) ; (61) does not possess an analytical solution. For completeness, we also report \(x_{s}\approx 3.98521\) and the area,

$$\begin{aligned} \tilde{a}_{3} := 4x_{1,3}^{\mathrm {R}} := 4\left( x_{31}^{0} + 1 \right) \approx 23.53419 . \end{aligned}$$

The values of \(x_{31}^{0}\) and \(x_{1,3}^{\mathrm {R}}\) can also be used to derive good upper bounds, \(\tilde{a}_{n} = 4x_{1,n}^{\mathrm {R}}\), on the area of rectangles for \(n\) identical ellipses.

For \(n\ge 7\), a general formula is

$$\begin{aligned} x_{1,n}^{\mathrm {R}}=\left( x_{1,n-2}^{\mathrm {R}}-1\right) + x_3, \end{aligned}$$

with \(x_3 \equiv x_{31}^{0} \approx 4.88355\) as derived for the three ellipse case. If the configuration is symmetric, we have

$$\begin{aligned} x_{1,n}^{\mathrm {R}}=2\left\{ \begin{array}{ll} x_{1,1+\left\lfloor n/2\right\rfloor }^{\mathrm {R}}-1, &{} \qquad \text {for }\; n=2k+(k-1)=3k-1 \wedge k=2m \\ x_{1,1+\left\lfloor n/2\right\rfloor }^{\mathrm {R}}-2, &{} \qquad \text {for }\; n=2k+(k-1)=3k-1 \wedge k=2m+1 \\ x_{1,1+\left\lfloor n/2\right\rfloor }^{\mathrm {R}}-2, &{} \qquad \text {for }\; n=2k+(k+1)=3k+1 \wedge k=2m+1 \\ x_{1,1+\left\lfloor n/2\right\rfloor }^{\mathrm {R}}-1, &{} \qquad \text {for }\; n=2k+(k+1)=3k+1 \wedge k=2m \\ \end{array}\right. \end{aligned}$$

We summarize the resulting symmetric cuttings in Table 6. Figure 7a, b, d illustrate the notation in Table 6 for 3, 8 and 9 ellipses, respectively.

Table 6 Cuttings obtained for “symmetric” placing of ellipses
Full size table

We start with a series of computations for identical ellipses using the monolith formulation (EP\(_{\mathrm{QP}}\)), as summarized in Table 7. With only 20 min of CPU time, the lower bounds do not increases above the sum of the area of all ellipses. This picture does not change when allowing 45 min. However, the runs terminated after 45 min tend to reveal improved solutions compared to the shorter runs of 20 min. Note that the lower bounds obtained by LindoGlobal are slightly larger when compared to those obtained by the other two solvers.

Table 7 Identical ellipses with (EP\(_{\mathrm{QP}}\)) (no MINLP extensions)
Full size table

As long as the upper bound on \(x^P_2\) equals 4 (test cases TS02, TS03, TS04), \(\tilde{a}_n\) yields the optimal area of the design rectangle. They are obtained by the three solvers (cf. Table 7). For \(x^R_2>4\) (all other test cases), the solutions obtained are often slightly better than the analytic bounds \(\tilde{a}\) because additional topological placements to the symmetric ones become possible. We observe this the first time for TC08. Figure 7b, c contrast the “symmetrical” to the better “asymmetrical” placement.

Computations exploiting the lexicographic ordering—the MINLP extension as discussed in Sect. 2.4—are summarized in Table 8. For eight ellipses, the lower bounds are improved compared to the monolith formulation without the lexicographic ordering; cf. Table 7. Because the MINLP is more difficult to solve than the pure NLP formulation, we are not surprised to see the upper bound weaker. However, the advantage of the lexicographic ordering becomes obvious when we try to close the gap; at least for three ellipses.

Table 8 Identical ellipses with (EP\(_{\mathrm{QP}}\)) exploiting lexicographic ordering.
Full size table

On platform 3, GAMS 23.8, GloMIQO, and the lexicographic MINLP approach, the gap is closed after 128,329 seconds (35 h 38 m 49 s) within a tolerance of \(\Delta =10^{-5}\). The global solution has objective function value \(a=23.53347\). The gap could neither be closed using GloMIQO embedded in GAMS 23.9 to GAMS 24.1, nor by the other two global solvers, with 48 h of computational time. Baron computed a cutting with area \(23.53383\); cf. Table 8. It turns out that this is smaller than the lower bound obtained by GloMIQO. The explanation lies in the different feasibility tolerances of the two global solvers.

4.3 Polylithic

For the larger test instances (TC20, TC30, TC50 and TC100), none of the global or local NLP solvers available in GAMS can compute a feasible point. Therefore, we analyze these cases using our polylithic approaches; cf. Table 9.

Table 9 Heuristic methods H1 (\(n_1=10\)) and H2 (\(n_1=10, n_3=5\)) for cutting ellipses; \(\vert S \vert = 8\)
Full size table

We choose value 10 for parameter \(n_1\) for both heuristics, because we can obtain reasonable solutions within approximately 5–15 minutes. The second parameter is \(n_2\), the number of ellipses placed during the sequential phase. We experienced with \(n_2=1\) and \(n_2=2\). While, from the underlying mathematical idea, we expect that the solutions are better for \(n_2=2\), the computing effort is higher. This in turn, can lead—and sometimes does—to worse solutions if the time limit is reached before the gap is closed. Thus, considering this trade-off, we recommend and prefer \(n_2=1\).

We benchmark the polylithic approach by comparing it to the best results obtained by the monolith one (Table 3) for TC11 and TC14. For TC11, the monolith yields \(A^-=47.31238\) and \(A^+=64.59177\) (LindoGlobal) whereas H1 provides \(A^-=37.11006\) and \(A^+=57.24034\) (BARON) and H2 provides \(A^+ = 57.73518\) (BARON) and for TC14, the monolith yields \(A^-=20.61650\) and \(A^+=29.65886\) (GloMIQO) whereas H1 provides \(A^-=13.69538\) and \(A^+ = 24.67185\) (BARON) and H2 provides \(A^+=24.84634\) (GloMIQO). Thus, for TC11 and TC14 both heuristics find better cuttings than the monolith formulation.

We reach the limits of H1 when we approach 30 and more ellipses (the solvers cannot compute a feasible cutting for the resulting (EP) in step H1_1.2.4). The front heuristics, H2, works fine for all cases TC11, TC14, TC20, TC30, TC50 and TC100. For both H1 and H2, results with \(n_2=2\) are superior to \(n_2=1\) but are somewhat more computational expensive. Computations for \(n_2=3\) are even more challenging and do not provide a clear direction.

Figure 8a shows a feasible cutting computed by BARON with H1 (\(n_2=1\)) and Fig. 8b the cutting computed by GloMIQO with H2 (\(n_2=1\)).

Fig. 8
figure 8

Feasible cuttings computed by the heuristics. a TC14: \(A^+ = 24.67185\). b TC20: \(A^+ = 67.83459\)

Full size image

5 Conclusions

We developed non-convex (MI)NLP models describing the problem of cutting ellipses from a design rectangular plate. Small problem instances can be solved with the current state-of-the art global solvers available in GAMS. The more the ellipses deviate from circles, the more difficult it is to close the gap. As it is expected from the NP-hard nature of the ellipse cutting problem, global solvers reach their limitations fast and it becomes a very challenging task for the solvers just to compute a feasible point. For these cases, we have developed two polylithic methods, generating good ellipse cuttings.

The developed (MI)NLP formulations lean themselves naturally to higher dimensional extensions. The 3-D case is of particular practical interest. Who was never curious on how to pack smarties, a German chocolate sweet, optimally?