Packing ellipses in an optimized convex polygon

Abstract

Packing ellipses with arbitrary orientation into a convex polygonal container which has a given shape is considered. The objective is to find a minimum scaling (homothetic) coefficient for the polygon still containing a given collection of ellipses. New phi-functions and quasi phi-functions to describe non-overlapping and containment constraints are introduced. The packing problem is then stated as a continuous nonlinear programming problem. A solution approach is proposed combining a new starting point algorithm and a new modification of the LOFRT procedure (J Glob Optim 65(2):283–307, 2016) to search for locally optimal solutions. Computational results are provided to demonstrate the efficiency of our approach. The computational results are presented for new problem instances, as well as for instances presented in the recent paper (http://www.optimization-online.org/DB_FILE/2016/03/5348.pdf, 2016).

1 Introduction

Packing ellipses in a container is a benchmark problem for two-dimensional packing. The problem is NP-hard [3] and has multiple applications in molecular dynamics (structure and properties of liquid crystals, the structure of liquids and glasses, chromosome packing in cell nucleus mineral, powder metallurgy, mineral industries), logistics (packing rolls of wallpaper, transportation of the pipes, transportation of paint buckets), cutting of industrial materials (mirror manufacturers, furniture making, 3D modeling of granular, structures and substances), robotics (see, e.g. [4,5,6,7,8] and the references therein).

Many authors tackled placement problems for ellipses. In [6] the following problem is considered: a set of ellipses with given axes has to be cut from a rectangular design plate, while minimizing the area of the design rectangle. The design plate is subject to lower and upper bounds of its width and length while orientations of ellipses are free. A mathematical programming formulation for this ellipse cutting problem is presented. Separating lines are used to derive non-overlapping conditions. For a small number of ellipses the authors report globally optimal solutions. However, for more than 14 ellipses none of the local or global NLP solvers available in GAMS can even compute a feasible point. So called polylithic approaches are proposed where ellipses are added sequentially in a strip-packing fashion to the rectangle restricted in width, but unrestricted in length. The rectangle’s area is minimized in each step in a greedy fashion.

The problem of placing a given collection of ellipses into a rectangular container of minimum area is studied in [1]. Quasi phi-functions for an analytical description of non-overlapping and containment constraints for ellipses under continuous rotation and translation are introduced. A corresponding nonlinear programming problem is stated and an efficient solution algorithm is proposed. Computational results of new instances and instances that compare favorably with those published elsewhere before are considered in the paper.

In [7] continuous and differentiable nonlinear programming models and algorithms for packing multidimensional ellipsoids in a container (a cuboid and a sphere) of minimum area are considered. Two different models for non-overlapping and containment conditions are presented. A simple multi-start strategy is combined with an intelligent choice of starting points and a nonlinear programming local solver. The number of variables (constraints) for non-overlapping models grows quadratically with the number of ellipsoids to be packed. Numerical experiments are suggested for instances with up to 100 ellipsoids to obtain acceptable solutions in a reasonable time.

In [8] the authors present a nonlinear programming model for packing ellipses and ellipsoids that contains a linear number of variables and constraints. The proposed model finds its basis in a transformation-based non-overlapping model introduced in [7]. Numerical experiments in [8] show the efficiency and effectiveness of the proposed model and methodology for solving large-sized instances.

Regular grids are used in [9, 10] to approximate a container resulting in corresponding linear integer programming models for optimal packing. Packing different shapes including so-called circular-like objects (ellipses, rectangles, rhombuses, octagons, etc.) is considered as well as nesting objects inside one another (recursive packing). However, it is assumed that all objects have the same orientation and no rotation is allowed.

In the recent paper [2] the authors present a model and a numerical solution approach to packing ellipses into an optimized regular polygon. Specifically, the optimization strategy is based on the concept of embedded Lagrange multipliers. In this Lagrangian setting the apothem (and thereby the area) of a regular polygon is optimizing while preventing ellipses overlapping. They proceed simultaneously towards these objectives using the LGO solver system for global–local nonlinear optimization. The numerical results given in the paper demonstrate the applicability of the embedded Lagrange multipliers based modeling approach combined with global optimization to tackle a broad class of highly non-convex ellipse packing problems.

In this work a problem of packing a given collection of ellipses into a fixed shape convex polygonal container is considered. The ellipses can be continuously rotated, while the container can be homothetically scaled. The objective is to minimize the scaling coefficient for the container subject to non-overlapping and containment constraints.

The main contributions of this work are as follows:

• It is demonstrated that the original problem is closely related to packing homothetically scaling ellipses in a fixed container while maximizing the scaling coefficient for the ellipses.

• New tools for mathematical modelling of placement constraints are proposed: a quasi phi-function to describe non-overlapping of ellipses and a phi-function to describe the containment of an ellipse in a convex polygon analytically;

• An exact mathematical model for optimal packing ellipses under rotation is stated as a continuous nonlinear programming problem;

• An efficient algorithm for finding a good solution (local optimum) to the original packing problem is proposed. The method involves problem reformulation and employs two principal steps: a simple technique to find a starting point and a local optimization algorithm. The optimization algorithm results in a sequence of NLP subproblems of considerably smaller dimension.

2 Problem formulation

A set of ellipses $E_{i} ,i \in \{ 1,2, \ldots ,n\} = I_{n}$, is given. Each ellipse $E_{i}$ is defined by its semi-axes $a_{i}$ and $b_{i}$.

The position of the ellipse $E_{i}$ is characterized by the vector of variable object placement parameters $u_{i} = (v_{i} ,\theta_{i} )$, where $v_{i} = (x_{i} ,y_{i} )$ is a translation vector, and $\theta_{i}$ is a rotation angle. The center of the ellipse coincides with the origin of its own coordinate system. Rotated by angle $\theta_{i}$ and translated by vector $v_{i}$ ellipse $E_{i}$ is defined as $E_{i} (u_{i} ) = \{ p \in R^{2} :p = v_{i} + M(\theta_{i} ) \cdot p^{0} ,\forall p^{0} \in E_{i}^{0} \}$, where $E_{i}^{0}$ denotes non-translated and non-rotated ellipse $E_{i}$, $M(\theta_{i} )$ is a rotation matrix, $M(\theta_{i} ) = \left( {\begin{array}{*{20}c} {\cos \theta_{i} } & {\sin \theta_{i} } \\ { - \sin \theta_{i} } & {\cos \theta_{i} } \\ \end{array} } \right).$

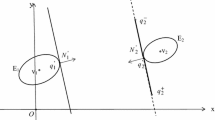
Let $\varOmega (\lambda )$ be a convex m-polygonal domain given by its vertices $\{ \lambda p_{1} ,\lambda p_{2} , \ldots ,\lambda p_{m} \}$ in the global coordinate system XOY. Here we define and use the variable homothetic coefficient $\lambda > 0$, $\lambda p_{s} = (\lambda x_{s}^{p} ,\lambda y_{s}^{p} ),s = 1,2, \ldots ,m$, and it is assumed that the origin $O$ is an interior point of $\varOmega$$\equiv \varOmega (\lambda )$.

In what follows we will also use the presentation of $\varOmega$ in the form $\varOmega = \bigcap\nolimits_{s = 1}^{m} {P_{s} (\lambda )} ,$ where $P_{s} (\lambda ) = \{ (x,y):\mu_{s} (x,y,\lambda ) = \cos \phi_{s} \cdot x + \sin \phi_{s} \cdot y + \lambda \gamma_{s} \ge 0\}$ is a half plane. Here the equation $\mu_{s} (x,y,\lambda ) = 0$ corresponds to a straight line $L_{s} (\lambda ) = \{ (x,y):\mu_{s} (x,y,\lambda ) = 0\}$ passing through the s-th side of $\varOmega (\lambda )$; $\phi_{s}$ is the angle between axis OX and the normal ${\mathbf{n}}_{s}$ to the straight line $L_{s} (\lambda )$ (Fig. 1), $\varphi_{s} = const,$$\gamma_{s} = const$, $s = 1,2, \ldots ,m$, and it is assumed that $\mu_{s} (O,\lambda ) > 0$.

Fig. 1

Illustration of the angle $\phi_{s}$

In what follows two related problems are considered: (1) packing the set of ellipses in a homothetically scaled convex polygonal container minimizing the scaling coefficient for the container; (2) packing a set of homothetically scaled ellipses in a fixed polygonal container maximizing the scaling coefficient for the ellipses. More specifically, these two problems are as follows.

Ellipse packing problem EPP_1. Pack the set of ellipses $E_{i} (u_{i} )$, $i \in I_{n}$ in a convex polygonal domain $\lambda \varOmega$ minimizing the homothetic coefficient $\lambda \ge 0$.

In EPP_1 the following placement constraints have to be satisfied:

• Non-overlapping constraints: $\text{int } E_{i} (u_{i} ) \cap \text{int } E_{j} (u_{j} ) = \emptyset$, for $i > j \in I_{n} ,$

• Containment constraints: $E_{i} (u_{i} ) \subset \varOmega (\lambda )$ for each $i \in I_{n}$.

Let each ellipse $E_{i} (u_{i} )$ be defined by its semi-axes $\beta \cdot a_{i}$ and $\beta \cdot b_{i}$, where $\beta \ge 0$ is a homothetic coefficient of the ellipse $E_{i} (u_{i} )$, $i \in I_{n}$. In what follows the notation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} (u_{i} ,\beta ) = \beta \cdot E_{i} (u_{i} )$, $i \in I_{n}$ is used.

Ellipse packing problem EPP_2. Place the set of ellipses $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} (u_{i} ,\beta )$,$i \in I_{n}$ into a fixed convex polygonal domain $\varOmega (\lambda = 1)$ maximizing the ellipse homothetic coefficient $\beta \ge 0$.

In EPP_2 the following placement constraints have to be satisfied:

• Non-overlapping constraints: $\text{int } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} (u_{i} ,\beta ) \cap \text{int } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} (u_{j} ,\beta ) = \emptyset$, for $i > j \in I_{n} ,$

• Containment constraints: $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} (u_{i} ,\beta ) \subset \varOmega$ for each $i \in I_{n}$.

It will be demonstrated in Sect. 5 that although these two problems are closely related, the second is more attractive from the computational point of view and will be used further in algorithmic constructions.

3 Mathematical modeling tools

In this study we use the phi-function technique which provides a powerful tool for mathematical modeling of placement constraints in the field of Packing& Cutting (see, e.g. [11,12,13,14]).

We introduce a new phi-function to describe containment constraints and a new quasi phi-function to describe non-overlapping constraints in the ellipse packing problem. These new tools allow us reducing considerably the number of auxiliary variables and using simpler mathematical model than in [1] proposed for the ellipse packing problem in a rectangular container.

For the reader’s convenience we provide here definitions of a phi-function and a quasi phi-function (see [2, 11] for more details).

Let $A \subset R^{2}$ and $B \subset R^{2}$ be two objects. The position of object $A$ is defined by a vector of placement parameters$u_{A} = (v_{A} ,\theta_{A} )$, where: $v_{A} = (x_{A} ,y_{A} )$ is a translation vector and $\theta_{A}$ is a rotation angle. The object A, rotated by angle $\theta_{A}$ and translated by vector $v_{A}$ will be denoted by $A(u_{A} )$.

Phi-functions allow us to distinguish the following three cases: $A(u_{A} )$ and $B(u_{B} )$ are intersecting so that $A(u_{A} )$ and $B(u_{B} )$ have common interior points; $A(u_{A} )$ and $B(u_{B} )$ do not intersect, i.e. $A(u_{A} )$ and $B(u_{B} )$ do not have common points; $A(u_{A} )$ and $B(u_{B} )$ are in contact, i.e. $A(u_{A} )$ and $B(u_{B} )$ have only common frontier points. We denote by $frA( \cdot )$ the frontier of set $( \cdot )$.

Definition

[11]. A continuous and everywhere defined function $\varPhi^{AB} (u_{A} ,u_{B} )$ is called a phi-function for objects $A(u_{A} )$ and $B(u_{B} )$ if

$$ \varPhi^{AB} \left( {u_{A} ,u_{B} } \right) < 0,\quad {\text{if}}\;\text{int } \;A\left( {u_{A} } \right) \cap \text{int } \;B\left( {u_{B} } \right) \ne \emptyset ; $$

$$ \varPhi^{AB} \left( {u_{A} ,u_{B} } \right) = 0,\quad {\text{if}}\;\text{int } \;A\left( {u_{A} } \right) \cap \text{int } \;B\left( {u_{B} } \right) = \emptyset \;{\text{and}}\;frA\left( {u_{A} } \right) \cap frB\left( {u_{B} } \right) \ne \emptyset ; $$

$$ \varPhi^{AB} \left( {u_{A} ,u_{B} } \right) > 0,\quad {\text{if}}\;A\left( {u_{A} } \right) \cap B\left( {u_{B} } \right) = \emptyset . $$

It should be noted that inequality $\varPhi^{AB} (u_{A} ,u_{B} ) \ge 0$ provides the non-overlapping constraint, i.e., $\text{int } A(u_{A} ) \cap \text{int } B(u_{B} ) = \emptyset$, and inequality $\varPhi^{{AB^{*} }} (u_{A} ,u_{B} ) \ge 0$ provides the containment constraint $A(u_{A} ) \subset$$B(u_{B} )$, i.e. $\text{int } A(u_{A} ) \cap \text{int } B^{*} (u_{B} ) = \emptyset$, where $B^{ * } = R^{2} \backslash \text{int } B.$

Definition

[1]. A continuous and everywhere defined function $\varPhi^{\prime AB} (u_{A} ,u_{B} ,u^{\prime})$ is called a quasi phi-function for two objects $A(u_{A} )$ and $B(u_{B} )$ if $\mathop {\hbox{max} }\nolimits_{{u^{\prime}}} \varPhi^{\prime AB} (u_{A} ,u_{B} ,u^{\prime})$ is a phi-function for the objects.

Here $u^{\prime}$ is a vector of auxiliary continuous variables that belongs to Euclidean space.

Based on features of a quasi phi-function [1] the non-overlapping constraint can be describe in the form:

$$ {\text{if}}\;\varPhi^{\prime AB} \left( {u_{A} ,u_{B} ,u^{\prime}} \right) \ge 0\;{\text{for}}\;{\text{some}}\;u^{\prime},{\text{ then}}\;\text{int } \;A\left( {u_{A} } \right) \cap \text{int } \;B\left( {u_{B} } \right) = \emptyset . $$

3.1 Phi-function for containment constraints

Let us construct a phi-function for containment constraints for the problem EPP_1:

$$ E_{i} \subset \varOmega (\lambda ) \Leftrightarrow \text{int } \;E_{i} \left( {u_{i} } \right) \cap \varOmega^{*} (\lambda ) = \emptyset ,{\text{ where}}\;\varOmega^{ * } (\lambda ) = R^{2} \backslash int\;\varOmega (\lambda ). $$

Proposition 1

A function defined by

$$ \varPhi^{{E_{i} \varOmega^{ * } }} \left( {u_{i} ,\lambda } \right) = \hbox{min} \left\{ {\varPhi_{is}^{*} \left( {u_{i} ,\lambda } \right),s \in I_{m} } \right\}, $$

(1)

is a phi-function of$E_{i} (u_{i} )$and$\varOmega^{ * } (\lambda )$, where$\varPhi_{is}^{*} (u_{i} ,\lambda )$is a phi-function of ellipse$E_{i} (u_{i} )$and half plane$P_{s}^{*} (\lambda )$, $P_{s}^{*} (\lambda ) = R^{2} \backslash \text{int } P_{s} (\lambda ).$

Proof

It is clear that ellipse $E_{i} (u_{i} )$ is arranged inside a convex polygon $\varOmega (\lambda )$ if and only if ellipse $E_{i} (u_{i} )$ does not overlap with each half plane $P_{s}^{*} (\lambda )$, i.e. $E_{i} (u_{i} ) \cap \text{int } P_{s}^{*} (\lambda ) = \emptyset$, for each $s \in I_{m}$. In terms of phi-functions it means that a phi-function of $E_{i} (u_{i} )$ and half plane $P_{s}^{*} (\lambda )$ should take nonnegative value for all $s \in I_{m}$. Q.E.D.

Therefore, according to (1), the inequality $\varPhi^{{E_{i} \varOmega^{ * } }} (u_{i} ,\lambda ) \ge 0$ provides the containment constraint $E_{i} (u_{i} ) \subset$$\varOmega$, i.e. $\text{int } E_{i} (u_{i} ) \cap \text{int } \varOmega^{*} (\lambda ) = \emptyset .$

Now we define a phi-function $\varPhi_{is}^{*} (u_{i} ,\lambda )$ of ellipse $E_{i} (u_{i} )$ and half plane $P_{s}^{*} (\lambda )$.

Proposition 2

A phi-function of $E_{i} (u_{i} )$ and half plane $P_{s}^{*} (\lambda )$ has the form

$$ \varPhi_{is}^{*} \left( {u_{i} ,\lambda } \right) = \delta_{is} \left( {v_{i} ,\lambda } \right) - d_{is} \left( {\theta_{i} } \right), $$

(2)

where

$$ \delta_{is} \left( {v_{i} ,\lambda } \right) = x_{i} cos\phi_{s} + y_{i} \sin \phi_{s} + \lambda \gamma_{s} ,d_{is} \left( {\theta_{i} } \right) = \sqrt {\Delta_{i} \cdot cos^{2} \left( {\theta_{i} + \phi_{s} } \right) + b_{i}^{2} } ,\quad \Delta_{i} = \left( {a_{i}^{2} - b_{i}^{2} } \right) \cdot $$

Proof

A deviation of $v_{i}$ to $L_{s} (\lambda )$ is derived as $\delta_{is} (v_{i} ,\lambda ) = x_{i} cos\phi_{s} + y_{i} \sin \phi_{s} + \lambda \gamma_{s}$ (Fig. 2a).

Fig. 2

Illustration for phi-function $\varPhi_{is}^{*}$: a the given position of ellipse $E_{i} (v_{i} ,\theta_{i} )$ and $L_{s} (\lambda );$b the position of the rotated ellipse $E_{i}$ and the rotated straight line $L_{s}^{\prime } (\lambda )$

Now let us get the expression for the semi length $d_{is} (\theta_{i} )$ of the orthogonal projection of $E_{i} (v_{i} ,\theta_{i} )$ on the straight line $L_{s}^{ \bot } (\lambda )$ that is perpendicular to $L_{s} (\lambda )$ (Fig. 2a). To this aim we rotate ellipse $E_{i} (v_{i} ,\theta_{i} )$ and straight line $L_{s} (\lambda )$ by angle $\pi - \phi_{s}$. As a result we obtain $L^{\prime}_{s} (\lambda ) \bot OX$ (Fig. 2b).

Now, based on the idea proposed in [6], we can derive the semi length of the projection of $E_{i} (v^{\prime}_{i} ,\theta^{\prime}_{i} )$ on OX in the form $d_{is} (\theta_{i} ) = \sqrt {\Delta_{i} \cdot cos^{2} (\theta_{i} + \phi_{s} ) + b_{i}^{2} }$.

Function (2) is everywhere defined and continuous. It addition, since $d_{is} (\theta_{i} )$ is always positive, then either $\delta_{is} (v_{i} ,\lambda ) > d_{is} (\theta_{i} )$ or $\delta_{is} (v_{i} ,\lambda ) = d_{is} (\theta_{i} )$, or $\delta_{is} (v_{i} ,\lambda ) < d_{is} (\theta_{i} )$. Thus: (1) $\varPhi_{is}^{*} (u_{i} ,\lambda ) > 0$ if and only if $\delta_{is} (v_{i} ,\lambda ) - d_{is} (\theta_{i} ) > 0$ (it means that $E_{i} (u_{i} ) \cap P_{s}^{*} (\lambda ) = \emptyset$); (2) $\varPhi_{is}^{*} (u_{i} ,\lambda ) = 0$ if and only if $\delta_{is} (v_{i} ,\lambda ) - d_{is} (\theta_{i} ) = 0$ (it means that $\text{int } E_{i} (u_{i} ) \cap P_{s}^{*} (\lambda ) = \emptyset$ and $frE_{i} (u_{i} ) \cap L_{s} (\lambda ) \ne \emptyset$); (3) $\varPhi_{is}^{*} (u_{i} ,\lambda ) < 0$ if and only if $\delta_{is} (v_{i} ,\lambda ) - d_{is} (\theta_{i} ) < 0$ (it means that $\text{int } E_{i} (u_{i} ) \cap P_{s}^{*} (\lambda ) \ne \emptyset$). Therefore function (1) is a phi-function of the ellipse $E_{i} (u_{i} )$ and the half plane $P_{s}^{*} (\lambda )$. Q.E.D.

The inequality $\varPhi_{is}^{*} (u_{i} ,\lambda ) \ge 0$ guarantees the non-overlapping of $E_{i} (u_{i} )$ and $P_{s}^{*} (\lambda ).$

Now let us construct a phi-function for containment constraints for the problem EPP_2:

Based on (2) and assuming $\lambda = 1$ we define a phi-function for containment of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} (u_{i} ,\beta )$ into $\varOmega$ that we present as follows:

$$ \varPhi^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \varOmega^{ * } }} \left( {u_{i} ,\beta } \right) = \hbox{min} \left\{ {\varPhi_{is}^{*} \left( {u_{i} ,\beta } \right),s \in I_{m} } \right\}, $$

(3)

$$ \varPhi_{is}^{*} \left( {u_{i} ,\beta } \right) = x_{i} \cdot \cos \phi_{s} + y_{i} \cdot \sin \phi_{s} + \gamma_{s} - \beta \sqrt {\Delta_{i} cos^{2} \left( {\theta_{i} + \phi_{k} } \right) + b_{i}^{2} } . $$

(4)

3.2 Quasi-phi-function for non-overlapping constraints

Next, we construct a quasi phi-function of two ellipses $E_{i} (u_{i} )$ and $E_{j} (u_{j} )$ for the problem EPP_1, that is considerably simpler than a quasi phi-function considered in [2].

The key idea is based on the following statement: if two ellipses do not intersect each other, then there exists a straight line, passing through the center of the coordinate system XOY, such that the projections of the ellipses on this line do not intersect each other. In fact, let two ellipses have no common interior points. Then, there exists a line that divides the plane into two half-planes in such a way that the two ellipses lie in different half-planes. Consequently, the projections of the ellipses on any straight line, that is perpendicular to the separating line (in particular, passing through the center of the coordinate system), do not have common interior points in $R^{1}$.

We denote the straight line, that is perpendicular to a separating line $L_{ij}$ and passing through the origin O, by $L_{ij}^{ \bot }$. Let $\phi_{ij}$ be the angle between the line $L_{ij}^{ \bot }$ and axis OX, while $E_{ij}$ and $E_{ji}$ be projections (line segments with the appropriate centers $t_{ij} = (x_{ij} ,y_{ij} )$ and $t_{ji} = (x_{ji} ,y_{ji} )$) of ellipses $E_{i} (u_{i} )$ and $E_{j} (u_{j} )$ (Fig. 3).

Fig. 3

Illustration for the construction of quasi-phi function $\varPhi^{{\prime E_{i} E_{j} }}$

Rotating the straight line $L_{ij}^{ \bot }$ around the origin O by the angle $- \phi_{ij}$, we obtain two segments $E^{\prime}_{ij} \subset OX$ and $E^{\prime}_{ji} \subset OX$ with centers $x^{\prime}_{ij} (v_{i} ,\phi_{ij} )$ and $x^{\prime}_{ji} (v_{j} ,\phi_{ij} )$ (Fig. 3) and semi lengths $d_{ij} (\theta_{i} ,\phi_{ij} )$ and $d_{ji} (\theta_{i} ,\phi_{ij} )$, where

$$ x^{\prime}_{ij} \left( {v_{i} ,\phi_{ij} } \right) = x_{i} cos\phi_{ij} - y_{i} sin\phi_{ij} ,x^{\prime}_{ji} \left( {v_{j} ,\phi_{ij} } \right) = x_{j} cos\phi_{ij} - y_{j} sin\phi_{ij} , $$

(5)

$$ d_{ij} \left( {\theta_{i} ,\phi_{ij} } \right) = \sqrt {b_{i}^{2} + \Delta_{i} cos^{2} \left( {\theta_{i} - \phi_{ij} } \right)} ,d_{ji} \left( {\theta_{j} ,\phi_{ij} } \right) = \sqrt {b_{j}^{2} + \Delta_{j} cos^{2} \left( {\theta_{j} - \phi_{ij} } \right)} , $$

(6)

$$ \Delta_{i} = \left( {a_{i}^{2} - b_{i}^{2} } \right),\Delta_{j} = \left( {a_{j}^{2} - b_{j}^{2} } \right). $$

Proposition 3

A function defined by

$$ \varPhi^{{\prime E_{i} E_{j} }} \left( {u_{i} ,u_{j} ,\phi_{ij} } \right) = x^{\prime}_{ij} \left( {v_{i} ,\phi_{ij} } \right) - x^{\prime}_{ji} \left( {v_{j} ,\phi_{ij} } \right) - \left( {d_{ij} \left( {\theta_{i} ,\phi_{ij} } \right) + d_{ji} \left( {\theta_{j} ,\phi_{ij} } \right)} \right) $$

(7)

is a quasi phi-function of ellipses $E_{i} (u_{i} )$ and $E_{j} (u_{j} ).$

Proof

To show that function $\varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} )$ is a quasi phi-function of ellipses $E_{i} (u_{i} )$ and $E_{j} (u_{j} )$ we need to prove that $\mathop {\hbox{max} }\nolimits_{{\phi_{ij} \in [0,2\pi ]}} \varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} )$ is a phi-function for ellipses $E_{i} (u_{i} )$ and $E_{j} (u_{j} )$ (see definitions of a phi-function and a quasi phi-function at the beginning of this section).

Further we show that the function possesses the following characteristics:

• (1) $\mathop {\hbox{max} }\nolimits_{{\phi_{ij} \in [0,2\pi ]}} \varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) > 0$ if $E_{i} (u_{i} ) \cap E_{j} (u_{j} ) = \emptyset$;

• (2) $\mathop {\hbox{max} }\nolimits_{{\phi_{ij} \in [0,2\pi ]}} \varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) = 0$ if $\text{int } E_{i} (u_{i} ) \cap \text{int } E_{j} (u_{j} ) = \emptyset$ and $frE_{i} (u_{i} ) \cap frE_{j} (u_{j} ) \ne \emptyset$;

• (3) $\mathop {\hbox{max} }\nolimits_{{\phi_{ij} \in [0,2\pi ]}} \varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) < 0$ if $\text{int } E_{i} (u_{i} ) \cap \text{int } E_{j} (u_{j} ) \ne \emptyset$.

First we show that the following equation

$$ \mathop {\hbox{max} }\limits_{{\phi_{ij} \in [0,2\pi ]}} \varPhi^{{\prime E_{i} E_{j} }} \left( {u_{i} ,u_{j} ,\phi_{ij} } \right) = \mathop {\hbox{max} }\limits_{{\phi_{ij} \in [0,\pi ]}} \left( {|x^{\prime}_{ij} \left( {v_{i} ,\phi_{ij} } \right) - x^{\prime}_{ji} \left( {v_{j} ,\phi_{ij} } \right)| - \left( {d_{ij} \left( {\theta_{i} ,\phi_{ij} } \right) + d_{ji} \left( {\theta_{j} ,\phi_{ij} } \right)} \right)} \right). $$

(8)

is valid.

Based on (5) we have

$$ x^{\prime}_{ij} \left( {v_{i} ,\phi_{ij} + \pi } \right) - x^{\prime}_{ji} \left( {v_{j} ,\phi_{ij} + \pi } \right) = x^{\prime}_{ij} \left( {v_{i} ,\phi_{ij} } \right) - x^{\prime}_{ji} \left( {v_{j} ,\phi_{ij} } \right),{\text{since}} $$

$$ x^{\prime}_{ij} \left( {v_{i} ,\phi_{ij} + \pi } \right) = x_{i} cos\left( {\phi_{ij} + \pi } \right) - y_{i} sin\left( {\phi_{ij} + \pi } \right) = - x_{i} cos\phi_{ij} + y_{i} sin\phi_{ij} = - x^{\prime}_{ij} \left( {v_{i} ,\phi_{ij} } \right). $$

Similarly we get

$$ x^{\prime}_{ji} \left( {v_{j} ,\phi_{ij} + \pi } \right) = - x_{j} cos\phi_{ij} + y_{j} sin\phi_{ij} = - x^{\prime}_{ji} \left( {v_{j} ,\phi_{ij} } \right). $$

Based on (6) we have

$$ d_{ij} \left( {\theta_{i} ,\phi_{ij} + \pi } \right) + d_{ji} \left( {\theta_{j} ,\phi_{ij} + \pi } \right) = d_{ij} \left( {\theta_{i} ,\phi_{ij} } \right) + d_{ji} \left( {\theta_{j} ,\phi_{ij} } \right) $$

Then we consider three cases.

• 1. Let $E_{i} (u_{i} ) \cap E_{j} (u_{j} ) = \emptyset$. It is known that if two ellipses $E_{i} (u_{i} )$ and $E_{j} (u_{j} )$ do not overlap each other then there exists a straight line such that orthogonal projections $E_{ij}$ and $E_{ji}$ of the ellipses on the straight line have no common interior points. It means that there exists a separating line $L_{ij}$ and therefore the straight line $L_{ij}^{ \bot }$, that is perpendicular to $L_{ij}$ and passing through the origin O with the angle $\phi_{ij}$ between the line $L_{ij}^{ \bot }$ and axis OX (Fig. 4a).

  Fig. 4

  

  Illustration to case 1: a$\varPhi^{{\prime E_{i} E_{j} }} = 0$, b$\varPhi^{{\prime E_{i} E_{j} }} > 0$, c$\varPhi^{{\prime E_{i} E_{j} }} < 0$

Based on (8) the non-overlapping constraint, $E_{i} (u_{i} ) \cap E_{j} (u_{j} ) = \emptyset$, can be described by the following inequality:

$$ \left| {x^{\prime}_{ij} \left( {v_{i} ,\phi_{ij} } \right) - x^{\prime}_{ji} \left( {v_{j} ,\phi_{ij} } \right)} \right| > d_{ij} \left( {\theta_{i} ,\phi_{ij} } \right) + d_{ji} \left( {\theta_{j} ,\phi_{ij} } \right). $$

Therefore $\mathop {\hbox{max} }\nolimits_{{\phi_{ij} \in [0,2\pi ]}} \varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) > 0.$

It should be noted that for some values of the angle $\phi_{ij}$ quasi phi-function (7) can take zero value (Fig. 4b) or be negative (Fig. 4c).

• 2. Let $\text{int } E_{i} (u_{i} ) \cap \text{int } E_{j} (u_{j} ) = \emptyset$ and $frE_{i} (u_{i} ) \cap frE_{j} (u_{j} ) \ne \emptyset$. Then either (a)$\text{int } E^{\prime}_{ij} (x_{ij} ,0) \cap \text{int } E^{\prime}_{ji} (x_{ji} ,0) \ne \emptyset$ or (b) $\text{int } E^{\prime}_{ij} (x_{ij} ,0) \cap \text{int } E^{\prime}_{ji} (x_{ji} ,0) = \emptyset$ and $frE^{\prime}_{ij} (x_{ij} ,0) \cap frE^{\prime}_{ji} (x_{ji} ,0) \ne \emptyset$. Therefore, $\left| {x^{\prime}_{ij} (v_{i} ,\phi_{ij} ) - x^{\prime}_{ji} (v_{j} ,\phi_{ij} )} \right| < d_{ij} (\theta_{i} ,\phi_{ij} ) + d_{ji} (\theta_{j} ,\phi_{ij} )$ and $\varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) < 0$ for case (a) or $\left| {x^{\prime}_{ij} (v_{i} ,\phi_{ij} ) - x^{\prime}_{ji} (v_{j} ,\phi_{ij} )} \right| = d_{ij} (\theta_{i} ,\phi_{ij} ) + d_{ji} (\theta_{j} ,\phi_{ij} )$ and $\varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) = 0$ for case (b). Thus, there is always exists $\phi_{ij}$ with $\mathop {\hbox{max} }\nolimits_{{\phi_{ij} \in [0,2\pi ]}} \varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) = 0$.

• 3. Let $\text{int } E_{i} (u_{i} ) \cap \text{int } E_{j} (u_{j} ) \ne \emptyset$. Then also $\text{int } E^{\prime}_{ij} (x_{ij} ,0) \cap \text{int } E^{\prime}_{ji} (x_{ji} ,0) \ne \emptyset .$

  It means that $\left| {x^{\prime}_{ij} (v_{i} ,\phi_{ij} ) - x^{\prime}_{ji} (v_{j} ,\phi_{ij} )} \right| < d_{ij} (\theta_{i} ,\phi_{ij} ) + d_{ji} (\theta_{j} ,\phi_{ij} )$ for any $\phi_{ij} , \text{i.e. } \mathop {\hbox{max} }\nolimits_{{\phi_{ij} \in [0,2\pi ]}} \varPhi^{{\prime E_{i} E_{j} }} \left( {u_{i} ,u_{j} ,\phi_{ij} } \right) < 0.\;{\text{Q}}.{\text{E}}.{\text{D}}.$

Thus, according to the main property of a quasi phi-function [1], we can conclude that, if $\varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) \ge 0$ for some $\phi_{ij}$, then $\text{int } E_{i} (u_{i} ) \cap \text{int } E_{j} (u_{j} ) = \emptyset$.

Now based on (7), we define a quasi phi-function to describe non-overlapping of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} (u_{i} ,\beta )$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} (u_{j} ,\beta )$ in problem EPP_2

$$ \begin{aligned} \varPhi^{{\prime \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} }} \left( {u_{i} ,u_{j} ,\phi_{ij} ,\beta } \right) & = \left( {x_{i} - x_{j} } \right)cos\phi_{ij} + \left( {y_{j} - y_{i} } \right)sin\phi_{ij} \\ & \quad - \,\beta \left( {\sqrt {b_{i}^{2} + \Delta_{i} cos^{2} \left( {\theta_{i} - \phi_{ij} } \right)} + \sqrt {b_{j}^{2} + \Delta_{j} cos^{2} \left( {\theta_{j} - \phi_{ij} } \right)} } \right), \\ \end{aligned} $$

(9)

4 Mathematical models for ellipse packings

Let us state a mathematical model of the problem EPP_1. A mathematical model for packing rotatable ellipses in a convex polygonal domain Ω of minimum homothetic coefficient can be formulated in the form

$$ \mathop {min}\limits_{{(t,\phi ) \in V \subset R^{\sigma } }} \lambda , $$

(10)

$V = \{ (t,\phi ) \in R^{\sigma } :\varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} ) \ge 0,(i,j) \in \varXi ,\varPhi^{{E_{i} \varOmega^{ * } }} (u_{i} ,\lambda ) \ge 0,i \in I_{n} ,\lambda \ge 0\} ,$ where $t = (v,\theta ,\lambda )$ is a vector of variables, $v = (v_{1} ,v_{2} , \ldots ,v_{n} )$, $\theta = (\theta_{1} ,\theta_{2} , \ldots ,\theta_{n} )$, $\phi = (\phi_{ij} ,(i,j) \in \varXi )$, $\varXi = \{ (i,j):i < j \in I_{n} \} ,$$\varPhi^{{\prime E_{i} E_{j} }} (u_{i} ,u_{j} ,\phi_{ij} )$ is defined in (7), $\varPhi^{{E_{i} \varOmega^{ * } }} (u_{i} ,\lambda )$ is defined in (1), $u_{i} = (v_{i} ,\theta_{i} )$, $v_{i} = (x_{i} ,y_{i} )$, $\sigma = 3n + 0.5 \cdot n(n - 1) + 1$ is the number of the problem variables.

Based on (1) the inequality $\varPhi^{{E_{i} \varOmega^{ * } }} (u_{i} ,\lambda ) \ge 0$ can be substituted by m inequalities $\varPhi_{is}^{*} (u_{i} ,\lambda ) \ge 0,s \in I_{m}$, where $\varPhi_{is}^{*} (u_{i} ,\lambda )$ is defined in (2). Therefore we can rewrite the feasible region $V$ in the form

$$ V = \left\{ {(t,\phi ) \in R^{\sigma } :\varPhi^{{\prime E_{i} E_{j} }} \left( {u_{i} ,u_{j} ,\phi_{ij} } \right) \ge 0,\quad (i,j) \in \varXi ,\varPhi_{is}^{*} \left( {u_{i} ,\lambda } \right) \ge 0,s \in I_{m} ,i \in I_{n} ,\lambda \ge 0} \right\}, $$

(11)

The number of inequalities that describes feasible region (11) is $N = 0.5n(n - 1) + nm$.

Feasible region $V$ given by (11) is defined by a system of inequalities with differentiable functions. Our model (10)–(11) is a non-convex and continuous nonlinear programming problem. This is an exact formulation in the sense that it gives all optimal solutions to the ellipse packing problem. It is possible, at least in theory, using a global solver for this nonlinear programming problem to get an optimal packing.

However in practice, the model has a large number of variables and inequalities. The model (10)–(11) involves O(n²) nonlinear inequalities and O(n²) variables due to the auxiliary variables in quasi phi-functions. As a result, even finding a locally optimal solution becomes a complicated procedure for the available state of the art NLP-solvers employed directly to model (10)–(11).

Therefore developing an efficient algorithm combining a fast and simple (feasible) starting point selection technique and local optimization procedure (linear to the number of ellipses) is of very important.

Then we state a mathematical model of EPP_2 in the form:

$$ \mathop {\hbox{max} }\limits_{{(u,\phi ) \in W \subset R^{\sigma } }} \beta , $$

(12)

$$ W = \left\{ {(u,\phi ) \in R^{\sigma } :\varPhi^{{\prime \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} }} \left( {u_{i} ,u_{j} ,\beta ,\phi_{ij} } \right) \ge 0,\quad (i,j) \in \varXi ,\varPhi_{is}^{*} \left( {u_{i} ,\beta } \right) \ge 0,s \in I_{m} ,i \in I_{n} ,\beta \ge 0} \right\}, $$

(13)

where, $u = (v,\theta ,\beta )$, $v = (v_{1} ,v_{2} , \ldots ,v_{n} )$, $\theta = (\theta_{1} ,\theta_{2} , \ldots ,\theta_{n} )$,$\phi = (\phi_{ij} ,(i,j) \in \varXi )$,$\varXi = \{ (i,j):i < j \in I_{n} \} ,$$u_{i} = (v_{i} ,\theta_{i} )$, $v_{i} = (x_{i} ,y_{i} )$,$\varPhi^{{\prime \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} }} (u_{i} ,u_{j} ,\beta ,\phi_{ij} )$ is defined in (9), $\varPhi_{is}^{*} (u_{i} ,\beta )$ is defined in (4), $\sigma = 3n + 0.5 \cdot n(n - 1) + 1$ is the number of the problem variables. The number of inequalities that describe the feasible region (13) is $N = 0.5n(n - 1) + nm.$

It is not hard to verify the following relation between the models (10)–(11) and (12)–(13). The problem (10)–(11) is equivalent to the problem (12)–(13) for β > 0 in the sense that there exists the following one-to-one correspondence between the appropriate feasible solutions of these problems:

$$ \left( {\frac{v}{\beta },\theta ,\lambda = \frac{1}{\beta },\phi } \right) \leftrightarrow (v,\theta ,\beta ,\phi ),\quad \forall (t,\phi ) \in V,\forall (u,\phi ) \in W,\beta > 0 . $$

(14)

Further we refer to (14) as a scaling transformation.

To find “good” locally optimal solutions of the problem (10)–(11) within a reasonable computational time we propose in Sect. 5 an efficient solution algorithm for the problem (12)–(13). We focus on the problem (12)–(13) and provide a fast and simple procedure to generate a good initial feasible solution. In most cases the approach reduces our problem with O(n²) variables and nonlinear constraints to a sequence of nonlinear programming subproblems of considerably smaller dimension, with O(n) variables and nonlinear constraints.

5 Solution algorithm

Our solution strategy consists of four stages:

• Stage 1. Generate a set of vectors of feasible placement parameters of ellipses in problem (12)–(13) provided that $\beta = 0$ (see Sect. 5.1).

• Stage 2. Search for a set of local maxima of problem (12)–(13) starting from each starting point obtained at Stage 1 (see Sect. 5.2).

• Stage 3. Derive local minima of problem (10)–(11) based on local maxima found at Stage 2, using scaling transformation (14).

• Stage 4. Choose the best local minimum from those found at Stage 3.

We note that this is a heuristic local solution strategy which produces good results as shown below.

5.1 Starting feasible parameters algorithm (SFP)

Let us consider problem (12)–(13). Let $\varOmega$ given by its vertices $p_{s} = (x_{s}^{p} ,y_{s}^{p} ),s \in I_{m} .$ We assume $\beta = 0$.

• Step 1. Generate within $\varOmega$ a set of $n$ randomly chosen centers $v_{i}^{1} = (x_{i}^{1} ,y_{i}^{1} ),$ of ellipses $E_{i}$,$i \in I_{n} ,$ using the formula $v_{i}^{0} = \sum\nolimits_{s = 1}^{m} {\alpha_{is} } p_{s}^{{}} ,$$\sum\nolimits_{s = 1}^{m} {\alpha_{is} } = 1,0 \le \alpha_{is} \le 1,s \in I_{m} .$

• To find $\alpha_{is} ,s \in I_{m}$ we randomly generate m positive numbers $n_{is} ,s \in I_{m}$, and derive $\alpha_{is} = \frac{{n_{is} }}{{\sum\nolimits_{s = 1}^{m} {n_{is} } }},s \in I_{m}$.

• Step 2. Generate random rotation parameters $\theta_{i}^{1} \in [0,\pi )$ of ellipses $E_{i}$,$i \in I_{n}$ (Fig. 5a).

  Fig. 5

  

  Illustrations to the SFP algorithm: a Steps 1–3; b Step 4

• Step 3. Form a vector $u^{1} = (v^{1} ,\theta^{1} ,\beta^{1} = 0)$.

• Step 4. Form a vector $\phi^{1}$ of auxiliary variables based on the elementary geometrical calculations. Each element of the vector $\phi^{1}$ is defined as an angle $\phi_{ij}^{1}$ between axis OX and a straight line paralleled to $L_{ij}^{ \bot }$ and passing through points $v_{i}^{1}$ and $v_{j}^{1}$ (Fig. 5b).

• Step 5. Return a starting point $(u^{1} ,\phi^{1} )$ for a subsequent search for a local maximum of the problem (12)–(13).

Note that the starting feasible point obtained by the algorithm for the problem (12)–(13) can not be transformed to a feasible point of the problem (10)–(11) using relation (14) for $\beta = 0$. This is the reason for considering the problem EPP_2 instead of the problem EPP_1.

5.2 Local optimization algorithm (LOFRT_P)

We propose a decomposition algorithm (LOFRT_P) to search for local maxima of the problem (12)–(13) with O(n²) variables and O(n²) nonlinear constraints.

The iterative algorithm reduces the large scale problem to a sequence of nonlinear programming subproblems of smaller dimension (O(n) variables and O(n) nonlinear constraints). It is based on a modification of the LOFRT procedure introduced in [1] for the packing problem of ellipses of given sizes in a rectangular domain of minimum area.

The key idea of the LOFRT_P algorithm is as follows. At each iteration a fixed individual rectangular $\varepsilon$-container centered at the feasible staring point is constructed for each ellipse. Then each ellipse can be moved within its individual $\varepsilon$-container. The motion of each ellipse is described by a system of four $\varepsilon$-inequalities. Then a subregion of the feasible region W is formed in the following way: we add 4n$\varepsilon$-inequalities to constraints (13) and then delete O(n²) phi-inequalities corresponding to pairs of ellipses with non-overlapping individual containers. Some redundant containment constraints are also deleted.

While deleting quasi phi-functions for some pairs of ellipses we also delete O(n²) corresponding auxiliary variables. This results in reducing the number of variables in our subproblem. Then we search for a local maximum for the subproblem with O(n) variables and nonlinear constraints. This local maximum is then used as a starting point for the next iteration. On the last iteration of our algorithm we find a local maximum of the problem (12)–(13).

The LOFRT_P algorithm comparing to the LOFRT procedure deals with an arbitrary convex polygon (vs. a rectangular container in LOFRT); does not use circular approximation of ellipses to generate $\varepsilon$-inequalities (vs. circumscribed circles around ellipses of given sizes); takes into account variable scaling parameters of ellipses while generating individual containers (vs. given sizes of ellipses); orientation of the individual container is associated with the ellipse orientation (vs. the fixed orientation of the individual container); maximizes the scaling parameter for ellipses (vs. minimizing area of the rectangular container).

Let us consider the algorithm in details. Let $u^{1}$ be one of the points found by the SFP algorithm. Now we describe the LOFRT_P algorithm which is an iterative decomposition procedure.

We denote the value of the decomposition step of the algorithm by $\varepsilon$ and assume that $\varepsilon = \frac{\gamma }{2n} \cdot \sum\nolimits_{i = 1}^{n} {b_{i} }$, where $\gamma = \frac{{S_{\varOmega } }}{{\sum\nolimits_{i = 1}^{n} {S_{i} } }}$, $S_{\varOmega }$ is the area of container $\varOmega (\lambda = 1),$$S_{i} = \pi \cdot a_{i} \cdot b_{i}$ is the area of ellipse $E_{i}$.

Step 1. Let $k = 1.$

Step 2. Construct a fixed “individual” rectangular container $\varOmega_{i}^{k} \supset \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} (u_{i}^{k} ,\beta^{k} )$ of sizes $2(\beta^{k} \cdot a_{i} + \varepsilon )$ and $2(\beta^{k} \cdot b_{i} + \varepsilon )$ with the center point $v_{i}^{k}$ for each $i \in I_{n}$ (Fig. 6).

Fig. 6

Illustration to construction of individual containers of ellipses for Steps 2–6

Step 3. Create a system of auxiliary “artificial” inequality constraints on the vector $(u_{i} ,\beta )$ of each ellipse $E_{i}$ in the form: $\varPhi^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \varOmega_{i}^{k * } }} (u_{i} ,\beta ) \ge 0$, $i \in I_{n}$, where $\varPhi^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \varOmega_{i}^{k * } }} (u_{i} ,\beta )$ is defined based on (3)

$$ \varPhi^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \varOmega_{i}^{k * } }} \left( {u_{i} ,\beta } \right) = \hbox{min} \left\{ {f_{i1}^{k} \left( {u_{i} ,\beta } \right),f_{i2}^{k} \left( {u_{i} ,\beta } \right),f_{i3}^{k} \left( {u_{i} ,\beta } \right),f_{i4}^{k} \left( {u_{i} ,\beta } \right)} \right\}. $$

The inequality $\varPhi^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \varOmega_{i}^{k * } }} (u_{i} ,\beta ) \ge 0$ is equivalent to the system of four inequalities

$$ f_{i1}^{k} \left( {u_{i} ,\beta } \right) \ge 0,f_{i2}^{k} \left( {u_{i} ,\beta } \right) \ge 0,f_{i3}^{k} \left( {u_{i} ,\beta } \right) \ge 0,f_{i4}^{k} \left( {u_{i} ,\beta } \right) \ge 0, $$

where

$$ f_{i1}^{k} \left( {u_{i} ,\beta } \right) = \left( {x_{i} - x_{i}^{k} } \right) \cdot \cos \theta_{i}^{k} + \left( {y_{i} - y_{i}^{k} } \right) \cdot \sin \theta_{i}^{k} + \beta^{k} \cdot a_{i} + \varepsilon - \beta \sqrt {\Delta_{i} cos^{2} \left( {\theta_{i} + \theta_{i}^{k} } \right) + b_{i}^{2} } , $$

$$ f_{i2}^{k} \left( {u_{i} ,\beta } \right) = - \left( {x_{i} - x_{i}^{k} } \right) \cdot \cos \theta_{i}^{k} - \left( {y_{i} - y_{i}^{k} } \right) \cdot \sin \theta_{i}^{k} + \beta^{k} \cdot a_{i} + \varepsilon - \beta \sqrt {\Delta_{i} cos^{2} \left( {\theta_{i} + \theta_{i}^{k} } \right) + b_{i}^{2} } , $$

$f_{i3}^{k} (u_{i} ,\beta ) = (x_{i} - x_{i}^{k} ) \cdot \sin \theta_{i}^{k} - (y_{i} - y_{i}^{k} ) \cdot \cos \theta_{i}^{k} + \beta^{k} \cdot b_{i} + \varepsilon - \beta \sqrt {\Delta_{i} \sin^{2} (\theta_{i} + \theta_{i}^{k} ) + b_{i}^{2} } ,\quad$$f_{i4}^{k} (u_{i} ,\beta ) = - (x_{i} - x_{i}^{k} ) \cdot \sin \theta_{i}^{k} + (y_{i} - y_{i}^{k} ) \cdot \cos \theta_{i}^{k} + \beta^{k} \cdot b_{i} + \varepsilon - \beta \sqrt {\Delta_{i} \sin^{2} (\theta_{i} + \theta_{i}^{k} ) + b_{i}^{2} } .$We note that $v_{{}}^{k} ,\theta^{k} ,\varphi^{k} ,\beta^{k} ,a_{i} ,b_{i} ,\Delta_{i}$ are constant.

Step 4. Construct an index set

$$ \varXi^{k} = \left\{ {(i,j):\varPhi^{{\varOmega_{i}^{k} \varOmega_{j}^{k} }} \left( {u_{i}^{k} ,u_{j}^{k} ,\beta^{k} } \right) < 0,\quad i > j \in I_{n} } \right\}, $$

where $\varPhi^{{\varOmega_{i}^{k} \varOmega_{j}^{k} }} (u_{i}^{k} ,u_{j}^{k} ,\beta^{k} )$ is a phi-function for two polygons $\varOmega_{i}^{k} (u_{i}^{k} ,\beta^{k} )$ and $\varOmega_{j}^{k} (u_{j}^{k} ,\beta^{k} )$ [13].

It is clear that if two individual containers $\varOmega_{i}^{k}$ and $\varOmega_{j}^{k}$ do not have common interior points (i.e. $\varPhi^{{\varOmega_{i}^{k} \varOmega_{j}^{k} }} (u_{i}^{k} ,u_{j}^{k} ,\beta^{k} ) \ge 0$), then we do not need to check the non-overlapping constraint for the corresponding pair of ellipses $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} (u_{i}^{k} ,\beta^{k} )$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} (u_{j}^{k} ,\beta^{k} )$ (e.g., the ellipses $E_{1}$ and $E_{3}$ in Fig. 6. In the case $\varXi^{k} = \{ (1,2),(2,3)\} ).$

Step 5. Form an subset

$$ \varPi_{k}^{\varepsilon } = \left\{ {\left( {u,\phi_{{w_{k} }} } \right) \in R^{{\sigma - \sigma_{k} }} :f_{i1}^{k} \left( {u_{i} ,\beta } \right) \ge 0,f_{i2}^{k} \left( {u_{i} ,\beta } \right) \ge 0,f_{i3}^{k} \left( {u_{i} ,\beta } \right) \ge 0,f_{i4}^{k} \left( {u_{i} ,\beta } \right) \ge 0,\quad i \in I_{n} } \right\}, $$

(15)

where $\sigma_{k} = card(\varXi \backslash \varXi^{k} )$.

Step 6. Construct an index set

$$ \varXi_{{}}^{*k} = \left\{ {(i,s):\varPhi^{{\varOmega_{i}^{k} P_{s}^{*} }} \left( {u_{i}^{k} ,\beta^{k} } \right) < 0,\quad s \in I_{m} ,i \in I_{n} } \right\}, $$

where $\varPhi^{{\varOmega_{i}^{k} P_{s}^{*} }} (u_{i}^{k} ,\beta^{k} )$ is a phi-function for polygon $\varOmega_{i}^{k} (u_{i}^{k} ,\beta^{k} )$ and a half plane $P_{s}^{*}$ [13].

In other words, if individual container $\varOmega_{i}^{k}$ and half plane $P_{s}^{*}$ have common interior points (i.e.$\varPhi^{{\varOmega_{i}^{k} P_{s}^{*} }} (u_{i}^{k} ,\beta^{k} ) < 0$), then we need to take into account the containment constraint for the corresponding pair of objects. For example, we need to monitor pairs $E_{1}$ and $P_{1}^{*}$, $E_{1}$ and $P_{2}^{*}$, $E_{3}$ and $P_{4}^{*}$ shown in Fig. 6. In the case $\varXi^{*k} = \{ (1,1),(1,2),(3,4)\} ).$

Step 7. Construct a vector of starting values for auxiliary variables $\phi_{{w_{k} }}^{k} = (\phi_{ij}^{k} ,(i,j) \in \varXi^{k} ).$

For each pair $(i,j) \in \varXi^{k}$ we search for the maximum value of auxiliary variable $\phi_{ij}$ (see Fig. 3), using the following non-constrained nonlinear optimization problem:

$$ \phi_{ij}^{k} = \arg \mathop {\hbox{max} }\limits_{{\phi_{ij} \in [0,2\pi ] \subset R^{1} }} \varPhi^{{\prime \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} }} \left( {u_{i}^{k} ,u_{j}^{k} ,\beta^{k} ,\phi_{ij} } \right), $$

where $u_{i}^{k} ,u_{j}^{k} ,\beta^{k}$ are fixed parameters.

Step 8. Solve the k-th subproblem, starting from point $(u_{{}}^{k} ,\phi_{{w_{k} }}^{k} ) = (v^{k} ,\theta^{k} ,\beta^{k} ,\phi_{{w_{k} }}^{k} )$:

$$ \mathop {\hbox{max} }\limits_{{(u_{{}}^{k} ,\phi_{{w_{k} }}^{k} ) \in W_{k} }} \beta , $$

(16)

$$ W_{k}^{{}} = \left\{ {\left( {u_{{}}^{k} ,\phi_{{w_{k} }}^{k} } \right) \in R^{{\sigma - \sigma_{k} }} :\varPhi^{{\prime \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} }} \left( {u_{i} ,u_{j} ,\beta ,\phi_{ij} } \right) \ge 0,\quad (i,j) \in \varXi_{k} } \right\}, $$

(17)

$$ \varPhi_{is}^{*} \left( {u_{i} ,\beta } \right) \ge 0,(i,s) \in \varXi_{k}^{*} ,\varPhi^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \varOmega_{i}^{k * } }} \left( {u_{i} ,\beta } \right) \ge 0,\quad i \in I_{n} \} , $$

where $(u,\phi_{{w_{k} }} ) = (v,\theta ,\beta ,\phi_{{w_{k} }} ),$$\varPhi^{{\prime \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} }} (u_{i} ,u_{j} ,\beta ,\phi_{ij} )$ is defined in (9), $\varPhi_{is}^{*} (u_{i} ,\beta )$ is defined by (4), $\varPhi^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \varOmega_{i}^{k * } }} (u_{i} ,\beta )$ is defined at Step 3, $\varXi_{k}$ is defined at Step 4, $\sigma_{k}$ is defined at Step 5, $\varXi_{k}^{*}$ is defined at Step 6.

Step 9. If the point $(u_{{}}^{k*} ,\phi_{{w_{k} }}^{*} )$ of local maximum of the k-th subproblem (16)–(17) belongs to the frontier of the subset $\varPi_{k}^{\varepsilon }$ described by (15) then we set $u^{k + 1} = u^{k*}$, take k = k+1 and go to Step 2, otherwise (i.e. $(u_{{}}^{k*} ,\phi_{{w_{k} }}^{*} ) \in \text{int } \varPi_{\varepsilon }^{k}$) set $u^{*} = u^{k*}$ and go to Step 10.

Remark

We do not need to redefine the deleted auxiliary variables at the last step of our algorithm based on the following reasons. Let $(u_{{w_{k} }}^{*} ,\phi_{{w_{k} }}^{*} ) \in R^{{\sigma - \sigma_{k} }}$ be the last point of our iterative procedure. We can construct vector $\phi^{k*}$ by means of redefining values of the previously deleted auxiliary variables for $(i,j) \in \varXi \backslash \varXi^{k}$ (see Step 7). The point $(u_{{}}^{*} ,\phi_{{}}^{*} ) = (u_{{}}^{k*} = u_{{w_{k} }}^{*} ,\phi^{k * } ) \in R^{\sigma }$ is a point of local maximum of the problem (12)–(13). The assertion comes from the property of quasi phi-functions: any arrangement of each pair of non-overlapping ellipses $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i}$ for $(i,j) \in \varXi \backslash \varXi^{k}$ guarantees that there always exists a vector $\phi^{k*}$ of auxiliary variables $\phi_{ij}^{*}$ such that $\varPhi^{{\prime \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{j} }} (u_{i}^{*} ,u_{j}^{*} ,\beta^{*} ,\phi_{ij}^{*} ) \ge 0,(i,j) \in \varXi \backslash \varXi^{k}$. Therefore the values of auxiliary variables of the vector $\phi^{k*}$ have no effect on the objective function value, i.e. $F(u_{{w_{k} }}^{*} ,\phi_{{w_{k} }}^{*} ) = F(u_{{}}^{k*} ,\phi_{{_{{}} }}^{k*} )$.

Figure 7 shows a diagram for local optimization of problem EPP_2: maximization of $\beta$ assuming $\lambda = 1$, starting from $\beta = 0$. We grow ellipses as much as possible in the fixed container $\varOmega (\lambda = 1)$.

Fig. 7

Illustration to LOFRT_P algorithm

Step 10. Get a local minimum solution of the problem (10)–(11) using the local maximum of the k-th subproblem (16)–(17) and scaling transformation (14)

$$ u^{*} = \left( {v^{*} ,\theta^{*} ,\beta^{*} } \right) \to t^{*} = \left( {\frac{{v^{*} }}{{\beta^{*} }},\theta^{*} ,\lambda^{*} = \frac{1}{{\beta^{*} }}} \right) $$

and stop our LOFRT_P procedure.

Figures 8 and 9 show diagrams for the Step 10 corresponding to $\beta^{*} > 1$ and $0 < \beta^{*} < 1$. Using the correspondence (14) between the problem EPP_2 (maximizing the homothetic coefficient $\beta$ of ellipses $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{i}$) and the problem EPP_1 (minimizing the homothetic coefficient $\lambda$ of the convex polygon) we find $\lambda^{*} = \frac{1}{{\beta^{*} }}$.

Fig. 8

Illustration to Step 10 for $\beta^{*} > 1$: a$\beta^{*} > 1,$$\lambda = 1$; b$\lambda^{*} = \frac{1}{{\beta^{*} }} < 1$

Fig. 9

Illustration to Step 10 for $\beta^{*} < 1$: a$\beta^{*} < 1,$$\lambda = 1$; b$\lambda^{*} = \frac{1}{{\beta^{*} }} > 1$

Note that if $\beta^{*} > 1$ (each ellipse size is larger than the original ellipse), then $\lambda^{*} < 1$ (Fig. 8), otherwise $0 < \beta^{*} \le 1$ (each ellipse size is smaller than the original ellipse), then $\lambda^{*} \ge 1$ (Fig. 9).

Our algorithm can in most cases actively control only $O(n)$ pairs of ellipses from $O(n^{2} )$ since for each ellipse only its “$\varepsilon$-neighbors” have to be monitored. This depends on the sizes of ellipses and the value of $\varepsilon$ [1]. The $\varepsilon$ parameter provides a balance between the number of inequalities in each NLP sub-problem and the number of the subproblems (16)–(17) have to be generated and solved to get a locally optimal solution of the problem (12)–(13). The LOFTR_P procedure allows us to reduce considerably the computational time.

6 Computational results

Here we present a number of examples to demonstrate the efficiency of our methodology. We have run all experiments on an AMD FX(tm)-6100, 3.30 GHz computer, programming language C++, OS: Windows 7. For local optimisation we use the IPOPT code https://projects.coin-or.org/Ipopt), developed in [15], with default options.

First we present our new instances for the ellipse packing problem.

Example 1

A convex polygonal domain with m = 5 sides is given by its vertices {(x_s, y_s), s = 1,…,5} = {(− 7.266244, 1.593456), (− 5.941336, − 6.880334), (2.310916, − 10.663272), (6.702019, − 10.663272), (20.670273, 2.387873)}. Collections of ellipses are taken from [6]: (a) n = 20 (TC20), (b) n = 30 (TC30), c() n = 50 (TC50). Corresponding optimized packings are presented in Fig. 10a, b, c.

Fig. 10

Ellipse packings: an = 20, bn = 30, cn = 50, in the optimized convex polygon with m = 5 in Example 1

Example 2

A convex polygonal domain with m = 9 sides is given by its vertices {(x_s, y_s), s = 1,…,9} = {(− 7.266244, 1.593456), (− 5.941336, − 6.880334), (− 3.291530, − 8.733971), (2.310916, − 10.663272), (6.702019, − 10.663272), (16.052038, − 4.080957), (20.670273, 2.387873), (7.118418, 9.915923), (− 1.853066, 7.948795)}. We consider collections of ellipses: (c) n = 50 (TC50) is taken from [6], (d) n = 20 $\times$ 7 = 140 is produced from [2]. Corresponding optimized packings are presented in Fig. 11a, b.

Fig. 11

Ellipse packings: an = 50, bn = 140, in the optimized convex irregular polygon with m = 9 in Example 2

We used 100 runs for the LOFTR_P procedure in our multistart strategy for each instance in Examples 1 and 2.

For these examples the optimized value of the homothetic coefficient $\lambda^{*}$ and the corresponding CPU time are as follows: (a) $\lambda^{*} =$ 0.536303, CPU = 654.96 s., (b) $\lambda^{*} =$ 0.640662, CPU = 1222.99 s., (c) $\lambda^{*} =$ 0.810372, CPU = 3764.04 s. in Example 1; (a) $\lambda^{*} =$ 0.6307, CPU = 298.125 s., (b) $\lambda^{*} =$ 0.419, CPU = 35840.98 s. in Example 2.

Further we apply our approach to the problem instances considered in [2]. The ellipse packing problem instances in [2] were designed as follows: $a_{i} = \frac{1}{\sqrt i },b_{i} = \frac{{a_{i} }}{c}$, $i \in I_{n}$, for ellipses with eccentricity $e = \sqrt {1 - \frac{1}{{c^{2} }}}$ and a regular polygonal domain with m sides for the container.

Two groups of instances presented in [2] were running by our approach:

• The first group of instances: for c = 1.00, 1.05, 1.15, 1.35, 1.50, 1.75, 2.00, n = 3, 4, 5, 6, 8, 10 and m = 3, 4, 5, 6, 8.

• The second group of instances: for c = 1.00, 1.05, 1.15, 1.35, 1.50, 1.75, 2.00, n = 10,15, 20 and m = 40.

Comparative results for 210 instances of the first group are presented in Tables 1, 2, 3, 4, 5, 6 and 7, while Table 8 summarizes computational results for 21 instances of the second group. For each problem instance we present the area of the optimized container (line Area) and CPU time in sec. (line Time) corresponding to our algorithm (column our result). The area of the optimized container obtained in [2] is also presented (column [2]). Since our computer, computing platform and solver used for subproblems are different from those used in [2], we do not compare here CPU times for both techniques. The column “impr. %” corresponds to the area of the optimized container and gives the value (result of [2] minus our result)/(result of [2]) in %. Thus positive values in this column indicate the better performance of our approach, while zero or negative (highlighted in bold) show that results of [2] were not improved. We used 10 runs for the LOFTR_P procedure in our multistart strategy for each instance.

Table 1 Comparison of results for c = 1

Table 2 Comparison of results for c = 1.05

Table 3 Comparison of results for c = 1.15

Table 4 Comparison of results for c = 1.25

Table 5 Comparison of results for c = 1.50

Table 6 Comparison of results for c = 1.75

Table 7 Comparison of results for c = 2

Table 8 Comparison results for m = 40

Figures 12 and 13 demonstrate our optimized packings for some problem instances of the first group. In [2] one can find configurations obtained for the same instances by their approach.

Fig. 12

Packings for n = 8 ellipses with parameter c = 1.25 in a regular polygon of m = 3, 4, 5, 6 sides

Fig. 13

Packings for n = 8 ellipses with parameter c = 1.0, 1.05, 1.15, 1.25, 1.50, 1.75, 2.0 in a regular polygon of m = 8 sides

Figure 14 provides our optimized packings for some problem instances of the second group: packing n = 20 ellipses with six different values of parameter $c = \frac{{a_{i} }}{{b_{i} }}$, $i \in I_{n}$, in a regular polygon of m = 40 sides. In [2] one can find configurations for the same instances obtained by their approach.

Fig. 14

Packings for n = 20 ellipses with parameter c = 1.05, 1.15, 1.25, 1.50, 1.75, 2.0, in a regular polygon of m = 40 sides

7 Conclusions

In this work we study a packing problem of a set of n arbitrary ellipses into an optimized convex polygon. The packed ellipses are given by their semi-axes and can be continuously translated and rotated. We propose new tools of mathematical modelling of placement constraints: a quasi phi-function to describe non-overlapping ellipses and a phi-function for containment constraints. Our quasi phi-function is considerably simpler than the quasi phi-function presented in [1, 12]: it has only one auxiliary variable and does not involve the “min” operator. An exact mathematical formulation for the ellipse packing problem is stated as the large scale nonlinear programming problem with $O(n^{2} )$ continuous variables and $O(n^{2} )$ nonlinear inequalities. We propose a simple algorithm to construct feasible starting points and the LOFTR_P procedure to search for good local optimal solutions. The LOFTR_P typically reduces our problem to a sequence of nonlinear programming subproblems of smaller dimension with $O(n)$ variables and $O(n)$ constraints. Computational results are provided to demonstrate the efficiency of our approach. The experiments were performed by solving new problem instances, as well as for the instances presented in [2]. In this work an open source local solver IPOPT [15] was used for implementing the algorithms. However, open source or commercial global solvers (i.e., COUENNE [16] or LGO [17]) can be used directly for the exact formulations (NLP-models) of the problems EPP_1 or EPP_2. Using global solvers in combination with the proposed starting point algorithm is an interesting direction for the future research.