Thermodynamically consistent non-local damage formulation for fluid-driven fracture in poro-viscoelastic media

Abstract

We present a novel non-local integral-type damage formulation for hydraulic fracture of poro-viscoelastic media under the framework of irreversible thermodynamics. The poro-viscoelastic material is modeled by a generalized Maxwell model, whose shear modulus is described in terms of Prony series. A bilinear damage law is assumed, which is driven by three equivalent strain invariants. Darcy’s law is employed to describe the fluid flow in the entire domain including the fracture process zone, where the permeability is assumed to be nonlinear and anisotropic. A monolithic two-field (${\varvec{u}}-p$) mixed finite element method is employed to discretize the coupled hydromechanical system. A Newton–Raphson method is utilized to solve the nonlinear system, and a backward Euler scheme is applied to evolve the system in time. Several numerical examples are presented to investigate the time-dependent deformation response of saturated porous media. In particular, we study the effects of relaxation time and the ratios of anisotropic initial permeability on the strongly coupled processes of the solid deformation, fluid transport and damage evolution of geomaterials. In addition, the different modes of energy dissipation mechanisms including damage and solid viscous response are presented and discussed.

1 Introduction

Hydraulic fracture has gained significant interest in petroleum engineering since it was first introduced in 1949 [24]. This process is used to create high-permeability flow channels in tight low permeability reservoirs resulting in an efficient exploitation of underground resources [9, 73]. In addition, hydraulic fracture gained interest in closely related applications, including: deep ground-water excavation [40], deep geothermal energy-plant technologies [101], measurement of in-situ stresses [33], earth dams disaster prevention [51], carbon sequestration [66] and others.

The interaction of fluid with porous media can be described by Biot’s theory of poroelasticity [10], a formulation that provides the basic governing equations including the mechanical equilibrium and fluid mass conservation. These balance laws are complemented by a linear stress–strain constitutive law for solid and a Darcy-type law for the fluid transport. A wide range of studies on poromechanics have been reported in the literature with applications to, e.g., geomaterials [2, 3] and biomaterials [92].

While many studies focus on linear poro-elasticity, in reality, the solid skeleton experiences time-dependent deformation such as creep and relaxation under long-term loading and strain-rate dependence under impact conditions as shown by in both in-situ measurements and laboratory creep tests on several geomaterials, e.g., shale [109], carbonates [105], welded tuff [82], tight sandstone [34] and calcite [108]. In particular, in cases of extreme complex loading at deeper reservoirs featuring high-temperature and high-stress conditions, time-dependent poro-viscoelasticity becomes important, but is typically neglected in traditional hydraulic fracturing models [35, 119].

Various rheological models have been utilized to characterize the time-dependent deformation behavior of a solid, for instance, Maxwell model [104], Kelvin model [96], Burgers model [132], generalized Maxwell model [80, 116], generalized Kelvin model [138], Glen’s creep law [37], fractional model [36, 75, 142] and some hybrid approaches like fractional Maxwell model [34] and fractional Kelvin model [131]. Biot [11] analytically derived the relaxation models via a correspondence principle for the fluid-solid media. Ehlers and Markert [41] established a poro-viscoelastic framework based on the generalized Maxwell model to describe the time-dependent motion in cartilage tissues. However, these works do not consider damage or fracture behavior in the porous media. Huang and Ghassemi [59] constructed a poro-viscoelastic model based on the Maxwell model to simulate the coupled processes of the gas depletion and compressible fluid flow in the fractured shale while lacking the description of crack propagation.

Fracture modeling in fluid-saturated porous media involves complex physical processes and their mutual couplings, in which the solid skeleton deforms with the fluid flowing into the pores and the fractured area [95]. To resolve such coupled systems, a variety of numerical strategies have been developed to predict fracture initiation and propagation in porous media. These methods can be grouped into two common categories: discrete approaches and continuum damage approaches [47]. In discrete methods, the discontinuous displacement introduced by the crack is resolved exactly. Examples in this category include: linear elastic fracture mechanics (LEFM) [12], extended finite element methods (XFEM) [29, 43, 107], generalized finite element methods (GFEM) [68, 113, 114] and cohesive zone models (CZM) [77]. Song et al. [120] numerically modeled fluid-driven fracture propagation using the extended finite element method (XFEM)-based cohesive zone model (CZM) model in which the viscoelastic properties are obtained via creep tests of shale samples. Suo et al. [122] and Ding et al. [35] employed the CZM to investigate hydraulic fracture propagation in poro-viscoelastic formation with Maxwell and fractional-Maxwell models. Nevertheless, the shortcomings and challenges of the aforementioned fracture mechanics approaches are the need for (i) criteria for fracture initiation [46], (ii) tracking the quite complex fracturing pattern, e.g., multi-cracks and 3D non-planar crack propagation [94], and (iii) non-traditional integration algorithms for stiffness matrices [128].

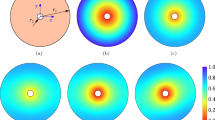
As opposed to discrete fracture methods, continuum damage methods (CDM) do not attempt to resolve the fracture geometry explicitly. Instead internal variables are introduced at specific points (typically at all Gauss points in the domain), with empirical evolution laws that are used to degrade/reduce the stiffness at those points [67, 71]. Typically, the damage parameter ranges from 0 in an undamaged state to 1 in a fully damaged state (see Fig. 1a). To this end, a wide range of empirical evolution laws have been proposed in the literature, e.g., the bilinear type [90] and exponential type by Mazars [85] with further improvements of Peerlings et al. [98]. Phenomenological and numerical models have been proposed to describe CDM in poroelastic domains for different applications e.g., rock mechanics [57, 81], geotechnical engineering [23], hydraulic fracture [111, 133], indentation problems [110] and others. Carmeliet [18] adopted a poro-viscoelastic model in conjunction with CDM to investigate a multi-physics coupling of fluid mass transfer, time-dependent deformation of solid and damage propagation. Wilson et al. [130] investigated the relation between the structural properties and degenerative changes of the highly viscoelastic articular cartilage. In the case of classical CDM where damage grows independently at each material point, once damage growth is triggered, the deformation increases sharply and rapidly, displaying a more pronounced strain softening (localization) phenomenon [1]. Further, the size of fracture process zone is governed by the mesh size resulting in the lack of uniqueness, i.e., one may obtain unreliable numerical solutions due to the loss of ellipticity of the governing equations [100].

To tackle this issue, some damage regularization methods have been presented, e.g., non-local integral-type [26, 100], non-local gradient-type [30, 90] and phase field [15, 50] methods. These approaches introduce an auxiliary length scale to smear localized quantities and alleviate the dependence on element size (see Fig. 1b). Such regularization strategies can effectively alleviate the mesh dependence in fracture simulations, leading to robust solutions. In addition, the issue of crack coalescence, branching, crossing and kinking can be readily represented. Several studies [70, 72, 86, 129, 134, 140] have employed the phase field method to investigate hydraulic fracture propagation in poroelastic media, while others utilized the non-local gradient damage for the same [89,90,91]. Both of these methods introduce additional degrees of freedom. However, none of these studies accounted for time-dependent response of the solid. We note that the non-local integral-type approach leads to a solution strategy that avoids the need for additional degrees of freedom, required by most of the other non-local methods [118]. However, downgraded performance is documented for non-convex boundaries (e.g., near notches and re-entrant corners) for which a special treatment of the non-locality operators is required [32, 106]; it may also be cumbersome to obtain the explicit derivation of non-local damage-related quantities for the consistent Jacobian in fully implicit implementations, and the system matrix bandwidth might increase due to the introduction of the length scale, which requires some additional strategies (e.g., domain partitioning or adaptive mesh refinement) to reduce the computational cost for large-scale simulations. Nevertheless, the non-local integral-type approach can more easily be extended to any multi-physics coupling problems without major modifications to the FEM code and the system of equations, and especially do not need extra degrees of freedom, which has motivated us in this work.

Fig. 1

Schematic illustration of two-dimensional fracture problem: a sharp fracture and b diffusive fracture topology in which the sharp fracture is smeared over a characteristic length scale $l_\mathrm{c}$. The fracture is modeled by the damage variable, which takes the value 1 in a fully damaged state and 0 in a undamaged state

Darcy’s law is widely employed in geomechanics to describe the fluid flow within the pores. Darcy’s law assumes that the fluid flow is laminar with a low Reynolds number, which is especially valid in deep formations due to the high compaction level of the solid phase [49]. Armitage et al. [4] experimentally confirmed the existence of initial anisotropy permeability in deep formations, even before fracture initiation. In reality, an existing fracture process zone, which serves as a infiltration channel, can effectively induce fluid preferential transport leading to a high velocity flow inside that fracturing domain [25, 137]. Based on the available experimental data, attempts have been made in the past to develop empirical permeability–strain [90], permeability–stress [91], permeability–damage [137], and permeability–pressure gradient [74] relationships. Additionally, lubrication (Poiseuille’s) equation is also widely employed in the literature to describe a laminar fluid flow rule inside a hydraulically driven fracture [6, 54]. However, such model needs an explicit definition of fracture opening. While it can be straightforward to obtain the fracture opening with discrete fracture approaches, e.g., LEFM [12], XFEM [78] and GFEM [55], it is knotty to calculate the fracture-width-like quantities in continuum fracture approaches [129].

In the current work, our objective is to present a thermodynamically consistent framework for time-dependent hydromechanical systems coupled with non-local damage to model hydraulic fracture processes. In particular we assume that the porous media are viscoelastic and may exhibit creep and relaxation-type phenomenon. The proposed model has several novel contributions compared with our previous work [23]. This includes: (a) a thermodynamically consistent formulation for poro-viscoelastic-damage model incorporating the generalized Maxwell model and non-local regularization formulation, (b) discussion of the energy dissipation processes and the interplay between viscous and damage effects and (c) introduction of an initial anisotropy permeability to highlight that horizontal permeability is higher than that in vertical direction in deep formations.

The structure of this paper is organized as follows. In Sect. 2, conservation laws for saturated porous media are revisited. Subsequently, the Helmholtz free energy function is specified and a thermodynamically consistent framework is constructed to derive the state laws and dissipated energy formulations. Section 3 details the constitutive framework for the solid skeleton, the damage evolution and the nonlinear Darcy’s transport law with anisotropic initial permeability. A two-field mixed finite element formulation of the fully coupled hydromechanical system and its solution algorithm are described in Sect. 4. Finally, in Sect. 5, numerical examples are presented to demonstrate the predictive capability of the proposed model. Results from the hydraulic fracture configuration show that both fluid diffusion and fracture propagation tend to be slower as relaxation time increases due to a slower shear relaxation modulus degradation. Poro-viscoelasticity experiences significant dissipation during fracture development with viscous dissipation domination. In addition, the larger horizontal permeability facilitates the fracture initiation. Also, in the anisotropic initial permeability cases, the fluid pressure, damage and effective stress exhibit a more flattened elliptical distribution than that in isotropic initial permeability case.

Throughout this paper, note that scalars and scalar-valued functions are written in light letters (e.g., p, D), first- and second-order tensors and tensor-valued functions are written in bold letters (e.g., ${\varvec{u}}$, $\varvec{\sigma }$), fourth-order tensors with blackboard bold letters (e.g., $\tilde{{\mathbb {C}}}$). Additionally, the following notions of the tensorial product are used, i.e., ${\varvec{A}} \otimes {\varvec{B}}={\varvec{A}}_{i j} {\varvec{B}}_{k l}$, ${\varvec{A}}: {\varvec{B}}={\varvec{A}}_{ij} {\varvec{B}}_{ij}$. We also define the corresponding identity tensors as ${\varvec{I}}=\delta _{i j}$, ${\mathbb {I}}=\frac{1}{2}(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})$, ${\mathbb {I}}_\mathrm{vol}=\frac{1}{3}\delta _{ij}\delta _{kl}$, ${\mathbb {I}}_\mathrm{dev}={\mathbb {I}}-{\mathbb {I}}_\mathrm{vol}$, where $\delta _{i j}$ is the Kronecker delta. $\nabla \cdot (\cdot )$, $\nabla (\cdot )$ and $\nabla ^{s}(\cdot )$ are the divergence, gradient and symmetric gradient of $(\cdot )$, respectively. $(\cdot )^{T}$, $(\cdot )^{-1}$ and $\dot{(\cdot )}$ denote the transpose, inverse and time derivative of $(\cdot )$, respectively. As for the sign convention, unless otherwise specified, we consider tensile stresses as positive.

2 Poro-viscoelasticity with damage

2.1 Conservation laws

Poroelasticity as introduced by Biot [10] provides a rigorous theory for coupling the deformation of a porous solid skeleton with a fluid that flows in the pores. The governing partial differential equations for fluid-saturated porous media describing the balance of linear momentum for the mixture, assuming that pore air pressure is negligible, can be written as follows [2, 28, 61]

$$\begin{aligned} \nabla \cdot \varvec{\sigma }+{\varvec{b}}={\varvec{0}} \end{aligned}$$

(1)

and balance of mass given by

$$\begin{aligned} {\dot{\zeta }}+\nabla \cdot {\varvec{v}}_\mathrm{f}=0 \end{aligned}$$

(2)

where $\varvec{\sigma }$ denotes the Cauchy stress tensor, ${\varvec{b}}$ is the mechanical body load vector, $\zeta$ is the increment in fluid volume content, and ${\varvec{v}}_\mathrm{f}$ is the fluid flow velocity. Note that we assume that inertia terms are negligible.

According to the formulations in [91, 134], the internal energy production rate for a fluid-saturated porous media is given as

$$\begin{aligned} \rho \dot{{\mathscr {E}}}=\varvec{\sigma }: \dot{\varvec{\varepsilon }}+ p {\dot{\zeta }} \end{aligned}$$

(3)

where $\rho$ is the mass density of the media, ${\mathscr {E}}$ denotes the entropy per unit mass, $\varvec{\varepsilon }$ represents the total strain as $\varvec{\varepsilon } \equiv \nabla ^{s} {\varvec{u}}=\frac{1}{2}\left( \nabla {\varvec{u}}+\nabla {\varvec{u}}^{T}\right)$ under the hypothesis of infinitesimal deformation, with ${\varvec{u}}$ being the displacement field of the solid phase, and p is the fluid pressure.

2.2 Thermodynamics of the porous media including damage

2.2.1 Specification of the Helmholtz free energy function

In the current work, a non-local damage method is introduced to study the damage propagation in fluid-saturated porous media. In particular, an internal damage variable is used to degrade the material stiffness, which in turn increases the fluid permeability. It is therefore necessary to derive a consistent thermodynamic poro-viscoelastic model for fracture of a saturated porous media.

A free energy per unit volume $\psi$ expression is introduced in the solid-fluid-damage system and is additively decomposed into two parts

$$\begin{aligned} \psi (\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i},\zeta ,\breve{D}) =\psi _{ve}(\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i}, \breve{D}) +\psi _\mathrm{f}(\varvec{\varepsilon },\zeta ,\breve{D}) \end{aligned}$$

(4)

where $\psi _\mathrm{ve}$ is the viscoelastic strain energy, $\psi _\mathrm{f}$ denotes the fluid contribution to the total free energy per unit volume, and $\breve{D}$ is a non-local damage measure that will be defined in Sect. 4.2. In this work, we utilize the generalized Maxwell model constructed as a set of parallel branches that consist of springs and dashpots to describe the viscoelastic response of the solid skeleton (see Fig. 2). This model assumes that the elastic volumetric response is time-independent, while the deviatoric component of the stress is time-dependent. The effective stress in this viscoelastic model is given as [117, 124]

$$\begin{aligned} \tilde{\varvec{\sigma }}(t)=\tilde{\varvec{\sigma }}_\mathrm{vol}+ \tilde{\varvec{\sigma }}_\mathrm{dev}^{\infty }+\sum _{i=1}^{n} \tilde{\varvec{\sigma }}_\mathrm{dev}^{i}(t) \end{aligned}$$

(5)

with $\tilde{\varvec{\sigma }}_\mathrm{vol}$ and $\tilde{\varvec{\sigma }}_\mathrm{dev}^{\infty }$ being the effective volumetric and deviatoric stresses in the pure spring branch, and $\tilde{\varvec{\sigma }}_\mathrm{dev}^{i}(t)$ is the time-dependent effective deviatoric stress in the ith Maxwell unit branch. The total deviatoric strain is defined as ${\varvec{e}}={\varvec{e}}_\mathrm{e}^{i}+\varvec{\alpha }_\mathrm{v}^{i}$, with ${\varvec{e}}_\mathrm{e}^{i}$ and $\varvec{\alpha }_\mathrm{v}^{i}$ being the elastic deviatoric strain of the spring and the viscous strain due to the dashpot of the ith Maxwell unit branch, respectively.

Fig. 2

Schematic showing the generalized Maxwell model [117]. K and $G^{\infty }$ are the bulk modulus and shear modulus corresponding to the pure spring branch, $G^{i}$ and $\eta ^{i}$ are the spring shear modulus and viscosity of the corresponding dashpot in ith Maxwell branch, respectively, and n is the number of Maxwell branches

The viscoelastic free energy degraded by a non-local damage can be expressed as [116]

$$\begin{aligned} \psi _{ve}(\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i}, \breve{D})= & {} (1-\breve{D}) {\tilde{\psi }}_{ve}(\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i}) =(1-\breve{D}) \left[ \frac{1}{2} K {\text {tr}}(\varvec{\varepsilon }) {\text {tr}}(\varvec{\varepsilon }) \right. \nonumber \\&\left. +G^{\infty } {\varvec{e}}: {\varvec{e}} +\sum _{i=1}^{n} G^{i} \left( {\varvec{e}}-\varvec{\alpha }_\mathrm{v}^{i}\right) : \left( {\varvec{e}}-\varvec{\alpha }_\mathrm{v}^{i}\right) \right] \end{aligned}$$

(6)

where ${\tilde{\psi }}_\mathrm{ve}(\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i})$ is the viscoelastic free energy in the undamaged state.

The fluid contribution to the total free energy, $\psi _\mathrm{f}(\varvec{\varepsilon },\zeta ,\breve{D})$, can be written as follows [87, 134]

$$\begin{aligned} \psi _\mathrm{f}(\varvec{\varepsilon },\zeta ,\breve{D}) =\frac{M(\breve{D})}{2}\left[ \zeta -\alpha (\breve{D}) {\text {tr}}(\varvec{\varepsilon })\right] ^{2} \end{aligned}$$

(7)

where M and $\alpha$ are Biot’s coefficient and Biot’s modulus, respectively, which provide measures for the solid and fluid compressibility. In this work, we allow both Biot parameters to vary with the damage growth provided in Sect. 3.1, which indicates that the compressibility of materials is functions of the damage [112].

2.2.2 Thermodynamic consistency

The second law of thermodynamics constructed in the form of the Clausius–Duhem inequality [56], is used to verify the dissipated and stored energies of the proposed poro-viscoelastic non-local damage model. Specifically, under an isothermal process, the total mechanical dissipation ${\mathscr {D}}$ should be non-negative [56]. In the presence of non-local phenomena, the Clausius–Duhem inequality must be expressed in its integral form over volume because the energy dissipation is non-local [14, 102], which reads

$$\begin{aligned} \int _{{\varOmega }} {\mathscr {D}} \hbox {d}{\varOmega }=\int _{{\varOmega }} \left( \rho \dot{{\mathscr {E}}}-{\dot{\psi }}\right) \hbox {d}{\varOmega } \ge 0 \end{aligned}$$

(8)

where ${\varOmega }$ is the volume of the domain, and ${\dot{\psi }}$ is the rate of the free energy. According to the suggestion by Polizzotto et al. [103] and Borino et al. [13], Eq. (8) can be rewritten in a pointwise form by introducing a non-locality residual function ${\mathscr {P}}$ which accounts for the energy exchanges between neighbor particles. As a consequence, Eq. (8) is recast into the following form

$$\begin{aligned} {\mathscr {D}}=\rho \dot{{\mathscr {E}}}-{\dot{\psi }}+{\mathscr {P}} \ge 0 \end{aligned}$$

(9)

with

$$\begin{aligned} \int _{{\varOmega }} {\mathscr {P}} \hbox {d} {\varOmega }=0 \end{aligned}$$

(10)

Recalling the definition in Eq. (4), the rate of free energy is obtained as

$$\begin{aligned} {\dot{\psi }}={\dot{\psi }}_\mathrm{ve}+{\dot{\psi }}_\mathrm{f} \end{aligned}$$

(11)

Applying the chain rule and expanding the rate of free energy in Eq. (11), and in addition considering Eqs. (6) and (7), we have

$$\begin{aligned} {\dot{\psi }}_\mathrm{ve}&=\frac{\partial \psi _\mathrm{ve}}{\partial \varvec{\varepsilon }}: \dot{\varvec{\varepsilon }} +\frac{\partial \psi _\mathrm{ve}}{\partial \varvec{\alpha }_\mathrm{v}^{i}} \dot{\varvec{\alpha }}_\mathrm{v}^{i} +\frac{\partial \psi _\mathrm{ve}}{\partial \breve{D}} \dot{\breve{D}} \end{aligned}$$

(12)

$$\begin{aligned} {\dot{\psi }}_\mathrm{f}&=\frac{\partial \psi _\mathrm{f}}{\partial \varvec{\varepsilon }}: \dot{\varvec{\varepsilon }} +\frac{\partial \psi _\mathrm{f}}{\partial \zeta } {\dot{\zeta }} +\frac{\partial \psi _\mathrm{f}}{\partial \breve{D}} \dot{\breve{D}} \end{aligned}$$

(13)

Substituting Eqs. (3) and (11)–(13) into Eq. (9) and rearranging terms, the inequality can be expanded as

$$\begin{aligned} {\mathscr {D}}&= \left( \varvec{\sigma } -\frac{\partial \psi _\mathrm{ve}}{\partial \varvec{\varepsilon }} -\frac{\partial \psi _\mathrm{f}}{\partial \varvec{\varepsilon }}\right) : \dot{\varvec{\varepsilon }} +\left( p-\frac{\partial \psi _\mathrm{f}}{\partial \zeta }\right) {\dot{\zeta }} \nonumber \\&\quad -\frac{\partial \psi _\mathrm{ve}}{\partial \varvec{\alpha }_\mathrm{v}^{i}} \dot{\varvec{\alpha }}_\mathrm{v}^{i} -\frac{\partial \psi _\mathrm{ve}}{\partial \breve{D}} \dot{\breve{D}} -\frac{\partial \psi _\mathrm{f}}{\partial \breve{D}} \dot{\breve{D}} +{\mathscr {P}} \ge 0 \end{aligned}$$

(14)

The above inequality must hold for any arbitrary thermodynamic process. Thus, the coefficients $\dot{\varvec{\varepsilon }}$ and ${\dot{\zeta }}$ which represent non-dissipative terms must vanish, for otherwise the rate may be chosen to violate inequality (14). Therefore, the first and second terms vanish and together with the definition in Eqs. (6) and (7), one gets

$$\begin{aligned} \varvec{\sigma }&=\frac{\partial \psi _\mathrm{ve}}{\partial \varvec{\varepsilon }} +\frac{\partial \psi _\mathrm{f}}{\partial \varvec{\varepsilon }} \end{aligned}$$

(15)

$$\begin{aligned} p&=\frac{\partial \psi _\mathrm{f}}{\partial \zeta } \end{aligned}$$

(16)

Then, the rate of the total dissipated energy per unit volume, ${\dot{\psi }}_{t}^\mathrm{dis}$, consists of the third to sixth terms of Eq. (14) that accounts for a viscous dissipation from the dashpots ${\dot{\psi }}_\mathrm{v}^\mathrm{dis}$, dissipation due to damage ${\dot{\psi }}_\mathrm{d}^\mathrm{dis}$, fluid ${\dot{\psi }}_\mathrm{f}^\mathrm{dis}$ and non-locality energy exchanges ${\mathscr {P}}$ such that

$$\begin{aligned} {\dot{\psi }}_\mathrm{t}^\mathrm{dis}&={\dot{\psi }}_\mathrm{v}^\mathrm{dis}+{\dot{\psi }}_{d}^\mathrm{dis}+{\dot{\psi }}_\mathrm{f}^\mathrm{dis}+{\mathscr {P}} =-\frac{\partial \psi _{ve}}{\partial \varvec{\alpha }_\mathrm{v}^{i}}: \dot{\varvec{\alpha }}_\mathrm{v}^{i} -\frac{\partial \psi _{ve}}{\partial \breve{D}} \dot{\breve{D}} \nonumber \\&\quad -\frac{\partial \psi _\mathrm{f}}{\partial \breve{D}} \dot{\breve{D}} +{\mathscr {P}} \ge 0 \end{aligned}$$

(17)

The detailed derivations of the terms $\frac{\partial \psi _\mathrm{ve}}{\partial \varvec{\alpha }_\mathrm{v}^{i}}$, $\frac{\partial \psi _\mathrm{ve}}{\partial \breve{D}}$ and $\frac{\partial \psi _\mathrm{f}}{\partial \breve{D}}$ in Eq. (17) are given in the Appendix 1. Furthermore, the dissipated energy density of viscous $\psi _\mathrm{v}^\mathrm{dis}$, damage $\psi _\mathrm{d}^\mathrm{dis}$ and fluid $\psi _\mathrm{f}^\mathrm{dis}$ over the time domain can be obtained from the rate of dissipated energy (17) as

$$\begin{aligned} \psi _\mathrm{v}^\mathrm{dis}= & {} \int _{0}^{t} {\dot{\psi }}_\mathrm{v}^\mathrm{dis} \hbox {d}t, \qquad \psi _\mathrm{d}^\mathrm{dis}=\int _{0}^{t} {\dot{\psi }}_\mathrm{d}^\mathrm{dis} \hbox {d}t, \qquad \nonumber \\ \psi _\mathrm{f}^\mathrm{dis}= & {} \int _{0}^{t} {\dot{\psi }}_\mathrm{f}^\mathrm{dis} \hbox {d}t \end{aligned}$$

(18)

and the total dissipated energy of viscous $\psi _{v,T}^\mathrm{dis}$, damage $\psi _{d,T}^\mathrm{dis}$ and fluid $\psi _{f,T}^\mathrm{dis}$ over the domain can be defined as

$$\begin{aligned} \psi _{v,T}^\mathrm{dis}= & {} \int _{{\varOmega }} \psi _\mathrm{v}^\mathrm{dis} \hbox{d}{\varOmega }, \qquad \psi _{d,T}^\mathrm{dis}=\int _{{\varOmega }} \psi _{d}^\mathrm{dis} \hbox{d}{\varOmega }, \qquad \nonumber \\ \psi _{f,T}^\mathrm{dis}= & {} \int _{{\varOmega }} \psi _\mathrm{f}^\mathrm{dis} \hbox{d}{\varOmega } \end{aligned}$$

(19)

Remark 1

The deviatoric stress of the spring in the ith Maxwell branch is equal to that in the dashpot as $2 G^{i} {\varvec{e}}_{e}^{i}=\eta ^{i} \dot{\varvec{\alpha }}_\mathrm{v}^{i}$, and yields $2 G^{i} {\varvec{e}}_{e}^{i}:\dot{\varvec{\alpha }}_\mathrm{v}^{i}=\eta ^{i} \dot{\varvec{\alpha }}_\mathrm{v}^{i}:\dot{\varvec{\alpha }}_\mathrm{v}^{i}\ge 0$ [116]. Since the non-local damage varies from 0 to 1, the viscous dissipated energy is positive. The rate of non-local damage satisfies the relation $\dot{\breve{D}} \ge 0$ since damage healing or recovery is not considered in this work; thus, we have positive damage and fluid dissipated energy based on the definition in Eqs. (61) and (63). Then, the total dissipated energy in the system in Eq. (17) naturally satisfies the non-negative condition and the first two dissipated energy is the dominant terms.

3 Constitutive relations and evolution laws

3.1 Poro-viscoelastic damage relationships

The constitutive relationship defining the fluid pressure can be obtained by substituting Eq. (7) into Eq. (16), such that

$$\begin{aligned} p=\frac{\partial \psi _\mathrm{f}}{\partial \zeta } =M(\breve{D})\left[ \zeta -\alpha (\breve{D}) {\text {tr}} (\varvec{\varepsilon }) \right] \end{aligned}$$

(20)

According to the derivations in the literatures [21, 22, 112], the damage-dependent Biot’s coefficient and modulus can be expressed as

$$\begin{aligned} \alpha (\breve{D})=1-\frac{K(\breve{D})}{K_{s}} \end{aligned}$$

(21)

and

$$\begin{aligned} M(\breve{D})=\frac{K_{u}-K(\breve{D})}{\alpha (\breve{D})^{2}} \end{aligned}$$

(22)

where the damaged bulk modulus is $K(\breve{D})=(1-\breve{D})K$, $K_{s}$ denotes the solid grain bulk modulus, and $K_{u}$ is the undrained bulk modulus given as

$$\begin{aligned} K^{u}=\frac{2 G(t) \left( 1+\nu _{u}\right) }{3\left( 1-2 \nu _{u}\right) } \end{aligned}$$

(23)

with

$$\begin{aligned} G(t)=G^{\infty }+\sum _{i=1}^{n} G^{i} e^{-\frac{t}{\lambda ^{i}}} \end{aligned}$$

(24)

where $\nu _{u}$ is the undrained Poisson’s ratio of the porous media, G(t) denotes the time-dependent shear modulus of the solid skeleton in the context of the generalized Maxwell model, and $\lambda ^{i}=\frac{\eta ^{i}}{G^{i}}$ denotes the relaxation time of the ith dashpot branch.

The total Cauchy stress $\varvec{\sigma }$ can be derived by combining Eqs. (6), (7) and (15) as follows

$$\begin{aligned} \varvec{\sigma }(t)=&\frac{\partial \psi _{e}}{\partial \varvec{\varepsilon }}+\frac{\partial \psi _\mathrm{f}}{\partial \varvec{\varepsilon }} =(1-\breve{D}) \left[ K {\text {tr}}(\varvec{\varepsilon }) {\varvec{I}}+2 G ^{\infty } {\varvec{e}}\right. \nonumber \\&\left. +\sum _{i=1}^{n} 2 G^{i} {\varvec{e}}_{e}^{i}(t) \right] -\alpha (\breve{D}) p {\varvec{I}} \end{aligned}$$

(25)

For the generalized Maxwell model, the deviatoric strain component ${\varvec{e}}_{e}^{i}(t)$ is considered to be time-dependent, which can be described using a Prony series form [124]. Detailed discussion on Prony series can be found in [80, 116, 117]. Here, we directly provide the explicit Prony series expression at the current time step $t=t_{n+1}=t_{n}+\Delta t$ with $\Delta t$ being the time step size

$$\begin{aligned} {\varvec{e}}_{e}^{i}(t) =e^{-\frac{\Delta t}{\lambda ^{i}}} {\varvec{e}}_{e,n}^{i} +\lambda ^{i}\left( 1-e^{-\frac{\Delta t}{\lambda ^{i}}}\right) \frac{{\varvec{e}}-{\varvec{e}}_{n}}{\Delta t} \end{aligned}$$

(26)

Moreover, in saturated poro-viscoelastic geomaterials considering damage of the media, the total Cauchy stress $\varvec{\sigma }(t)$ can be taken as a combination of a homogenized solid stress $\varvec{\sigma }_{s}$ and a fluid stress $\varvec{\sigma }_\mathrm{f}$ based on the effective stress principle attributed to Terzaghi [126], such that

$$\begin{aligned} \varvec{\sigma }(t) =\varvec{\sigma }_{s}(t)+\varvec{\sigma }_\mathrm{f} =(1-\breve{D}) \tilde{\varvec{\sigma }}(t)-\alpha (\breve{D}) p {\varvec{I}} \end{aligned}$$

(27)

The effective stress $\tilde{\varvec{\sigma }}(t)$ in the undamaged state can be obtained by comparing Eqs. (25) and (27), such that

$$\begin{aligned} \tilde{\varvec{\sigma }}(t)&=K {\text {tr}}(\varvec{\varepsilon }) {\varvec{I}}+2 G ^{\infty } {\varvec{e}}+\sum _{i=1}^{n} 2 G^{i} \left[ e^{-\frac{\Delta t}{\lambda ^{i}}} {\varvec{e}}_{e,n}^{i}\right. \nonumber \\&\quad \left. +\lambda ^{i}\left( 1-e^{-\frac{\Delta t}{\lambda ^{i}}}\right) \frac{{\varvec{e}}-{\varvec{e}}_{n}}{\Delta t} \right] \end{aligned}$$

(28)

Finally, the undamaged tangent stiffness tensor $\tilde{{\mathbb {C}}}$ for viscoelastic materials can be obtained by linearizing Eq. (28) which yields

$$\begin{aligned} \tilde{{\mathbb {C}}}=\frac{\partial \tilde{\varvec{\sigma }}(t)}{\partial \varvec{\varepsilon }}=3 K {\mathbb {I}}_\mathrm{vol}+\left[ 2 G^{\infty }+\sum _{i=1}^{n} 2 G^{i} \frac{\lambda ^{i}}{\Delta t}\left( 1-e^{-\frac{\Delta t}{\lambda ^{i}}}\right) \right] {\mathbb {I}}_\mathrm{dev} \end{aligned}$$

(29)

with the operators ${\mathbb {I}}_\mathrm{vol}$ and ${\mathbb {I}}_\mathrm{dev}$ defined in Sect. 1.

3.2 Equivalent strain measure

Failure analysis in porous media has been investigated by experiments [52, 84, 97] and numerical studies [88, 89, 136]. These studies concluded that the increasing damage and therefore the permeability is mainly resulting from three inducement (i) tensile loads cause an increase in the micro-crack aperture size, (ii) shear dilation occurs, while the shear stresses exceed the shear strength at a material point, and (iii) direct volumetric expansion causes the pore dilation. Hayhurst [58] established a damage loading function that consists of the maximum principal tensile stress and the first and second stress invariants to recognize the creep rupture behavior. Recently, Mobasher et al. employed a deviatoric-volumetric split equivalent strain measure [90] and a Hayhurst-type equivalent stress formulation [89, 91] to control the damage evolution in multi-axial directions. This approach enables the use of a scalar damage model and alleviates the costly computations with damage tensors [127]. Motivated by the above studies, we assume the local damage and permeability evolution to be a function of a three-invariant equivalent strain measurements, which can be written as

$$\begin{aligned} {\tilde{\varepsilon }}_\mathrm{eq}= {\left\{ \begin{array}{ll} \chi , &{}\quad \text { if } \chi \ge 0 \\ 0, &{}\quad \text { otherwise } \end{array}\right. } \end{aligned}$$

(30)

with

$$\begin{aligned} \chi =\xi _{1} \varepsilon _{1}+\xi _{2} \sqrt{J_{2}^{\varepsilon }}+(1-\xi _{1}-\xi _{2}) I_{1}^{\varepsilon } \end{aligned}$$

(31)

where the constants $\xi _{1}$ and $\xi _{2}$ are material parameters, calibrated from experiments, that control the material failure. For consistency, these parameters should satisfy the conditions: $0 \le \xi _{1}, \xi _{2} \le 1$ and $\xi _{1}+\xi _{2} \le 1$. The equivalent strain formulation in Eq. (31) provides three strain invariants: (a) $\varepsilon _{1}$ is the highest eigenvalue of strain that controls model-I like crack opening mechanism, (b) $J_{2}^{\varepsilon }=\frac{1}{2} \varvec{\varepsilon }(t):\varvec{\varepsilon }(t)-\frac{1}{6} (I_{1}^{\varepsilon })^2$ is the second invariant of the deviatoric strain, which accounts for the shear component of the deformation, and (c) $I_{1}^{\varepsilon }={\text {tr}}(\varvec{\varepsilon }(t))$ is the volumetric strain contributing directly to pore dilation.

3.3 Local damage evolution law

The damage criterion, also known as the loading function, governs the damage development based on the equivalent strain measure, such that [19, 44]

$$\begin{aligned} f \left( {\tilde{\varepsilon }}_\mathrm{eq},\kappa \right) ={\tilde{\varepsilon }}_\mathrm{eq}-\kappa \end{aligned}$$

(32)

where $\kappa$ is a strain-like threshold which denotes the maximum value of the corresponding local equivalent strain ever reached during the loading history. At a prescribed material point, the irreversible nature of the history variable is updated by means of the Karush−Kuhn−Tucker (KKT) loading/unloading conditions, which can be expressed as [93]

$$\begin{aligned} f \left( {\tilde{\varepsilon }}_\mathrm{eq},\kappa \right) \le 0, \quad {\dot{\kappa }} \ge 0, \quad f \left( {\tilde{\varepsilon }}_\mathrm{eq},\kappa \right) {\dot{\kappa }}=0 \end{aligned}$$

(33)

The above KKT conditions can be further explained as: (1) the first condition means that the local equivalent strain ${\tilde{\varepsilon }}_\mathrm{eq}$ can never exceed the history state variable $\kappa$; (2) the second conditions describe that the history state variable $\kappa$ monotonically increases to impose the irreversibility of damage, i.e., no-healing; (3) the third condition ensures the irreversible of damage growth postulated in Remark 1 by enforcing that the model satisfies either, damage increases if ${\dot{\kappa }}>0$ and $f \left( {\tilde{\varepsilon }}_\mathrm{e q},\kappa \right) =0$, or damage stagnation if ${\dot{\kappa }}=0$ and $f \left( {\tilde{\varepsilon }}_\mathrm{e q},\kappa \right) <0$ [67, 71].

A valid formulation that describes the damage initiation and propagation depends on the material at hand and requires sufficient experimental data to calibrate parameters. According to the available experimental data, researchers have proposed empirical damage–strain [20, 63, 90] and damage–stress [89, 133] relationships through bilinear or exponential laws. In the current work, the local damage evolution is evaluated by adopting a bilinear damage law as a function of the internal state variable of the equivalent strain measure $\kappa$ [23], defined as

$$\begin{aligned} D(\kappa )=\left\{ \begin{array}{ll} 0, &{} \text{ if } \kappa<\varepsilon _\mathrm{e q}^{i} \\ \frac{\varepsilon _\mathrm{e q}^\mathrm{f}(\kappa -\varepsilon _\mathrm{e q}^{i})}{\kappa (\varepsilon _\mathrm{e q}^\mathrm{f}-\varepsilon _\mathrm{e q}^{i})}, &{} \text{ if } \varepsilon _\mathrm{e q}^{i} \le \kappa \le \varepsilon _{e q}^{th} \\ D_\mathrm{max}, &{} \text{ if } \varepsilon _\mathrm{e q}^{th}<\kappa \end{array}\right. \end{aligned}$$

(34)

where $\varepsilon _\mathrm{eq}^{i}$ is the initiation damage of the equivalent strain, and $\varepsilon _\mathrm{eq}^\mathrm{f}$ is the failure damage of the equivalent strain, that require to be calibrated against experimental data. $D_\mathrm{max}$ denotes the maximum damage, usually set to slightly less than 1, to maintain the well-posedness of the governing equations. The corresponding equivalent strain value $\varepsilon _\mathrm{e q}^{th}$ is formulated as

$$\begin{aligned} \varepsilon _\mathrm{e q}^{th}=-\frac{\varepsilon _\mathrm{e q}^\mathrm{f} \varepsilon _\mathrm{e q}^{i}}{\varepsilon _\mathrm{e q}^\mathrm{f} - \varepsilon _\mathrm{e q}^{i}} \left[ D_\mathrm{max} - \frac{\varepsilon _\mathrm{e q}^\mathrm{f}}{\varepsilon _\mathrm{e q}^\mathrm{f}-\varepsilon _\mathrm{e q}^{i}} \right] ^{-1}. \end{aligned}$$

(35)

3.4 Anisotropic Darcy law

The fluid transport law inside the porous media needs to be specified to complete the model. Darcy’s law [27] has been widely employed to describe fluid transport for similar problems. Darcy law assumes that the fluid velocity is a linear function of the pressure gradient, which is valid for most geomaterial applications with laminar flow cases and low Reynolds number due to the narrow inter-granular voids [49]. The expression of this transport law is given as

$$\begin{aligned} {\varvec{v}}_\mathrm{f}=-k \nabla p \end{aligned}$$

(36)

${k}$ denotes the permeability coefficient defined as $k=\frac{{\bar{k}}}{\mu }$, with ${\bar{k}}$ being the intrinsic permeability with dimensional units in length squared and $\mu$ the dynamic viscosity of the fluid.

According to the preferentially oriented fracture process zone in the geomaterial, it is expected that the fluid transports predominantly along the direction of fissures, which means that the permeability would increase within its domain and essentially be direction dependent [90, 134, 137]. It should also be noted that porous media (even before fracture is initiated) is considered anisotropic where the horizontal permeability is higher than the vertical component as confirmed by Armitage et al. [4] for deep formations. In this work, we adopt a nonlinear anisotropic permeability tensor in which the permeability component in the tangential direction to the fracture will increase significantly, while the normal or vertical direction to the fracture will only be mildly impacted. Under two-dimensional conditions, the anisotropic permeability tensor can be written as

$$\begin{aligned} {\varvec{k}}(\kappa )=\left[ \begin{array}{cc} k_{xx} &{} 0 \\ 0 &{} k_{yy} \end{array}\right] \\ =\left[ \begin{array}{cc} k_{0,h}+\breve{k}(\kappa ) \sin \theta &{} 0 \\ 0 &{} k_{0,v}+\breve{k}(\kappa ) \cos \theta \end{array}\right] \end{aligned}$$

(37)

where $k_{xx}$ and $k_{yy}$ are the permeability components in x- and y-directions, respectively, $k_{0,h}$ and $k_{0,v}$ are the horizontal and vertical permeabilities in an intact domain, which can characterize the anisotropic nature of the permeability in deep formations prior to fracture initiation, and $\breve{k}(\kappa )$ denotes the evolving permeability due to fracture-induced fluid flow. Note that since damage can be driven by shear, we assume that the permeability can also be impacted by shear dilation when $\kappa$ is dominated by a shear state. The angle $\theta =\arctan \left[ \frac{\gamma _{xy}}{2(\varepsilon _{1}-\varepsilon _{yy})}\right]$ corresponds to the direction of the maximum principal strain $\varepsilon _{1}$, with $\gamma _{xy}$ being the engineering shear strain and $\varepsilon _{yy}$ the strain component in y-direction. In this work, we utilize an exponential relationship to define $\breve{k}(\kappa )$ as a function of the internal variable of the equivalent strain $\kappa$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{k} (\kappa ) = \left\{ {\begin{array}{*{20}l} {k_{{\text{f}}} \left[ {1 - e^{{ - b_{1} \left( {\kappa - \varepsilon _{\text{eq}}^{i} } \right)}} } \right],} \hfill & {{\text{if}}}& {\kappa \geq \varepsilon _{\text{eq}}^{i} } \hfill \\ {0,} \hfill & {{\text{if}}}& {\kappa < \varepsilon _{{{\text{eq}}}}^{i} } \hfill \\ \end{array} } \right.{\text{ }}$$

(38)

where $k_\mathrm{f}$ is the fracture permeability, and $b_{1}$ is a constant that needs to be calibrated from experiments. The diagram in Fig. 3 shows the variation of $\breve{k}(\kappa )$ with $\kappa$. Figure 3 demonstrates how $b_{1}$ controls the rate of permeability evolution, in which the transition from low permeability to high permeability behavior occurs within the fracture process zone. Taking $b_{1}=0$ means that the permeability tensor recovers a constant permeability. Substituting the variable permeability tensor ${\varvec{k}}(\kappa )$ in Eq. (37) into the standard Darcy’s law in Eq. (36), yields a nonlinear strain-dependent anisotropic law

$$\begin{aligned} {\varvec{v}}_\mathrm{f}=-{\varvec{k}}(\kappa ) \nabla p. \end{aligned}$$

(39)

Fig. 3

Variation of the permeability enhancement factor $\breve{k} (\kappa )$ with the internal variable of equivalent strain $\kappa$

4 Computer implementation of the poro-damage-viscoelastic model

4.1 Boundary value problem

The governing equation of the poro-damage-viscoelastic model can be written as follows

$$\begin{aligned} \nabla \cdot [(1-\breve{D}) \tilde{\varvec{\sigma }}(t)-\alpha (\breve{D}) p {\varvec{I}}]+{\varvec{b}}={\varvec{0}}, \quad&\text{ in } {\varOmega } \end{aligned}$$

(40)

$$\begin{aligned} \frac{\partial }{\partial t}\left[ \frac{p}{M(\breve{D})}+\alpha (\breve{D}) {\text {tr}}(\varvec{\varepsilon })\right] -\nabla \cdot [{\varvec{k}}(\kappa ) \nabla p]=0, \quad&\text{ in } {\varOmega } \end{aligned}$$

(41)

where Eq. (40) is derived by substituting the definition of the total Cauchy stress from Eq. (25) into momentum equation (1). Equation (41) is derived by substituting the definition of $\zeta$ from Eq. (20) and the nonlinear Darcy’s law from Eq. (39) into fluid mass balance equation (2). The damage-dependent Biot’s coefficient $\alpha (\breve{D})$ and modulus $M(\breve{D})$ are calculated according to Eqs. (21) and (22), respectively, which are implicit functions of time since damage evolves with stress and time. The local damage variable D and anisotropic permeability tensors are defined as a function of the internal state variable $\kappa$ based on the loading function in Eq. (32), which is related to an equivalent strain measure according to Eq. (30). The non-local damage $\breve{D}$ will be defined in Sect. 4.2. Boundary conditions are given to complete the boundary value problem, as follows

$$\begin{aligned}&\left\{ \begin{array}{ll} {\varvec{u}}=\overline{{\varvec{u}}}, &{} \text{ on } {\Gamma }_{u} \\ \varvec{\sigma } \cdot {\varvec{n}}=\overline{{\varvec{t}}}, &{} \text{ on } {\Gamma }_{t} \end{array}\right. \end{aligned}$$

(42)

$$\begin{aligned}&\left\{ \begin{array}{ll} p={\bar{p}}, &{} \text{ on } {\Gamma }_{p} \\ -{\varvec{v}}_\mathrm{f} \cdot {\varvec{n}}={\bar{q}}, &{} \text{ on } {\Gamma }_{q} \end{array}\right. \end{aligned}$$

(43)

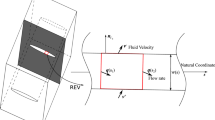
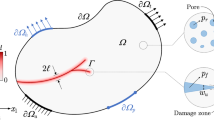
where ${\Gamma }_{u}$ and ${\Gamma }_{t}$ denote complementary subsurfaces of the boundary ${\Gamma }$, in which the displacement $\overline{{\varvec{u}}}$ is prescribed on ${\Gamma }_{u}$ and the surface traction $\overline{{\varvec{t}}}$ on ${\Gamma }_{t}$; ${\Gamma }_{p}$ and ${\Gamma }_{q}$ are also complementary subsurfaces of the boundary ${\Gamma }$, where the fluid pressure is specified on ${\Gamma }_{p}$ and the normal fluid flux on ${\Gamma }_{q}$, as shown in Fig. 4. Note that quantities with an overbar are prescribed boundary data.

In addition, the governing equations are supplemented with the following set of initial conditions

$$\begin{aligned} \left\{ \begin{array}{ll} {\varvec{u}}({\varvec{x}}, 0)=0, &{} \text{ in } {\varOmega } \\ \dot{{\varvec{u}}}({\varvec{x}}, 0)=0, &{} \text{ in } {\varOmega } \\ p({\varvec{x}}, 0)=0, &{} \text{ in } {\varOmega } \\ \breve{D}({\varvec{x}}, 0)=\breve{D}_{0}, &{} \text{ in } {\varOmega } \end{array}\right. \end{aligned}$$

(44)

The coupled set of Eqs. (40) and (41), along with boundary conditions (42) and (43), and initial conditions (44), yield the initial boundary-value problem for the primary variables of interest ${\varvec{u}}({\varvec{x}},t)$ and $p({\varvec{x}},t)$ coupled with the explicit non-local damage variable $\breve{D}$.

Fig. 4

Schematic illustration of the boundary and loading conditions for a fluid-saturated porous media. The non-local damage that develops due to these conditions is illustrated by the colorbar

4.2 Non-local integral-type regularization

It is well known that classical local damage models may suffer from significant mesh size and alignment dependence [31, 64] and may also suffer from severe spurious oscillations of field variables in porous media [90]. Particularly, once damage occurs the material exhibits strain softening (localization) pattern that is often confined to one element, which is due to the fact that the only existing length scale in the problem is the element size. This is of course an undesirable numerical phenomena associated with the change of the type of governing equations [7, 100]. To that end, a non-local integral-type technique is employed in the current work to regularize the local damage variable. As compared with gradient damage approaches, the non-local integral formulation has two important advantages: (i) simple numerical implementation which requires only a neighbor search algorithm that records the Gauss point information within the non-local interaction zone at the beginning of the analysis [38] and (ii) avoids introducing additional degrees of freedom, which significantly reduces the computational burden [118].

The non-local damage variable $\breve{D}$ at a certain point is calculated by a weighted average of all the local counterparts within its neighboring material points, such that [99]

$$\begin{aligned} \breve{D}\left( {\varvec{X}}_{g}^{0}\right) =\frac{\int _{{\varOmega }} \Phi \left( {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}\right) D\left( {\varvec{X}}_{g}\right) \hbox {d}{\varOmega }}{\int _{{\varOmega }} \Phi \left( {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}\right) \hbox {d}{\varOmega }} \end{aligned}$$

(45)

where ${\varvec{X}}_{g}^{0}$ and ${\varvec{X}}_{g}$ are coordinate vectors of the evaluated point and the surrounding point, respectively, $\Phi \left( {\varvec{X}}_{g}^{0}, {\varvec{X}}_{g}\right)$ is the weighting function taken here as the following bell-shaped function [62, 65]

$$\begin{aligned} \Phi \left( {\varvec{X}}_{g}^{0}, {\varvec{X}}_{g}\right) = {\left\{ \begin{array}{ll} \left( 1-\frac{\left\| {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}\right\| ^{2}}{l_{c}^{2}}\right) ^{2}, &{} \text{ if } 0 \leqslant \left\| {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}\right\| \leqslant l_{c} \\ 0, &{} \text{ if } \left\| {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}\right\| >l_{c} \end{array}\right. } \end{aligned}$$

(46)

where $l_{c}$ is the internal length scale, which relates the diffusion width of the fracture process zone, and can be considered to be the same order of material inhomogeneities [69]. Note however that the length scale automatically determines the upper limit on the finite element size, as at least two elements must introduced within the length scale, i.e., $h \le 0.5 l_\mathrm{c}$. Providing a more rigorous quantitative form for the length scale is a research direction that requires additional experimental exploration. According to the experimental observations by Bavzant and Pijaudier-Cabot [8] on concrete structures, the length scale $l_\mathrm{c}$ is suggested to be related with the maximum aggregate size $d_\mathrm{a}$, e.g., $l_\mathrm{c}=2.7d_\mathrm{a}$. The shape of the weighting function is displayed in Fig. 5a. It can be clearly seen that a maximum weighting value occurs at the position of that material point itself, and the weighting value decreases monotonically with increase of the distance between ${\varvec{X}}_\mathrm{g}^{0}$ and ${\varvec{X}}_\mathrm{g}$ and tends to zero.

To motivate our subsequent finite element implementation, the non-local regularization formulation can be further rewritten as [38]

$$\begin{aligned} \breve{D}\left( {\varvec{X}}_\mathrm{g}^{0}\right) =\frac{\sum _{j=1}^{N_\mathrm{g}} \Phi \left( {\varvec{X}}_\mathrm{g}^{0}-{\varvec{X}}_\mathrm{g}^{j}\right) D\left( {\varvec{X}}_\mathrm{g}^{j}\right) }{\sum _{j=1}^{N_\mathrm{g}} \Phi \left( {\varvec{X}}_\mathrm{g}^{0}-{\varvec{X}}_\mathrm{g}^{j}\right) } \end{aligned}$$

(47)

where $N_\mathrm{g}$ denotes the number of neighboring Gauss points within the window of interaction bounded by a circle of radius $l_\mathrm{c}$, as shown in Fig. 5b. Note that Eq. (47) is a weighted average that is an approximation of Eq. (45). To reduce the computational cost, one can identify and store the coordinates of the neighboring Gauss points within the regularization domain for each Gauss point at the first time step. Then the weights of all neighboring Gauss points and their sum are evaluated and stored.

Fig. 5

a A bell-shaped weighting function for the non-local integral $\Phi \left( {\varvec{X}}_\mathrm{g}^{i},{\varvec{X}}_\mathrm{g}\right)$. b Schematic diagram showing neighboring Gauss points of ${\varvec{X}}_\mathrm{g}$ indicated by “$\times$” mark within the window of the influence bounded by a circle of radius $l_\mathrm{c}$. The Gauss point ${\varvec{X}}_\mathrm{g}^{0}$ is colored in red and its neighbors are colored in blue

4.3 Mixed finite element formulation

A mixed finite element formulation is employed to solve the boundary value problem presented in Sect. 4.1 with the primary variables in the equations being ${\varvec{u}}$ and p. The weak form can be obtained by multiplying the strong forms in Eqs. (40) and (41) with trial functions ${\varvec{w}}_{u}$ and $w_{p}$, respectively, and then integrating the equations over the domain ${\varOmega }$. Using the integration by parts or divergence theorem where appropriate, together with the corresponding boundary conditions, yields the following residual equations

$$\begin{aligned} {\varvec{R}}_{{\varvec{u}}}({\varvec{u}}, p)&=\int _{{\varOmega }} \nabla {\varvec{w}}_{u}^{T} (1-\breve{D}) \tilde{\varvec{\sigma }}(t) \hbox {d}{\varOmega } -\int _{{\varOmega }} \nabla {\varvec{w}}_{u}^{T} \alpha (\breve{D}) {\varvec{I}} p \hbox {d}{\varOmega }\nonumber \\&\quad -\int _{{\varOmega }} {\varvec{w}}_{u}^{T} {\varvec{b}} \hbox {d}{\varOmega } -\int _{{\varGamma }_{t}} {\varvec{w}}_{u}^{T} \bar{{\varvec{t}}} \hbox {d}{\Gamma }_{t}=0 \end{aligned}$$

(48)

$$\begin{aligned} R_{p}({\varvec{u}}, p)&=\int _{{\varOmega }} w_{p}^{T} \left[ \frac{\partial p}{\partial t} \frac{1}{M(\breve{D})} +p \frac{\partial ( 1/M(\breve{D}) )}{\partial t} \right. \nonumber \\&\quad \left. \quad+\alpha (\breve{D}) \frac{\partial {\text {tr}} (\varvec{\varepsilon })}{\partial t} +{\text {tr}} (\varvec{\varepsilon }) \frac{\partial \alpha (\breve{D})}{\partial t} \right] \hbox {d}{\varOmega }\nonumber \\&\quad +\int _{{\varOmega }} \nabla w_{p}^{T} {\varvec{k}} (\kappa ) \nabla p \hbox {d}{\varOmega } -\int _{{\varGamma }_{q}} w_{p}^{T} {\bar{q}} \hbox {d}{\Gamma }_{q}=0 \end{aligned}$$

(49)

where ${\varvec{w}}_{u}$ and $w_{p}$ are the test functions for displacement ${\varvec{u}}$ and fluid pressure p, respectively. The problem domain is discretized into finite elements in which the two-field variables ${\varvec{u}}$ and p, and the corresponding test functions are approximated by Galerkin’s method as

$$\begin{aligned} {\varvec{u}} \approx {\varvec{N}}_{u} \hat{{\varvec{u}}}, \quad {\varvec{w}}_{u} \approx {\varvec{N}}_{u} \hat{{\varvec{w}}}_{u}, \quad p \approx {\varvec{N}}_{p} \hat{{\varvec{p}}}, \quad p \approx {\varvec{N}}_{p} \hat{{\varvec{p}}} \end{aligned}$$

(50)

where ${\varvec{N}}_{u}$ and ${\varvec{N}}_{p}$ are the shape functions for the displacement ${\varvec{u}}$ and fluid pressure p, respectively. The variables $\hat{{\varvec{u}}}$ and ${\hat{p}}$ with an over-hat indicate nodal values at the element level. It should be noted that a well-known unstable numerical issue featuring spurious oscillations may exist when using the same order of the shape functions for displacement and fluid pressure fields [3], also known as the Babuska–Brezzi stability criteria in mixed finite element formulations. To satisfy the Babuska–Brezzi condition [5, 16, 125] for two-field (${\varvec{u}}-p$) system, the displacement shape function matrix is taken to correspond to a quadratic 8-node quadrilateral serendipity element, while the pressure shape function matrix is taken to be continuous bilinear 4-node element, which has proven to minimize observed oscillations [3, 90, 91].

In order to continue with the linearization of the weak form presented in Eqs. (48) and (49), the generalized residuals ${\varvec{R}}$ and the generalized unknowns ${\varvec{X}}$ can be recast at the element level as

$$\begin{aligned} {\varvec{R}}=\left\{ \begin{array}{c} \hat{{\varvec{R}}}_{u} \\ \hat{{\varvec{R}}}_{p} \end{array}\right\} ; \quad {\varvec{X}}=\left\{ \begin{array}{l} \hat{{\varvec{u}}} \\ \hat{{\varvec{p}}} \end{array}\right\} \end{aligned}$$

(51)

The FEM discretization of the coupled system in Eqs. (40) and (41) leads to the following time-continuous version as

$$\begin{aligned} {\varvec{R}}={\varvec{C}} \dot{{\varvec{X}}}+{\varvec{K}} {\varvec{X}}-{\varvec{F}}_\mathrm{e x t}={\mathbf {0}} \end{aligned}$$

(52)

where ${\varvec{C}}$ and ${\varvec{K}}$ are the generalized damping and stiffness matrix, respectively, and ${\varvec{F}}_\mathrm{ext}$ denotes external force vector. Using a time difference scheme to evolve the system in time, the velocity vector $\dot{{\varvec{X}}}$ can be expressed as [60]

$$\begin{aligned} \dot{{\varvec{X}}}=\frac{1}{\beta \Delta t}\left[ {\varvec{X}}-{\varvec{X}}_{n}\right] -\frac{1-\beta }{\beta } \dot{{\varvec{X}}}_{n} \end{aligned}$$

(53)

where $\beta$ is the parameter that defines the family of time integration schemes. Note that the subscript $n+1$, which denotes the next time step, has been removed for notational clarity.

Due to the damage and permeability growth, the coupled system is strongly nonlinear in the solid displacements and fluid pressure response. In order to solve the nonlinear system of equations at every time step, we adopt the Newton–Raphson method resulting in the following linearized system

$$\begin{aligned} {\varvec{J}}^{i} \delta {\varvec{X}}=-{\varvec{R}}^{i} \end{aligned}$$

(54)

where $\delta {\varvec{X}}$ is the incremental-iteration solution vector obtained at the current Newton iteration $i+1$. Note that the superscript $i+1$ that stands for the next iteration step has been removed for notational clarity. ${\varvec{J}}$ is the tangent stiffness operator associated with the nonlinear system, also called the Jacobian. In this coupled problem, ${\varvec{J}}$ takes the following form

$$\begin{aligned} {\varvec{J}}=\frac{\partial {\varvec{R}}}{\partial {\varvec{X}}} =\left[ \frac{1}{\beta \Delta t} {\varvec{C}}+{\varvec{K}}\right] =\left[ \begin{array}{ll} {\varvec{J}}_{\textit{\textbf{u u}}} &{} {\varvec{J}}_{{\varvec{u}} p} \\ {\varvec{J}}_{p {\varvec{u}}} &{} {\varvec{J}}_{p p} \end{array}\right] \end{aligned}$$

(55)

The components of the Jacobian matrix ${\varvec{J}}$ are provided in Appendix 2. In the current work, we set $\beta =1$ for the backward Euler scheme. The Newton–Raphson iteration continues until convergence is reached, in which case the primary fields of displacement and fluid pressure at $i+1$ nonlinear iteration are updated as

$$\begin{aligned} {\varvec{X}}={\varvec{X}}^{i}+\delta {\varvec{X}} \end{aligned}$$

(56)

The proposed model in this work is implemented as a user-defined element within the FEAP software [123]. In addition, the FEAP built-in adaptive time-stepping strategy is employed to update the time step size for each solution step. A detailed solution scheme is summarized in Algorithm 1.

5 Numerical examples

In this section, we study several geomechanics fracture problems employing the proposed poro-damage-viscoelastic model under various loading conditions. We first study the effect of different relaxation times on soil consolidation response without damage considering a poro-viscoelastic column. The final (long-term) settlement of the column is verified against an analytical solution available for one-dimension poro-elastic consolidation. Next, we study the viscous effects on the hydraulic fracturing propagation via a fluid flux injection. Three different relaxation time cases are considered. Finally, a fluid-driven crack propagation problem is investigated while comparing the different ratios of the initial permeability coefficient in x-direction $k_{0,h}$ with respect to y-direction $k_{0,v}$ for lherzolite rock. In these two hydraulic fracture examples the horizontal fracture propagation is assumed to be driven by mode-I fracturing. The evolution of damage, fluid velocity, fluid pressure and damaged solid stresses are investigated. All aforementioned cases are modeled in plane strain conditions. It is noteworthy that the viscoelastic parameters in Sect. 5.1 are chosen to test the sensitivity of the model, while the more realistic values in 5.2 and 5.3 are calibrated from experimental data.

5.1 Consolidation of a poro-viscoelastic column without damage: test case

We employ a soil column under a uniform vertical surcharge to test the accuracy and reliability of the proposed formulation and investigate the effect of different relaxation times on the consolidation process without damage. The column, shown in Fig. 6a, is subjected to a constant compressive loading with the magnitude of $f=3000 ~{\mathrm{Pa}}$ at the fully drained upper edge [76], while the other edges are impermeable. The bottom boundary is mechanically constrained in all directions and the two lateral boundaries are fixed in their normal direction. We employ uniform quadrilateral elements to discretize the problem domain with the mesh size of $h=0.5$ m. In addition, a fixed time step of $d t=0.005$ s is selected. The mechanical and fluid parameters used in the simulations are listed in Table 1 in which the poro-elastic properties are taken from [23]. Note that we assume the shear modulus of the spring $G^{i}$ in the Maxwell branch to be equal to that in the pure spring branch $G^{\infty }$. The behavior of the soil column is investigated in the following cases:

• Linear poro-elastic model (PE)

• Poro-viscoelastic model with one Maxwell branch, with relaxation time of $\lambda ^{1}=3~\mathrm {s}$ (PVE1)

• Poro-viscoelastic model with one Maxwell branch, with relaxation time of $\lambda ^{1}=6~\mathrm {s}$ (PVE2)

• Poro-viscoelastic model with two Maxwell branch, with relaxation time of $\lambda ^{1}=\lambda ^{2}=3~\mathrm {s}$ (PVE3)

Fig. 6

a Schematic diagram demonstrating a poro-viscoelastic column with boundary conditions and FEM mesh. b Contours of the vertical displacement $u_{y}$ and viscous dissipated energy density $\psi _\mathrm{v}^\mathrm{dis}$ are plotted at 40 s from PVE3 case

Table 1 Mechanical and fluid parameters used in the soil consolidation example problem

The numerical results from the poro-elastic and poro-viscoelastic analyses are compared with each other. The poro-elastic case can be regarded as a poro-viscoelastic model with the relaxation time tending to $\lambda ^{i} \rightarrow 0$ for the solid skeleton. Time histories of the vertical displacement recorded at the top boundary are presented in Fig. 7a. Figure 7a shows a comparison between the model vertical displacement and the analytical solution given by Terzaghi [126], which provides an expression for the final settlement $\Delta H$ at the steady state. Terzaghi’s expression is given as

$$\begin{aligned} \Delta H=\frac{fH}{M_\mathrm{c}(t)} \end{aligned}$$

(57)

with

$$\begin{aligned} M_\mathrm{c}(t)=K+\frac{4}{3}G(t) \end{aligned}$$

(58)

where f is the applied total load, H denotes the height of the soil column, and $M_\mathrm{c}(t)$ is the constrained modulus of the solid skeleton. Note that the shear relaxation modulus G(t) defined in Eq. (24) recovers the shear modulus in the pure spring branch $G^{\infty }$ in steady state. Figure 7a shows that the vertical displacements obtained by the proposed model converge to Terzaghi’s steady-state analytical solutions. It is also observed that the time to reach the final settlement increases with the relaxation time. In addition, as the number of Maxwell branches increases, the consolidation rate decreases significantly due to the larger constrained modulus in the early stage. We also plotted the vertical displacement contour at the steady state from the PVE3 model in Fig. 6b. One can observe that the top of the column has a maximum settlement, while there is no settlement at the bottom due to fully mechanical constraints.

By analyzing the distribution of viscous dissipated energy density $\psi _\mathrm{v}^\mathrm{dis}$ in Fig. 6b at steady state from PVE3 model, the contour displays the $\psi _\mathrm{v}^\mathrm{dis}$ decreases with the increase of the depth, which can be explained that the fluid pressure diffuses more easier at the top part leading to a significant increase in effective stress and viscous strain than that at the bottom part. In order to have a better understanding of the viscous behaviors, we plot the total viscous energy dissipating from the system $\psi _{v,T}^\mathrm{dis}$ as function of time, as shown in Fig. 7b. As expected, the PE model has no viscous energy dissipation, since there are no Maxwell branches employed for the solid skeleton. For the PVE1 and PVE2 models, the rate of the total viscous energy dissipation decreases with the increase of relaxation time, while the larger relaxation time case has a greater final dissipated energy. The PVE3 model with two Maxwell branches has a greater final viscous energy dissipation due to the higher number of Maxwell branches. From these results, one can conclude that changing the relaxation rate alters the rate at which the energy dissipates, and dissipating more energy with a larger relaxation time. However, adding a second Maxwell branch creates an additional path through which energy can be dissipated, thus leading to a larger overall energy dissipation. This can be better understood by analyzing the terms in Eqs. (17) and (60).

In order to further investigate the viscous effects on the consolidation process, the effective stress and fluid pressure evolution with time at the bottom are presented in Fig. 8. It can be observed that the effective stress acting on the solid phase increases gradually as the fluid pressure diffuses away, and the sum of the solid effective stress and fluid pressure is equal to the intensity of the compressive loading at the top edge, which satisfies the effective stress principal in Eq. (27). This observation can be interpreted as a state in which the solid skeleton behaves as a “spring” and the fluid acts as “dashpot.” Moreover, when the viscous effects are included in the solid skeleton response, the effective stress for the solid skeleton increases more quickly at the early stage than that from the PE model. This interesting phenomena can be explained as a result of material stiffness of viscous (PVE) model in the early stage is larger than that of PE model and can bear more external load; especially, the difference is even more pronounced in the larger relaxation time case due to the slower shear modulus degradation or more Maxwell branches with an overall greater shear modulus, see Eq. (24).

Fig. 7

Time histories of a vertical displacement recorded at the top and b viscous energy dissipation from the dashpots over the domain

Fig. 8

Time histories of a effective stress and b fluid pressure recorded at the bottom

5.2 The effect of viscoelasticity on the fluid-driven fracture problem

In order to increase oil and gas production from tight formations, hydraulic fracturing techniques are often used to create channels in low permeability reservoir for fluid flow [42, 121]. Although many geomaterials may exhibit time-dependent deformations as observed in laboratory experiments and field observations, only few works in the literature have taken into consideration the rheological transient aspects of the solid skeleton in hydraulic fracture processes [35]. The anisotropic nature of permeability in fully intact state of deep formations has been established by researchers using experimental [4, 17, 45, 115] and numerical studies [135]. In this section, we tackle the fluid-driven fracture problem at deep rock formations with initial anisotropic permeability and consider the effects of viscoelasticity on the damage propagation and fluid pressure evolution.

The problem domain and computational configuration are depicted in Fig. 9. A fluid flux of ${\bar{q}}=5.6 \times 10^{-4}~\mathrm {m/s}$ is applied on the center zone with 0.2 m edge (red zone in Fig. 9a). Considering the double symmetry in Fig. 9a, only the top-right quarter of the domain is represented in the simulation with symmetric boundary conditions as shown in Fig. 9b. In order to determine the viscoelastic parameters, we firstly derive the analytical solution for the creep strain response $\varepsilon _{1}(t)$ under tri-axial constant stress state using the correspondence principle and Laplace transform mathematical tool [2, 48]. Note that we only consider one Maxwell branch in this closed-form solution which is directly given as follows

$$\begin{aligned} \varepsilon _{1}(t)= & {} \frac{\sigma _{1}+2 \sigma _{3}}{9 K}+\frac{\sigma _{1}-\sigma _{3}}{3 G^{\infty }}\nonumber \\&-\frac{\sigma _{1}-\sigma _{3}}{3} \left( \frac{1}{G^{\infty }}-\frac{1}{G^{\infty }+G^{1}} \right) e^{-\frac{G^{\infty } t}{\left( G^{\infty }+G^{1}\right) \lambda ^{1}}} \end{aligned}$$

(59)

Then the viscoelastic parameters $\left( G^{\infty }, K, G^{1}, \lambda ^{1}\right)$ are calibrated with a nonlinear least squares fitting technique. To this end, we take experimental results from Zhao [139] for lherzolite rock to perform data fitting, and the axial strain evolution with time from experimental and theoretical fitting are presented in Fig. 10. The calibrated viscoelastic parameters and other parameters employed in the simulation are summarized in Table 2. In order to study the effect of relaxation time on the hydraulic fracturing process, we consider an alternative case with only half of the relaxation time $\lambda ^{1}=3535 ~\mathrm {s}$. For comparison, the poroelastic (PE) model is also investigated. Similar to the approach in Sect. 5.1, the poroelastic model is achieved by introducing small $\lambda ^{1}$ value, such that the relaxation time $\lambda ^{1} \rightarrow 0$ in the Maxwell branch, which restores the elastic response of the solid skeleton. In the following, we define the fracture length $L_\mathrm{F}$ and width $W_\mathrm{F}$ to characterize the morphology of the damaged domain where damage is larger than 0.6.

Fig. 9

a Geometry and boundary conditions of the deep rock formation subjected to a fluid injection. b The top right of the specimen is selected for the numerical simulation due to symmetry

Fig. 10

The axial creep strain response for lherzolite rock under deviatoric stress $\sigma _{1}-\sigma _{3}=-29.50 ~{\mathrm{MPa}}$ and confining pressure $\sigma _{3}=-6 ~{\mathrm{MPa}}$, where the dot symbols are extracted from experimental data [139]

Table 2 Material properties and numerical parameters for lherzolite rock used in fluid-driven fracture simulations

The variations of damage, anisotropic permeability in x-direction $k_{xx}$ and fluid pressure recorded at Point A (on Fig. 9b), and fracture length $L_\mathrm{F}$ under different relaxation times are presented in Fig. 11. As shown in Fig. 11a, the damage growth obtained from the PE model grows faster than that from the PVE models. In the PVE models, as the relaxation time increases, a slower damage evolution is observed, which is the same conclusion reported in the numerical study based on the fractional model [79]. The trends of the permeability $k_{xx}$ evolution nearly coincide with the damage growth. This is due to the proposed model setup in which both permeability and damage are driven by the same equivalent strain $\kappa$ defined in Eqs. (34) and (38). It also can be found that the fluid pressure in Fig. 11c rapidly ascents to a maximum value and then descends to a constant value within the fracture domain. This is observed in both of the PE and PVE models. The maximum pressure is often referred to as the breakdown pressure [53] and the pressure drop to a constant value corresponding to a flow in an open channel. These model observations conform with experimental and field data in [83]. As the relaxation time decreases, a slower decline in the fluid pressure is observed. In addition, it can be seen in Fig. 11d that a faster fracture length $L_\mathrm{F}$ buildup occurs when a lower relaxation time is modeled, which is confirmed by the abrupt fracture propagation observed in the PE model. We conclude that the larger relaxation time leads to a slower degradation of the shear relaxation modulus, which in turn leads to slower fracture initiation and propagation processes.

In order to facilitate the investigation of the viscous effects on the fluid-driven fracture propagation, the positions of fracture aperture at $\breve{D}=0.6$ for three cases at several representative times are extracted and displayed in Fig. 12. Note that the horizontal and vertical axes are in different scale sizes. It can be observed that the fracture indeed develops along the horizontal direction due to the preferential direction provided by the anisotropic permeability. By analyzing the trends in Fig. 12a–c, we can observe faster fracture propagation as the relaxation time decreases. The hydraulic fracture profiles at the 20,000 s from each modeling case are demonstrated in Fig. 12d. In Fig. 12d, one can observe that the PVE models yield larger fracture widths than that from the PE model, while the fracture length decreases with the increase in relaxation time, which agree qualitatively with the fracture evolution patterns recorded in a previous study [35].

The evolution of fluid pressure for the three modeling cases is better demonstrated in Fig. 13 where the positions of the fluid pressure contour at $p=3$ MPa at several representative times are extracted. The contour of fluid pressure expands rapidly and then converges to a narrower range which is consistent with the evolution patterns recorded in several numerical studies [91, 94] and experimental observations of hydraulic fracture width evolution [83]. The reason for this phenomenon can be explained by the continuous development of the fracture domain which provides more space to accommodate the fluid. Once the fracture is developed, the volume of the injected fluid is in equilibrium with the rate of infiltration into the boundary, and the fluid flow in the fracture behaves like an open channel flow. This observation is consistent with the observations from Fig. 11c that were discussed earlier and observations in [89]. Additionally, it can be observed that the larger relaxation time model generates a wider pressure contours which could be attributed to the fact that the shear relaxation modulus relaxes more slowly with the increase of relaxation time which results in less concentration at the crack front leading to a wider pressure and damage distribution.

It is well-established from previous studies [91] that the fluid flow velocity inside the fractured media is considerably higher than that infiltration into the host matrix. Without loss of generality, we consider the relaxation time $\lambda ^{1}$ = 7070 s case as an example to investigate the evolution of permeability $k_{xx}$ profiles. As shown in Fig. 14, one can find that the permeability within the fluid-driven fracture could be several orders of magnitudes larger than that in the intact domain. By analyzing the damage profiles in Fig. 12c and fluid pressure profiles in Fig. 13c, we can observe that the variable anisotropic permeability approach in Eq. (37) provides a strong preferential direction for fluid transport. This definition leads to a significant increase in the permeability component $k_{xx}$, while the $k_{yy}$ component remains almost constant in the fractured domain. This observation is confirmed by the damage development along the horizontal direction, which results in an ellipse-like shape of fluid pressure distribution following the damage evolution. These observations show that the proposed model formulation provides a strong coupling among the damage, permeability and fluid pressure.

The evolution of total damage $\psi _{d,T}^\mathrm{dis}$ and viscous $\psi _{v,T}^\mathrm{dis}$ dissipated energies over the domain for different relaxation times is presented in Fig. 15. The total damage dissipated energy from the PE case quickly approaches a constant value, while the $\psi _{d,T}^\mathrm{dis}$ from the PVE case progressively increases in line with the fracture propagation in Fig. 11d. One can also observe that the PE case yields a smaller final damage dissipated energy than the PVE case. This can be interpreted as the PE case with infinitesimal relaxation time $\lambda ^{i} \rightarrow 0$ leads to a rapid deformation release in dashpot $\varvec{\alpha }_\mathrm{v}^{i} \rightarrow {\varvec{e}}$ and spring part in the Maxwell branch returns to origin state ${\varvec{e}}_{e}^{i}(t) \rightarrow 0$ (see Eq. (26)); then, the Maxwell branch contributes very little part to the damage dissipated energy based on the third term in Eq. (61). In addition, the total viscous dissipated energy grows more quickly in the $\lambda ^{1}$ = 3535 s case, which can be explained by the fact that the viscous effect is more quickly relaxed with smaller relaxation times. It is also interesting to point out that the larger relaxation time case possess a higher final viscous dissipated energy, which is in agreement with the observations made in the previous section.

Fig. 11

Evolution of a damage, b permeability $k_{xx}$ and c fluid pressure recorded at the Point A (on Fig. 9b) and d fracture length with time. Note that we select different time histories for different field variables to display their pronounced features

Fig. 12

Profiles of the fracture aperture ($\breve{D}=0.6$) for a PE model, b PVE model: $\lambda ^{1}$ = 3535 s, c PVE model: $\lambda ^{1} = 7070$ s at representative times, and d comparison of the fracture profiles at 20,000 s for three models. Note that we select the different time sets for PE and PVE models for highlighting their evolution features due to the discrepancy of the damage growth rates in Fig. 11d

Fig. 13

Profiles of the fluid pressure ($p=3$ MPa) for a PE model, b PVE model: $\lambda ^{1} = 3535$ s, c PVE model: $\lambda ^{1} = 7070$ s at representative times

Fig. 14

Contour of the permeability in x-direction for the PVE model: $\lambda ^{1}$ = 7070 s at several representative times

Fig. 15

Evolution of a total damage dissipated energy $\psi _{d,T}^\mathrm{dis}$ and b total viscous dissipated energy $\psi _{v,T}^\mathrm{dis}$ over the domain for two different relaxation times cases and PE case

5.3 The effect of anisotropic initial permeability on the pressure-driven fracture problem

The anisotropic nature of permeability in deep formation even before fracture initiation has been well-established by several studies [4, 45]. The initial anisotropic permeability gives a better field representation, including the representation of the effect of the in situ confining stresses on initial permeability, which is close to the idealized physical reality especially in the deep formation [17, 115]. In this section, we study the effect of the ratio of initial horizontal permeability $k_{0,h}$ to vertical component $k_{0,v}$ on the interactions of deformation, damage and fluid pressure, and we define the anisotropy ratio as ${\mathcal {N}}=k_{0,h}/k_{0,v}$. Considering the schematic illustration in Fig. 16, the external boundaries of a porous domain with dimensions 4 m $\times$ 4 m are permeable and restrained in both directions, with an initial pre-fracture of a length of 0.25 m. Following the approach in [39, 141], a prescribed increasing fluid pressure loading is applied to resemble hydraulic fracturing. In this setup, a gradually increasing pressure as ${\bar{p}}(t)=500 t ~[{\mathrm{Pa}}]$ is applied over a time interval of 20000 s and then remains constant at 10 MPa, as depicted in Fig. 16a. The poro-viscoelastic parameters used in the calculation are listed in Table 3. We consider four different anisotropy ratios ${\mathcal {N}}=\{1,5,10,20\}$, respectively.

Fig. 16

Geometry and boundary conditions of the pre-fractured specimen subjected to an increasing internal fluid pressure ${\bar{p}}$ and FEM mesh. The four boundaries of the domain are fully mechanical fixed and permeable

Table 3 Material properties and numerical parameters for deep formation used in pressure-driven fracture simulations

Snapshots illustrating the evolution of damage and fluid velocity in x-direction at three representative times are presented in Fig. 17 for the ${\mathcal {N}}=20$ case. The fracture initiates when the pore pressure ${\bar{p}}(t)$ reaches 5 MPa at 10000 s and then continuous fracture propagation is observed along the horizontal direction as the pressure increases. The fluid velocity component $v_{f,x}$ contours show that the fluid velocity predominantly increases horizontally due to the preferentially oriented fracture and larger initial horizontal permeability than vertical component.

Furthermore, we plot the fluid pressure contours for each modeling case at 10000 s and 20000 s in Fig. 18. In order to have a closer look at the fluid flow pattern, the streamlines are also depicted showing the flow transport path. As the physical time increases, one can observe that the fluid pressure has a pronounced elliptical distribution around the fracture. In particular, a higher anisotropy ratio ${\mathcal {N}}$ yields a more ellipse-like shape of fluid pressure distributions. From the streamline layouts, it is interesting to observe that the fluid flows firstly along the fracture propagation direction and then perpendicularly penetrates the fracture wall into the intact rock region and finally perpendicular to the external effusion boundaries. The fluid flow tendency toward the horizontal direction is attributed to the increase of anisotropy ratios ${\mathcal {N}}$.

Figure 19 shows the maximum principal value of the homogenized (damaged) solid stress distributions, where the black dash lines on nephograms are stress isolines. The damage region with $\breve{D}>0.7$ is clipped from the host matrix to highlight the fracture zone. It can be concluded that a significant stress concentration phenomenon appears around the fracture tips, which is similar to the results presented in Zhuang et al. [143] based on the phase field method. Note that the sharp fracture is smeared using the non-local integral formulation which reduces the stress intensity. Meanwhile, the isotropic initial permeability model ${\mathcal {N}}=1$ yields a more diffused stress intensity zones and requires more energy, compared with the anisotropic case, to trigger fracture initiation. By comparing the stress isolines, it is concluded that the localized stress intensity zone around the fracture tips significantly expands, while it tends to shrink near the fracture sides as ${\mathcal {N}}$ increases.

We examine the resulting fluid velocity in x-direction $v_{f,x}$ recorded at the Point A (on Fig. 16a) and fracture length $L_\mathrm{F}$ obtained from the four different ${\mathcal {N}}$ case, as shown in Fig. 20. The results in Fig. 20 display that the fluid velocity $v_{f,x}$ keeps increasing as the applied pressure increases till ${\bar{p}}=10$ MPa at 20000 s; then, $v_{f,x}$ shows a much slower rise as the applied pressure remains constant. The velocity $v_{f,x}$ is higher in larger ${\mathcal {N}}$ case, which means that more fluid flow occurs along the horizontal direction.

Additionally, the evolution of total damage $\psi _{d,T}^\mathrm{dis}$ and viscous $\psi _{v,T}^\mathrm{dis}$ dissipated energies over the domain for different ratios of ${\mathcal {N}}$ is presented in Fig. 21. The total damage dissipated energy in anisotropic initial permeability is triggered earlier than that in the isotropic case, which indicates that the configuration of anisotropic initial permeability facilitates the fracture initiation. The difference between the total viscous and damage dissipation is about two orders of magnitude, which may be explained by the fact that the contribution to the damage dissipated energy comes only from the fracture process region, as there is no damage development $\dot{\breve{D}}=0$ in the intact region away from the damage, while the viscous dissipated energy gets contributions from the whole domain. Furthermore, as the ratio ${\mathcal {N}}$ increases, the total dissipated energy for both damage and viscous parts grows slower, since the stronger anisotropy permeability provides a more localized damage zone (See Figs. 18, 19) and thus results in smaller energy dissipation in the intact zone.

Fig. 17

The ${\mathcal {N}}=20$ case: damage (left column) and fluid velocity in x-direction $v_{f,x}$ (right column) distribution profiles at three different times

Fig. 18

Comparison of the fluid pressure distribution profiles together with the streamlines for four different anisotropy ratios ${\mathcal {N}}$ cases at 10,000 s (left column) and 20,000 s (right column)

Fig. 19

Comparison of the maximum principal value of homogenized (damaged) solid stress $\sigma _{s,1}$ profiles for four different anisotropy ratios ${\mathcal {N}}$ cases at 10,000 s. Note that the region with $\breve{D}>0.7$ is removed for highlighting the fracture morphology

Fig. 20

Evolution of fluid velocity in x-direction $v_{f,x}$ recorded at the Point A (on Fig. 16a) for four different anisotropy ratios ${\mathcal {N}}$ cases

Fig. 21

Evolution of a total damage dissipated energy $\psi _{d,T}^\mathrm{dis}$ and b total viscous dissipated energy $\psi _{v,T}^\mathrm{dis}$ over the domain for four different anisotropy ratios ${\mathcal {N}}$ cases

6 Summary and conclusion

We propose a novel thermodynamic formulation for a poro-damage-viscoelasticity model in saturated porous media in geomechanics applications of consolidation and hydraulic fracture. The approach is based on a non-local integral-type damage method and leads to a strongly coupled hydromechanical-damage system. The solid is modeled as a viscoelastic material using a generalized Maxwell model, and the fluid flow is described by Darcy’s law. The damage and permeability evolve in time following a three-invariant equivalent strain measurement. Additionally, an initial permeability is assumed to be anisotropic to describe the fluid flow behavior in deep formations. The state laws are derived analytically using a thermodynamically consistent definition. The problem is discretized using a mixed finite element framework, and the resulting nonlinear system of equations is linearized using a Newton–Raphson approach with an analytically derived consistent tangent. Numerical results show agreement with previously published numerical and experimental data.

First, a benchmark example of soil column consolidation problem without damage is presented by considering a poro-elastic and poro-viscoelastic models. While the elastic and viscoelastic soil column settlements are shown to converge to the steady-state analytical solution, a slower settlement is observed for the viscoelastic column. Further, the viscoelastic settlement becomes slower with increase of the relaxation time and/or increase of the number of Maxwell branches, which is due to the significant increase in viscous energy dissipation.

The proposed model is then applied to hydraulic fracturing problems, for which the effect of relaxation times and the degree of anisotropic initial permeability are studied. The numerical results show that the proposed model can well capture the essential features of hydraulic fracture, such as expected fracture propagation, and fluid pressure/velocity response. The permeability is enhanced in the damaged region to provide a strong preferential fluid flow. We conclude that larger relaxation times in viscoelasticity yield slower fracture propagation and slower fluid diffusion away from the crack. Furthermore, larger initial permeability anisotropy results in larger fluid velocity along the horizontal fracture direction, more flattened elliptic pressure distributions and earlier fracture initiation.

In conclusion, for some geomechanics application such as deep reservoirs featuring high-temperature and high-stress conditions, time-dependent creep and relaxation phenomena of the porous media become important. In these cases, one has to employ poro-damage-viscoelasticity theory, which has been shown herein to have pronounced impact on the damage growth and fluid flow in the medium. Future efforts will extend this work to other weighting functions for the non-local regularization considering more complex fracture patterns which may result from mixed-mode fracturing, fracture branching and coalescence.

Appendices

Appendix 1: The derivations of the terms $\frac{\partial \psi _{ve}}{\partial \alpha _\mathrm{v}^{i}}$, $\frac{\partial \psi _{ve}}{\partial \breve{D}}$ and $\frac{\partial \psi _\mathrm{f}}{\partial \breve{D}}$

Following the viscoelastic strain energy $\psi _\mathrm{ve}(\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i}, \breve{D})$ in (6), the $\frac{\partial \psi _\mathrm{ve}}{\partial \varvec{\alpha }_\mathrm{v}^{i}}$ and $\frac{\partial \psi _\mathrm{ve}}{\partial \breve{D}}$ can be written as

$$\begin{aligned}&\frac{\partial \psi _\mathrm{ve}(\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i}, \breve{D})}{\partial \varvec{\alpha }_\mathrm{v}^{i}} =-(1-\breve{D}) \sum _{i=1}^{n} 2 G^{i} {\varvec{e}}_{e}^{i} \end{aligned}$$

(60)

$$\begin{aligned}&\frac{\partial \psi _\mathrm{ve}(\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i}, \breve{D})}{\partial \breve{D}}=-{\tilde{\psi }}_\mathrm{ve}(\varvec{\varepsilon },\varvec{\alpha }_\mathrm{v}^{i}) =-\left[ \frac{1}{2} K {\text {tr}}(\varvec{\varepsilon }) {\text {tr}}(\varvec{\varepsilon }) \right. \nonumber \\&\quad \left. +G^{\infty } {\varvec{e}}: {\varvec{e}} +\sum _{i=1}^{n} G^{i} \left( {\varvec{e}}-\varvec{\alpha }_\mathrm{v}^{i}\right) : \left( {\varvec{e}}-\varvec{\alpha }_\mathrm{v}^{i}\right) \right] \end{aligned}$$

(61)

Combining the constitutive relationship defining the fluid pressure in Eq. (20), the fluid free energy $\psi _\mathrm{f}(\varvec{\varepsilon },\zeta ,\breve{D})$ in Eq. (7) can be recast as the $\psi _\mathrm{f}(p,\breve{D})$ form [87, 134]

$$\begin{aligned} \psi _\mathrm{f}(p,\breve{D}) =\frac{p^{2}}{2M(\breve{D})} \end{aligned}$$

(62)

Then

$$\begin{aligned} \frac{\partial \psi _\mathrm{f}}{\partial \breve{D}}=\frac{p^{2}}{2} \frac{\partial (1 / M(\breve{D}))}{\partial \breve{D}} \end{aligned}$$

(63)

with

$$\begin{aligned}&\frac{\partial (1 / M(\breve{D}))}{\partial \breve{D}} =\frac{2 \alpha (\breve{D}) \frac{\partial \alpha (\breve{D})}{\partial \breve{D}}}{K_{u}-K(\breve{D})} -\frac{K \alpha ^{2}(\breve{D})}{\left( K_{u}-K(\breve{D})\right) ^{2}} \end{aligned}$$

(64)

$$\begin{aligned}&\frac{\partial \alpha (\breve{D})}{\partial \breve{D}}=\frac{K}{K_{s}} \end{aligned}$$

(65)

Appendix 2: The components of the Jacobian matrix J

$$\begin{aligned}&{\varvec{J}}_{\varvec{u u}} =\frac{\partial \hat{{\varvec{R}}}_{{\varvec{u}}}}{\partial \hat{{\varvec{u}}}} =\int _{{\varOmega }} {\varvec{B}}_{u}^{T} (1-\breve{D}) \tilde{{\mathbb {C}}} {\varvec{B}}_{u}\hbox {d}{\varOmega } \nonumber \\&\quad -\int _{{\varOmega }} {\varvec{B}}_{u}^{T} \tilde{\varvec{\sigma }}(t) \otimes \frac{\partial {\breve{D}}}{\partial \varvec{\varepsilon }} {\varvec{B}}_{u} \hbox {d}{\varOmega } \nonumber \\&\quad -\int _{{\varOmega }} {\varvec{B}}_{u}^{T} {\varvec{I}} p \frac{\partial \alpha (\breve{D})}{\partial \varvec{\varepsilon }} {\varvec{B}}_{u} \hbox {d}{\varOmega } \end{aligned}$$

(66)

$$\begin{aligned}&{\varvec{J}}_{{\varvec{u}} p} =\frac{\partial \hat{{\varvec{R}}}_{{\varvec{u}}}}{\partial {\hat{p}}} =-\int _{{\varOmega }} {\varvec{B}}_{u}^{T} \alpha (\breve{D}) {\varvec{I}} {\varvec{N}}_{p} \hbox {d}{\varOmega } \end{aligned}$$

(67)

$$\begin{aligned}&{\varvec{J}}_{p {\varvec{u}}} =\frac{\partial \hat{{\varvec{R}}}_{p}}{\partial \hat{{\varvec{u}}}} =\frac{1}{\beta \Delta t} \int _{{\varOmega }} {\varvec{N}}_{p}^{T} \alpha (\breve{D}) {\varvec{B}}_{u}^\mathrm{vol} \hbox {d}{\varOmega } \nonumber \\&\quad +\int _{{\varOmega }} {\varvec{N}}_{p}^{T} \frac{\partial \alpha (\breve{D})}{\partial t} {\varvec{B}}_{u}^\mathrm{vol} \hbox {d}{\varOmega }\nonumber \\&\quad +\int _{{\varOmega }} {\varvec{B}}_{p}^{T} \frac{\partial {\varvec{k}} (\kappa ) }{\partial \kappa } \nabla p \frac{\partial \kappa }{\partial \varepsilon _{eq}} \frac{\partial \varepsilon _\mathrm{eq} }{\partial \varvec{\varepsilon }} {\varvec{B}}_{u} \hbox {d}{\varOmega } \nonumber \\&\quad +\int _{{\varOmega }} {\varvec{B}}_{p}^{T} \frac{\partial {\varvec{k}} (\kappa ) }{\partial \theta } \nabla p \frac{\partial \theta }{\partial \varvec{\varepsilon }} {\varvec{B}}_{u} \hbox {d}{\varOmega }\nonumber \\&\quad +\int _{{\varOmega }} {\varvec{N}}_{p}^{T} \left[ \frac{\partial p}{\partial t} \frac{\partial (1/M(\breve{D}))}{\partial \varvec{\varepsilon }} +p \frac{\partial ^{2} (1/M(\breve{D}) )}{\partial t \partial \varvec{\varepsilon }}\right. \nonumber \\&\quad \left. +\frac{\partial {\text {tr}} (\varvec{\varepsilon })}{\partial t} \frac{\partial \alpha (\breve{D})}{\partial \varvec{\varepsilon }} +{\text {tr}} (\varvec{\varepsilon }) \frac{\partial ^{2} \alpha (\breve{D}) }{\partial t \partial \varvec{\varepsilon }} \right] {\varvec{B}}_{u} \hbox {d}{\varOmega } \end{aligned}$$

(68)

$$\begin{aligned}&{\varvec{J}}_{p p} =\frac{\partial \hat{{\varvec{R}}}_{p}}{\partial {\hat{p}}} =\frac{1}{\beta \Delta t} \int _{{\varOmega }} {\varvec{N}}_{p}^{T} \frac{1}{M(\breve{D})} {\varvec{N}}_{p} \hbox {d}{\varOmega }\nonumber \\&\quad +\int _{{\varOmega }} {\varvec{N}}_{p}^{T} \frac{\partial (1/M(\breve{D}) )}{\partial t} {\varvec{N}}_{p} \hbox {d}{\varOmega } +\int _{{\varOmega }} {\varvec{B}}_{p}^{T} {\varvec{k}} (\kappa ) {\varvec{B}}_{p} \hbox {d}{\varOmega } \end{aligned}$$

(69)

and the corresponding expansion of the terms $\frac{\partial {\breve{D}}}{\partial \varvec{\varepsilon }}$, $\frac{\partial ^{2} {D}}{\partial \kappa ^{2}}$ and $\frac{\partial ^{2} {\tilde{\varepsilon }}_\mathrm{e q}}{\partial \varvec{\varepsilon }^{2}}$ are as follows:

$$\begin{aligned}&\frac{\partial {\breve{D}}}{\partial \varvec{\varepsilon }} =\frac{\int _{{\varOmega }} \Phi \left( {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}\right) \frac{\partial D\left( {\varvec{X}}_{g}\right) }{\partial \varvec{\varepsilon }} \hbox {d}{\varOmega }}{\int _{{\varOmega }} \Phi \left( {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}\right) \hbox {d}{\varOmega }} \nonumber \\&\quad =\frac{\sum _{j=1}^{N_{g}} \Phi \left( {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}^{j}\right) \frac{\partial D\left( {\varvec{X}}_{g}^{j}\right) }{\partial \varvec{\varepsilon }}}{\sum _{j=1}^{N_{g}} \Phi \left( {\varvec{X}}_{g}^{0}-{\varvec{X}}_{g}^{j}\right) } \end{aligned}$$

(70)

$$\begin{aligned}&\frac{\partial D}{\partial \varvec{\varepsilon }}= \frac{\partial {D}}{\kappa } \frac{\kappa }{\partial {\tilde{\varepsilon }}_\mathrm{e q}} \frac{\partial {\tilde{\varepsilon }}_\mathrm{e q}}{\partial \varvec{\varepsilon }} \end{aligned}$$

(71)

$$\begin{aligned}&\frac{\partial D}{\partial \kappa }= \left\{ \begin{array}{ll} 0,&{} \text{ if } \kappa \le \varepsilon _\mathrm{e q}^{i} \\ \frac{\varepsilon _\mathrm{e q}^\mathrm{f}\varepsilon _\mathrm{e q}^{i}}{\kappa ^2\left( \varepsilon _\mathrm{e q}^\mathrm{f}-\varepsilon _\mathrm{e q}^{i}\right) }, &{} \text{ if } \varepsilon _\mathrm{e q}^{i}< \kappa \le \varepsilon _\mathrm{e q}^{th} \\ 0,&{} \text{ if } \varepsilon _\mathrm{e q}^{th} < \kappa \end{array}\right. \end{aligned}$$

(72)

$$\begin{aligned}&\frac{\partial ^{2} {D}}{\partial \kappa ^{2}} =\left\{ \begin{array}{ll} 0,&{} \text{ if } \kappa \le \varepsilon _\mathrm{e q}^{i} \\ -\frac{2\varepsilon _\mathrm{e q}^\mathrm{f}\varepsilon _\mathrm{e q}^{i}}{\kappa ^3\left( \varepsilon _\mathrm{e q}^\mathrm{f}-\varepsilon _\mathrm{e q}^{i}\right) }, &{} \text{ if } \varepsilon _\mathrm{e q}^{i}< \kappa \le \varepsilon _\mathrm{e q}^{th} \\ 0,&{} \text{ if } \varepsilon _\mathrm{e q}^{th} < \kappa \end{array}\right. \end{aligned}$$

(73)

$$\begin{aligned}&\frac{\partial \kappa }{\partial {\tilde{\varepsilon }}_\mathrm{e q}}= \left\{ \begin{array}{ll} 1,&{} \text{ if } f \left( {\tilde{\varepsilon }}_\mathrm{e q},\kappa \right) =0 \\ 0,&{} \text{ if } f \left( {\tilde{\varepsilon }}_\mathrm{e q},\kappa \right) <0 \end{array}\right. \end{aligned}$$

(74)

$$\begin{aligned}&\frac{\partial {\tilde{\varepsilon }}_\mathrm{e q}}{\partial \varvec{\varepsilon }}= {\left\{ \begin{array}{ll} \frac{\partial \chi }{\partial \varvec{\varepsilon }}, &{} \text{ if } \chi \ge 0 \\ 0, &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

(75)

$$\begin{aligned}&\frac{\partial \chi }{\partial \varvec{\varepsilon }}= \xi _{1} \frac{\partial \varepsilon _{1}}{\partial \varvec{\varepsilon }} +\frac{\xi _{2}}{2 \sqrt{J_{2}^{\varepsilon }}} \varvec{\varepsilon } +(1-\xi _{1}-\xi _{2}-\frac{\xi _{2} I_{1}^{\varepsilon }}{6 \sqrt{J_{2}^{\varepsilon }}}) {\varvec{I}} \end{aligned}$$

(76)

$$\begin{aligned}&\frac{\partial ^{2} {\tilde{\varepsilon }}_\mathrm{e q}}{\partial \varvec{\varepsilon }^{2}}= {\left\{ \begin{array}{ll} \frac{\partial ^{2} \chi }{\partial \varvec{\varepsilon }^{2}} , &{} \text{ if } \chi \ge 0 \\ 0, &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

(77)

$$\begin{aligned}&\frac{\partial ^{2} \chi }{\partial \varvec{\varepsilon }^{2}}= \xi _{1} \frac{\partial ^{2} \varepsilon _{1}}{\partial \varvec{\varepsilon }^{2}} -\frac{\xi _{2}}{4 \left( \sqrt{J_{2}^{\varepsilon }}\right) ^{3}} \left( \varvec{\varepsilon }-\frac{1}{3} I_{1}^{\varepsilon } {\varvec{I}}\right) \otimes \left( \varvec{\varepsilon }-\frac{1}{3} I_{1}^{\varepsilon } {\varvec{I}}\right) \nonumber \\&\quad +\frac{\xi _{2}}{2 \sqrt{J_{2}^{\varepsilon }}} \left( {\mathbb {I}}-\frac{1}{3} {\varvec{I}} \otimes {\varvec{I}}\right) \end{aligned}$$

(78)

(2) $\frac{\partial \alpha (\breve{D})}{\partial \varvec{\varepsilon }}$, $\frac{\partial \alpha (\breve{D}) }{\partial t}$ and $\frac{\partial ^{2} \alpha (\breve{D}) }{\partial t \partial \varvec{\varepsilon }}$

$$\begin{aligned}&\frac{\partial \alpha (\breve{D})}{\partial \varvec{\varepsilon }} =\frac{\partial \alpha (\breve{D})}{\partial {\breve{D}}} \frac{\partial {\breve{D}}}{\partial \varvec{\varepsilon }} \end{aligned}$$

(79)

$$\begin{aligned}&\frac{\partial \alpha (\breve{D})}{\partial {\breve{D}}}=\frac{K}{K_{s}} \end{aligned}$$

(80)

$$\begin{aligned}&\frac{\partial \alpha (\breve{D}) }{\partial t} =\frac{\partial \alpha (\breve{D})}{\partial \breve{D}} \frac{\partial {\breve{D}}}{\partial \varvec{\varepsilon }} \frac{\partial \varvec{\varepsilon }}{\partial t} \end{aligned}$$

(81)

$$\begin{aligned}&\frac{\partial ^{2} \alpha (\breve{D}) }{\partial t \partial \varvec{\varepsilon }} =\frac{\partial \alpha (\breve{D})}{\partial \breve{D}} \frac{\partial {\breve{D}}}{\partial {D}} \frac{\partial ^{2} {D}}{\partial \kappa \partial \varvec{\varepsilon }} \frac{\partial \kappa }{\partial \varepsilon _{eq}} \frac{\partial {\varepsilon _{eq}}}{\partial \varvec{\varepsilon }} \frac{\partial \varvec{\varepsilon }}{\partial t}\nonumber \\&\quad +\frac{\partial \alpha (\breve{D})}{\partial \breve{D}} \frac{\partial {\breve{D}}}{\partial {D}} \frac{\partial {D}}{\partial \kappa } \frac{\partial \kappa }{\partial \varepsilon _{eq}} \frac{\partial ^{2} {\varepsilon _{eq}}}{\partial \varvec{\varepsilon }^{2}} \frac{\partial \varvec{\varepsilon }}{\partial t} \end{aligned}$$

(82)

$$\begin{aligned}&\frac{\partial ^{2} {D}}{\partial \kappa \partial \varvec{\varepsilon }} =\frac{\partial ^{2} {D}}{\partial \kappa ^{2}} \frac{\partial \kappa }{\partial \varepsilon _{eq}} \frac{\partial {\varepsilon _{eq}}}{\partial \varvec{\varepsilon }} \end{aligned}$$

(83)

(3) $\frac{\partial (1/M(\breve{D}))}{\partial \varvec{\varepsilon }}$, $\frac{\partial (1/M(\breve{D})) }{\partial t}$ and $\frac{\partial ^{2} (1/M(\breve{D}))}{\partial t \partial \varvec{\varepsilon }}$

$$\begin{aligned}&\frac{\partial (1/M(\breve{D}))}{\partial \varvec{\varepsilon }} =\frac{\partial (1/M(\breve{D}))}{\partial {\breve{D}}} \frac{\partial {\breve{D}}}{\partial \varvec{\varepsilon }} \end{aligned}$$

(84)

$$\begin{aligned}&\frac{\partial (1/M(\breve{D}))}{\partial {\breve{D}}} =\frac{2 \alpha (\breve{D}) \frac{\partial \alpha (\breve{D})}{\partial \breve{D}}}{K_{u}-K(\breve{D})} -\frac{K \alpha (\breve{D})^{2}}{(K_{u}-K(\breve{D}))^2} \end{aligned}$$

(85)

$$\begin{aligned}&\frac{\partial (1/M(\breve{D})) }{\partial t} =\frac{\partial (1/M(\breve{D}))}{\partial {\breve{D}}} \frac{\partial {\breve{D}}}{\partial \varvec{\varepsilon }} \frac{\partial \varvec{\varepsilon }}{\partial t} \end{aligned}$$

(86)

$$\begin{aligned}&\frac{\partial ^{2} (1/M({\hat{D}})) }{\partial t \partial \varvec{\varepsilon }} =\frac{\partial ^{2} (1/M({\hat{D}}))}{\partial {\hat{D}} \partial \varvec{\varepsilon }} \frac{\partial {{{\hat{D}}}}}{\partial {D}} \frac{\partial {D}}{\partial \kappa } \frac{\partial \kappa }{\partial \varepsilon _{eq}} \frac{\partial {\varepsilon _{eq}}}{\partial \varvec{\varepsilon }} \frac{\partial \varvec{\varepsilon }}{\partial t} \nonumber \\&\quad +\frac{\partial (1/M({\hat{D}}))}{\partial {\hat{D}}} \frac{\partial {\breve{D}}}{\partial {D}} \frac{\partial ^{2} {D}}{\partial \kappa \partial \varvec{\varepsilon }} \frac{\partial \kappa }{\partial \varepsilon _{eq}} \frac{\partial {\varepsilon _{eq}}}{\partial \varvec{\varepsilon }} \frac{\partial \varvec{\varepsilon }}{\partial t}\nonumber \\&\quad +\frac{\partial (1/M(\breve{D}))}{\partial \breve{D}} \frac{\partial {\breve{D}}}{\partial {D}} \frac{\partial {D}}{\partial \kappa } \frac{\partial \kappa }{\partial \varepsilon _{eq}} \frac{\partial ^{2} {\varepsilon _{eq}}}{\partial \varvec{\varepsilon }^{2}} \frac{\partial \varvec{\varepsilon }}{\partial t} \end{aligned}$$

(87)

$$\begin{aligned}&\frac{\partial ^{2} (1/M(\breve{D}))}{\partial \breve{D} \partial \varvec{\varepsilon }} =\frac{\partial ^{2} (1/M(\breve{D}))}{\partial \breve{D}^{2}} \frac{\partial {\breve{D}}}{\partial \varvec{\varepsilon }} \end{aligned}$$

(88)

$$\begin{aligned}&\frac{\partial ^{2} (1/M(\breve{D}))}{\partial \breve{D}^{2}} =\frac{2 \left( \frac{\partial \alpha (\breve{D})}{\partial \breve{D}} \right) ^{2}}{K_{u}-K(\breve{D})} -\frac{4 K \alpha (\breve{D}) \frac{\partial \alpha (\breve{D})}{\partial \breve{D}}}{(K_{u}-K(\breve{D}))^{2}} \nonumber \\&\quad +\frac{2 K^{2} \alpha (\breve{D})^{2}}{(K_{u}-K(\breve{D}))^3} \end{aligned}$$

(89)

(4) $\frac{\partial {\varvec{k}} (\kappa ) }{\partial \kappa }$ and $\frac{\partial {\varvec{k}} (\kappa ) }{\partial \theta }$

$$\begin{aligned}&\frac{\partial {\varvec{k}} (\kappa ) }{\partial \kappa } =\left[ \begin{array}{cc} \frac{\partial \breve{k} (\kappa )}{\partial \kappa } \sin \theta &{} 0 \\ 0 &{} \frac{\partial \breve{k} (\kappa )}{\partial \kappa } \cos \theta \end{array}\right] \end{aligned}$$

(90)

$$\begin{aligned}&\frac{\partial \breve{k} (\kappa ) }{\partial \kappa } ={\left\{ \begin{array}{ll} b_{1} k_\mathrm{f} e^{-b_{1} \left( \kappa -\varepsilon _\mathrm{e q}^{i}\right) }, &{} \text{ if } \kappa \geqslant \varepsilon _\mathrm{e q}^{i} \\ 0, &{} \text{ if } \kappa < \varepsilon _\mathrm{e q}^{i} \end{array}\right. } \end{aligned}$$

(91)

$$\begin{aligned}&\frac{\partial {\varvec{k}} (\kappa ) }{\partial \theta } =\left[ \begin{array}{cc} \breve{k} (\kappa ) \cos \theta &{} 0 \\ 0 &{} -\breve{k} (\kappa ) \sin \theta \end{array}\right] \end{aligned}$$

(92)