1 Introduction

One of the most important features needed in hydraulic fracture design is the ability to predict the geometry and the characteristics of hydraulically induced fracture.

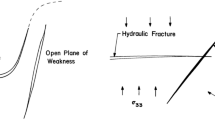
Due to the presence of discontinuities in rock mass, a better understanding of how a hydraulic fracture interacts with a NF is fundamental for predicting the ultimate size and shape of hydraulic fractures formed by a treatment.

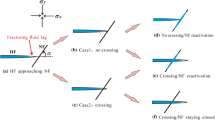
Some experimental research revealed the effect of NF on hydraulic fracture propagation [3–5, 9–11, 21, 22, 26]. Blanton [4] demonstrated that at low interaction angles and differential stresses, the NF can prevent the crack propagation. However, at high interaction angles and differential stresses, hydraulic fracture crosses the NF. Zhou et al. [26] showed that in addition to differential in situ stresses and interacting angle, friction coefficient is often a main and effective parameter. The obtained results indicate that the most significant factors affecting hydraulic fracture propagation are interacting angle of the hydraulic fracture with natural fracture, in situ stress condition, and NF shear strength.

Some numerical studies were developed to study the effect of natural fracture on hydraulic fracture [6, 20, 24, 25].

Boundary element method has been extensively used in fracture mechanics and stress analysis [1, 2]. Displacement discontinuity method (DDM) is an indirect boundary element method, which has been used for analysis of crack problems related to rock fracture mechanics. It should be noted that DDM does not have the re-meshing problem. The higher-order variation of the displacement discontinuities with special crack tip elements is usually used for the treatment of crack problems [13, 15–18]. Fracture modeling and crack propagation were also investigated using meshless [27, 28] and finite element [14] methods.

In this study, a general higher-order displacement discontinuity method implementing crack tip element is used to study the interaction of pressurized fracture with discontinuities. This paper shows how the interaction affects the behavior of the natural fractures and activates them, and consequently, the hydraulic fracture propagation path and locations with potential to re-initiate the tensile crack along the opposite side of NF are determined.

2 Displacement discontinuity method

A displacement discontinuity element (DDE) with length of 2a along the x-axis is shown in Fig. 1a, which is characterized by a general displacement discontinuity distribution of \( \hat{u}(\xi ) \). By taking the u x and u y components of the general displacement discontinuity to be constant and equal to D x and D y , respectively, in the interval (−a, +a) as shown in Fig. 1b, two DDE surfaces can be distinguished, one on the positive side of y (y = 0+) and another one on the negative side (y = 0−). The displacements undergo a constant change in value when passing from one side of the DDE to the other side. Therefore, the constant element displacement discontinuities D x and D y can be written as:

Fig. 1
figure 1

a DDE and the distribution of u(ξ). b Constant element displacement discontinuity

Full size image
$$ D_{x} = u_{x} (x,0_{ - } ) - u_{x} (x,0_{ + } ),D_{y} = u_{y} (x,0_{ - } ) - u_{y} (x,0_{ + } ) $$
(1)

The positive sign conversion of D x and D y is shown in Fig. 1b [8].

2.1 The quadratic element formulation

The quadratic element displacement discontinuity is based on analytical integration of quadratic collocation shape functions over collinear, straight-line displacement discontinuity elements [18]. Figure 2 shows the quadratic displacement discontinuity distribution, which can be written in a general form as:

$$ D_{i} (\varepsilon \,\,) = N_{1} (\varepsilon \,\,)D_{i}^{1} + N_{2} (\varepsilon \,\,)D_{i}^{2} + N_{3} (\varepsilon \,\,)D_{i}^{3} \,,\,\,\,\,\,\,\,\,i = x,y $$
(2)

where D 1 i , D 2 i and D 3 i are the quadratic nodal displacement discontinuities, and,

$$ N_{1} (\xi ) = \xi (\xi - 2a_{1} )/8a_{1}^{2}, \quad N_{2} (\xi ) = - (\xi^{2} - 4a_{1}^{2} )/4a_{1}^{2} , \quad N_{3} (\xi ) = \xi (\xi + 2a_{1} )/8a_{1}^{2} $$
(3)

are the quadratic collocation shape functions using a 1 = a 2 = a 3. A quadratic element has 3 nodes, which are at the centers of its three sub-elements.

Fig. 2
figure 2

Quadratic collocations for the higher-order displacement discontinuity elements

Full size image

The displacements and stresses for a line crack in an infinite body along the x-axis, in terms of single harmonic functions g(x,y) and f(x,y), are given by Crouch and Starfield [8] as:

$$ \begin{aligned} u_{x} = & \left[ {2(1 - \nu \,\,)f_{,y} - yf_{,xx} } \right] + \left[ { - (1 - 2\nu \,\,)g_{,x} - yg_{.xy} } \right] \\ u_{y} = & \left[ {(1 - 2\nu \,\,)f_{,x} - yf_{,xy} } \right] + \left[ {2(1 - \nu \,\,)g_{,y} - yg_{.yy} } \right] \, \\ \end{aligned} $$
(4)

and the stresses are

$$ \begin{aligned} \sigma_{xx} = \,& 2\mu \left[ {2f_{,xy} + yf_{,xyy} } \right] + 2\mu \left[ {g_{,yy} + yg_{,yyy} } \right] \\ \sigma_{yy} = \,& 2\mu \left[ { - yf_{,xyy} } \right] + 2\mu \left[ {g_{,yy} - yg_{,yyy} } \right] \, \\ \sigma_{xy} = \,& 2\mu \left[ {f_{,yy} + yf_{,yyy} } \right] + 2\mu \left[ { - yg_{,xyy} } \right] \\ \end{aligned} $$
(5)

μ is shear modulus and, f ,x ,g ,x ,f ,y , g ,y , etc. are the partial derivatives of the single harmonic functions f(x,y) and g(x,y) with respect to x and y, in which these potential functions for the quadratic element case can be find from:

$$ f(x,y) = \frac{ -1}{4\pi(1 - \nu)}\sum\limits_{j = 1}^{3} {D_{x}^{j} F_{j} (I_{0} ,I_{1} ,I_{2})}, g(x,y) = \frac{ - 1}{4\pi \,\,(1 - \nu \,\,)}\sum\limits_{j = 1}^{3} {D_{y}^{j} F_{j} (I_{0} ,I_{1} ,I_{2} )\,\,} $$
(6)

in which, the common function F j is defined as:

$$ F_{j} (I_{0} ,I_{1} ,I_{2} ) = \int {N_{j} (\xi )\ln \left[ {(x - \xi )^{2} + y^{2} } \right]}^{\frac{1}{2}} {\text{d}}\xi ,\quad {\text{j = 1, to 3}} $$
(7)

where the integrals I 0 , I 1 and I 2 are expressed as follows:

$$ I_{0} (x,y) = \int\limits_{ - a}^{a} {\ln \left[ {(x - \xi \,\,)^{2} + y^{2} } \right]}^{\frac{1}{2}} {\text{d}}\xi = y(\theta_{1} - \theta_{2} ) - (x - a)\ln (r_{1} ) + (x + a)\ln (r_{2} ) - 2a $$
(8-a)
$$ I_{1} (x,y) = \int\limits_{ - a}^{a} {\xi \,\,\,\ln \left[ {(x - \xi \,\,)^{2} + y^{2} } \right]}^{\frac{1}{2}} d\xi = xy(\theta_{1} - \theta_{2} ) + 0.5\left( {y^{2} - x^{2} + a^{2} } \right)\ln \frac{{r_{1} }}{{r_{2} }} - ax $$
(8-b)
$$ \begin{aligned} I_{2} (x,y) =& \int\limits_{ - a}^{a} {\xi^{\,2} \,\ln \left[ {(x - \xi )^{2} + y^{2} } \right]}^{\frac{1}{2}} d\xi \, = \frac{y}{3}\left( {3x^{2} - y^{2} } \right)(\theta_{1} - \theta_{2} ) + \hfill \\ &\frac{1}{3}\left( {3xy^{2} - x^{3} + a^{3} } \right)\ln (r_{1} ) - \frac{1}{3}\left( {3xy^{2} - x^{3} - a^{3} } \right)\ln (r_{2} ) - \frac{2a}{3}\left( {x^{2} - y^{2} + \frac{{a^{2} }}{3}} \right) \hfill \\ \end{aligned} $$
(8-c)

The terms θ 1,θ 2, r 1 and r 2 in this equation are defined as:

$$ \begin{aligned} \theta_{1} &= { \arctan }\left( {\frac{y}{x - a}} \right),\quad \theta_{2} = { \arctan }\left( {\frac{y}{x + a}} \right), \hfill \\ r_{1} &= \left[ {\left( {x - a^{2} } \right) + y^{2} } \right]^{\frac{1}{2}} ,\quad {\text{and}}\quad r_{2} = \left[ {\left( {x + a} \right)^{2} + y^{2} } \right]^{\frac{1}{2}} \hfill \\ \end{aligned} $$

2.2 Crack tip element and stress intensity factor

Analytical solutions of crack problems for various loading conditions show that the stresses at the distance r from the crack tip always vary as r −0.5 if r is small. Due to the singularity variations \( 1/\sqrt r \) and \( \sqrt r \) for the stresses and displacements at the vicinity of the crack tip, the accuracy of the displacement discontinuity method decreases, and usually, a special treatment of the crack at the tip is necessary to increase the accuracy and make the method more efficient. A special crack tip element that already has been introduced in literature e.g., [18] is used here, to represent the singularity feature of the crack tip. Using the special crack tip element of length 2a, as shown in Fig. 3, the parabolic displacement discontinuity variations along this element are given as:

$$ D_{i} (\varepsilon ) = D_{i} (a)\left( {\xi /a} \right)^{\frac{1}{2}} \, ,\quad \, i = x,y $$
(9)

where ξ is the distance from tip along the crack and D y (a) and D x (a) are the opening (normal) and sliding (shear) displacement discontinuities at the center of special crack tip element.

Fig. 3
figure 3

Displacement correlation technique for the special crack tip element

Full size image

Substituting Eq. (9) into Eqs. (4) and (5), the displacement and stresses can be expressed in terms of D i (a). Then, the potential functions f C (x, y) and g C (x, y) for the crack tip element can be expressed as:

$$ \begin{aligned} f_{C} (x,y) &= \frac{ - 1}{4\pi \,\,(1 - \nu \,)}\int\limits_{ = a}^{a} {\frac{{D_{x} (a)}}{{a^{\frac{1}{2}} }}\xi^{\frac{1}{2}} \ln \left[ {(x - \xi )^{2} + y^{2} } \right]^{\frac{1}{2}} {\text{d}}\xi } \hfill \\ g_{C} (x,y) &= \frac{ - 1}{4\pi \,\,(1 - \nu \,)}\int\limits_{ = a}^{a} {\frac{{D_{y} (a)}}{{a^{\frac{1}{2}} }}\xi^{\frac{1}{2}} \ln \left[ {(x - \xi )^{2} + y^{2} } \right]^{\frac{1}{2}} {\text{d}}\xi } \hfill \\ \end{aligned} $$
(10)

These functions have a common integral of the following form:

$$ I_{C} = \int\limits_{0}^{2a} \xi^{\frac{1}{2}} \ln \left[ {(x - \xi )^{2} + y^{2} } \right]^{\frac{1}{2}} {\text{d}}\xi $$
(11)

3 Numerical discretization

Numerical solution to any problem by discretizing a curved or straight-line crack with enough elements and summing the effects of all N elements can be found (Fig. 4).

Fig. 4
figure 4

Representation of a crack by N elemental displacement discontinuities

Full size image

The discretized form of displacement discontinuity equation can be formed based on the principle of superposition as:

$$ \left. \begin{array}{ll} {\mathop{\sigma} \limits^{i}}_{s} = \sum\limits_{j = 1}^{N} {A_{ss}^{ij} {\mathop {D}\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{sn}^{ij} \,{\mathop{D}\limits^{j}}_{n} } } \\ {\mathop{\sigma}\limits^{i}}_{n} = \sum\limits_{j = 1}^{N} {A_{ns}^{ij} {\mathop{D}\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{nn}^{ij} \,{\mathop{D}\limits^{j}}_{n} } } \end{array} \right\}\quad 1 \le i \le N $$
(12)
$$ \left. \begin{aligned} {\mathop u\limits^{i}}_{s} &= \sum\limits_{j = 1}^{N} {B_{ss}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {B_{sn}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\ {\mathop u\limits^{i}}_{n} &= \sum\limits_{j = 1}^{N} {B_{ns}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {B_{nn}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\ \end{aligned} \right\}\,\,\,\,1 \le i \le N $$
(13)

where D j s and D j n are the shear and normal components of discontinuity with respect to the local coordinates s and n at the jth element. σ j s and σ j n are the shear and normal stress at the midpoint of the ith element. A ij and B ij are the influence coefficient matrix accounting for the different positions and orientations of each element. The coefficient \( A_{ns}^{ij} \), for example, gives the normal stress at the ith segment (σ i n ) in terms of the shear component of displacement discontinuity at the jth segment (D j s ). Finally, a system of 2(3 N) simultaneous linear equations in 2(3 N) unknowns (DD) is made. Given the boundary conditions on each element, the system of algebraic equations is solved. These equations can be solved by standard methods of numerical analysis, e.g., elimination or iteration, and the values of elemental DD, element by element along the boundary can be gotten. In this study, the LU factorization method is used in this study. The four basic steps of the numerical program (2DFPM), which is developed by authors, are shown in the following flowchart (Fig. 5).

Fig. 5
figure 5

General flowchart of 2DFPM

Full size image

It’s necessary to declare that the fluid pressure distribution along the HF is assumed constant in this study for simplicity. Because of the less effect of fluid pressure distribution on the HF and NF interaction, this assumption does not have significant consequence on the accuracy of the results.

4 Fracture propagation criterion

The “stress intensity factor” is an important concept in fracture mechanics. Since the DDM is used in this research, it is necessary to use the formulations given for the SIF (K I and K II) in terms of the normal and shear displacement discontinuities [17, 23]. Based on liner elastic fracture mechanics (LEFM) theory, the mode I and mode II stress intensity factors K I and K II can be written in terms of the normal and shear displacement discontinuities as [18]:

$$ K_{\text{I}} = \frac{\mu }{{4\left( {1 - \nu } \right)}}\left( {\frac{2\pi }{a}} \right)^{\frac{1}{2}} D_{y}(a),\,{\text{and}}\,K_{\text{II}} = \frac{\mu }{{4\left( {1 - \nu } \right)}}\left( {\frac{2\pi }{a}} \right)^{\frac{1}{2}} D_{x} \left( a \right) $$
(14)

Then, the mixed mode of stress intensity factors (i.e., mode I and mode II fractures, which are the most commonly fracture modes occur in rock fracture mechanics) is numerically computed.

Several mixed mode fracture criteria have been used in the literature to investigate the crack initiation direction and its path [23]. As most of rocks have brittle behavior under tension, the mode I fracture toughness KIC (under plain strain condition) with the maximum tangential stress fracture criterion (σ-criterion) introduced by Erdogan and Sih [12] mostly is used to predict the crack propagation direction.

Based on this criterion, the crack tip will start to propagate when:

$$ { \cos }\frac{{\theta_{0} }}{2}\left[ {K_{\text{I}} { \cos }^{2} \frac{{\theta_{0} }}{2} - \frac{3}{2}K_{\text{II}} { \sin }\frac{{\theta_{0} }}{2}} \right] = K_{\text{IC}(14)} $$
(15)

where θ 0 is the crack propagation angle follows that

$$ \theta_{0} = 2\arctan \left[ {\frac{1}{4}\left( {\frac{{K_{\text{I}} }}{{K_{\text{II}} }}} \right) - \frac{1}{4}\sqrt {\left( {\frac{{K_{\text{I}} }}{{K_{\text{II}} }}} \right)^{2} + 8} } \right] $$
(16)

The latter value corresponding to the crack tip should satisfy the condition:

$$ K_{\text{I}} { \sin }\theta_{0} + K_{\text{II}} \left( {3{ \cos }\theta_{0} - 1} \right) = 0 $$
(17)

For a given crack length of 2a, under a certain loading condition, the crack propagation angle θ 0 is predicted (based on LEFM principles and σ-criterion, i.e., Eqs. (15) and (16)). Then, the original crack for each tip is extended by an amount Δa that has equal length with crack tip element. This element will be perpendicular to the maximum tangential stress near the crack tip. So a new crack length (2a + 2Δa) is obtained and again Eqs. (15) and (16) are used to predict the new conditions of crack propagation for this new crack.

5 Joint element

For an elastic joint element with zero initial deformations, the joint element deforms only in response to the induced stress caused, for example, by an approaching hydraulic fracture. The relation between tractions and the displacement discontinuities on the joint surface (having N elements) is [8]:

$$ \left. \begin{aligned} &0 = ({\mathop {K_{s} )(}\limits^{i}}{ \mathop D\limits^{i}}_{s} ) + \sum\limits_{j = 1}^{N} {A_{{_{ss} }}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{{_{sn} }}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\& 0 = ({\mathop {K_{n} )(}\limits^{i}} {\mathop D\limits^{i}}_{n} ) + \sum\limits_{j = 1}^{N} {A_{{_{ns} }}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{{_{nn} }}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\ \end{aligned} \right\}\,\,\,\,1 \le i \le N $$
(18)

K i n and K i s are the normal and shear rigidity of the joint and A ss (i, j), etc. are the corresponding influence coefficient. D i n and D i s are the total joint deformation which can be expressed as the sum of the initial total joint deformation ((D i n )0 and (D i s )0) and the induced deformation (D ′i n and D ′i s ). In this type of joint element, the natural fracture has reached equilibrium with geological time, and it does not deform elastically or plastically under far field stresses prior to the process of hydraulic fracturing, and the initial stress field around a hydraulic fracture was not affected by the presence of natural fracture.

During elastic deformation, there is a constraint between the normal (σ i n ) and shear (σ i s ) stresses across the joint, which is given by Mohr–Coulomb condition (shown Fig. 6). The total shear stress across a Mohr–Coulomb joint element cannot exceed the value specified by Eq. 19.

$$ \left| {\mathop {\sigma_{s} }\limits^{i} } \right| \le \mathop c\limits^{i} + ( - \mathop {\sigma_{n} }\limits^{i} )\tan \mathop \phi \limits^{i} $$
(19)

where ϕ i is the angle of friction and c i is the cohesion. It is required that the element be allowed to undergo a certain amount of inelastic deformation or permanent slip, when the total shear stress on the joint element, |σ i s |, exceeds the total yield stress.

Fig. 6
figure 6

Mohr diagram for a joint element under different contact mode and different stress conditions

Full size image

If the element is yielding, the total shear stress must equal the yield stress. The initial joint deformation is zero for a joint in this case (D i n  = D ′i n and D i s  = D ′i s ), and then, the governing equations for the normal and shear deformation can be written as:

$$ \begin{aligned}& \pm {\mathop \sigma \limits^{i}}_{s,yield} = ({\mathop \sigma \limits^{i}}_{s} )_{0} + \sum\limits_{j = 1}^{N} {A_{{_{ss} }}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{{_{sn} }}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\ &0 = ({\mathop {K_{n} )(}\limits^{i}} {\mathop D\limits^{i}}_{n} ) + \sum\limits_{j = 1}^{N} {A_{{_{ns} }}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{{_{nn} }}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\ \end{aligned} $$
(20)

where

$$ {\text{Sign}}\left( {\sigma^{i}_{{s,{\text{yield}}}} } \right) = {\text{sign}}\left( {\left( {\sigma_{s}^{i} } \right)_{\text{total}} } \right) $$
(21)

Joint separation or tensile cracking is another possible failure mode for the joint elements. According to the Mohr–Coulomb condition, the tensile strength of a joint element can be expresses as:

$$ {\mathop \sigma \limits^{i}}_{n}^{{}} = {\mathop c\limits^{i}} \cot {\mathop \phi \limits^{i}} $$
(22)

The tensile stress transmitted across an element cannot be greater than this, so the element must be allowed to crack open whenever σ i n  = c i cot ϕ i. Alternatively, and perhaps more realistically, we can use a tensile strength cutoff, σ i n  = T i0 (0 ≤ T i0  ≤ c i cot φ i), and allow the element to open whenever σ i n  = T i0 . In both cases, when the tensile stress across an element is greater than the tensile strength, the total normal and shear stresses become zero for an open element. For a joint with N elements, if element i becomes an open joint element, the following equations must be used:

$$ \begin{aligned} - ({\mathop \sigma \limits^{i}}_{s} )_{0} =& \sum\limits_{j = 1}^{N} {A_{ss}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{sn}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\& - ({\mathop \sigma \limits^{i}}_{n} )_{0} = \sum\limits_{j = 1}^{N} {A_{ns}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{nn}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\ \end{aligned} $$
(23)

6 Numerical procedure

If there are N elements altogether, with M displacement discontinuity stress elements along the HF boundary and N–M displacement discontinuity elements along the joint, then, the first 2(3 M) equations in the system are:

$$ \left. \begin{aligned} - ({\mathop \sigma \limits^{i}}_{s} )_{0} =& \sum\limits_{j = 1}^{N} {A_{ss} (i,j)\,D_{s}^{j} + \sum\limits_{j = 1}^{N} {A_{sn} (i,j)\,D_{n}^{j} } } \hfill \\ &- ({\mathop \sigma \limits^{i}}_{n} )_{0} = \sum\limits_{j = 1}^{N} {A_{ns} (i,j)\,D_{s}^{j} + \sum\limits_{j = 1}^{N} {A_{nn} (i,j)\,D_{n}^{j} } } \, \hfill \\ \end{aligned} \right\}\,\,\,\,1 \le i \le M $$
(24)

The remaining 2(3(N–M)) equations are:

$$ \left. \begin{aligned} &0 = ({\mathop {K_{s} )(}\limits^{i}} {\mathop D\limits^{i}}_{s} ) + \sum\limits_{j = 1}^{N} {A_{{_{ss} }}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{{_{sn} }}^{ij} \,{\mathop D\limits^{j}}_{n} } } \hfill \\& 0 = ({\mathop {K_{n} )(}\limits^{i}} {\mathop D\limits^{i}}_{n} ) + \sum\limits_{j = 1}^{N} {A_{{_{ns} }}^{ij} {\mathop D\limits^{j}}_{s} + \sum\limits_{j = 1}^{N} {A_{{_{nn} }}^{ij} \,{\mathop D\limits^{j}}_{n} } } \\ \end{aligned} \right\}\quad M + 1 \le i \le N $$
(25)

The numerical algorithm employed for joint modeling is based on incremental loading of boundary tractions. The initial tractions are divided into K increments with equal size and are applied step by step.

$$ ({\mathop \sigma \limits^{i}}_{s} )_{0}^{k} = \frac{k}{K}({\mathop \sigma \limits^{i}}_{s} )_{0}^{{}},\,\,\,\,({\mathop \sigma \limits^{i}}_{n} )_{0}^{k} = \frac{k}{K}({\mathop \sigma \limits^{i}}_{n} )_{0} $$
(26)

The incremental loading is continued until all K load increments are applied [8]. In each time step, at kth iteration and at element i, first, a joint contact type (for example, stick mode) is assumed, and the shear and normal displacements \( {\mathop {D}\limits^{i}}_{s}^{(k)} \), \( {\mathop{D}\limits^{i}}_{n}^{(k)} \)at the ith element are achieved using Eq. 18. Then, the total stresses at the ith element can be obtained and the yield stress at the kth iteration according to Eq. 19 can be calculated. After that a check is made to see whether the yield/opening condition is met or not according to Eqs. 19 and 22. The Eqs. 20, 18 and 23 are used to compute the next approximation of the normal and shear displacements at the ith elements (\( {\mathop D\limits^{i}}_{n}^{(k + 1)} \) and \( {\mathop D\limits^{i}}_{s}^{(k + 1)} \)) for the yield, stick and opening conditions, respectively. Lastly, the total stresses can be found and used to check the contact state again. If the new and the previous contact modes are not in agreement, the assumed contact mode must be changed and DD must be solved again. The process will be stopped when the new and the assumed contact modes are the same and resultant DD and stresses at each element i along the joint converge. The incremental technique (k) that is used for applying the boundary tractions in 2DFPM is shown in Fig. 7. At the end of the incremental loading, the procedure continues to calculate the characteristics of the new crack length (2a + 2Δa) and after that the iterative technique (CP) is used for fracture propagation steps.

Fig. 7
figure 7

General flowchart of incremental and iterative technique in 2DFPM

Full size image

The algorithm of calculation of tangential stress along the NF is presented in “Appendix”.

7 Verification of higher-order displacement discontinuity

For verification of the numerical program (2DFPM), a problem with analytical solution is solved and the results of numerical program compared with analytical results and the validity of the program in calculation of tangential stresses are confirmed.

7.1 Bonded interface

The accuracy of the program is demonstrated by examining the shear stress along a bonded interface just ahead of the fracture (x = 0) that subjected to an isotropic remote tensile stress (5 MPa) and its tip is s = 0.5 cm from the interface. The analytical solution for stresses around a 1 m long, open crack within a homogeneous, isotropic and linear-elastic body subjected to uniform remote tension can be derived from the Westergaard function (e.g., [19]).

The comparison between numerical results and the analytical values of the shear stresses is shown in the Fig. 8, and good agreement between the numerical and analytical results (the error <5 %) is displayed.

Fig. 8
figure 8

Shear stress along the interface when the fracture tip is s = 0.5 cm from the interface

Full size image

8 Interaction between hydraulic and natural fractures

In order to study the interaction between HF and NF, some problems of hydraulic fracture propagation near discontinuities are modeled. Then, shear, normal and tangential stresses on the other side of NF are calculated by 2DFPM and the HF propagation path and the change in its direction near the NF is investigated.

To reduce the number of independent variables and for simplicity, the dimensionless parameters are used [6].

$$ \bar{\sigma }_{ij} = \frac{{\sigma_{ij} }}{{\sigma_{m} }},\,\,\,\bar{\sigma }_{ij}^{\infty } = \frac{{\sigma_{ij}^{\infty } }}{{\sigma_{m} }}\,\, $$
(27)

where σ m  = (σ 1 + σ 3)/2 is the mean in situ stress and σ ij is the stress tensor components. The distance and spacing are normalized by the initial length of hydraulic fracture (L HF).

$$ \bar{x} = \frac{x}{{L_{\text{HF}} }},\,\,\,\,\,\bar{y} = \frac{y}{{L_{\text{HF}} }},\,\,\,\,\bar{r} = \frac{r}{{L_{\text{HF}} }},\,\,\,\,\bar{\rho } = \frac{\rho }{{L_{\text{HF}} }} $$
(28)

where ρ is the distance between the tip of hydraulic fracture and NF.

The shear and normal displacements (D s,n ) along the NF are normalized as follows:

$$ \bar{D}_{k} = \frac{{D_{k} }}{{L_{\text{HF}} }}\frac{G}{{(1 - \upsilon )\sigma_{m} }} $$
(29)

where G and ν are shear modulus and Poisson ratio of rock, respectively.

8.1 Interaction between hydraulic fracture and inclined natural fracture

Interactions between the hydraulic fracture and the inclined natural fracture are investigated in an infinite space (Fig. 9). For studying the effect of cross angle of HF on interaction process, the interaction between HF and NF with 40-degree angle related to the x-axis is modeled here. The strength and shear properties of rock and NF are mentioned in Table 1. The NF with shear strength properties equal to moderate strength (φ = 26.6°, c = 2.2 MPa and T 0 = 0.2 MPa) is investigated here. The fluid pressure inside the HF is constant along the HF and equal to −3.9 MPa, and maximum and minimum horizontal stresses are −2.1 and −1.9 MPa, respectively.

Fig. 9
figure 9

The geometry of interaction between the HF and inclined NF

Full size image
Table 1 Rock and NF parameters
Full size table

The NF (length of 20 m) was discretized with quadratic DD elements with an equal length and the HF (length of 2 m) was discretized with quadratic DD elements with equal length and 2 crack tip elements for HF tip. Elements with 0.5 mm length are selected for 2 m of central NF and 2.5 cm length for other elements. The distance between the HF tip and NF is equal to 0.1 m for this problem.

The maximum tangential stress (maximum principal stress) that is created on the other side of the NF is calculated. This parameter can characterize the ability of HF to cross the NF or arrest by that. For better description of this process, the normal and shear stresses along the NF are estimated too.

Normalized normal and shear displacement curves of NF are shown in Fig. 10. It can be seen that the normal and shear displacements are equal to zero along most of NF length and the opening and sliding are happening along the NF only near the HF tip. In this problem, we suppose that the NF has initial aperture and the normal stresses can close it. The results show the elements (598–602) in −0.092 < y < −0.079 range slipped, while the elements (603–647) that are in the—0.076 < y < 0.066 range opened (opening section).

Fig. 10
figure 10

Profiles of opening and sliding along the NF (40°), (L 0 = 0.1 m)

Full size image

Normalize profiles of normal, shear and tangential stresses along the NF are shown in Fig. 11. As shown in this Fig, the maximum principal stress has two different peak points along the opposite side of NF. These two points could become most probable locations for HF re-initiation at the NF before the HF cross the NF. The results show the positions of two peaks locate on the end of the opening section. It should be mentioned that in the opening section the normal and shear stresses are zero.

Fig. 11
figure 11

Stress distribution along a moderate NF that inclined with 40°(L 0 = 0.1 m)

Full size image

Normalize curves of normal and shear displacements for L 0 = 0 are shown in Fig. 12. The values of displacements are several times greater than the displacements in the previous case. For this case the results show, the elements (627–677) that are in the 0.002 < y < 0.162 range opened, while the elements (678–689) in 0.166 < y < 0.201 range slipped.

Fig. 12
figure 12

Profiles of opening and sliding along the inclined NF (40°), (L 0 = 0.0 m)

Full size image

The maximum principal stress has two different peak points along the opposite side of NF, but one peak is very greater than another (Fig. 13). The location of the greater peak that shows the potential points for hydraulic fracture re-orientation is located on the positive side (y > 0) of NF. For better understanding the movement of peak location along the NF (y > 0), the maximum principal stress for different distances (L 0) is calculated (Fig. 14). The results show when the distance is decreased, the maximum principal stress is increased and the location of peak is farther from the center of NF. The distance between the peak location and the center of the NF is equal 0.4 m for this case.

Fig. 13
figure 13

Stress distribution along a moderate NF that inclined with 40° (L 0 = 0)

Full size image
Fig. 14
figure 14

Maximum principle stress distribution along a moderate NF that inclined with 40° for different tip distances

Full size image

8.2 Fluid flow into the natural fracture

Modeling of the fluid flow into the NF after the coalescence with the HF is studied in this section. Parameters and geometry of HF and NF in previous section are used to study this process. The previous results show the elements of NF in the positive side of y axis are opened (Fig. 12), and then, the fluid-filled zone (L b) is selected for these elements (Fig. 15). The zone of pressurized NF is extended gradually and the profile of normalizes principle stress along the NF is studied.

Fig. 15
figure 15

The geometry of interaction between the HF and NF partly filled with fluid

Full size image

The results show the fluid-filled zone can shift the peak of principal stress along the NF. These peaks indicate the most probable points of HF re-initiation along the NF that move along the NF with increasing the length of fluid-filled zone and locate at the end of this zone (Fig. 16).

Fig. 16
figure 16

Maximum principal stress distribution along NF for different fluid-filled lengths (L b) (p = 3.9 MPa)

Full size image

The normal opening along the NF for different fluid-filled lengths is shown in Fig. 17. As a result, the fluid pressure front never coincides with the HF tip, allowing finite lag zone (empty open zone without fluid) to be created in front of the pressurized zone.

Fig. 17
figure 17

Normalized normal displacement (D n ) along NF at different fluid-filled lengths of NF (L b) (p = 3.9 MPa)

Full size image

For studying the effect of fluid pressure on location of maximum principle stress peak, the maximum principle stress is calculated for different fluid pressure in L b = 0.6 m (Fig. 18). The results show with increasing the fluid pressure inside the NF, the location of peaks move further to the right part of NF and then fluid pressure increasing cause the HF to deviate from original path. These results are in agreement with those of Cooke and Underwood [7], Chuprakov et al. [6] and Xue [24].

Fig. 18
figure 18

Normalized principal stress along NF at different fluid pressures (p) (L b = 0.6)

Full size image

9 Hydraulic fracture path near the natural fracture

A better understanding of how a HF interacts with a NF is fundamental for predicting the ultimate size and shape of the hydraulic fractures formed by a treatment. Thus, the propagation path of the HF near the NF which can be considered as a closed crack is investigated. The Poisson ratio and Young modulus are considered ν = 0.2, E = 20,000 MPa, respectively. The friction coefficient between the NF surfaces is assumed to be 0.2 and the material cohesion is zero. The lengths of the HF and the NF are 0.5 and 2 m, respectively, and the fluid pressure inside the HF is 29.1 MPa. The minimum and maximum horizontal stresses are 9.7 and 19.4 MPa, respectively.

The NF has various inclination (15°, 30° and 90°) related to the \( \sigma_{{h,{ \hbox{min} }}} \) direction. The crack paths for three different NF inclination angles are shown in Fig. 19. The results show, when the inclination angle is 90°, the HF grows along x-direction until cross the left surface of the NF and the maximum deviation is occurred for NF with 15° inclination. The results show the NF can deviate the HF in high inclination angles in spite of high differential stresses. NF changes the field stress near its surface and causes the principal stresses to be locally parallel and perpendicular to the surface; therefore, all hydraulic fractures tend to interact with NF at right angle.

Fig. 19
figure 19

Propagation paths of pressurized crack for different NF inclination angles

Full size image

For calculating the effect of shear strength of NF on HF path near the NF, HF propagation near the NF with zero and infinite strength is modeled too. As is shown in Fig. 20, for a bonded NF (without opening and sliding) with 30° inclination, the HF propagates in its direction, but for unbonded NF (with opening and sliding), the HF deviates from its original direction.

Fig. 20
figure 20

Propagation paths of HF for NF with different shear strengths

Full size image

10 Conclusion

In this study, the problem of interaction between a hydraulic fracture and a pre-existing natural fracture in an impermeable media is investigated numerically with constant pressure distribution assumption along the hydraulic fracture. Furthermore, the numerical program (2DFPM) is developed to study the mechanical activation of a NF because of the propagation of the HF. Joint elements are employed to describe different NF contact modes (stick, slip and open mode). The maximum tangential stress criterion is implemented sequentially to trace the crack propagation path. The stages of hydraulic fracturing tip approaching, coalescence and fluid penetration along the NF is modeled. By coupling the finite difference and boundary element (DDM), the tangential stress along the both side of the NF is calculated and the maximum principal stress peaks (tensile stress) that are the locations of new tensile fractures are founded.

The results display before the HF reaches a NF, the fracture re-initiation across the NF and with an offset is probable. The results show that the probable re-initiation points are located in the end of the open zone along the NF, which shift with decreasing the distance between the HF tip and NF. After that, HF trajectories near a NF and prior to coalesce with the NF are examined using different joint properties. The results show HF trajectories near a NF deviate from the direction of the maximum horizontal stress because of NF inclination angle and shear strength. It is found that the position, distance and inclination of the HF relative to the natural fractures have a strong influence on the HF propagation path.