Abstract
In this paper, a numerical method is proposed to simulate multi-scale fracture propagation driven by fluid injection in transversely isotropic porous media. Intrinsic anisotropy is accounted for at the continuum scale, by using a damage model in which two equivalent strains are defined to distinguish mechanical behavior in the direction parallel and perpendicular to the layer. Nonlocal equivalent strains are calculated by integration and are directly introduced in the damage evolution law. When the weighted damage exceeds a certain threshold, the transition from continuum damage to cohesive fracture is performed by dynamically inserting cohesive segments. Diffusion equations are used to model fluid flow inside the porous matrix and within the macro-fracture, in which conductivity is obtained by Darcy’s law and the cubic law, respectively. In the fractured elements, the displacement and pore pressure fields are discretized by using the XFEM technique. Interpolation on fracture elements is enriched with jump functions for displacements and with level set-based distance functions for fluid pressure, which ensures that displacements are discontinuous across the fracture, but that the pressure field remains continuous. After spatial and temporal discretization, the model is implemented in a Matlab code. Simulations are carried out in plane strain. The results validate the formulation and implementation of the proposed model and further demonstrate that it can account for material and stress anisotropy.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The study of damage and fracture in brittle solids has numerous engineering applications, such as aerospace metal optimization, construction design and hydraulic fracturing techniques used in the oil and gas industry. Hydraulic fracturing is used to stimulate well production, both in regular and tight formations. It is a complex process that involves host rock deformation, fracture propagation, fluid flow and fluid leak-off. Solving the problem of hydraulic fracturing either analytically or numerically is still very challenging because of the nonlinear, history dependent fluid flow with moving boundary conditions and also because of the anisotropic nonlinear behavior of the host rock.
Pioneering work on hydraulic fracturing dates back from the 1950s [36, 50, 78]. Classical solutions are based on the so-called PKN and KDG models. In 1961, Perkins and Kern [68] used the theory of elasticity to solve for the fracture width w and the fluid pressure p along the fracture length l in plane strain conditions, in which the fracture height h was constant. Later, Nordgren [60] improved the model by accounting for the fluid leak-off into the surrounding rock matrix (hence the name, PKN model). By further assuming that the width of the fracture w is constant in the direction perpendicular to the fracture plane, Khristianvic and Zheltov [50] and Geertsma and De Klerk [32] independently developed another set of analytical solutions for hydraulic fracturing—the so-called KGD model. Spence and Sharp [80] extended the KGD model with self-similar relations (power law relations between the cavity volume and the injection time), and they accounted for rock toughness. In addition to the plane strain models, analytical solutions for the radial or penny-shaped fracture growth under constant fluid injection pressure was obtained by Sneddon [78] and later extended to elliptical fracture growth [36]. The penny-shaped fracture growth model was further applied to hot, dry rock [1, 2]. Note that by invoking scaling laws, Detournay [17] found that there are three competing energy dissipation mechanisms that control the process of hydraulic fracturing, depending on the value of the fracture toughness, the fluid viscosity and the leak-off term. Based on Detournay’s analyses, numerous semi-analytical solutions were developed for plane strain conditions [3, 4, 27,28,29, 38] and for penny-shaped fractures [7, 8, 72]. These solutions, based on a variety of governing laws for fluid rheology (viscosity), fluid flow in the matrix (leak-off) and rock toughness, are important tools to understand hydraulic fracture propagation regimes. As pointed out by Detournay and Peirce [18], the analytical solutions reviewed above were all obtained with ad hoc assumptions and did not properly account for the boundary conditions at the tip and near the tip. To address these limitations, a number of studies were carried out to find analytical solutions for the singularity of the tip and to predict the limiting propagation regimes, such as the toughness dominated regime (index k), the leak-off dominated regime (index \({{\tilde{m}}}\)), and the viscous dominated regime (index m). The \(m-\)vertex solution was explained by Desroches et al. [16] for the zero-toughness and impermeable case, the \({{\tilde{m}}}\)-vertex solution was presented by Lenoach [53] for the zero-toughness and leak-off dominated case, and the k-vertex solution was obtained from Linear Elastic Fracture Mechanics (LEFM) asymptotes. In the general case, fracture propagation may evolve within the parametric space of the three limiting cases. Recently, Garagash et al. [30] and Dontsov and Peirce [20] obtained the universal tip asymptotic solution that can be used for any location in the parametric space.
Analytical solutions were used for industry applications at the inception of hydraulic fracturing. However, the overly constraining assumptions limit their application. So-called pseudo-3D (P3D) models were the first numerical simulators developed to relax those constraints. Numerical P3D models are still based on the assumption that a vertical plane fracture propagates in a homogeneous rock formation, but fracture height growth is accounted for. In lumped P3D models, fractures are assumed to be ellipsoids [55]. In cell-based P3D models, fractures are regarded as connected rectangular elements [61, 74]. The latest P3D models include the stacked height [11] and the enhanced [19] models. The planar 3D numerical models (PL3D) were proposed to account for the variation of elasticity, toughness and confining pressure across formation layers [5, 67, 75, 84], which relaxes analytical constraints even further. Either the adaptive mesh method or the structured mesh enhanced with level set method is used to obtain the dynamic planar fracture footprint. The two-dimensional fluid flow as well as the elastic equilibrium are considered. The PL3D model significantly increases the accuracy of the hydraulic fracturing model, but also increases dramatically its computational cost.
In the past years, research on hydraulic fracturing modeling focused on three major objectives. The first one is to reduce the computational cost while maintaining solution accuracy in P3D and PL3D models, by incorporating the tip asymptotic solutions [21, 22, 66] into the simulation code. The second is to relax the constraints of the P3D and PL3D models, by considering non-planar fracture geometries [9, 37], by simulating the simultaneous propagation of multiple hydraulic fractures [21, 83] and by incorporating the interaction with natural fractures [46, 48, 51]. To meet these two first objectives, the force equilibrium in elastic formation, the mass balance equation for the fluid with leak-off and the propagation of fracture tip are accounted for. However, the process of fluid flow within the porous matrix, as well as the nonlinear rock deformation and the cohesive fracture propagation are ignored. The third objective is thus to incorporate these physical processes by employing advanced numerical methods, such as interface elements [10], the eXtended Finite Element Method (XFEM) [24] and the phase field method [56].
The XFEM allows simulating fracture propagation in arbitrary directions explicitly, without remeshing. The XFEM was used extensively in the last decade to simulate hydraulic fracturing. For instance, considering an impermeable matrix, Gordeliy and Peirce [33,34,35] investigated the enrichment strategy, the coupling scheme, and the convergence of the XFEM hydraulic fracturing models. Dontsov and Peirce [21] later enriched the fracture tip with a universal tip asymptotic solution to account for all possible cases in the toughness/viscosity/leak-off dominated regimes. Considering a fully saturated matrix, De Borst et al. [15] pioneered the formulation of XFEM models for stationary fractures. Afterward, fracture propagation in saturated porous media was simulated using XFEM-cohesive segments [49, 57, 59, 69], in which different enrichment functions were adopted to represent the pore pressure distribution across the fracture. This idea was further extended to model the propagation of multiple fluid-driven fractures [83] and to model the intersection with natural fractures [47]. Considering a partially unsaturated matrix, Salimzadeh and Khalili [71] employed the XFEM to model hydraulic fracturing in a three-phase system.
The numerical methods reviewed above for modeling hydraulic fracturing have addressed a wide range of challenges and have significant value; however, some assumptions on host rock deformation and fracture propagation are overly simplified. As explained in [12, 14, 45, 77, 85], quasi-brittle materials fail following two stages: diffused damage inception followed by extensive damage localization leading to macro-fracture propagation. The singularity at the fracture tip from LEFM does not exist physically, and the cohesive segment concept by which the diffuse damage process zone is condensed into a surface or line was never assessed for its accurate representation of fracture propagation. In addition, most of reservoir sedimentary host rocks (e.g., shale) behave anisotropically [54, 73]. The propagation direction of fluid-driven fractures remains as a puzzle when material anisotropy and stress anisotropy compete.
In this paper, we thus propose a numerical scheme to predict multi-scale hydraulic fracture propagation in transversely isotropic porous materials based on the XFEM. To capture the two-stage fracture propagation process, we couple a nonlocal damage model with a cohesive zone method, following the methods previously presented by the authors [42]. We first present the strong and weak forms of the governing equations of the problem of hydraulic fracturing in saturated porous media, in Sect. 2. We detail the momentum balance equations for the solid and fluid phases as well as the mass balance equations for the fluid phase inside the solid skeleton and inside the fracture. Constitutive equations include a nonlocal anisotropic damage model (for the deformation and damage of the porous matrix), the Park–Paulino–Roesler (PPR) cohesive model (for fracture propagation), Darcy’s law (for fluid flow in the solid matrix) and the cubic law (for fluid flow within the fractures). In Sect. 3, we present the XFEM used for space discretization and the finite difference method used for time discretization. A Newton–Raphson iterative scheme is employed to solve the global nonlinear system of equations. In Sect. 4, we first validate the formulation and implementation of the computational model by simulating the Khristianovic–Geertsma–de Klerk (KGD) problem; we then conduct parametric studies in plane strain conditions to understand the mechanisms that control fracture path formation in the presence of both material and stress anisotropy.
2 Coupled hydro-mechanical governing equations for saturated porous media with intrinsic transverse isotropy
2.1 Strong formulation
Hydraulic fracturing in porous media is a complex problem, which involves coupled physical processes that happen simultaneously, mainly micro-crack propagation and coalescence in the solid porous matrix; fluid flow through the porous medium; fluid flow within the macro-fracture; fluid exchange between the porous matrix and the fracture. Correspondingly, the governing equations required to model these processes shall include: momentum balance equations and constitutive laws for predicting the deformation field, micro-crack development in the solid matrix and the propagation of macro-fractures; fluid mass balance equation and fluid transport constitutive equation, both in the solid matrix and in the macro-fracture.
We start with the classical Biot theory [6] to describe the mechanical behavior of elastic porous media saturated with a single-phase fluid. Following Dormieux’s approach [23], we consider that the development of micro-cracks (damage) will have a direct influence on elasticity parameters and on porosity. For the sake of simplicity, we assume that damage development (i.e., the initiation and propagation of micro-cracks) does not generate inelastic deformation, i.e., damage only affects the stiffness tensor. Porosity and permeability are affected indirectly by damage, through the expression of Biot’s effective stress. Consequently, the potential energy density of a Representative Elementary Volume (REV) of transversely isotropic porous material can be expressed as:
where \(H_s\) is also called Helmholtz free energy, \(\varvec{\epsilon }\) is the strain tensor, p is the fluid pressure, \(\varvec{\omega }\) stands for the damage variable, \({\mathbb {C}}\) is the elastoplastic stiffness tensor and \(\alpha _{ij}=-\partial ^2H_s/\partial \epsilon _{ij}\partial p\) is Biot’s coefficient tensor. \(\varvec{\alpha }\) linearly relates the porosity change to the strain variation when pressure is held constant (\(p=0\)). Due to Maxwell’s symmetry [13], \(\varvec{\alpha }\) also linearly relates the stress increment to the pressure increment when strain is held constant (\(\varvec{\epsilon }=0\)). \(1/N=-\partial ^2H_s/\partial p^2\) is the inverse of Biot’s skeleton modulus, linking pressure variation dp with the porosity variation when strain is held constant (\(\varvec{\epsilon }=0\)). According to the thermodynamic conjugation relationships, the Biot’s effective stress tensor \(\varvec{\sigma }\) and the porosity \(\phi\) can be expressed in following state equations:
where \(\phi _0\) is the initial porosity.
2.1.1 Mixture governing equations
Under quasi-static conditions, the momentum balance equation of the REV (made of the mixture solid + fluid) is:
where \(\rho\) is the average mass density of the mixture, defined as \(\rho = (1-\phi )\rho _s+\phi \rho _{\text {f}}\), in which \(\rho _s\) (respectively \(\rho _{\text {f}}\)) stands for the mass density of the solid phase (respectively, density of the fluid phase). \(\varvec{g}\) is the body force vector. Substituting the state Eq. 2 into Eq. 3, we get the strong form of the governing equation for the mixture, as follows:
2.1.2 Fluid governing equations in the saturated porous matrix
Fluid flow inside the porous matrix is fundamentally governed by the fluid mass balance equation, which expresses that the mass change within the considered REV should be equal to the difference between the fluid mass flowing out the REV and the fluid mass flowing in the REV, as follows:
where \(\varvec{v}\) is the velocity vector of the fluid. \(\rho _{\text {f}}\) and \(m_{\text {f}}\) represent the mass density and the mass of the fluid, respectively. Since the porous medium is saturated with the fluid, we have: \(m_{\text {f}} = \rho _{\text {f}} \phi\), where \(\phi\) is the porosity. According to the state equation of the fluid, the mass density of the fluid is related to the pore pressure through the following equation:
where \(K_{\text {f}}\) is the bulk modulus of the fluid. We assume that fluid flow inside the porous matrix is laminar and that it is governed by Darcy’s seepage equation as:
where \(\mu\) is the dynamic viscosity of the fluid, \(\varvec{k}_{\rm m}\) is the intrinsic anisotropic permeability tensor of the solid skeleton. For simplicity, we assume that permeability remains constant in this paper. Note that future developments are necessary to account for the dependence of permeability to the geometry and connectivity of pores and cracks within the solid skeleton. By substituting the state equations (Eqs. 2, 6), the Darcy’s law (Eq. 7) into Eq. 5, we get the governing equation for the fluid flow through the permeable porous medium surrounding the fracture, as follows:
where it is assumed that the spatial variability of the fluid mass density is negligible (i.e., \(\nabla \rho _{\text {f}}\ne 0\)). M is the so-called Biot’s modulus, defined by
2.1.3 Fluid governing equations along the fracture
Different from the fluid flow inside the porous matrix, the mass balance equation that governs the fluid flow inside the fracture involves a direction-dependent hydraulic conductivity. Consider a plane strain REV such that a face of the REV is a unit fracture surface, as sketched in Fig. 1. The local fracture width is noted w (perpendicular to fracture faces). The fluid mass change per unit of time within the REV is equal to the variation of flow rate in the direction of the fracture plane, plus the variation of flow rate in the direction perpendicular to the fracture surfaces. The mass balance equation is thus expressed as:
where \(\nabla _s\) represents the gradient in the tangent direction of the local fracture surface, in which \(\varvec{s}\) denotes the natural coordinate of the fracture. \(\varvec{q}\) is the flow rate inside the fracture. Accordingly, the first term represents the change of fluid mass due to a flow rate variation within the fracture. The velocity \(\varvec{v}\) is related to the flow in the matrix and can be discontinuous at the two fracture surfaces: \(\varvec{v}^+\ne \varvec{v}^-\). We note \([\![ \varvec{v}( \varvec{ s}) ]\!]\) the velocity jump across the fracture. After multiplying by the normal direction of the fracture surfaces \(\varvec{n}_{\varGamma _d}\) and the fluid density \(\rho _{\text {f}}\), the second term represents the amount of fluid exchanged between the matrix and the fracture.
Sketch of a unit plane strain REV for fluid flow along the fracture. \(\varvec{s}\) is the natural coordinate along fracture surface, \(\varvec{q}(\varvec{s})\) is the flow rate across the fracture width w at \(\varvec{s}\), \(\varvec{v}\) is the fluid velocity inside matrix and \(\varvec{n}_{\varGamma _d}\) is the unit normal direction of the fracture
The flow rate \(\varvec{q}\) is typically computed by the integral of the velocity over the thickness of the fracture. It can vary with the location s of the point on the fracture surface, and it is related to the pressure gradient in the fracture surface by the following law:
where \(c (\varvec{ s})\) is the hydraulic conductivity of the fracture at the natural coordinate \(\varvec{ s}\). Here, we use Poiseuille fluid flow equation and accordingly, we calculate \(c (\varvec{ s})\) from the cubic law.
By substituting the constitutive law (Eq. 11) and the state equation (Eq. 6) into Eq. 10, we get the governing equation for the fluid flow within the fracture, as follows:
Since \(\varvec{\epsilon }\) and w can be both expressed in terms of the displacement field in the solid skeleton and of the fluid pressure, the unknowns in Eqs. 4, 8, and 12 can all be related to \(\varvec{u}\) and p. Thus, these governing equations are usually referred to as the \(\varvec{u} - p\) formulation.
2.2 Weak formulation
In order to obtain the weak formulation of the problem from its strong formulation, it is necessary to define the essential and natural boundary conditions at the exterior and interior boundaries of the domain. In this chapter, we focus on two-dimensional problems, as described in Fig. 2. The domain \(\varOmega\) with exterior boundary \(\varGamma\) has a discontinuity \(\varGamma _d\), which is treated as an interior boundary and may evolve due to fluid pressurization. The two surfaces of the discontinuity \(\varGamma _d\) are noted \(\varGamma _d^+\) and \(\varGamma _d^-\). We note \(\varvec{n}_{\varGamma _d}\) the unit normal vector on the fracture surface, pointing toward \(\varOmega ^+\), i.e., \((\varvec{n}_{\varGamma _d}=\varvec{n}_{\varGamma _d^-}=-\varvec{n}_{\varGamma _d^+})\).
Boundary conditions on a domain \(\varOmega\) that contains a discontinuity \(\varGamma _d\). \(\varOmega\) is subjected to boundary conditions, as follows: \(\varGamma _u\) (respectively, \(\varGamma _p\)) is subjected to displacement \(\varvec{\bar{u}}\) (respectively, pore pressure \({\bar{p}}\)); and \(\varGamma _t\) (respectively, \(\varGamma _q\)) is subjected to traction \(\bar{\varvec{t}}\) (respectively, fluid flux \({\bar{q}}\)). \(\varGamma _u \cup \varGamma _t = \varGamma\) and \(\varGamma _u \cap \varGamma _t = \emptyset\) hold for the solid phase, \(\varGamma _p \cup \varGamma _q = \varGamma\) and \(\varGamma _p \cap \varGamma _q = \emptyset\) hold for the fluid phase. The discontinuity \(\varGamma _d\) is treated as an interior boundary with a positive surface \({\varGamma _d^+}\) and a negative surface \({\varGamma _d^-}\), subjected to cohesive traction \(\varvec{t}_d^+\) and \(\varvec{t}_d^-\), respectively. Unit normal vectors are noted \(\varvec{n}_{\varGamma _d^+}\) and \(\varvec{n}_{\varGamma _d^-}\) for the positive and negative fracture surface, respectively. Note that the level set function \(\phi\) is defined so as that it is positive on the side of the domain that contains \({\varGamma _d^+}\), and negative on the side of the domain that contains \({\varGamma _d^-}\)
As shown in Fig. 2, the essential boundary conditions (respectively, natural boundary conditions) are imposed on the external boundary of the domain by the prescribing the primary variables \(\varvec{\bar{u}}\) and \(\bar{p}\) (respectively, the secondary variables, traction \(\varvec{\bar{t}}\) and fluid outflow rate \({{\bar{q}}}\)), as follows:
and
where \(\varvec{n}_\varGamma\) is the unit outward normal vector to the external boundary \(\varGamma\). Note: \(\varGamma _u \cup \varGamma _t = \varGamma\) and \(\varGamma _u \cap \varGamma _t = \emptyset\) hold for the solid phase, and \(\varGamma _p \cup \varGamma _q = \varGamma\) and \(\varGamma _p \cap \varGamma _q = \emptyset\) hold for the fluid phase.
From a physics perspective, the existence of the fracture \(\varGamma _d\) in the domain \(\varOmega\) leads to a hydro-mechanical coupling between the fracture and the bounding matrix. Fluid flow along the fracture exerts pressure on the two fracture surfaces and pushes them apart, while the two surfaces transmit cohesive traction. Reversely, pressure gradients drive fluid flow into/out of the bounding matrix surrounding the fracture. Thus, the essential and natural boundary conditions at the interior boundary \(\varGamma _d\) are expressed as
where \(\varvec{t}_d\) is the cohesive traction which governs the mechanical behavior of the macro-fracture once the fracture is initiated. In this paper, we employ the potential-based PPR [65] cohesive model detailed in Sect. 2.4. Moreover, \(q_d\) represents the fluid flow into the matrix, i.e., leak-off in the fracture flow model.
For the hydraulic fracturing problem, an additional boundary conditions needs to be specified at the fracture tip and at the fracture mouth (i.e., at the intersection point between the domain surface \(\varGamma\) and the fracture \(\varGamma _d\)). In typical field operations, a fluid injection rate \(Q_{\text {in}}\) is applied at the fracture mouth \((\varvec{s} = \varvec{0})\) and a zero flux is applied at the fracture tip \((\varvec{s} = \varvec{s}_{\text {max}})\):
We first obtain the weak form of the mixture governing equation by multiplying Eq. 4 with a virtual displacement \(\delta \varvec{u}\) and by integrating over the whole domain \(\varOmega\). After applying the divergence theorem and the boundary conditions, we have:
where the kinematic strain-displacement relation \(\nabla ^s \varvec{u} = \varvec{\epsilon }\) is used. We use \(\nabla ^s\) to denote the symmetric part of the gradient operator. Note that Ritz method is adopted, in which the interpolation functions (shape functions) used to approximate the displacement field also serve as weight functions to calculate the weighted integral residuals. In order to ensure that the above equation holds for all admissible solutions of displacement, the virtual displacement must satisfy the essential boundary condition \(\delta \varvec{u}|_ {\varGamma _u} = 0\). It is worth noting that the mechanical coupling term comes from the boundary condition along the fracture surfaces \(\varGamma _d\), derived as follows:
We recall that \((\varvec{n}_{\varGamma _d}=\varvec{n}_{\varGamma _d^-}=-\varvec{n}_{\varGamma _d^+})\).
Similarly, we can obtain the weak form of the governing equation of the fluid flowing in the matrix (Eq. 8), as follows:
Note that \(\delta p\) is the virtual pressure that satisfies \(\delta p |_{\varGamma _p} = 0\). The boundary condition \(\frac{\varvec{k}_{\rm m}}{\mu }( - \nabla p + \rho _{\text {f}} \varvec{g} ) \cdot \varvec{n}_{\varGamma } = \varvec{v} \cdot \varvec{n}_{\varGamma }= {{\bar{q}}}\) is used for the exterior boundary \(\varGamma _q\). Note that the hydraulic coupling term in the above formula results from the interior boundary conditions at the fracture surfaces, in virtue of the following equation:
The above equation states that the velocity of the fluid normal to the fracture is discontinuous, which indicates, according to Darcy’s law, that the gradient of fluid pressure along the normal to the fracture surface is discontinuous. At the same time, the fluid pressure field as well as the virtual pressure should be continuous across the fracture so that Darcy’s law can be applied. Thus, we use the same virtual pressure \(\delta p\) as in Eq. 19 to multiply the governing equation of the fluid flowing in the fracture (Eq. 12), and we integrate it over the fracture domain \(\varGamma _d\) to obtain the following weak form:
where \(\nabla _{m}\) denotes the one-dimensional gradient along the fracture tangent direction (\(\varvec{m}_{\varGamma _d}\), as shown in Fig. 2). The width of the fracture is computed through the following relationship:
The weak form of governing equation for the fluid flow inside the fracture can be directly injected into the weak form of the governing equation for the fluid flowing in the matrix (Eq. 19), since the same virtual field \(\delta p\) is used.
2.3 Nonlocal continuum damage model for transversely isotropic materials
As explained by Roth et al. [70], Wang and Waisman [85] and Leclerc et al. [52], the mechanical failure of quasi-brittle materials occurs in two phases: the process starts with diffused material degradation due to microscopic defects inception and evolution and continues with localized macroscopic fracture propagation. The first phase can be modeled with continuum damage mechanics. Nonlocal enhancement is needed to capture softening. The evolution of damage can then be used to predict the initiation of a localized macroscopic fracture in the second phase.
In the following, we briefly introduce the nonlocal damage model for transversely isotropic materials, proposed by the authors in [40, 41] and used to govern matrix behavior in this paper. Note that we focus on plane strain conditions with tensile damage development. The model is built on the principle of strain equivalence, which states that the deformation of the damaged material under the actual stress \(\varvec{\sigma }\) is the same as that of the non-damaged material under the so-called effective stress, \(\varvec{\hat{\sigma }}\), defined as:
where \({\mathbb {M}}\) is a fourth-order damage operator (second-order with Voigt notation \({\mathcal {M}}\)). Assuming that damage components in each direction evolve independently, the damage operator \({\mathcal {M}}\) has a diagonal form, as follows:
where \(\omega _i\) are the components of damage variable \(\varvec{\omega }\) ( in Eq. 1). Note that Voigt notations are adopted here, so that \({\hat{\sigma }}_4={\hat{\tau }}_{12}=\frac{\tau _{12}}{1-\omega _4}\), in which \(\omega _4=1-(1-\omega _{1})(1-\omega _{2})\). The diagonal form of \({\mathcal {M}}\) ensures that the damaged compliance matrix resulting from Eq. 23 is symmetric. We consider transversely isotropic materials, in which the local coordinate system is oriented so that direction 1, called the axial direction, is perpendicular to the bedding plane. Directions 2 and 3, along the bedding plane, are called transverse directions. Correspondingly, in Eq. 24, \(\omega _1\) is called axial damage and \(\omega _2\) and \(\omega _3\) are the transverse damage variables. Damage components are directly related to equivalent strains, as explained below. We focus on plane strain conditions, in which the equivalent strain in the out-of-plane direction is zero, which implies that the damage component \(\omega _3\) is zero.
We focus on quasi-brittle materials, in which the nonlinear stress/strain relation results from damage evolution only (micro-crack development), with negligible inelastic deformation. Adopting the principle of strain equivalence, the constitutive relation is expressed as
where \({\mathbb {S}}^0\) is the material elastic compliance matrix, which depends on 5 independent parameters for transversely isotropic materials, and they are Young’s modulus in axial and transverse direction \((E_{1}/E_2\)), shear modulus \(G_{12}\), Poisson’s ratio in the bedding plane \(\nu _{23}\) and in the plane perpendicular to the bedding plane \((\nu _{12})\). In plane strain conditions, the damaged stiffness tensor \({\mathbb {C}}(\varvec{\omega }) = ({\mathbb {S}}^0\,:\,{\mathbb {M}})^{-1}\) can be explicitly expressed by using Voigt notation, as follows:
in which
where \({E_2}\nu _{12} = {E_1}\nu _{21}\), and \(D= (1-\omega _2)\nu _{23}^2 + 2(1-\omega _1)(1-\omega _2)\nu _{12}\nu _{21}\nu _{23}+(1-\omega _1)(2-\omega _2)\nu _{12}\nu _{21}-1.\)
In order to distinguish damage development in axial and transverse directions, two loading surfaces \(g_{1}/g_2\) are defined as:
where the equivalent strains \(\epsilon _1^{\rm eq}/\epsilon _2^{\rm eq}\) are scalar measures of strain defined in the axial and transverse directions. \(\kappa _1\) and \(\kappa _2\) are the internal state variables that control the evolution of damage: they represent the equivalent strain thresholds before the initiation of damage in directions 1 and 2, respectively. After damage initiation, \(\kappa _1\) and \(\kappa _2\) are the largest equivalent strains ever reached during the past loading history of the material.
Field investigation and laboratory experiments [26, 81] indicate that there are two primary failure modes in transversely isotropic rock (Fig. 3): the sliding mode, in which failure is controlled by the tensile and shear strength of the bedding planes, and the non-sliding mode, in which failure is controlled by the strength of the matrix material. Correspondingly, the two equivalent strains in two loading surfaces (Eq. 28) for direction-dependent transverse isotropic materials under plane strain condition are defined as:
where \(\epsilon _{11}^{t0}\) (respectively \(\epsilon _{22}^{t0}\)) is the initial tensile strain threshold for the sliding mode (respectively for the non-sliding mode), and \(\epsilon _{12}^{s0}\) is the initial out-of-bedding-plane shear strain threshold. They are all material properties and are calibrated from experimental data.
The loading surfaces in Eq. 28, together with the definition of equivalent strains in Eq. 29, determine the current boundary of the elastic domain \(g_i<0\). Damage can only grow if the current strain state reaches the boundary \(g_i=0\). Karush-Kuhn-Tucker complementary conditions are used to account for loading-unloading stress paths:
Now, we establish a relationship between the internal state variables \(\kappa _1\), \(\kappa _2\), defined as the maximum equivalent strains ever encountered in the material, and the damage variable components \(\omega _i, (i=1, 2)\). Since both the internal variables and the damage components grow monotonically, it is admissible to postulate the evolution law of damage in the form \(\omega _i = f (\kappa _i),\,i=1,2\). The exact form of the function f should be identified from actual stress paths monitored in experiments, such as uniaxial stress–strain curve in axial and transverse directions. In the absence of such data, we assume that in tension, the axial damage component follows an exponential law, which reflects rapid micro-crack propagation in mixed I–II mode:
where \(\alpha _{11}^t\) is a material parameter that controls the damage growth rate. We use a similar evolution law for tensile damage growth in the transverse directions:
where \(\alpha _{22}^t\) controls the ductility of the response in the transverse directions.
The constitutive law in Eq. 25 leads to stress-strain softening behavior, which results in the well-known mesh dependence issue in finite element simulations. Specifically, the size of the damage zone, which is linearly related to energy release rate and should be a material constant, does not converge upon mesh refinement [43]. Mathematically, the partial differential equations governing quasi-static problems loose ellipticity, which makes the boundary problem ill-posed. To address this issue, we adopt the integral-based nonlocal regularization technique, in which the damage evolution at a material point not only depends on the stress state at that point, but also on the stress of points located within a certain neighborhood, the size of which is controlled by internal length parameters. Numerically, we replace the local equivalent strains \(\epsilon _{i}^{\rm eq}\) in the loading surfaces (Eq. 28) by their nonlocal counterparts \({\overline{\epsilon }}_{i}^{\rm eq}\), which are calculated as the weighted averages of the local equivalent strains over an influence volume V:
where \(\varvec{x}\) and \(\varvec{\xi }\) are the position vectors of the local point considered and of a point located in the influence volume, respectively. \(\alpha (\varvec{x}, \varvec{\xi })\) is a weight function and is normalized to preserve constant fields, as follows:
where the function \(\alpha _0 (r)\) monotonically decreases with the increasing distance \(r=\Vert \varvec{x} - \varvec{\xi }\Vert\). We choose \(\alpha _0(r)\) to be a bell-shaped function with a bounded nonlocal influence zone \(l_c\) as
in which \(l_c\) provides an internal length parameter that serves as a localization limiter to alleviate mesh sensitivity. In addition, the size of \(l_c\) also determines the size of the damage process zone.
2.4 Macro cohesive zone model: PPR
The nonlocal damage model performs well for modeling diffused damage development during micro-crack propagation. However, it suffers spurious damage growth during macro-fracture localization because the fixed interaction domain used in the nonlocal formulation enables the transfer of energy from the damage process zone to a neighboring unloading elastic region [31, 76]. In addition, macro-fracture surfaces are not explicitly represented. Therefore, in this paper, we employ the nonlocal damage model to simulate micro-crack propagation (i.e., the damage process zone development) and we define a damage threshold \(\omega _{crit}\) above which a macroscopic fracture segment represented by a cohesive zone model is inserted to simulate the macro-fracture localization. We adopt the potential-based PPR cohesive model [65]. The main traction-separation equations are explained in the following.
PPR cohesive model of macro-fracture propagation. \(\sigma _{\max }\) (respectively, \(\tau _{\max }\)) denotes normal (respectively, shear) cohesive strength at normal separation \(\delta _{nc}\) (respectively, at shear separation \(\delta _{tc}\)). \(\delta _{n}\) (respectively, \(\delta _{t}\)) is the normal (respectively, shear) separation at which cohesive traction is zero. \(\phi _n\) and \(\phi _t\) are the mode I and mode II cohesive energy release rates, respectively
The PPR meets the following requirements: (1) Complete normal and shear failure are reached when normal or tangential separation reaches a maximum value; (2) the traction rate is equal to zero when the traction is equal to the cohesive strength; (3) the energy release rate is equal to the area enclosed by the traction-separation curve. The expression of the potential is
where \(\varDelta _n\) and \(\varDelta _t\) (respectively \(\delta _n\) and \(\delta _t\)) stand for the separations in the normal and shear directions at the current time (respectively, at failure) as shown in Fig. 4. \(\phi _n\) (respectively \(\phi _t\)) is the mode I (respectively, mode II) cohesive energy release rate. \(\alpha\) and \(\beta\) are the shape factors that control the concave or convex nature of the softening curve. The mechanical response of brittle materials is best represented by power law softening equations or bilinear softening laws [79]. Accordingly, we use \(\alpha =\beta =4\), which allows representing concave shaped softening curves with a power law. \(\varGamma _n\) and \(\varGamma _t\) are energy constants, related to \(\phi _n\) and \(\phi _t\) as follows:
where m, n, called the non-dimensional exponents, are expressed in terms of the shape factors \(\alpha , \beta\) (\(\alpha =\beta =4\) in this study) and of the initial slope indicator \((\lambda _n, \lambda _t)\), as follows:
The initial slope indicators are defined as the ratios of critical crack opening width to the final crack opening width (Fig. 4), i.e., \(\lambda _n = \delta _{nc}/\delta _n, \lambda _t = \delta _{tc}/\delta _t\).
According to thermodynamic principles, the traction vector in the local coordinate system \((T_n, T_t)\), noted \(\varvec{t}_d\) in the global coordinate system shown in Fig. 2, is obtained directly from the derivative of the potential in equation 36:
Usually, the extrinsic CZM, in which the elastic behavior (or initial ascending slope) is excluded, is used to model fracture propagation when a cohesive segment or a cohesive interface element is adaptively inserted. Only the softening branch is used, because the elastic deformation of the material is already accounted for by the continuum damage model. However, numerical simulations indicate that the absence of one-to-one relationship at the point \(\varDelta _n=\varDelta _t=0\) causes stability issues. In the following, we use the intrinsic cohesive zone model with \(\lambda _n=\lambda _t=0.01\) to improve the convergence rate, and to avoid unwanted elastic separation.
To close the formulation of the PPR cohesive model, relationships between the cohesive strengths \((\sigma _{\text {max}}, \tau _{\text {max}})\) and the final normal and shear crack opening widths \((\delta _n, \delta _t)\) are needed. The traction rate is equal to zero when traction is equal to the cohesive strength, so we have:
As explained in [63], the tangent Jacobian matrix can be calculated analytically from the potential-based cohesive segment model, which is critical to achieve quadratic convergence in the Newton–Raphson iterative scheme. The reader is referred to [64, 65] for the expression of the Jacobian matrix for loading, unloading and reloading stress paths.
3 Discretization and resolution procedure
3.1 XFEM spatial discretization for displacement and pressure
To model fracture propagation without remeshing, we adopt the XFEM to discretize the primary variables. The Heaviside enrichment function is employed to account for the displacement jump across the macro-fracture. Note that the bounding medium is modeled by the proposed anisotropic damage model with softening, so there is no singularity at the macro-fracture tip. Thus, the classical branching functions are not necessary here. As a result, the approximate function of displacement \(\varvec{u}^h(\varvec{x},t)\) is expressed in the following form:
where \(N_{ui}(\varvec{x})\) is the standard shape function associated with node i, S is the set of all nodal points and \(S_H\) is the set of enriched nodes, the supports of which are bisected by the fracture. \(\varvec{u}_i(t)\) and \(\varvec{a}_i(t)\) denote the nodal value of the displacement field associated with the standard and enriched degree of freedoms respectively. The Heaviside jump function \({H}(\varvec{x})\) is defined as
where \(\phi (\varvec{x})\) is the level set function, which is defined as the closest distance from the fracture surface, with positive or negative, depending on which side of the fracture the point \(\varvec{x}\) is located—see Fig. 2. It is worth noting that the shifted jump function \(1/2\left[ H_{\varGamma _d}(\varvec{x}) - H_{\varGamma _d}(\varvec{x}_i) \right]\) is used to avoid the problem of postprocessing and blending elements [25]. The analytical form of the displacement jump across the fracture \(\varGamma _d\) is:
Note that the displacement jump is directly used to calculate the fracture aperture w in the fluid flow governing equation, as \(w = [\![ \varvec{u}(\varvec{x},t) ]\!]\cdot \varvec{n}_{\varGamma _d}\) (Eq. 22). For the fluid pressure field, enrichment is done with the distance function. The approximate pressure field is expressed as:
where \(N_{pi}(\varvec{x})\) is the standard finite element shape function associated with node i. Nodal sets S and \(S_H\) are the same as for the displacement field. \(p_i(t)\) and \({b}_i(t)\) denote the nodal value of the fluid pressure associated with the standard and enriched degree of freedom, respectively. \(D_{\varGamma _d}(\varvec{x})\) is the distance function, defined as:
The gradient of the distance function along the direction normal to the fracture is discontinuous, with: \(\nabla D_{\varGamma _d} \cdot \varvec{n}_ {\varGamma _d} = H_{\varGamma _d}\). As a result, enriching the FEM with the distance function for the pressure field allows ensuring a continuous pressure field and a discontinuous gradient of pressure across the fracture. Thus, the fluid exchange between the fracture and the matrix can be accounted for. Similar to the displacement approximation, the shifted enrichment function \(\left[ D_{\varGamma _d}(\varvec{x}) - D_{\varGamma _d}(\varvec{x}_i) \right]\) is used and \(R(\varvec{x})\) is a weight function, defined as \(R(\varvec{x}) = \sum _{i \in S_H} N_{pi}(\varvec{x})\) as proposed by Mohammadnejad and Khoei [58]. It is worth noting that the pressure field at the tip of the fracture does not need to be enriched to satisfy the “no leakage flux” boundary condition.
From now on, we use the following (simplified) notations: \(\varvec{N}_{u}(\varvec{x})\) and \(\varvec{N}_{p}(\varvec{x})\) (respectively, \(\varvec{N}_{a}(\varvec{x})\) and \(\varvec{N}_{b}(\varvec{x})\)) are the matrices of standard (respectively, enriched) shape functions for the displacement field \(\varvec{u}\) and for the pressure field p, respectively. \(\varvec{U}(t)\) and \(\varvec{P}(t)\) (respectively, \(\varvec{A}(t)\) and \(\varvec{B}(t)\)) are the vectors of the standard (respectively, enriched) displacement and pressure degrees of freedom, respectively. By substituting the approximations (Eqs. 41, 44) into the governing weak form equations (Eqs. 4, 8, 12 ), we can obtain the discretized form of the governing equations, as follows:
where the Ritz method is used, i.e., in which the virtual displacement \(\delta \varvec{u}\) and the virtual pressure \(\delta p\) are used as weight functions. The matrices \(\varvec{K}_{\alpha \beta } (\alpha ,\beta = u,a)\) are the mechanical stiffness matrices, which can be expressed as:
where \(\varvec{B}\) is the strain–displacement matrix (derivative of shape functions with respect to the coordinates), and \({\mathcal {C}}\) is the Voigt matrix of damage stiffness tensor \({\mathbb {C}}\).
The matrices \(\varvec{Q}_{\alpha \beta } (\alpha ,\beta = u,p)\) are hydro-mechanical coupling terms, which can be expressed as:
in which \(\varvec{N}\) is the shape function vector.
The matrices \(\varvec{M}_{\alpha \beta } (\alpha ,\beta = p,b)\) represent the compressibility of the fluid and of the solid skeleton and they are expressed as:
where M is the Biot modulus defined in Eq. 9. The matrices \(\varvec{H}_{\alpha \beta } (\alpha ,\beta = p,b)\) represent the hydraulic conductivity and are expressed as
It is worth noting that the mass balance equation for the fluid flow in the fracture does not explicitly appear in the discrete form (Eq. 46). Instead, we introduce the internal force (flux) vector \((\varvec{F}_p^{\text {int}}, \varvec{F}_b^{\text {int}})\) to account for the mass exchange between the matrix and the fracture, as follows:
The mechanical coupling term between the fracture and the matrix constitutes another internal force vector \(\varvec{F}_a^{\text {int}}\) in the equilibrium equation, expressed as
where the fluid pressure p and the cohesive traction \(\varvec{t}_d\) are both exerted on the fracture surfaces. The remainder of the external force (flux) vectors in Eq. 46 are listed in the following:
3.2 Finite difference temporal discretization and resolution procedure
In order to further simplify the notations in the following derivations for time discretization, we condense the enriched and standard degree of freedoms for displacement and pressure as \({\mathbb {U}}(\varvec{U}, \varvec{A})\) and \({\mathbb {P}} (\varvec{P}, \varvec{B})\). The weak form of the governing equation discretized in space (Eq. 46) can be rewritten as
To solve the above equations, we use a linear discretization scheme in time: first-order time derivatives \(\varvec{{\dot{X}}}\) are expressed in terms of the difference between \(\varvec{X}\) at time step \(n+1\) and \(\varvec{X}\) at time step n:
where \(\varDelta t\) is the time step. \(\varvec{X}\) at the current time is the weighted value between time step \(n+1\) and time step n:
in which the weight \(\theta\) can be any value between 0 and 1. If \(\theta = 0\), the time discretization method is the explicit forward Euler scheme; if \(\theta = 1\), the time discretization method is the implicit Euler scheme. We use \(\theta = 2/3\) to ensure unconditional stability. After injecting the time discretization equations into the spatially discretized governing equations (Eq. 54), we obtain the residual at time step \(n+1\), as follows:
where \(G_{{\mathbb {P}}_{n+1}}\) is the vector of known values at time step n, expressed as:
and \(F_{{\mathbb {P}}_{n+1}}^{{\text {int}}}\) is the flux vector that accounts for the mass exchange between the matrix and the fracture at time step \(n+1\):
The nonlinear system (Eq. 57) is solved iteratively. We adopt the Newton–Raphson method to linearize the system with respect to displacement and pressure at the equilibrium iteration i within the time step \(n+1\), as follows:
The derivative of the residual with respect to the unknown degrees of freedom is the Jacobian matrix \(\varvec{J}\). Note that the mechanical stiffness \(\varvec{K}(\varvec{\omega })\) depends on damage and is therefore a function of the unknown displacement. The internal forces and flux vectors \((F_{{\mathbb {U}}}^{\text {int}}, F_{{\mathbb {P}}}^{\text {int}})\) are also functions of the unknowns at time step \(n+1\). As a result, the full consistent tangent matrix \(\varvec{J}\) is:
where \(\widetilde{\varvec{K}} = \varvec{K} + \frac{ \partial \varvec{K} }{\partial {\mathbb {U}}} {\mathbb {U}}\). The analytical expression for \(\widetilde{\varvec{K}}\) is complex due to the nonlocal contribution, detailed in Sect. 3.3. The other terms in Eq. 61 are expressed as:
in which \(\varvec{\varLambda }\) is the rotation matrix used to transform the expression of the displacement jumps from the local coordinate system \((\varDelta _n, \varDelta _t)\) to the global coordinate system \([\![ \varvec{u} ]\!]\). It is defined as
where \({{\overline{\theta }}}\) is the angle between the fracture path and the horizontal axis.
\(\varvec{T}_{\text{ c }oh}\) in Eq. 62 is the derivative of the cohesive traction force \(\varvec{t}_d(T_n, T_t)\) with respect to the local displacement jump \((\varDelta _n, \varDelta _t)\). Since we adopt the PPR cohesive model, \(\varvec{T}_{coh}\) can be explicitly calculated from the expression of \(\partial (T_n, T_t) / \partial (\varDelta _n, \varDelta _t)\), as shown by Park and Paulino [64]. Note that the above formulation does not account for fluid flow within the fracture explicitly. Instead, for those elements with enriched degrees of freedom, the XFEM is used to account for the influence of the fracture on the permeability matrix \(\varvec{H}\), on the coupling term \(\varvec{Q}\) and on the compressibility term \(\varvec{M}\), through the terms \((\partial F_{{\mathbb {U}}}^{\text {int}} / \partial {{\mathbb {U}}}, \partial F_{{\mathbb {P}}}^{\text {int}} / \partial {{\mathbb {P}}})\). This approach integrates fluid flow in both the fracture and the matrix and requires few degrees of freedom, which makes the implementation of the model easier and allows achieving faster convergence rates. It is also important to note that the extra terms \(\frac{ \partial F^{{\text {int}}} }{\partial {\mathbb {P}}}\) are added to the coupling and permeability matrixes, which allows using the same linear interpolation function without concerning stability issue.
3.3 Analytical expression of the mechanical tangent stiffness matrix
Due to the adopted nonlocal formulation, the calculation of internal variables at a point requires calculating the average of the values taken by those variables at the Gauss points located in the influence zone. Consequently, additional terms need to be added to the consistent stiffness matrix \(\widetilde{\varvec{K}}_{\alpha \beta } ( \alpha ,\beta = u,a)\) due to nonlocal enhancement. Following the procedure of Jirásek and Patzák [44], we have
where the first term on the right-hand side is the local Gauss point contribution, which can be numerically expressed as
where \(N_I\) is the total number of Gauss points, and \(w_I\) are the corresponding integration weights. The second term on the right-hand side of Eq. 64 constitutes the nonlocal Gauss points contribution. According to the chain rule, the derivative of the stiffness tensor with respect to the displacement reads:
For the plane strain case studied in this paper, it is possible to obtain the explicit expression of each of the partial derivatives involved in the above equation. In particular, the derivative of stiffness with respect to damage is:
in which
According to Eqs. 31 and 32, the partial derivatives of the damage components with respect to \(\kappa _i\) can be calculated as
Note that the partial derivative terms
are actually the loading-unloading indicators.
Differentiating the nonlocal strains defined in Eq. 33 with respect to displacement, we obtain
in which:
and in which the notation of \(w_J\) in Eqs. 71 and 72 is the volume \(\varDelta V\) associated to Gauss point J. \(N_J\) is the total number of Gauss points within the nonlocal influence zone for Gauss point I. \({ \text {d} \epsilon _{i}^{\rm eq} }\) and \({ \text {d} \varvec{\epsilon } }\) are vectors, which can be calculated from the definition of the equivalent strains as
Combining all the above expressions, we can obtain the analytical expression of the consistent tangent stiffness \(( \widetilde{\varvec{K}}_{\alpha \beta }, \alpha ,\beta = u,a)\) as:
3.4 Damage-driven cohesive fracture propagation
The transition from continuum damage to macro-fracture is modeled by inserting cohesive segments to regular finite elements when damage reaches a critical threshold. Because the damage model employed in this paper is phenomenological, the transition can be triggered at any level of damage. We set \(\omega _{crit}= 0.1\) for all simulation cases presented in this paper. To compute the damage value at the crack tip, we adopt the method proposed by Wang and Waisman [85] and Wells et al. [86]. As shown in Fig. 5, we assume that the fracture propagates when the maximum component of the weighted damage vector (\(\omega _i, i= 1, 2\) for 2D) over the half-circle patch (shaded in blue) exceeds the threshold \(\omega _{crit} = 0.1\). Mathematically, we first obtain \(\bar{ \omega _i}\) by using the bell-shaped weight function \(\alpha _0(\Vert \varvec{x}- \varvec{\xi }\Vert )\), through
where \(\varvec{x}_{tip}\) and \(\varvec{\xi }\) are the global coordinates of fracture tip and the Gauss points in \(\varOmega _T\), respectively. \(N_{GP}\) is the total number of Gauss points in \(\varOmega _T\), and \(\varDelta V_J\) is the geometrical volume associated with Gauss point j. Note that the size of \(\varOmega _T\) is controlled by the internal length \(l_c\) because the weight function used for nonlocal enhancement is the bell-shaped function (Eq. 35).
The macro-fracture propagates in the direction \(\bar{\varvec{d}_i}\), calculated as the weighted average of the damage directions in the half-circle patch, as follows:
where \(\varvec{d} = \varvec{\xi }- \varvec{x}_{tip}\), as shown in Fig. 5. To summarize, we first compare \({\text {max}}(\bar{\omega _i}), i = 1,2\) with \(\omega _{crit}\). If \({\text {max}}(\bar{\omega _i}) \ge \omega _{crit}\), we propagate the fracture in the direction of \(\bar{\varvec{d}_i}\) with a user-defined growth length \(\varDelta a\). For all the simulations presented in this chapter, we choose \(\varDelta a = l_c\). Since only the Heaviside function is used for XFEM discretization, no cohesive segment is inserted into the tip element if the fracture tip is located inside an element. It is worth noting that for a given time increment, the size of the zone in which damage satisfies the transition criterion may exceed the growth length \(\varDelta a\). Thus, we repeat the above calculation until \({\text {max}}(\bar{\omega _{i}}) < \omega _{crit}\). Within a single time increment, the length of the propagated fracture equals several times \(\varDelta a\). Every time the fractures grows by a length \(\varDelta a\), we add extra degrees of freedom at the enriched nodes and we add enriched shaped functions for the elements that contain newly enriched nodes. In addition, to ensure consistent displacement jumps across the fracture, we adopt the classical sub-region quadrature technique to divide a quadrilateral element into multiple triangles, as illustrated in Fig. 5. We use three Gauss points within each triangle to calculate the Jacobian matrix and the residual. To transform the internal and state variables from the initial to the new set of Gauss points, we adopt the super-convergent patch recovery method proposed by Zienkiewicz and Zhu [87]. After remapping, we recheck the propagation criterion and repeat all the follow-up steps. Once the propagation criterion is not satisfied, we march to the next increment and construct the global matrix equations, and the problem is iteratively solved. When convergence is reached and the results are postprocessed, the fracture propagation procedure is repeated. For clarification, the overall computational steps of the proposed numerical tool is presented in Algorithm 1.

4 Engineering applications
We implemented the proposed numerical framework in MATLAB for modeling fluid-driven multi-scale fracture propagation in transversely isotropic porous media. In the following, we validate the formulation and implementation of the multi-scale hydraulic fracturing model by comparing simulation results to analytical solutions for the classical Khristianovic–Geertsma–de Klerk (KGD) problem of hydraulic fracturing. Then, we investigate the relative influence of material and stress anisotropy on the fracture path during hydraulic fracturing. Note that linear quadrilateral plane strain elements are used to discretize the domain in all cases.
4.1 Model verification: KGD Injection Problem
The KGD problem is that of fracture propagation due to the injection of a viscous fluid in a borehole embedded in an infinite isotropic porous medium. Figure 6 presents the geometry, dimensions, boundary conditions and mesh used for the simulations. Only a half of the plane strain domain is modeled due to symmetry, and the size of the domain is chosen to avoid boundary effects. The internal length \(l_c\) is set to 0.05 m. We refine the mesh along the expected fracture propagation path with an element size 0.015 m. Note this element size satisfies the requirement of nonlocal regularization as it is less than 1/3 of the internal length \(l_c = 0.05\) m. In addition, the proposed cohesive element size is 10 times smaller than the cohesive process zone, which can be estimated as \(l_p = 0.1EG/\sigma _{max}^2\) according to Turon et al. [82]. An initial fracture with length 0.1 m is placed at the borehole, and a constant injection rate of \(Q=0.0002 m^2/s\) is applied at the fracture mouth. For all the simulation cases in this section, we set the initial effective stress and fluid pressure to zero, and we employ a constant time increment \(\varDelta t = 0.01 s\) for a total simulation time of 10 s. The remainder of the material parameters for the porous medium is given in Table 1.
Trial and error calibration process for the multi-scale model of hydraulic fracturing: (1) Simulation of a splitting test with pre-inserted cohesive segments without damage evolution inside the matrix to obtain the global force-displacement curve; (2) simulation of the same splitting test with the proposed multi-scale framework, in which cohesive segments are dynamically inserted, to obtain the \(F-u\) curve; (3) adjustment of the material parameters used in simulation (2) until the two \(F-u\) curves match
Given that the considered domain is isotropic, the elastic constants as well as the damage evolution parameters are not direction dependent (Table 1). In addition, we assume that the cohesive strength and the cohesive energy release rate have the same value for mode I and mode II fracture propagation (\(\phi _n=\phi _t=G, \sigma _{\text {max}}=\tau _{\text {max}}\)) in all simulation cases. It is also worth noting that the damage initiation and evolution parameters (\(\epsilon _{11}^{t0}, \epsilon _{12}^{t0}, \alpha _{11}^{t}\)) as well as the cohesive fracture parameters (\(G, \sigma _{\text {max}}\)) are calibrated to ensure a consistent transition from damage to fracture. In this work, a constant cohesive strength and a constant energy release rate are assigned to each new cohesive segment inserted during fracture propagation. Note that it is possible to track the amount of energy dissipated by damage and to dynamically calculate the cohesive energy release rate as the difference between the total energy release rate and the damage energy release rate (see [39, 42]). The calibration of the multi-scale fracture propagation model is explained in Fig. 7. We first simulate a mode I splitting test using cohesive segments without damage development within the matrix. All the cohesive segments are inserted along the predefined fracture path (assumed to be known a priori in this particular case) and we use \(G = 100 N/m, \sigma _{\text {max}} = 1MPa\). We choose the rest of the parameters of the PPR cohesive model (\(m=n=4, \lambda _n = \lambda _t =0.01\)) so as to represent brittle fracture propagation and to ensure fast convergence. We track the global response of the opening displacement (u) and the reaction force (F) at the point where the displacement boundary is applied and we obtain the displacement–force curve marked with red circles in Fig. 7. We carry out another simulation with the same boundary conditions, with the proposed multi-scale fracturing model this time, in which nonlocal damage is modeled in the matrix at the first place, and cohesive segments are dynamically inserted once the maximum weighted damage component exceeds the threshold \((\omega _{crit})\). We adjust the damage initiation and evolution parameters (\(\epsilon _{11}^{t0}, \epsilon _{12}^{t0}, \alpha _{11}^{t}\)) and the cohesive fracture parameters (\(G, \sigma _{\text {max}}\)) by trial and error, until the global response (\(u-F\) curve marked with blue plus signs in Fig. 7) matches the response obtained when only cohesive segments are considered. For both simulation cases, the same Young’s modulus and Poisson ratio are used (Table 1), and the nonlocal internal length is \(l_c = 0.05 m\). After calibration, we obtain the same cohesive strength \(\sigma _{\text {max}} = 1 MPa\) for the multi-scale framework as for the cohesive segment model, but a lower cohesive energy release rate \(G_I = 90 N/m\). In summary, simulating multi-scale fracture propagation with the calibrated parameters represents fracture propagation in a porous material that has a 1 MPa strength and a total 100 N / m energy release rate according to laboratory measurements.
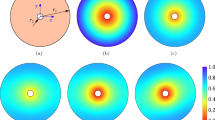
Distribution of damage component \(\omega _2\), nonlocal equivalent strain \({\bar{\epsilon }}^{\rm eq}\), pore pressure, and stress component \(\sigma _2\) on the deformed mesh (displacements multiplied \(10^3\) times) at the end of the simulation (\(t=10\) s). Note that the fracture propagates in direction 1 (x-axis)
Figure 8 shows the distribution of damage, nonlocal equivalent strain, pore pressure and stress on the deformed mesh (displacements multiplied by 1000) at \(t=10\) s. As expected, diffused damage \(\omega _2\) (horizontal micro-cracks) is obtained within the process zone surrounding the macro-fracture. Note that damaged elements are replaced by cohesive segments when the weighted damage exceeds the threshold \(\omega _{crit}=0.1\), and not when a particular component of damage exceeds that threshold. That explains why the fracture tip does not advance when \({\text {max}}(\bar{\omega _i}) < \omega _{crit}\), even when the value of damage components at a few Gauss points within the tip detection region \(\varOmega _T\) exceed the threshold, \({\text {max}}( {\omega _i}) \ge \omega _{crit}\) (Fig. 5). The distribution of the nonlocal equivalent strain \(\bar{\epsilon }^{\rm eq}\) shown in Fig. 8 indicates that tensile strains only exist in the area near the fracture tip. The fracture surface behind the tip is under compressive strain even when the pore pressure in this area is positive. Note that we assume that the entire simulation domain including the macro-fracture is saturated, i.e., the fluid lag is not considered. However, a suction zone with negative pore pressure is obtained at the fracture tip, which indicates that a mathematical fluid lag exists. We will consider multi-phase flow with explicit consideration of fluid lag in future studies. The distribution of \(\sigma _2\) further confirms that only a limited zone close to the fracture tip is under tension during hydraulic fracturing; the rest of the domain is under compression.
An analytical solution to the KGD problem was obtained for an elastic and impermeable medium in which a fracture propagates due to the injection of an incompressible fluid [32], as follows:
where \(G_s\) is the shear modulus, L is the fracture length at time t, CMOD stands for crack mouth opening displacement, and CMP stands for crack mouth pressure. The other notations are the same as in Table 1.
Figure 9 shows our simulation results of CMP, CMOD and L, plotted against injection time. We also simulated the KGD test with different permeabilities (\(\kappa = 2\times 10^{-13} m^2\), and \(\kappa =2\times 10^{-15} m^2\)), keeping the rest of the parameters the same (Table 1). Results are compared to the analytical KGD solution [32]. As expected, results highlight the significant influence of the intrinsic permeability on the evolution of the fracture geometry (\(\kappa = 2\times 10^{-13} m^2\) vs \(\kappa = 2\times 10^{-14} m^2\)). The CMP builds up and lasts longer for porous media with high permeability (Fig. 9a). Because the fluid leak-off decreases the fluid pressure in the fracture, the final fracture length is smaller in porous media with higher permeability. On the contrary, the CMP quickly decreases for porous media with low permeability, because the macro-fracture propagates quickly, thus creating space for the fluid to flow into. This phenomenon does not hold for all permeabilities. Below a certain permeability value, the CMP does not change any longer (\(\kappa = 2\times 10^{-14} m^2\) vs \(\kappa = 2\times 10^{-15} m^2\)). For \(t\le 1\)s, with a very low intrinsic permeability, the evolutions of L and of the CMOD found numerically match the analytical solution, in which the bounding medium is assumed to be impermeable. After 1s, the analytical solution overestimates the fracture length L and underestimates the CMOD. This discrepancy is because: (1) even for media with very low permeability, the assumption of impermeability does not hold because the fluid flow into the matrix decreases the effective stress that applies to the fracture faces; (2) the proposed multi-scale hydraulic fracture propagation model depends on the material’s strength and energy release rate, while the analytical solution is for a purely brittle fracture propagation problem, independent of strength or energy release rate.
We further investigate the influence of the fluid injection rate on hydraulic fracturing for the KGD problem. All the material parameters are kept the same as in Table 1, and we vary the injection rate from \(Q=0.0002 m^2/s\) to \(Q=0.0005 m^2/s\). Figure 10 shows the calculated CMOD and fracture length evolution against the injection time, and the fracture opening displacement profile, the hydraulic water pressure profile as well as the effective cohesive attraction profile along the propagated fracture surface at the end of the simulation (at \(t=10\) s). The evolution of the CMOD and of the fracture length show that a higher injection rate results in faster fracture propagation and a wider fracture mouth opening. The profile of fracture opening at the end of the simulation further confirms that both the length and the width of the fracture increase with the injection rate. However, the increase rate is not linear, since the difference of CMOD and fracture length for the same injection rate interval \(d Q=0.0001 m^2/s\) at the same time is not the same. Due to the assumption of saturation, water pressure profile shown in Fig. 10d show negative value near the fracture tip area, and the magnitude of which increases with increasing injection rate. Figure 10e plot the effective cohesive attraction along the propagated fracture surface at time of \(t=10s\). For all of the injection rates, the cohesive attraction starts at the fracture tip and increases to cohesive strength \(\sigma _{\max } = 1 MPa\) and then gradually decreases to zero as the displacement jump increases. It is worth noting that the starting cohesive attraction for COD = 0 mm varies with the injection rate, because that the transition from continuum damage to discrete fracture is triggered from weighted damage, not from stress.
4.2 Influence of material and stress anisotropy on hydraulic fracturing
The following engineering problem illustrates the performance of the proposed computational framework in modeling the hydro-mechanical behavior of saturated media subjected to both material and stress anisotropy. A square domain 500 mm by 500 mm is considered. The solid skeleton is transversely isotropic with horizontal layers. We carry out three series of simulations (Fig. 11). In test 1, all normal displacements at the boundary are fixed. An initial fracture, 40 mm in length, oriented at an angle \(\theta\) with respect to the horizontal axis, is placed at the center of the domain (Fig. 11a). We investigate the effect of material anisotropy on hydraulic fracturing by varying the angle \(\theta\) under a constant fluid injection rate \(Q = 10\,{mm}^2/s\). About 6500 linear plane strain elements were used to discretize the domain. We set the initial pore pressure to zero, and we run the simulation in 0.2 s with the time increment \(\varDelta t = 0.005\) s. In test 2, we use the same initial and boundary conditions, but we change the fluid injection rate from \(Q = 10\,{mm}^2/s\) to \(Q = 20\,{mm}^2/s\). Comparing the results of tests 1 and 2 informs on the influence of injection rate on hydraulic fracturing in an anisotropic material. In test 3, anisotropic in situ stress is applied at the boundary and the injection angle \(\theta\) is nonzero, as shown in Fig. 11b. The other initial and boundary conditions are the same as in the previous two cases. The parameters used for the three simulations are listed in Table 2.
Like in the KGD case, we calibrate by trial and error the material parameters that control damage evolution (\(\epsilon _{11}^{t0}, \epsilon _{22}^{t0}, \epsilon _{12}^{t0}, \alpha _{11}^{t},\alpha _{22}^{t}\)) and those that govern the cohesive fracture behavior (\(G_{,1}, G_{,2}, \sigma _{\text {max},1} , \sigma _{\text {max},2}\)) in the directions perpendicular and parallel to the layer. We use the local coordinate system in which axis-1 is perpendicular to the layer, and axis-2 is parallel to the layer. Note that in the following simulations, we fix the local coordinate system in such a way that axis-1 is always vertical. As explained in Fig. 12, we first simulate two splitting tests with pre-inserted cohesive segments parallel and perpendicular the layer, for which the cohesive energy values are \(G_{,1} = 0.1\,{N/mm}, G_{,2} =0.2 \,{N/mm}\) and the cohesive strengths are \(\sigma _{\text {max},1} =1\) MPa, \(\sigma _{\text {max},2} = 2\) MPa. Let us recall that in the PPR cohesive model, we employ \(\phi _n=\phi _t=G, \sigma _{\text {max}}=\tau _{\text {max}}, m=n=4, \lambda _n = \lambda _t =0.01\) to account for mixed mode fracture propagation and brittle fracture propagation [62, 64, 65]. We extract the global force–displacement curves (red circles for fractures parallel to the layer and green squares for fractures perpendicular to the layer). Then we run the same two simulations using the multi-scale hydraulic fracturing model, in which cohesive segments are dynamically inserted when the weighted damage at the fracture tip exceeds the critical value \(\omega _{crit}=0.1\). After a number of simulations with different input parameters, which control meso-scale damage evolution and macro-scale cohesive fracture propagation, we find the best match for the \(F-u\) curve, as shown in Fig. 12. The calibrated parameters are listed in Table 2. In summary, the calibrated multi-scale fracture propagation model is globally equivalent to a model of fracture propagation in a transversely isotropic material with \(G_{,1} = 0.1 {N/mm}, \sigma _{\text {max},1} =1\) MPa in direction parallel to the layer, and \(G_{,2} =0.2 {N/mm}, \sigma _{\text {max},2} = 2\) MPa in direction perpendicular to the layer.
Trial and error calibration process for coupling nonlocal damage with cohesive fracture for transversely isotropic materials: (1) simulation of two splitting tests with pre-inserted cohesive segments parallel (respectively perpendicular) to the layer to obtain the global force-displacement curve in the case of horizontal (respectively vertical) bedding; (2) simulation of the same splitting tests with the multi-scale hydraulic fracturing model, in which the cohesive segments are dynamically inserted, to obtain the \(F-u\) curves; (3) adjustment of the multi-scale hydraulic fracturing model parameters until the \(F-u\) curves match for both fracture propagation directions
The calibration process only provides the cohesive parameters when the fracture propagates in the direction parallel or perpendicular to the bedding. To determine the cohesive parameters when the fracture propagation direction is neither parallel or perpendicular to the bedding, a whole series of laboratory experiments would need to be carried out. In this paper, we propose to obtain the cohesive parameters by projection on an elliptical failure curve, as shown in Fig. 13. The cohesive strength and the energy release rate of a fracture that propagate at an angle \(\theta\) to the layer are expressed as:
Fundamentally, we assume that the strength and the energy release rate at different propagation angles form an ellipse in plane strain condition.
Figure 14 shows the pore pressure p, the effective stress component \(\sigma _x\) and the fracture paths at the end of the simulation (at \(t=0.02\) s) for test 3 with the boundary conditions \(\sigma _v = 4\) MPa, \(\sigma _h = 2\) MPa, and \(Q = 20\,{mm}^2/s\). The increased pore pressure near the fracture in Fig. 14a, b demonstrates that the proposed numerical tool can predict the fluid leak-off from the macro-fracture to the porous matrix. Compared to the case \(\theta =90^\circ\), the higher pore pressure observed for \(\theta =0^\circ\) is due to the lower permeability in the direction perpendicular to the layer (Table 2): more fluid pressure builds up and less fracture space is created (less fracture length and less width). In agreement with physical expectations, for \(\theta =30^\circ , 60^\circ\), compressive effective stress is observed in the area behind the fracture tip, and tensile effective stress only concentrates in the areas ahead of fracture tip. For \(\theta =30^\circ , 60^\circ , 90^\circ\), the fracture propagates in the direction of maximum compressive in situ stress, which is exactly what is reported in the literature. For \(\theta =0^\circ\), we expect to see two branches emerging from the tips of the initial horizontal fracture, that finally form vertical fractures. Instead, we obtain the horizontal fracture shown in Fig. 14a, because of the continuum damage to fracture transition criterion, based on a weighted damage threshold (Sect. 3.4). Even if the continuum damage model predicts damage development in the two vertical branch directions, the weighted damage direction is horizontal.
Figure 15 shows the pore pressure distribution and the fracture paths at the end of the simulations (at \(t=0.02 s\)) for the three tests, when \(\theta = 30 ^\circ\) and when \(\theta = 60 ^\circ\). In test 1 (no in situ stress, \(Q=10\,{mm}^2/s\)), the fracture propagates in the horizontal direction parallel to the layer, for both \(\theta = 30 ^\circ\) (Fig. 15a) and \(\theta = 60 ^\circ\) (Fig. 15b). However, when the injection rate increases to \(Q=20\,{mm}^2/s\) (tests 2 and 3), the fracture path is horizontal only for \(\theta = 30 ^\circ\) under zero in situ stress (Fig. 15c), while a vertical fracture path is predicted for \(\theta = 60 ^\circ\) under the same boundary conditions (Fig. 15d). This questionable result can be attributed to: (1) The weighted damage-driven fracture propagation criterion, which, similar to all other continuum theory based propagation criteria, is not capable of predicting fracture branching; (2) the rapid injection of the fluid, which can change the fracture propagation direction if it does not align with the weak layer. Further laboratory experiments are needed to understand which of these two phenomena is the primary cause of the discrepancy. In tests 3, the fracture path is parallel to maximum compressive stress, irrespective of the initial fracture direction (the figure shows the case of \(\sigma _v= 4 MPa, \sigma _h = 2 MPa\)).
We further extracted the propagated fracture paths for all the tests simulated, as illustrated in Fig. 16. When only material anisotropy is considered, results show that a horizontal fracture path parallel to the layer forms (Fig. 16a). Typically, the fracture length and width increase with the injection rate. Questionable results are obtained in some of the cases with \(\theta \ge 60 ^\circ\), due to the weighted damage-driven fracture proposition criterion. Figure 16b presents a comparison between the cases with material anisotropy only (tests 1 and 2) and the cases with both material and stress anisotropy (test 3). For all orientations \(\theta\) considered, the predicted fracture length is shorter when in situ stress is applied. This is because a part of the energy is dissipated to overcome the compressive in situ stress. Some cases need further experimental assessment and more advanced fracture propagation criteria, especially when a horizontal fracture path is predicted under nonzero in situ stress or when a vertical fracture is predicted under zero in situ stress.
5 Conclusions
In this paper, we formulated and implemented a numerical tool to model multi-scale mixed mode fluid-driven fracture propagation in transversely isotropic porous media. We first presented the strong and weak forms of the governing equations for the hydraulic fracturing problem, including the equilibrium of forces for the mixture, the balance of fluid mass within the matrix, and the balance of fluid mass along the fracture. A nonlocal anisotropic damage model was coupled to the PPR cohesive macro-fracture model to simulate the transition between microscopic crack propagation and macroscopic fracture localization. The transition from continuum damage to cohesive fracture is done by dynamically inserting cohesive segments once the weighted damage exceeds a certain threshold. Diffusion equations are used to model fluid flow inside the porous matrix and within the macro-fracture, in which conductivity is obtained by Darcy’s law and the cubic law, respectively. The XFEM is employed to approximate the solution for the fully coupled \(\varvec{u}-p\) formulation: The macro-fracture is modeled with Heaviside jump functions for the displacement field and with modified distance functions for the fluid pressure. After discretizing the system of equations in time, the entire nonlinear system is linearized and solved by using a Newton–Raphson iteration scheme, in which the consistent tangent stiffness is derived analytically, accounting for the nonlocal terms, in the plane strain case.
We validate the formulation and implementation by simulating the KGD mode I fracture propagation problem in an infinite porous medium. We check that for low volumes of fluid injected in a porous medium of low permeability, the model provides predictions that are in agreement with the analytical solution proposed for impermeable media. We then examine the effect of material and stress anisotropy on hydraulic fracturing by simulating a series of injection tests in an inclined fracture embedded in a transversely anisotropic porous medium. As expected, the fracture propagates along the bedding direction in the absence of in situ stress and along the direction of maximum compressive stress when anisotropic stress boundary conditions are applied. The length and width of the fracture increase with the injection rate.
The validation against the KGD analytical solution shows that the widely used LEFM model might over-predict the propagation length. The proposed computational framework, the first of its kind, allows simulating multi-scale hydraulic fracturing. Improvements are still needed. For example, some discrepancies are noted, especially when both material and stress anisotropy are accounted for, because of the choice of the damage-to-fracture transition criterion, which cannot account for fracture branching (but works perfectly well for unidirectional fractures). On the one hand, a more detailed algorithm is needed to process the evolution of damage at the tip and predict branching paths; on the other hand, the level set method used to identify fracture paths in the XFEM has inherent limitations to account for multiple fracture branches and intersections, especially in 3D. To overcome these limitations, other numerical methods will be explored in future work, such as techniques based on the dynamic insertion of cohesive interface elements, peridynamics and the phase field method.
Abbreviations
- \(\alpha (\beta )\) :
-
Mode I (mode II) cohesive law shape factor
- \(\alpha (\varvec{x})\) :
-
Nonlocal weight function
- \(\alpha _{ii}^t\) :
-
Material parameters controlling damage growth rate
- \(\bar{p}\) :
-
Prescribed pore pressure
- \(\bar{\varvec{t}}\) :
-
Prescribed traction on exterior boundary
- \(\bar{\varvec{t}}_d\) :
-
Cohesive traction vector on fracture surfaces in global coordinate
- \(\bar{\varvec{u}}\) :
-
Prescribed displacement
- \(\bar{\epsilon }_i^{\rm eq}\) :
-
Nonlocal equivalent strain components
- \(\bar{q}\) :
-
Prescribed flow rate
- \(\bar{q}_d\) :
-
Flow rate difference across fracture
- \(\varvec{\alpha }\) :
-
Biot coefficient tensor
- \(\varvec{\epsilon }\) :
-
Strain tensor
- \(\varvec{\omega }\) :
-
Damage variables
- \(\varvec{\sigma }\) :
-
Stress tensor
- \(\varvec{a}\) :
-
Enriched degree of freedom on displacement
- \(\varvec{b}\) :
-
Enriched degree of freedom on pore pressure
- \(\varvec{g}\) :
-
Gravity vector
- \(\varvec{m}_{\varGamma _d}\) :
-
Unit tangent vector along fracture
- \(\varvec{n}_{\varGamma _d}\) :
-
Unit normal vector along fracture
- \(\varvec{q}\) :
-
Fluid flow rate
- \(\varvec{s}\) :
-
Fracture natural coordinate
- \(\varvec{v}\) :
-
Fluid velocity
- \(\varvec{\kappa }_{\rm m}\) :
-
Matrix permeability tensor
- \(\varDelta _n(\varDelta _t)\) :
-
Separations in the normal (shear) direction at current time
- \(\delta _n(\delta _t)\) :
-
Separations in the normal (shear) direction at failure
- \(\epsilon _i^{\rm eq}\) :
-
Local equivalent strain components
- \(\epsilon _{12}^{s0}\) :
-
Initial out-of-bedding-plane shear strain threshold
- \(\epsilon _{ii}^{t0}\) :
-
Initial tensile strain thresholds
- \(\varGamma _{n}(\varGamma _{t})\) :
-
Mode I (mode II) energy constants
- \(\kappa _i\) :
-
Internal state variables controlling damage evolution
- \(\lambda _{n}(\lambda _{t})\) :
-
Mode I (mode II) initial slope indicator
- \(\mathbb {C}\) :
-
Stiffness tensor
- \(\mathbf M\) :
-
Damage operator in Voigt notation
- \(\mathbf {S/C}\) :
-
Compliance/stiffness matrix in Voigt notation
- \(\mu\) :
-
Fluid viscosity
- \(\phi\) :
-
Matrix porosity
- \(\phi (\varvec{x})\) :
-
Level set function
- \(\phi _n(\phi _t)\) :
-
Mode I (mode II) cohesive energy release rate
- \(\rho _{\text {f}}\) :
-
Fluid density
- \(\sigma _{max}(\tau _{max})\) :
-
Mode I (mode II) cohesive strength
- c :
-
Fracture hydraulic conductivity
- \(H_s\) :
-
Helmholtz free energy
- \(H_{\varGamma _d}\) :
-
Heaviside jump function
- \(K_{\text {f}}\) :
-
Fluid bulk modulus
- \(l_c\) :
-
Nonlocal internal length parameter
- M :
-
Biot modulus
- m(n):
-
Mode I (mode II) non-dimensional exponents
- \(m_{\text {f}}\) :
-
Fluid mass
- N :
-
Biot skeleton modulus
- \(N_{ui}(N_{pi})\) :
-
Shape functions for displacement (pore pressure)
- p :
-
Pore pressure
- \(Q_{\rm in}\) :
-
Fluid injection rate
- \(T_n(T_t)\) :
-
Normal (shear) cohesive traction in local coordinate
- w :
-
Fracture aperture
References
Abe H, Keer L, Mura T (1979) Theoretical study of hydraulically fractured penny-shaped cracks in hot, dry rocks. Int J Numer Anal Methods Geomech 3(1):79–96
Abe H, Keer LM, Mura T (1976) Growth rate of a penny-shaped crack in hydraulic fracturing of rocks, 2. J Geophys Res 81(35):6292–6298
Adachi JI, Detournay E (2002) Self-similar solution of a plane-strain fracture driven by a power-law fluid. Int J Numer Anal Methods Geomech 26(6):579–604
Adachi JI, Detournay E (2008) Plane strain propagation of a hydraulic fracture in a permeable rock. Eng Fract Mech 75(16):4666–4694
Advani S, Lee T, Lee J (1990) Three-dimensional modeling of hydraulic fractures in layered media: Part I—finite element formulations. J Energy Resourc Technol 112(1):1–9
Biot MA (1941) General theory of three-dimensional consolidation. J Appl Phys 12(2):155–164
Bunger AP, Detournay E (2005) Asymptotic solution for a penny-shaped near-surface hydraulic fracture. Eng Fract Mech 72(16):2468–2486
Bunger AP, Detournay E (2007) Early-time solution for a radial hydraulic fracture. J Eng Mech 133(5):534–540
Carter B, Desroches J, Ingraffea A, Wawrzynek P (2000) Simulating fully 3d hydraulic fracturing. Model Geomech 200:525–557
Chen Z (2012) Finite element modelling of viscosity-dominated hydraulic fractures. J Pet Sci Eng 88:136–144
Cohen CE, Kresse O, Weng X et al (2015) A new stacked height growth model for hydraulic fracturing simulation. In: 49th US rock mechanics/geomechanics symposium. American Rock Mechanics Association
Comi C, Mariani S, Perego U (2007) An extended fe strategy for transition from continuum damage to mode i cohesive crack propagation. Int J Numer Anal Methods Geomech 31(2):213
Coussy O (2004) Poromechanics. Wiley, New York
Cuvilliez S, Feyel F, Lorentz E, Michel-Ponnelle S (2012) A finite element approach coupling a continuous gradient damage model and a cohesive zone model within the framework of quasi-brittle failure. Comput Methods Appl Mech Eng 237:244–259
De Borst R, Réthoré J, Abellan MA (2006) A numerical approach for arbitrary cracks in a fluid-saturated medium. Arch Appl Mech 75(10–12):595–606
Desroches J, Detournay E, Lenoach B, Papanastasiou P, Pearson JRA, Thiercelin M, Cheng A (1994) The crack tip region in hydraulic fracturing. Proc R Soc Lond A 447(1929):39–48
Detournay E (2004) Propagation regimes of fluid-driven fractures in impermeable rocks. Int J Geomech 4(1):35–45
Detournay E, Peirce A (2014) On the moving boundary conditions for a hydraulic fracture. Int J Eng Sci 84:147–155
Dontsov E, Peirce A (2015) An enhanced pseudo-3d model for hydraulic fracturing accounting for viscous height growth, non-local elasticity, and lateral toughness. Eng Fract Mech 142:116–139
Dontsov E, Peirce A (2015) A non-singular integral equation formulation to analyse multiscale behaviour in semi-infinite hydraulic fractures. J Fluid Mech 781:R1
Dontsov E, Peirce A (2016) Implementing a universal tip asymptotic solution into an implicit level set algorithm (ilsa) for multiple parallel hydraulic fractures. In: 50th US rock mechanics/geomechanics symposium. American Rock Mechanics Association
Dontsov E, Peirce A (2017) A multiscale implicit level set algorithm (ilsa) to model hydraulic fracture propagation incorporating combined viscous, toughness, and leak-off asymptotics. Comput Methods Appl Mech Eng 313:53–84
Dormieux L, Kondo D, Ulm FJ (2006) Microporomechanics. Wiley, New York
Faivre M, Paul B, Golfier F, Giot R, Massin P, Colombo D (2016) 2d coupled hm-xfem modeling with cohesive zone model and applications to fluid-driven fracture network. Eng Fract Mech 159:115–143
Fries TP (2008) A corrected xfem approximation without problems in blending elements. Int J Numer Methods Eng 75(5):503–532
Gallant C, Zhang J, Wolfe CA, Freeman J, Al-Bazali TM, Reese M et al (2007) Wellbore stability considerations for drilling high-angle wells through finely laminated shale: a case study from terra nova. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Garagash D (2006) Transient solution for a plane-strain fracture driven by a shear-thinning, power-law fluid. Int J Numer Anal Methods Geomech 30(14):1439–1475
Garagash DI (2006) Plane-strain propagation of a fluid-driven fracture during injection and shut-in: asymptotics of large toughness. Eng Fract Mech 73(4):456–481
Garagash DI, Detournay E (2005) Plane-strain propagation of a fluid-driven fracture: small toughness solution. J Appl Mech 72(6):916–928
Garagash DI, Detournay E, Adachi J (2011) Multiscale tip asymptotics in hydraulic fracture with leak-off. J Fluid Mech 669:260–297
Geers M, De Borst R, Brekelmans W, Peerlings R (1998) Strain-based transient-gradient damage model for failure analyses. Comput Methods Appl Mech Eng 160(1):133–153
Geertsma J, De Klerk F et al (1969) A rapid method of predicting width and extent of hydraulically induced fractures. J Pet Technol 21(12):1–571
Gordeliy E, Peirce A (2013) Coupling schemes for modeling hydraulic fracture propagation using the xfem. Comput Methods Appl Mech Eng 253:305–322
Gordeliy E, Peirce A (2013) Implicit level set schemes for modeling hydraulic fractures using the xfem. Comput Methods Appl Mech Eng 266:125–143
Gordeliy E, Peirce A (2015) Enrichment strategies and convergence properties of the xfem for hydraulic fracture problems. Comput Methods Appl Mech Eng 283:474–502
Green A, Sneddon I (1950) The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid. In: Mathematical Proceedings of the Cambridge Philosophical Society, vol 46. Cambridge University Press, pp. 159–163
Gupta P, Duarte CA (2014) Simulation of non-planar three-dimensional hydraulic fracture propagation. Int J Numer Anal Methods Geomech 38(13):1397–1430
Hu J, Garagash DI (2010) Plane-strain propagation of a fluid-driven crack in a permeable rock with fracture toughness. J Eng Mech 136(9):1152–1166
Jin W (2018) Computational modeling of the transition from damage to fracture in intrinsically anisotropic porous media. Ph.D. thesis, Georgia Institute of Technology
Jin W, Arson C (2017) Modeling of tensile and compressive damage in layered sedimentary rock: a direction dependent non-local model. In: 51st US Rock Mechanics/Geomechanics Symposium. American Rock Mechanics Association
Jin W, Arson C (2018) Anisotropic nonlocal damage model for materials with intrinsic transverse isotropy. Int J Solids Struct 139:29–42
Jin W, Arson C (2019) Xfem to couple nonlocal micromechanics damage with discrete mode i cohesive fracture. Comput Methods Appl Mech Eng (under review)
Jirasek M (1998) Nonlocal models for damage and fracture: comparison of approaches. Int J Solids Struct 35(31):4133–4145
Jirásek M, Patzák B (2002) Consistent tangent stiffness for nonlocal damage models. Comput Struct 80(14):1279–1293
Jirasek M, Zimmermann T (2001) Embedded crack model. Part II: combination with smeared cracks. Int J Numer Methods Eng 50(6):1291–1305
Khoei A, Vahab M, Hirmand M (2016) Modeling the interaction between fluid-driven fracture and natural fault using an enriched-fem technique. Int J Fract 197(1):1–24
Khoei A, Vahab M, Hirmand M (2018) An enriched-fem technique for numerical simulation of interacting discontinuities in naturally fractured porous media. Comput Methods Appl Mech Eng 331:197–231
Khoei AR, Hirmand M, Vahab M, Bazargan M (2015) An enriched fem technique for modeling hydraulically driven cohesive fracture propagation in impermeable media with frictional natural faults: Numerical and experimental investigations. Int J Numer Methods Eng 104(6):439–468
Khoei AR, Vahab M, Haghighat E, Moallemi S (2014) A mesh-independent finite element formulation for modeling crack growth in saturated porous media based on an enriched-fem technique. Int J Fract 188(1):79–108
Khristianovic S, Zheltov Y (1955) Formation of vertical fractures by means of highly viscous fluids. In: Proceedings of 4th world petroleum congress, Rome, vol 2, pp 579–586
Kresse O, Weng X, Gu H, Wu R (2013) Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations. Rock Mech Rock Eng 46(3):555–568
Leclerc J, Wu L, Nguyen VD, Noels L (2018) A damage to crack transition model accounting for stress triaxiality formulated in a hybrid nonlocal implicit discontinuous galerkin-cohesive band model framework. Int J Numer Methods Eng 113(3):374–410
Lenoach B (1995) The crack tip solution for hydraulic fracturing in a permeable solid. J Mech Phys Solids 43(7):1025–1043
Li C, Caner FC, Chau VT, Bažant ZP (2017) Spherocylindrical microplane constitutive model for shale and other anisotropic rocks. J Mech Phys Solids 103:155–178
McLennan JD, Picardy JC et al (1985) Pseudo-three-dimensional fracture growth modeling. In: The 26th US Symposium on Rock Mechanics (USRMS). American Rock Mechanics Association
Miehe C, Mauthe S, Teichtmeister S (2015) Minimization principles for the coupled problem of darcy-biot-type fluid transport in porous media linked to phase field modeling of fracture. J Mech Phys Solids 82:186–217
Mohammadnejad T, Andrade J (2016) Numerical modeling of hydraulic fracture propagation, closure and reopening using xfem with application to in-situ stress estimation. Int J Numer Anal Methods Geomech 40(15):2033–2060
Mohammadnejad T, Khoei A (2013) An extended finite element method for fluid flow in partially saturated porous media with weak discontinuities; the convergence analysis of local enrichment strategies. Comput Mech 51(3):327–345
Mohammadnejad T, Khoei A (2013) An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model. Finite Elements Anal Des 73:77–95
Nordgren R et al (1972) Propagation of a vertical hydraulic fracture. Soc Pet Eng J 12(04):306–314
Palmer I, Carroll Jr H et al (1983) Numerical solution for height and elongated hydraulic fractures. In: SPE/DOE Low Permeability Gas Reservoirs Symposium. Society of Petroleum Engineers
Park K, Choi H, Paulino GH (2016) Assessment of cohesive traction-separation relationships in abaqus: a comparative study. Mech Res Commun 78:71–78
Park K, Paulino GH (2011) Cohesive zone models: a critical review of traction-separation relationships across fracture surfaces. Appl Mech Rev 64(6):060802
Park K, Paulino GH (2012) Computational implementation of the ppr potential-based cohesive model in abaqus: educational perspective. Eng Fract Mech 93:239–262
Park K, Paulino GH, Roesler JR (2009) A unified potential-based cohesive model of mixed-mode fracture. J Mech Phys Solids 57(6):891–908
Peirce A (2015) Modeling multi-scale processes in hydraulic fracture propagation using the implicit level set algorithm. Comput Methods Appl Mech Eng 283:881–908
Peirce A, Detournay E (2008) An implicit level set method for modeling hydraulically driven fractures. Comput Methods Appl Mech Eng 197(33–40):2858–2885
Perkins T, Kern L et al (1961) Widths of hydraulic fractures. J Pet Technol 13(09):937–949
Remij E, Remmers J, Huyghe J, Smeulders D (2015) The enhanced local pressure model for the accurate analysis of fluid pressure driven fracture in porous materials. Comput Methods Appl Mech Eng 286:293–312
Roth SN, Léger P, Soulaïmani A (2015) A combined xfem-damage mechanics approach for concrete crack propagation. Comput Methods Appl Mech Eng 283:923–955
Salimzadeh S, Khalili N (2015) A three-phase xfem model for hydraulic fracturing with cohesive crack propagation. Comput Geotech 69:82–92
Savitski A, Detournay E (2002) Propagation of a penny-shaped fluid-driven fracture in an impermeable rock: asymptotic solutions. Int J Solids Struct 39(26):6311–6337
Semnani SJ, White JA, Borja RI (2016) Thermoplasticity and strain localization in transversely isotropic materials based on anisotropic critical state plasticity. Int J Numer Anal Methods Geomech 40(18):2423–2449
Settari A, Cleary MP et al (1986) Development and testing of a pseudo-three-dimensional model of hydraulic fracture geometry. SPE Prod Eng 1(06):449–466
Siebrits E, Peirce AP (2002) An efficient multi-layer planar 3d fracture growth algorithm using a fixed mesh approach. Int J Numer Methods Eng 53(3):691–717
Simone A, Askes H, Sluys LJ (2004) Incorrect initiation and propagation of failure in non-local and gradient-enhanced media. Int J Solids Struct 41(2):351–363
Simone A, Wells GN, Sluys LJ (2003) From continuous to discontinuous failure in a gradient-enhanced continuum damage model. Comput Methods Appl Mech Eng 192(41):4581–4607
Sneddon IN (1946) The distribution of stress in the neighbourhood of a crack in an elastic solid. Proc R Soc Lond A 187(1009):229–260
Song SH, Paulino GH, Buttlar WG (2006) A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material. Eng Fract Mech 73(18):2829–2848
Spence DA, Sharp P (1985) Self-similar solutions for elastohydrodynamic cavity flow. Proc R Soc Lond A 400(1819):289–313
Tien YM, Kuo MC (2001) A failure criterion for transversely isotropic rocks. Int J Rock Mech Mining Sci 38(3):399–412
Turon A, Davila CG, Camanho PP, Costa J (2007) An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng Fract Mech 74(10):1665–1682
Vahab M, Khalili N (2018) X-fem modeling of multizone hydraulic fracturing treatments within saturated porous media. Rock Mech Rock Eng 51:3219–3239
Vandamme L, Curran JH (1989) A three-dimensional hydraulic fracturing simulator. Int J Numer Methods Eng 28(4):909–927
Wang Y, Waisman H (2016) From diffuse damage to sharp cohesive cracks: a coupled xfem framework for failure analysis of quasi-brittle materials. Comput Methods Appl Mech Eng 299:57–89
Wells G, Sluys L, De Borst R (2002) Simulating the propagation of displacement discontinuities in a regularized strain-softening medium. Int J Numer Methods Eng 53(5):1235–1256
Zienkiewicz OC, Zhu JZ (1992) The superconvergent patch recovery and a posteriori error estimates. Part 1: the recovery technique. Int J Numer Methods Eng 33(7):1331–1364
Acknowledgements
Financial support for this research was provided by the U.S. National Science Foundation, under Grant 1552368: “CAREER: Multiphysics Damage and Healing of Rocks for Performance Enhancement of Geo-Storage Systems—A Bottom–Up Research and Education Approach”
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jin, W., Arson, C. Fluid-driven transition from damage to fracture in anisotropic porous media: a multi-scale XFEM approach. Acta Geotech. 15, 113–144 (2020). https://doi.org/10.1007/s11440-019-00813-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-019-00813-x