A unified non-local damage model for hydraulic fracture in porous media

Abstract

We present a unified non-local damage model for modeling hydraulic fracture processes in porous media, in which damage evolves as a function of fluid pressure. This setup allows for a non-local damage model that resembles gradient-type models without the need for additional degrees of freedom. In other words, we propose a non-local damage formulation at the same cost of a local damage approach. Nonlinear anisotropic permeability is employed to distinguish between the fluid flow velocity in the damage zone and the intact porous media. The permeability evolves as a function of an equivalent strain measure, where its anisotropic evolution behavior is controlled by the direction of principle strain. The length scale of the proposed model is analytically derived as a function of material point variables and is shown to be dependent on the pressure rate. A mixed finite element method is proposed to monolithically solve the coupled displacement–pressure system. The nonlinear system is linearized and solved using Newton’s method with analytically derived consistent Jacobian matrix and residual vector, and the evolution of the system in time is performed by a backward Euler scheme. Numerical examples of 1D and 2D hydraulic fracture problems are presented and discussed. The numerical results show that the proposed model is insensitive to the mesh size as well as the time step size and can well capture the features of hydraulic fracture in porous media.

1 Introduction

Hydraulic fracture can be described as the initiation and propagation process of fracture, which is driven by a pressurized fluid in order to disintegrate tight bedrock formations with low permeability [23]. The hydraulic fracture technique is broadly applied in petroleum exploitation and shale gas production [81], to crack the impervious rock through which gas or oil can flow out more easily. This process has been investigated on a wide range of materials in hydraulic engineering, e.g., clay core wall [46, 120] and concrete [63, 132]. In order to optimize hydraulic fracture processes, several modeling approaches were proposed, such as the extended finite element method (XFEM) [55], generalized finite element method (GFEM) [37], discrete element method [110], peridynamics method [113], continuum damage mechanics (CDM) method [114], and phase-field method [74, 75, 128]. Further, the CDM models used to model hydraulic fracture may be classified into local [58, 104] and non-local damage mechanics methods [17, 41, 48, 79].

In CDM model, material failure is represented by the introduction of a state variable that degrades the material capacity to carry loads. Damage evolution is usually defined as a function of material point variables such as equivalent stress and strain, and leads to gradual softening of the solid skeleton stiffness [57]. The accumulation process of damage at a material point represents the formation and growth process of microcracks or micro-voids [49]. Therefore, the CDM model is well suited to represent the nonlinear response of porous media, including the evolution of poroelastic parameters during failure [49, 57, 101], and it can readily capture crack initiation, propagation, interaction, and possible branching [104].

The CDM model is naturally different from the linear elastic fracture mechanics (LEFM) in considering the hydraulic fracture of solids. While CDM models suppose that a macro-fracture is formed by the accumulation of microcracks, LEFM models assume one dominant fracture at the macroscale and does not consider processes at smaller scales. Although LEFM models can capture macroscopic crack initiation and propagation [27], they are challenging to account for the surrounding diffusive processes of micro-crack formation which has been observed via experiments on porous media [25, 131]. Additionally, they are challenged by the difficulty of tracking complicated fracture behavior such as curved cracks, crack coalescence, branching, and crossing [38, 121].

The local CDM approach exhibits loss of ellipticity of governing equations, which leads to the lack of uniqueness of the solution and mesh dependence of numerical results [87]. In order to overcome these drawbacks, non-local definition of damage has been introduced in [9], in which the damage growth at a material point is related to a neighboring interaction zone [7] sometimes referred to as the fracture process zone (FPZ). The FPZ represents the region in which the material variables contribute to the damage growth rate. The size of the FPZ is controlled by a material characteristic length scale which is typically considered to be an inherent property of the material and used as a localization limiter [36, 76]. Estimation of the characteristic length scale parameter remains an open challenge that has been studied by many researchers, see for example [3], but it is often related to particle size [10], size of representative volume element [71], or other micromechanics features of the solid [44].

The non-local CDM is often implemented in the form of either integral non-local model [8, 11, 17] or gradient-type model [86, 112]. The integral non-local model, while being cheaper computationally (requiring less degrees of freedom), is challenged by the calculation of damage in the vicinity of external edges and the difficulty of the derivation of fully consistent tangent matrices. The gradient model is based on transformation of the spatial averaging operator into a diffusion equation which results into a system of equations that requires an additional degree of freedom to represent the non-local internal variable field [86]. The gradient non-local damage model has been previously employed to investigate hydraulic fracture in porous media [17, 18, 41, 77, 79, 80]. The phase-field method, which is closely related to the gradient damage model [26], also requires additional degrees of freedom and a specific length scale. The phase-field method has been used for the description of hydraulic fracture in porous media for example in [40, 74, 75, 128].

Previous efforts to model hydraulic fracturing using diffuse damage approaches, including those by the authors, are mostly based on either gradient damage model [18, 41, 77, 80], or phase-field model [40, 74, 75, 128]. Both of these approaches are known to require the solution of additional partial differential equations on the top of the balance of momentum and mass balance equations which represent the fundamental poroelastic response. In gradient damage, the additional equation provides the non-local strain; and in phase field, the additional equation describes the growth of the effectively non-local damage parameter [26]. The need for the additional PDEs leads to additional FEM degrees of freedom, and consequently elevated computational costs.

In this paper, we introduce a novel unified non-local damage model that can retrieve the advantages of the gradient damage model while eliminating the need and cost of an additional regularization equation for a non-local variable. Following the experimental and numerical investigations of the relation between damage, porosity, permeability, pore pressure, and damage [2, 39, 51, 66, 84, 92, 125, 135, 136], we define a damage variable that is driven by fluid pressure. We hypothesize that the fluid mass balance equation is analogous to a gradient non-local damage model, in which fluid pressure can be used to regularize the governing equations and lead to mesh insensitivity. Darcy’s law is used to describe the fluid flow inside and outside the damage zone, while a nonlinear anisotropic permeability is introduced to enhance the fluid flow behavior in the fracture domain. The founding damage mechanics and nonlinear permeability approaches have been extensively developed and validated by the authors in [18, 19, 77, 79, 80, 128] and others [61, 65, 85, 90, 102]. Given the intrinsic non-locality in the model setup, the size of the interaction zone is dictated by the material point variables including the pressure rate. Hence, the size of the characteristic length is derived analytically using an analogy between the fluid mass balance equation and the non-local anisotropic gradient equation. The proposed model is implemented within a mixed finite element formulation for poroelasticity with pressure-dependent damage, for which a Newton–Raphson approach is used to linearize the nonlinear system of equation by means of an analytically derived tangent matrix. The proposed model is used for the analysis of several benchmark problems. The model results are shown to be mesh independent and provide physically sound results, thus proving our hypothesis. The major advantage of this model is the ability to demonstrate a non-local damage behavior without the extra effort needed for non-local integral computations or the additional computational cost of the non-local gradient model, hence leading to a unified non-local damage model.

The paper is organized as follows: first, in Sect. 2, the poroelastic damage theory is introduced briefly in terms of equilibrium equation and fluid flow continuity equation as well as some essential constitutive definitions. Section 3 discusses the non-local characteristic of fluid pressure due to the governing continuity equation. In Sect. 4, we propose a unified damage model which involves fluid pressure-dependent damage evolution and nonlinear anisotropic permeability, and the non-local characteristics of the proposed model are discussed. Then, in Sect. 5, a monolithic mixed finite element setup is proposed to solve the coupled displacement-pressure nonlinear system. In Sect. 6, a poroelastic column is employed to illustrate that fluid-driven failure behavior of porous media is insensitive to the time step size in the range of investigated parameters. In addition, the underlying characteristic length scale of the proposed model is analyzed in details, and the mesh independence characteristic of the proposed model is confirmed. In Sect. 7, a 2D hydraulic fracture problem is investigated to illustrate the capability of the proposed model for capturing hydraulic fracture features. We draw the summary and conclusions in Sect. 8.

2 Introduction to poroelastic damage theory

2.1 Poroelastic equilibrium

In saturated porous media, the relationships between total stress tensor $\sigma _{ij}$, solid damaged stress tensor $\sigma _{ij}^{s}$, and fluid pressure P are described by the following Biot’s mixture theory definition [12].

$$\begin{aligned} \sigma _{ij}=\sigma _{ij}^{s}-\alpha (D) \delta _{ij} P \end{aligned}$$

(1)

in which $\alpha (D)$ denotes the damaged Biot’s coefficient [101]. D is a scalar damage variable which reflects the damage status of the material. $D=0$ represents undamaged material, and $D=1$ represents a complete loss of stiffness of the material at that point. $\delta _{ij}$ is the Kronecker delta.

According to continuum damage mechanics [57], the solid damaged stress tensor $\sigma _{ij}^{s}$ is given by

$$\begin{aligned} \sigma _{i j}^{s}=C_{ijkl}(D) \varepsilon _{kl} \end{aligned}$$

(2)

where $C_{ijkl}(D)$ denotes the damaged drained stiffness tensor that is described by $C_{ijkl}(D)=(1-D)C^{e}_{ijkl}$. Here $C^{e}_{ijkl}$ is the elastic drained stiffness tensor that is given by $C^{e}_{ijkl}=K \delta _{ij} \delta _{kl}+G(\delta _{ik} \delta _{jl}+\delta _{il} \delta _{jk}-\frac{2}{3} \delta _{ij} \delta _{kl})$, where K is the undamaged bulk modulus, and G is the undamaged shear modulus. Under the assumption of small strain, the total strain is given by $\varepsilon _{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})$, with $u_{i}$ being the displacement field.

The damaged Biot’s coefficient $\alpha (D)$ can be written as [101]:

$$\begin{aligned} \alpha (D)=1-\frac{K_{D}}{K_{s}} \end{aligned}$$

(3)

where $K_{D}$ is the damaged bulk modulus of the mixture described by $K_{D}=(1-D)K$. $K_{s}$ is the solid grain bulk modulus. The undamaged Biot’s coefficient is $\alpha (D)|_{D=0}= \alpha _{0}=1-K/K_{s}$. Biot’s coefficient approaches a value of $\alpha (D)=1$ as the damage reaches $D=1$, which means that the fluid has completely dominated the total stress tensor. Biot’s coefficient $\alpha (D)$ increases with damage D [6, 93, 101].

In the absence of inertia terms, the balance of momentum equation can be expressed as:

$$\begin{aligned} \sigma _{ij,j}+b_{i}=0 \end{aligned}$$

(4)

where $b_{i}$ is a body force. Substituting Eqs. (1) and (2) into Eq. (4) yields:

$$\begin{aligned} \left[ C_{ijkl}(D) \varepsilon _{kl}-\alpha (D) \delta _{ij} P\right] _{,j}+b_{i}=0 \end{aligned}$$

(5)

2.2 Fluid mass balance

The fluid mass balance equation in saturated porous media can be expressed by:

$$\begin{aligned} \frac{\partial \zeta }{\partial t}+v_{i,i}=0 \end{aligned}$$

(6)

where $\zeta$ denotes the fluid content change at a material point, t is time, and $v_{i}$ is the fluid velocity vector. The relationship between fluid pressure P and fluid content change $\zeta$ is given by [28, 101]:

$$\begin{aligned}&\zeta =\frac{P}{M(D)}+\alpha (D) \varepsilon _{ii} \end{aligned}$$

(7a)

$$\begin{aligned}&\text {with} \nonumber \\&M(D)=\frac{K^{u}-K_{D}}{\alpha (D)^{2}} \end{aligned}$$

(7b)

where M(D) is the damaged Biot’s modulus which is related to the storage coefficient of the poroelastic medium [101]. The storage coefficient is defined as the decrease in the fluid amount in a unit volume of porous medium due to a unit decrease in fluid pressure under constant volumetric strain. Biot’s modulus M(D) increases with damage D [79, 101]. In the case of complete damage ($D=1$), $M|_{D=1}=K^u$, and $M|_{D=0}=M_{0}$ when the material is intact ($D=0$), where $M_{0}$ is the Biot’s modulus of intact porous media. $\varepsilon _{i i}$ is solid volumetric strain given by $\varepsilon _{ii}=\varepsilon _{xx}+\varepsilon _{yy}+\varepsilon _{zz}$. $K^{u}$ is the undrained bulk modulus defined as $K^{u}=\frac{2}{3}G(1+\nu ^{u}) / (1-2\nu ^{u})$, where $\nu ^{u}$ is the undrained Poisson’s ratio.

Darcy’s law is often adopted to describe the relationship between fluid velocity $v_i$ and fluid pressure gradient $P_{,i}$. The reason is that Darcy’s law describes the flow as a laminar flow between grains [33, 42] which is the characteristic of many geomechanics applications. Darcy’s law featuring anisotropic permeability can be expressed as:

$$\begin{aligned} v_{i}=-k_{ij} P_{,j} \end{aligned}$$

(8)

where $k_{ij}$, a variable tensor during the damage process of porous media, denotes anisotropic permeability tensor which can be described by Eq. (9) in 2D framework [60] under the assumption that permeability off-diagonal components are equal to zero.

$$\begin{aligned} k_{ij}=\left[ \begin{array}{cc} k_{xx} &{} 0 \\ 0 &{} k_{yy} \end{array} \right] \end{aligned}$$

(9)

where $k_{xx}$ and $k_{yy}$ are the x and y components of the permeability tensor. In this anisotropic permeability definition, the changes in permeability ($k_{xx},k_{yy}$) are sought to be represented by the strain dependent permeability definition detailed later in Sect. 4.2. In this tensorial representation with zero off-diagonals, the anisotropy is retrieved through the resultant of the flow in these two directions. This is a similar approach to the previous numerical and experimental investigations in [1, 77, 80, 90]. It is worth mentioning that the permeability has been attempted to be represented as a function of damage [68, 127], equivalent stress [80, 108], or equivalent strain [79, 100] during the damage process of porous media. By substituting Eqs. (8) and (7a) into Eq. (6), the fluid flow continuity equation, for a damaged saturated porous media, can be described as:

$$\begin{aligned} \frac{\partial }{\partial t}\left[ \frac{P}{M(D)}+\alpha (D) \varepsilon _{ii} \right] -\left[ k_{ij}P_{,j}\right] _{,i}=0 \end{aligned}$$

(10)

3 Non-local characteristic of fluid pressure

This section focuses on the implicit gradient feature of the fluid flow continuity equation which is used to illustrate the non-local characteristic of fluid pressure. We first introduce a variation of a previously published anisotropic gradient non-local model as a reference point, and then we construct an analogy with the continuity equation Eq. (10). We show that the fluid pressure can essentially be treated as a non-local variable in poroelastic damage theory, hence leading to a unified non-local damage model without the need for extra degrees of freedom.

3.1 Non-local gradient model

Isotropic implicit gradient non-local model can be expressed as [35]:

$$\begin{aligned} {X^{NL}} - g^{b}c X_{,ii}^{NL} = {X^L} \end{aligned}$$

(11)

where $X^{N L}$ and $X^{L}$ denote the non-local and local variables, respectively. Herein, $g^{b}$ is denoted as variable gradient activity function, which is a dimensionless scalar quantity. c is a scalar gradient parameter that is determined by the size of the averaging domain, which has the square of length dimension, i.e., $\mathrm L^{2}$. In 2D framework, the non-local averaging in the averaging domain is performed over an isotropic, circular area. Equation 11 is also called as transient-gradient damage model since the gradient activity evolves with a variable [35]. Note that in the case of a constant $g^{b}c$, Eq. (11) reduces to the classical gradient model published in [86].

Anisotropic implicit gradient-enhanced formula in tensor form can be expressed as follows [115]:

$$\begin{aligned} {X^{NL}} - {\left( {g_{ij}^{a}X_{,j}^{NL}} \right) _{,i}} = {X^L} \end{aligned}$$

(12)

where $g_{ij}^{a}$ is an anisotropic tensor, which controls the size and shape of non-local interaction zone. The non-local averaging is performed over an ellipse in [115], which illustrated the influence of $g_{ij}^{a}$ components on non-local variable in details. The dimensions of the components of $g^{a}_{ij}$ have the dimension of square of length dimension ($\mathrm L^{2}$) and should not be less than zero. However, in the special case that $g^{a}_{ij}$ is isotropic, except that $g_{ij}^{a}$ is a constant, Eq. (12) does not reduce to Eq. (11) due to the presence of $g_{ij,i}^{a}X^{NL}_{,j}$ in the expansion of $\left( {g_{ij}^{a}X_{,j}^{NL}} \right) _{,i}$. Thus, we propose the following implicit gradient-enhanced formula to unify the mathematical forms of anisotropic and isotropic implicit gradient models.

$$\begin{aligned} {X^{NL}} - g^{b}{\left( {g_{ij}^{a}X_{,j}^{NL}} \right) _{,i}} = {X^L} \end{aligned}$$

(13)

where $g^{b}$ is dimensionless. With this modification, Eq. (13) reduces to the transient-gradient isotropic model in Eq. (11) when $g^{a}_{ij}$ is isotropic and space independent. Additionally, the constant $g^{b}$ will retrieve the original implicit gradient formula in [86, 88]. Moreover, when $g^{b}$ is not a function of space, Eq. (13) will reduce to the anisotropic implicit gradient-enhanced formula in Eq. (12).

The non-local averaging effects can be reflected by the coefficient of the second derivative of non-local variable [13], so the $g^{b}g^{a}_{ij}$ is used to represent the size, shape, and orientation of the non-local interaction zone in this paper, which is referred to as gradient activity tensor. We note that the components in $g^{b}g^{a}_{ij}$ have square of length dimension ($\mathrm L^{2}$), and all the components should not be less than zero.

Following [98], Eq. (13) can be rewritten as $\frac{1}{g^{b}}{X^{NL}} - {\left( {g_{ij}^{a}X_{,j}^{NL}} \right) _{,i}} = \frac{1}{g^{b}}{X^L}$, and implemented in a FEM code following similar approach as in [115]. The effect of $g^{b}g^{a}_{ij}$ on the non-local variable $X^{NL}$ in Fig. 1 is presented based on an annulus with an inner radius $r_{2}=0.1$ m and outer radius $r_{1}=1.0$ m. The value of local variable $X^{L}$ is set as $\frac{1}{r_{1}-r_{2}}\left[ \left( x^{2}+y^{2}\right) ^{0.5}r_{1}-r_{2}\right]$ which results in $X^{L}=1.0$ at the outer edge and $X^{L}=0.0$ at the inner edge of the annulus as shown in Fig. 1b. The maximum element size of the annulus is 0.02 m. The contours of non-local variable $X^{NL}$ in Fig. 1c–f correspond to case 1 ($g^{a}_{11}=g^{a}_{22}=0.1X^{L}$, $g^{a}_{12}=g^{a}_{21}=0.0$, $g^{b}=1.0$); case 2 ($g^{a}_{11}=0.4X^{L}$, $g^{a}_{22}=0.1X^{L}$, $g^{a}_{12}=g^{a}_{21}=0.0$, $g^{b}=1.0$); case 3 ($g^{a}_{11}=0.4X^{L}$, $g^{a}_{22}=0.1X^{L}$, $g^{a}_{12}=g^{a}_{21}=0.0$, $g^{b}=X^{L}$); and case 4 ($g^{a}_{11}=0.4X^{L}$, $g^{a}_{22}=0.1X^{L}$, $g^{a}_{12}=g^{a}_{21}=0.1X^{L}$, $g^{b}=X^{L}$), respectively. The non-local variable $X^{NL}$ contour of case 1 in Fig. 1c is isotropic since the gradient activity $g^{b}g^{a}_{ij}$ is isotropic. The anisotropic $g_{ij}^{a}$ changes the shape and value of the non-local variable (see Fig. 1c–f), and the $g^{b}$ only changes its value (see Fig. 1d, e).

Fig. 1

Representation of the effect of gradient activity term $g^{b}g^{a}_{ij}$ on the non-local variable $X^{NL}$. a The geometry of an annulus with that inner radius $r_{2}$ and outer radius $r_{1}$ are 0.1 and 1.0 m, respectively. b The value of local variable $X^{L}=\frac{1}{r_{1}-r_{2}}\left[ \left( x^{2}+y^{2}\right) ^{0.5}r_{1}-r_{2}\right]$. c The value of $X^{NL}$ when $g^{a}_{11}=g^{a}_{22}=0.1X^{L}$, $g^{a}_{12}=g^{a}_{21}=0.0$, and $g^{b}=1.0$. d The value of $X^{NL}$ when $g^{a}_{11}=0.4X^{L}$, $g^{a}_{22}=0.1X^{L}$, $g^{a}_{12}=g^{a}_{21}=0.0$, and $g^{b}=1.0$. e The value of $X^{NL}$ when $g^{a}_{11}=0.4X^{L}$, $g^{a}_{22}=0.1X^{L}$, $g^{a}_{12}=g^{a}_{21}=0.0$, and $g^{b}=X^{L}$. f The value of $X^{NL}$ when $g^{a}_{11}=0.4X^{L}$, $g^{a}_{22}=0.1X^{L}$, $g^{a}_{12}=g^{a}_{21}=0.1X^{L}$, and $g^{b}=X^{L}$

3.2 Analogy between mass balance and non-local gradient equations

The fluid flow continuity Eq. (10) can be expanded as:

$$\begin{aligned} \frac{\partial [1 / M(D)]}{\partial t}P+\frac{\partial P}{\partial t}\frac{1}{M(D)}-\left[ {k_{ij}}P_{,j}\right] _{,i}=-\frac{\partial \alpha (D)}{\partial t}\varepsilon _{ii}-\frac{\partial \varepsilon _{ii}}{\partial t}\alpha (D) \end{aligned}$$

(14)

Equation (14) explicitly involves fluid pressure P and its second derivative in space, which is analogous to the non-local gradient models reviewed in Sect. 3.1. In addition, the expression in Eq. (14) includes a term that constitutes the pressure derivative in time $\frac{\partial P}{\partial t}$ which is not included in the aforementioned section. In order to proceed with the derivation, we introduce the discretization of variables in time using a backward Euler operator as follows: $\frac{{\partial H}}{{\partial t}} = \frac{1}{{\Delta t}}\left( {{H^n} - {H^{n - 1}}} \right)$ for any function H(t) that is a continuous variable with time, where $\Delta t$ is the time step size. $H^{n}$ and $H^{n-1}$ are the values of variable H at the current and previous time step, respectively.

Following the derivation process in Appendix A, the discrete form of Eq. (14) can be expressed as follows:

$$\begin{aligned} \begin{aligned}&\left[ {\frac{2}{{M(D)}} - \frac{1}{{{{[M(D)]}^{n - 1}}}}} \right] P - \frac{{{P^{n - 1}}}}{{M(D)}} - {\left[ {{k_{ij}}{P_{,j}}} \right] _{,i}}\Delta t\\ {}&= {\left[ {{\varepsilon _{ii}}} \right] ^{n - 1}}\alpha (D) - \left[ {2\alpha (D) - {{[\alpha (D)]}^{n - 1}}} \right] {\varepsilon _{ii}} \end{aligned} \end{aligned}$$

(15)

Note that the superscript n, which denotes the current time step, was removed for notational convenience. Re-arranging Eq. (15) in order to keep the pressure and its derivatives on the left hand side leads to:

$$\begin{aligned}&P-\left[ \frac{2M_{0}}{M(D)}-\frac{M_{0}}{[M(D)]^{n-1}}\right] ^{-1} \left[ M_{0}k_{ij}\Delta t P_{,j}\right] _{,i}=P^{L} \end{aligned}$$

(16a)

$$\begin{aligned}&\text {with} \nonumber \\&P^{L}= \left[ \frac{2}{M(D)}-\frac{1}{[M(D)]^{n-1}}\right] ^{-1}\left[ \frac{P^{n-1}}{M(D)}-\left[ 2 \alpha (D)-[\alpha (D)]^{n-1}\right] \varepsilon _{ii}+\left[ \varepsilon _{i i}\right] ^{n-1} \alpha (D)\right] \end{aligned}$$

(16b)

Note that the second term in Eq. (16a) is transformed using the undamaged Biot’s modulus $M_{0}$ so that the $M_{0}k_{ij} \Delta t$ term has the square of length dimension ($\mathrm L^{2}$) and $\left[ \frac{2M_{0}}{M(D)}-\frac{M_{0}}{[M(D)]^{n-1}}\right] ^{-1}$ is dimensionless. The dimension of variable $P^{L}$ is $\mathrm {M L^{-1} T^{-2} }$, and the M and T have dimensions of mass and time, respectively. It follows that the variable $P^{L}$ has the same dimension as fluid pressure P, i.e., pressure dimension.

By comparing the implicit gradient formula Eq. (13) and Eq. (16a), the analogy between the continuity equation and the non-local anisotropic gradient formula can be constructed where P is analogous to $X^{NL}$ and $P^L$ is analogous to $X^L$. Therefore, Eq. (16) can be regarded as a variant of the gradient equation in which the non-local variable is fluid pressure P. The $P^{L}$ will be referred to in this paper as “driving pressure load”which drives the evolution of the fluid pressure P. The driving pressure load $P^{L}$ is a function of current damage D, volumetric strain $\varepsilon _{ii}$, and history variables (e.g., previous fluid pressure $P^{n-1}$, damage $D^{n-1}$, volumetric strain $\left[ \varepsilon _{ii}\right] ^{n-1}$); therefore, it implicitly involves the time step size $\Delta t$.

By further exploring the analogy between Eq. (16) and Eq. (13), gradient activity tensor in Eq. (16) can be written as:

$$\begin{aligned} \begin{aligned} g_{ij}&= \left[ \begin{array}{cc} g_{xx} &{} 0 \\ 0 &{} g_{yy} \end{array} \right] =\left[ \frac{2}{M(D)}-\frac{1}{[M(D)]^{n-1}}\right] ^{-1} k_{ij} \Delta t\\&=\left[ \frac{2}{M(D)}-\frac{1}{[M(D)]^{n-1}}\right] ^{-1} \left[ \begin{array}{cc} k_{xx} &{} 0 \\ 0 &{} k_{yy} \end{array} \right] \Delta t \end{aligned} \end{aligned}$$

(17)

where $g_{ij}$ denotes the gradient activity tensor in fluid flow continuity equation. Equation (17) indicates that gradient activity, which depends on the permeability $k_{ij}$ tensor, is a symmetric second-order tensor as long as the permeability is symmetric.

Remark 1

The presented setup leads to the impression that the non-local gradient activity tensor formula involves time step size. However, the actual dependency of the model can be better understood dividing Eq. (16a) and rearranging its terms:

$$\begin{aligned} \frac{P}{\Delta t}-\left[ \frac{2M_{0}}{M(D)}-\frac{M_{0}}{[M(D)]^{n-1}}\right] ^{-1} \left[ M_{0}k_{ij}P_{,j}\right] _{,i}=\frac{P^{L}}{\Delta t} \end{aligned}$$

(18)

In this relationship, and by drawing analogy to Eq. (13), the non-local variable is $\frac{P}{{\Delta t}}$ and the local variable is $\frac{{{P^L}}}{{\Delta t}}$. By looking at the mathematical expressions in this equation, we conclude that the non-local relationship is actually based on the pressure rate being the non-local variable. In this case, the time step $\Delta t$ does not appear in the second term, and the resulting length scale is time step free.

The problem with the direct implementation of this equation is that it leads to complications when being used within the FEM model derivation. Therefore, we opt for multiplying both sides by $\Delta t$, which leads to Eq. (16) and the resulting length scale equivalent expressions in Eqs. (17) and (27) and the length scale expression Eq. (28).

Therefore, we can conclude that the contribution of the time step in the length scale equivalent expressions in Eqs. (17) and (27) and the length scale expression Eq. (28) is only an artifact of the non-local behavior being truly function of the pressure rate rather than the pressure. The fact that a material model is a function of strain rate or pressure rate is widely acceptable and is often observed in the damage modeling of geomaterials and metals [64, 72, 73, 107, 111, 130].

As mentioned earlier, all the components of gradient activity tensor should not be less than zero [13, 115]. Introducing this condition to Eq. (17) leads to a positivity condition that is defined as: $\left[ \frac{2}{M(D)}-\frac{1}{[M(D)]^{n-1}}\right] >0$, provided that the components of the anisotropic permeability $k_{ij}$ and the time step $\Delta t$ are always positive. The latter is a condition for the well-posedness of the continuity equation [24]. As for most porous geomaterials, the difference between $\frac{2}{M(D)}$ and $\frac{1}{[M(D)]^{n-1}}$ is greater than zero, as proved in Appendix B.

In order to understand the impact of gradient activity $g_{ij}$ on fluid pressure, we present the fluid pressure contour of a circular domain with isotropic and anisotropic permeabilities in Fig. 2. One can observe that the anisotropy of the gradient activity is a function of permeability tensor according to Eq. (17). The circular domain is subjected to a fluid pressure $P_{\max }$ at the center point and a fluid pressure $P_{\min }$ at the edge of the circle, and the displacement of the circle domain is zero. It can be observed that the fluid pressure appears a circle under the condition of $g_{xx}= g_{yy}$ (achieved by $k_{xx}= k_{yy}$) while the fluid pressure shape is an ellipse for $g_{xx}= 5g_{yy}$ (achieved by $k_{xx}= 5k_{yy}$). This indicates that the anisotropic gradient activity term leads to an anisotropic localization behavior of the fluid pressure. The anisotropic localization phenomenon, with the influence of gradient activity components, is similar to the anisotropic gradient formula described in [115] for the non-local variable.

Fig. 2

Representation of the effect of gradient activity on fluid pressure in a circular domain. a The circular domain is subjected to a high fluid pressure $P_{\max }$ at the circle center while a fluid pressure $P_{\min }$ at circle edge is zero. b $g_{xx}= g_{yy}$. c $g_{xx}= 5g_{yy}$

Moreover, when $D=0$, $M(D)=M_{0}$, and $\alpha (D)=\alpha _{0}$, Eq. (16) can be written as:

$$\begin{aligned} P-[ \underbrace{M_{0}k_{ij} \Delta t}_{g_{ij}} P_{,j}]_{,i}= \underbrace{P^{n-1}-M_{0}\alpha _{0} \left[ \varepsilon _{ii}-\left[ \varepsilon _{ii}\right] ^{n-1}\right] }_{P^{L}} \end{aligned}$$

(19)

Equation (19) illustrates that the gradient activity and driving pressure load in an undamaged porous media is not zero, which means that the fluid pressure is also a non-local variable even in the absence of solid damage. Once damage D reaches its maximum value $D_{\max }$, $M(D)=[M(D)]^{n-1}=M(D_{\max })$ and $\alpha (D)=[\alpha (D)]^{n-1}=\alpha (D_{\max })$, and $\alpha (D_{\max })$ and $M(D_{\max })$ remain constant, at which point, Eq. (16) reduces to:

$$\begin{aligned} P-[ \underbrace{M(D_{\max })k_{ij} \Delta t}_{g_{ij}} P_{,j}]_{,i}= \underbrace{P^{n-1}-M(D_{\max })\alpha (D_{\max }) \overbrace{\left[ \varepsilon _{ii}-\left[ \varepsilon _{ii}\right] ^{n-1}\right] }^{\Delta \varepsilon _{ii}} }_{P^{L}} \end{aligned}$$

(20)

where $\Delta \varepsilon _{ii}$ denotes the variation in volumetric strain. Equation (20) shows that the gradient activity and driving pressure load will not vanish when the damage arrives to its maximum value, which suggests that the fluid non-local diffusive behavior will continue even if the fracture is completely developed. In the case of fluid-driven fracture, the volumetric strain and permeability of porous media monotonically increase in the fracture zone during damage evolution. Therefore, in this model, the driving pressure load $P^{L}$ will continue varying in response to variation in volumetric strain $\Delta \varepsilon _{ii}$ and fluid pressure $P^{n-1}$, and the averaging zone controlled by $g_{ij}$ will increase in the damaged zone which is consistent with [88]. We emphasize that the proposed model is different from the localizing gradient damage model [91, 94] or the phase-field method [26, 69], in which the gradient activity will decrease to a number close to zero or the driving term will vanish when fracture is completely formed, so that the non-local behavior is terminated.

Therefore, based on the derivations in this section, it is confirmed that the fluid pressure described in the continuity equation is in fact a non-local variable, and interestingly. The gradient activity tensor of fluid pressure depends on material point variables.

4 Unified non-local damage model

The majority of damage mechanics models describing material failure assume that the damage variable is a function of strain or stress type invariants. In hydraulic fracture, the process of material failure is the result of a high fluid pressure that leads to a localized fracture front [54, 95, 133]. Thus, for modeling hydraulic fracture, another way that defines the damage evolution is through fluid pressure at a material point.

However, once the onset of damage is reached, the characterization of the damage dependence on fluid pressure becomes a non-trivial task. The relationship between damage and fluid pressure can be established via an intermediate variable. For example, hydraulic fracture experiments can be monitored by computerized tomography (CT) scanning technique [47, 52, 53], or acoustic emission (AE) method [21, 31, 59]. Thus, the fluid pressure can be related to some CT or AE quantity for which relationships with damage have been previously established [34, 82, 122]. Hence, the damage evolution law can be indirectly defined based on hydraulic fracture experiments. Alternatively, the relationship between damage and fluid pressure can be defined on the basis of the relationship between damage and permeability [68, 89, 127] and the relationship between permeability and fluid pressure [22, 118].

Moreover, thanks to the analogy between non-local damage and the fluid pressure as established in Sect. 3, fluid pressure-dependent damage evolution allows us to reach a non-local damage behavior without additional computational effort. That is, the pressure-dependent damage is readily regularized leading to efficient mesh-independent hydraulic fracture model.

In this section, we propose a novel damage evolution law that is a function of the fluid pressure, for which a nonlinear anisotropic permeability is employed to describe the permeability evolution. Finally, we discuss the gradient activity and characteristic length scale in the proposed model.

4.1 Fluid pressure-dependent damage

Fracture in porous media occurs when sufficient mechanical stress is applied to the solid skeleton to begin local dislocations which leads to micro-void nucleation and expansion into macroscale damage. In CDM phenomenological idealizations [57], evolving damage is represented as growing porosity. Applying any diffuse fracture (CDM or phase-field) to porous media requires underlying assumptions to distinguish between the intrinsic porosity of the porous media, and the gained porosity vs. damage evolution as mechanical loading is applied. Some studies have attempted to establish distinguished porosity and damage evolution functions based on thermodynamic derivations, micromechanical assumptions, and experimental data [39, 125]. In cases where fluid flow in porous media is of primary interest, such as the subject case of modeling fluid-driven fracture, the interplay between permeability, porosity, damage, and pressure becomes even a more complex task for phenomenological modeling. This has been an active subject of research, and several studies have investigated: a)pore pressure-fracture dependency [2, 92], b) permeability dependency on pressure, stress, porosity, and damage [51, 84], c) and other aspects of the dependencies of these four variables [66, 135, 136]. Based on these studies, it is possible to establish a range of pore pressure in which the material can transform from a fully intact state to a fully damaged state.

In this study, a logistic function is used to describe the damage evolution law, in which the relationship between damage D and fluid pressure P is given by:

$$\begin{aligned} D(P)=D_{\max }\dfrac{1}{1+e^{-a_{1}(P-a_{2})}} \end{aligned}$$

(21)

where $D_{\max } = 1 - \eta$ with $\eta$ is a small value that allows for a smoother convergence. $a_{1}$ and $a_{2}$ are constants. The characterization, verification, and validation of this relationship require additional research efforts which should be ideally focused on specific material responses. Figure 3 shows the role of the two parameters in Eq. (21) on the damage evolution. The variable $a_{1}$ controls the increase rate of damage. The variable $a_{2}$ controls the onset of damage, and $D(P)=0.5D_{\max }$ in case of fluid pressure $P=a_{2}$. Thus, the $a_{1}$ and $a_{2}$ parameters can be referred to as damage growth rate parameter and onset of damage parameter, respectively, and they can be calibrated from experimental data. Since fluid pressure P can increase or decrease during the hydraulic fracture, the Karush–Kuhn–Tucker condition [83, 103] $D=\max \left\{ D^{n}, D^{n-1}\right\}$ is applied to implement an irreversible damage growth. When fluid pressure decreases, the irreversible condition will lead to a monotonic increase in damage as presented by a 1D column model in Sect. 6.1.

Fig. 3

Plots of damage evolution with fluid pressure. a $a_{2}=50$ and $D_{\max }=0.99$. b $a_{1}=0.5$ and $D_{\max }=0.99$

4.2 Nonlinear anisotropic permeability

In this paper, we employ Darcy’s law to describe the behavior of fluid flow in the entire poroelastic domain. In order to distinguish between fluid flow in the fracture and the intact poroelastic region surrounding the fracture, [80] proposed an anisotropic stress-dependent permeability function which evolves with the direction of the principal stress in a non-local transport-damage model. [128] proposed an anisotropic permeability evolution law which depends on an equivalent strain and direction of principal strain in phase-field method. Similarly, in this study, a nonlinear anisotropic permeability is employed to describe permeability evolution in the bulk. This definition can present the different permeability evolution mechanisms following the directions of damage propagation. The $k_{xx}$ and $k_{yy}$ in Eq. (9) are considered to evolve as a function of an equivalent strain measure, and the anisotropic evolution behavior is controlled by the direction of the principal strain in tension. Hence, $k_{xx}$ and $k_{yy}$ are defined as:

$$\begin{aligned} \begin{aligned}&k_{xx}=k_{0}+\left( k(\varepsilon ^{eq})-k_{0}\right) \cos \varphi \\&k_{yy}=k_{0}+\left( k(\varepsilon ^{eq})-k_{0}\right) \sin \varphi \end{aligned} \end{aligned}$$

(22)

where $\varepsilon ^{eq}$ is the equivalent strain measure described by Eq. (24). $k(\varepsilon ^{eq})$ is a scalar material permeability, which evolves nonlinearly with equivalent strain measure $\varepsilon ^{eq}$. $\varphi$ is the angle corresponding to the direction of the principal strain, which is given by $\varphi =\dfrac{1}{2}\arctan \left( \frac{\varepsilon _{xy}}{ \varepsilon _{xx}-\varepsilon _{yy}} \right)$ in a 2D framework used herein. $k_{0}$ is the initial permeability defined as $k_{0}=k^{^{\prime }}/\gamma$, where $k^{^{\prime }}$ and $\gamma$ are solid hydraulic conductivity and dynamic viscosity of fluid, respectively.

In this paper, a polynomial function is employed to describe the nonlinear relationship between permeability and equivalent strain measure [67, 100], given by:

$$\begin{aligned} k(\varepsilon ^{eq})=\left[ 1+b_{1} (\varepsilon ^{eq})^{b_{2}}\right] k_{0} \end{aligned}$$

(23)

where $b_{1}$ and $b_{2}$ are material constants. $b_{1}>0$ and $b_{2}> 0$, which ensures that the permeability will increase with the increase in the equivalent strain. This relationship has been used in [19, 77, 79, 80] that be focused on damage mechanics modeling of hydraulic fracturing. $b_{1}$ and $b_{2}$ can be calibrated from experimental data.

In addition, we follow the work in [128] to employ tensile principal strain as the equivalent strain measure, as follows:

$$\begin{aligned} \varepsilon ^{eq}=\left\{ \begin{array}{ll} \varepsilon ^{(1)} &{} \text{ if } \varepsilon ^{(1)} > 0 \\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

(24)

where $\varepsilon ^{(1)}$ is the first principal strain given by:

$$\begin{aligned} \varepsilon ^{(1)}=\frac{{{\varepsilon _{xx}} + {\varepsilon _{yy}}}}{2} + \frac{1}{2}\sqrt{{{\left( {{\varepsilon _{xx}} - {\varepsilon _{yy}}} \right) }^2} + 4\varepsilon _{xy}^2} \end{aligned}$$

(25)

Substituting Eqs. (23) and (22) into Eq. (9) yields the nonlinear anisotropic permeability expressed as:

$$\begin{aligned} k_{ij}=\left[ \begin{array}{cc} k_{xx} &{} 0 \\ 0 &{} k_{yy} \end{array} \right] =k_{0}\left[ \begin{array}{cc} 1+b_{1}(\varepsilon ^{eq})^{b_{2}}\cos \varphi &{} 0 \\ 0 &{} 1+b_{1}(\varepsilon ^{eq})^{b_{2}}\sin \varphi \end{array} \right] \end{aligned}$$

(26)

The tensorial definition of the anisotropic permeability defined in Eq.(26) follows the definitions used in several experimental and numerical studies [1, 77, 80, 90]. The anisotropic permeability evolves from an initial isotropic value of $k_{0}$. This relationship suggests that the permeability is isotropic in the initial state, and evolves to be anisotropic once strain growth initiates. Similar to damage growth, we introduce $k_{xx}=\max \left\{ [k_{xx}]^{n}, [k_{xx}]^{n-1}\right\}$ and $k_{yy}=\max \left\{ [k_{yy}]^{n}, [k_{yy}]^{n-1}\right\}$ in order to avoid permeability oscillations and ease numerical convergence.

4.3 Discussion on the physical length scale

Due to the non-local characteristic of fluid pressure, the proposed damage model is naturally regularized as discussed in Sect. 3. Substituting Eq. (26) into Eq. (17) yields the gradient activity term as follows:

$$\begin{aligned} \begin{aligned} g_{ij}= \underbrace{M_{0}k_{0}\Delta t}_{c_{0}}\underbrace{\left[ \frac{2M_{0}}{M(D)}-\frac{M_{0}}{[M(D)]^{n-1}}\right] ^{-1}}_{s} \underbrace{\left[ \begin{array}{cc} 1+b_{1}(\varepsilon ^{eq})^{b_{2}}\cos \varphi &{} 0 \\ 0 &{} 1+b_{1} (\varepsilon ^{eq})^{b_{2}}\sin \varphi \end{array} \right] }_{m_{ij}} \end{aligned} \end{aligned}$$

(27)

where $c_{0}$ is initial gradient parameter. s is called a scaling factor, which is a dimensionless coefficient with minimum value of 1.0. Furthermore, s increases with damage D (elaborated in Appendix C) and expands the initial gradient parameter. It is dependent on initial, current, and previous Biot’s modulus. $m_{ij}$ is an anisotropic matrix which decides the anisotropy of gradient activity, and the diagonal components of $m_{ij}$ do not decrease due to the introduction of irreversible permeability condition in Sect. 4.2. Also, $m_{ij}$ evolves with equivalent strain measure and the direction of the first principle strain. The gradient activity $g_{ij}$ is expressed as $c_{0}sm_{ij}$ in this paper, which is consistent with the expression of anisotropic gradient activity in [115]. This expression clarifies the constituents and evolution of anisotropic gradient activity in the proposed damage model.

Figure 4 presents the averaging zone generated by the gradient activity $g_{ij}$. The initial gradient parameter $c_{0}$ defines the inner circle (solid line in magenta) which is similar to the isotropic non-local model. The inner circle is enlarged by the scaling factor s to be the circle with red dotted line. Increasing the anisotropic component $m_{ij}$ leads to the elliptical shape (dashed blue line). Clearly, the averaging zone determined by $c_{0}$ is the smallest.

Fig. 4

Graphical representation of the averaging zone due to the gradient activity $g_{ij}$ term. The inner circle (solid line in magenta) represents an isotropic interaction kernel determined by $c_{0}$. The scaling factor s expands the inner circle to a new averaging zone (red dotted line). The anisotropy matrix $m_{ij}$ leads to the ellipse interaction zone (blue dashed line)

The characteristic length scale is often used to present the size of the averaging zone. Following Eq. (27), we present a length scale tensor as follows:

$$\begin{aligned} \begin{aligned} l_{ij}&=\sqrt{2g_{ij}} =\left[ \begin{array}{cc} l_{xx} &{} 0 \\ 0 &{} l_{yy} \end{array} \right] =\sqrt{2\Delta t}\left[ \frac{2}{M(D)}-\frac{1}{[M(D)]^{n-1}}\right] ^{-0.5} \left[ \begin{array}{cc} \left( k_{xx}\right) ^{0.5} &{} 0 \\ 0 &{} \left( k_{yy}\right) ^{0.5} \end{array} \right] \\&= \underbrace{\sqrt{2M_{0}k_{0}\Delta t}}_{l_{ct}}\left[ \frac{2M_{0}}{M(D)}-\frac{M_{0}}{[M(D)]^{n-1}}\right] ^{-0.5} \left[ \begin{array}{cc} \left( 1+b_{1}(\varepsilon ^{eq})^{b_{2}}\cos \varphi \right) ^{0.5} &{} 0 \\ 0 &{} \left( 1+b_{1} (\varepsilon ^{eq})^{b_{2}}\sin \varphi \right) ^{0.5} \end{array} \right] \end{aligned} \end{aligned}$$

(28)

Equation (28) suggests that the length scale tensor $l_{ij}$ is described by an expression that is a function of Biot’s modulus, initial permeability, equivalent strain measure, and direction of principle strain. Additionally, the length scale also depends on pressure rate according to the analysis in Remark 1. Thus, the length scale tensor can be interpreted as a physical length scale tensor that is dependent on physical parameters including the pressure rate. The dependency of a material model on strain rate or pressure rate is a common aspect of many physics-based material models, e.g., [64, 72, 73, 107, 111, 130]. As opposed to models in which the length scale tensor is somehow assumed based on mesostructure properties [3, 10] or strongly imposed as in phase-field method [74, 128], herein, the physical length scale tensor $l_{ij}$ can be directly calculated from experimental data and numerical parameters. It is interesting to note that the concept of a physical length scale was discussed in other multi-physics problems. For examples, [72] presented a physical length scale based on thermal diffusivity for shear bands problems, and [16] presented a physical length scale in the context of dispersive wave propagation in composite materials. In this paper, the physical length scale is an anisotropic tensor, where we obtain its explicit expression based on analytical arguments. Moreover, the diagonal components of the physical length scale tensor $l_{xx}$ and $l_{yy}$ increase with the increase in damage D (see Appendix (C)) and equivalent strain measure $\varepsilon ^{eq}$.

According to Eq. (28), an initial physical length scale is defined as $l_{ct}=\sqrt{2c_{0}}=\sqrt{2M_{0}k_{0}\Delta t}$ which is a scalar and easily obtained from the initial Biot’s modulus, initial permeability, and time step size. The anisotropic physical length scale tensor $l_{ij}$ evolves from an initial physical length scale $l_{ct}$, and increases. Further, the initial time step size is no smaller than time step size in subsequent iteration step in this paper via setting the appropriate numerical parameters (see Sect. 5.3). These indicate that the initial physical length scale $l_{ct}$ controls the size of the smallest averaging zone.

Generally, in order to obtain mesh-independent results, the characteristic length scale should be larger than the element size, $\omega h_{e}$, in which $h_{e}$ is a typical element size and $\omega$ is a constant often taken between 2 and 3 in non-local damage model [9, 79]. Similarly, provided the finite element mesh size $h_{e}< \frac{l_{ct}}{\omega }$ in the proposed model, the damage regularization can be achieved automatically to obtain mesh-independent results because the averaging zone controlled by $l_{ct}$ is the smallest. It indicates the damage regularization in the proposed model eliminates the need for additional equations and degrees of freedom as in gradient damage and phase-field methods. Therefore, the proposed model is computationally more efficient than the other aforementioned methods.

Once the damage D reaches its preset maximum value $D_{\max }$, the current Biot’s modulus $M\left( D_{\max }\right)$ equals to Biot’s modulus from the previous time step which results in that length scale tensor in Eq. (28) reduces to:

$$\begin{aligned} l_{ij}^{m}=\sqrt{2k_{0}\Delta tM\left( D_{\max }\right) } \left[ \begin{array}{cc} \left( 1+b_{1}(\varepsilon ^{eq})^{b_{2}}\cos \varphi \right) ^{0.5} &{} 0 \\ 0 &{} \left( 1+b_{1} (\varepsilon ^{eq})^{b_{2}}\sin \varphi \right) ^{0.5} \end{array} \right] \end{aligned}$$

(29)

It is observed that the components of length scale tensor $l_{ij}^{m}$ continue to increase even if the porous solid is fully damaged due to the increase in equivalent strain measure $\varepsilon ^{eq}$. This property of $l_{ij}^{m}$ is remarkably consistent with the increasing length scale in [88] for isotropic non-local damage model.

In Sect. 6.2, we analyze the evolution of the physical length scale tensor based on the numerical results of 1D fluid-driven failure model. Moreover, the reader is also referred to Sect. 6.3 where the effect of time stepping $\Delta t$ on the results of the proposed model is investigated and Sect. 6.4 in which we estimate if this approach leads to mesh insensitivity.

5 Computational implementation

5.1 Boundary value problem

The governing equations of the proposed unified damage-poroelasticity model can be written as:

$$\begin{aligned}&\left[ C_{ijkl}(D) \varepsilon _{kl}-\alpha (D) \delta _{ij} P\right] _{,j}+b_{i}=0 \end{aligned}$$

(30a)

$$\begin{aligned}&\frac{\partial [1 / M(D)]}{\partial t}P+\frac{\partial P}{\partial t}\frac{1}{M(D)}+\frac{\partial \alpha (D)}{\partial t}\varepsilon _{ii}+\frac{\partial \varepsilon _{ii}}{\partial t}\alpha (D)-\left[ {k_{ij}}P_{,j}\right] _{,i}=0 \end{aligned}$$

(30b)

where the damaged Biot’s Modulus M(D) and coefficient $\alpha (D)$ are obtained according to Eqs. (7b) and (3), respectively. Note that these parameters are implicit functions of fluid pressure P since damage in Eq. (21) evolves with fluid pressure. The anisotropic nonlinear permeability $k_{ij}$ is defined as a function of the equivalent strain measure in Eq. (24) according to Eq. (26). We emphasize that the fluid pressure-dependent damage ensures that the damage regularization can be readily achieved so that no additional equations are needed to regularize the damage. Thus, there are only two governing partial differential equations (PDE), Eqs. (30a) and (30b), in the proposed model. The former describes the momentum balance and the latter fluid mass balance.

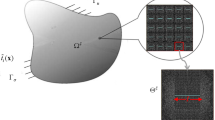
The above nonlinear PDE system is derived in a continuous domain space $\Omega$. The following boundary conditions are required to complete the boundary value problem:

$$\begin{aligned} \begin{aligned}&u_{i}=\bar{u}_{i} \quad \text{ on } \varGamma _{u}^{u}; \quad \quad \sigma _{ij} n_{j} =t_{i}\quad \text{ on } \varGamma ^{t}_{u} \\&P=\bar{P} \quad \text{ on } \varGamma _{P}^{P}; \quad \quad v_{i} n_{i}=q \quad \text{ on } \varGamma _{P}^{q} \\ \end{aligned} \end{aligned}$$

(31)

where $\bar{u}_{i}$, $\bar{P}$, $t_{i}$, and q denote the displacements, pressure, tractions, and normal flow flux boundary conditions, respectively. The boundary conditions $\bar{u}_{i}$, $\bar{P}$, $t_{i}$, and q correspond to the boundary segments $\varGamma _{u}^{u}$, $\varGamma _{P}^{P}$, $\varGamma ^{t}_{u}$, and $\varGamma _{P}^{q}$, respectively, as shown in Fig. 5.

Fig. 5

Schematic illustration of the proposed unified damage-poroelastic boundary value problem. The contours represent damage value in damage zone

In addition, the following set of initial conditions is given to supplement the mathematical model.

$$\begin{aligned} u_{i}|_{t=0} =0; \quad \quad P|_{t=0} =0; \quad \quad D|_{t=0} =0 \quad \text { in } \Omega \end{aligned}$$

(32)

The coupled nonlinear PDE, Eqs. (30a) and (30b), along with the boundary conditions, Eq. (31), and initial conditions, Eq. (32), yield the initial boundary value problem for the primary variables of interest $u_{i}$ and P coupled with damage D.

5.2 Mixed finite element formulation

A monolithic mixed finite element formulation is proposed to solve Eqs. (30)–(32) with the primary unknowns displacement ${\textbf {u}}$ and fluid pressure P. Herein, we define the two trial solution function spaces $S_{\textbf {u}}$ for displacement and $S_{P}$ for the fluid pressure as:

$$\begin{aligned} \begin{aligned}&S_{\textbf {u}}=\left\{ {\textbf {u}}\left( \textbf{x},t\right) |{\textbf {u}}\in H^{1},{\textbf {u}}=\bar{\textbf{u}}\quad \text {on}\quad \varGamma _{u}^{u} \right\} \\&S_{P}=\left\{ P\left( {\textbf {x}},t\right) |P\in H^{1},P=\bar{P}\quad \text {on}\quad \varGamma _{P}^{P} \right\} \end{aligned} \end{aligned}$$

(33)

where $H^{1}$ represents the Sobolev space of functions with degree one. Similarly, the corresponding test function spaces, $V_{{\textbf {u}}}$ and $V_{P}$, are expressed as:

$$\begin{aligned} \begin{aligned}&V_{\textbf {u}}=\left\{ {\textbf {w}}_{u}\left( \textbf{x}\right) |{\textbf {w}}_{u}\in H^{1},{\textbf {w}}_{u}=0\quad \text {on}\quad \varGamma _{u}^{u} \right\} \\&V_{P}=\left\{ w_{P}\left( \textbf{x}\right) |w_{P}\in H^{1},w_{P}=0\quad \text {on}\quad \varGamma _{P}^{P} \right\} \end{aligned} \end{aligned}$$

(34)

where ${\textbf {w}}_{u}$ and $w_{P}$ are the test functions for displacement and fluid pressure fields, respectively. The residual functions corresponding to Eq. (30) can be obtained in their weak forms as shown in Eq. (35).

$$\begin{aligned} \begin{aligned} {\textbf {R}}_{u}({\textbf {u}}, P)&=\int _{\Omega } {\textbf {w}}^{u}\left[ \nabla \cdot \left[ (1-D){\textbf {C}}^{e} \mathbf {\varepsilon }-\alpha (D) {\textbf {I}}_{v} P\right] +{\textbf {b}}\right] d\Omega \\ R_{P}({\textbf {u}}, P)&=\int _{\Omega } w^{P}\left[ \frac{\partial [1 /M(D)]}{\partial t}P+\frac{\partial P}{\partial t}\frac{1}{M(D)} \quad +\frac{\partial \alpha (D)}{\partial t}\varepsilon _{v}+\frac{\partial \varepsilon _{v}}{\partial t}\alpha (D)-\nabla \cdot \left[ {\textbf {k}}\nabla P\right] \right] d \Omega \end{aligned} \end{aligned}$$

(35)

where ${\textbf {C}}^{e}$ denotes the matrix form of the stiffness tensor $C^{e}_{ijkl}$. Matrix ${\textbf {I}}_{v}$ is defined as $\left\{ 1, \ 1, \ 0\right\} ^{T}$. $\mathbf {\varepsilon }$, ${\textbf {b}}$, and ${\textbf {k}}$ are the matrix notations of $\varepsilon _{ij}$, $b_{i}$, and $k_{ij}$, respectively. $\nabla \cdot (*)$, $\nabla (*)$, and $\varepsilon _{v}$ denote the divergence of $(*)$, gradient of $(*)$, and volumetric strain, respectively. The weak forms are approximated by Galerkin’s method for the ${\textbf {u}}$ and P field variables, defined by:

$$\begin{aligned} \begin{aligned}&{\textbf {u}}={\textbf {N}}_{u}{} {\textbf {u}}^{h},\quad \mathbf {\varepsilon }={\textbf {B}}_{u}{} {\textbf {u}}^{h},\quad {\textbf {w}}_{u}={\textbf {N}}_{u}{} {\textbf {w}}_{u}^{h},\quad \nabla {\textbf {w}}_{u}={\textbf {B}}_{u}{} {\textbf {w}}_{u}^{h}\\&P={\textbf {N}}_{P}{} {\textbf {P}}^{h},\quad \nabla P={\textbf {B}}_{P}{} {\textbf {P}}^{h},\quad w_{P}={\textbf {N}}_{P}{} {\textbf {w}}_{P}^{h},\quad \nabla w_{p}={\textbf {B}}_{P}{} {\textbf {w}}^{h}_{P} \end{aligned} \end{aligned}$$

(36)

where superscript h denotes discretization, i.e., the nodal values of the corresponding variables. ${\textbf {N}}_{u}$ and ${\textbf {N}}_{P}$ are the shape functions for each field. ${\textbf {B}}_{u}$ and ${\textbf {B}}_{P}$ are the shape function derivatives of ${\textbf {N}}_{u}$ and ${\textbf {N}}_{P}$ consistent with the definitions in Eq. (36), respectively.

If the trial functions for displacement and pressure in poroelasticity are of the same order, then the numerical results may be unstable and spurious pressure oscillations are likely to be observed [116, 129]. Thus, it is necessary to select suitable shape functions for the fluid pressure and displacement fields to satisfy the Babuška-Brezzi condition [4, 5, 14].

In this paper, we adopt a mixed element interpolation function (as shown in Fig. 6) in which the displacement shape functions correspond to a quadratic eight-node quadrilateral serendipity element and fluid pressure functions correspond to a continuous bilinear four-node quadrilateral element. A $3 \times 3$ Gauss quadrature rule is employed to integrate element quantities. This selection of shape functions for damaged poroelasticity was also adopted by [17, 79, 80, 99] for which good convergence behavior and stable numerical results were demonstrated.

Fig. 6

The degrees of freedom and Gauss integration points in the $u-P$ mixed finite element scheme

The solution vector ${\textbf {x}}$ and the residual vector ${\textbf {R}}$ are defined as:

$$\begin{aligned} {\textbf {x}}=\left\{ \begin{array}{l} {\textbf {u}} \\ P \end{array} \right\} , \qquad {\textbf {R}}=\left\{ \begin{array}{l} {\textbf {R}}_{u} \\ R_{P} \end{array} \right\} \end{aligned}$$

(37)

In this paper, a Newton–Raphson method is adopted to solve the resulting system of nonlinear equations at every time step, for which the linearized system is given by:

$$\begin{aligned} {\textbf {J}}^{n}\delta {\textbf {x}}^{n}=-{\textbf {R}}^{n} \end{aligned}$$

(38)

where $\delta {\textbf {x}}^{n}$ is the incremental solution vector at each Newton iteration, and ${\textbf {J}}^{n}$ is the Jacobian (tangent stiffness) matrix. A backward Euler scheme is used to evolve the system in time, consequently, the Jacobian matrix ${\textbf {J}}^{n}$ can be written as:

$$\begin{aligned} {\textbf {J}}^{n}=\frac{\partial {\textbf {R}}^{n}}{\partial {\textbf {x}}^{n}}=\left[ \frac{1}{\Delta t}{} {\textbf {C}}+{\textbf {K}}\right] =\left[ \begin{array}{ll} {\textbf {J}}_{uu} &{} {\textbf {J}}_{uP} \\ {\textbf {J}}_{Pu} &{} {\textbf {J}}_{PP} \end{array} \right] \end{aligned}$$

(39)

where ${\textbf {C}}$ and ${\textbf {K}}$ are square matrices that represent the damping and stiffness matrices, respectively. Analytical derivation of the blocks leads to the following consistent Jacobian matrix ${\textbf {J}}^{n}$.

$$\begin{aligned} \begin{aligned}&\begin{aligned} {\textbf {J}}_{uu}=\frac{\partial {\textbf {R}}_{u}}{\partial {\textbf {u}}}= \int _{\Omega }{} {\textbf {B}}_{u}^{T}(1-D){\textbf {C}}^{e}{} {\textbf {B}}_{u}d\Omega \end{aligned}\\&\begin{aligned} {\textbf {J}}_{uP}=\frac{\partial {\textbf {R}}_{u}}{\partial P}= -\int _{\Omega }{} {\textbf {B}}_{u}^{T}\frac{\partial D}{\partial P}{} {\textbf {C}}^{e} \mathbf {\varepsilon } {\textbf {N}}_{P}d\Omega \quad -\int _{\Omega }{} {\textbf {B}}_{u}^{T}\frac{\partial \alpha \left( D\right) }{\partial D}\frac{\partial D}{\partial P}{} {\textbf {I}}_{v}P{\textbf {N}}_{P}d\Omega \,\,\,-\int _{\Omega }{} {\textbf {B}}_{u}^{T}\alpha \left( D\right) {\textbf {I}}_{v}{} {\textbf {N}}_{P}d\Omega \end{aligned}\\&\begin{aligned} {\textbf {J}}_{Pu}=\frac{\partial R_{P}}{\partial {\textbf {u}}}=\frac{1}{\Delta t}\int _{\Omega }{} {\textbf {N}}_{P}^{T}\alpha \left( D\right) {\textbf {B}}_{u,vol}d\Omega \quad \,\,\,+\int _{\Omega }{} {\textbf {N}}_{P}^{T}\frac{\partial \alpha \left( D\right) }{\partial t}{} {\textbf {B}}_{u,vol}d\Omega +\int _{\Omega }{} {\textbf {B}}_{P}^{T}\frac{\partial {\textbf { k}}}{\partial {\textbf {u}} }{} {\textbf {B}}_{P}P^{h}d\Omega \end{aligned}\\&\begin{aligned} {\textbf {J}}_{PP}=\frac{\partial R_{P}}{\partial P}=\; &2\int _{\Omega }{} {\textbf {N}}_{P}^{T}\frac{\partial \left[ 1/M(D)\right] }{\partial t}{} {\textbf {N}}_{P}d\Omega +\frac{1}{\Delta t}\int _{\Omega }{} {\textbf {N}}_{P}^{T}\frac{1}{M(D)}{} {\textbf {N}}_{P}d\Omega +\int _{\Omega }{} {\textbf {N}}_{P}^{T}\frac{\partial \frac{\partial \left[ 1/M(D)\right] }{\partial t}}{\partial P}P{\textbf {N}}_{P}d\Omega \\&+\int _{\Omega }{} {\textbf {N}}_{P}^{T}\frac{\partial \alpha \left( D\right) }{\partial D}\frac{\partial D}{\partial P}\frac{\partial \varepsilon _{v}}{\partial t}{} {\textbf {N}}_{P}d\Omega +\int _{\Omega }{} {\textbf {N}}_{P}^{T}\frac{\partial \frac{\partial \left[ \alpha (D)\right] }{\partial t}}{\partial P}\varepsilon _{v}{} {\textbf {N}}_{P}d\Omega +\int _{\Omega }{} {\textbf {B}}_{P}^{T}{} {\textbf {k}} {\textbf {B}}_{P}d\Omega \end{aligned} \end{aligned} \end{aligned}$$

(40)

where the superscript T indicates matrix transpose. ${\textbf {B}}_{u,vol}$ is the shape function derivative of ${\textbf {N}}_{u}$, which is used to calculate volumetric strain as $\varepsilon _{v}={\textbf {B}}_{u,vol}{} {\textbf {u}}^{h}$. The expressions of the partial derivatives in Eq. (40) are provided in details in Appendix D.

5.3 Solution algorithm

The proposed model is implemented in the FEAP program [109] as a user-defined element to solve the nonlinear PDE system in Eqs. (30), (31), and (32). A psuedo-code outlining the solution algorithm is summarized in Algorithm 1. Material point variables are calculated between steps 4 and 16, and the solution of the equations is obtained in step 14. Once the convergence requirement is met in step 3, the time step for the next time increment is obtained by the FEAP built-in fixed time stepping or adaptive time stepping technique, which is defined by:

$$\begin{aligned} \Delta t =\left\{ \begin{array}{cc} \min {(\Delta t_{\max },10^{\left[ \log {(\Delta t^{n-1})}+0.2\right] })}{} &{} \text {if}\quad I^{n-1}<I_{\min } \\ \max {(\Delta t_{\min },10^{\left[ \log {(\Delta t^{n-1})}-0.2\right] })}{} &{} \text {if}\quad I^{n-1}>I_{\max } \end{array}\right. \end{aligned}$$

(41)

where the operators min and max are used to limit time step size $\Delta t$ to a user-defined target range $\left[ \Delta t_{\min },\Delta t_{\max }\right]$. $\Delta t^{n-1}$ represents the $(n-1)^{th}$ time step size. $I^{n-1}$ denotes the number of Newton–Raphson iterations at the $(n-1)^{th}$ time step. $I_{\min }$ and $I_{\max }$ are the user-defined target minimum and maximum number of iterations for each time step size, respectively.

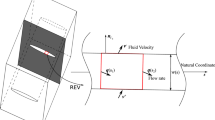
6 Fluid-driven failure of a poroelastic column

A 1D fluid-driven failure model of a poroelastic column is presented in this section, which follows the example that was previously analyzed by [79]. The column is shown in Fig. 7a, and the bottom of the column is fixed ($u_{y}|_{y=0}=0$). A sinusoidal fluid flux $q+\frac{q}{2}\sin (\frac{\pi }{10000}t)$ in Fig. 7b is injected at the bottom of the column in Sect. 6.1 to verify the implementation of irreversible damage and permeability evolution. The applied fluid flux in Sects. 6.2–6.4 is $q=k_{yy}\frac{\partial P}{\partial y}|_{y=0}$. At the top of the column, the fluid pressure is set to zero ($P|_{y=H}=0$). The behavior of the column is considered for the following cases:

• LM: damage-free poroelastic model with variable permeability,

• LD: local damage and variable permeability model that evolves as a function of an equivalent strain variable. The model is defined in Appendix E [79],

• ND: the proposed model, variable permeability, and non-local damage model based on fluid pressure.

Fig. 7

a 1D poroelastic column and its boundaries. b Fluid flux q and $q+\frac{q}{2}\sin (\frac{\pi }{10000}t)$. c Fluid pressure contour of the column with fluid flux of $q+\frac{q}{2}\sin (\frac{\pi }{10000}t)$ at 0.9978$\times 10^{6}$ s. d Fluid pressure contour of the column with fluid flux of $q+\frac{q}{2}\sin (\frac{\pi }{10000}t)$ at 1.0077$\times 10^{6}$ s

The LM and LD models are employed herein as reference models to illustrate the advantage of the ND model proposed in this paper for fluid-driven fracture. The multi-dimensional stress equilibrium in Eq. (5) is modified into Eq. (42) to model the 1D problem with the absence of body forces. The fluid pressure term is multiplied by $\delta _{yy}$ so that the fluid pressure is only added to the stress in y-direction. That is

$$\begin{aligned} \left[ C_{i j k l}(D) \varepsilon _{k l}-\alpha (D) \delta _{ij} P\delta _{yy} \right] _{,j}=0 \end{aligned}$$

(42)

In this example, the value of Poisson’s ratio is set to zero in order to neglect transverse effects. Additionally, the maximum allowable damage $D_{max}$ is limited to 0.75. The complete set of model parameters is listed in Table 1. A fixed time step is taken in this simulation, and the values of time steps considered will be detailed in the following subsections. The allowable maximum number of nonlinear iterations is 20.

Table 1 Material parameters for Sect. 6

6.1 Irreversible damage evolution

In order to illustrate the irreversibility condition of damage growth and the effectiveness of permeability in the ND model, the sinusoidal fluid flux $q+\frac{q}{2}\sin (\frac{\pi }{10000}t)$ in Fig. 7b is applied to investigate the evolution of damage and permeability. Figures 7c, d shows the fluid pressure contour of the 1D column at 0.9978$\times 10^{6}$ s and 1.0077$\times 10^{6}$ s, and the temporal evolution of fluid pressure, damage, and permeability are presented in Fig. 8. Clearly, the fluid pressure is oscillatory and both the damage and permeability have a staircase rise. These observations confirm the irreversible condition for damage growth and permeability prescribed in the solution algorithm.

Fig. 8

The temporal evolution of results at the bottom of the column with the ND model applied a sinusoidal fluid flux. a Fluid pressure. b Damage. c Permeability. The plots illustrate that the irreversible condition for damage growth and permeability is effective in ND model

6.2 Physical length scale $l_{yy}$ for 1D porous media

Based on the 1D poroelastic column idealization in Fig. 7a, the physical length scale $l_{yy}$ is given by Eq. (43) as a special 1D simplification of Eq. (28).

$$\begin{aligned} l_{yy}=\left[ \frac{2}{M(D)}-\frac{1}{[M(D)]^{n-1}}\right] ^{-0.5}\sqrt{2\Delta t k_{0}\left[ 1+b_{1} (\varepsilon _{y})^{b_{2}}\right] } \end{aligned}$$

(43)

Following Eq. (28), one can observe that $l_{yy}$ increases with the increase in damage and strain $\varepsilon _{y}$. In order to better understand the physical length scale evolution, the column is modeled with the element size of 1.00 m and time step size of 1.0 s. The initial permeability $k_{0}=1.0\times 10^{-7}$, $5.0\times 10^{-8}$, and $1.0\times 10^{-8}$ m$^{2}$/Pa s, and the corresponding initial physical length scale $l_{ct}$ of the ND model is 7.07, 5.00, and 2.24 m, respectively. The physical length scale $l_{yy}$ evolution over the column at different time instances is plotted in Figs. 9, 10, and 11. The results show that the physical length scale is varying in space with increasing values closer to the bottom of the column. This is likely related to the larger strain $\varepsilon _{y}$. Also, the physical length scale $l_{yy}$ tends to converge to a fixed value at steady state, which is caused by the convergence of Biot’s Modulus M(D) and the strain $\varepsilon _{y}$ to a constant value at steady state, as shown in Figs. 9a, 10a, and 11a.

Fig. 9

The evolution of strain $\varepsilon _{y}$ physical length scale over column at different time instances of the ND model with different permeability. Initial permeability $k_{0} = 1.0\times 10^{-7}$ m$^{2}$/Pa s. The closer to column bottom and the larger value of physical length scale

Fig. 10

The evolution of strain $\varepsilon _{y}$ physical length scale over column at different time instances of the ND model with different permeability. Initial permeability $k_{0} = 5.0\times 10^{-8}$ m$^{2}$/Pa s. The closer to column bottom and the larger value of physical length scale

Fig. 11

The evolution of strain $\varepsilon _{y}$ physical length scale over column at different time instances of the ND model with different permeability. Initial permeability $k_{0} = 1.0\times 10^{-8}$ m$^{2}$/Pa s. The closer to column bottom and the larger value of physical length scale

The physical length scale arises from the diffusive fluid behavior in the proposed model, and it is not enforced by a special gradient/phase-field approach. It can go to a larger value due to the increase in equivalent strain and damage, and tends to converge to a fixed value according to Figs. 9, 10, and 11. The larger value of physical length scale does not have an adverse effect in the proposed model as shown later in Sect. 6.4 for mesh independence.

6.3 Effect of time step size $\Delta t$ in the ND model

In the proposed model, the physical length scale $l_{ij}$ formula involves the size of the time step as given in Eq. (17). In this example, we investigate the effect of time step size $\Delta t$ on the ND model response in the idealized 1D scenario. The different time step sizes considered are 0.01, 0.1, 1.0, 10.0, and 100.0 s. An element size of 1.00 m is chosen, and the initial permeability is taken to be $k_{0}=1.0\times 10^{-7}$ m$^{2}$/Pa s.

The temporal and spatial evolution of fluid pressure P, damage D, strain in y direction $\varepsilon _{y}$, and permeability $k_{yy}$ are presented in Figs. 12 and 13, respectively. Figures 12 and 13 show that all the results are the same even if time step sizes are different. Therefore, in the range of $\Delta t$ and the set of material parameters presented in Table 1, the proposed model is insensitive to the time step size $\Delta t$. This is attributed to the large resulting values of the physical length scale in this range of $\Delta t$, which guarantees the non-local response of damage evolution and hence leading to time step independent results.

Fig. 12

The temporal evolution of results at the bottom of the column with the ND model with different time step sizes. a Fluid pressure. b Damage. c Strain. d Permeability. The plots show that the ND model is insensitive to time step size within the range of parameters that we use in the example

Fig. 13

Fluid pressure P, damage D, strain $\varepsilon _{y}$, and permeability $k_{yy}$ over the 1D column at steady state of ND model with different time step sizes when initial permeability $k_{0}= 1.0\times 10^{-7}$ m$^{2}$/Pa s. a Fluid pressure. b Damage. c Strain. d Permeability. The plots show that time step size $\Delta t$ has no effect on the spatial distributions of results

Next, since the lower initial permeability leads to a smaller physical length scale, we need to investigate the effect of the time step size under the lower initial permeability. To this end, the initial permeability is considered to be $5.0\times 10^{-8}$ and $1.0\times 10^{-8}$ m$^{2}$/Pa s in the following set of results. The temporal and spatial evolution of fluid pressure P and strain $\varepsilon _{y}$ are plotted in Figs. 14 and 15, respectively. Similar to the previous results, herein one can also observe the insensitive feature to time step size. In conclusion, the proposed model is insensitive to time step size under the range of investigated parameters in this section.

Fig. 14

Fluid pressure P and strain $\varepsilon _{y}$ evolution with time of ND model with different time step sizes when initial permeability is $5.0\times 10^{-8}$ and $1.0\times 10^{-8}$ m$^{2}$/Pa s, respectively. The plots show that time step size $\Delta t$ has no effect on the temporal evolution of results

Fig. 15

Fluid pressure P and strain $\varepsilon _{y}$ over the 1D column at steady state of ND model with different time step sizes when initial permeability is $5.0\times 10^{-8}$ m$^{2}$/Pa s and $1.0\times 10^{-8}$ m$^{2}$/Pa s, respectively. The plots show that there is no effect of time step size $\Delta t$ on the spacial distributions of results

6.4 Mesh independence

Four different element sizes ($h_{e}$ =3.3, 2.0, 1.0, and 0.5 m) are considered to investigate mesh independence. The column is modeled using the LM, LD, and ND models with fixed time step size of 1.0 s. The initial permeability is chosen to be $k_{0}$ is $1.0\times 10^{-7}$ m$^{2}$/Pa s, which results in an initial physical length scale $l_{ct}$ of 7.07 m.

The spatial distributions of fluid pressure P, damage D, strain in y direction $\varepsilon _{y}$, and permeability $k_{yy}$ at steady state are presented in Figs. 16, 17, and 18, respectively. The fluid pressure P of the LD model in Fig. 16b is regarded as mesh dependent, while the values of fluid pressure of the ND model with different element sizes in Fig. 16c are mesh independent. Figure 17 shows that the evolution of the strain tensor $\varepsilon _{y}$ in the ND model are smooth while there is a discontinuity in the slope of the strain $\varepsilon _{y}$ of the LD model in the transition between the no-damage to damage zones. The same observations are reported for the spatial distributions of the permeability field in Fig. 18. These observations show that the proposed ND model exhibits the non-local behavior characteristics of damage and leads to a diffusive and gradual transition between the intact and highly damaged regions of the domain. This is a property of non-local damage model that has been documented in earlier studies [17, 79]. In other words, the strain $\varepsilon _{y}$ and permeability $k_{yy}$ of the LD model tend toward a narrower and stronger jump in the middle of the column if the smaller meshed size is applied. Thus, it is considered that the LD model is mesh-dependent at steady state for all element sizes in this section. As for the ND model, it is observed that the localization zone tends to converge as the element size decreases leading to mesh-independent results.

Fig. 16

Fluid pressure P over column at steady state of damage-free poroelastic model (LM), local damage model (LD), and the proposed model (ND)

Fig. 17

Stain $\varepsilon _{y}$ over column at steady state of damage-free poroelastic model (LM), local damage model (LD), and the proposed model (ND)

Fig. 18

Permeability $k_{yy}$ over column at steady state of damage-free poroelastic model (LM), local damage model (LD), and the proposed model (ND)

In order to have a better understanding of mesh independence characteristic of the proposed model, the temporal evolution of key variables is further examined. The evolution of fluid pressure, damage, strain, and permeability at point $y=0$ are presented in Figs. 19, 20, 21, and 22. The fluid pressure in Fig. 19b, strain in Fig. 21b, and permeability in Fig. 22b of the LD model experience spurious oscillations, and the irreversible damage growth condition is introduced into the LD model, so the damage experiences staircase rise in Fig. 20a. The mesh dependence of the LD model is observed clearly during the growth of fluid pressure and at the steady state. These suggest that the LD model results suffer from significant mesh dependence which is also confirmed in [79]. On the other hand, the temporal evolution profiles of fluid pressure in ND model are in good agreement with the numerical [97, 127] and experimental [56, 134] results for fluid-driven fracture problems. The results of the ND model evolve smoothly and converge to similar steady state values. The error of the ND model results continues to reduce with the decrease in element mesh size, which illustrates the mesh independence of the proposed model.

Fig. 19

Fluid pressure P evolution of damage-free poroelastic model (LM), local damage model (LD), and the proposed model (ND). Results are presented at the point $y=0$

Fig. 20

Damage D evolution of local damage model (LD) and the proposed model (ND). Results are presented at the point $y=0$

Fig. 21

Stain $\varepsilon _{z}$ evolution of damage-free poroelastic model (LM), local damage model (LD), and the proposed model (ND). Results are presented at the point $y=0$

Fig. 22

Permeability $k_{yy}$ evolution of damage-free poroelastic model (LM), local damage model (LD), and the proposed model (ND). Results are presented at the point $y=0$

The results in Figs. 16, 17, 18, 19, 20, 21, and 22 suggest that the proposed model can be regarded as mesh independent under the investigated element sizes in which the maximum element size is 3.3 m, and the initial physical length scale $l_\textrm{ct}$ is 7.07 m. This confirms that for an element size that is sufficiently smaller than the length scale, mesh independence will be achieved as postulated in Sect. 4.

In summary, according to the results of 1D fluid-driven failure example, it is confirmed that the proposed unified model is not sensitive to time step size $\Delta t$ in the range of investigated parameters, and the initial physical length scale $l_{ct}$ can be used to advise element size for mesh-independent results.

7 Hydraulic fracture in porous media

In this section, the proposed model is used to analyze hydraulic fracture in a poroelastic domain with dimensions $2L \times 2L$ as shown in Fig. 23a. The center of the domain is injected with fluid to drive the fracture. Considering the symmetry in Fig. 23a, the right half part of the domain is represented in the simulation with symmetric boundary conditions as shown in Fig. 23b. A zero-flux condition ($\frac{\partial P}{\partial n}=0$) and a horizontal translation constraint ($u_{x}=0$) are applied to the left edge. The external boundaries (right, top and bottom edges) of the domain are constrained, which leads to $u_x=u_y=0$ and $P=0$. The middle of the left edge is subjected to an injection fluid with flux of $q =1.0\times 10^{-3}$ $\mathrm m^{3} s^{-1}$. The width L of the poroelastic domain is considered to be 100 m.

In this simulation, the initial time step size $\Delta t$ is 0.1 s, and the minimum and maximum number of iterations for each time step are $I_{\min }=20$ and $I_{\max }=50$, respectively. The parameters chosen for this problem are listed in Table 2. The set of material and numerical parameters results in the initial physical length scale $l_{ct}$ is 3.1 m according to the analysis in Sect. 4.3. The finite element mesh size is 1.0 m which is smaller than one-third of the initial physical length scale, and it is expected to lead to mesh-independent results according to the analysis in section 6.4.

Fig. 23

Schematic diagram of the hydraulic fracture domain. a The domain is $2L \times 2L$ and the center of the domain is injected with fluid. b The symmetric model for modeling hydraulic fracture. The left side of the domain is regarded as symmetry boundary ($u_{x}=0$ and $\frac{\partial P}{\partial n}=0$) and other boundaries are mechanically restrained ($u_{x}=u_{y} = 0$) and permeable ($P = 0$). The middle of the left edge is subjected to the injection fluid with the flux of q

Table 2 Material parameters for Sect. 7

In order to investigate the effect of time step size on results in this model, the target minimum time step size is $\Delta t_{\min }=$0.1 s, and the target maximum time step size $\Delta t_{\max }$ is considered as 5.0 and 10.0 s, respectively. The variations in time step size $\Delta t$, inlet pressure, and damage evolution at the injection point over the period of the simulation are plotted in Fig. 24. Although the time step sizes for $\Delta t_{\max }=$ 5.0 and 10.0 s are different, the inlet pressure and damage evolution with time are the same. It suggests that the hydraulic fracture behavior is insensitive to time step size in the range of investigated parameters. In addition, the inlet pressure increases up to approximately 1.22 MPa which can be referred to as the breakdown pressure [43], and it coincides with the onset of damage. Then, the inlet pressure decreases to a slightly lower value and approximately remains the value in an open crack ($D=0.99$). This behavior of inlet pressure is consistent with the previous study on fluid-driven fracture [127].

Fig. 24

The evolution of time step size $\Delta t$, inlet pressure, and damage at the injection point. a time step size $\Delta t$ with total time. b inlet pressure evolution. c damage evolution at the injection point. The plots suggest that the hydraulic fracture behavior is insensitive to time step size in the range of investigated parameters

In order to have a closer look at the behavior of hydraulic fracture, the evolution of damage D, permeability $k_{xx}$, and fluid pressure P in the poroelastic domain contours are demonstrated by the contours in Fig. 25. The lengths of high damage band, permeability $k_{xx}$ zone, and high fluid pressure zone continue to grow with injection time. The damage contours show that the damage propagates along the expected horizontal direction. The damage evolution provides a major direction for strain evolution which drives the anisotropic growth of the permeability component $k_{xx}$. This leads to the result that fluid preferentially flows along the direction of damage evolution. The fluid pressure contours show that the high pressure is confined inside and around the fracture which is presented by high damage band, and the phenomenon is also reported in previous literature [77, 80, 124].

Fig. 25

Damage D, permeability $k_{xx}$ ($\text {m}^{2}\text {Pa}^{-1}\text {s}^{-1}$), and fluid pressure P (MPa) contours of 2D hydraulic fracture model

There exists a difference between the widths of high pressure band and high damage band, which is attributed to the $k_{yy}$ permeability component. The presence and evolution of $k_{yy}$ lead to fluid leakage from the sides of fracture which is observed in the fluid pressure results. The leakage may cause additional damage around the fracture [32] which is observed in the damage contours. This leakage is commonly referred to as leak-off [29], and it has been observed in many field cases and experiments [106, 119, 126]. Other formulations introduce an artificial flux to the hydraulic fracture boundary in order to account for the leak-off phenomena, e.g., phase-field [75], LEFM [117], cohesive element method [15, 62], and XFEM [45]. The numerical implementation of these models encounters inherent difficulties in capturing the fluid leakage caused by the material properties evolution of the fracture process zone. This is attributed to the fact that the tangential flow within the crack is calculated based on a Poiseuille flow equation which assumes an impermeable channel flow, this requires the artificial addition of an empirical leak-off effect that does not represent the nonlinear evolution of damage and permeability in the fracture process zone. In addition, the artificial leak-off in these models does not contribute to damage growth because the damage or fracture grows only in the defined zone while the external domain remains elastic or poroelastic. The leakage phenomenon and the corresponding damage are readily captured in the proposed model due to the continuous definition of the fluid constitutive law inside and outside the fracture, which is achieved by the nonlinear anisotropic permeability relationship.

In order to better understand the fluid flow, the profiles of damage D, permeability component $k_{xx}$, and fluid velocity in x-direction $v_{x}$ are plotted along a line that is 10 m away from the flux input point. Snapshots of these plots at different time steps (192, 609, 998, and 1771s) are shown in Fig. 26. The plots show that damage, permeability, and velocity increase with injection time, which illustrates the growth of the fluid-driven fracture. The location of high permeability component $k_{xx}$ and high fluid velocity $v_{x}$ correspond to the location of high damage, which demonstrates that the fracture is hydraulically driven. The high velocity fluid flow inside the fluid-driven fracture is a key feature for the simulation of hydraulic fracture process [123]. This key feature can be captured using the proposed model, and it is demonstrated by that the fluid velocity inside the fracture is several orders of magnitudes higher than the fluid velocity in the intact porous media.

Fig. 26

The profiles of damage D, permeability component $k_{xx}$, and fluid velocity $v_{x}$ along a line 10 m away from the left edge of the domain in Fig. 23

Moreover, the effect of initial permeability on the evolution of hydraulic fracture is investigated. We plot the profiles of damage D, permeability component $k_{xx}$, and fluid velocity in x-direction $v_{x}$ along a line 10 m away from the left edge of the domain in Fig. 23 at 789 s when the values of initial permeability are 0.5$k_{0}$, $k_{0}$, and $1.5k_{0}$, respectively. The plots suggest that using higher values of initial permeability leads to wider hydraulic fracture, and elevates permeability and fluid velocity in the fracture driven by fluid.

Fig. 27

The profiles of damage D, permeability component $k_{xx}$, and fluid velocity $v_{x}$ along a line 10 m away from the left edge of the domain in Fig. 23 of the model with different permeability at 609 s

In order to analyze fracture propagation in damage theory, the fracture length $L_{F}$ and average fracture width $W_{F}$ were introduced in [77, 78]. $L_{F}$ is defined as the distance from the injection point to the farthest point experiencing damage ($D=0$) along the fracture center line. $W_{F}$ is approximated as the value of the damage zone volume divided by the fracture length, i.e., $W_{F}=\frac{\int _{V}D\text {d}V}{L_{F}}$. The temporal evolution of the fracture length and average fracture width are presented in Fig. 28. During the initial injection stage, there is no damage in the poroelastic media, and the fracture has not formed. During the subsequent stage, the fracture propagates quickly once it is initiated, and then fracture propagation is relatively slow. The evolution of fracture average width leads to the formation of the wide fluid pool observed in Fig. 25. The propagation behavior of fluid-driven fracture in the proposed model agrees qualitatively with results found in previous studies [15, 30, 45, 48, 50, 70, 77, 96, 105].

Fig. 28

The temporal evolution of the fracture length and average fracture width. a The temporal evolution of fracture length. b The temporal evolution of average fracture width

Therefore, the results in Figs. 25, 26, 27, and 28 confirm that the proposed model has an excellent ability to naturally capture the features of hydraulic fracture.

8 Summary and conclusions

In this paper, we prove that the fluid flow continuity equation in poroelastic damage theory is analogous to the implicit gradient formula, in which the fluid pressure is a non-local variable. Hence, a unified non-local damage model based on fluid pressure damage dependence for hydraulic fracture in poroelastic media is proposed. In the proposed model, the damage variable is driven by the inherently non-local fluid pressure, and the damage evolution law is described by a logistic growth curve. The permeability of the porous media evolves as a function of equivalent strain measure, and an anisotropic evolution is induced by decomposition into principal strains.

In the proposed model, the damage regularization can be achieved automatically without the need for an additional regularization equation or a spatial integral non-local operator. The physical length scale is analytically derived as a function of material point variable, and it can be estimated directly from model parameters. The physical length scale is transient which evolves with damage and an equivalent strain measure.

A monolithic, mixed finite element method is proposed to solve the coupled deformation and fluid flow system with a displacement-pressure ($u-p$) element. Newton’s method is used to solve the nonlinear system at every time step, in which a consistent Jacobian matrix and residual vector are derived analytically. A backward Euler scheme is employed to advance the system in time.

The proposed model is used to analyze the fluid-driven failure of a poroelastic column. The results are shown to be insensitive to the time step size in the range of the physical parameters used. While the damage, strain, and permeability are dependent on mesh size in the local damage model, all results are mesh independent and respond smoothly in the proposed unified model. In addition, hydraulic fracture in a 2D poroelastic domain is investigated using the proposed model, which confirmed that the proposed model has an excellent capacity to capture the features of hydraulic fracture in porous media.

In conclusion, the proposed model is found to be robust, mesh insensitive, and elegant, and in particular, computationally more efficient than implicit gradient damage or phase-field methods, which require additional degrees of freedom to model the damage.

Appendices

Derivation for discrete form of fluid flow continuity equation

The terms including time derivative in Eq. (14) are interpolated with values of current time step n and previous time step $n-1$, which are shown as Eq. (A.1).

$$\begin{aligned} \begin{aligned}&\frac{\partial [1 / M(D)]}{\partial t}=\frac{\frac{1}{[M(D)]^{n}}-\frac{1}{[M(D)]^{n-1}}}{\Delta t} \\&\frac{\partial \alpha (D)}{\partial t}=\frac{[\alpha (D)]^{n}-[\alpha (D)]^{n-1}}{\Delta t} \\&\frac{\partial \varepsilon _{ii}}{\partial t}=\frac{\left[ \varepsilon _{ii}\right] ^{n}-\left[ \varepsilon _{ii}\right] ^{n-1}}{\Delta t} \\&\frac{\partial P}{\partial t}=\frac{P^{n}-P^{n-1}}{\Delta t} \end{aligned} \end{aligned}$$

(A.1)

The subscripts n are removed from all functions in Eq. (A.1) for convenience, then substituting Eq. (A.1) into Eq. (14) and multiplying $\Delta t$ yield Eq. (A.2).

$$\begin{aligned} \begin{aligned}&\left( {\frac{1}{{M(D)}} - \frac{1}{{{{[M(D)]}^{n - 1}}}}} \right) P + \left( {P - {P^{n - 1}}} \right) \frac{1}{{M(D)}} - \Delta t{\left[ {{k_{ij}}{P_{,j}}} \right] _{,i}} \\&= \left( {{[\alpha (D)]}^{n - 1}}-{\alpha (D)} \right) {\varepsilon _{ii}} - \left( {{\varepsilon _{ii}} - {{\left[ {{\varepsilon _{ii}}} \right] }^{n - 1}}} \right) \alpha (D) \end{aligned} \end{aligned}$$

(A.2)

Equation (A.2) can be arranged into Eq. (15).

Proof of $\frac{2}{M(D)} > \frac{1}{[M(D)]^{n-1}}$

The partial derivative of damage Biot’s modulus M(D) with respect to damage D is written by:

$$\begin{aligned} \frac{\partial M(D)}{\partial D}=\frac{K\alpha (D)-2\frac{\partial \alpha (D)}{\partial D}\left( K^{u}-K_{D}\right) }{\alpha (D)^{3}} =\frac{K\alpha (D)K_{s}+2K\left( K^{u}-K_{D}\right) }{K_{s}\alpha (D)^{3}} \end{aligned}$$

(B.1)

Obviously, $\frac{\partial M(D)}{\partial D}$ is more than zero. It suggests that the damage Biot’s modulus M(D) increases with the increase in damage D. Thus, $M(D)\geqslant M(D)|_{D=0}= \frac{K^{u}-K}{\left( K_{s}-K\right) ^{2}} {K_{s}}^{2}>0$.

Given that the solid grain bulk modulus $K_{s}$ is much larger than the drained bulk modulus K, $K_{s} \gg K$, for most geomaterials, and the undrained bulk modulus $K^{u}$ can be defined as Eq. (B.2) [20, 28].

$$\begin{aligned} K^{u}=K\left( 1+\frac{K_{f}}{\phi K}\right) \end{aligned}$$

(B.2)

where $\phi$ is material porosity which is less than 1. $K_{f}$ is the bulk modulus of fluid. $K_{f}$ is larger than $\phi K$ for general materials filled fully by water or other difficultly compressible fluid, so $K^{u} > 2K$.

On the other hand, the damaged Biot’s modulus M(D) increases with damage. $M(D)=K^{u}$ when $D=1$, and $M(D)=\frac{K^{u}-K}{\left( K_{s}-K\right) ^{2}} {K_{s}}^{2}$ when $D=0$. Thus, we can obtain the upper and lower limit value of M(D) which are presented by:

$$\begin{aligned}&M(D) \leqslant M(D)|_{D=1}=K^{u} \end{aligned}$$

(B.3a)

$$\begin{aligned}&\frac{K^{u}-K}{\left( K_{s}-K\right) ^{2}} {K_{s}}^{2}=M(D)|_{D=0} \leqslant [M(D)]^{n-1} \leqslant M(D) \end{aligned}$$

(B.3b)

Because $0< K^{u}-K<\frac{K^{u}-K}{\left( K_{s}-K\right) ^{2}} {K_{s}}^{2}$, Eq. (B.4) is obtained.

$$\begin{aligned} 0<K^{u}-K<[M(D)]^{n-1} \leqslant M(D) \end{aligned}$$

(B.4)

According to Eqs. (B.3a) and (B.4), we can get $2[M(D)]^{n-1} > 2(K^{u}-K)$ and $K^{u} \geqslant M(D)$. Given that $2(K^{u}-K) > K^{u}$, $2[M(D)]^{n-1}> M(D)$. Therefore, inequality formula $\frac{2}{M(D)} > \frac{1}{[M(D)]^{n-1}}$ is obtained.

s and $l_{ij}$ increase with damage

The partial derivative of s with respect to damage D is expressed as:

$$\begin{aligned} \frac{\partial s}{\partial D}=\left[ \frac{2}{M(D)}-\frac{1}{[M(D)]^{n-1}}\right] ^{-2} \frac{2}{[M(D)]^{2}}\frac{\partial M(D)}{\partial D}\geqslant 0 \end{aligned}$$

(C.1)

Equation (C.1) indicates that s increases as damage D increases.

The partial derivative of physical length scale $l_{ij}$ with respect to damage D is written by:

$$\begin{aligned} \frac{\partial l_{ij}}{\partial D}=\left[ \frac{2}{M(D)}-\frac{1}{[M(D)]_{n-1}}\right] ^{-\dfrac{3}{2}} \frac{\sqrt{2k_{0}\Delta t}}{[M(D)]^{2}}\frac{\partial M(D)}{\partial D} \left[ \begin{array}{cc} \left( 1+b_{1}(\varepsilon ^{eq})^{b_{2}}\cos \varphi \right) ^{\dfrac{1}{2}} &{} 0 \\ 0 &{} \left( 1+b_{1} (\varepsilon ^{eq})^{b_{2}}\sin \varphi \right) ^{\dfrac{1}{2}} \end{array} \right] \end{aligned}$$

(C.2)

Equation (C.2) suggests that diagonal components of the partial derivative of characteristic length scale with respect to damage are more than zero. Thus, the diagonal components of characteristic length scale $l_{ij}$ increase with the increase in damage.

Derivatives used in the Jacobian matrix derivation

Details of partial derivatives in the Jacobian matrix for 2D plane strain framework:

$$\begin{aligned}&\frac{\partial k_{ij} }{\partial \textbf{u}} =\left[ \begin{array}{cc} \frac{\partial k_{xx} }{\partial \mathbf {\varepsilon }}\frac{\partial \mathbf {\varepsilon }}{\partial \textbf{u}} &{} 0\\ 0 &{} \frac{\partial k_{yy} }{\partial \mathbf {\varepsilon }}\frac{\partial \mathbf {\varepsilon }}{\partial \textbf{u}} \end{array} \right] \end{aligned}$$

(D.1)

$$\begin{aligned}&\frac{\partial \alpha \left( D\right) }{\partial D}=-\frac{K}{K_{s}} \end{aligned}$$

(D.2)

$$\begin{aligned}&\frac{\partial \left[ 1/M(D)\right] }{\partial D}=2\alpha \left( D\right) \frac{\partial \alpha \left( D\right) }{\partial D}\left[ K^{u}-K(D)\right] ^{-1}-\alpha \left( D\right) ^{2}K\left[ K^{u}-K(D)\right] ^{-2} \end{aligned}$$

(D.3)

$$\begin{aligned}&\frac{\partial \alpha \left( D\right) }{\partial t}=\frac{\partial \alpha \left( D\right) }{\partial D}\frac{\partial D}{\partial P}\frac{\partial P}{\partial t} \end{aligned}$$

(D.4)

$$\begin{aligned}&\frac{\partial \left[ 1/M(D)\right] }{\partial t}=\frac{\partial \left[ 1/M(D)\right] }{\partial D}\frac{\partial D}{\partial P}\frac{\partial P}{\partial t} \end{aligned}$$

(D.5)

$$\begin{aligned}&\frac{\partial D}{\partial P}=D_{\max }a_{1}e^{-a_{1}\left( P-a_{2}\right) }\left[ 1+e^{-a_{1}\left( P-a_{2}\right) }\right] ^{-2} \end{aligned}$$

(D.6)

$$\begin{aligned}&\frac{\partial ^{2}D}{\partial P^{2}}=D_{\max }\left[ 2\left[ a_{1}e^{-a_{1}\left( P-a_{2}\right) }\right] ^{2}-a_{1}^{2}e^{-a_{1}\left( P-a_{2}\right) }\left[ 1+e^{-a_{1}\left( P-a_{2}\right) }\right] \right] \left[ 1+e^{-a_{1}\left( P-a_{2}\right) }\right] ^{-3} \end{aligned}$$

(D.7)

$$\begin{aligned}&\frac{\partial \frac{\partial \left[ \alpha (D)\right] }{\partial t}}{\partial P} = \underbrace{\frac{\partial ^{2} \alpha (D)}{\partial D\partial P}}_{\text {0}}\frac{\partial D}{\partial P}\frac{\partial P}{\partial t}+\frac{\partial \alpha (D)}{\partial D}\frac{\partial ^{2}D}{\partial P^{2}}\frac{\partial P}{\partial t}+\frac{1}{\Delta t}\frac{\partial \alpha (D)}{\partial D}\frac{\partial D}{\partial P}{} {\textbf {N}}^{P} \nonumber \\&=\frac{\partial \alpha (D)}{\partial D}\frac{\partial ^{2}D}{\partial P^{2}}\frac{\partial P}{\partial t}+\frac{1}{\Delta t}\frac{\partial \alpha (D)}{\partial D}\frac{\partial D}{\partial P}{} {\textbf {N}}^{P} \end{aligned}$$

(D.8)

$$\begin{aligned}&\frac{\partial \frac{\partial \left[ 1/M(D)\right] }{\partial t}}{\partial P}=\frac{\partial ^{2}\left[ 1/M(D)\right] }{\partial D\partial P}\frac{\partial D}{\partial P}\frac{\partial P}{\partial t}+\frac{\partial \left[ 1/M(D)\right] }{\partial D}\frac{\partial ^{2}D}{\partial P^{2}}\frac{\partial P}{\partial t}+\frac{1}{\Delta t}\frac{\partial \left[ 1/M(D)\right] )}{\partial D}\frac{\partial D}{\partial P}{} {\textbf {N}}^{P} \end{aligned}$$

(D.9)

$$\begin{aligned}&\frac{\partial ^{2}\left[ 1/M(D)\right] }{\partial D\partial P}=&2\left[ \frac{\partial \alpha \left( D\right) }{\partial D}\right] ^{2}\frac{\partial D}{\partial P}\left[ K^{u}-K(D)\right] ^{-1}-4\alpha \left( D\right) \frac{\partial \alpha \left( D\right) }{\partial D}K\left[ K^{u}-K(D)\right] ^{-2}\nonumber \\&+2\alpha \left( D\right) ^{2}K^{2}\left[ K^{u}-K(D)\right] ^{-3} \end{aligned}$$

(D.10)

The derivative matrix of shape functions of mixed finite element method for 2D framework:

$$\begin{aligned}&\begin{aligned}&{\textbf {B}}^{{\textbf {u}}}=\left[ {\textbf {B}}_{1}^{{\textbf {u}}},\ ...,\ {\textbf {B}}_{i}^{{\textbf {u}}},\ ...,\ {\textbf {B}}_{8}^{{\textbf {u}}}\right] ,\qquad {\textbf {B}}_{i}^{{\textbf {u}}}=\left[ \begin{array}{ll} \frac{\partial {\textbf {N}}_{i}^{u}}{\partial x} &{} 0 \\ 0 &{} \frac{\partial {\textbf {N}}_{i}^{u}}{\partial y} \\ \frac{\partial {\textbf {N}}_{i}^{u}}{\partial y} &{} \frac{\partial {\textbf {N}}_{i}^{u}}{\partial x} \end{array} \right] \end{aligned} \end{aligned}$$

(D.11)

$$\begin{aligned}&{\textbf {B}}^{{\textbf {u,vol}}}=\left[ {\textbf {B}}_{1}^{{\textbf {u,vol}}},\ ...,\ {\textbf {B}}_{i}^{{\textbf {u,vol}}},\ ...,\ {\textbf {B}}_{8}^{{\textbf {u,vol}}}\right] ,\qquad {\textbf {B}}_{i}^{{\textbf {u,vol}}}=\left[ \frac{\partial {\textbf {N}}_{i}^{u}}{\partial x},\ \frac{\partial {\textbf {N}}_{i}^{u}}{\partial y}\right] \end{aligned}$$

(D.12)

$$\begin{aligned}&{\textbf {B}}^{P}=\left[ \begin{array}{llll} \frac{\partial {\textbf {N}}_{1}^{P}}{\partial x} &{} \frac{\partial {\textbf {N}}_{2}^{P}}{\partial x} &{} \frac{\partial {\textbf {N}}_{3}^{P}}{\partial x} &{} \frac{\partial {\textbf {N}}_{4}^{P}}{\partial x} \\ \frac{\partial {\textbf {N}}_{1}^{P}}{\partial y} &{} \frac{\partial {\textbf {N}}_{2}^{P}}{\partial y} &{} \frac{\partial {\textbf {N}}_{3}^{P}}{\partial y} &{} \frac{\partial {\textbf {N}}_{4}^{P}}{\partial y} \end{array} \right] \end{aligned}$$

(D.13)

Local damage model based on equivalent strain

In local damage model based on equivalent strain, the permeability evolution law and equivalent strain measure are, respectively, described as Eqs. (26) and (24), which are the same to non-local damage model based on the fluid pressure. The bilinear damage law is taken to describe damage evolution, which is written by:

$$\begin{aligned} D\left( \varepsilon ^{eq}\right) =\left\{ \begin{array}{ll} 0 &{} \text {if }\varepsilon ^{eq}\leqslant \varepsilon _{i}^{eq} \\ \frac{\varepsilon _{f}^{eq}\left( \varepsilon ^{eq}-\varepsilon _{i}^{eq}\right) }{\varepsilon ^{eq}\left( \varepsilon _{f}^{eq}-\varepsilon _{i}^{eq}\right) } &{} \text {if }\varepsilon _{i}^{eq}\leqslant \varepsilon ^{eq}\leqslant \varepsilon _{j}^{eq} \\ D_{\max } &{} \text {if }\varepsilon _{j}^{eq}\leqslant \varepsilon ^{eq} \end{array} \right. \end{aligned}$$

(E.1)

where $\varepsilon _{i}^{eq}$ and $\varepsilon _{f}^{eq}$ denote the damage initiation and failure strains, respectively. They can be obtained from experiment. $\varepsilon _{j}^{eq}$ is a value of equivalent strain which can be given by:

$$\begin{aligned} \varepsilon _{j}^{eq}=-\frac{\varepsilon _{f}^{eq}\varepsilon _{i}^{eq}}{\varepsilon _{f}^{eq}-\varepsilon _{i}^{eq}}\left( D_{\max }-\frac{\varepsilon _{f}^{eq}}{\varepsilon _{f}^{eq}-\varepsilon _{i}^{eq}}\right) ^{-1} \end{aligned}$$

(E.2)