1 Introduction

The modelling and numerical simulation of large deformation problem have aroused much interest in geotechnical engineering for many decades. Since large deformation phenomena occur frequently in various geotechnical practices (i.e., the deep penetration of CPT, installation of spudcan foundations into seabed soils and run-out of landslides). In modelling such large deformation problems, application of the traditional finite element method is often inappropriate, because it suffers from excessive mesh distortion and results in errors, inaccuracy, and premature termination of the calculation.

To solve the large deformation problems, various numerical approaches have been proposed over the past decades. For example, the framework of Arbitrary Lagrangian–Eulerian (ALE) is the most common approach to deal with large deformation in geotechnical engineering [45]. Three ALE-based approaches that are widely used in geotechnical engineering are the so-called interpolation technique by small strain (RITSS) proposed by Hu and Randolph [14, 15, 35], the efficient ALE approach (EALE) developed by Nazem [25, 26] and the Abaqus built-in Coupled Eulerian–Lagrangian (CEL) method [1, 32]. Another class of approach commonly utilized is the so-called particle-based method, in which the mesh distortion is avoided by utilizing a set of particles to replace the mesh that used in ALE-based approaches. Various particle-based methods for large deformation analysis have been proposed and applied in geotechnical engineering, such as smoothed-particle hydrodynamics (SPH) [2, 5– 7, 30], material point method (MPM) [9–11, 38, 40], and particle finite element method (PFEM) [27].

The particle finite element method (PFEM) was originally developed by Oñate et al. [27] and has been widely used in geotechnical analyses. In PFEM, a set of nodal points or particles are used to represent the continuum body, and the computational mesh is built by connecting these points using the Delaunay triangulation. A large deformation analysis is divided into standard Lagrangian increments with periodic remeshing. After each remeshing, the state variables are remapped from the old mesh to the new mesh. This remeshing and mapping process prevents mesh distortion and allows modelling very large deformations. Therefore, PFEM approach has distinct advantages as it inherits both the flexibility of mesh-free particle methods on the arbitrary changes in geometry, and the solid mathematical foundation of the FEM. Moreover, the independence of the remeshing and mapping from the standard Lagrangian incremental analysis allows PFEM to be implemented easily based on the existing standard finite element program.

The PFEM was originally developed to solve problems of fluid mechanics [27] as well as fluid–structure interaction problems [17, 28, 29]. It has recently been developed for solving large deformation problems in geotechnical engineering, in which applications such as granular flow problems [8, 53, 54], slope stability problems and landslides [34, 54–57, 59, 60], structure–soil interaction [3, 4, 22, 23], and coupled analysis of a fluid-saturated porous media [22, 24, 50]. Very recently, the so-called smoothed-particle finite element method (SPFEM) [51, 52, 58, 61] was developed, in which a node integration technique is incorporated into the PFEM framework. The SPFEM allows storing and calculating the state variables at the node/particles, and thus, the frequent state variable transfer between old Gauss points and new Gauss points associated with the remeshing procedure is avoided. In addition, linear elements can be used directly without suffering from volumetric locking.

To date, the ALE-based approaches (i.e., RITSS and CEL) were mainly implemented in commercial FEM software Abaqus, which make those methods be widely used in geotechnical engineering [42–45]. However, there is yet no PFEM software package commercially available for analyzing practical problems in geotechnical engineering. The available PFEM implementations were mainly based on in-house codes, which require users to handle a large amount of coding work. This is now considered as the major obstacle that hinders a wide application of the PFEM approach. Thus, it is worth implementing PFEM in an existing commercial software package. In this paper, the Abaqus software is chosen as a platform to implement PFEM approach, due to its popularity in geotechnical engineering. It is known that Abaqus is a well-recognized commercial software that been widely used in various industries, including the field of geotechnical engineering. Furthermore, complicated soil behaviours (e.g. [18, 19, 44, 46–48) can also be considered in Abaqus through user subroutines. The combination of the PFEM and the commercial software Abaqus is obviously an appropriate alternative approach to tackle the large deformation problems. The implementation of PFEM at the platform provided by the Abaqus is able to make the use of PFEM more convenient, owing to the powerful pre- and post-processing functions, as well as the special modules built in the software. Moreover, it will then help promote the applicability and popularity of PFEM in the fields of computational mechanics and geotechnical engineering.

This paper presents a PFEM implementation in the commercial FEM package Abaqus for large deformation problem analysis in geotechnical engineering. This simple implementation allows using the built-in Abaqus capabilities for solving standard incremental FEM analysis and the mapping state variables. Moreover, this simple implementation has additional advantages as it can make use of the constitutive models, structure–soil interaction analysis algorithm and pre- and post-processing features in Abaqus. Therefore, it is especially helpful for the inexperienced user, as problems involving large deformation can be solved without the use of a large amount of user defined code. The following sections are organized as: First, fundamentals of PFEM solving procedures are given. Then, details of the PFEM implementation in Abaqus are given. Finally, four numerical examples are presented to benchmark and validate the proposed Abaqus-PFEM implementation against the published results.

2 Fundamentals of PFEM approach

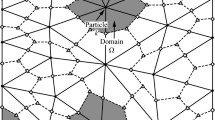
2.1 Basic idea of PFEM

In PFEM, a Lagrangian description of the motion is employed, thus, the governing equation of a continuum body is solved in an updated Lagrangian (UL) manner. A cloud of Lagrangian particles is used to discretize the continuum body, in which the information such as mass and velocity, as well as other state variables such as stress and strain, are stored. Then, a computational mesh is generated by connecting the cloud of Lagrangian particles using the Delaunay triangulation. After that, the so-called alpha shape method is utilized to identify the boundaries of the computational domain. The computational mesh is then used to solve the governing equations via a standard FEM solving procedure. The particle positions are updated after each computational step, and thus the motion of the continuum body is tracked during the solution, which is a standard updated Lagrangian approach. Excessive mesh distortion is avoided by frequently rebuilding the mesh, and the state variables are remapped from the old mesh to the new mesh. Now, considering a typical load incremental step with mesh rebuilding, the primary procedures of PFEM are as follows (see also Fig. 1):

Fig. 1
figure 1

Sequence of steps in the PFEM approach

Full size image
  1. 1.

    Discretize a continuum body into a cloud of particles.

  2. 2.

    On the basis of a cloud of particles, build the triangular finite element mesh based on Delaunay triangulation, and identify the boundaries of the computational domain via alpha-shape method.

  3. 3.

    Mapping the state variables from the old mesh to the new mesh.

  4. 4.

    Solve the discrete governing equations via a standard finite element approach to obtain the node displacements.

  5. 5.

    Update the positions of particles to form a new cloud of particles.

  6. 6.

    Go back to step 2 and repeat until problem-dependent stop condition is satisfied.

A flowchart of the PFEM solving procedure is given in Fig. 2. In PFEM, the computation steps 2–5 are repeated until the problem-dependent stop condition is achieved, obviously step 4 is the most computational time consuming step among steps 2–5, and thus, the computation efficiency of a PFEM implementation can be improved significantly by conducting step 4 with the commercial FEM package Abaqus by enabling the parallel computing features of the solver. Moreover, from the above computational cycles of PFEM, we notice that step 4 is a standard FEM analysis process, and it actually can be conducted with any FEM package. Therefore, the PFEM approach can be easily implemented into Abaqus software package, which requires limited amount of coding work and contributes to high computation efficiency.

Fig. 2
figure 2

General flow of the PFEM procedure

Full size image

2.2 Governing equations

In PFEM, the motion of a continuum is modelled in an updated Lagrangian fashion, in order to solve the governing equation; all quantities are transferred to the current configuration. The stress equilibrium equation of the boundary value problem for a simple body Ω with boundary S in the current configuration can be expressed by

$$\begin{aligned} & \nabla \cdot {\varvec{\upsigma}} + {\mathbf{b}} = {\mathbf{0}} \\ & {\mathbf{u}}({\mathbf{X}},t_{0} ) = {\mathbf{u}}_{0} \quad {\text{in }}^{0} \varOmega_{{\mathbf{u}}} \, \\ & {\mathbf{u}}({\mathbf{X}},t) = {\bar{\mathbf{u}}}\quad \,\,\,{\text{on }}^{t} S_{{\mathbf{u}}} \, \\ & {\mathbf{n}} \cdot {\varvec{\upsigma}}^{t} { = }{\mathbf{t}}\quad \quad \,\,\,\,\,{\text{on }}^{t} S_{{\mathbf{t}}} , \\ \end{aligned}$$
(1)

where σ represents the total Cauchy stress vector and b represents the body force vector, u0 stands for the initial displacement, \({\bar{\mathbf{u}}} \,\) and t are prescribed displacement tractions on the boundary of the domain, and n is the outward normal to the boundary. Thus, the virtual work equation for a deformable body of volume \({}^{t}\varOmega\) written in the current configuration may be expressed as:

$$\int\limits_{{{}^{t}\varOmega }} {\delta^{t + \Delta t} {\mathbf{ E}}\text{:}{}^{t + \Delta t}{\mathbf{S}}{\text{d}}V} = {}^{t + \Delta t}{\mathbf{R}}$$
(2)

where \({\mathbf{ E}} = - \frac{1}{2}(\nabla {\mathbf{u}} + (\nabla {\mathbf{u}})^{\text{T}} + (\nabla {\mathbf{u}})^{\text{T}} \cdot \nabla {\mathbf{u}})\) is the Green–Lagrange strain tensor, S is the second Piola–Kirchhoff (PK2) stress tensor, and δu are the virtual displacements. R is the external forces in the current deformed configuration at time t, and is given by

$${}^{t + \Delta t}{\mathbf{R}} = \int\limits_{{{}^{t}\varOmega }} {\delta {\mathbf{u}} \cdot^{t + \Delta t} {\mathbf{b}}{\text{d}}V} + \int\limits_{{{}^{t}S}} {\delta {\mathbf{u}} \cdot {}^{t + \Delta t}{\mathbf{t}}{\text{d}}S^{t} }$$
(3)

where b, t and S are the body force, prescribed traction vectors and surface area, respectively. Since the above mentioned large strain updated Lagrangian formulation has been implemented in Abaqus originally, the details of the finite element discretization and solution of the governing equations are not introduced. Moreover, the discretized stress equilibrium equation is solved directly in Abaqus using an implicit iterative solution scheme.

3 Implementation framework in Abaqus

The PFEM approach is integrated into the Abaqus FE software mainly due to its powerful pre- and post-processing tools and computational efficiency. In addition, another advantage of using Abaqus FE package is that the Abaqus’s built-in mesh-to-mesh solution mapping (MSM) algorithm provides comparable accuracy and efficiency as compared with user-coded solution mapping algorithm [42, 43]. The Abaqus-based PFEM is implemented using the Abaqus built-in script language Python. The whole process is controlled by a single master Python script, which repeatedly calls Python subroutines and Abaqus solver to accomplish the analysis automatically without the intervention of the user. A flow diagram is given in Fig. 3 to describe the detailed flow of the general algorithm and the data exchanges between Python script and Abaqus FE package.

Fig. 3
figure 3

Implementation of PFEM in ABAQUS

Full size image

A detailed explanation of the implementation is given: an initial mesh is generated with proper boundary conditions and soil geometry for the first incremental step of analysis. The model input file (Abaqus usually uses a file extension “.inp” to read model input information) is submitted to standard Abaqus solver with large deformation considered.

Upon the completion of the first standard analysis step, the Abaqus output database (odb) file (Abaqus usually uses a file extension “odb” to store model solution for all nodes (i.e., displacements, pore pressure, reaction forces) and element (i.e., stress and strain) variables) are read by a Python subroutine. The structure of an “odb” file generally includes two blocks: model data and results data. Model data contain the information of the mesh, i.e., the coordination of nodes, the element connectivity and the type of elements. On the other hand, the results data comprise all of the results of finite element computation (e.g., stress, strain, displacements, etc.). Only the node coordinates and element connectivity needed to be read/extract from the “odb” file.

The deformed mesh is extracted from the “odb” file in the form of node/particle coordinates/positions using the built-in Python function in Abaqus. Then, a new mesh is generated using Delaunay triangulation technique based on a cloud of deformed particles. In the current implementation, the Delaunay triangulation is done by adopting a function called scipy.spatial.Delaunay in the scipy library (other computational geometry libraries (i.e., CGAL [41], Triangle [36]) in Python are available for Delaunay triangulation as well). In order to improve the quality of the newly constructed mesh, additional mesh-adaptive or mesh-smoothing techniques have been employed [33], such as addition of particles based on distance between particles and optimization of particle positions using Laplacian smoothing algorithm. More specifically, if the distance of two nodes is smaller than a characteristic length in the domain boundary, one of the nodes is moved to the domain; on the contrary, if the distance of two nodes is larger than a characteristic length in the domain boundary or radius of the element circumcircle in the domain a new particle is added. Moreover, the external boundary of the computational domain is identified via an alpha-shape method. The general flowchart of mesh refinement procedure is given in Fig. 4. Again, the above mentioned new techniques in mesh generation, mesh quality improvement and external boundary identification are accomplished by the corresponding Python subroutines.

Fig. 4
figure 4

General flow of the mesh refinement procedure

Full size image

After the new mesh is generated, the boundary conditions need to be recovered. For the loading boundaries, because the node/particle positions are continuously updated during the computation process, it is easy to trace the location of these boundaries in every step. Thus, the boundary conditions can be easily recovered. For contact boundaries, besides the location of the boundary, the contact normal stress also needs to be recovered after each remeshing. For this purpose, a dummy step defined in each step (but not the first step) before the real loads is applied [49]. In the dummy step, no external loads or prescribed displacement are applied, the only purpose of this step is to let Abaqus iterates and re-balance the contact stress based on the field stress mapped. For other boundaries, their geometry is kept unchanged during the computational process, so they can be recovered directly. Next, a model is set up with the newly generated mesh containing the boundary conditions and soil geometry for the next incremental step of analysis, and the model is written into an Abaqus input file using another Python subroutine.

In order to proceed with the analysis, the state variables (such as stress and strain) stored in the Abaqus output database file (“odb” file) are needed to be recovered from old Gauss points to new Gauss points. In this paper, the Abaqus built-in solution mapping or state variable transferring method MSM is used, the Abaqus automatically maps the necessary information from the old database file to the new analysis by writing the keyword of MSM into the Abaqus input file. The mesh-to-mesh solution mapping (MSM) is a built-in Abaqus function that used to map field variables from mesh to mesh. It can be applied between meshes with different topologies. The field variables are extrapolated from the Gauss points to the node points in the old mesh and then interpolate to the Gauss points in the new mesh. To use the MSM, the users need to insert the keyword “map solution” into the Abaqus input file and specify the old “odb” file name where the state variables are mapped from. However, there is no need to specify which variables to map, and the Abaqus automatically maps the necessary variables for successful continuation of the analysis [13]. The MSM method has been proven to possess acceptable accuracy and numerical stability [42, 43], and more importantly, it greatly reduces the coding work for implementing solution mapping algorithms. Note that the MSM is not yet applicable for dynamic problems in Abaqus, and to further extend the Abaqus-PFEM implementation for dynamic problems, in-house code for state variables remapping is needed.

Finally, a new incremental analysis is executed by submitting the new input file to Abaqus Solver, and the incremental analysis steps are repeated until the desired stop condition is achieved. By organizing the above mentioned Python subroutines as a single Abaqus Python script, the computation cycles of PFEM analysis is automated. The PFEM analysis is executed by submitting the single master Python script to Abaqus-FEM package.

4 Numerical examples

In this section, four numerical examples are presented to first verify and further illustrate the accuracy and robustness of the proposed approach. For all examples in this section, only quasi-static single phase is considered and the governing equations are solved using the implicit solver in Abaqus. The first example studies the large deformation bending of an elastic cantilever beam; the second one involves the penetration of rigid footing into a soft Tresca soil. Afterward, two more deep penetration problems involving soil–structure interactions, namely the T-Bar and pipeline–soil interaction are discussed to demonstrate the efficacy of proposed Abaqus-PFEM approach.

4.1 Bending of an elastic cantilever beam

The first demonstration problem is the elastic cantilever bending beam subjected to a point load at the vertical midpoint of its free end. As shown in Fig. 5, the beam is 10 m long and 1 m deep, and the following linear elastic parameters are assumed: Young’s modulus of 12 MPa and a Poisson’s ratio of 0.2. The left hand end of the beam is fully fixed; a point load of 100 kN is applied at the vertical midpoint of the right hand end over 50 equal load steps. Figure 6 shows the normalized horizontal and vertical displacements at the loading point versus the load force. The load–displacement curves predicted by the Abaqus-PFEM approach agree well with the results obtained by both the analytical and traditional FEM solutions. The Abaqus-PFEM analysis is carried out using six-node triangular elements. The FEM analysis is carried out using eight-node quadratic elements with reduced integration, and the domain is discretized into 1000 elements with mesh size of 0.1 m to ensure the accuracy of the results. The analytical solution of the elastic beam bending problem considering large deformation is elaborated in the thesis of Molstad [21]. In addition, the final configuration and the vertical stress σy distribution of both Abaqus-PFEM and FEM are given in Fig. 7; again, good agreement in vertical stress distribution can be seen between Abaqus-PFEM and FEM, indicating the accuracy of the proposed approach.

Fig. 5
figure 5

Geometry and boundary conditions of the elastic cantilever beam problem

Full size image
Fig. 6
figure 6

Normalized load versus horizontal and vertical displacements

Full size image
Fig. 7
figure 7

Deformed configurations and the vertical stress σy distribution

Full size image

In order to further study the performances of the proposed approach, the influence of the load steps per analysis as well as mesh size is investigated. Figure 8 shows the curves of load versus displacement for 20 steps, 50 steps and 100 steps per analysis. The load–displacement curves of all cases are identical to the analytical solution, which indicates that the mapping error introduced during remeshing after each step is limited and the results converge for different number of steps per analysis. The load–displacement curves of h = 0.25 m, h = 0.125 m and h = 0.1 m (h is the characteristic length of the element) are shown in Fig. 9. The relations of load versus displacement for h = 0.25 m, h = 0.125 m and h = 0.1 m show good agreement with the analytical solution and there is very little difference in the numerical results of the three mesh sizes. The response of load versus displacement converges on h = 0.125 m, and further decreasing the characteristic element length to h = 0.1 m would not improve the numerical results.

Fig. 8
figure 8

Normalized load versus horizontal and vertical displacements with different number of steps per analysis

Full size image
Fig. 9
figure 9

Normalized load versus horizontal and vertical displacements with different mesh sizes

Full size image

4.2 Penetration of rigid footing

The second numerical example considers the penetration of a rigid footing into weightless homogeneous clay in plane-strain condition. The clay is modeled as an elastic-perfectly plastic Tresca material with undrained shear strength of cu and Young’s modulus E. The footing is gradually pushed into the clay to a depth equal to the footing width by prescribing an incremental vertical displacement. This benchmark example has been considered by PFEM, ALE and MPM and the analytical solutions of both small and large deformation are also available. Thus, it can be used to further validate the proposed Abaqus-PFEM approach. The following Tresca material parameters are considered: undrained shear strength cu = 1 kPa, Young’s modulus is E = 100 kPa and Poisson’s ratio is υ = 0.495.

Due to symmetry, only the right half of the problem geometry is considered, with the boundary conditions properly applied along the symmetry plane. The simulated rigid footing B is assumed to be 2 m wide, the computation domain has a depth of 5B and a width of 5B, with the bottom boundary fixed in both vertical and horizontal direction, and the lateral boundary is fixed only in horizontal direction, as illustrated in Fig. 10. A prescribed vertical displacement of 2 m is applied on the footing over 200 load steps, with an incremental displacement of 0.01 m per step. To maintain reasonable computation efficiency, a 3-node linear plane-strain triangle element with hybrid formulation of pressure in Abaqus is used for the analysis. The CPU time consumed for simulating this problem (200 incremental steps) is 39 min on a Laptop with Intel Core i7-4700MQ 2.4 GHz processor using four cores.

Fig. 10
figure 10

Rigid footing on Tresca soil

Full size image

The normalized vertical resistance force (q/cu) versus penetration depth (z/B) obtained from the proposed approach is shown in Fig. 11. This result is comparable to results obtained from the analytical solutions (da Silva et al. [37], Prandtl [31], and Meyerhof [20]) as well as from numerical solutions such as PFEM (which used an in-house developed program) [23], MPM [39], ALE [16] and SPFEM [51, 58]. It is shown that all results lie between the analytical solution obtained by Prandtl [31] (in small strain assumptions: \(\left( {\pi + 2} \right)c_{\text{u}} = 5.14c_{\text{u}}\)) and by Meyerhof [20] (in large strain assumptions: \(\left( {2\pi + 2} \right)c_{\text{u}} = 8.28c_{\text{u}}\)). In general, the resistance force verse penetration depth response of the proposed Abaqus-PFEM implementation agrees well with the solutions of PFEM, MPM and ALE, and is higher than that obtained by the SPFEM. Note that the small oscillations in the curve (black line) of resistance force versus penetration depth are related to the errors caused by remeshing which changes the element topology relations and also by the mapping of state variables. It is apparent that these oscillations are relatively small and acceptable; the oscillations can be reduced by fining the particle density near the footing region.

Fig. 11
figure 11

Normalized resistance force versus penetration depth

Full size image

The contours of incremental displacement magnitude, accumulated plastic strain invariant \(\varepsilon_{q}^{\text{p}} = \sqrt {\frac{2}{3}{\varvec{\upvarepsilon}}^{\text{p}} \text{:}{\varvec{\upvarepsilon}}^{\text{p}} }\), vertical stress σy, and the shear stress τxy, are given in Fig. 12. The failure extends up to the free surface according to the classical bearing capacity rules, as depicted by the contours of incremental displacement magnitude shown in Fig. 12a. A wedge-shaped zone develops below the loaded area, which is defined by the failure surface starting from the edges of the footing. Below this wedge-shaped zone is a transition zone with plastic strain, as shown in Fig. 12b. In addition, Fig. 12c shows that a zone of high vertical stress (up to − 7.0 kPa) occurs right below the footing and it decrease with depth. It is seen from Fig. 12d that there is a shear stress bulb with a maximum value of 1.0 kPa (which exactly equals to the cohesion of the soil) below the footing corner, and it spreads downwards to the bottom of the domain. Moreover, another wing-shaped shear stress bulb develops next to corner of the footing and spreads upwards into the soil, and the shear stress in this region shows a minimum value of − 1.0 kPa. Moreover, the mesh evolution during the large deformation penetration process is given in Fig. 13.

Fig. 12
figure 12

Contour of incremental displacements (a), accumulated plastic strain invariant (b), vertical stress (c) and shear stress (d) at a penetration depth of 1B

Full size image
Fig. 13
figure 13

Mesh evolutions during the large deformation process

Full size image

4.3 Penetration of T-bar

This numerical example considers a deep embedded T-bar penetrating into elastic-perfectly plastic and weightless Tresca clay. This case has been studied by researchers with various large deformation numerical methods, and thus, it is considered here to further validate the accuracy and efficiency of the proposed approach. The following Tresca material parameters are considered: undrained shear strength cu = 5 kPa, Young’s modulus is E = 2.5 MPa and Poisson’s ratio is υ = 0.49. As shown in Fig. 14, the width and depth of computation domain are taken as 10 times and 20 times the T-bar diameter, respectively. The T-bar penetrometer has a diameter D = 0.04 m and it is initially embedded at a depth of 9D. A plane-strain condition is assumed and only half of the T-bar and soil domain is considered due to symmetry. The bottom boundary is fixed in both vertical and horizontal direction while the lateral boundary is fixed only in horizontal direction, as illustrated in Fig. 14. To guarantee the full contact between the T-bar and the soil during the whole penetration process, a uniform vertical pressure of 100 kPa is applied at the top surface. The penetration is executed in 200 displacement intervals, and each interval is equal to 0.0002 m (D/200). Two roughness conditions are considered for the interface between T-bar and soil: frictionless and rough contact. A 3-node linear plane-strain triangle element with hybrid formulation of pressure in Abaqus is used for the analysis. The structural (T-bar) is simplified as a rigid body, and the standard surface to surface contact method with hard core contact model and penalty algorithm in Abaqus is used. The CPU time consumed is 0.5 h for frictionless contact and 1.0 h for rough contact on a Laptop with Intel Core i7-4700MQ 2.4 GHz processor using four cores.

Fig. 14
figure 14

T-bar penetration on Tresca soil

Full size image

The normalized limit resistance force gives a resistance factor of T-bar, Nc= q/Dcu, which is the vertical stress (exerted by the T-bar) divided by the projected area. The calculated relationship between the normalized resistance force and the normalized penetration depth is shown in Fig. 15. The results of the proposed Abaqus-PFEM approach are compared with the upper bound solutions [12]. It is seen that the Abaqus-PFEM results are slightly larger than those given by the upper bound solution. Moreover, the T-bar ultimate resistance factor, Nc, is 9.78 and 12.22 for frictionless and rough contact, respectively. The upper bound solution method gives the ultimate resistance factor as 9.22 and 11.94 for frictionless and rough contact. The differences between the Abaqus-PFEM and upper bound solutions are 6.3% and 2.3% for frictionless and rough contact, respectively. In order to compare the results obtained by Abaqus-PFEM with other methods, Fig. 16 presents the results on the same problem, which are obtained by PFEM (which used an in-house developed program) [23], RITSS [42] and the upper bound solutions [12], showing that the result differences among the concerned numerical methods are around 2–6%.

Fig. 15
figure 15

Normalized resistance force versus penetration depth

Full size image
Fig. 16
figure 16

Comparison of T-bar resistance factors of different numerical methods

Full size image

Figure 17 presents the contours of incremental displacement magnitude, accumulated plastic strain invariant, and the shear stress τxy of the frictionless case at a penetration depth of 1D. From Fig. 17a, it is seen that the soil deformation is fully localized around the T-bar, and the incremental displacement profile indicates a rotational flow mechanism, which is consistent with the results of PFEM analysis on the same problem [23]. The accumulated plastic strain profile shown in Fig. 17b further confirms the rotational failure mechanism, since there is a wedge of clay moving together with the T-bar. Figure 17c shows that two wing-shaped shear stress bulbs (with a maximum value equal to the cohesion of the clay) develop next to the T-bar cylinder and spread out upwards and downwards at approximately 45° relative to the horizontal direction, respectively. In addition, another stress bulb with a minimum shear stress of − 5.0 kPa spreads out horizontally.

Fig. 17
figure 17

Contour of incremental displacements (a), accumulated plastic strain invariant (b) and shear stress (c) at a penetration depth of 1D

Full size image

4.4 Pipeline interaction with Tresca soil

To further demonstrate the performance of the proposed method, the fourth numerical example considers the interaction of a rigid weightless pipeline with an elastic-perfectly plastic Tresca soil. Deep-water offshore pipeline is often penetrated into the seabed at a depth of a fraction of its diameter due to wave force and self-weight; on the other hand, large lateral movement of pipeline may be induced by thermal expansion combined with high internal pressure. In this section the vertical penetration and lateral movement of offshore pipelines are simulated using the proposed Abaqus-PFEM approach.

The Tresca material parameters used in this section are as follows: undrained shear strength is cu = 5 kPa, Young’s modulus is E = 1.0 MPa, Poisson’s ratio is υ = 0.49 and soil density is ρ = 1600 kg/m3. The pipeline has a diameter D = 0.04 m and is initially located at the top of surface with a distance of 6D from the left domain boundary, and the computation domain is taken as 15D and 5D in width and depth, respectively. A plane-strain condition is assumed and the bottom boundary is fixed in both vertical and horizontal direction while the lateral boundaries are fixed only in horizontal direction, as illustrated in Fig. 18. The pipeline is first subjected to a vertical penetration of 0.5D, which is followed by a horizontal movement of 2.0D. The analysis is performed through 250 displacement intervals (50 for the vertical penetration and 200 for the subsequent horizontal movement), and each interval is equal to 0.008 m (D/100). The pipeline-soil interface is assumed to be frictionless. The element type and contact setup used are the same as in the Sect. 4.3. The CPU time consumed for simulating this problem (250 incremental steps) is around 8 h on a Laptop with Intel Core i7-4700MQ 2.4 GHz processor using four cores.

Fig. 18
figure 18

Pipeline soil interaction problem

Full size image

The normalized resistance force (q/Dcu) obtained from the Abaqus-PFEM approach is plotted against the vertical and horizontal displacements (Ux/D, Uy/D), as shown in Fig. 19. In the vertical penetration stage, the maximum normalized vertical resistance force reaches around 5.7, while the normalized horizontal resistance force remains zero. In the subsequent horizontal movement stage, the vertical displacement of the pipeline is fixed at 0.5D, and the pipeline is only allowed to move horizontally, which results in a rapid increase in horizontal resistance force and a decrease in vertical resistance force. After that, the horizontal resistance force experiences a mild linear increase and eventually reaches around 3.5 at a final horizontal displacement of 2.0D. On the other hand, the vertical resistance force decreases in an approximately linear manner down to around 2.5 at a final horizontal displacement of 2.0D.

Fig. 19
figure 19

Normalized resistance force versus displacements

Full size image

The contours of incremental plastic strain invariant at various vertical and horizontal displacements are given in Fig. 20. A classical Prandtl-type failure mechanism is observed as illustrated in Fig. 20a. A W-shaped strain localization shear band is observed, and the shear band starts from the bottom of the pipeline and develops in the soil layer before intersecting the free surface. Figure 20b–e shows the soil failure mechanisms at various subsequent movement stages. It can be seen that a shear band starts from the bottom of the pipeline and spreads upwards almost in a straight line to the soil surface. The pipeline pushes the soil to the right side and forms an active berm next to the pipeline, as the pipeline keeps moving horizontally, the volume of the active berm increases. This also explains why the horizontal resistance force increases linearly during the later movement stage in Fig. 19.

Fig. 20
figure 20

Contour of incremental plastic strains invariant at various displacements

Full size image

5 Conclusions

A PFEM program for analyzing geotechnical problems involving large deformation is implemented in the commercial FEM package Abaqus in this study. The presented approach combines the built-in Abaqus capabilities for solving standard incremental FEM analysis and the powerful MSM state variables mapping technique. The Abaqus built-in script language Python is used to implement the whole solution procedure. A single master Python script is developed, which repeatedly calls Python subroutines and Abaqus solver to accomplish the large deformation analysis automatically without the intervention of the user.

The theoretical background of the PFEM approach is briefly introduced first. Then, the detailed implementation of PFEM in Abaqus is given. The proposed approach is first verified through a simple elastic cantilever beam bending problem. Good agreement is found between the Abaqus-PFEM results and the analytical solution. The results obtained by the Abaqus-PFEM approach are convergent in terms of different mesh sizes and computation steps. Additionally, the performance of the proposed Abaqus-PFEM approach is further examined by two numerical examples: penetration of rigid footing and penetration of T-bar. Also, good agreement with published results of other numerical methods has further validated the accuracy and robustness of the proposed approach. Finally, an illustrative numerical example, the pipeline-soil interaction problem, is simulated by the proposed Abaqus-PFEM approach with Tresca soil model. The results show that the proposed Abaqus-PFEM approach can well handle these large deformation problems in geotechnical engineering.

Although only quasi-static single-phase problems are studied in this paper, the proposed approach can be easily extended to other geotechnical applications, including the axisymmetric and three-dimensional problems, the dynamic problems, and hydro-mechanical coupled consolidation problems.