Modelling of tunnelling processes and rock cutting tool wear with the particle finite element method

Abstract

Underground construction involves all sort of challenges in analysis, design, project and execution phases. The dimension of tunnels and their structural requirements are growing, and so safety and security demands do. New engineering tools are needed to perform a safer planning and design. This work presents the advances in the particle finite element method (PFEM) for the modelling and the analysis of tunneling processes including the wear of the cutting tools. The PFEM has its foundation on the Lagrangian description of the motion of a continuum built from a set of particles with known physical properties. The method uses a remeshing process combined with the alpha-shape technique to detect the contacting surfaces and a finite element method for the mechanical computations. A contact procedure has been developed for the PFEM which is combined with a constitutive model for predicting the excavation front and the wear of cutting tools. The material parameters govern the coupling of frictional contact and wear between the interacting domains at the excavation front. The PFEM allows predicting several parameters which are relevant for estimating the performance of a tunnelling boring machine such as wear in the cutting tools, the pressure distribution on the face of the boring machine and the vibrations produced in the machinery and the adjacent soil/rock. The final aim is to help in the design of the excavating tools and in the planning of the tunnelling operations. The applications presented show that the PFEM is a promising technique for the analysis of tunnelling problems.

1 Introduction

Tunneling is a very challenging discipline in constant demand of new technologies. The sizes on caverns and tunnels have experienced a considerable increase during last years. Consequently the sizes of the tunnel boring machines (TBMs) and their diameters have also grown. The performance demands on these machines are focused on the increase of effectiveness and reduction of the operation time. The current research is looking for new technologies in order to help and improve the design of the TBMs. The present work focuses on the numerical simulation of tunnelling processes with the particle finite element method (PFEM). The purpose is to predict the effects produced by the mechanical excavation on the tunnel and its environment. With this numerical technique we start with the ambitious challenge of modelling an excavation in a tunnel.

The analysis of a boring machine excavating a massive rock is usually undertaken nowadays by the study of a single cutting tool. The study of a characteristic tool is commonly performed by laboratory tests. With the obtained results analytical formulas are applied in order to find out the parameters that will describe the behavior of the whole tunnelling machine. This type of studies mainly rely on tunnelling experience of analysts and on experimental tests.

Modelling excavation using numerical simulation is something relatively new. The breakthrough comes from the development of new computational mechanics techniques. An example is the discrete element method (DEM) [12, 17, 23, 24]. DEM can simulate the cutting process induced by the excavation tools. However, a high computational cost is required for this type of simulations.

The present work opens new possibilities for the modelling of an excavation process with the PFEM focussing on the global analysis of the whole machine-tool ground interaction.

The PFEM is founded on the Lagrangian description of particles and motion and it combines a meshless definition of the continuum containing a cloud of particles with standard mesh-based finite element techniques.

The PFEM had its origins on computational fluid dynamics (CFD) applications [10, 18] and lately was applied to fluid-structure interaction problems [19–21] and solid mechanics [7, 14, 15]. In this work the PFEM is extended to the modelling of ground excavation processes. The continuum, representing a solid or a fluid, is described by a collection of particles in space. The particles contain enough information to generate the correct boundaries of the analysis domain. Meshing techniques like the Delaunay tessellation and the alpha-shape concept [6] are used to discretize the continuum with finite elements starting from the particle distribution. The meshing process creates continuum sub-domains and identifies the geometrical contacts between sub-domains.

Contact constraints are applied between the interacting domains. The contact forces produced at the interface of these domains can be predicted. When there is an interaction between a tunnelling machine and the ground the contact forces depend on the geometry of the machine and the distribution of the tools on the cutting heads. These forces change when the geomaterial is excavated. The boundary of the ground experiences large changes as the digging goes forward.

The crushing and fracture of the geomaterial at the excavation front is modelled by combining a rate law and a damage law. The first one estimates the excavated material and the second one models the general behavior of the geomaterial.

The basis of the PFEM is described in the next section. Then the particular extension of the method for analysis of excavation problems is detailed. Some examples are presented showing that the PFEM is a promising numerical technique for the modelling and simulation of excavation processes and the prediction of wear in rock cutting tools.

2 The particle finite element method (PFEM)

The particularities of the PFEM makes it very suitable for capturing free surface motions. This fact was the main reason for introducing the PFEM for solid mechanics problems where important changes in the boundary geometry occur. Initially the PFEM was applied to model all kind of continua. The basis of the PFEM computations is a finite element mesh and this allows combining the PFEM with the standard FEM to model different parts of a continuum with one or other method. Existing material models for geomaterial typically used in the FEM can be directly used into the PFEM, and this is another advantage of this method.

2.1 Basic steps of the PFEM

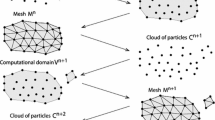
In the PFEM the continuum are modelled using an updated Lagrangian formulation. That is, all variables are assumed to be known in the current configuration at time $t$. The new set of variables is sought for in the next or updated configuration at time $t+\Delta t$ (Fig. 1). The finite element method (FEM) is used to solve the continuum equations. Hence a mesh discretizing the domain must be generated in order to solve the governing equations in the standard FEM fashion. Recall that the nodes discretizing the analysis domain are treated as material particles which motion is tracked during the transient solution. This is useful to model the separation of particles from the main domain such as soil/rock particles in an excacation problem, and to follow their subsequent motion as individual particles with a known density, an initial acceleration and velocity and subject to gravity forces. The mass of a given domain is obtained by integrating the density at the different material points over the domain.

Fig. 1

Sequence of steps to update in time a “cloud” of nodes representing a rock mass that is progressively fragmented the action of a boundary force $q$ using the PFEM. Crossed circles denote fixed nodes at the boundary

The quality of the numerical solution depends on the discretization chosen as in the standard FEM. Adaptive mesh refinement techniques can be used to improve the solution.

For clarity purposes we will define the collection or cloud of nodes (C) pertaining to the analysis domain, the volume (V) defining the analysis domain and the mesh (M) discretizing the domain.

Fig. 2

Clamped shallow circular arch. Three curves representing the theoretical solution, the FEM solution, the PFEM solution for the same mesh of 18959 3-noded triangular elements

A typical solution with the PFEM involves the following steps.

• 1. The starting point at each time step is the cloud of points in the analysis domains. For instance ${}^nC$ denotes the cloud at time $t=t_n$ (Fig. 2).

• 2. Identify the boundaries defining the analysis domain ${}^nV$. This is an essential step as some boundaries may be severely distorted during the solution, including separation and re-entering of nodes. The alpha shape method [6] is used for the boundary definition.

• 3. Discretize the fluid and solid domains with a finite element mesh ${}^nM$.

• 4. Solve the Lagrangian equations of motion in the domain. Compute the state variables at the next (updated) configuration for $t+\Delta t$: displacements, stresses, strains and temperature, etc.

• 5. Move the mesh nodes to a new position ${}^{n+1} C$ where $n+1$ denotes the time $t_n+\Delta t$, in terms of the time increment size. This step is typically a consequence of the solution process of step 4.

• 6. Go back to step 1 and repeat the solution process for the next time step to obtain ${}^{n+2} C$. The process is shown in Fig. 1.

Figure 1 shows a conceptual example of application of the PFEM to model the progressive fragmentation of a rock mass under the action of external surface forces $q$.

2.2 Particle concept and variable updating

In the PFEM the continuum is described using material points in space. These points are entities that store the domain information. Each point has a label identifying the sub-domain to which it belongs (i.e. a point belonging to the ground) and a material label (i.e. sandstone). When certain properties are assigned to the space coordinates of a point, it changes from a simple spatial reference to a larger entity. This point is then called a particle. The kinematics and mechanical properties of the continuum domain are described by these particles. All the practical information of the model is simply stored on the particles.

Differently from the discrete methods based on particles representing an area or volume in the space, in the PFEM a particle does not represent a physical entitling with a certain volume. It is only a geometrical entity that contains the information of its immediate volume or area. This means that the description of the whole continuum can be recovered from the particles. The simplest form of doing this is by considering each particle as a node and then connecting all the nodes with a finite element mesh (Fig.  1). Once the continuum has been discretized by a mesh, a computation is performed using the standard FEM.

From this description it arises a key feature of the PFEM. It is possible to recover the physical domain from a cloud of points but some information necessary for the mechanical computations is not located at the proper position. Kinematic variables (displacements, velocities and accelerations) are defined on each particle and therefore they describe correctly the particle (node) motions. However, the variables which are usually defined at the integration points of a finite element mesh have not a direct correspondence with the mesh nodes. This means that the information must be transferred adequately from the particles to the integration points to perform the mechanical computation on the underlying continuum. Box 1 shows a simple and natural scheme to transfer the information from particles to elements. An incremental transfer and update for the stresses is performed in order to minimize the smoothing during the transfer. We have checked that after this transfer the equilibrium position is not largely perturbed. Therefore, the next analysis step can be performed without any additional equilibrium re-computation. Figure 2 shows the structural response of a clamped shallow circular arch under a point load. The solution using PFEM is compared with the solution with the standard FEM.

Box 1 Flowchart of the information transfer for the stresses update: particles-elements-particles

More elaborated methods, such as the superconvergence patch recovery (SPR) technique [11] can be used for transferring the information from particles to elements. For transient problems the variables are updated on the particles. It takes in account the particle contributive volume concerning to the variable. The recover of element information is done if all nodes of a new element contain the relevant variable. For a damage model, the internal variables concerning damage are transferred to an element if all nodes of a new element have already some damage active. A fragmentation process modeled with damage is useful when well defined zone with traction stresses is identified for the numerical solution. The damage implementation used in this work is the one described in [13] and [16] and we use it only at locations of the structures, where tensile stresses are recorded. It is taken also as an example of implementation of a constitutive model that goes a little bit further than the elastic one. In the modelling of the constitutive behavior of the geomaterials the laws are complex and they need the transfer of several internal variables. In order to show the smoothing for the damage field modeled by the PFEM a comparison of the results of a problem modeled with FEM and PFEM is presented (see Fig.  4). The calculation is done in 244 steps. A re-meshing of the model and a transfer of the constitutive variables are performed in each one of these steps. The selected benchmark is the case of the classical problem of a notched shear beam (see [2, 25]) where loading conditions are non-symmetric with respect to the notch. For the response of the beam, the load is compared with the crack mouth sliding displacement (CMSD), which coincides with the relative vertical displacement on the lower points of the notch $\partial u$. Figure 3 shows the non-linear response of the beam in terms of load-CMSD for the Simo-Ju model with exponential softening.

Fig. 3

Load versus CMSD response for fracture problem using Simo-Ju model with exponential softening

Fig. 4

Crack pattern and stresses at-peak using Simo-Ju model with exponential softening. Analysis with the FEM on the right and with the PFEM on the left

2.3 Boundary definition via remeshing process

As previously mentioned, the particles are the basis of the continuum definition in the PFEM. From these particles the continuum is defined by interconnecting the particles and building a mesh. A Delaunay tessellation into 3-noded triangles or 4-noded tetrahedra is used for this purpose [9]. This creates a discretized continuum domain, but does not necessarily recover exactly the previous domain. In order to define the shape of the boundary another concept is needed.

In our work we use the $\alpha$-shape technique to characterize the element size when a Delaunay tessellation is performed [6, 9, 10, 18]. The convex hull defined by a cloud of points is meshed taking an account a certain predefined $\alpha$-size ratio. Every particle has information concerning the $\alpha$-size of the elements in its surroundings. This provides a methodology for an accurate boundary definition after meshing the domain (Fig.  5) [6].

Fig. 5

Boundary recognition of a set of particles using the $\alpha$-shape method [19]

The first distribution of particles determines the characteristic length for each particle. This is translated to a characteristic $\alpha$-size which defines every new boundary when the Delaunay tessellation is performed. The correct value of $\alpha$ is computed using the average distance between neighboring particles as follows:

$$\begin{aligned} \alpha _{j}=\sum _{i=1}^{{n}_{b}}\frac{\left|\mathbf{x}_{i}- \mathbf{x}_{j}\right|}{{n}_{b}} \end{aligned}$$

(1)

where $n_b$ is the number of neighboring particles $i$, that are defined as particles contained in the same sub-domain as particle $j$ and $\mathbf{x}_{k}$ is the spatial position of a particle. In order to set the tolerance of alpha in non-structured meshes, a characteristic $\alpha$-size is assigned to the new elements of the mesh from the $\alpha$-size of their nodes. The $\alpha$-size of the particles has been computed using the previous mesh and stored as geometrical information of the particle. The obtained elemental value for the $\alpha$-size is compared with the minimum radius of circle which contains all nodes of the new element. Certain tolerance on the circle radius is admitted to set the level of accuracy of the selection. The performed comparison is summarized as follows:

$$\begin{aligned} \frac{1}{N}\sum _{j=1}^{N}\alpha _{j} \le {r}_{tol}*{R}^{(e)} \end{aligned}$$

(2)

where $N$ is the number nodes of the element, $\alpha _j$ the $\alpha$-size of the node $j, R^{(e)}$ is the minimum radius of the circle which contains all particles and $r_{tol}$ a value between 0.5 and 1.

Any geometry in 2D and 3D can be recovered after the particle definition using the $\alpha$-shape technique. Some extra refining must be however applied to detect the boundaries of empty holes in the domain. Usually the $\alpha$-shape method fails in the definition of sharp corners, as depicted in Fig.  6.

Fig. 6

Lack of definition in convex corners after remeshing a set of particles using the $\alpha$-shape concept

To overcome this handicap in the boundary detection an additional refining algorithm can be applied after mesh generation. The algorithm is based in the convex nature of the elements formed in edges or in holes, which must be polished. The criteria to consider or not the elements is based on the boundary inward normals to the element nodes. Box 2 summarizes the refining scheme.

Box 2 Flowchart of the boundary refinement. The refining scheme is complementary to the $\alpha$-shape process

The main conceptual steps of the PFEM during one time increment are presented in Fig.  7.

Fig. 7

Main steps followed in PFEM solution during a time increment (from left to rightand up to down)

2.4 Governing equations and solution scheme

Once a domain is defined the mechanical behavior of the system can be computed. A discretization of the continuum is automatically available after meshing the particle domain. This allows us to perform a finite element computation on the given domain. A summary of the main governing equations using an updated Lagrangian formulation is presented below. The relevant dependent variables are the initial density $\rho _0(\mathbf{X},t)$, the displacement $\mathbf{u}(\mathbf{X},t)$, and the Lagrangian measures of stress and strain in the current configuration ${\pmb \varphi }(\mathcal B )$ [26, 29].

Mass conservation

$$\begin{aligned} \rho (\mathbf{X},t) J (\mathbf{X},t)= \rho _{0}(\mathbf{X},t) \end{aligned}$$

(3)

Conservation of linear momentum.

$$\begin{aligned} \frac{\partial \sigma _{ij}}{\partial {x}_{j}}+\rho \bar{b}_{i} = \rho \ddot{{u}_{i}} \end{aligned}$$

(4)

Constitutive equation (In our work we use a damage model).

$$\begin{aligned} \sigma _{ij}= (1-d) {C}_{ijkl} {E}_{kl} \end{aligned}$$

(5)

where $E_{kl}$ is the linear part of the Green-Lagrange strain tensor and $d$ is the damage internal variable. Note that any constitutive model of continuous mechanics can be used in the context of the PFEM.

The weak form of the balance of linear momentum equation (Eq. 4) is obtained by applying the principle of virtual work. This yields

$$\begin{aligned} g({\pmb \varphi },{\pmb \eta })&= \int _{{\pmb \varphi } (\mathcal B )}{\pmb \sigma }\cdot \nabla ^{S}{\pmb \eta }\,dV -\int _{{\pmb \varphi }(\mathcal B )}\rho (\bar{\mathbf{b}}- \dot{\mathbf{v}})\cdot {\pmb \eta }\,dV \nonumber \\&-\int _{{\pmb \varphi }(\partial \mathcal{B })}\bar{\mathbf{t}} \cdot {\pmb \eta }\,dS=0 \end{aligned}$$

(6)

where ${\pmb \eta }$ is a vector valued function ${\pmb \eta }=\left\{ {\pmb \eta }\,|\,{\pmb \eta }= \mathbf{0}\;\mathrm{on}\;\partial {\mathrm{B}_{\mathrm{u}}}\right\}$, representing virtual displacements; $\bar{\mathbf{t}}$ are the surface tractions, $\rho \bar{\mathbf{b}}$ are the body forces and $\rho \dot{\mathbf{v}}$ are the inertia forces.

In Eq. (6), all integrals, stresses and gradients are computed in the current configuration. This introduces a nonlinearity in the solution for large displacement problems. The discretization procedure follows the general FEM methodology for solid mechanics [26, 29].

Note that the main difference introduced by the PFEM in the discretization process is that the basic discrete unit is the particle, while the mesh is a consequence of a distribution of particles. This offers a flexible adaptation of the geometry to the continuum kinematics. This description is suitable for a good conjunction between the rapid changes in the domain boundary and the numerical computations for predicting the mechanical behavior.

When large displacements and large deformations occur, as for excavation problems, other mechanical phenomena are present. Usually the continuum breaks, discontinuities appear and large domains are split into small ones. The PFEM allows to reproduce these complex phenomena. For the numerical modeling of excavation we have focused on the characterization of contact mechanics and the boring of the material. The treatment of frictional contact is detailed in the next section.

3 Contact mechanics with the PFEM

3.1 Geometrical detection

The geometrical detection of contact is a complex problem. The geometric search is especially complex when the contact of more than two bodies has to be considered. In excavation problems this happens when the solids break, and hence several discrete elements are originated from the initial set up during the solution process.

Static contact problems with large deformations also need fast and reliable search algorithms, as contact areas are not known a priori and can change much within a load step. The search for an active set of contact constraints is not trivial in this case, since a surface point of a body may contact any portion of the surface of another body. Thus the search for the correct contact detection eventually needs considerable effort, depending on the problem. This is especially true when self-contact is possible.

Classically, the contact search task is split into two phases: the spatial search for objects (finite element subdomains) which might possibly come into contact, and the determination of pairs of objects (finite element subdomains) which actually intersect and hence are in contact.

Usually in the first phase the finite elements lying on the surface of the solid are ordered by a sorting algorithm. After that, a hierarchical structure is set up to find out which bodies, part of the bodies, surfaces or parts of the surfaces are able to come into contact. This is a global search within a given time step or displacement increment. Search algorithms combine complex structures of cell decompositions, binary tree searches or more advanced spatial methods [27].

The complicated phases in the spatial search are simplified in the PFEM as the spatial search is intrinsically bound up with the generation of the mesh. Contact is detected when the domains are so close as to generate contact elements between the interacting subdomains (Fig.  8) [7, 10, 14, 15, 18]. An interface mesh is created anticipating the spatial contact. Hence, a mesh for the domain and another one for the interface are generated. This permits to anticipate the collision of the different subdomains.

Fig. 8

Using the alpha-shape method in the detection of contact between subdomains is done automatically. This generates contact elements when the sub-domains are close enough

Usually the mesh identification is performed comparing labels between domain particles. A contact element is detected when the element contains particles of two or more different subdomains. This yields a rapid and automatic detection of the contact interface mesh. However this detection procedure is not possible when the same subdomain enters in contact. This can happen due to large deformations or when parts of the same subdomain are segregated during the detection of boundaries with the $\alpha$-shape procedure. Then the contact is produced between subdomains with the same identification label and has to be treated as self contacting subdomains. In order to include self-contact in the spatial search, new tools have to be added to the contact search algorithm.

The algorithm for detecting self-contact elements in this work is based on the evaluation of the surface normals. Let us consider that every particle that belongs to the surface of a subdomain has an associated inward normal vector which points towards the inner side. After applying the $\alpha$-shape criteria, a self-contact element must fulfill the conditions stated in Box 3:

Box 3 Definition of a self-contact element in the PFEM

Fig. 9

Self-contact elements in 3D formed between two exterior surfaces of the domain: a Node to face element, b Edge to edge element

The conditions in Box 3 are illustrated in Fig.  9 for a 3D self-contact tetrahedron. Note that the contact domain in 3D has two different modalities, Node to face element and Edge to edge element.

The first modality simplifies the number of elements to be analyzed. Only elements on the edges and self-contacting elements will be formed entirely by particles on the boundary of the same subdomain. The second modality rejects contact elements that are formed in the convex edges of the subdomain and also helps to identify the position of the element. Hence, if the element is located outside the subdomain it is then a self-contact element.

Self-contact conditions have been written for determining the contact elements for meshes of 3-noded triangles and 4-noded tetrahedra. Once the set of contact elements is determined and fixed for each time step, the contact constraint can be formulated in a fictitious continuum domain composed by the contact element set. In the PFEM, the same finite elements used for discretizing the continuum are used to model the contact domain (Fig.  3). This is an advantage of the PFEM, which provides a simple discretization procedure for modelling contact.

3.2 Treatment of contact constraint

The treatment of the contact constraint is based in the interface mesh created in the contact detection. This procedure has been named in this work as the continuum constraint method (CCM). The CMM was originally developed in 2009 and it shares many similarities with the contact domain method (CDM) developed by Oliver et al. [7, 15]. In both the CCM and the CDM the contact constraint is formulated in the fictitious domain created between the contacting bodies $\mathcal B ^{c}$ when the geometrical detection is performed. When the constraint is active on $\partial \mathcal B ^{c}$, the contact term is then related to the continuum and acts as an internal work term in the continuum formulation (Eq. 6).

Fig. 10

Deformed configuration $\mathcal B ^{\alpha }$ and minimum distance between bodies [27]

The first particular feature of the CCM is related to the definition of the contact kinematics. Usually the kinematics are defined by two sub-domains where a contact gap function describes the spatial interaction between them. In the PFEM the normal contact gap function $\bar{g}_N$ defines if the contact is active or not and determines a reference value for the penetration condition. Firstly it is necessary to define $\mathbf{x}^{\alpha }$ as the coordinates of the current configuration ${\pmb \varphi }(\mathcal B ^{\alpha })$ of the body and $\mathbf{n}^1$ as the normal vector associated with body $\mathcal B ^{1}$ at the minimum distance point (see Fig. 10). After that, the inequality constraint for the non-penetration condition is started as

$$\begin{aligned} {g}_{N}=(\mathbf{x}^2-\bar{\mathbf{x}}^1)\cdot \bar{\mathbf{n}}^1-\hat{g}_{N}\ge 0 \end{aligned}$$

(7)

where $\hat{g}_N$ is the prior gap between the two bodies. In this case, the penetration function defines if the contact is active or not; i.e.

$$\begin{aligned} \bar{g}_{N}=\left\{ \begin{array}{lll} true&\rightarrow \mathrm{if}\quad (\mathbf{x}^2- \bar{\mathbf{x}}^1)\cdot \bar{\mathbf{n}}^1-\hat{g}_{N}<0\\ false&\rightarrow \qquad \mathrm{otherwise} \end{array}\right. \end{aligned}$$

(8)

when $\bar{g}_N=true$, then $g_N=(\mathbf{x}^2- \bar{\mathbf{x}}^1)\cdot \bar{\mathbf{n}}^1-\hat{g}_{N}$. This is necessary for notation consistency in the imposition of the correct contact constraints.

For the tangential contact, the tangential gap $\mathbf{g}_{T}$ defines the length of the frictional path and is computed for the slip condition as

$$\begin{aligned} \mathbf{g}_{T}=\int ^{t}_{t_{0}}\,\Vert \dot{\pmb \xi }^{\alpha }\, \bar{\mathbf{x}}^1_{,\alpha }\Vert dt \end{aligned}$$

(9)

where $t$ is the time used to parameterize the path of point $\mathbf{x}^2, \pmb \xi$ are the convective coordinates of $\mathbf{x}^1$ during the motion and $\alpha$ is the index of the deformed configuration $\mathcal B ^{\alpha }$, as illustrated in Fig.  10.

The definitions presented for the gap in Eqs.  (7) and (9) fulfill the Kuhn-Tucker conditions for contact [27].

The contact constraint for the PFEM is finally written as:

$$\begin{aligned} {C}_{c}&= \int _{{\pmb \varphi }(\mathcal{B }^c)}(\mathbb P \, {\pmb \sigma }_c +\mathbb T \,{\pmb \sigma }_c)\cdot \nabla ^{S} {\pmb \eta }_c\,dv\nonumber \\&= \int _{{\pmb \varphi }(\mathcal{B }^c)}{\pmb \sigma }_c\cdot \nabla ^{S}{\pmb \eta }_c\,dv \end{aligned}$$

(10)

In Eq. (10) $\mathbb P$ is the projection tensor $\mathbb{P =\bar{\mathbf{n}}^1\!\!~\otimes \!\!~\bar{\mathbf{n}}^1}$ and $\bar{\mathbf{n}}^1$ is the normal to the contact surface at the minimum distance point. Tensor $\mathbb T$ can be written for the stick case as $\mathbb T =(\mathbb I -\mathbb P )$. Equation (10) expresses the virtual internal work within the contact domain.

The integration is performed with respect to the continuum domain ${\pmb \varphi }(\mathcal B ^c)$ instead of the contact surface $\partial \mathcal{B }_{c}\equiv \Gamma _c$. Note that ${\pmb \varphi }(\mathcal B ^c)$ is the sub-domain occupied by the interface contact domain $\mathcal B ^c$ in the current configuration. The virtual displacements ${\pmb \eta }^{\gamma }_c$ in Eq. (10) are equivalent to the ones in Eq. (6); i.e. ${\pmb \eta }_c\equiv {\pmb \eta }$.

Tensor $\pmb \sigma _c$ in Eq. (10) is the Cauchy stress tensor for the contact domain which depends on $\delta \bar{g}_{N}$ and $\delta \mathbf{g}_{T}$. This is defined as

$$\begin{aligned} {\pmb \sigma }_c=\left\{ \begin{array}{lll} (\frac{K}{J^n}\,\ln J^n)\,\mathbb 1&\rightarrow \mathrm{if}\quad (\bar{g}_{N}=true \quad \mathrm{and}\quad {p}_{N}<0)\\ \mathbf{0}&\rightarrow \mathrm{if}\quad (\bar{g}_{N}=false \quad \mathrm{or}\quad {p}_{N}\ge 0) \end{array} \right.\nonumber \\ \end{aligned}$$

(11)

The constitutive law used to compute $\pmb \sigma _c$ is equivalent to a penalty law where $K$ is the bulk modulus $K=\lambda +\dfrac{2\,\mu }{3}$ and $J^n$ is the Jacobian determinant computed using the projected displacements:

$$\begin{aligned} (\mathbf{u}\cdot \bar{\mathbf{n}}^1)>0\rightarrow \mathbf{u}^n= (\mathbf{u}\cdot \bar{\mathbf{n}}^1)\cdot \bar{\mathbf{n}}^1= \mathbb P \,\mathbf{u} \end{aligned}$$

(12)

The discretization of the constant constraint (10) for the normal forces is analogous to the first term of the principle of virtual work (see Eq. 6) [26]. Considering the normal force vector produced by the normal contact as $\mathbf{F}_{N}:=(C^{\,CC}_{c})_N$, yields

$$\begin{aligned} \mathbf{F}_{N}:=({C}_{c})_{N}=\int _{{\pmb \varphi }(\mathcal{B }^c)} (\mathbb P \,{\pmb \sigma }_{c})\cdot \nabla ^{S}{\pmb \eta }_c\,dv \end{aligned}$$

(13)

Using the variation of the contact test functions $\nabla ^{S}{\pmb \eta }_c$ (6) for the projected displacements (12) and using the isoparametric concept [26], the contact constraint can be written on a parent configuration $\square$ as

$$\begin{aligned} ({\pmb \eta }_c)^T\,(C_c)_N=\bigcup _{ce=1}^{n_{ce}}\, \mathbb P \,\sum _{I=1}^{n_n}\,{\pmb \eta }_{I}^{T} \int _{{\pmb \Omega }_{\square }}{\mathbf{B}_{0I}^n}^{T} \,{\pmb \sigma }_{ce}\,\det \mathbf{j}^{n}_{ce}\,d{\square }\nonumber \\ \end{aligned}$$

(14)

where subscript $(.)_{ce}$ means contact element and superscript $(.)^n$ means that the variables are computed using the normal projected displacements (12). The $\square$ means that it is expressed on the parent configuration. The projection tensor is $\mathbb P =\bar{\mathbf{n}}^1\otimes \bar{\mathbf{n}}^1$, considering that the normal in the contact surface $\bar{\mathbf{n}}^1$ is rate independent. ${\mathbf{B}_{0I}^n}^{T}$ contains the derivative of the shape functions commonly used in the finite element approximation.

The tangential contact constraint for the CCM formulation in the slip case, considering Coulomb law [28], is written as

$$\begin{aligned} \mathbf{F}_{T}:=({C}_{c})_{T}&= \int _{{\pmb \varphi }(\mathcal{B }^{c})} {\pmb \kappa }_{c}\cdot \nabla ^{S}{\pmb \eta }_{c} dV\nonumber \\&= \int _{{\pmb \varphi }(\mathcal{B }^c)}-\mu \;\mathbb T \, \pmb \sigma _c\cdot \nabla ^{S}{\pmb \eta }_{c} dV \end{aligned}$$

(15)

where $\mathbb T =\bar{\mathbf{t}}^1\otimes \bar{\mathbf{n}}^{1}$ and $\pmb \sigma _c$ is described by (11). When the friction coefficient $\mu$, the normal $\bar{\mathbf{n}}^1$ and tangent $\bar{\mathbf{t}}^1$ are rate independent, the previous equation can be written as

$$\begin{aligned} (C_c)_T=-\mu \,\mathbb T \,\int _{{\pmb \varphi }(\mathcal{B }^c)} \pmb \sigma _c\cdot \nabla ^{S}{\pmb \eta }_c dV \end{aligned}$$

(16)

This expression can be applied when the contact surface does not suffer big changes in one time step. When the sliding condition is applied, the discretization of the tangential contact constraint for the CCM method is given by

$$\begin{aligned} ({\pmb \eta }_c)^T(C^{\,CC}_c)_T&= \int _{{\pmb \varphi } (\mathcal B ^c)}-\,\mu \,\mathbb T {\pmb \sigma }_c\cdot \nabla ^{S}{\pmb \eta }_{c}\;dV\nonumber \\&= \bigcup _{ce=1}^{n_{ce}}\,-\,\mu \,\mathbb T \int _{{\pmb \varphi }(\Omega _{ce})} (\nabla ^{S}{\pmb \eta }_c)^{T}\,{\pmb \sigma }_{ce}\,dV\nonumber \\&= \bigcup _{ce=1}^{n_{ce}}-\,\mu \,\mathbb T \sum _{I=1}^{n_n}{\pmb \eta }_{I}^{T}\int _{{\pmb \varphi } (\Omega _{ce})}{\mathbf{B}_{0I}^n}^{T}{\pmb \sigma }_{ce}\,dV\nonumber \\&= \bigcup _{ce=1}^{n_{ce}}-\,\mu \mathbb T \sum _{I=1} ^{n_n}{\pmb \eta }_{I}^{T} \int _{{\pmb \Omega }_{\square }} {\mathbf{B}_{0I}^n}^{T}{\pmb \sigma }_{ce}\det \mathbf{j} ^{n}_{ce}\,d{\square } \nonumber \\ \end{aligned}$$

(17)

The contact constraint is inserted in an implicit solution scheme using a rotational approach. This means that the convergence for the uniqueness of the contact active set is checked within the Newton iteration. Contact is not a conservative contribution. The linearization of the contact equations introduces additional terms in the consistent tangent matrix which must be taken into account during the implicit solution. In a rotational approach of an iterative scheme the quadratic convergence of a Newton-Raphson method is lost. In this case an approximation of the consistent tangent matrix is suitable enough for the computation. The approximated tangent matrix for the contact contribution is given by

$$\begin{aligned} \mathbf{K}^{con}=\bigcup _{ce=1}^{n_{ce}}(\mathbb P \, (\hat{\mathbf{K}}^{con}_{ce})\,\mathbb P -\mu \,\mathbb T \,(\hat{\mathbf{K}}^{con}_{ce})\mathbb P ) \end{aligned}$$

(18)

with

$$\begin{aligned} \hat{\mathbf{K}}^{con}_{ce}=\hat{\mathbf{K}}^{mat}_{ce}+ \hat{\mathbf{K}}^{geo}_{ce} \end{aligned}$$

(19)

and matrices $\hat{\mathbf{K}}^{mat}_{ce}$ and $\hat{\mathbf{K}}^{geo}_{ce}$ defined by

$$\begin{aligned} \hat{\mathbf{K}}^{mat}_{ce}&= \bigcup _{ce=1}^{n_{ce}}\,\sum _{I=1}^{n_n}\, \sum _{K=1}^{n_n}\,\int _{{\pmb \varphi }(\Omega _{ce})} \,[{\bar{\mathbf{B}}^{n}_{0I}}\!^{T}\;\bar{\mathbf{D}} ^{vol}\;\bar{\mathbf{B}}^{n}_{0K}]\,dV \end{aligned}$$

(20)

$$\begin{aligned} \hat{\mathbf{K}}^{geo}_{ce}&= \bigcup _{ce=1}^{n_{ce}}\,\sum _{I=1}^{n_n}\,\sum _{K=1}^{n_n}\, \int _{{\pmb \varphi }(\Omega _{ce})} [({\nabla _{{\bar{ \mathbf{x}}}}{N}_{I}}^{T})\,\bar{\pmb \sigma }_{ce}\, \nabla _{{\bar{\mathbf{x}}}}{N}_{K}] \;\mathbb I \,dV\nonumber \\ \end{aligned}$$

(21)

where $\bar{\mathbf{D}}^{vol}$ is the volumetric part of the incremental material constitutive tensor $\bar{\hat{\mathbf{c}\!\!\mathbf{c}}}$ expressed in the current configuration. ${N}_{J}$ are the shape functions for the elements in the contact interface. The convergence properties in case of contact varies depending on the stability of the contact active set and the deformation on the contact area. For a stable active set we observe quadratic convergence when the deformation of the contact area is low. When the contact area experiences a larger deformation the quadratic convergence is lost and the convergence rate decreases to linear and in some cases sublinear.

To model an excavation process, not only the computation of the contact forces between solid domains is needed. Also a scheme to capture and treat the changing geometries is required. The features of the PFEM allow us to model rapidly changing boundaries and adapt the geometry to every mechanical process. This opens a new way for the treatment of wear in rock cutting materials and also for modeling excavation problems with dynamic boundary generation.

4 Modelling tunneling processes

The better knowledge of the excavation process is a matter of great interest in tunnelling engineering. The process of crushing and digging a solid material introduces several complicated phenomena that must be taken in account in the analysis. The wear produced on the cutting tools is another relevant phenomenon when a massive rock material is bored.

Most of these phenomena are related to the constitutive behavior of materials and to the mechanical contact. To pay a specific attention to each particular physical problem distinct multi-scale analyses are needed. To simplify these processes usually the problem is seen from the macro-scale and modeled with particular laws.

In the next sections, the general theory for modelling wear of rock cutting tools is introduced. From that theory the macroscopic model for excavation is developed. The model is independent from the constitutive behavior of the bodies in order to not restrict its general application.

In general, wear is related with the sliding contact and can involve different mechanisms at various stages of the mechanical process. It depends upon the properties of the material surfaces, the surface roughness, the sliding distance, the sliding velocity and the temperature. For processes involved in excavation it is important to reduce the wear mechanisms. Abrasive wear is chosen as the most relevant type of wear for the analysis.

4.1 Abrasive wear of rock cutting tools

Abrasive wear arises when a hard rough surface slides against a softer surface, digs into it, and plows a series of grooves. The material originally in the grooves is normally removed in the form of loose fragments, or else it forms a pair of mounds along each groove. The material in the mounds is then vulnerable to subsequent complete removal from the surface.

To quantify abrasive wear through constitutive equations, the properties or effects that play a major role have to be determined. In our work a simple wear model is considered. In this model, the asperities on the hard surface are assumed to be conical (Fig.  11). A conical asperity, carrying a load $\Delta F_N$ penetrates into a softer surface removing certain volume. Taking in account all asperities of the contact surface leads to an expression that was proposed initially by Archard for adhesive wear in [1] and [8], and later also applied to abrasive wear [22],

$$\begin{aligned} {V}_{wear}={k}_{abr}\frac{F_{N}\,{g}_{T}}{H} \end{aligned}$$

(22)

where $g_T$ is the relative sliding distance and $k_{abr}$ is the abrasive wear coefficient that physically represents the average geometry of the asperities. The range of $k_{abr}$ is between $10^{-2}$ and $10^{-5}$. The penetration hardness coefficient $H$ is specified by the Brinell test or the Vickers test, the last one is performed by pressing a square pyramid into a flat surface and then measuring the diagonals of the square indentation.

Fig. 11

A much simplified abrasive wear model showing how a cone removes material from a surface

The hardness coefficient is the basis of the Mohs’s hardness scale, widely used by mineralogists. The effect of hardness on the abrasive wear rate is the fact that an abrasive material must be harder than the surface to be abraded, thought not enormously harder. This is an important feature, as a no abrasive material will cut anything harder than itself.

4.2 Excavation

The mechanism of cutting and digging on the ground is not so much different compared to wear of a solid surface. The most significant difference is the scale where the process takes place. The wear of materials usually is associated with the micro-scale of solid surfaces. When one refers to the erosion of a fluid on a solid surface the scale starts to change. The same happens when a solid surface digs onto another. Excavation processes can be described with the same physical variables and with similar laws as wear. Figure 12 shows how a macro-scale model for excavation is analogue to the micro-scale model used for wear.

Fig. 12

A simplified excavation model for a removal of a solid material by means of a cutting tool

The volume loss rate of the excavated material depends on the relative displacement of the cutting tool and the hardness of the material. A rate function is used for the description of excavation as was done with wear. Similar analogies have been employed by other researchers in order to model fracture of hard cutting indenters in a brittle material [5, 17].

The asperities of the surfaces are now cutting tools with a specific geometry. The characteristic cutting tools for TBMs are discs and for roadheaders are drag picks. In the case of picks the excavation model can be represented with the basic model of Fig.  12. Hence the estimation of the volume loss of material for the particular case of drag picks is:

$$\begin{aligned} {V}_{dp}={K}_{dp}\,\frac{{F}_{N}\,{g}_{T}}{{H}_{d}} \end{aligned}$$

(23)

where $K_{dp}$ is a measure of the boreability or excavability of the pick which depends on extra variables like the clearance angle in the cutting direction $\beta$ and the rake angle of the bit $\alpha$ (Fig.  13). $H_{d}$ is the hardness of the material.

Fig. 13

Drag tools parallel to the cutting direction. $\alpha$: rake angle; $\beta$: clearance angle

The derivation of (23) is analogue to the one performed for abrasive wear. A physical definition of $K_{dp}$ is

$$\begin{aligned} {K}_{dp}=\frac{\tan \theta }{\pi } \end{aligned}$$

(24)

where $\theta =\bar{\beta }+\bar{\alpha }$ is the sum of the average clearance angle and the average rake angle for the roadheader bits.

In the case of discs, a more detailed model has to be studied as shown in Fig.  14.

Fig. 14

A simplified excavation model for removal of solid material by means of a cutting disc. $s$ is the cutter spacing and $w$ is the disc edge width

The volume loss of material produced by a disc cutting a geomaterial is expressed as

$$\begin{aligned} {V}_{d}={{K}_{d}}\,\frac{{F}_{N}}{UCS}\,{g}_{T} \end{aligned}$$

(25)

where UCS is the uniaxial compressive strength, the most widely test for rock strength. $K_d$ is the boreability coefficient that physically represents the weighted average of the values of spacing $\bar{s}=\sum _{i=1}^{n_d}{\left({s}_i/n_d\right)}$ and the disc width $\bar{w}=\sum _{i=1}^{n_d}{\left({w}_i/n_d\right)}$ (where $n_d$ is the number of discs).

$$\begin{aligned} {K}_{d}=\frac{{k}_{p}\,(\bar{w}+\bar{s})}{10^3} \end{aligned}$$

(26)

where ${k}_{p}$ is a constant that depends on the material (${k}_{p}=3940$ for hard rocks) and the $1/{10^3}$ appears due to the conversion of disc penetration from millimeters to meters. A more detailed development of the Eq. 26 can be found in [3]. ${K}_{d}$ is a parameter that has to be calibrated using the properties of the excavated material and the geometrical properties of the TBM cutter head: discs distribution and disc geometry.

Equation (25) depends on the normal force applied to the excavation front $F_N$, which is only a component of the contact forces received by the head of the TBM.

Equations (22), (23) and (25) are applied in the context of the PFEM formulation described. In the PFEM every particle represents a part of the domain volume. The surface of a body is composed by particles that represent the volume of the same body associated to them. By means of the contact model the interaction between two solid domains can be quantified. The result is the normal force $F_N$ associated to the surface particles, and the relative velocities or the sliding distances. Therefore, for each particle laying on the surface, the volume loss of material can be estimated in time by the excavation model. Equation (22) can be written in its more general form as:

$$\begin{aligned} {V}_{d}^{t+\triangle t}= {V}_{d}^{t}+{K}_{d}\;\frac{\Vert \mathbf{F}_{N}\Vert }{H_d}\;(\Vert \mathbf{v}_{t}\Vert \cdot \triangle t) \end{aligned}$$

(27)

where $\mathbf{v}_{t}$ is the relative tangent velocity between the contact surfaces and $\triangle t$ is the time step. The volume loss of material $V_{d}$ can be compared with the volume associated to each contact particle. From this comparison different strategies for geometry shaping can be formulated.

The global concept of shaping the surface after computing wear and excavation is presented in Fig.  15. When the volume associated to the patch of the particle is reached the particle is released from the material volume.

Fig. 15

Excavation strategy consisting in a Shaping the Surface using the computed volume loss

4.3 Constitutive models and excavation

The damage from the stresses generated in the excavation can be extended inwards and affect other parts of the excavated material. The damage not directly produced by the excavation crush is described by the constitutive model, but not by the excavation model. On the other hand, the damage which fractures the ground due to excavation is considered within the excavation model. The boreability coefficient $K_{d}$ includes this phenomenon (see Eq. 26). This coefficient defines the material properties that quantify the damage produced on the surface of the geomaterial, but only in the cutting region.

When damage occurs on some part of the massive ground, the boreability coefficient of this zone ($K_{d}$) is modified in order to include the effect. Material properties change and is easier to dig on it. Therefore the damage model affects the excavation model by means of this coupling. The modification on the boreability coefficient is applied using the damage variable $d$ as follows:

$$\begin{aligned} \hat{K}_{d}=\frac{K_{d}}{1-d}\quad \text{ with}\quad d\in [0,1) \end{aligned}$$

(28)

where $\hat{K}_d$ includes the damage influence in the volume loss rate. Using the general form of Eq.  (23) and introducing the damage influence yields

$$\begin{aligned} V_{d}=\hat{K}_{d}\,\frac{F_N\,g_T}{H_{d}}=\left(\frac{1}{1-d}\right)\,K_{d}\,\frac{F_N\,g_T}{H_{d}} \end{aligned}$$

(29)

The layer of elements in the contact surface is not described by the geomaterial constitutive law. Instead of that, an elastic layer is used. This is applied in order to avoid the local effects that contact forces produce in contact surfaces. Damage produced in the surface area is computed by the excavation model. Once a damaged element is reached by the excavation front, the amount of accumulated damage is accounted for in the model by using Eq. (28).

Similarly as for worn particles, totally damaged particles do not contribute to the mechanical behavior of the domain. Therefore when particles on the body surface reach the maximum damage level ($d=1$) they are removed from the analysis domain.

4.4 General solution scheme

Box 4 presents the flowchart for modelling an excavation problem with the PFEM using a rotational execution of an implicit time integration scheme.

Box 4 Flowchart for the analysis of an excavation with the PFEM

5 Simulation of tunneling problems

The PFEM formulation described previously has been implemented in a computational code written in C++ [4]. The simulation models are created using the same procedure as in the classical FEM. The materials contain certain properties related to excavation. Some particular parameters about the contact strategy and the mesh regeneration are also included in the definition of the model. Some examples are presented in order to show how an excavation is modeled using the PFEM accounting for the wear of the rock cutting tools. All examples presented have been run in a single processor Pentium IV PC. In Table 1 an indicative computing time for the main processes of these examples is presented.

Table 1 Time consuming with the programmed code for the PFEM (2,4 GHz processor)

Note that to capture the surface wear and excavation the cutting tools have to travel across the whole ground surface. This must be managed with a suitable combination of the rotation and penetration speeds on each case of study. In some examples the penetration velocity has been forced to be larger than the realistic one in order to get results in a more reasonable time.

5.1 2D roadheader tools

The first application example is a simplified model of an elastic roadheader in 2D. Usually excavation problems are fully 3D. However, some simplifications can be made to model the problem in 2D. The purpose of the example is to check the suitability of the PFEM for modelling and simulating a real excavation. The roadheader has a circular center which has an imposed rotation and displacement. This transfers the rotation to the dentated ring on the roadheader surface which generates friction when contacting with the ground. Figure 16 shows the 2D model with the material properties and boundary conditions.

Fig. 16

2D model of an excavation problem with a roadheader

The problem is solved as a dynamic interaction between two continuum domains. A small Rayleigh damping has been included in order to reduce the frequencies induced by the excavation impacts [3]. For the elastic ground material Rayleigh parameters are $a_1=0$ and $a_2=0.05$ and for the roadheader $a_1=0$ and $a_2=0.01$. The geomaterial in the excavation region is modelled with a damage constitutive law using a Drucker-Prager damage surface and linear softening [16]. The soil region far from the excavation front has been modeled with a simple hyperelastic model. The visco-elastic behavior considered for this material is introduced by the Rayleigh damping. The values considered for the damping coefficients are $a_1=0$ and $a_2=0.01$.

Figure 17 shows the excavation in the initial, intermediate and final states. The impacting forces are depicted using the resulting accelerations in the excavation front.

Fig. 17

2D excavation with a roadheader

The wear coefficient $K_w$ and the material hardness $H$ are shown for each material. A model of cutting picks has been considered on the surface of the roadheader (see Eq. 23). The hardness of the geomaterial is $H_{dp}=10^7\;Pa$ and the boreability coefficient $K_{dp}=2500$. The friction coefficients are $\mu _s=0.3$ and $\mu _d=0.25$. The thickness of the model is $t=1$ m. The total excavation time studied was about 100 s.

In Fig.  18 the results after approximately 32 s of analysis are depicted. Stresses, strains and accelerations in the ground as well as wear produced on the surface of the roadheader after 2 revolutions of the tunneling machine are presented.

Fig. 18

2D excavation with roadheader. Mesh used for the PFEM computation. Stresses, strains and accelerations on the ground due to excavation and accumulated wear on the roadheader surface after 32” of excavation

Some conclusions can be extracted from this simplified excavation analysis. The first one is that the computing time is very large compared with the real time simulated. Around 4 h of computing time were needed to obtain 10 s of actual excavation time. The numerical treatment of contact and crushing in the excavation front has a temporary scale much smaller than the time for the operational excavation.

Note that in the presented example the imposed advance velocity of the roadheader is large. This increases the excavation velocity generating a more demanding test for the performance of the method. In 32 s the roadheader penetrates almost 1 meter in the ground. As a result of this imposition the computed contact forces are extremely large (see Fig.  19) and can not be directly compared with the usual parameters of an excavation with a roadheader.

The penetration velocity has been forced to be larger than the realistic one in order to get results in a more reasonable time. To capture the surface wear and excavation, the cutting tools have to travel across the whole ground surface. A suitable combination of the rotation and penetration speeds can be a solution for the characterization of the excavation in a shorter time. This is a first attempt to accelerate the numerical simulation but it would require an appropriate correction factor in order to estimate the magnitude of the excavation forces when the excavation has different parameters.

Fig. 19

Computed contact forces on the 2D roadheader and averaged contact interaction curve

5.2 3D Roadheader

In this example an excavation with a roadheader is modeled in 3D. The objective is to reproduce a real excavation as well as checking the times and the performance of the method. The simulation considers a ripping process. Firstly the ripping head is pushed towards the rock-solid with a constant rotation. After 18 s, when the roadheader has excavated a considerable portion of the rock, it moves over a lateral part. To reproduce the work a rotation of 2 rpm is imposed at the center of the roadheader during the entire analysis. An imposed velocity of $\mathbf{v}=(0,0,-0.01)\,$m/s is applied at the first 18 s and a velocity of $\mathbf{v}=(0.01,0,0)\,$m/s in the following time steps. Prescribed velocities are applied in the cylindrical axis of the machine only. The external part of the roadheader is set free. The geometry of the model is displayed in Fig.  20. The rock-solid is fixed on the base. Points in the lateral walls are allowed to move vertically.

Fig. 20

3D model of a roadheader cutting a ground

Table 2 lists the material properties of the model. The wear coefficient $K_w$ and the material hardness $H$ are defined as properties of each material. A cutting pick model has been considered on the surface of the roadheader (see Eq. 23). The hardness of the geomaterial is $H_{dp}=0.5\times 10^7\;Pa$ and the boreability coefficient $K_{dp}=100$. These properties are assigned to the surface of the roadheader head considering 50 picks on it.

Table 2 Material properties for the 3D roadheader excavation example

The discretization of the model was done with an initial mesh of 270463 4-noded tetrahedra with 52551 nodes. The time step used in the analysis is $\Delta t=0.04$ s.

The simulation permits to characterize some important excavation variables. Firstly, the most important unknowns are the contact forces. Contact occurs when the disc edges come near the ground wall. An interface mesh of contact elements is generated and it anticipates the contact area. The contacting forces are transmitted through the contact elements to each domain. This interaction damages the solid material and digs into it. With the normal contact force and the relative sliding velocity an excavated volume and a worn volume are computed for each surface particle. The geometry of the ground is shaped at the same time the excavation moves forward. Figure 21 shows the distribution of wear on the head of the roadheader after the initial penetration on the massive rock and some seconds later when it rips onto the left side.

Fig. 21

Wear on the cutting tool after 20.9 s penetrating on the massive rock and at 158.12 s, when the roadheader is moving towards the side

The resultant of the surface forces can be translated to the axis of the roadheader in order to yield force and momentum reactions. This gives practical information of the power and torque needed for the excavation. At the same time, excavation forces generate accelerations on the rock which are transmitted to the surface. The foundation located on the top of the model vibrates due to the excavation. Figure 22 shows the produced acceleration for different stages of the excavation. This information is very useful in order to predict possible damages in buildings located on the ground surface.

Fig. 22

3D roadheader excavation. Contour lines of accelerations produced by the excavation forces

5.3 TBM excavation

The simulation of the actual functioning of a tunnel boring machine (TBM) is performed in this example. Figure 23 shows the actual geometry of the TMB head. It is a rock cutting head of small size. This machine is usually used when large water canalizations must go underground. That happens when the water piping crosses a highway or a populated area. This type of machines are used only for excavating hard rock. For soft rock grounds discs are not used and are generally replaced by picks.

Fig. 23

Geometry of TBM head

Fig. 24

Model of the real rock cutting head of the TBM

The geometry of a TBM is very complex. Therefore, a simplified model is created from the machine depicted in Fig.  23. Figure 24 shows the cutting head model of the TMB which will be used to excavate the piece of solid rock. In Table 3 the material properties for the rock-solid and the TMB head are presented. To model the excavation, the characteristics of the ground and the boreability of the cutting parts have to be defined. These properties are assigned to the TBM head surface for each disc. Generic values has been assigned for the boreability $K_d \subset (150,300)$, for the hardness of the rock material $H_d\sim 1.0\times 10^8 Pa$ and for the uniaxial compressive strength of the rock ${UCS}\sim 1.88\times 10^8 Pa$.

Table 3 Material properties for the TBM excavation example

The TBM kinematics are the head rotation and the forward movement. In order to reproduce them, a velocity of $\mathbf{v}=(0.01,0,0)$ m/s and a rotation of 4 rpm are imposed to the rear support of the TBM head. These movements are kept constant during the entire analysis. The rock-solid domain is fixed at the base.

The problem is analyzed using a mesh of 704475 4-noded tetrahedra with 127299 nodes. The mesh is finer in the excavation zone (see Fig.  25). The time step used in the analysis is $\Delta t=0.01$ s.

Fig. 25

Discretization of the model. The initial mesh has 704475 tetrahedra and 127299 nodes

Fig. 26

TBM simulations. Excavation rate and stresses on the rock surface in the initial interaction

Fig. 27

Normal forces and strains due to the excavation at the early stage of the excavation

Figures 26 and 27 show some results of the initial interaction between the TBM and the ground. The computed force evolution on the TMB cutting wheel is very irregular. Instantaneous action and reaction forces appear when discs impact on the rock face. Figure 27 shows the instantaneous forces of the TBM discs against the massive rock. From that results the power required for the TBM operation can be estimated.

Fig. 28

Volume loss due to wear on the TBM discs at time $t=1.79$s

The model also reproduces the volume loss due to excavation. Some volume on the surface of the ground is taken away automatically when discs dig on it. The prior geometry is shaped to the new geometry at each time step. The results provide a reference for the TMB excavation advance and prediction of wear on the cutting tools of the machine (Fig.  28).

Wear values are useful for predicting how many times the discs must be changed during the excavation of the tunnel. The most outworn tools can be also determined using the wear distribution on the TMB head. This is shown in Fig. 28 which depicts the wear produced on the TBM discs after some rotation and pressure over the rock surface.

6 Conclusions

This work presents advances of the PFEM for the modelling and simulation of ground excavation and wear of rock cutting tools in tunnelling processes. The algorithms for the particle transfer scheme, the definition of the geometrical boundary, the treatment of frictional contact, the models for predicting tool wear and excavation have been explained.

The derivation of the discretized equations in the PFEM is based on the standard FEM. This permits the use of well-known constitutive equations of continuum mechanics and all the existing background theoretical and numerical knowledge in the FEM.

Preliminary results show that the PFEM is a good method to model complex excavation problems and wear of rock cutting tools. As such, it promises to be a powerful technique for solving a wide range of complex 3D problems of practical interest in underground constructions in civil and mining engineering.

The next challenge in the proposed method is its detailed validation with experimental data on excavation and wear for different geomaterials and rock cutting tools and machinery.