ESPFEM2D: A MATLAB 2D explicit smoothed particle finite element method code for geotechnical large deformation analysis

Abstract

The Smoothed Particle Finite Element Method (SPFEM) has gained popularity as an effective numerical method for modelling geotechnical problems involving large deformations. To promote the research and application of SPFEM in geotechnical engineering, we present ESPFEM2D, an open-source two-dimensional SPFEM solver developed using MATLAB. ESPFEM2D discretizes the problem domain into computable particle clouds and generates the finite element mesh using Delaunay triangulation and the $\alpha$-shape technique to resolve mesh distortion issues. Additionally, it incorporates a nodal integration technique based on strain smoothing, effectively eliminating defects associated with the state variable mapping after remeshing. Furthermore, the solver adopts a simple yet robust approach to prevent the rank-deficiency problem due to under-integration by using only nodes as integration points. The Drucker-Prager model is adopted to describe the soil’s constitutive behavior as a demonstration. Implemented in MATLAB, this open-source solver ensures easy accessibility and readability for researchers interested in utilizing SPFEM. ESPFEM2D can be easily extended and effectively coupled with other existing codes, enabling its application to simulate a wide range of large geomechanical deformation problems. Through rigorous validation using four numerical examples, namely the oscillation of an elastic cantilever beam, non-cohesive soil collapse, cohesive soil collapse, and slope stability analysis, the accuracy, effectiveness and stability of this open-source solver have been thoroughly confirmed.

1 Introduction

Numerous geotechnical engineering topics involve large deformations, such as landslides, avalanches, debris flows, cone penetration tests, pile installation, et al. With the development of geotechnical numerical analysis, the large deformation simulation has become increasingly popular in addressing these issues, garnering significant research attention in recent years. Effective numerical methods for large deformation analysis must accurately capture the geometric changes in surface profiles and soil layers. However, traditional mesh-based numerical methods (e.g., finite element method (FEM), finite difference method (FDM)) are prone to mesh distortion during large deformation. Even if only a few meshes are severely distorted, the calculation will be interrupted.

To address the issue of mesh distortion in traditional FEM during large deformation, numerous alternative methods have been proposed. Some representative methods include Arbitrary Lagrangian–Eulerian (ALE), Coupled Eulerian-Lagrangian (CEL) and Remeshing and Interpolation Technique with Small Strain (RITSS). In ALE [1, 2], an excessively deformed mesh is substituted by another one with regularly-shaped elements and the state variables are mapped from the old mesh to the new one. This approach has been called ALE because the transfer of state variables from one mesh to another is perceived as a convection process similar to that in classical Eulerian analysis. CEL, which is a method very similar to ALE, has gained popularity in geotechnical analysis, especially due to its presence in the commercial codes Abaqus/Explicit [3, 4] and LS-DYNA[5]. The basis of CEL is that there are two domains, one Eulerian domain and one Lagrangian domain, that interact with each other via a suitable contact formulation. RITSS was first proposed by Hu and Randolph [6], which is based on implicit time integration for Lagrangian computation with mesh re-profiling techniques and state variable interpolation techniques to solve the mesh distortion problem.

Another class of numerical methods for solving large deformation problems is the particle-based methods, which discretize the geotechnical body into a series of particles that can freely move within the computational domain, thereby overcoming the mesh distortion problem encountered by traditional mesh-based methods during large deformation. Currently, the commonly used particle-based methods include Smoothed Particle Hydrodynamics (SPH), Material Point Method (MPM), and Particle Finite Element Method (PFEM). Initially proposed for solving astrophysical problems [7], SPH has found widespread applications in solving geotechnical problems [8,9,10]. Two key difficulties with SPH for solid modelling are the imposing of essential boundary conditions and the so-called tensile instability. MPM combines the advantages of particle-based and mesh-based methods by discretizing the continuum into material points. It preserves the state variable information on these material points while maintaining a fixed background mesh to solve the governing momentum equations [11,12,13,14]. However, MPM is prone to computational inaccuracies, particularly stress oscillations and inaccuracies [15]. PFEM was initially proposed by O$\tilde{\text {n}}$ate et al. [16,17,18] with the primary goal of solving fluid dynamics and fluid–structure interaction problems. In recent years, it has gained significant popularity for solid large deformation analysis [19,20,21,22]. PFEM treats the nodes in the FEM mesh as particles, and addresses mesh distortion during large deformation through frequent mesh re-discretization and state variable mapping. The updated Lagrangian FEM is utilized for solving the governing equation.

Among the three particle-based methods, PFEM inherits the sound theoretical basis of FEM while maintaining the flexibility of the particle-based method, and thus has been widely used in geotechnical large deformation analysis. However, PFEM performs numerical integration on Gaussian points while storing state variable information on particles. This necessitates frequent information transfer between Gaussian points and particles (i.e. nodes), adding complexity and introducing errors. To overcome this defect, a nodal integration technique based on strain smoothing has been introduced by the authors to improve PFEM, leading to a novel framework, known as Smooth Particle Finite Element Method (SPFEM) [23,24,25,26,27]. With the nodal integration technique, all state variables are calculated and stored on particles. This approach simplifies the computational procedure, eliminates errors caused by mapping, and helps mitigate volume-locking issues.

To this end, it is important for geotechnical researchers who are already utilizing the aforementioned methods, as well as for new users looking to adopt them, to have access to an efficient open-source solver. ABAQUS software [3, 4] and LS-DYNA [5] provide options for implementing CEL, ALE, and SPH methods. However, the underlying codes are hidden from users, which hinders the promotion of applications and in-depth research on numerical methods. In terms of SPH, many open-source codes are available, such as GADGET [28, 29], GIZMO [30, 31], SPHysics [32, 33], DualSPHyiscs [34, 35], and GPU SPH [36], et al. SPH open-source solvers specific to geotechnical problems have been developed as well, such as the 3D GPU-accelerated SPH open-source solver LOQUAT proposed by Peng et al. [37]. For open-source solvers of MPM, many codes are available, such as NairnMPM, Uintah and Cb-Geo [38]. Uintah is a massively parallel, multi-physics process simulation platform that implements MPM and can be used to simulate the behavior of solid materials [39]. The open-source solvers of PFEM are few in comparison with SPH and MPM. Kratos, which is an object-oriented framework of FEM, has implemented PFEM by linking with an external mesh generation library [40]. Guo and Yang [38] proposed NSPFEM2D, a 2D SPFEM open-source solver based on C++ and Python. However, the hybrid programming of C++ and Python is less readable and less easy to use for mechanical researchers in comparison to the MATLAB language. Herein, this paper introduces a MATLAB-based open-source solver for SPFEM named ESPFEM2D, aiming to enable interested researchers to more easily grasp the method and promote the research and application of SPFEM. ESPFEM2D employs an explicit time integration scheme and utilizes the Drucker-Prager model to describe the soil constitutive behavior as a demonstration. It can be easily extended and effectively coupled with other existing codes to simulate various geotechnical large deformation problems.

The following sections are organized as follows. Section 2 provides an introduction to the fundamental theory of explicit SPFEM. Section 3 elaborates on the implementation details of the ESPFEM2D code. In Sect. 4, the open-source solver is demonstrated through application examples, including simulations of the oscillation of an elastic cantilever beam, non-cohesive soil collapse, cohesive soil collapse, and slope stability analysis. These examples serve to verify the accuracy, validity, and robustness of the solver. Finally, a summary is presented in Sect. 5.

2 Theory of ESPFEM2D

2.1 Governing equations

The explicit SPFEM [25, 27] employs the same governing equations with the FEM. The linear momentum conservation of the continuum in the computational domain can be represented as

$$\begin{aligned} \rho {\varvec{a}} = \nabla \cdot {\varvec{\sigma }} + \rho {\varvec{b}} \end{aligned}$$

(1)

where $\rho$ represents the material density, ${\varvec{a}}$ denotes the acceleration, ${\varvec{\sigma }}$ represents the Cauchy stress tensor, and ${\varvec{b}}$ represents the specific body density acting on the object. By considering the principle of virtual displacement and the divergence theorem, the weak form of the governing equation can be expressed as

$$\begin{aligned} \int _{\Omega } \delta {\varvec{u}} \cdot \rho {\varvec{a}} \textrm{d} \Omega= & {} \int _{S}\delta {\varvec{u}} \cdot {\varvec{\tau }} \textrm{d}S\nonumber \\{} & {} + \int _{\Omega } \delta {\varvec{u}} \cdot \rho {\varvec{b}} \textrm{d} \Omega - \int _{\Omega } \nabla \delta {\varvec{u}}: {\varvec{\sigma }} \textrm{d} \Omega \end{aligned}$$

(2)

where ${\varvec{u}}$ represents the displacement vector, $\Omega$ denotes the configuration domain, $S$ represents the boundary domain, and ${\varvec{\tau }}$ is the prescribed traction force.

2.2 Spatial discretization

The SPFEM first discretizes the problem domain into a particle cloud and then generates a finite element mesh by combining Delaunay triangulation and $\alpha$-shape techniques [41]. Furthermore, the nodal integration technique based on strain smoothing [42, 43] is used to solve Eq. (2).

Fig. 1

Smoothing sub-cells associated with particles

As shown in Fig. 1, the problem domain $\Omega$ is divided into $N _{n}$ strain-smoothed sub-cells associated with particle such that $\Omega = {\textstyle \sum _{k=1}^{N_{n}}} \Omega ^{k}$ and $\Omega ^{i} \bigcap \Omega ^{j} = \phi$, $i\ne j$ where $\phi$ denotes the empty set. Each smoothing sub-cell associated with particle $k$ is created by sequentially connecting the midpoints of the edges of the triangular elements around particle $k$ to their centroids. Thus, each triangular element is divided into three quadrilateral subdomains. Afterward, the strain tensor $\tilde{{\varvec{\varepsilon }}}_{k}$ associated with particle $k$ is obtained as

$$\begin{aligned} \tilde{{\varvec{\varepsilon }}}_{k} = \sum _{I = 1}^{N^{k}} \tilde{{\varvec{B}}}_{I}\left( {\varvec{x}}_{k} \right) {\varvec{u}}_{I} \end{aligned}$$

(3)

where $I$ is the particle number, ${\varvec{x}}_{k}$ is the coordinate of particle $k$, $N ^{k}$ is the number of particles connected to particle $k$, ${\varvec{u}}_{I}$ is the displacement of particle $I$, and $\tilde{{\varvec{B}}}$ is the smoothed strain matrix.

For triangular elements, due to the constant element strain, the smooth strain matrix can be simply calculated as follows

$$\begin{aligned} \tilde{{\varvec{B}}}_{I}\left( {\varvec{x}}_{k}\right) = \frac{1}{A_{k}} \sum _{j=1}^{N_{e}^{k}} \frac{1}{3} A_{e}^{j} {\varvec{B}}_{j} \end{aligned}$$

(4)

where $N _{e}^{k}$ is the number of elements around particle $k$, $j$ is the element number, $A _{e}^{j}$ and ${\varvec{B}}_{j}$ are respectively the area and strain gradient matrix of the $\textit{j}$th triangular element around particle $k$, and $A_{k}$ is the area of smoothing sub-cell associated with particle $k$ which can be calculated by the following equation:

$$\begin{aligned} A_{k} = \int _{\Omega ^{k}} \textrm{d} \Omega = \frac{1}{3} \sum _{j=1}^{N_{e}^{k}} A_{e}^{j} \end{aligned}$$

(5)

Using the standard Galerkin method and performing the node-based discretization, the global discretized formulation of the weak form Eq. (2) can be expressed as

$$\begin{aligned} {\varvec{M}} {\varvec{a}} = {\varvec{F}}^{ext} - {\varvec{F}}^{int} \end{aligned}$$

(6)

in which

$$\begin{aligned} {\varvec{F}}^{ext}= & {} \sum _{k=1}^{N_{n}} \int _{S} {\varvec{N}}_{k} {\varvec{\tau }} \textrm{d} S + \sum _{k=1}^{N_{n}} \rho {\varvec{b}}_{k} A_{k} \end{aligned}$$

(7)

$$\begin{aligned} {\varvec{F}}^{int}= & {} \sum _{k=1}^{N_{n}} \tilde{{\varvec{B}}}_{k} {\varvec{\sigma }}_{k} A_{k} \end{aligned}$$

(8)

$$\begin{aligned} {\varvec{M}}= & {} \sum _{k=1}^{N_{n}} \rho A_{k} \end{aligned}$$

(9)

where ${\varvec{F}}^{ext}$ represents the external force, ${\varvec{F}}^{int}$ denotes the internal force, and ${\varvec{M}}$ represents the diagonal mass matrix.

2.3 Temporal discretization

The present SPFEM utilizes the explicit time integration scheme. The leapfrog approach is implemented, which is a second-order accuracy method [25]. Equation (10) is used to update the acceleration of particles at the $n$-th step, followed by Eqs. (11) and (12) applied to update the velocity and position of particles, i.e.

$$\begin{aligned} {\varvec{a}}^{n}= & {} {\varvec{M}}^{-1}\left( {\varvec{F}}^{ext} - {\varvec{F}}^{int}\right) \end{aligned}$$

(10)

$$\begin{aligned} {\varvec{v}}^{n + \frac{1}{2}}= & {} {\varvec{v}}^{n - \frac{1}{2}} + \Delta t {\varvec{a}}^{n} \end{aligned}$$

(11)

$$\begin{aligned} {\textbf{u}}^{n + 1}= & {} {\textbf{u}}^{n} + \Delta t {\varvec{v}}^{n + \frac{1}{2}} \end{aligned}$$

(12)

In addition, to simulate static problems with the dynamic relaxation method, a local damping force term is added to the system, which is calculated as

$$\begin{aligned} {\varvec{F}}^{\xi } = - \xi \cdot \left| ({\varvec{F}}^{ext} - {\varvec{F}}^{int}) \right| \textrm{sign}({\varvec{v}}^{n - \frac{1}{2}}) \end{aligned}$$

(13)

where $\xi$ is the damping constant.

2.4 Constitutive model

To obtain a smooth yield surface that approximates the classic Mohr-Coulomb surface for numerical convenience, Drucker-Prager introduced the following yielding criterion,

$$\begin{aligned} f = \alpha I_{1} + \sqrt{J_{2}} - k \end{aligned}$$

(14)

where $I_{1}$ represents the first invariant of the stress tensor, $J_{2}$ denotes the second invariant of the deviatoric stress tensor, $\alpha$ and $k$ represent the material constants, respectively. To align with the Mohr-Coulomb yield surface, three schemes can be adopted. In the first two schemes, we use

$$\begin{aligned} \alpha = \frac{2 \textrm{sin} \varphi }{\sqrt{3} \left( 3 {\mp } \textrm{sin} \varphi \right) }, k = \frac{6c \textrm{cos} \varphi }{\sqrt{3} \left( 3 {\mp } \textrm{sin} \varphi \right) } \end{aligned}$$

(15)

where $c$ represents the cohesion and $\varphi$ denotes the friction angle. The plus sign in Eq. (15) represents the Drucker-Prager yield surface passing through the inner apexes of the Mohr-Coulomb yield surface in the $\pi$-plane, while the minus sign represents the outer apexes. In the third scheme, we use

$$\begin{aligned} \alpha = \frac{\textrm{tan} \varphi }{\sqrt{9 + 12 \textrm{tan}^{2} \varphi }}, k = \frac{3c}{\sqrt{9 + 12 \textrm{tan}^{2} \varphi }} \end{aligned}$$

(16)

which indicates that the Drucker–Prager yield surface inscribes the Mohr-Coulomb yield surface in the $\pi$-plane.

The same plastic potential function as the yield function is used, which is given by

$$\begin{aligned} g = \sqrt{J_{2}} + \alpha _{ \Phi } I_{1} \end{aligned}$$

(17)

where $\alpha _{ \Phi }$ represents the dilatancy coefficient, which is associated with the ratio of plastic volume change to plastic shear strain.

The classic return-mapping algorithm is used to implement stress point integration. Although more complicated soil constitutive models can be used, we use the Drucker-Prager elastic perfectly-plastic model for demonstration purposes. The extension to other constitutive models for the ESPFEM2D solver is straightforward.

2.5 Rigid boundary contact

A rigid boundary contact algorithm is employed to account for the soil interaction with a rigid boundary. As shown in Fig. 2, the interaction between soil particles and a rigid boundary must satisfy the following contact constraints, also known as Signorini conditions [44]:

$$\begin{aligned} \begin{matrix} g_{n} \ge 0, \sigma _{n} \ge 0, \sigma _{n} g_{n} = 0 \\ \left| \sigma _{t}\right| - \mu \sigma _{n}\le 0 \end{matrix} \end{aligned}$$

(18)

where $g _{n}$ represents the gap between the particle and the boundary, $\sigma _{n}$ denotes the normal contact pressure, $\sigma _{t}$ represents the tangential stress, and $\mu$ is the friction coefficient.

A prediction-correction algorithm is employed to ensure the contact constraint. First, the positions and velocities of all particles are predicted assuming that no contact occurs. Then, contact is activated when the gap between particles and line segments is less than zero. It is assumed that the normal contact force can completely suppress the normal penetration velocity of the particles during the time step, resulting in:

$$\begin{aligned} {\varvec{f}}_{I}^{n} = -\frac{m_{I} v_{I}^{n}}{\Delta t} {\varvec{e}}_{n} \end{aligned}$$

(19)

where $m_{I}$ represents the mass of particle $I$, $v _{I}^{n}\left( = {\varvec{v}}_{I} \cdot {\varvec{e}}_{n}\right)$ denotes the normal projection of the relative velocity between the particle and the rigid boundary, which is negative upon contact, $\Delta t$ is the time step, and ${\varvec{e}}_{n}$ represents the normal vector of the rigid boundary. Similarly, the tangential contact force ${\varvec{f}}_{I}^{t}$ is calculated by assuming viscous conditions as follows:

$$\begin{aligned} {\varvec{f}}_{I}^{t} = - \frac{m_{I}\left( {\varvec{v}}_{I} - v_{I}^{n} \cdot {\varvec{e}}_{n}\right) }{\Delta t} \end{aligned}$$

(20)

The tangential force is also subject to Coulomb friction, which sets a limit $\left| {\varvec{f}}_{I}^{t}\right| \le \mu \left| {\varvec{f}}_{I}^{n}\right|$ to the magnitude of the tangential force, where $\mu$ is the friction coefficient. It should be pointed out that the current prediction-correction method does not involve additional penalty parameters and thus does not affect the time step.

After determining the contact force, the corrected velocity of the particle is calculated as follows:

$$\begin{aligned} \bar{{\varvec{v}}} _{I} = {\varvec{v}}_{I} +\Delta t \frac{{\varvec{f}}_{n}^{c} + {\varvec{f}}_{t}^{c}}{m_{I}} \end{aligned}$$

(21)

where ${\varvec{v}}_{I}$ represents the predicted velocity of particle $I$.

Fig. 2

The contact between a deformable body and a rigid surface

2.6 Remeshing

The mesh reconstruction technique is a crucial aspect of SPFEM to prevent mesh distortion during large deformations. In SPFEM, the mesh reconstruction technique combines the Delaunay triangulation technique with the $\alpha$-shape algorithm, forming a two-step mesh reconstruction algorithm [45]. First, the Delaunay triangulation is performed based on the particle cloud to generate a convex domain and reconstruct the triangular mesh. Then, the $\alpha$-shape algorithm is employed to calculate the radius of the sphere for each triangular element and delete the triangular elements with a radius greater than $\alpha h$ where $\alpha$ is a predefined parameter generally ranging from 1.2$\sim$1.6 and $h$ is the characteristic spacing of particles. As a result, the remaining triangular elements correspond to the computational domain [16].

In SPFEM, due to the nodal integration technique based on strain smoothing, more distorted meshes can be utilized without significant loss of accuracy. Thus, the requirements for mesh quality are not as stringent as in the original PFEM. However, a mesh smoothing technique is still necessary to enhance the mesh quality and to increase the critical time step. Specifically, the Laplacian smoothing technique [46, 47] is utilized when a few particles are too close to their adjacent particles. Although other mesh smoothing techniques (e.g. Meduri et al. [48], Vartziotis et al. [49]) can also be employed, we use the Laplacian smoothing technique due to its simplicity and high efficiency.

Fig. 3

Primary procedures of PFEM for a typical calculation step

2.7 Rank-deficiency treatment

Despite the success of the nodal integration technique in many applications, in some cases, the results may be not reliable due to spurious low-energy instability. This instability associated with the under-integrating using only nodes is also known as rank-deficiency or rank-instability in the literature [23, 50,51,52,53,54,55,56,57].

To circumvent this instability associated with nodal integration, we proposed a simple yet robust coping control approach [58], which has also been implemented in ESPFEM2D. The key idea of the approach is to ensure that all the particles in the smoothing element follow a single linear velocity field by adding correction forces. The correction force on particle $i$ due to all neighbors $j$ in the smoothing cell is computed as

$$\begin{aligned} {\varvec{f}}_{ij} = \sum _{I=1}^{N_{k}} \frac{\beta }{2\left\| {\varvec{x}}_{ij}^{t}\right\| }\left( E_{i} \mathrm {\Omega }_{i} \frac{\delta _{ij}^{i}}{\left\| {\varvec{x}}_{ij}^{t}\right\| } + E_{j} \mathrm {\Omega }_{j} \frac{\delta _{ij}^{j}}{\left\| {\varvec{x}}_{ij}^{t}\right\| }\right) {\varvec{n}}_{ij}^{t + \Delta t} \end{aligned}$$

(22)

where $\beta$ represents the artificial control parameter ranging from 0.1 to 1.0, $\left\| {\varvec{x}}_{ij}^{t}\right\|$ represents the actual distance vector of the deformed coordinates at time $t$, $E _{i}$ and $E _{j}$ are Young’s modulus of smoothing cells $i$ and $j$ respectively, $\mathrm {\Omega }_{i}$ and $\mathrm {\Omega }_{j}$ represent the area of smoothing cells $i$ and $j$ respectively, $\delta _{ij}^{i}$ represents the projected length of the error vector, ${\varvec{n}}_{ij}^{t + \Delta t}$ represents the unit normal of distance vector ${\varvec{x}}_{ij}^{t + \Delta t}$ which can be calculated as ${\varvec{n}}_{ij}^{t + \Delta t} = {\varvec{x}}_{ij}^{t + \Delta t} / \left\| {\varvec{x}}_{ij}^{t}\right\|$. Readers can refer to Yuan et al. [58] for a detailed description.

3 Description of the open-source solver ESPFEM2D

3.1 Overview

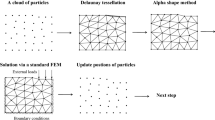
The primary procedures of PFEM for a typical calculation step is shown in Fig. 3. First, we discretize the region into a set of nodes/particles. Then, we obtain the FEM mesh by consequently using the Delaunay triangulation technique and the $\alpha$-shape algorithm. With the FEM mesh generated, we solve the governing equation using the incremental FEM. The nodal coordinates of the FEM mesh are then updated according to the incremental displacement results. If the FEM mesh is too distorted, we discard the old mesh and generate a new one based on the set of nodes/particles.

The code workflow diagram of the open-source solver ESPFEM2D is shown in Fig. 4. All the 10 steps in the workflow diagram are implemented in the form of MATLAB functions except that the MATLAB script named $\texttt {SPFEM.m}$ is used as the main program. The MATLAB function names corresponding to all the 10 computational steps are shown in Fig. 5.

The installation of the ESPFEM2D can be done by simply adding a path of \$\texttt {ESPFEM2D}$ directory to the MATLAB search path. The practical usage of ESPFEM2D can be simply realized by running the main MATLAB script $\texttt {SPFEM.m}$.

To facilitate the users, we provide 4 demo examples, i.e., all the validation and verification examples in Sect. 4. A total of 7 simulations are available for these 4 examples, as two simulation stages are required for the last 3 examples. Each simulation has a separate ID. By changing the variable $\texttt {iEX}$ in $\texttt {SPFEM.m}$, the simulation ID is selected and the corresponding pre-processing for the simulation is implemented in the function $\texttt {input\_data.m}$. These demonstration examples can be used as the reference for the ESPFEM2D users to create new geotechnical large deformation simulation applications.

Fig. 4

Code workflow diagram of the open-source solver ESPFEM2D

Fig. 5

MATLAB function names corresponding to all the computational steps

3.2 The ESPFEM2D repository

The MATLAB open-source solver ESPFEM2D is freely available from the repository: https://github.com/WeiZhang-2023/ESPFEM2D. The structure of the repository, illustrated in Fig. 6, is described in this section.

The directory $\texttt {ESPFEM2D}$ comprises four subdirectories of the comprehensive open-source solver ESPFEM2D, and the main script $\texttt {SPFEM.m}$, which can be executed to initiate the simulation.

The directory $\texttt {comp}$ contains the MATLAB functions associated with the core computational procedure of the explicit SPFEM, including Step 1, Step 10, and Steps 4$\sim$9 in Fig. 4.

The directory $\texttt {constitutive\_model}$ contains the MATLAB functions associated with the numerical implementation of constitutive models. The linear elastic constitutive model and the Druker-Prager elastic perfect-plastic model are available. New constitutive models can be implemented by simply adding a new MATLAB function similar to the MATLAB function $\texttt {mat\_model\_DP.m}$ (see Fig. 5).

The directory $\texttt {mesh}$ contains the MATLAB functions associated with the mesh generation and remeshing, including the Delaunay triangulation and $\alpha$-shape techniques, the calculation of element quality, the nodal integration technique based on strain smoothing, and the retrieval of related particle and element data. It should be pointed out that in PFEM, it is beneficial to add new nodes in those areas we are interested in. However, we choose to use a simple yet robust remeshing algorithm in the open-source code ESPFEM2D for demonstration purposes. With the basic remeshing algorithm mastered, the readers can realize complex remeshing algorithms (including adding nodes, deleting nodes, mesh optimization, Yuan et al. [59, 60]) by modifying the MATLAB codes in the directory $\texttt {mesh}$.

The directory $\texttt {example}$ includes the MATLAB functions associated with the pre-processing for simulations. A MATLAB function corresponds to a simulation, including the particle distribution, the material model and parameters, the definition of the boundary conditions, the initial condition settings, and the monitoring and output settings.

The directory $\texttt {documentation}$ contains a $\texttt {.pdf}$ file that provides a systematic tutorial on setting up a basic problem, along with explanations of code functions and variable definitions.

The directory $\texttt {out\_put}$ is used to save computational result files. $\texttt {.vtk}$ files are created to save the field information intermittently, while a $\texttt {.csv}$ file is created to monitor the evolution of the interested results for particular particles.

Fig. 6

Structure of the open-source solver ESPEM2D repository

3.3 Variables

The primary variables in ESPFEM2D are introduced as follows:

• $\texttt {iEX}$: a separate ID of each simulation.

• $\texttt {nCoor}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 containing the x - and y - coordinates of each node/ particle.

• $\texttt {eNode}$: array of dimension $\texttt {par}$-$>\texttt {element\_cnt}\times$3 containing three node/particle IDs corresponding to each element.

• $\texttt {nMat}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$1 containing the type of constitutive model for each node/particle.

• $\texttt {nAccel}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 containing the accelerations in the x - and y - directions of each node/particle.

• $\texttt {nVel}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 containing the velocities in the x - and y - directions of each node/particle.

• $\texttt {nDisp}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 containing the total displacements in the x - and y - directions of each node/particle.

• $\texttt {nDdisp}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 containing the incremental displacements in the x - and y - directions of each node/particle.

• $\texttt {nStress}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$4 containing the stresses of each node/particle.

• $\texttt {nPstrain\_eq}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$1 containing the equivalent plastic strain of each node/particle.

• $\texttt {nBoundT}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 specifying the boundary condition type in the x - and y - directions of each node/particle.

• $\texttt {nBoundV}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 containing the value of boundary conditions in the x - and y - directions of each node/particle.

• $\texttt {nREN}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$1 containing the number of elements around each node/particle.

• $\texttt {nREs}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times \texttt {par}$-$>\texttt {MN}$ containing the element IDs around each node/particle.

• $\texttt {nRNN}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$1 containing the number of nodes/particles around each node/particle.

• $\texttt {nRNs}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times \texttt {par}$-$>\texttt {MN}\cdot$3 containing the node/particle IDs around each node/particle.

• $\texttt {nFrd}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 containing the rank-deficiency correction forces in the x - and y - direction for each node/particle.

• $\texttt {nFint}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$2 containing the internal forces in the x - and y - directions of each node/particle.

• $\texttt {eArea}$: array of dimension $\texttt {par}$-$>\texttt {element\_cnt}\times$1 containing the area of each element.

• $\texttt {eDNdx}$, $\texttt {eDNdy}$: array of dimension $\texttt {par}$-$>\texttt {element\_cnt}\times$3 containing the partial derivatives of the shape function concerning x and y for the three nodes/particles corresponding to each element, respectively.

• $\texttt {nArea}$: array of dimension $\texttt {par}$-$>\texttt {node\_cnt}\times$1 containing the area of each strain smoothing cell associated with node/particle.

• $\texttt {nDNdx}$, $\texttt {nDNdy}$: array of dimension $\texttt {par}$-$>\texttt {element\_cnt}\times \texttt {par}$-$>\texttt {MN}\cdot$3 containing the partial derivatives of the shape function concerning x and y for each node/particle, respectively.

3.4 Functions

The primary functions in ESPFEM2D are summarized as follows:

• $\texttt {input\_data.m}$: set up a problem.

• $\texttt {initializing.m}$: prepare for the calculation process of ESPFEM2D.

• $\texttt {mesh\_alpha\_shape.m}$: identify the computational domain boundary using the $\alpha$-shape technique (see Sect. 2.6).

• $\texttt {mesh\_get\_related\_element\_node.m}$: get related particle and element information (see Sect. 2.6).

• $\texttt {mesh\_remesh.m}$: reconstruct the finite element mesh (see Sect. 2.6).

• $\texttt {mesh\_quality.m}$: get the mesh quality (see Sect. 2.6).

• $\texttt {element\_data\_prepare.m}$: get element information (see Sect. 2.2).

• $\texttt {node\_data\_prepare.m}$: get node/particle information (see Sect. 2.2).

• $\texttt {mesh\_lap\_smoothing.m}$: perform Laplacian smoothing for the mesh (see Sect. 2.2).

• $\texttt {constitutive\_model.m}$: select constitutive model (see Sect. 2.4).

• $\texttt {mat\_model\_elas.m}$: implement the elasticity constitutive model (see Sect. 2.4).

• $\texttt {mat\_model\_DP.m}$: implement the Drucker-Prager constitutive model (see Sect. 2.4).

• $\texttt {force\_int.m}$: calculate the nodal internal forces (see Sect. 2.2).

• $\texttt {update\_half\_velocity.m}$: prepare for the leapfrog time integration (see Sect. 2.3).

• $\texttt {force\_rank\_deficiency.m}$: calculate the rank-deficiency correction forces (see Sect. 2.7).

• $\texttt {time\_integration.m}$: perform time integration (see Sect. 2.3).

• $\texttt {contact\_wall.m}$: treatment of rigid boundary contact (see Sect. 2.5).

• $\texttt {output\_vtk.m}$: output the field results.

• $\texttt {save\_monitor\_data.m}$: output the monitoring results.

3.5 Main program

This section concentrates on the essential component of the code, SPFEM.m, which orchestrates and executes all functions required for simulation. Listing 1 presents the MATLAB code snippet contained within $\texttt {SPFEM.m}$. The code workflow diagram for the open-source solver ESPFEM2D shown in Fig. 4 can be better understood by reading the codes in $\texttt {SPFEM.m}$.

4 Verification and demonstration examples

To verify the accuracy, effectiveness, and stability of the open-source solver ESPFEM2D, four numerical examples are given in this section, i.e., the oscillation of an elastic cantilever beam, non-cohesive soil collapse under gravity loading, cohesive soil collapse, and the failure of Mohr-Coulomb soil slope. All these examples verify the accuracy and effectiveness of the ESPFEM2D. Moreover, with the first example, we primarily aim to demonstrate the effectiveness of the rank-deficiency treatment technique to maintain numerical stability. Meanwhile, we compare the computational efficiency between the ESPFEM2D and an existing SPFEM open-source code.

4.1 Oscillation of an elastic cantilever beam

An undamped elastic cantilever beam experiencing vibrations induced by a sudden application of gravitational acceleration is considered. The problem’s geometry and model setup are depicted in Fig. 7. The cantilever beam measures 2.0 m in length and 0.2 m in height, with its left end fixed and other edges of the beam free. The material parameters are as follows: Young’s modulus $E =$ 80.0 MPa, Poisson’s ratio $\nu =$ 0.25, and density $\rho = 1850$ $\textrm{kg}/\textrm{m}^{3}$. We investigate the problem using a total time of $t =$ 4.0 s and a constant time step of $\Delta t = 1 \times 10^{-5}$ s. The domain is discretized into 1111 particles. The rank-deficiency correction parameter $\beta$ in Eq. (22) is taken to be 0.0 and 0.1 sequentially to solve this problem, corresponding to SPFEM without rank-deficiency correction and SPFEM with rank-deficiency correction, respectively. The results obtained by the FEM [61] are used as a reference.

Fig. 7

Oscillation of an elastic cantilever beam: setup and geometry

The final stress distribution is depicted in Fig. 8. It is evident that the SPFEM with rank-deficiency correction exhibits a smoother stress field compared to the SPFEM without rank-deficiency correction, effectively mitigating stress distribution oscillations (e.g., inhomogeneity of stress distribution) caused by rank-instability associated with the nodal integration technique [50,51,52,53,54,55,56,57]. Figures 9 and 10 display the vertical displacements and velocities to time at the end of the cantilever beam. Figure 11 displays the evolution of the axial stress at the fixed end. Remarkably, the results obtained through the SPFEM with rank-deficiency treatment show excellent agreement with the corresponding FEM results [61]. In contrast, the SPFEM without rank-deficiency treatment demonstrates a gradual deviation, which clearly demonstrates the rank-instability. It is clear that the rank-instability issue is mitigated and smoother stress and displacement fields can be obtained by employing the SPFEM with rank-deficiency treatment.

We note that in terms of explicit SPFEM, an open-source code NSPFEM2D [38], which is built using hybrid C++ and Python programming, is also available to the public. It would be interesting to compare the computational efficiency between the NSPFEM2D and the ESPFEM2D presented in this paper. For the same problem, a total of 7 simulations with different numbers of nodes/particles are performed using NSPFEM2D and ESPFEM2D respectively, using a personal computer with an Intel(R) Core(TM) i5-8500 CPU, the main frequency of which is 3.00 GHz. The computational time costs are compared in Table 1. The results clearly show that when the number of nodes exceeds 729, the computational efficiency of ESPFEM2D outperforms that of NSPFEM2D. When the number of nodes is relatively large, the efficiency advantage is more apparent. The chief reason may be that in NSPFEM2D the computational procedure is driven by Python which runs much slower than MATLAB.

Fig. 8

Stress distributions at t = 4 s. ${{\textbf {a}}}$ SPFEM without rank-deficiency treatment. ${{\textbf {b}}}$ SPFEM with rank-deficiency treatment

Fig. 9

Vertical displacement of point B (see Fig. 7) on the end of the cantilever as a function of time

Fig. 10

Vertical velocity of point B (see Fig. 7) on the end of the cantilever as a function of time

Fig. 11

Stress $\sigma _{xx}$ history of point A (see Fig. 7)

Table 1 Efficiency comparison between ESPFEM2D and NSPFEM2D

4.2 Non-cohesive soil collapse

The following examples involve geotechnical applications. The collapse of non-cohesive soil is considered first. The problem setup and geometric model involve a rectangular soil column with dimensions of 0.2 m in width and 0.1 m in height, as illustrated in Fig. 12. The boundary conditions consist of a fixed constraint at the bottom and a normal constraint on the left side. The corresponding physical experiment has been conducted by Nguyen et al. [62], and their results can serve as a reference for comparison in this analysis. The soil material properties are as follows: Young’s modulus $E =$ 5.84 MPa, Poisson’s ratio $\nu =$ 0.3, density $\rho = 26.5$ $\textrm{kN}/\textrm{m}^{3}$, friction angle $\varphi = 19.8^{\circ }$, dilation angle $\Phi = 0^{\circ }$, and cohesion $c =$ 0 kPa. We investigate the problem using a total time of $t =$ 0.6 s and a constant time step of $\Delta t = 1 \times 10^{-6}$ s. The domain is discretized into 5894 particles.

Fig. 12

Non-cohesive soil collapse: setup and geometry of the analysis

The simulation results of the non-cohesive soil collapse process using ESPFEM2D are illustrated in Fig. 13, which shows the distribution of equivalent plastic strain during non-cohesive soil collapse at different time steps, and compares the simulation results with experimental observations from the literature [62]. The simulation results obtained from ESPFEM2D are in good agreement with the results reported by Nguyen et al. [62] at different time steps. Under the influence of gravity, the right end of the non-cohesive soil column initiates the collapse process, with deformation starting in the top region while a portion remains undisturbed. As the collapse progresses, the undisturbed area gradually decreases, and the granular material flows and undergoes deformation, forming a slope-like deposit that propagates from the lower right corner toward the top. Throughout the collapse process, a stationary region is observed in the lower left corner of the soil column, with the surface of this region defined as the slip line. The damage state of the non-cohesive soil column in Fig. 13 shows that the slip line obtained from the ESPFEM2D simulation aligns with the experimental observations.

Fig. 13

Comparison of equivalent plastic strain between the experiment results (left) and the simulation results obtained from ESPFEM2D (right)

Fig. 14

Cohesive soil collapse: setup and geometry of the analysis

4.3 Cohesive soil collapse

The cohesive soil collapse problem was originally presented by Bui et al. [9] and has been previously investigated as a benchmark example by some researchers [63, 64]. The problem setup and geometric model are illustrated in Fig. 14. The rectangular domain has dimensions of height (H) = 2 m and width (L) = 4 m. The material parameters, as reported by Chalk et al. [63], are as follows: Young’s modulus $E =$ 1.8 MPa, Poisson’s ratio $\nu =$ 0.2, density $\rho = 1850$ $\textrm{kg}/\textrm{m}^{3}$, friction angle $\varphi = 25^{\circ }$, dilation angle $\Phi = 0^{\circ }$, and cohesion $c =$ 5 kPa. The boundary conditions include complete fixation at the left and lower surfaces, while the front and upper surfaces remain free. We investigate the problem using a total time of $t =$ 2.5 s and a constant time step of $\Delta t = 5 \times 10^{-5}$ s. The domain is discretized as 23,256 particles.

Fig. 15

Comparison of equivalent plastic strain between the SPH simulation results (left) and the simulation results obtained from ESPFEM2D (right)

The simulation results are compared with the SPH simulation results from the literature [63]. Figure 15 illustrates the distribution of equivalent plastic strains during the progressive destruction process of cohesive soil at different time steps. Throughout the progressive damage process, the first appearance of equivalent plastic strain is observed at the lower right corner of the granular column, and the destruction of the granular column gradually unfolds as the irreversible deformation region propagates through the specimen, forming a shear zone. The damage initiates from the upper right corner and progressively develops, resulting in the formation of a triangular damage region. From Fig. 15, it can be observed that the simulation results obtained from ESPFEM2D generally agree with those reported by Chalk et al. [63].

4.4 Failure of a Mohr–Coulomb soil slope

The problem setup and geometric model for the failure of a Mohr-Coulomb soil slope are presented in Fig. 16. The soil material properties are as follows: Young’s modulus $E =$ 100 MPa, Poisson’s ratio $\nu =$ 0.3, density $\rho = 2000$ $\textrm{kg}/\textrm{m}^{3}$, friction angle $\varphi = 20^{\circ }$, dilation angle $\Phi = 0^{\circ }$, and cohesion $c =$ 10 kPa. The discretization of the domain consists of 7,912 particles.

Fig. 16

Failure of a Mohr–Coulomb soil slope: setup and geometry of the analysis

Fig. 17

Maximum displacement with different values of SRF

Fig. 18

Mohr–Coulomb slope with SRF=1.385: ${{\textbf {a}}}$ Equivalent plastic strain distribution; ${{\textbf {b}}}$ Total displacement distribution

Fig. 19

Mohr–Coulomb slope: ${\textbf {a, c and e}}$ Equivalent plastic strain distribution with SRF=1.0, 2.0 and 3.0; ${\textbf {b, d and f}}$ Total displacement distribution with SRF=1.0, 2.0 and 3.0

ESPFEM2D is utilized to simulate the whole failure process of the slope, including both pre-failure and post-failure stages. The strength reduction method is used to obtain the safety factor of the slope, in which the shear strength parameters are decreases gradually with increasing strength reduction factor (SRF) as follows:

$$\begin{aligned} \varphi _{f}= & {} \textrm{arctan} \left( \textrm{tan} \varphi / \textrm{SRF} \right) \nonumber \\ c_{f}= & {} c / \textrm{SRF} \end{aligned}$$

(23)

where $\varphi _{f}$ and $c_{f}$ are the friction angle and cohesion used in the simulation while $\varphi$ and c are the soil friction angle and cohesion. The factor of safety (FOS) is defined as the minimum SRF value inducing slope failure. The whole simulation process is divided into two phases: In the first phase, the initial stress field is generated by applying gravity load. At the end of this phase, the displacements of all the particles are discarded with the stress state preserved. Since the ESPFEM2D uses an explicit time integration scheme, the dynamic relaxation method is employed in this phase to obtain the quasi-static solution with a local damping factor of 0.7. In the second phase, the slope failure process is simulated using the strength reduction technique, with a total time of $t =$ 5.0 s and a constant time step $\Delta t = 1 \times 10^{-4}$ s. The total time of 5.0 s is found to be large enough to engender large deformation if the slope is unstable.

The maximum nodal displacements with different SRFs are depicted in Fig. 17. By examining the criterion of slope factor of safety based on the abrupt increase in nodal displacements (the maximum curvature radius are used here to identify the abrupt increase and all the curvature radius with different SRFs are indicated in Fig. 17b by numbers in brackets), it is evident that the FOS of the slope is 1.385. Figure 18a illustrates that the plastic zone has fully penetrated the slope when SRF $=$ 1.385, and the displacement distribution in Fig. 18b reveals the sliding zone associated with slope failure. The obtained factor of safety of 1.385 agrees with Bishop and Morgenstern’s definition of 1.38 with the limit equilibrium method in 1960 [65].

It should be pointed out that, thanks to the large deformation simulation capability of the ESPFEM2D, problems with a large range of SRF values can be successfully solved, including both stable and unstable cases. Figure 19 illustrates the final plastic zone and displacement distributions for the simulation with SRF $=$ 1.0, 2.0 and 3.0. Note that for the traditional strength reduction method for slope stability analysis [66], no convergent result can be obtained when the SRF value exceeds the safety factor of the slope. As shown in Fig. 19e, a plastic zone that fully penetrates the slope with SRF $=$ 3.0 is successfully captured with the ESPFEM2D. Meanwhile, an intuitive sliding can be observed in Fig. 19f. It is clear that by combining the present ESPFEM2D with the strength reduction method, an in-depth slope stability analysis can be performed.

5 Conclusions

We propose ESPFEM2D, an open-source solver that implements a two-dimensional explicit Smooth Particle Finite Element Method (SPFEM), aiming to facilitate the understanding and application of SPFEM in geotechnical engineering. The solver incorporates all the state-of-art techniques for explicit SPFEM, addressing challenges related to mesh distortion, state variable mapping, volume locking and rank-instability.

ESPFEM2D utilizes explicit time integration and the Drucker-Prager constitutive model to describe soil behavior for demonstration purposes. The solver’s performance is validated through a series of numerical examples, ensuring its accuracy, validity, and stability. ESPFEM2D, being an open-source solver based on MATLAB programming, offers advantages such as generality, simplicity, and accessibility, making it convenient for researchers to grasp the methodology and promote the application of SPFEM in geotechnical engineering.